BERTULANG INDONESIA 1971(PBI-71)
(Skripsi)Oleh
DIAN SETIAWAN
JURUSAN TEKNIK SIPIL
FAKULTAS TEKNIK
UNIVERSITAS LAMPUNG
ABSTRAK
ANALISIS PERBANDINGAN MOMEN LENTUR PELAT DUA
ARAH ANTARA METODE LEVY DENGAN PERATURAN
BETON BERTULANG INDONESIA 1971(PBI-71)
Oleh
DIAN SETIAWAN
Pada suatu perancangan dan analisis pelat dua arah yang berlaku di Indonesia
terdapat dua metode perhitungan yakni dengan metode desain langsung (Direct
Design Method) dan metode PBI-71(metode koofisien momen). Selain itu ada dua metode lain yang dapat digunakan dalam perhitungan desain pelat yakni metode portal ekivalen (Equivalent Frame Method) dan metoda garis leleh (Yield Line Method). Pada perhitungan pelat menggunakan metode DDM (Direct Design Method) dan metode PBI-71 terdapat perbedaan nilai momen lentur yang dapat berpengaruh terhadap perancangan tulangan pelat yang cenderung boros di dalam pelaksanaan di lapangan.
Dalam hal ini dilakukan studi analisis menggunakan metode M. Levy dengan beberapa simulasi kondisi tumpuan. Selanjutnya, membandingkan nilai faktor momen dari hasil analisis pada metode M. Levy dengan nilai faktor momen pada PBI-71 Tabel 13.3.1. Hasil analisis menunjukan nilai faktor momen pada PBI-71 lebih besar dibandingkan metode M. Levy.
ABSTRACT
COMPARATIVE ANALYSIS OF FLEXIBLE MOMENTS
BETWEEN TWO-WAY PLATE METHOD LEVY BY
REGULATION REINFORCED CONCRETE INDONESIA 1971
(PBI-71)
By
DIAN SETIAWAN
In a design and analysis of two-way plate that apply in Indonesia, there are two methods of calculation with Direct Design Method and PBI-71 method (method of moment coefficient). then there are two other methods that can be used in the calculation of plate design, namely the Equivalent Frame Method and Yield Line Method. In the calculation of plates using DDM (Direct Design Method) and methods of PBI-71 there is a difference in the value of the bending moment that can affect the design of reinforcement plates are wasteful in implementation.
Analysis study will be conducted using the method of M. Levy with some simulation edge conditions. Furthermore, compared to the value of factors moments from the analysis on methods M. Levy to the value of factors moments on PBI-71. Results of the analysis showed the value of factors moments on PBI-71 is greater than the method of M. Levy.
ANALISIS PERBANDINGAN MOMEN LENTUR PELAT DUA ARAH
ANTARA METODE LEVY DENGAN PERATURAN BETON
BERTULANG INDONESIA 1971(PBI-71)
(Skripsi)Oleh
DIAN SETIAWAN
Skripsi
Sebagai Salah Satu Syarat untuk Mencapai Gelar SARJANA TEKNIK
Pada
Jurusan Teknik Sipil
Fakultas Teknik Universitas Lampung
JURUSAN TEKNIK SIPIL
FAKULTAS TEKNIK
UNIVERSITAS LAMPUNG
RIWAYAT HIDUP
Penulis dilahirkan di Lampung Selatan, pada tanggal 11
Januari 1993, sebagai anak pertama dari Bapak Mistam
dan Ibu Siti Fatimah. Penulis memiliki satu saudara
laki-laki bernama Firmansyah Aji Wijaya dan satu saudara
perempuan bernama Bella Arinda.
Pendidikan Sekolah Dasar (SD) di SDN 2 Baktirasa
diselesaikan pada tahun 2004, Sekolah Menengah Pertama (SMP) di SMPN 2 Sragi
diselesaikan pada tahun 2007, Sekolah Menengah Atas (SMA) di SMAN 1
Kalianda diselesaikan pada tahun 2010. Tahun 2010, penulis terdaftar sebagai
mahasiwa Jurusan Teknik Sipil Fakultas Teknik Unila melalui jalur Ujian Mandiri
(UM). Selama menjadi mahasiswa penulis pernah menjadi anggota Bidang
Musholla dan Kesekretariatan organisasi FOSSI FT Unila, Kepala Bidang
Pembinaan Mahasiswa Baru organisasi HIMATEKS Unila dan mengikuti Latihan
Kepemimpinan (LK) 1 pada organisasi Himpunan Mahasiswa Islam (HMI)
Kombisariat Teknik (KomTek) Unila. Pada tahun 2013, penulis melakukan kerja
praktik di proyek mall Bintaro Xchange, yang berlokasi di Jalan Tegal Rotan,
Bintaro Sektor 7, Tanggerang Barat, dan melakukan Kerja Kuliah Nyata (KKN) di
Desa Banjar Dewa, Kecamatan Banjar Agung, Kabupaten Tulang Bawang pada
Persembahan
Alhamdulillahirabbil’alamiin
Puji syukur kehadirat Allah SWT. atas karunia dan rahmatnya sehingga aku
sampai juga pada titik ini
Hasil kerja kerasku ini tidak terlepas dari orang-orang disekitarku
Kupersembahkan karya ini
Untuk orang yang selalu tidak lelah menyemangatiku, kedua orang tuaku
Bapak Mistam dan Ibu Siti Fatimah serta saudaraku Bella Arinda dan
Firmansyah Aji Wijaya
Terima kasih atas segala dukungan dan motivasinya baik secara moril maupun
materil
Teman-teman dekatku F. Afrie Adi S., Dedy Dwi Pujiyanto, Rifki Ananda
Saputra, Sapto Nugroho, Riko Berliardian dan Chandra R.S.
Terima kasih atas segala masukan dan semangatnya
Kemudian untuk teman-teman seperjuangan Teknik Sipil Unila 2010 dan adik
tingkat 2012 yang tidak dapat tersebutkan namanya
Terima kasih banyak untuk semuanya
SANWACANA
Puji syukur mutlak milik Allah swt. karena atas rahmat, karunia, dan hidayah-Nya penulis
dapat menyelesaikan skripsi yang berjudul “ANALISIS PERBANDINGAN MOMEN LENTUR PELAT DUA ARAH ANTARA METODE LEVY DENGAN PERATURAN BETON BERTULANG INDONESIA 1971 (PBI-71)“ sebagai salah satu syarat untuk
memperoleh gelar sarjana Teknik Sipil di Universitas Lampung.
Pada penyusunan skripsi ini penulis banyak mendapatkan bantuan, dukungan, bimbingan, dan
pengarahan dari berbagai pihak. Untuk itu penulis mengucapkan terimakasih yang
sebesar-besarnya kepada :
1. Bapak. Prof. Dr. Suharno, M.Sc. selaku Dekan Fakultas Teknik Universitas Lampung.
2. Bapak Dr. Gatot Eko Susilo, S.T., M.Sc. selaku Ketua Jurusan Teknik Sipil Fakultas
Teknik Universitas Lampung sekaligus sebagai Dosen Penguji Kerja Praktik.
3. Bapak Suyadi, S.T., M.T. selaku Dosen Pembimbing Utama atas kesediaannya untuk
memberikan bimbingan, saran dan kritik dalam proses penyelesaian skripsi ini.
4. Bapak Bayzoni, S.T., M.T. selaku Dosen Pembimbing Kedua atas kesediaannya untuk
memberikan bimbingan, saran dan kritik dalam proses penyelesaian skripsi ini.
5. Bapak Andi Kusnadi, S.T., M.T., M.M. selaku Penguji Utama pada ujian skripsi.
Terimakasih untuk masukan dan saran-saran dalam proses penyelesaian skripsi ini.
6. Ibu Hasti Riakara Husni S.T., M.T. selaku Dosen Pembimbing Akademik.
7. Seluruh Dosen Jurusan Teknik Sipil yang telah membimbing dan memberikan ilmu
Arinda dan Firmansyah Aji Wijaya yang sudah menjadi charger dalam mengisi
semangatku.
9. Teman-teman Teknik Sipil khususnya angkatan 2010 dan 2012 yang sudah banyak
membantu dan memberi semangat.
10.Semua pihak yang tidak dapat disebutkan satu persatu, yang telah membantu dalam
penyelesaian skripsi ini.
Penulis sangat menyadari bahwa skripsi ini masih banyak kesalahan dan kekurangan. Untuk
itu penulis mengharapkan saran dan kritik yang bersifat membangun di kemudian hari. Penulis
berharap semoga skripsi ini dapat bermanfaat bagi pembaca.
Bandar Lampung, Januari 2017
Penulis,
i
E. Manfaat Penelitian ...4
BAB II. TINJAUAN PUSTAKA A. Teori Elastisitas ...5
B. Persamaan Differensial Pelat dalam Sistem Koordinat Kartesius ...15
BAB III. METODE PENELITIAN
A. Pendekatan Penelitian ...42
B. Lokasi Penelitian ...42
C. Data Penelitian ...42
D. Prosedur Penelitian ...43
E. Kerangka Penelitian ...45
BAB IV. ANALISIS DAN PEMBAHASAN A. Alisis Pelat Persegi Sederhana ...47
B. Pelat Persegi yang Mengalami Momen Akibat Jepit...58
C. Pelat Persegi Dengan Dua Tepi yang Berhadapan Ditumpu Secara Sederhana dan Dua Sisi Lainnya Terjepit ...67
D. Pelat Persegi di mana Ketiga Tepinya Ditumpu Secara Sederhana dan Satu Tepinya Terjepit ...73
E. Pelat Persegi yang Semua Tepinya Terjepit ...78
BAB V. PENUTUP A. Kesimpulan ...107
B. Saran ...108
iii
DAFTAR GAMBAR
Halaman
Gambar 2.1. Respon suatu benda elastis tehadap gaya luar ...6
Gambar 2.2. Metode Irisan ...8
Gambar 2.3. Elemen tiga dimensi ...9
Gambar 2.4. Deformasi suatu elemen ...12
Gambar 2.5. Distorsi yang diproyeksi...13
Gambar 2.6. Pelat persegi yang memikul beban lateral ...17
Gambar 2.7. Pelat persegi yang memikul beban lateral ...18
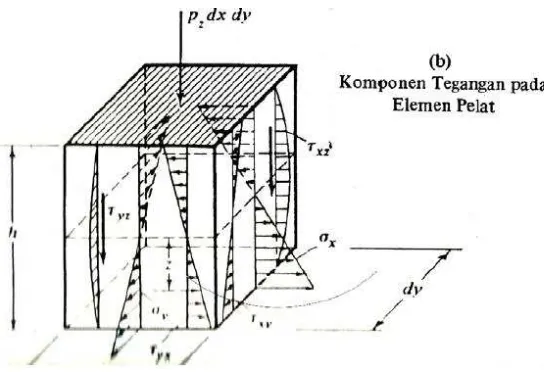
Gambar 2.8. Tegangan pada suatu elemen pelat ...22
Gambar 2.9. Penampang sebelum dan sesudah berubah bentuk ...23
Gambar 2.10. Distorsi Sudut ...24
Gambar 2.11. Berbagai Kondisi Tepi ...29
Gambar 2.12. Pengaruh tepi dari momen puntir ...30
Gambar 2.13 Fungsi periodik sembarang ...33
Gambar 2.14 Analisis Harmonis ...34
Gambar 2.15. (a) Harmonisasi ganjil, (b) harmonisasi genap...35
Gambar 2.16. (b) Harmonisasi ganjil, (a) harmonisasi genap...36
Gambar 2.17 Fungsi yang akan diekspansikan menjadi deret Fourier ...37
Gambar 2.18. Grafik ekspansi deret Fourier ...38
Gambar 3.1 Kondisi tumpuan pelat Tabel 13.3.1 PBI-71 ...43
Gambar 3.3 Kondisi tumpuan dua tepi jepit dan dua tepi lainya jepit ...44
Gambar 3.4 Kondisi tumpuan tiga tepi sederhana dan tepi lain jepit ...44
Gambar 3.5 Kondisi tumpuan semua tepinya terjepit ...44
Gambar 3.6 flow chart...46
Gambar 4.1 Sistem koordinat metode M. Levy ...47
Gambar 4.2 Distribusi momen lentur sepanjang tepi ...59
Gambar 4.3 Pelat persegi panjang dengan dua tepi yang berhadapan di tumpu secara sederhana dan dua sisi lainnya terjepit ...67
Gambar 4.4 Pelat persegi panjang dimana ketiga tepinya ditumpu secara sederhana dan satu tepinya terjepit ...74
Gambar 4.5 Prinsip superposisi dalam perhitungan pelat persegi panjang yang semua tepinya terjepit. ...79
Gambar 4.6 Pelat persegi yang semua tepinya terjepit ...79
Gambar 4.7 Perubahan koordinat persamaan lendutan pelat yang ditumpu secara sederhana. ...80
Gambar 4.8 Momen yang terdistribusi merata sepanjang tepi y = b/2 ...81
Gambar 4.9 Momen yang terdistribusi merata sepanjang tepi x = ± a/2 ...83
Gambar 4.10 Syarat kondisit tepi menurut persamaan (4.60) ...85
Gambar 4.11 Syarat kondisit tepi menurut persamaan (4.61) ...85
Gambar 4.12a Grafik Nilai Faktor Bilangan Mlx (PBI-71) dan Mx (Levy)...96
Gambar 4.12b Grafik Nilai Faktor Bilangan Mly (PBI-71) dan My (Levy) ...96
Gambar 4.13a Grafik Nilai Faktor Bilangan Mlx (PBI-71) dan Mx (Levy)...98
v
Gambar 4.13c Grafik Nilai Faktor Bilangan Mtx (PBI-71) dan My y=±b/2
(Levy) ...99
Gambar 4.14a Grafik Nilai Faktor Bilangan Mlx (PBI-71) dan Mx (Levy)...101
Gambar 4.14b Grafik Nilai Faktor Bilangan Mly (PBI-71) dan My (Levy) ...102
Gambar 4.14c Grafik Nilai Faktor Bilangan Mtx (PBI-71) dan My y=±b/2
(Levy) ...102
Gambar 4.15a Grafik Nilai Faktor Bilangan Mtx (PBI-71) dan Mx x=0, y=0
(Levy) ...105
Gambar 4.15b Grafik Nilai Faktor Bilangan Mty (PBI-71) dan My x=0, y=0
(Levy) ...105
Gambar 4.15c Grafik Nilai Faktor Bilangan Mlx (PBI-71) dan Mxx=±a/2, y=0
(Levy) ...106
Gambar 4.15d Grafik Nilai Faktor Bilangan Mly (PBI-71) dan Myx=0, y=±b/2
DAFTAR TABEL
Halaman
Tabel 4.1 Nilai Rata Perbandingan Poisson Rasio ...57
vii
DAFTAR NOTASI
a,b : Dimensi linier pelat dalam arah X dan Y
D, Dx, Dy : Ketegaran lentur pelat
E : Modulus elastisitas
Fm, Fi, f(x), Em, Ei : Fungsi gaya
G : Modulus geser
h : Tebal pelat
I : Momen inersia
i, m, n : Bilangan ganjil positif (1,3,5....) yang menyatakan suku
deret
K : Kekakuan suatu struktur
lx, ly : Dimensi linier pelat dalam X dan Y
M0 : Momen lentur yang didistribusikan disepanjang tepi terjepit
Mx, My, Mxy, Myx : Momen lentur arah X, Y, XY dan YX
Qx, Qy : Gaya geser transversal per satuan panjang
q : Gaya lateran berupa beban merata
εx, εy, εz : Komponen regangan normal
, x, y : Koefisien momen lapangan
γ, γx, γy : Koefisien momen tumpuan
x, y, z : Komponen regangan normal
, xy : Tegangan geser
ω : Frekuensi sudut getaran bebas
∆ : Selisih, pertambahan kecil yang berhingga
I. PENDAHULUAN
A. Latar Belakang
Rekayasa adalah penerapan kaidah-kaidah ilmu di pelaksanaan (seperti perancangan,
pembuatan konstruksi, serta pengoperasian kerangka, peralatan, dan sistem yg
ekonomis dan efisien). Pada penerapan rekayasa dalam bidang ilmu teknik berkaitan
erat dengan merekayasa gaya-gaya dalam yang bekerja pada perancangan dan analisis
suatu bidang konstuksi, gaya-gaya dalam yang sering kita jumpai dalam menganalisis
suatu kontruksi diantaranya gaya momen, lintang dan normal.
Pada hakekatnya dalam suatu rekayasa pada perancangan dan analisis suatu kontruksi
menitikberatkan pada aspek keamanan, kenyamanan, keindahan dan efisiensi. Dari
segi keamanan ditinjau bahwa suatu kontruksi dapat menahan gaya-gaya yang bekerja
pada kontruksi tersebut, dari segi kenyamanan dan keindahan ditinjau bahwa suatu
kontruksi diperuntukan untuk umat manusia, sedangkan ditinjau dari segi efisiensi
mengarah kepada pemilihan metode pendekatan yang efisien dalam perancangan atau
analisis.
Perancangan adalah proses penerapan berbagai teknik dan prinsip yang bertujuan
untuk mendefinisikan sebuah peralatan, satu proses atau satu sistem secara detail yang
membolehkan dilakukan realisasi fisik. Perancangan memberikan pegangan bagi
perancangan kontruksi gedung, terdapat sub bagian perancangan yakni : perancangan
pondasi, perancangan atas (berupa kolom, balok dan pelat lantai) dan atap.
Pelat adalah struktur bidang yang datar/tidak melengkung yang tebalnya jauh lebih
kecil dari dua dimensi yang lain. Sistem perancangan tulangan pelat beton pada
dasarnya dibagi menjadi 2 macam yaitu : Sistem perancangan pelat dengan tulangan
pokok satu arah (arah x) disebut pelat satu arah/ one way slab dan Sistem perancangan
pelat dengan tulangan pokok dua arah (arah x dan arah y) disebut pelat dua arah/ two
way slab.
Pada suatu perancangan dan analisis pelat dua arah yang berlaku di Indonesia terdapat
dua metode perhitungan yakni dengan metode desain langsung (Direct Design
Method) dan metode PBI-71(metode koofisien momen). Selain itu ada dua metode
lain yang dapat digunakan dalam perhitungan desain pelat yakni metode portal
ekivalen (Equivalent Frame Method) dan metoda garis leleh (Yield Line Method).
Pada perhitungan pelat menggunakan metode DDM (Direct Design Method) dan
metode PBI-71 terdapat perbedaan nilai momen lentur yang dapat berpengaruh
terhadap perancangan tulangan pelat yang cenderung boros di dalam pelaksanaan di
lapangan. Hal ini yang mendorong penulis untuk melakukan pengkajian ulang
terhadap nilai faktor momen lentur Tabel 13.3.1 pada metode PBI-71 dengan
menggunakan pendekatan metode M. Levy.
B. Rumusan Masalah
Dari permasalahan yang ada, maka dapat diambil suatu rumusan masalahnya yaitu
melakukan pengkajian terhadap nilai faktor momen lentur pelat dua arah pada PBI-71
3
C. Batasan Masalah
Batasan masalah dalam penelitian ini meliputi hal-hal sebagai berikut :
1. Perhitungan analisis nilai momen lentur pada pelat tipis yang kondisi tegangan
dalamnya menyerupai kondisi kontinyu tiga-dimensi.
2. Perhitungan hanya pada pelat dua arah yang berbentuk persegi.
3. Beban yang digunakan hanya beban terbagi rata.
4. Asumsi kondisi pelat berdasarkan teori pelat dengan lendutan kecil berdasarkan
teori Kirchhoff dan Love.
5. Kondisi tumpuan pelat yang akan ditinjau antara lain :
a. Pelat persegi dengan tumpuan sederhana.
b. Pelat persegi yang mengalami momen akibat jepit.
c. Pelat persegi dengan dua tepi yang berhadapan ditumpu secara sederhana dan
dua sisi lainnya terjepit.
d. Pelat persegi di mana ketiga tepinya ditumpu secara sederhana dan satu
tepinya terjepit.
e. Pelat persegi yang semua tepinya terjepit.
6. Peraturan yang digunakan pada skripsi ini menggunakan peraturan yaitu
berdasarkan Tabel 13.3.1 dari metode PBI-71.
D. Tujuan Penelitian
Tujuan penelitian pada Tugas Akhir ini adalah melakukan analisis perbandingan nilai
faktor momen lentur berdasarkan Tabel 13.3.1 pada metode PBI-71 dengan
E. Manfaat Penelitian
Dari hasil penelitian yang diperoleh, diharapkan dapat memberikan manfaat sebagai
berikut :
1. Mengetahui perbandingan nilai faktor momen lentur berdasarkan Tabel 13.3.1
pada metode PBI-71 dengan pendekatan metode M. Levy.
2. Hasil analisis ini dapat digunakan oleh para perencana untuk bahan pertimbangan
dalam pemilihan metode perancangan penulangan pelat lantai dua arah.
3. Untuk mengetahui nilai momen lentur pada koordinat tertentu pada suatu pelat
II. TINJAUAN PUSTAKA
A. Teori Elastisitas
Teori elastisitas merupakan cabang yang penting dari fisika matematis
yang mengkaji hubungan antara gaya, tegangan dan regangan dalam benda
elastis. Elastisitas adalah sifat benda yang mengalami perubahan bentuk
atau deformasi secara tidak permanen. Bila suatu benda pejal dibebani
gaya luar, benda tersebut akan berubah bentuk/ deformasi, sehingga timbul
tegangan dan regangan dalam.
Perubahan bentuk ini tergantung pada konfigurasi geometris dari benda
tersebut dan pada sifat mekanis bahannya. Dalam pembahasan sifat elastik
pada benda perlu diasumsikan bahwa benda-benda tersebut mempunyai
sifat-sifat berikut :
- Homogen artinya setiap bagian benda mempunyai kerapatan yang
sama.
- Isotropik artinya pada setiap titik pada benda mempunyai sifat-sifat
Dalam teori elastisitas pembahasan dibatasi hanya pada bahan yang elastis
linier, yaitu keadaan dimana hubungan tegangan dan regangan bersifat
linier. Dan perubahan bentuk serta tegangan akan hilang bila gaya luar
dihilangkan. Selain itu, teori elastisitas menganggap bahan bersifat
homogennya dan isotropis; dengan demikian, sifat mekanis bahan sama
dalam segala arah. Walaupun bahan-bahan struktural tidak tepat
memenuhi semua anggapan ini, tapi pengujian menunjukkan bahwa teori
elastisitas memberikan hasil dengan ketepatan yang tinggi, asalkan
tegangannya masih di bawah titik leleh (yield point).
Teori pelat klasik yang merumuskan dan menyelesaikan masalah pelat
berdasarkan analisis matematis yang eksak, merupakan penerapan khusus
yang penting dari teori elastisitas. Oleh karena itu, pengertian menyeluruh
tentang konsep dasarnya, notasi, definisi, dan lainnya, sangat penting.
Tujuan dari bagian ini ialah mengenalkan dasar tersebut dalam bentuk
yang ringkas.
7
1. Keadaan tegangan pada saat benda elastis
Dalam statika benda tegar (rigid body), disini akan dikaji gaya luar
yang bekerja pada suatu benda tidak meninjau perubahan bentuk yang
timbul. Sebaliknya, dalam teori elastisitas, ditinjau perubahan bentuk
akibat gaya luar. Melalui perubahan bentuk pada benda tersebut,
gaya-gaya luar dikonversi menjadi gaya-gaya-gaya-gaya dalam.
Kita mulai dengan meninjau suatu benda elastis dengan bentuk
sembarang dalam system koordinat cartesius X, Y, Z, yang memikul
gaya luar yang berada dalam keseimbangan. Untuk menentukan gaya
dalam yang timbul di antara partikel-partikel benda tersebut, kita
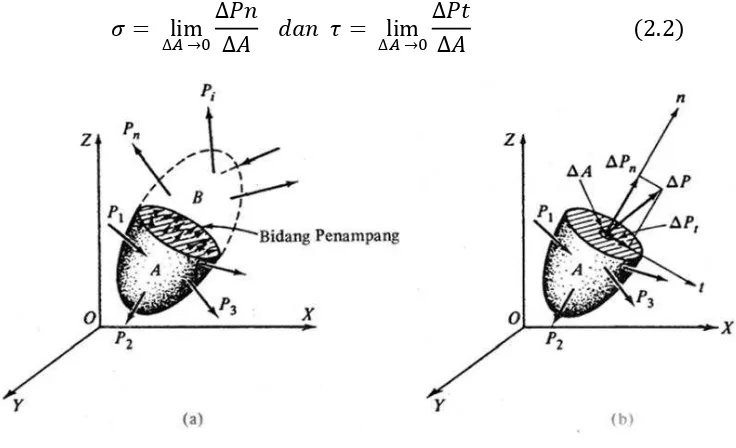
bayangkan benda tersebut dipenggal menjadi dua bagian oleh suatu
bidang, seperti pada Gambar 2.2a. Jika sekarang kita bayangkan bahwa
bagian B dihilangkan, keseimbangan benda tersebut harus
dipertahankan oleh gaya-gaya luar yang bekerja pada permukaan
penampangnya.
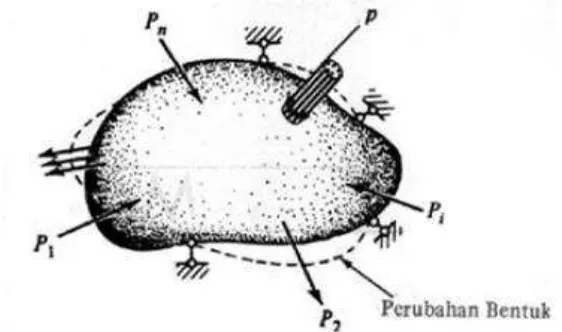
Marilah kita ambil suatu luas ΔA yang kecil pada penampang tersebut
dan kita nyatakan gaya dalam yang bekerja pada luas ini sebagai ΔP
(Gambar 2.2b). Perbandingan ΔP/ΔA adalah tegangan rata rata, yang
didefinisikan sebagai limit dari perbandingan; jadi
� = lim∆� → ∆∆ .
Karena ΔP umumnya tidak tegak lurus penampang, kita lebih mudah
(sebidang). Dengan demikian definisi tegangan normal ( ) dan
tegangan geser ( ) (Gambar 2.2b) adalah
� = lim∆� → ∆∆ � = lim∆� → ∆∆ .
Gambar 2.2 Metode Irisan
Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Perlu diperhatikan bahwa tegangan pada suatu bidang adalah vektor
tegangan. Resultan tegangan dengan mudah dapat dicari dengan
penjumlahan vektor dari komponen-komponennya. Keadaan tegangan
pada benda elastis biasanya bervariasi dari satu titik ke titik lainnya;
jadi, kita dapat tuliskan (x,y,z) dan (x,y,z).
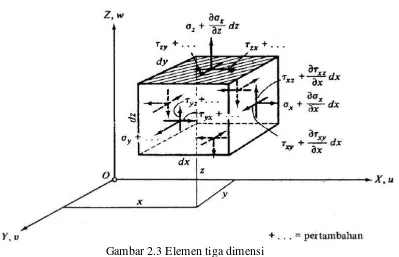
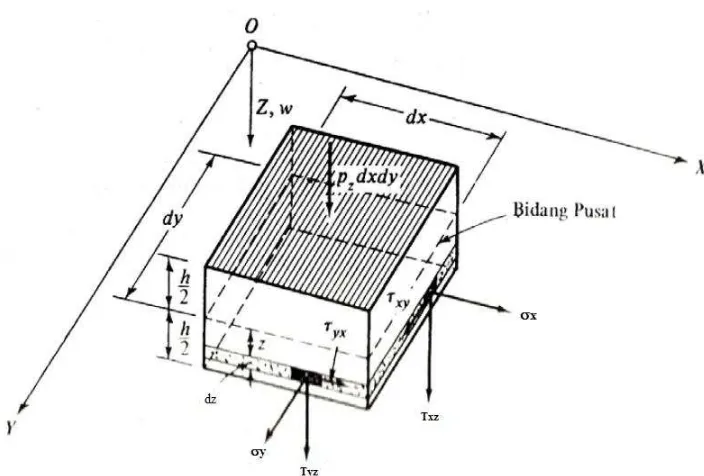
Untuk menggambarkan keadaan tegangan tiga-dimensi, kita ambil
suatu elemen yang kecil dalam bentuk kontak (dx dy dz) yang mukanya
sejajar dengan bidang koordinat, seperti yang ditunjukan Gambar 2.3.
Komponen tegangan normal X, Y, dan Z, masing-masing diberi notasi
x, y dan z . Subskribnya ( subscript/ huruf bawah) menunjukkan
9
bekerja. Tegangan geser biasanya memiliki dua subskrib. Subskrib
pertama menunjukkan arah garis normal permukaan, sedang subskrib
kedua menunjukkan arah arah vektor
tegangan . Karena tegangan merupakan fungsi dari letaknya pada
suatu benda, intensitasnya akan berubah bila bidang rujuknya
digerakkan sejauh dx, dy, dz. Pertambahan yang timbul dinyatakan
oleh dua suku pertama dari deret Taylor (Gambar 2.3)
Gambar 2.3 Elemen tiga dimensi
Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Perjanjian tanda berikut akan digunakan dalam pembahasan
berikutnya. Pada bidang dekat suatu elemen yang dipandang dari
ujung-ujung sumbu koordinat positif dianggap positif. Pada bidang
jauh suatu elemen, semua tegangan yang bekerja pada arah sumbuh
aturan umum yang dipakai dalam praktek bidang teknik; yakni,
tarikan bertanda positif dan tekanan bertanda negatif.
Keadaan tegangan tiga-dimensi di sembarang titik benda elastis
ditentukan oleh sembilan komponen tensor tegangan dengan matriks.
[�] = [�� �� ��
� � � ] .
yang simetris terhadap diagonal utama. Dimana Tensor adalah besaran
yang memiliki arti fisik yang memenuhi hukum transformasi tertentu.
Hukum transformasi ini dalam teori elastis adalah rotasi sumbu.
Tensor orde dua dinyatakan dalam bentuk (Szilard,1974:15). Karena
sifat simetris ini,
� = � � = � � = � .
Dalam beberapa literatur, Persamaan (2.1) disebut hukum timbal-balik
tegangan geser dan mudah dibuktikan dengan mengambil momen dari
tegangan-tegangan terhadap sumbu koordinat. Sementara keadaan
tegangan dalam pelat yang tebal bersifat tiga-dimensi, pelat tipis yang
memiliki ketegangan lentur yang mempunyai keadaan tiga-dimensi
yang tidak sempurna; yakni, semua komponen tegangan permukaan
yang sejajar bidang XY sama dengan nol.
Dalam analisis pelat elastis, keadaan tegangan dua-dimensi berperan
penting. Pada keadaan ini, z = yz = xz = 0; dengan demikian,
matriks tensor tegangan yang bersangkutan menjadi
11
dimana � = � = �
2. Regangan dan perpindahan
Benda elastis yang diperlihatkan pada Gambar 2.1 ditumpu sedemikian
rupa sehingga perpindahan benda tegar/ rigid body (translasi dan
rotasi) tidak terjadi. Karena benda elastis tersebut berubah bentuk
akibat gaya luar, setiap titik padanya mengalami perpindahan elastis
yang kecil. Dengan menyatakan komponen perpindahan translasional
dalam arah X, Y, Z sebagai u, v, w, dapat dituliskan
= , , = , , = , , .
yang menunjukkan bahwa komponen perpindahan juga merupakan
fungsi dari letaknya.
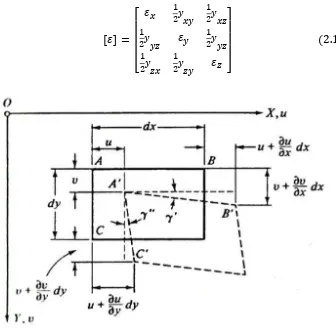
Untuk menghubungkan perpindahan dan berubah bentuk, kita tinjau
kembali kotak yang sangat kecil dengan sisi dx, dy, dan dz pada suatu
benda elastis (Gambar 2.3). Karena keseluruhan benda elastis ini
berubah bentuk, elemen kecil tersebut juga akan berubah bentuk, yakni
panjang sisi dan sudut-sudut antara yang semula siku-siku juga akan
berubah (Gambar 2.4). Dengan membatasi pembatasan kita pada
perubahan bentuk yang kecil, kita definisikan regangan normal (ε)
sebagai perubahan satuan panjang. Misalnya, regangan normal dalam
arah X adalah
dimana pertambahan Δdx dapat dinyatakan dengan suku kedua deret
Taylor (Δdx = (∂u / ∂x)dx); jadi, dapat ditulis
� = , � = � = .
Akibat pengaruh tegangan geser, permukaan elemen tersebut akan
berputar (Gambar 2.4b). Sebagai contoh, dengan mengambil proyeksi
elemen tersebut pada bidang XY seperti yang ditunjukkan dalam
Gambar 2.5, dapat didefinisikan regangan geser sebagai distorsi sudut;
Gambar 2.4 Deformasi suatu elemen Sumber : Teori dan Analisis Pelat (Szilard, 1974)
jadi
� = �′+ �"
= + = � . Dengan cara yang sama, kita peroleh
� = + = � � = + = � .
Sama halnya dengan tensor tegangan [Persamaan (2.3)] di suatu titik
13
Gambar 2.5 Distorsi yang diproyeksi Sumber : Teori dan Analisis Pelat (Szilard, 1974)
3. Hukum Hooke
Untuk bahan struktur yang menunjukkan batas elastis linear yang jelas,
hukum Hooke suatu dimensi menghubungkan tegangan dan regangan
normal sebagai
� = � .
dimana E adalah modulus elastis young. Jika tegangan normal bekerja
dalam arah X, perpanjangan εx, diikuti oleh perpendekan lateral; jadi,
regangan dalam arah X,Y, dan Z adalah
dengan ν adalah angka poisson yang bekisar antara 0.15 dan 0.35
untuk kebanyakan bahan struktur. Untuk struktur linear yang
mengikuti Hukum Hooke, prinsip superposisi dapat diterapkan; dengan
demikian, jika tegangan x, y, dan z bekerja secara bersamaan pada
elemen yang kecil tersebut, hukum Hooke diperluas menjadi
� = [ � − (� + � )] .
� = [ � − � + � ]
� = [ � − (� + � )]
Dengan cara yang sama, hubungan antara tegangan dan regangan geser
adalah [lihat persamaan (2.14)]
� = � .�
dimana G adalah modulus elaslisitas geser atau modulus geser/
gelincir. Jika tegangan geser bekerja pada semua permukaan elemen,
Persamaan (2.15) menjadi
� = � � ,� = � � � = � � .
Hubungan antaara modulus elastisitas Young E dan modulus geser G
adalah
15
B. Persamaan Differensial Pelat dalam Sistem Koordinat Kartesius
1. Sistem Koordinat dan Perjanjian Tanda.
Bentuk pelat cukup ditentukan dengan menunjukkan geometri bidang
pusatnya (middle surface), yang merupakan bidang /permukaan yang
membagi dua tebal pelat h setiap titik (Gambar 2.6). Szilard (1974)
mengatakan teori pelat dengan lendutan kecil, yang sering kali disebut
teori Kirchhoff dan Love, didasarkan pada anggapan berikut:
a. Bahan pelat bersifat elastis, homogen, dan isotropis
b. Pelat pada mulanya datar.
c. Tebal pelat relatif kecil dibandingkan dengan dimensi lainnya.
Dimensi lateral terkecil pada pelat paling sedikit sepuluh kali lebih
besar daripada ketebalannya.
d. Lendutan sangat kecil dibandingkan dengan tebal pelat. Lendutan
maksimum sebesar sepersepuluh sampai seperlima tebal pelat
dianggap sebagai batasan untuk teori lendutan yang kecil. Batasan
ini juga dapat dinyatakan dalam panjang pelat; misalnya, lendutan
maksimum lebih kecil dari satu perlima puluh panjang bentang
yang terkecil.
e. Kemiringan bidang pusat yang melendut jauh lebih kecil dari satu
f. Perubahan bentuk pelat bersifat sedemikian rupa sehingga garis
lurus yang semula tegak lurus bidang pusat pelat, tetap berupa
garis lurus dan tetap tegak lurus bidang (perubahan bentuk gaya
g. Lendutan pelat diakibatkan oleh perpindahan titik-titik bidang
pusat yang tegak lurus awalnya.
h. Besarnya tegangan yang lurus bidang pusat sangat kecil sehingga
bisa diabaikan. Banyak dari anggapan ini terkenal karena sama
seperti balok dasar. Pengujian dengan skala kecil dan besar telah
membuktikan berlakunya anggapan-anggapan tersebut.
i. Regangan pada bidang pusat akibat gaya-gaya sebidang biasanya
dapat diabaikan jika dibandingkan dengan regangan akibat lentur
(teori pelat inekstensional).
Untuk pelat segiempat (persegi), pemakaian sistem koordinat kartesius
merupakan cara yang paling mudah (Gambar 2.6). Gaya luar dan
dalam serta komponen lendutan u, v, dan w dianggap positif bila
searah dengan arah positif sumbu koordinat X, Y, dan Z. Dalam praktik
bidang teknik, momen positif menimbulkan tarikan pada serat yang
terletak dibagian bawah struktur. Perjanjian tanda seperti ini juga
berlaku untuk pelat.
Kita tinjau suatu kotak kecil yang dipotong dari sebuah pelat pada
(Gambar 2.7). Kemudian kita berikan gaya dalam dan momen positif
pada bidang-bidang dekat (near face). Agar elemen tersebut seimbang,
gaya dalam momen negatif harus bekerja pada bidang jauh (far side).
Subkrip pertama pada gaya dalam menunjukkan arah garis normal
(garis tegak lurus) permukaan penampang tempat momen atau gaya
17
Gambar 2.6. Pelat persegi yang memikul beban lateral Sumber : Teori dan Analisis Pelat (Szilard, 1974)
2.7. Pelat persegi yang memikul beban lateral Sumber : Teori dan Analisis Pelat (Szilard, 1974)
2. Keseimbangan elemen pelat
Dengan menganggap pelat hanya memikul beban lateral, di antara ke
enam persamaan keseimbangan dasar hanya tiga persamaan berikut
yang digunakan:
∑ = ∑ = ∑ = .
Perilaku pelat dalam banyak hal analog dengan perilaku jaringan
19
Qx dan Qy serta oleh momen lentur Mx dan My. perbedaan yang jelas
dengan aksi jaringan balok silang dua-dimensi ialah adanya momen
puntir Mxy dan Myx (Gambar 2.7a). Dalam teori pelat, umumnya gaya
dalam dan momen dinyatakan persatuan panjang bidang pusat
(Gambar 2.7b). Untuk membedakan gaya dalam ini dengan resultan
yang disebut diatas, notasi Qx, Qy, Mx, My, Mxy, dan Myx, akan
digunakan disini.
Prosedur untuk menurunkan persamaan differensial keseimbangan
adalah sebagai berikut:
a. Pilih sistem koordinat yang memudahkan dan menggambarkan
suatu elemen pelat (Gambar 2.7)
b. Tinjaulah semua gaya dalam dan luar yang bekerja pada elemen
tersebut
c. Berikan gaya dalam positif dengan penambahannya
(qx+…qy+…dan seterusnya) pada bidang dekat
d. Berikan gaya dalam negatif pada bidang jauh
e. Nyatakan pertambahan tersebut dalam deret Taylor yang
dipenggal:
+ = + , + = + , . .
f. Tuliskan keseimbangan gaya dalam dan luar yang bekerja pada
elemen tersebut.
Sebagai contoh, kita samakan jumlah momen semua gaya dalam
( + ) − + + −
− ( + ) − = .
Setelah disederhanakan, kita abaikan suku yang mengandung besaran
���
� . Karena merupakan suku berorde tinggi yang sangat
kecil. Dengan demikian, persamaan (2.19) menjadi
. + . − . . = .
Dan, setelah dibagi dengan dx dy, kita peroleh
+ = .
Dengan cara yang sama, perjumlahan momen-momen terhadap sumbu
X menghasilkan
+ = .
Penjumlahan semua gaya dalam arah Z menghasilkan persamaan
keseimbangan ketiga [lihat persamaan (2.23)]
. + . − . . = .
Yang setelah dibagi oleh dx dy menjadi :
+ = − .
Dengan memasukkan persamaan (2.21) dan (2.22) ke persamaan (2.24)
dan memperhatikan bahwa = , kita peroleh
21
Momen lentur dan puntir dalam persamaan (2.25) tergantung pada
regangan, sedang regangan merupakan fungsi dari komponen
perpindahan. Oleh karena itu, langkah selanjutnya ialah mencari
hubungan antara momen dalam dan komponen perpindahan.
3. Hubungan Antara Tegangan, Regangan, dan Perpindahan
Anggapan bahwa bahan bersifat elastis memungkinkan pemakaian
hukum Hooke dua-dimensi (yang diperoleh dari persamaan (2.13)
dengan � = ),
� = � + � .
dan
� = � + � .
Yang menghubungkan tegangan dan regangan pada suatu elemen pelat.
Subtitusi persamaan (2.26b) ke persamaan (2.26a) menghasilkan
� = − (� + � ) .
Dengan cara yang sama, akan diperoleh [lihat persamaan (2.28)]
� = − (� + � ) .
Momen puntir Mxy dan Myx menimbulkan tegangan sebidang (in-plane
shear) xy dan yx(Gambar 2.8), yang berhubungan dengan regangan
geser γ melalui persamaan yang sejenis dengan hukum Hooke
Persamaan (2.15)
Gambar 2.8 Tegangan pada suatu elemen pelat Sumber : Teori dan Analisis Pelat (Szilard, 1974)
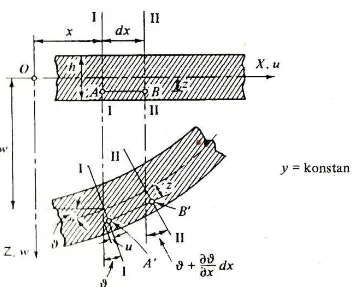
Selanjutnya, ditinjau geometri pelat yang melendut untuk menyatakan
regangan dalam koefesien perpindahan. Dengan mengambil satu irisan
pada nilai y yang konstan, seperti ditunjukkan dalam (Gambar 2.9),
kita bandingkan penampang (irisan) sebelum dan sesudah melendut.
Dengan memakai anggapan e dan f, yang disebutkan di muka bagian
ini, kita bisa nyatakan sudut rotasi garis I-I dan II-II sebagai [lihat
persamaan (2.30)].
= − + ⋯ = + .
Setelah berubah bentuk, panjang suatu deret ̅̅̅̅ yang terletak pada
jarak Z dari bidang pusat menjadi ̅̅̅̅̅̅′ ′ (Gambar 2.9). Dengan memakai
defenisi regangan yang diberikan dalam persamaan (2.13), dapat
23
Gambar 2.9 Penampang sebelum dan sesudah berubah bentuk Sumber : Teori dan Analisis Pelat (Szilard, 1974)
� =∆ = ̅̅̅̅̅̅ − ̅̅̅̅′ ′̅̅̅̅ = [ + ]= .
Kemudian persamaan pertama disubtitusi dari persamaan ( 2.30 ) ke
persamaan ini akan menghasilkan
� = − .
Dengan cara yang sama, kita bisa memperoleh regangan
� = − .
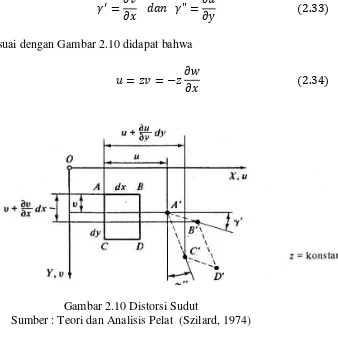
Selanjutnya ditentukan distorsi sudut xy = ’ + ” dengan
suatu jarak konstan dari bidang pusat, dengan keadaannya setelah
berubah bentuk A’B’C’D’ pada permukaan pelat yang melendut. Dari
kedua segitiga kecil dalam Gambar 2.10 dan dari persamaan ( 2.8 )
jelas terlihat bahwa
�′= �" = .
Sesuai dengan Gambar 2.10 didapat bahwa
= = − .
Gambar 2.10 Distorsi Sudut
Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Dengan cara yang sama,
= − .
Sehingga,
� = �′+ �" = − .
Perubahan kelengkungan pada bidang pusat yang melendut
25
= − , = − , � = − .
Dimana χ menyatakan pemilinan (warping) pelat.
4. Gaya dalam yang dinyatakan dalam w
Komponen tegangan x dan y (Gambar 2.8) menimbulkan momen
lentur pada elemen pelat dengan cara yang sama seperti pada teori
balok dasar. Jadi, dengan mengintegrasikan komponen tegangan
normal, kita peroleh momen lentur yang bekerja pada elemen pelat:
= ∫+ℎ �
lendutan lateral w. Jadi, dapat ditulis sebagai
� = − − + .
Dan
� = − − + .
Integrasi persamaan (2.38), setelah substitusi persamaan di atas x dan
= − ℎ− + = − +
Menyatakan ketegaran lentur/ kekakuan pelat (flextural rigidity) pelat.
Dengan cara yang sama, kita peroleh persamaan momen puntir dalam
lendutan lateral:
Jika persamaan (2.42), (2.43) dan (2.45) disubstitusikan ke persamaan
(2.25) akan menghasilkan persamaan differensial penentu untuk pelat
yang memikul beban lateral :
+ + = .
∇ ∇ =
Persamaan ini merupakan persamaan differensial parsial tak homogen,
berorde-empat yang termasuk jenis eliptis dengan koefesien konstan,
27
persamaan (2.46) bersifat liner karena turunan w tidak memiliki
eksponensial lebih dari satu (szilard, 1974:31). Selanjutnya,
merumuskan gaya geser transversal dalam lendutan lateral. Persamaan
(2.42) dan, (2.43), dan (2.45) disubstitusi ke persamaan (2.21) dan
(2.22) menghasilkan
= + = − + .
= + = − + .
5. Kondisi tepi menurut teori lentur
Penyelesaian eksak untuk persamaan pelat (persamaan 2.46) harus
juga memenuhi persamaan differensial tersebut dalam kondisi tepi
(syarat batas) masalah pelat tertentu. Karena persamaan (2.46)
merupakan persamaan differensial berorde–empat, dua kondisi tepi,
baik untuk perpindahan ataupun untuk gaya-gaya dalam, diperlukan
setiap tepi.
Dalam teori lentur pelat, ada tiga komponen gaya dalam yang harus
ditinjau: momen lentur, momen puntir dan gaya geser transversal.
Demikian pula, komponen perpindahan yang harus dipakai dalam
perumusan kondisi tepi adalah lendutan lateral dan kemiringan
(putaran sudut). Kondisi tepi pelat yang mengalami lentur umumnya
dapat digolongkan sebagai salah satu dari kondisi tersebut. Adapun
kondisi tepi yang digunakan dalam pembahasan tugas akhir ini adalah
a. Kondisi tepi geometris (jepit). Kondisi geometris tertentu yang
diperoleh berdasarkan besarnya perpindahan (translasi dan rotasi)
dapat digunakan untuk merumuskan kondisi tepi dalan bentuk
matematis. Misalnya, lendutan dan kemiringan permukaan pelat
yang melendut di tepi jepit (Gambar 2.11a) sama dengan nol, jadi,
dapat dituliskan
= , ( ) = = =
Dan (2.49)
= , ( ) = = =
Kondisi tepi seperti ini disebut kondisi tepi geometris
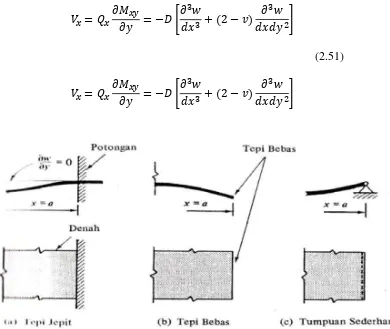
b. Kondisi tepi statis (tepi bebas). Untuk kondisi tepi statis, gaya-gaya
tepi memberikan persamaan matematis yang diperlukan. Misalnya,
di tepi bebas suatu pelat yang tidak dibebani lihat (Gambar 2.11b),
kita dapat katakan bahwa momen dan gaya geser transversal (V) di
tepi tersebut sama dengan nol. Jadi,
= � = � = ,
Atau (2.50)
= � = � = ,
Gaya geser di tepi pelat terdiri dari dua suku, yaitu gaya geser
transversal dan pengaruh momen puntir. Dengan memperhatikan
tepi-tepi pelat yang memiliki garis normal dalam arah X dan Y,
29
� = = − [ + − ]
(2.51)
� = = − [ + − ]
Gambar 2.11 Berbagai Kondisi Tepi Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Dimana Qx dan Qy adalah gaya geser lateral (persamaan 2.47 dan
2.48). Suku kedua ∂mxy/dy dan ∂myx/dx dalam persamaan (2.51)
menyatakan gaya geser tambahan di tepi tersebut yang diakibatkan
oleh momen puntir Mxy = Myx. Dengan mengganti momen puntir
dengan kopel ekivalen secara statis Mxy dy/dy dan Myx dx/dx
(Gambar 2.12), gaya-gaya ini saling menghapus di elemen-elemen
yang bersebelahan, kecuali bagian pertambahannya :
Dengan membagi persamaan ini masing-masing dengan dy dan dx,
kita peroleh gaya geser tambahan persatuan panjang :
= =
Gaya ini disebut gaya tambahan Kirchhoff (Kirchhoff Ersatzkrafte)
Gambar 2.12 Pengaruh tepi dari momen puntir Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Dengan mengganti momen puntir dengan gaya geser ekivalen ini,
Kirchhoff mengurangi jumlah gaya dalam yang harus ditinjau,
yakni dari tiga menjadi dua. Dengan demikian,dari persamaan
(2.42),dan (2.43), dan (2.50), dan (2.51) Kondisi tepi bebas adalah :
+ = , [ + − ] = .
31
+ = , [ + − ] = .
c. Kondisi tepi sederhana. Tepi yang memiliki tumpuan sederhana
(Gambar 2.11c) menghasilkan kondisi tepi campuran. Karena
lendutan dan momen lentur di sepanjang tepi ini melibatkan
persamaan yang berkaitan dengan perpindahan dan gaya. Jadi,
= , = + =
Dan (2.54)
= , = + =
C. Pengenalan Metode M. Levy
Deret Fourier merupakan alat yang ampuh untuk mendapatkan
penyelesaian analitis dari banyak masalah dalam bidang mekanika terapan
(applied mechanics ), seperti penyelesaian persamaan differensial parsial
pada teori elastisitas, getaran, aliran panas, transmisi listrik, dan
gelombang elektromagnetik. Begitu pula analisa pelat yang akan dibahas
kemudian, yaitu metode M. Levy. Perluasan deret Fourier menghasilkan
integral Fourier dan transformasi Fourier.
Untuk penyelesaian persamaan differensial dari persamaan yang
digunakan dalam penurunan rumus untuk metode M. Levy, hanya
digunakan deret Fourier tunggal untuk mendapatkan penyelesaian
Dalil Fourier menyatakan bahwa suatu fungsi sembarang y = f (x) dapat
dinyatakan dengan deret tak-hingga yang terdiri dari suku sinus dan
kosinus. Jadi, fungsi semula dapat diganti dengan superposisi sejumlah
gelombang sinus dan kosinus. Jika f(x) adalah fungsi periodik, dalil
(2.56) berlaku untuk sembarang fungsi periodik beraturan yang terdiri dari
sejumlah segmen (piecewise), yang boleh memiliki diskontinuitas.
Persamaan ini menyatakan fungsi periodic sembarang f(x) dalam seluruh
jangkauan dari x = -∞ sampai x = +∞, sehingga disebut ekspansi dengan
33
Gambar 2.13 Fungsi periodik sembarang
Sumber : Teori dan Analisis Pelat (Szilard, 1974)
= �∫� .
= �∫� cos .
Dan
= � ∫� sin , = , , , … .
Bila bentuk analitis dari fungsi f(x) tidak diketahui atau terlalu rumit untuk
diintegrasi, kita dapat memanfatkan analitis harmonis yang mengganti
integral dengan penjumlahan. Dengan membagi periode T menjadi
interval-interval yang sama sebesar 2m (lihat Gambar 2.14)
koefesien Fourier bisa ditentukan sebagai
Gambar 2.14 Analisis Harmonis
Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Dan
Metode pendekatan lainnya untuk menghitung konstanta ekspansi Fourier
ialah dengan menggambarkan kurva f(x), f(x) cos (2π/T) dan sin (2πx/T)
dan menentukan luas masing-masing kurva dengan planimeter (alat
pengukur luas). Jika suatu fungsi periodik, fungsi tersebut dapat dibuat
periodik dengan meneruskan fungsi secara sembarang keluar intervalnya.
Penerusan sembarang ini dapat berupa harmonis gelap, harmonis ganjil
(Gambar 2.15), atau genap ganjil (Gambar 2.16). Karena dalam banyak hal
tujuan kita adalah menyatakan fungsi f(x) hanya pada panjang tertentu L,
kita lebih mudah memakai ekspansi setengah-jangkauan (half-range
expansion) dengan pengulangan interval T = 2L dan dengan mengambil
35
Misalkan kita hendak menyatakan fungsi f(x) hanya dalam suku kosinus.
untuk itu, kita tambahkan secara sembarang suatu fungsi genap dalam x
pada fungsi tak-periodik semula (Gambar 2.16a) , sehingga hubungan
= − .
Gambar 2.15. (a) Harmonisasi ganjil, (b) harmonisasi genap Sumber : Teori dan Analisis Pelat (Szilard, 1974)
Berlaku, jadi suku sinus, dalam persamaan (2.56) menghilang selama
integrasi. Demikian pula, dengan membuat fungsi ganjil (Gambar 2.16b)
= − − .
Berlaku, suku sinus akan hilang dalam integrasi dan akan diperoleh deret
trigonometris sinus dengan cara ekspansi deret Fourier
setengah-jangkauan. Cara terakhir, karena deret ini mengandung konstanta A0
sebenarnya merupakan suku kosinus menurut [persamaan (2.64) dan
(2.65)] dan dapat menyatakan kondisi tepi geometris bagi tumpuan
sederhana,
37
Kita dapat mengekspansikan fungsi pada Gambar 2.17 menjadi deret
Fourier dengan tiga ( 3 ) cara :
Gambar 2.17 Fungsi yang akan diekspansikan menjadi deret Fourier Sumber : Teori dan Analisis Pelat (Szilard, 1974)
1. Ekspansi jangkauan-penuh, yang mengandung konstanta serta suku
sinus dan kosinus.
2. Ekspansi setengah-jangkauan, yang hanya mengandung suku sinus.
3. Ekspansi setengah-jangkauan, yang hanya mengandung suku kosinus
1. Untuk ekspansi jangkauan-penuh
Periode ekspansi adalah T = 2xo. Suku konstan diperoleh dari
persamaan (2.58) :
= ∫ � = .
Dan persamaan (2.59)
= ∫ � cos � = , = , , … .
= ∫ � sin � = ∫ � sin � +
= − � � − . Sehingga diperoleh
= � = , , , ….
Dan (2.69)
= , = , , , ….
Nilai-nilai tersebut disubtitusikan ke persamaan (2.56), menghasilkan
ekspansi deret Fourier penuh
= + � (sin� + sin � + sin � + ⋯) .
39
2. Berikutnya kita ubah fungsi yang sama (Gambar 2.17) menjadi deret
trigonometris yang hanya mengandung suku sinus. Untuk itu,
digunakan ekspansi setengah-jangkauan dengan periode T = 4x0.
Kemudian, fungsi ini secara sembarang diperpanjang melampaui titik
pusat sehingga diperoleh fungsi ganjil (Gambar 2.16b). Karena fungsi
dalam integral f(x) dan f(x) cos nωx. Merupakan fungsi ganjil,
persamaan (2.64) dan (2.65) menghasilkan A0 = An = 0. Namun, f(x)
sin nωx = f(x) adalah fungsi genap, dan untuk fungsi genap.
∫� = ∫� .
Dimana T = 2L. Dengan demikia persamaan (2.60) menjadi
= ∫� sin � .
Nilai-nilai untuk contoh ini kita subtitusikan ke persamaan (2.72), kita
peroleh
= ∫ 0 sin � = ∫ 0 � � +
= [ � cos � ] = − � cos �− .
Untuk berbagai nilai Bn, kita peroleh
= � , = , , , …
= � , = , , , … .
Dari nilai-nilai di atas dan persamaan (2.56), kita peroleh
= ∑
∞
sin
= � (sin� + sin� + sin � + sin � + ⋯ ) .
Grafik penjumlahan berbagai suku ini ditunjukan pada Gambar 2.18b
3. Selanjutnya, kita ekspansikan fungsi yang sama (Gambar 2.17) ke
deret trigonometris yang hanya mengandung suku kosinus. Kembali,
kita gunakan ekspansi setengah-jangkauan dengan periode T = 2L =
4x0. Akan tetapi, untuk kasus ini, perpanjangan sembarang yang
melampaui titik awal akan menghasilkan suatu fungsi genap seperti
yang diperlihatkan pada Gambar 2.16b.
Sekarang, fungsi dalam integral f(x) dan f(x) cosnωx dalam persamaan
(2.58) dan (2.59) merupakan fungsi genap, sedang f(x) sin nωx dalam
persamaan (2.60) adalah fungsi ganjil. Kita simpulkan bahwa Bn = 0,
dan dari persamaan (2.58) dan (2.59), diperoleh
= ∫� = ∫� cos � .
Dengan demikian, ekspansi Fourier untuk sembarang fungsi genap
berperiose 2L dapat dituliskan sebagai
= + ∑
∞
cos � .
Penyelesaian untuk koefesien-koefesien menghasilkan
41
= � sin �−
Untuk berbagai nilai n, kita peroleh [lihat persamaan (2.79)]
= � , = , , , …
= , = , , , … .
= − � , = , , , …
Subtitusi nilai-nilai ke persamaan (2.77) menghasilkan
= + � (cos � − cos � + cos� + ⋯ ) .
III. METODE PENELITIAN
A. Pendekatan Penelitian
Pendekatan penelitian yang digunakan adalah pendekatan kuantitatif, karena
hasil penelitian yang dilakukan berupa angka atau bilangan yaitu merupakan
hasil analisis perbandingan nilai faktor momen pada suatu pelat persegi antara
hasil analisis pada metode M. Levy dengan Tabel 13.3.1 pada PBI-71.
B. Lokasi Penelitian
Lokasi penelitian merupakan tempat dilakukannya penelitian. Dalam hal ini,
penelitian dilakukan di daerah Bandar Lampung.
C. Data Penelitian
Data penelitian merupakan penjelasan dari objek yang akan diteliti, objek
dalam penelitian ini yakni nilai momen pada pelat kondisi tumpuan sederhana
(tumpuan sendi), tumpuan jepit dan kombinasi jepit dan sederhana.
Kondisi-kondisi tersebut disesuaikan dengan Kondisi-kondisi yang terdapat pada Tabel 13.3.1
pada metode PBI-71.
Ada pun kondisi pelat yang sesuai dengan Tabel 13.3.1 pada metode PBI-71
43
Gambar 3.1 Kondisi tumpuan pelat Tabel 13.3.1 PBI-71
D. Prosedur Penelitian
Ada pun prosedur yang dilakukan dalam penelitian ini :
1. Melakukan analisis masalah yang terjadi saat menghitung nilai momen
lentur pada suatu pelat dua arah.
2. Melakukan studi literatur mengenai metode-metode pendekatan yang
dapat dilakukan dalam menentukan nilai momen pelat dua arah.
3. Menentukan jenis tumpuan pada pelat dua arah yang akan dianalisis
berdasarkan kondisi pelat yang dapat diterapkan di lapangan. Ada pun
a. Pelat persegi dengan tumpuan sederhana.
Gambar 3.2 Kondisi tumpuan sederhana
b. Pelat persegi yang mengalami momen akibat jepit.
c. Pelat persegi dengan dua tepi yang berhadapan ditumpu secara
sederhana dan dua sisi lainnya terjepit.
Gambar 3.3 Kondisi tumpuan dua tepi jepit dan dua tepi lainya jepit
d. Pelat persegi di mana ketiga tepinya ditumpu secara sederhana dan
satu tepinya terjepit.
Gambar 3.4 Kondisi tumpuan tiga tepi sederhana dan tepi lain jepit
e. Pelat persegi yang semua tepinya terjepit.
45
4. Melakukan analisis nilai faktor momen lentur dengan metode M. Levy
a. Menentukan variasi kondisi tumpuan pelat yang akan dianalisis,
kondisi tumpuan sesuai dengan prosedur ke 3.
b. Menghitung nilai w menggunakan deret Fourier tunggal pada kondisi
perbandingan panjang dan lebar pelat yang bervariasi.
c. Menghitung nilai Mx dan My pada kondisi perbandingan panjang dan
lebar pelat yang bervariasi.
d. Melakukan perbandingan nilai momen hasil analisis dengan metode
M. Levy dengan Tabel 13.3.1 pada metode PBI-71.
5. Melakukan pembahasan dan kesimpulan mengenai perbandingan kedua
metode ini.
E. Kerangka Penelitian
Kerangka penelitian merupakan sebuah benang merah tentang hal-hal yang
akan dilakukan dalam penelitian, ada pun kerangka penelitian dalam
menyusun skripsi ini dapat dilihat pada gambar 3.6.
Dalam gambar 3.6 tersebut, digambarkan hal-hal yang akan dilakukan dalam
menganalisis perbandingan nilai faktor momen pelat dua arah antara
Peraturan Beton Bertulang Indonesia (PBI-71) dan metode M. Levy (teori
Gambar 3.6 flow chart
Mulai
Hipoteisis awal : analisis masalah dalam perhitungan nilai momen pada pelat dua arah
Menentukan nilai tegangan & regangan
Menentukan nilai lendutan w dengan prosedur 3. Jenis tumpuan
V. PENUTUP
A. Kesimpulan
Adapun kesimpulan yang dapat diambil setelah melakukan penelitian ini
adalah sebagai berikut :
1. Terdapat perbedaan nilai faktor momen pada kedua metode hal ini
karenakan pada analisisnya penulis hanya memasukan nilai m = 1,3 dan 5
pada persamaan momen untuk setiap studi khasus.
2. Pada pelat persegi sederhana perbandingan momen lentur arah sumbu x dan
y yang diperoleh kedua metode hampir sama besar, tetapi secara
keseleruhunan nilai faktor pada motede M. levy cenderung lebih kecil.
3. Pada pelat persegi dengan dua tepi yang berhadapan ditumpu secara
sederhana dan dua sisi lainnya terjepit mengalami selisih nilai faktor
bilangan tertinggi pada momen tumpuan dengan perbandingan b/a = 1.5
yaitu : 0.00091 (0.87%).
4. Pelat persegi di mana ketiga tepinya ditumpu secara sederhana dan satu
tepinya terjepit mengalami selisih nilai faktor bilangan terbesar yakni pada
momen tumpuan perbandingan b/a = 1.9 dengan selisih 0.00265 atau
5. Selanjutnya pada pelat persegi yang semua tepinya terjepit terdapat
perbedaan nilai faktor bilangan yang paling besar pada momen tumpuan
(Mx y = ±a/2) perbandingan b/a = 1.7, pada metode M. Levy nilainya :
0.07938 dan momen tumpuan (Mtx) pada PBI-71 dengan nilainya : 0.081.
ada pun selisih nilai faktor bilangan kedua metode yakni : 0.00162 (2%).
6. Dengan memasuka nilai v (Poisson Rasio) pada persamaan dasar momen
lentur pada metode M. Levy untuk bahan yang berbeda, kita akan
mendapatkan nilai faktor bilangan yang berbeda untuk mendapatkan nilai
momen pada bahan struktur tertentu.
B. Saran
Adapun saran yang dapat diberikan setelah melakukan penelitian ini adalah
sebagai berikut :
1. Perlu dilakukan peninjauan kembali pada pelat persegi dengan kombinasi
tumpuan sesuai pada PBI-71 Tabel 13.3.2 menggunakan metode M. Levy.
2. Perlu dilakukan peninjauan kembali pada pelat berbentuk segitiga dan
lingkaran menggunakan metode M. Levy.
3. Sebelum melakukan perancangan pada suatu pelat persegi, sebaiknya kita
meninjau terlebih dahulu jenis bahan yang akan digunakan. Hal ini akan
berpengaruh pada nilai v (Poisson Rasio) dan momen lentur struktur
DAFTAR PUSTAKA
Universitas Lampung, 2013, Pedoman Penulisan Karya Ilmiah Universitas
Lampung, Unila Offset, Bandar Lampung.
PBI, 1971, Peraturan Beton Bertulang Indonesia, Departemen Pekerjaan Umum
dan Tenaga Listrik, Bandung.
Szilard, Rudolph, 1974, Teori dan Analisis Pelat Metode Klasik dan Numerik.
Diterjemahkan oleh : Ir. Wira, MSCE, Erlangga, Jakarta.
Timoshenko, S.P. dkk, 1986, Teori Elastisitas Edisi ke Tiga, Diterjemahkan oleh :
Ir. Darwin Sebayang, Erlangga, Jakarta.
Timoshenko, S.P. dkk, 1959, Theory of Plates and Shells Second Edition,
McGraw-Hill, Inc. Singapore.
Ventsel, Eduard. Dkk, 2001, Thin Plates and Shelss, Theory, Analysis, and
A. Pelat persegi dengan tumpuan sederhana.
1,0 90 1,5708 0,9172 2,5092 0,00406 -0,00896 0,00260 0,04396 0,04435
1,1 99 1,7279 0,9388 2,9032 0,00487 -0,00815 0,00225 0,05173 0,04495
1,2 108 1,8850 0,9549 3,3689 0,00565 -0,00737 0,00194 0,05914 0,04491
1,3 117 2,0420 0,9669 3,9180 0,00639 -0,00663 0,00167 0,06607 0,04442
1,4 126 2,1991 0,9757 4,5640 0,00708 -0,00594 0,00143 0,07247 0,04361
1,5 135 2,3562 0,9822 5,3228 0,00772 -0,00530 0,00123 0,07833 0,04259
1,6 144 2,5133 0,9870 6,2131 0,00831 -0,00471 0,00105 0,08364 0,04145
1,7 153 2,6704 0,9905 7,2572 0,00884 -0,00418 0,00090 0,08842 0,04025
1,8 162 2,8274 0,9930 8,4806 0,00932 -0,00371 0,00077 0,09270 0,03904
1,9 171 2,9845 0,9949 9,9137 0,00974 -0,00328 0,00066 0,09653 0,03785
2,0 180 3,1416 0,9963 11,5920 0,01013 -0,00289 0,00056 0,09994 0,03671
B. Pelat Persegi yang Mengalami Momen Akibat Jepit
1,0 90 1,5708 0,9172 2,5092 0,03703 0,3939 0,2150
1,1 99 1,7279 0,9388 2,9032 0,03604 0,3723 0,1540
1,2 108 1,8850 0,9549 3,3689 0,03446 0,3477 0,1058
1,3 117 2,0420 0,9669 3,9180 0,03250 0,3216 0,0683
1,4 126 2,1991 0,9757 4,5640 0,03033 0,2952 0,0395
1,5 135 2,3562 0,9822 5,3228 0,02804 0,2693 0,0178
1,6 144 2,5133 0,9870 6,2131 0,02575 0,2443 0,0016
1,7 153 2,6704 0,9905 7,2572 0,02351 0,2207 -0,0102
1,8 162 2,8274 0,9930 8,4806 0,02136 0,1986 -0,0185
1,9 171 2,9845 0,9949 9,9137 0,01932 0,1782 -0,0241
2,0 180 3,1416 0,9963 11,5920 0,01742 0,1595 -0,0277
1,0 90 1,5708 0,9172 2,5092 -0,00215 -0,02284 0,02112 -0,01247 0,03188 -0,06907
1,1 99 1,7279 0,9388 2,9032 -0,00234 -0,02420 0,02753 -0,01001 0,03494 -0,07799
1,2 108 1,8850 0,9549 3,3689 -0,00246 -0,02479 0,03435 -0,00755 0,03737 -0,08601
1,3 117 2,0420 0,9669 3,9180 -0,00250 -0,02471 0,04136 -0,00525 0,03917 -0,09302
1,4 126 2,1991 0,9757 4,5640 -0,00247 -0,02407 0,04840 -0,00322 0,04038 -0,09904
1,5 135 2,3562 0,9822 5,3228 -0,00240 -0,02302 0,05530 -0,00152 0,04107 -0,10409
1,6 144 2,5133 0,9870 6,2131 -0,00229 -0,02169 0,06194 -0,00014 0,04131 -0,10826
1,7 153 2,6704 0,9905 7,2572 -0,00215 -0,02018 0,06823 0,00093 0,04118 -0,11166
1,8 162 2,8274 0,9930 8,4806 -0,00200 -0,01859 0,07411 0,00173 0,04077 -0,11440
1,9 171 2,9845 0,9949 9,9137 -0,00184 -0,01699 0,07954 0,00230 0,04015 -0,11659
2,0 180 3,1416 0,9963 11,5920 -0,00168 -0,01542 0,08452 0,00268 0,03938 -0,11831
0,00533
D. Pelat persegi di mana ketiga tepinya ditumpu secara sederhana dan satu tepinya terjepit
1,0 90 1,5708 0,9172 2,5092 0,00128 0,01359 0,03037 0,00742 0,03693 -0,08608
1,1 99 1,7279 0,9388 2,9032 0,00136 0,01400 0,03773 0,00579 0,03915 -0,09400
1,2 108 1,8850 0,9549 3,3689 0,00139 0,01399 0,04514 0,00426 0,04065 -0,10068
1,3 117 2,0420 0,9669 3,9180 0,00138 0,01364 0,05243 0,00290 0,04152 -0,10621
1,4 126 2,1991 0,9757 4,5640 0,00134 0,01304 0,05943 0,00175 0,04186 -0,11072
1,5 135 2,3562 0,9822 5,3228 0,00128 0,01228 0,06605 0,00081 0,04178 -0,11434
1,6 144 2,5133 0,9870 6,2131 0,00120 0,01142 0,07222 0,00007 0,04137 -0,11722
1,7 153 2,6704 0,9905 7,2572 0,00112 0,01051 0,07790 -0,00048 0,04074 -0,11949
1,8 162 2,8274 0,9930 8,4806 0,00103 0,00960 0,08310 -0,00089 0,03993 -0,12127
1,9 171 2,9845 0,9949 9,9137 0,00094 0,00871 0,08782 -0,00118 0,03903 -0,12265
2,0 180 3,1416 0,9963 11,5920 0,00086 0,00786 0,09208 -0,00136 0,03807 -0,12372
E.Pelat Persegi yang Semua Tepinya Terjepit
1,0 90 1,5708 0,9172 2,5092 0,001399 0,021143 0,02114 -0,05112 -0,05112
1,1 99 1,7279 0,9388 2,9032 0,001679 0,025024 0,02098 -0,05785 -0,05362
1,2 108 1,8850 0,9549 3,3689 0,001962 0,02845 0,02030 -0,06362 -0,05518
1,3 117 2,0420 0,9669 3,9180 0,002240 0,031369 0,01930 -0,06839 -0,05608
1,4 126 2,1991 0,9757 4,5640 0,002508 0,03379 0,01818 -0,07224 -0,05655
1,5 135 2,3562 0,9822 5,3228 0,002763 0,035756 0,01690 -0,07527 -0,05677
1,6 144 2,5133 0,9870 6,2131 0,003004 0,037325 0,01569 -0,07761 -0,05683
1,7 153 2,6704 0,9905 7,2572 0,003228 0,038557 0,01456 -0,07938 -0,05682
1,8 162 2,8274 0,9930 8,4806 0,003435 0,039509 0,01352 -0,08069 -0,05677
1,9 171 2,9845 0,9949 9,9137 0,003624 0,040233 0,01261 -0,08164 -0,05672
2,0 180 3,1416 0,9963 11,5920 0,003798 0,040774 0,01181 -0,08231 -0,05667