SIMULASI INTENSITAS TERSENSOR KANAN TIPE 2 DENGAN BAHASA R DALAM PENDUGAAN PARAMETER DATA SURVIVAL BERDISTRIBUSI WEIBULL

(1)

SIMULASI INTENSITAS TERSENSOR KANAN TIPE 2 DENGAN BAHASA R DALAM PENDUGAAN PARAMETER

DATA SURVIVAL BERDISTRIBUSI WEIBULL

Oleh

Andro Pranajaya Ramadhan

Skripsi

Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS

Pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(2)

ABSTRAK

SIMULASI INTENSITAS TERSENSOR KANAN TIPE 2 DENGAN BAHASA R DALAM PENDUGAAN PARAMETER

DATA SURVIVAL BERDISTRIBUSI WEIBULL

Oleh

Andro Pranajaya Ramadhan

Analisis survival (survival analysis) bertujuan menduga probabilitas kelangsungan hidup, kekambuhan, kematian, dan peristiwa-peristiwa lainnya sampai pada periode waktu tertentu. Dalam analisis survival terdapat data tersensor yang terdiri dari beberapa jenis yaitu, data tersensor kiri, data tersensor kanan, data tersensor selang, dan data tersensor acak. Dari jenis data tersensor, terdapat 3 tipe penyensoran antara lain data penyensoran 1, penyensoran tipe 2, dan penyensoran maju. Dari berbagai macam distribusi yang ada, penelitian ini menggunakan fungsi survival berdistribusi Weibull, atau data waktu hidup diasumsikan mengikuti Distribusi Weibull. Tujuan dari penelitian ini adalah menduga parameter dari Distribusi Weibull terensor kanan tipe 2 dan melakukan simulasi dengan intensitas tersensor yang berbeda. Metode yang digunakan pada penelitian ini adalah metode kemungkinan maksimum, dan software yang digunakan pada penelitian ini adalah R x64 2.15.3.

(3)

(4)

(5)

(6)

DAFTAR ISI

Halaman

DAFTAR TABEL

I. PENDAHULUAN

1.1Latar Belakang ... 1

1.2Batasan Masalah ... 3

1.3Tujuan Penelitian ... 3

1.4Manfaat Penelitian ... 3

II. LANDASAN TEORI 2.1Analisis Survival ... 5

2.2Fungsi Survival ... 6

2.3Data Tersensor ... 7

2.4Tipe Tipe Penyensoran ... 9

2.5Model Survival Data Tersensor KananTipe II ... 10

2.6Distribusi Weibull ... 11

2.7Metode Kemungkinan Maksimum (maksimum likelihood estimation method) ... 13

2.8Metode Newton-Raphson ... 14

2.9Program R ... 14

III.METODOLOGI PENELITIAN 3.1Langkah Penelitian ... 16

3.2Flowchart Bahasa R Full Data ... 19

3.3Flowchart Bahasa R Data Tersensor ... 20

IV.HASIL DAN PEMBAHASAN 4.1Model Survival untuk Data Tersensor Kanan Tipe II ... 21

4.2Maximum Likelihood Estitamtion (MLE) Pada Model Distribusi Weibull untuk Data Tersensor Kanan ... 22

4.2.1 Penduga untuk Bagi Distribusi Weibull Untuk Data Tersensor Kanan ... 23

(7)

4.3.2 Penduga Bagi Distribusi Weibull Full Data……… 29 4.3.3 Iterasi Newton Rhapson Bagi Distribusi Weibull Untuk Data

Tersensor Kanan ... 31 4.3.4 Iterasi Newton Rhapson Bagi Distribusi Weibull Untuk

Full Data ... 33 4.4Hasil Numerik Proses Simulasi ... 35 4.5Grafik Distribusi Weibull Full Data ... 42

V. KESIMPULAN

DAFTAR PUSTAKA

(8)

I. PENDAHULUAN

1.1 Latar Belakang dan Masalah

Dalam bidang matematika terdapat cabang statistika yang telah banyak

mengalami perkembangan yang sangat pesat dengan ditemukanya berbagai alat

analisis yang bisa digunakan untuk menganalisis suatu permasalahan. Salah

satunya adalah analisis survival. Analisis survival (survival analysis) atau analisis kelangsungan hidup bertujuan menduga probabilitas kelangsungan hidup,

kekambuhan, kematian, dan peristiwa-peristiwa lainnya sampai pada periode

waktu tertentu. Analisis ini biasanya digunakan dalam bidang teknik, biologi,

kedokteran dan lain-lain. Variabel random positif pada analisis survival berupa

survival time (waktu tahan hidup) atau failure time (waktu kegagalan). Penelitian-penelitian tersebut biasanya menggunakan data yang berkaitan dengan waktu

hidup dari suatu individu yang akan diuji. Perbedaan antara analisis survival

dengan analisis statistik lainnya adalah adanya data tersensor. Menurut Pyke &

Thompson (1986) data dikatakan tersensor jika pengamatan waktu survival hanya

sebagian, tidak sampai kejadian gagal.

Dalam pengamatan, sensor dilakukan untuk memperpendek waktu percobaan

(9)

yang lama dan biaya yang tidak sedikit. Dalam analisis survival terdapat tiga jenis

sensor, yaitu sensor kiri (left censored), sensor kanan (right censored), sensor interval (interval censored), dan sensor acak (random censored).

Sensor kanan adalah tipe penyensoran di mana sampel ke-r merupakan observasi

terkecil dalam sampel random berukuran n (1 ≤r ≤ n). Dengan kata lain jika total sampel berukuran n, maka percobaan akan dihentikan sampai diperoleh r

kegagalan. Semua unit uji n masuk pada waktu yang sama. Pada sensor tipe ini, jika tidak terdapat individu yang hilang, maka waktu tahan hidup observasi

tersensor sama dengan waktu tahan hidup observasi tidak tersensor. Kelebihan

dari sensor ini adalah dapat menghemat waktu dan biaya.

Untuk menganalisis data survival dengan data tersensor diperlukan asumsi tertentu tentang distribusi populasinya. Beberapa distribusi parametrik yang

populer dan dapat digunakan untuk menganalisis model survival adalah Distribusi Weibull, Distribusi Eksponensial, Distribusi Log-normal, Distribusi Gamma,

Distribusi Log-logistik dan lain-lain.

Dari berbagai macam distribusi yang ada, dalam penelitian ini menggunakan

fungsi survival berdistribusi Weibull, atau data waktu hidup diasumsikan mengikuti Distribusi Weibull. Selain dapat digunakan untuk memodelkan

fenomena kerusakan dengan laju kerusakan tergantung pada usia pakai

komponen, Distribusi Weibull juga sering dipakai untuk menyelesaikan

masalah-masalah engineering, misalnya jangka waktu kerusakan dari kapasitor, transistor,

sel photo conductive, korosi, kelelahan logam dan sebagainya.

(10)

Dalam pembuatan skripsi ini penulis menggunakan bantuan software R 2.15.3

yang berbasis open source, guna membantu untuk membuat program pada proses iterasi yang nantinya akan diperlukan dalam penelitian ini.

1.2 Batasan Masalah

Penelitian ini membahas tentang penduga parameter distribusi Weibull untuk data

tersensor kanan dan penduga parameter distribusi Weibull untuk full data.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah:

1. Melakukan pendugaan parameter dengan menggunakan Maximum Likelihood Estimation (metode kemungkinan maksimum) pada distribusi Weibull dengan

intensitas data tersensor kanan.

2. Melakukan simulasi untuk melihat karakteristik penduga distribusi Weibull

dengan data sensor kanan.

3. Mengkaji karakteristik dan bias penduga dari distribusi Weibull dengan data

sensor kanan dan membandingannya dengan full data.

1.4 Manfaat Penelitian

Manfaat dari penelitian ini adalah untuk:

1. Memberikan sumbangan pemikiran bagi peneliti lain mengenai pendugaan

(11)

kemungkinan maksimum) pada distribusi Weibull dengan data tersensor

kanan.

2. Menunjukkan kepada peneliti lain tentang analisis perbandingan karakteristik

(12)

II. TINJAUAN PUSTAKA

2.1 Analisis Survival

Analisis survival (survival analysis) atau analisis kelangsungan hidup bertujuan

menduga probabilitas kelangsungan hidup, kekambuhan, kematian, dan

peristiwa-peristiwa lainnya sampai pada periode waktu tertentu. Dalam menentukan waktu

survival, terdapat tiga elemen yang harus diperhatikan yaitu

a. Time origin or starting point (titik awal) adalah waktu dimulainya suatu penelitian.

b. Ending event of interest (kejadian akhir) adalah kejadian yang menjadi inti dari penelitian

c. Measurement scale for the passage of time (skala ukuran untuk berlalunya waktu).

Perbedaan antara analisis survival dengan analisis statistik lainnya adalah adanya

data tersensor. data dikatakan tersensor jika pengamatan waktu survival hanya

sebagian, tidak sampai waktu kejadian.

Menurut Lee (1992), jika melambangkan waktu survival dan mempunyai fungsi

kepekatan peluang , maka fungsi sebaran kumulatif dinyatakan sebagai

∫

(13)

Dalam bidang kesehatan data ini diperoleh dari suatu pengamatan terhadap

sekelompok atau beberapa kelompok individu dan dalam hal ini adalah pasien,

yang diamati dan dicatat waktu terjadinya kegagalan dari setiap individu.

Kegagalan yang dimaksudkan antara lain adalah kematian karena penyakit

tertentu, keadaan sakit yang terulang kembali setelah pengobatan atau munculnya

penyakit baru. Apabila kegagalan yang diamati adalah terjadinya kematian pada

pasien maka waktu survival yang dicatat antara lain sebagai berikut :

a. Selisih waktu mulai dilakukannya pengamatan sampai terjadinya kematian dan

data tersebut termasuk data tidak terpotong (uncensored data).

b. Jika waktu kematiannya tidak diketahui, maka memakai selisih waktu mulai

dilakukannya pengamatan sampai waktu terakhir penelitian dan data tersebut

termasuk data terpotong (censored data).

2.2 Fungsi Survival

Menurut Lee (1992), jika variabel random yang menotasikan waktu bertahan

dari seorang individu, maka adalah probabilitas bahwa lebih besar dari .

Dalam statistik fungsi distribusi kumulatif didefinisikan :

∫

Karena maka ∫

(suatu individu bertahan lebih dari t)

(14)

∫

Dari definisi fungsi distribusi kumulatif dari , maka

2.3 Data Tersensor

Suatu data dikatakan tersensor jika lamanya hidup seseorang yang ingin diketahui

atau diobservasi hanya terjadi pada periode waktu yang telah ditentukan (interval

pengamatan), sedang info yang ingin diketahui tidak terjadi pada interval tersebut.

Dengan demikian kita tidak memperoleh informasi apapun yang diinginkan

selama interval pengamatan.

Menurut Collect (1997), data survival tidak memenuhi syarat prosedur standar

statistika yang digunakan pada analisis data. Alasan pertama karena data survival

biasanya berdistribusi tidak simetris. Model histogram waktu survival pada

sekelompok individu yang sangat sama akan cenderung “positive skewed”, oleh

karena itu histogram akan semakin miring ke kanan sesuai dengan interval waktu

dengan jumlah pengamatan terbesar, sehingga tidak ada alasan untuk

mengasumsikan bahwa data survival berdistribusi normal.

Ada empat jenis penyensoran yaitu sensor kanan (right censoring), sensor kiri (left censoring) , sensor selang (interval censoring), dan sensor acak (random censoring). Right cencoring, terjadi jika individu yang diamati masih tetap hidup

(15)

informasi yang ingin diketahui dari seorang individu telah dapat diperoleh pada

awal studi. Interval cencoring, jika informasi yang dibutuhkan telah dapat diketahui pada kejadian peristiwa didalam selang pengamatan. Random cencoring

terjadi apabila individu yang di amati meninggal karena sebab lain, bukan

disebabkan dari tujuan utama penelitian (Klein dan Moeschberger, 1997).

Dalam contoh yang di ilustrasikan oleh Klein dan Moeschberger (1997), misalkan

dalam sebuah penelitian untuk menentukan sebaran penggunaan ganja dikalangan

anak laki-laki di sebuah SMA di California. Dengan mengajukan pertanyaan

“kapan anda menggunakan ganja untuk pertama kalinya”. Ternyata ada beberapa

anak menjawab “saya tidak pernah menggunakan ganja”, dengan demikian anak

tersebut mengalami kejadian tersensor kanan. Dan jika ada anak yang menjawab

“saya pernah menggunakanya, tetapi saya tidak tahu tepatnya kapan pertama kali

menggunakanya”, pada kasus ini anak tersebut mengalami kejadian tersensor kiri

dikarenakan waktu awal dia menggunakan ganja tidak diketahui. Pada kasus lain,

misalkan untuk mengestimasi distribusi dari beberapa tikus yang diberikan zat

karsinogen pada makanannya, dilakukan studi selama 10 bulan kepada 10 tikus

dan penelitian dilakukan setiap akhir tahun, jika 2 dari 8 tikus tewas karena

kanker pada bulan ke-5 dan ke-7, maka 2 tikus tersebut mengalami kejadian

sensor selang, karna tidak didapat informasi kapan tepatnya tikus tersebut tewas

karena kanker. Dan jika ada 1 dari 10 tikus tersebut meninggal karena terinjak

(tewas bukan karena penilitian utam) bukan karena terkena kanker, maka tikus

(16)

2.4 Tipe-Tipe Penyensoran

Jenis penyensoran dapat dibagi lagi menjadi tipe-tipe penyensoran. Menurut

Johnson (1982), tipe-tipe penyensoran terdiri dari :

1. Penyensoran Tipe I

Pada penyensoran sebelah kanan tipe I, penelitian diakhiri apabila waktu

pengamatan yang ditentukan tercapai. Jika waktu pengamatan sama untuk semua

unit maka dikatakan penyensoran tunggal. Jika waktu pengamatan untuk setiap

unit berbeda maka dikatakan penyensoran ganda.

Pada penyensoran sebelah kiri tipe I, pengamatan dilakukan jika telah melampaui

awal waktu yang ditentukan. Karakteristik penyensoran tipe I adalah bahwa

kegagalan adalah acak.

2. Penyensoran Tipe II

Pada penyensoran tipe II, pengamatan diakhiri setelah sejumlah kegagalan yang

telah ditetapkan diperoleh, atau dapat dikatakan banyaknya kegagalan adalah tetap

dan waktu pengamatan adalah acak.

Pada sensor kanan jenis II, jumlah individu pada saat awal ditentukan dan waktu

penelitian ditentukan sampai terjadinya kematian dengan jumlah tertentu

3. Penyensoran Maju (Progressive Censoring)

Pada penyensoran maju, suatu jumlah yang ditentukan dari unit-unit bertahan

dikeluarkan dari penelitian berdasarkan kejadian dari tiap kegagalan terurut.

Secara konseptual, hal ini sama dengan suatu praktek yang dikenal sebagai

sudden-death testing, dimana tes secara serempak memuat beberapa pengetesan

(17)

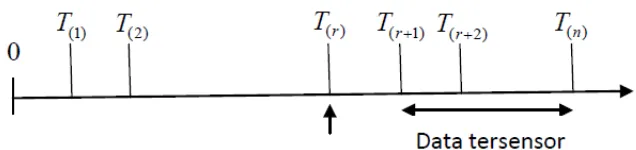
2.5 Model Survival Data Tersensor KananTipe II

Dalam data tersensor kanan tipe 2, terdapat pengamatan dari sampel yang

diamati, dan eksperimen akan dihentikan setelah kegagalan yang terjadi

sebelum waktu . Data terdiri dari tahan hidup terkecil

dari sampel random yang terdiri dari tahan hidup ,

seperti iliustrasi pada Gambar 2.1.

Gambar 2.1. Ilustrasi Model Tersensor Kanan

Misalkan merupakan variabel random dari individu yang diamati,

merupakan fungsi densitas peluang dari variabel random individu ,

merupakan fungsi densitas peluang dari variabel random individu , dan

seterusnya hingga untuk variabel random individu . Individu yang

gagal, yaitu individu sampai individu masing-masing sebanyak

satu komponen. Sedangkan individu yang masih bertahan melebihi kegagalan dari

individu dituliskan sebagai sebanyak . Sampel

random berukuran dengan kegagalan ini mengikuti distribusi multinomial,

sehingga terdapat

(18)

Fungsi densitas peluang bersama dari dari data yang diamati, dapat

ditulis sebagai berikut:

[ ]

_[∏

] [( ) ( )]

_[∏

] [( ) ( )]

_[∏

] [ ]

_[∏

] [ ]

Fungsi densitas peluang bersama data tersensor kanan dari , untuk

dengan order statistik adalah:

[∏ ][ ] _(2.1)

(Klein dan Moeschberger, 1997)

2.6 Distribusi Weibull

Distribusi Weibull dikembangkan oleh W. Weibull pada awal tahun 1950.

(19)

pada sistem kompleks di dalam sistem engineering. Secara umum, distribusi ini

dapat digunakan untuk menjelaskan data saat waktu menunggu hingga terjadi

kejadian dan untuk menyatakan berbagai fenomena fisika yang berbeda-beda.

Dengan demikian, distribusi ini dapat diterapkan pada analisa resiko karena dapat

menduga umur pakai (life time) komponen. Distribusi Weibull merupakan salah

satu jenis distribusi kontinu yang sering digunakan, khususnya dalam bidang

keandalan dan statistik karena kemampuannya untuk mendekati berbagai jenis

sebaran data.

Distribusi Weibull sering digunakan untuk memodelkan waktu kegagalan dari

banyak sistem fisik. Parameter dalam distribusi memungkinkan fleksibilitas untuk

memodelkan sistem dengan jumlah kegagalan bertambah terhadap waktu,

berkuran terhadap waktu atau tetap konstan terhadap waktu.

Menurut Al-Kanani (2011), fungsi kepekatan peluang dari suatu peubah acak

Weibull dengan parameter dan , adalah sebagai berikut:

[ ] ,

Distribusi Weibull dengan parameter dan dapat dinotasikan sebagai berikut

, dengan dan .

Dengan nilai Mean dan Varian berturut-turut sebagai berikut:

[ ( _)]

(20)

Dan commulatife density functions (cdf)dari Distribusi Weibull, yaitu : (₎

Dan fungsi survivalnya adalah

(₎

2.7 Metode Kemungkinan Maksimum (maksimum likelihood estimation

method)

Metode kemungkinan maksimum adalah metode untuk menduga satu sebaran

dengan memilih dugaan-dugaan yang nilai-nilai parameternya diduga dengan

memaksimalkan fungsi kemungkinanya, metode kemungkinan maksimum

merupakan salah satu metode yang paling sering digunakan untuk mencari nilai

estimasi dari suatu parameter.

Menurut Nar Herrhyanto (2003), misalkan adalah peubah acak kontinu atau

diskrit dengan fungsi kepekatan peluang , dengan adalah salah satu

sampel yang tidak diketahui. Misalkan merupakan sampel acak

berukuran maka fungsi kemungkinan (likelihood function) dari sampel acak itu

adalah:

Dalam hal ini, fungsi kemungkinan adalah fungsi dari parameter yang tidak

diketahui . Biasanya untuk mempermudah penganalisaan, fungsi kemungkinan

diberi log natural ( ). Penduga kemungkinan maksimum dari adalah nilai

(21)

2.8 Metode Newton-Raphson

Kebanyakan persoalan model matematika dalam bentuk yang rumit tidak dapat

diselesaikan dengan metode analitik yang sudah umum untuk mendapatkan solusi

eksak. Bila metode analitik tidak dapat lagi diterapkan, maka solusi dari persoalan

model matematika tersebut masih dapat diselesaikan dengan menggunakan

metode numerik.

Menurut Atkinson (1993) dalam metode numerik, pencarian akar

dilakukan dengan iterasi. Diantara semua metode akar, metode

Newton-Raphsonlah yang paling terkenal dan paling banayak dipakai dalam terapan sains

dan rekayasa. Metode ini paling disukai karena tingkat konvergensinya paling

cepat diantara metode lainnya

Dimana

adalah nilai awal

adalah fungsi yang ingin diketahui nilainya

adalah turunan pertama dari

2.9 Program R

R adalah perangkat lunak bebas untuk komputasi statistik dan grafik. Merupakan

proyek GNU General Public License Free Software Foundation yang mirip

dengan bahasa S yang dikembangkan di Bell Laboratories oleh Jhon Chambers

(22)

modeling, pengujian analisis klasik, analisis time-series, klasifikasi dan lainnya.

Sebuah rangkaian perangkat lunak yang digunakan untuk manipulasi data,

perhitungan, dan tampilan grafik yang mencakup antara lain sebagai berikut :

a. Penanganan data yang efektif dan penyimpanan data.

b. Rangkaian operator untuk perhitungan array dalam matriks tertentu.

c. Fasilitas grafik untuk analisis data dan menampilkan baik pada layar maupun

hardcopy.

d. Bahasa pemprograman yang sederhana, berkembang dengan baik dan efektif.

(23)

III. METODOLOGI PENELITIAN

3.1 Langkah Penelitian

Metode yang digunakan dalam penelitian ini adalah studi pustaka dengan

menggunakan buku-buku referensi, dan jurnal ilmiah yang berhubungan dengan

skripsi ini dan memberikan ilustrasi penerapannya dengan menggunakan software R 2.15.3. Adapun langkah-langkah dalam penelitian ini adalah sebagai berikut:

1. Menentukan model likelihood Distribusi Weibull untuk data tersensor kanan.

2. Menduga parameter distribusi Weibull dengan metode kemungkinan

maksimum (maximum likelihood estimation) pada data tersensor kanan.

a. Membentuk fungsi kemungkinan maksimum Distribusi Weibull

tersensor kanan.

b. Memaksimumkan fungsi yang diperoleh untuk mendapatkan dugaan

parameter

c. Dugaan parameter yang diperoleh dari metode kemungkinan maksimum

diperoleh dengan mencari turunan pertama dari logaritma natural fungsi

kepekatan peluang terhadap parameter-parameter yang akan diduga dan

(24)

3. Menduga parameter distribusi Weibull dengan metode kemungkinan

maksimum (maximum likelihood estimation) untuk full data.

a. Membentuk fungsi kemungkinan maksimum Distribusi Weibull full data.

b. Memaksimumkan fungsi yang diperoleh untuk mendapatkan dugaan

parameter

c. Dugaan parameter yang diperoleh dari metode kemungkinan maksimum

diperoleh dengan mencari turunan pertama dari logaritma natural fungsi

kepekatan peluang terhadap parameter-parameter yang akan diduga dan

menyamakannya dengan nol.

4. Mengkaji karakteristik penduga parameter distribusi Weibull secara simulasi,

dengan melakukan langkah-langkah sebagai berikut:

a. Membangkitkan data dengan distribusi Weibull ( dengan

dan nilai parameter ( yang berbeda-beda

yaitu (1,1), (1, 1.5), (0.5, 1) dan (0.5, 1.5) dengan perulangan setiap

sebanyak 1000 kali.

b. Menentukan nilai parameter ̂ dan ̂ Distribusi Weibull full data dengan

metode kemungkinan maksimum (maximum likelihood estimation).

c. Menghitung nilai rata-rata ̂ dan ̂ pada Distribusi Weibull full data.

d. Menentukan nilai parameter ̂ dan ̂ Distribusi Weibull tersensor kanan

dengan intensitas tersensor sebanyak (1%, 5%, 10%,15%) dengan metode

(25)

e. Menentukan ̂ dan ̂ pada distribusi Weibull tersensor kanan dengan

rumus yang diperoleh pada langkah d, dengan intensitas sensor yaitu r =

1%, 5%, 10%, dan 15% kemudian simulasi diulang sampai 1000 kali

f. Menghitung nilai rata-rata ̂ dan ̂ pada Distribusi Weibull tersensor

kanan

g. Membandingkan penduga parameter distribusi Weibull full data dengan

data tersensor kanan.

(26)

3.2 Flowchart Bahasa R Full Data

TIDAK miu 1 beta 1 miu 0,5 beta 1 miu 1 beta 1,5 miu 0,5 beta 1,5

MODEL ̂ MODEL ̂ DEFINISI FUNGSI

TULIS HASIL

SELESAI DEFINISI

FUNGSI DEFINISI

VARIABEL

YA ̂ ̂ START

(27)

3.3 Flowchart Bahasa R Data Tersensor

TIDAK miu 1 beta 1

miu 0,5 beta 1 miu 1 beta 1,5 miu 0,5 beta 1,5

r= 1%, 5%, 10%, 15%

MODEL ̂ MODEL ̂ DEFINISI FUNGSI

TULIS HASIL

SELESAI DEFINISI

FUNGSI DEFINISI VARIABEL

YA ̂ ̂ START

(28)

V. KESIMPULAN

Kesimpulan yang didapat pada penelitian mengenai Intensitas Tersensor Kanan

Dalam Analisis Data Survival Yang Berdistribusi Weiibull adalah

1. Penduga bagi Distribusi Weibull untuk data tersensor kanan adalah ̂

[ ̂ ∑ ̂_] ̂_{, dan penduga} _{bagi Distribusi Weibull untuk data}

tersensor kanan adalah

̂ [

̂_∑ ̂

_] ̂_∑

[ ∑ ̂ ̂_∑ ̂

]

(

̂

̂_∑ ̂

̂

)

̂

̂_∑ ̂

(

̂_∑ ̂

̂

)

2. Penduga bagi Distribusi Weibull untuk full data adalah ̂ [∑ ̂] ̂, dan

(29)

∑ ̂

̂

∑

3. Intensitas tersensor sangat mempengaruhi nilai penduga parameter ̂ dan ̂,

hal ini dapat dilihat pada tabel 4.1 karena semakin besar intensitas tersensor,

maka nilai penduga ̂ akan semakin berkurang seiring dengan besarnya

intensitas tersensor, begitu juga penduga bagi ̂ akan semakin besar seiring

besarnya intensitas tersensor

4. Bias yang dihasilkan oleh penduga dan pada data tersensor akan bernilai

semakin besar seiring dengan besarnya intensitas tersensor.

5. bias yang dihasilkan oleh parameter data tersensor dan tidak dipengaruhi

oleh banyaknya data n karena pada perhitungan bias yang dilakukan, karena semakin banyak jumlah data n maka bias yang dihasilkan penduga parameter

(30)

DAFTAR PUSTAKA

Al-Kanani, H.I. and A.J. Shaima, 2011. Estimate survival function for the brain cancer disease by using three parameters weibull distribution. J. Basrah Res. Sci., pp: 80.

Atkinson, Kendal (1993). Elementar Numerical Analysis. second edition. John Wiley & Sons, Singapore.

Bambey G. C.,dan Ibrahim A. N. 2013.” Methods for Estimating the 2-Parameter Weibull Distribution with Type-I Censored Data”. Journal

Collet, D. (1996). Modeling survival data in medical research. London: Chapman & Hall.

Engelhardt, M. and Bain, L. J. 1991. Statistical Analysis Of A Weibull Process With Left-Censored Data. Workshop On Survival Analysis and Related Topics. Columbus, OHIO.

Herrhyanto, Nar. 2003. Statistika Matematika Lanjutan. Pustaka Setia. Bandung. Hogg, R. V. and Craig, A. T. 1986. Introduction to Mathematical Statistics. Fifth

Edition. Prentice-Hall International Inc., New Jersey.

Jonhson, R.1982. Applied Multivariate Statisticals Analysis. Prentice-Hall Inc., New Jersey .

Klein, J. P. and Moeschberger, M. L. 1997. Survival Analysis : Techniques for Censored and Truncated Data. Springer-Verlag, New York.

Lawless, J. F. 1982 Statistical Model and Methods for Lifetime Data. New York: John Wiley and Sons, Inc.

(31)

Generate data berdistribusi Weibull dengan miu 0.5 dan beta 1.5

write.table(data.X100,file="D:/R/random1.50.5_X100.txt",sep= ,col.names = NA)

X200<-matrix(0,n2,ulangan)

Generate data berdistribusi Weibull dengan miu 1.5 dan beta 1

(32)

write.table(data.X100,file="D:/R/random1.51_X100.txt",sep= ,col.names = NA)

Generate data berdistribusi Weibull dengan miu 0.5 dan beta 1

n1<-100

(33)

Generate data berdistribusi Weibull dengan miu 1 dan beta 1

n1<-100

write.table(data.X100,file="D:/R/random11_X100.txt",sep= ,col.names = NA)

(34)

write.table(data.X400,file="D:/R/random11_X400.txt",sep= ,col.names = NA)

salah satu coding untung menduga nilai parameter dengan dengan perulangan sebanyak 1000 yang berdistribusi Weibull pada full data

 Menduga parameter dengan dan

beta<-1.5 miu<-0.5 ulangan<-1000 iterasi<-100

X100<-read.table(file = "D:/R/random1.50.5_X100.txt",header=TRUE)

# melakukan pendugaan parameter (beta,miu) dengan n=100 dimana pada program ini menggunakan fungsi array, dimana matriks yang akan terbuat adalah matriks 100 x 1000 dengan seratus adalah banyaknya data dan 1000 adalah banyaknya

(35)

A[i,k,j]<-X100[i,j]^b_duga100[1,k,j]

X100_sb[1,j] <- sum(X100[,j]^b_duga100[1,100,j]) }

miu_duga100<-matrix(0,1,ulangan) for (j in 1:ulangan)

{

miu_duga100[1,j] <- (X100_sb[1,j]/n1)^(1/b_duga100[1,100,j]) }

data.Beta_dugaX100=data.frame(b_duga100[1,100,])

write.table(data.Beta_dugaX100,file="D:/R/Bduga_X100.txt",sep= ,col.names = NA)

data.Miu_dugaX100=data.frame(miu_duga100)

write.table(data.Miu_dugaX100,file="D:/R/MIUduga_X100.txt",sep= ,col.names = NA)

Coding penduga parameter yang berdistribusi Weibull untuk data tersensor kanan dengan , intensitas tersensor (1%, 5%, 10%, 15%), dengan perulangan sebanyak 1000

(36)

 Menduga parameter dengan , , dengan intensitas tersensor 1%

X100 <- read.table (file = "D:/R/random1.50.5_X100.txt",header=TRUE)

#pendugaan parameter (beta,lamda) data tersensor kanan dengan n=100

#tersensor kanan 1%

beta<-1.5 miu<-0.5 n1<-100 r <-99

ulangan <- 1000

#proses penyensoran data, dimana data harus di urutkan terlebih dahulu menggunakan fungsi sort, kemudian tentukan banyaknya data tersensor bergantung pada intensitas tersensor yang telah di tentukan sebelumnya

X100_sort <-matrix(0,n1,ulangan) for (j in 1:ulangan)

{

X100_sort[,j] <- sort(X100[,j]) }

Xi<- matrix(0,n1-1,ulangan) for (j in 1:ulangan)

{

for (i in 1:99) {

Xi[i,j] <- X100_sort[i,j] }

}

Xr<-matrix(0,1,ulangan) for (j in 1:ulangan) {

Xr[1,j]<-Xi[99,j] }

(37)

x 1000 dengan seratus adalah banyaknya data dan 1000 adalah banyaknya

q[1,j] <- sum(log(Xi[,j])) }

for (j in 1:ulangan) {

s[1,j] <- sum( ((Xi[,j]/miu)^beta) * (log(Xi[,j]/miu)) ) }

t[1,j] <- (n1-r) * ((Xr[1,j]/miu)^beta) * (log(Xr[1,j]/miu)) }

(38)

z[1,j] <- sum((Xi[,j])^beta_duga[1,j]) }

miu_duga[1,j] <- ((1/r)*(y[1,j] + z[1,j]))^1/beta_duga[1,j] }

data.Miu_dugasensor1_X100=data.frame(miu_duga)

write.table(data.Miu_dugasensor1_X100,file="D:/R/miudugasensor_1%_1.50.5_X10 0.txt",sep= ,col.names = NA)

data.Beta_dugasensor1_X100=data.frame(beta_duga)

write.table(data.Beta_dugasensor1_X100,file="D:/R/betadugasensor_1%_1.50.5_X1 00.txt",sep= ,col.names = NA)

X100 <- read.table (file = "D:/R/random1.51_X100.txt",header=TRUE)

#tersensor kanan 1 %

beta<-1.5 miu<-1 n1<-100 r <-99

ulangan <- 1000

{

X100_sort[,j] <- sort(X100[,j]) }

(39)

{

for (i in 1:99) {

pengulangan

q[1,j] <- sum(log(Xi[,j])) }

(40)

{

beta_duga[1,j] <- r /(p[1,j] - q[1,j] + s[1,j] - t[1,j]) }

#penduga miu

y<-matrix(0,1,ulangan) z<-matrix(0,1,ulangan)

miu_duga<-matrix(0,1,ulangan)

y[1,j] <- (n1-r) * ((Xr[1,j])^beta_duga[1,j]) }

write.table(data.Miu_dugasensor1_X100,file="D:/R/miudugasensor_1%_1.51_X100. txt",sep= ,col.names = NA)

write.table(data.Beta_dugasensor1_X100,file="D:/R/betadugasensor_1%_1.51_X100 .txt",sep= ,col.names = NA)

(41)

ulangan <- 1000

{

X100_sort[,j] <- sort(X100[,j]) }

(42)

q[1,j] <- sum(log(Xi[,j])) }

(43)

X100 <- read.table (file = "D:/R/random11_X100.txt",header=TRUE)

beta<-1 miu<-1 n1<-100 r <-99

ulangan <- 1000

{

X100_sort[,j] <- sort(X100[,j]) }

(44)

p<-matrix(0,1,ulangan)

q[1,j] <- sum(log(Xi[,j])) }

(45)

write.table(data.Miu_dugasensor1_X100,file="D:/R/miudugasensor_1%_11_X100.tx t",sep= ,col.names = NA)

write.table(data.Beta_dugasensor1_X100,file="D:/R/betadugasensor_1%_11_X100.t xt",sep= ,col.names = NA)

beta<-1.5 miu<-0.5 n2<-200 r <-198

ulangan <- 1000

{

X200_sort[,j] <- sort(X200[,j]) }

{

(46)

{

pengulangan

q[1,j] <- sum(log(Xi[,j])) }

(47)

#penduga miu

beta<-1.5 miu<-1 n2<-200 r <-198

(48)

{

X200_sort[,j] <- sort(X200[,j]) }

pengulangan

(49)

}

(50)

beta<-1 miu<-0.5 n2<-200 r <-198

ulangan <- 1000

{

X200_sort[,j] <- sort(X200[,j]) }

(51)

p<-matrix(0,1,ulangan)

q[1,j] <- sum(log(Xi[,j])) }

(52)

beta<-1 miu<-1 n2<-200 r <-198

ulangan <- 1000

{

(53)

Xi[i,j] <- X200_sort[i,j]

pengulangan

q[1,j] <- sum(log(Xi[,j])) }

(54)

#penduga miu

(55)

ulangan <- 1000

{

X400_sort[,j] <- sort(X400[,j]) }

(56)

q[1,j] <- sum(log(Xi[,j])) }

(57)

beta<-1.5 miu<-1 n3<-400 r <-396

ulangan <- 1000

{

X400_sort[,j] <- sort(X400[,j]) }

{

for (i in 1:396) {

}

Xr<-matrix(0,1,ulangan) for (j in 1:ulangan) {

(58)

pengulangan

p<-matrix(0,1,ulangan) q<-matrix(0,1,ulangan) s<-matrix(0,1,ulangan) t<-matrix(0,1,ulangan)

beta_duga<-matrix(0,1,ulangan)

p[1,j] <- r * log(miu) }

q[1,j] <- sum(log(Xi[,j])) }

#penduga miu

(59)

{

beta<-1 miu<-0.5 n3<-400 r <-396

ulangan <- 1000

{

(60)

{

for (i in 1:396) {

pengulangan

q[1,j] <- sum(log(Xi[,j])) }

(61)

{

#penduga miu

(62)

beta<-1 miu<-1 n3<-400 r <-396

ulangan <- 1000

{

X400_sort[,j] <- sort(X400[,j]) }

(63)

for (j in 1:ulangan)

q[1,j] <- sum(log(Xi[,j])) }

(64)

Coding penduga parameter yang berdistribusi Weibull untuk data tersensor kanan dengan , intensitas tersensor 5%, dengan perulangan sebanyak 1000

beta<-1 miu<-1 n1<-100 r <-95

ulangan <- 1000

{

X100_sort[,j] <- sort(X100[,j]) }

{

(65)

Xi[i,j] <- X100_sort[i,j]

pengulangan

q[1,j] <- sum(log(Xi[,j])) }

(66)

#penduga miu

#rata-rata penduga parameter

mean_betaduga <- matrix(0,1,1)

{

mean_betaduga <- sum(beta_duga[1,])/ulangan }

mean_miuduga <- matrix(0,1,1)

{

mean_miuduga <- sum(miu_duga[1,])/ulangan }

(67)

beta<-1 miu<-1 n1<-100 r <-90

ulangan <- 1000

{

X100_sort[,j] <- sort(X100[,j]) }

(68)

p<-matrix(0,1,ulangan) q<-matrix(0,1,ulangan) s<-matrix(0,1,ulangan) t<-matrix(0,1,ulangan)

beta_duga<-matrix(0,1,iterasi)

p[1,j] <- r * log(miu) }

q[1,j] <- sum(log(Xi[,j])) }

#penduga miu

(69)

{

mean_betaduga <- sum(beta_duga[1,])/ulangan }

{

mean_miuduga <- sum(miu_duga[1,j])/ulangan }

write.table(data.Miu_dugasensor1_X100,file="D:/R/miudugasensor_10%_11_X100.t xt",sep= ,col.names = NA)

write.table(data.Beta_dugasensor1_X100,file="D:/R/betadugasensor_10%_11_X100. txt",sep= ,col.names = NA)

beta<-1 miu<-1 n1<-100 r <-85

(70)

{

X100_sort[,j] <- sort(X100[,j]) }

(71)

q[1,j] <- sum(log(Xi[,j])) }

{

(72)

{

mean_miuduga <- sum(miu_duga[1,])/ulangan }

write.table(data.Miu_dugasensor1_X100,file="D:/R/miudugasensor_15%_11_X100.t xt",sep= ,col.names = NA)

write.table(data.Beta_dugasensor1_X100,file="D:/R/betadugasensor_15%_11_X100. txt",sep= ,col.names = NA)

 Lampiran Coding untuk plot distribusi Weibull pada nilai miu1=1, miu2=0.5, dan beta=1

(73)

fw2[i]<-beta*(miu2^(-beta))*(x[i]^(beta-1))*(exp(-((x[i]/miu2)^beta))) }

}

plot(x,fw1,type="l",xlim=range(0,20),ylim=range(0,2.5),xlab="time",ylab="Pdf Weibull",col="green",lty=1)

lines(x, fw2,col="red", lty=2)

temp<-legend("topright",legend=c("beta=1 miu1=1","beta=1 miu2=0.5"),col = c("green","red","blue"),text.col = "green4", lty = c(1, -1, 0), pch = c(-1, 3, 21),merge = TRUE, bg = 'gray90')

 Lampiran Coding untuk plot distribusi Weibull pada nilai miu1=1, miu2=0.5, dan beta=1.5

(74)

plot(x,fw1,type="l",xlim=range(0,20),ylim=range(0,2.5),xlab="time",ylab="laju kegagalan",col="green",lty=1)

temp<-legend("topright",legend=c("beta=1.5 miu1=1","beta=1.5 miu2=0.5"),col = c("green","red","blue"),text.col = "green4", lty = c(1, -1, 0), pch = c(-1, 3, 21),merge = TRUE, bg = 'gray90')

(75)

temp<-legend("topright",legend=c("beta1=1 miu=0.5","beta2=1.5 miu=0.5"),col = c("green","red","blue"),text.col = "black", lty = c(1, -1, 2), pch = c(-1, 3, 4),merge = TRUE, bg = 'gray90')

 Coding untuk plot distribusi Weibull pada nilai miu=1 beta1=1 dan beta2=1.5

(76)