Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006)

(1)

FORMALISASI NAVIGASI MOBILE ROBOT

(STUDI KASUS ROBOT KRCI FATETA IPB 2006)

DIDIT WIDIYANTO

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

(2)

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006), adalah karya saya sendiri dengan arahan Komisi Pembimbing dan belum pernah diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, M e i 2007

(3)

ABSTRAK

DIDIT WIDIYANTO. Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006). Dibimbing oleh PRAPTO TRI SUPRIYO dan WISNU ANANTA KUSUMA.

Penelitian tesis ini dilatarbelakangi oleh kebutuhan rancangan kendali navigasi robot pada robot KRCI (Kontes Robot Cerdas Indonesia) 2006 milik Team AERS (Agricultural Engineering Robotic Squad) dari Fakultas Teknik Pertanian (FATETA) Institut Pertanian Bogor (IPB) yang diselenggarakan di Balairung Universitas Indonesia di Depok pada bulan Juni 2006. Kendala team robot yang saat itu adalah tidak memiliki konsep yang baik dalam memformulasikan sistem navigasi robotnya. Robot yang dibuat saat itu hanya merespon untuk menghindari halangan (obstacle avoidance) tanpa memperhatikan tata ruang lingkungannya (environment map). Akibatnya sangat mungkin robot tidak dapat kembali ke tempat semula, atau terdapat ruangan yang belum dikunjungi, atau terdapat ruangan yang dikunjungi lebih dari 1 (satu) kali. Kelemahan ini disebabkan tidak adanya formulasi navigasi dalam disain robot tersebut.

Inspirasi penelitian ini adalah mencoba menemukan formulasi sistem navigasi robot yang akurat, dengan terlebih dahulu mendeskripsikan sistem secara informal, merumuskan spesifikasi sistem secara formal dengan menggunakan bahasa spesifikasi Linear Temporal Logic (LTL), melakukan verifikasi sistem dengan menggunakan perangkat lunak pembanguan prototipe MOBOTSIM Versi 1.0.03, dan akhirnya menghasilkan sebuah prototipe sistem navigasi mobile robot yang dapat direkomendasikan untuk dipergunakan pada KRCI 2007 atau sesudahnya.

Akhirnya hasil penelitian ini diharapkan dapat membuktikan bahwa melalui eksperimen pada prototipe, bahasa spesifikasi formal LTL dapat digunakan untuk merumuskan sistem navigasi mobile robot pada studi kasus KRCI 2006 dengan baik.

(4)

© Hak Cipta milik Institut Pertanian Bogor, tahun 2007

Hak cipta dilindungi

(5)

FORMALISASI NAVIGASI MOBILE ROBOT

(STUDI KASUS ROBOT KRCI FATETA IPB 2006 )

DIDIT WIDIYANTO

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Ilmu Komputer

(6)

Nama : Didit Widiyanto N I M : G651040024

Disetujui

Komisi Pembimbing

Drs. Prapto Tri Supriyo, M.Kom. Wisnu Ananta Kusuma, S.T, M.T.

Ketua Anggota

Diketahui

Ketua Program Studi Ilmu Komputer Dekan Sekolah Pascasarjana

Dr. Sugi Guritman Prof. Dr. Ir. Khairil A. Notodiputro, MS.

(7)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karuniaNya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2006 ini adalah Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006).

Terima kasih penulis ucapkan kepada Bapak Drs. Prapto Tri Supriyo, M.Kom dan Bapak Wisnu Ananta Kusuma, S.T, M.T selaku pembimbing. Di samping itu, penghargaan penulis sampaikan kepada para dosen pengajar FATETA IPB yang telah berkenan mengajak penulis untuk terlibat dalam tim KRCI 2006 dan KRCI 2007 sehingga penulis memiliki makalah penelitian tesis ini diantaranya yaitu Bapak Ir. Mohamad Solahudin, M.Si, Bapak Dr. Ir. Radite Praeka Agus Setiawan, M.Agr, Bapak Dr. Ir. Dewa Made Subrata, M.Agr, dan Bapak Dr. Ir. Suroso, M.Agr. Ungkapan terima kasih juga disampaikan kepada orang tua, adik, mbak Nita beserta seluruh keluarga di Cepu Jawa-Tengah atas segala doa dan perhatiannya.

Semoga karya ilmiah ini bermanfaat.

Bogor, M e i 2007

(8)

Penulis dilahirkan di Semarang pada tanggal 14 Juli 1970 dari ayah Widodo W.S dan ibu Niniek Sri Harsini. Penulis merupakan anak pertama dari 2 bersaudara.

Tahun 1989 penulis lulus dari SMA Negeri 42 Halim Perdanakusuma, pada tahun 1993 lulus Program Diploma-3 Manajemen Informatika dan Komputer di UPN “Veteran” Jakarta, dan pada tahun 1998, lulus Strata-1 Manajemen informatika di STMIK “Budi Luhur” Jakarta.

(9)

viii DAFTAR ISI

Halaman

DAFTAR TABEL ……….. ix

DAFTAR GAMBAR……….. ix

PENDAHULUAN……….. 1

TINJAUAN PUSTAKA Robotik……… 3

Transformasi Lingkungan Kontinu ke Diskrit..……….. 4

Transformasi Lingkungan Diskrit ke Graf………... 5

Optimal Trajectory Vs Good Trajectory……… 6

Metode Formal……… 7

Bahasa Formal Linear Temporal Logic (LTL)... 8

Studi Terdahulu Yang Terkait... 10

BAHAN DAN METODE Metode Penelitian... 13

Bahan dan Alat Yang Digunakan... 15

Waktu dan Tempat Penelitian... 16

HASIL DAN PEMBAHASAN Deskripsi Informal Sistem………... 17

Pra-Spesifikasi Sistem………. 19

Spesifikasi Sistem……….. . 22

Prototipe Mobot………... 24

Verifikasi Sistem……… ………. 29

Rekomendasi Prototipe……….. . 44

SIMPULAN... 45

(10)

ix DAFTAR TABEL

Halaman

Tabel 2.1 Penjelasan Tuple MobotEnv……….. . 6

Tabel 2.2 Arti Operator Temporal………... 9

Tabel 4.2 Adjancy matriks w(si,sj)……….. 22

Tabel 4.3 Trajectory Yang Baik………. . 22

Tabel 4.4 Formula Proposisi Untuk Trajectory Yang Baik……. 23

Tabel 4.5 Perilaku Roda dan Pengaruh Arah Gerakan………… 24

Tabel 4.6 Penjelasan parameter fungsi SetSteering………. 25

Tabel 4.7 Karakteritik Kerangka dan Sensor………. . 26

Tabel 4.8 Karakteritik Kompas Robot dan Perbedaan Dengan Kompas Umumnya………. . 26

Tabel 4.9 Karakteristik trajectory t = 0,1,2……… . 29

DAFTAR GAMBAR Halaman Gambar 2.1 Abstraksi diskrit lingkungan mobot……… 4

Gambar 2.2 Directed Graph dan Adjancency-Matrix……… 5

Gambar 3.1 Kerangka pemikiran pembangunan Formalisasi Navigasi Mobile Robot……… 13

(11)

FORMALISASI NAVIGASI MOBILE ROBOT

(STUDI KASUS ROBOT KRCI FATETA IPB 2006)

DIDIT WIDIYANTO

(12)

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006), adalah karya saya sendiri dengan arahan Komisi Pembimbing dan belum pernah diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, M e i 2007

(13)

ABSTRAK

DIDIT WIDIYANTO. Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006). Dibimbing oleh PRAPTO TRI SUPRIYO dan WISNU ANANTA KUSUMA.

Penelitian tesis ini dilatarbelakangi oleh kebutuhan rancangan kendali navigasi robot pada robot KRCI (Kontes Robot Cerdas Indonesia) 2006 milik Team AERS (Agricultural Engineering Robotic Squad) dari Fakultas Teknik Pertanian (FATETA) Institut Pertanian Bogor (IPB) yang diselenggarakan di Balairung Universitas Indonesia di Depok pada bulan Juni 2006. Kendala team robot yang saat itu adalah tidak memiliki konsep yang baik dalam memformulasikan sistem navigasi robotnya. Robot yang dibuat saat itu hanya merespon untuk menghindari halangan (obstacle avoidance) tanpa memperhatikan tata ruang lingkungannya (environment map). Akibatnya sangat mungkin robot tidak dapat kembali ke tempat semula, atau terdapat ruangan yang belum dikunjungi, atau terdapat ruangan yang dikunjungi lebih dari 1 (satu) kali. Kelemahan ini disebabkan tidak adanya formulasi navigasi dalam disain robot tersebut.

Inspirasi penelitian ini adalah mencoba menemukan formulasi sistem navigasi robot yang akurat, dengan terlebih dahulu mendeskripsikan sistem secara informal, merumuskan spesifikasi sistem secara formal dengan menggunakan bahasa spesifikasi Linear Temporal Logic (LTL), melakukan verifikasi sistem dengan menggunakan perangkat lunak pembanguan prototipe MOBOTSIM Versi 1.0.03, dan akhirnya menghasilkan sebuah prototipe sistem navigasi mobile robot yang dapat direkomendasikan untuk dipergunakan pada KRCI 2007 atau sesudahnya.

Akhirnya hasil penelitian ini diharapkan dapat membuktikan bahwa melalui eksperimen pada prototipe, bahasa spesifikasi formal LTL dapat digunakan untuk merumuskan sistem navigasi mobile robot pada studi kasus KRCI 2006 dengan baik.

(14)

© Hak Cipta milik Institut Pertanian Bogor, tahun 2007

Hak cipta dilindungi

(15)

FORMALISASI NAVIGASI MOBILE ROBOT

(STUDI KASUS ROBOT KRCI FATETA IPB 2006 )

DIDIT WIDIYANTO

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Ilmu Komputer

(16)

Nama : Didit Widiyanto N I M : G651040024

Disetujui

Komisi Pembimbing

Drs. Prapto Tri Supriyo, M.Kom. Wisnu Ananta Kusuma, S.T, M.T.

Ketua Anggota

Diketahui

Ketua Program Studi Ilmu Komputer Dekan Sekolah Pascasarjana

Dr. Sugi Guritman Prof. Dr. Ir. Khairil A. Notodiputro, MS.

(17)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karuniaNya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2006 ini adalah Formalisasi Navigasi Mobile Robot (Studi Kasus Robot KRCI FATETA IPB 2006).

Terima kasih penulis ucapkan kepada Bapak Drs. Prapto Tri Supriyo, M.Kom dan Bapak Wisnu Ananta Kusuma, S.T, M.T selaku pembimbing. Di samping itu, penghargaan penulis sampaikan kepada para dosen pengajar FATETA IPB yang telah berkenan mengajak penulis untuk terlibat dalam tim KRCI 2006 dan KRCI 2007 sehingga penulis memiliki makalah penelitian tesis ini diantaranya yaitu Bapak Ir. Mohamad Solahudin, M.Si, Bapak Dr. Ir. Radite Praeka Agus Setiawan, M.Agr, Bapak Dr. Ir. Dewa Made Subrata, M.Agr, dan Bapak Dr. Ir. Suroso, M.Agr. Ungkapan terima kasih juga disampaikan kepada orang tua, adik, mbak Nita beserta seluruh keluarga di Cepu Jawa-Tengah atas segala doa dan perhatiannya.

Semoga karya ilmiah ini bermanfaat.

Bogor, M e i 2007

(18)

Penulis dilahirkan di Semarang pada tanggal 14 Juli 1970 dari ayah Widodo W.S dan ibu Niniek Sri Harsini. Penulis merupakan anak pertama dari 2 bersaudara.

Tahun 1989 penulis lulus dari SMA Negeri 42 Halim Perdanakusuma, pada tahun 1993 lulus Program Diploma-3 Manajemen Informatika dan Komputer di UPN “Veteran” Jakarta, dan pada tahun 1998, lulus Strata-1 Manajemen informatika di STMIK “Budi Luhur” Jakarta.

(19)

viii DAFTAR ISI

Halaman

DAFTAR TABEL ……….. ix

DAFTAR GAMBAR……….. ix

PENDAHULUAN……….. 1

TINJAUAN PUSTAKA Robotik……… 3

Transformasi Lingkungan Kontinu ke Diskrit..……….. 4

Transformasi Lingkungan Diskrit ke Graf………... 5

Optimal Trajectory Vs Good Trajectory……… 6

Metode Formal……… 7

Bahasa Formal Linear Temporal Logic (LTL)... 8

Studi Terdahulu Yang Terkait... 10

BAHAN DAN METODE Metode Penelitian... 13

Bahan dan Alat Yang Digunakan... 15

Waktu dan Tempat Penelitian... 16

HASIL DAN PEMBAHASAN Deskripsi Informal Sistem………... 17

Pra-Spesifikasi Sistem………. 19

Spesifikasi Sistem……….. . 22

Prototipe Mobot………... 24

Verifikasi Sistem……… ………. 29

Rekomendasi Prototipe……….. . 44

SIMPULAN... 45

(20)

ix DAFTAR TABEL

Halaman

Tabel 2.2 Arti Operator Temporal………... 9

Tabel 4.2 Adjancy matriks w(si,sj)……….. 22

Tabel 4.3 Trajectory Yang Baik………. . 22

Tabel 4.4 Formula Proposisi Untuk Trajectory Yang Baik……. 23

Tabel 4.5 Perilaku Roda dan Pengaruh Arah Gerakan………… 24

Tabel 4.6 Penjelasan parameter fungsi SetSteering………. 25

Tabel 4.7 Karakteritik Kerangka dan Sensor………. . 26

Tabel 4.8 Karakteritik Kompas Robot dan Perbedaan Dengan Kompas Umumnya………. . 26

Tabel 4.9 Karakteristik trajectory t = 0,1,2……… . 29

DAFTAR GAMBAR Halaman Gambar 2.1 Abstraksi diskrit lingkungan mobot……… 4

Gambar 2.2 Directed Graph dan Adjancency-Matrix……… 5

Gambar 3.1 Kerangka pemikiran pembangunan Formalisasi Navigasi Mobile Robot……… 13

(21)

1 PENDAHULUAN

1.1 Latar Belakang

Penelitian tesis ini dilatarbelakangi oleh kebutuhan rancangan kendali navigasi robot KRCI (Kontes Robot Cerdas Indonesia) 2006 milik tim AERS (Agricultural Engineering Robotic Squad) dari Fakultas Teknik Pertanian (FATETA) Institut Pertanian Bogor (IPB) yang diselenggarakan di Balairung Universitas Indonesia pada bulan Juni 2006.

Dalam kontes KRCI 2006 saat itu, panitia penyelenggara mensyaratkan robot start dari tempat yang telah ditentukan, dapat mengunjungi setiap ruangan tepat 1 (satu) kali, dan kembali ke tempat semula (DIRJEN DIKTI 2006). Robot yang dibuat oleh FATETA IPB saat itu hanya merespon untuk menghindari halangan (obstacle avoidance) tanpa memperhatikan peta lingkungannya (environment map). Akibatnya sangat mungkin robot tidak dapat kembali ke tempat semula, atau masih terdapat ruangan yang belum dikunjungi, atau terdapat ruangan yang dikunjungi lebih dari 1 (satu) kali. Kelemahan ini disebabkan karena tidak adanya formulasi navigasi dalam disain robot tersebut.

Di lain pihak metode formal (formal method) adalah teknik berdasarkan matematika untuk merepresentasikan spesifikasi sistem dengan bahasa spesifikasi tertentu (Supriyo 2003). Dalam metode formal banyak bahasa spesifikasi yang dapat digunakan. Salah satu bahasa spesifikasi tersebut adalah bahasa spesifikasi Linear Temporal Logic (LTL) yang dapat mengekspresikan keterurutan kondisi (conditional sequencing) sesuai urutan waktu (temporal ordering).

(22)

direkomendasikan untuk digunakan oleh FATETA IPB pada kontes robot KRCI mendatang.

1.2 T u j u a n

Tujuan penelitian ini adalah membangun suatu prototipe sistem navigasi mobile robot untuk KRCI yang telah dispesifikasikan dengan bahasa spesifikasi LTL dan diverifikasi pada simulasi program prototipe.

1.3 Ruang Lingkup

Spesifikasi sistem secara formal dilakukan dengan menggunakan bahasa spesifikasi LTL (Linear Temporal Logic).

Berdasarkan hasil spesifikasi sistem, verifikasi sistem dilakukan pada prototipe dengan menggunakan perangkat lunak MOBOTSIM Versi 1.0.03.

Sistem dikembangkan sampai pada prototipe sistem yang telah diverifikasi kebenarannya.

1.4 Manfaat Penelitian

(23)

2 TINJAUAN PUSTAKA

2.1 Robotik

Robot is a software-controllable mechanical device that uses

sensors to guide one or more end-effectors through programmed motions

in a workspace inorder to manipulate physical objects (Schilling J Robert

2000), yang artinya “Robot adalah perangkat mekanik yang dapat

dikendalikan oleh perangkat lunak yang menggunakan sensor untuk

memandu satu atau lebih efektor melalui gerakan terprogram dalam suatu

ruang kerja dalam hal untuk manipulasi obyek fisik.”

Terdapat 2 (dua) kendali robot yaitu high-level controller dan

low-level controler (Shanahan & Witkowski 2000). Low level control

digunakan untuk mendefinisikan aksi primitif dan mengkomunikasikan

status sensor kepada high level controller (Shanahan & Witkowski 2000).

Dalam high-level planning, terdapat 2 (dua) pendekatan yaitu

Robotic-Level Languages, dan Task- Level Languages (Fu 1987). Robotic level

languages memandang rangkaian task sebagai rangkaian gerakan robot,

dan setiap statement program secara kasar berkaitan dengan aksi robot.

Task level languages memandang rangkaian task sebagai rangkaian

positional goal dari obyek lebih lanjut (Fu 1987).

Kendali navigasi robot berada pada high-level controller. Kendali

robot high-level digunakan untuk mendefinisikan task (task planner)

berdasarkan sensor yang ada, menghasilkan trayek robot (robot

trajectory), dan aksi atau pergerakan robot (robot motion) dari suatu

tempat ke tempat lain.

Mobile robot atau mobot adalah robot yang memiliki mekanisme

penggerak berupa roda (wheel) atau kaki (leg), untuk dapat berpindah

(24)

2.2 Transformasi Lingkungan Kontinu ke Diskit

Lingkungan mobot adalah bentuk lingkungan kontinu, sedangkan

sistem navigasi yang dispesifikasikan dalam bahasa formal adalah diskrit.

Untuk itu perlu transformasi lingkungan kontinu ke bentuk diskrit yang

disebut sebagai abstraksi diskrit lingkungan mobot (Fainekos 2005a).

Transformasi lingkungan kontinu ke diskrit dilakukan dengan

rectangulasi (pembentukan ruang maya segiempat sebagai representasi

status atau daerah atau area yang dibuat berdasarkan kesamaan ciri letak

atau posisi penghalang) yang diterapkan pada hallway lingkungan mobot

KRCI 2006. Tujuan rectangulasi pada hallway agar gerakan robot dalam

hallway memiliki kepastian posisi dan arah, sehingga mengeliminasi

kesalahan interpretasi posisi mobot terhadap lingkungannya. Gambar 2.1

di bawah ini merupakan gambar hasil abstraksi diskrit lingkungan mobot

dalam KRCI 2006 lalu.

(25)

5

2.3 Transformasi Lingkungan Diskrit ke Graf (graph)

Graf (graph) adalah struktur data yang memiliki struktur G =

{V,E} (Cormen 1990). Di mana struktur tersebut adalah :

V : Himpunan verteks (vertice) yang terdapat dalam graf G

E : Himpunan tepi (edges) yang terdapat dalam graf G

Terdapat 2 (dua) bentuk struktur data untuk merepresentasikan graf

yaitu sebagai adjacency-list atau adjacency-matrix (Cormen 1990).

Untuk menyederhanakan model, maka dalam penelitian ini menggunakan

struktur data adjacency-matrix.

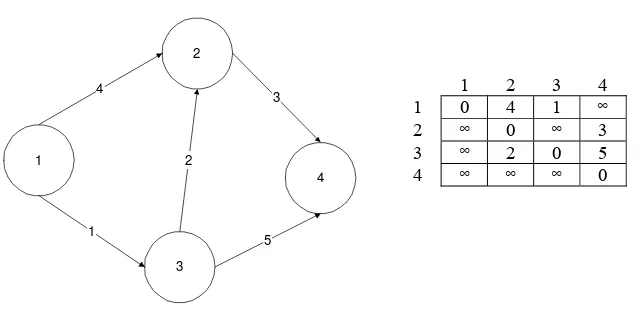
Dalam penelitian ini digunakan graf berarah (directed graph) untuk

transformasi abstraksi diskrit dengan :

V : Verteks sebagai representasi suatu ruang nyata maupun ruang

maya segiempat dalam lingkungan mobot.

E : Tepi berarah (directed edges) berupa anak panah sebagai

representasi suatu jalur atau jalan mobot dari suatu ruang yang

satu ke ruang yang lain.

Sebagai ilustrasi graf berarah secara umum terdapat dalam Gambar

2.2 di bawah ini.

1

3

4 2

2

5 3

1

4 1 2 3 4

1 0 4 1 ∞

2 ∞ 0 ∞ 3

3 ∞ 2 0 5

4 ∞ ∞ ∞ 0

(26)

Dalam konsep graf berarah secara umum adjacency-matrix berisi

bobot tepi. Adjacency-matrix dalam penelitian ini menyatakan jumlah hop

minimal atau jumlah minimal ruang yang harus dilalui untuk menuju ke

suatu ruang tujuan. Sebagai contoh dalam Gambar 2.1 untuk menuju

ruang s14 dari s0 minimal terdapat 4 hop yaitu s8, s7, s6, dan s14. Akhirnya

dalam penelitian ini graf dimodelkan ke dalam suatu bentuk tuple

Mobotenv = (S, I, F, T, G, P) yang penjelasannya terdapat dalam Tabel

2.1.

Tabel 2.1 Penjelasan Tuple Mobotenv Variabel Keterangan

S Himpunan seluruh status (state) di mana berlaku siЄ S.

I Himpunan status awal (initial state) di mana berlaku I C S.

F Status akhir (finish state) di mana berlaku F C S.

T Himpunan trajectory yang baik (good trajectory) di mana berlaku tiЄ T dan i = 0,1,2, …

ti ditentukan melalui penelusuran (walk) secara heuristik. G Himpunan status tujuan (goal) di mana berlaku G C S dan si

Є G jika dan hanya jika maxvisited(si) = 1, dan bila ¬(siЄ G)

maka maxvisited(si) ≥ 1. Fungsi Maxvisited(.)

mengembalikan nilai yang menyatakan jumlah maksimal status tersebut boleh dikunjungi.

P Himpunan fungsi proposisi di mana berlaku : p(t,s) Є P dan p(t,s) adalah fungsi p : T,G Æ {┬, ┴}, atau dengan kata lain fungsi yang memetakkan T dan G ke suatu nilai logika ┬ (true) atau ┴ (false) dalam himpunan nilai logika, di mana t

Є T dan s Є G.

2.4 Optimal Trajectory vs Good Trajectory

Trajectory mobot adalah representasi rangkaian Hamilton

(Hamilton circuit) dalam graf, artinya suatu siklus (cycle) dalam graf yang

dimulai dari suatu verteks awal melakukan kunjungan ke setiap verteks

(dalam kasus penelitian ini disebut status atau state) tepat 1 (satu) kali dan

kembali ke verteks asal (Siang 2002).

Menentukan trajectory optimal merupakan masalah yang sama

dengan Travelling Salesman Problem (TSP) yaitu menemukan rangkaian

Hamilton (Hamilton circuit) yang memiliki total bobot minimum pada

(27)

7

Hamilton yang ada dalam graf tersebut adalah sebanyak permutasi dari

verteks-verteks pembentuk rangkaian Hamilton, kecuali untuk verteks

pertama dan terakhir.

Dapat disimpulkan bahwa untuk menemukan trajectory optimal

membutuhkan waktu komputasi yang lama, karena harus mencoba seluruh

kemungkinan (permutasi) yang ada dalam graf tersebut (Utdirartatmo

1992). Hal ini dapat ditemukan dengan pendekatan heuristik, yaitu

pendekatan yang tidak menjamin optimalitas, tetapi berdasarkan aturan

yang baik untuk mencari solusi yang baik (Taha 1987).

Dua manfaat dalam pendekatan heuristik (Taha 1987) yaitu :

• Pendekatan heuristik memerlukan komputasi lebih sedikit

dibandingkan dengan algorithma pasti (exact algorithm).

Untuk itu pada model dengan skala besar, pendekatan heuristik

dapat mempercepat proses untuk mencari solusi yang

diharapkan optimal.

• Pendekatan heuristik akan menghasilkan solusi yang baik

(good solution) terhadap masalah, walaupun tidak menjamin

menemukan solusi optimal.

Kembali pada kasus graf setelah terbentuk sesuai dengan tuple di

atas, trajectory yang baik ditentukan melalui pendekatan heuristik.

Mulai dari status awal (s0), pendekatan heuristik dilakukan dengan

mengunjungi status tujuan (si Є G) terdekat yang terhubung (adjacency)

dengan status sekarang (present state) dan belum dikunjungi (unvisited),

demikian seterusnya berturut-turut.

2.5 Metode Formal

Dalam buku Software Engineering Practitional Approach 3-rd

Edition (Pressman 1992), definisi metode formal menurut Enclycopedia of

Software Engineering adalah sebagai berikut :

Metode formal yang digunakan di dalam pengembangan sistem

(28)

menggambarkan properti system. Metode formal semacam itu

memberikan kerangka kerja di mana manusia dapat menentukan,

mengembangkan dan memverifikasi sistem secara matematis ketimbang

secara ad hoc

Suatu metode dikatakan formal bila metode itu memiliki dasar

matematis yang secara khusus diberikan oleh suatu bahasa spesifikasi

formal. Basis ini memberikan alat yang dengan teliti menentukan

pemikiran seperti konsistensi dan kelengkapan, dan yang lebih penting,

spesifikasi, implementasi, dan kebenaran.

Metode formal dengan pendekatan ke arah matematis memiliki

daya tarik bagi beberapa perekayasa perangkat lunak, salah satunya adalah

ambiguitas dapat dikurangi. Berkurangnya ambiguitas dilakukan dengan

mendefinisikan sintaks formal pada bahasa spesifikasi yang

memungkinkan persyaratan atau desain diinterpretasikan hanya dengan

satu cara. Konsistensi dilakukan dengan cara suatu fakta yang dinyatakan

di dalam suatu tempat dalam suatu spesifikasi, tidak boleh

dikontradiksikan dengan yang ada di tempat lain. Artinya terdapat suatu

fakta dapat dipetakan (dengan aturan inferensi) ke dalam statement

selanjutnya dalam spesifikasi tersebut.

2.6 Bahasa Formal Linear Temporal Logic (LTL)

Dalam metode formal banyak bahasa formal yang dapat digunakan

sebagai bahasa spesifikasi antara lain seperti CSP, LARCH, VDM, dan

Spesifikasi-Z (Pressman 1992). Dalam penelitian ini digunakan bahasa

spesifikasi formal Linear Temporal Logic (LTL) (Fainekos 2005a), karena

kemampuannya mendefinisikan keterurutan status dan aksi secara linear.

Sejarah Temporal Logic awalnya dirancang oleh philosopher untuk

mempelajari bagaimana waktu digunakan dalam natural language. Lalu

dibawa ke dalam computer science (ilmu komputer) oleh Pnueli dalam 19th

Anual Symposium on Fondation on Computer Science dengan tulisannya

(29)

9

LTL terdiri dari logika proposisi standar dengan penambahan

operator temporal seperti eventually (◊), always (฀), next (O), dan until (U) (Fainekos 2005a). Arti operator temporal dijelaskan dalam Tabel 2.2

di bawah ini :

Tabel 2.2 : Arti Operator Temporal Operator

Temporal

Contoh Arti

next (O) Op Selanjutnya : Pada satuan waktu berikutnya akan terjadi proposisi p bernilai benar

always (฀) ฀p Selalu : Untuk saat ini dan di waktu mendatang proposisi p selalu bernilai benar

eventually (◊) ◊p Kadang-kadang atau pada akhirnya : Pada akhirnya di waktu mendatang entah kapan kepastian waktunya, akan terjadi proposisi p bernilai benar

until (U) pUq Hingga : Untuk saat ini dan di waktu mendatang proposisi p bernilai benar hingga ditemukan proposisi q bernilai benar

Bila Πi maupun oi adalah proposisi yang bernilai benar jika mobot

berada pada status i, maka beberapa contoh ekspresi penting dalam

navigasi robotika adalah :

• Mencapai tujuan sambil menghindari penghalang (reach

goals while avoiding obstacles) diekspresikan dengan

formula ¬(o1 v o2 v ... v on) U Π, yang artinya untuk terjadi Π akan bernilai benar, dan hingga Π tercapai, kita harus

menghindari penghalang oi di mana i = 1,2,...,n.

• Keterurutan (sequencing) diekspresikan dengan formula

◊(Π1 ^ ◊(Π2 ^ ◊Π3)) yang artinya mengunjungi secara

berturut-turut Π1, Π2, dan Π3.

• Pelingkupan (coverage) diekspresikan dengan formula ◊Π1

^ ◊Π2 ^ ◊Π3 ^ ... ^ ◊Πn yang artinya mensyaratkan robot

untuk mencapai semua wilayah Πi di mana i = 1,2,...,n

(30)

Bü_chi _Automata_{adalah pengembangan lanjut dari teori otomata}

dan sering digunakan sebagai model checking atau verifikasi spesifikasi

sistem dalam bahasa spesifikasi LTL. Bila dalam teori otomata memiliki

tuple A = (Q,Σ,δ,I,F) dengan F adalah himpunan status yang dapat

diterima, maka Bü_chi_Automata_{memiliki tuple A = (Q,}Σ_,δ_{,I,FT) di mana :}

Q : Himpunan status

Σ : Finite Alphabet

δ : Relasi Transisi

I : Himpunan status awal (initial state)

FT : Superset dari himpunan status yang dapat diterima (acceptance state) di mana FT = (F1, F2, F3, ... Fk) dengan Fi = himpunan

status yang dapat diterima otomata Büchi.

Eksekusi p dapat diterima bila Inf(p) ∩ Fi≠ Ø untuk setiap 1 < i <

k, dimana Inf(p) adalah fungsi yang mengembalikan rangkaian urutan

status dari eksekusi p.

Sehingga dapat disimpulkan bahwa otomata Büchi dapat

mendefinisikan lebih dari satu acceptance state F.

2.7 Studi Terdahulu Yang Terkait

a. Navigasi Robot dengan Kalkulus Kejadian (Event Calculus).

Penelitian metode formal untuk navigasi robot yang

dilakukan oleh Shanahan (2000) menerapkan kalkulus kejadian

(Event Calculus). Konsep dasarnya menggunakan 2 buah program

utama yaitu untuk navigasi dan deskripsi peta (map). Pada

program navigasi diterapkan model komputasi untuk controller

(pengendali) yaitu berupa siklus sense-plan-action. Untuk

perencanaan (planning) dan pembacaan sensor (Sensor Data

Assimilation), Shanahan menggunakan teori pencekalan (abductive

theorem) untuk mewujudkan tugas pencekalan (abductive task)

dengan menerapkan kalkulus kejadian. Pada proses pencekalan

dari sensor data menghasilkan pengetahuan status (apakah pintu

ruangan robot terbuka atau tertutup) selama robot berada dalam

ruangan. Hasilnya adalah pengetahuan mengenai layout ruangan

(31)

11

b. Navigasi Robot dengan Linear Temporal Logic (LTL)

Penelitian navigasi robot dengan bahasa spesifikasi Linear

Temporal Logic (LTL) telah dilakukan oleh Fainekos, Hadas, dan

Pappas pada tahun 2005. Fainekos, Hadas, dan Pappas (2005)

dalam sebuah artikel jurnalnya yang berjudul “Temporal Logic

Motion Planning for Mobile Robots” mengungkapkan

pemanfaatan Linear Temporal Logic (LTL) pada formalisasi

motion planning untuk mobile robot.

Dalam penelitiannya Fainekos menggunakan dalam 3 (tiga)

langkah untuk menghasilkan robot trajectory yaitu: mendefinisikan

abstraksi diskrit pergerakan robot, melakukan verifikasi temporal

logic planning menggunakan model checking, dan melakukan

transformasi rencana diskrit ke dalam bentuk terapan lingkungan

kontinu (continuous implementations of discrete plan) (Fainekos

2005a).

Untuk abstraksi diskrit-nya Fainekos melakukan triangulasi

(pembentukan ruang maya segitiga sebagai representasi status)

ruang mobot, yang mana sisi setiap segitiga bersinggungan dengan

sisi segitiga lainnya. Selanjutnya dari abstraksi diskrit dibentuk

status diskrit dari status kontinu dengan menggunakan fungsi T : P

Æ Q di mana P adalah status ruang kontinu dan Q adalah status ruang diskrit. Selanjutnya temporal logic planning melakukan

plan mobot trajectory berupa rangkaian status yang harus dilalui.

Model checking atau sebagai verifikasi spesifikasi sistem secara

formal dilakukan dengan Bü_{chi Automata}_{yang memeriksa apakah}

trajectory tersebut acceptable untuk diimplementasikan dalam

ruang kontinu. Untuk implementasi ruang kontinu dari

perencanaan diskrit, Fainekos menerapkan invers dari fungsi T:

(32)

Sedangkan yang membedakan dalam penelitian ini, untuk

alasan kemudahan dan kesederhanaan adalah :

• Abstraksi diskrit dari ruang kontinu tidak dilakukan

triangulasi seperti dalam penelitian Fainekos, melainkan

rectangulasi (pembentukan ruang maya segiempat sebagai

representasi status) yang diterapkan pada hallway mobot

KRCI 2006.

• Verifikasi spesifikasi sistem tidak dilakukan dengan otomata Büchi melainkan dengan mengamati secara

langsung pada simulator mobile robot saat program

(33)

3

BAHAN DAN METODE

3.1 Metode Penelitian

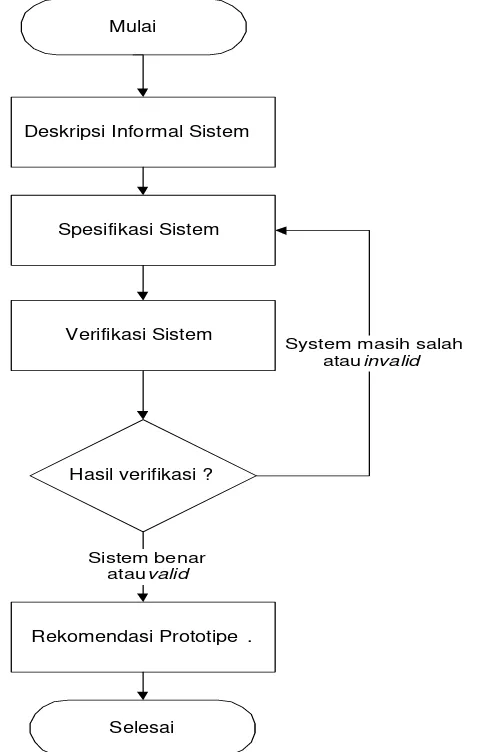
[image:33.612.201.442.303.679.2]

Dalam penelitian ini sistem terlebih dahulu dideskripsikan secara informal, selanjutnya spesifikasi sistem dibuat dengan bahasa spesifikasi Linear Temporal Logic (LTL), dan akhirnya dilaksanakan verifikasi sistem yang bertujuan untuk membuktikan kebenaran sistem (system correctness). Verifikasi sistem dilakukan melalui eksekusi prototipe yang dibuat dengan perangkat lunak MOBOTSIM Versi 1.0.03. Gambar 3.1 mengilustrasikan kerangka pemikiran dan dapat dijelaskan sebagai berikut:

Gambar 3.1 Kerangka pemikiran pembangunan Formalisasi Navigasi Mobile Robot. Mulai

Deskripsi Informal Sistem

Spesifikasi Sistem

Verifikasi Sistem

Hasil verifikasi ?

System masih salah atau invalid

Rekomendasi Prototipe .

Sistem benar atau valid

(34)

a. Deskripsi Informal Sistem.

Deskripsi informal sistem dibuat untuk memperoleh deskripsi umum sistem secara informal dengan bahasa alami (natural language) melalui akusisi pengetahuan berupa telaah sebagai berikut :

Telaah Pustaka

Telaah pustaka dilakukan terhadap pustaka yang berkaitan dengan konsep robotika, abstraksi diskrit lingkungan robot, bahasa spesifikasi LTL, dan pemrograman prototipe dengan menggunakan MOBOTSIM.

Telaah Persyaratan Sistem (system requirement) Navigasi

KRCI 2006

Telaah persyaratan sistem (system requirement) navigasi KRCI 2006 yang dimaksud adalah telaah peta lingkungan robot (map environment) dan persyaratan perilaku robot yang diharapkan dalam KRCI.

Telaah peta lingkungan robot (map environment) bertujuan mengidentifikasi navigasi pergerakan mobile robot dengan cara transformasi peta (map) lingkungan robot kedalam bentuk graf (graph).

Pembangunan Asumsi

Untuk menyederhanakan deskripsi sistem secara informal pembangunan asumsi dibuat seperlunya, dengan demikian akan memudahkan pula dalam menyusun spesifikasi sistem dengan bahasa formal.

b. Spesifikasi Sistem.

(35)

15

spesifikasi ini dipilih karena mampu mendeskripsikan keterurutan kondisi tujuan (conditional sequencing of goals) (Fainekos 2005b).

c. Verifikasi Sistem.

Berdasarkan spesifikasi sistem di atas, verifikasi sistem dilakukan dengan mengamati hasil eksekusi program prototipe. Bila hasil verifikasi sistem masih salah (invalid), maka perlu dikoreksi kembali spesifikasi sistem dan program prototipenya. Demikian seterusnya dilakukan hingga tercapai hasil verifikasi sistem yang benar (valid).

Adapun perangkat lunak pembangunan prototipe yang digunakan adalah MOBOTSIM Versi 1.0.03 dari Mobotsoft yang terdapat dalam situs www.mobotsoft.com dan diciptakan oleh Gonzalo Rondriquez Mir dengan bahasa pemrogramannya yang telah terintegrasi dalam MOBOTSIM adalah Sax Basic Versi 6.4.50/32 dari Polar Engineering. Perangkat lunak pembangunan prototipe ini dijalankan dengan menggunakan komputer dengan prosesor minimal setara Intel Pentium III, memori 128 Mbytes, Harddisk 10 Mbytes, dan sistem operasi minimal Microsoft Windows 98 (Tm).

d. Rekomendasi Prototipe.

Penelitian ini dilakukan hanya sampai pada pembangunan prototipe yang telah diverifikasi, untuk itu bila hasil verifikasi sudah benar (valid) maka penelitian berakhir, selanjutnya prototipe dapat direkomendasikan untuk diterapkan pada Robot KRCI FATETA IPB 2007 mendatang dan atau sesudahnya.

3.2 Bahan dan Alat yang Digunakan

(36)

menyatakan bahwa robot harus dapat mengunjungi setiap ruangan tepat 1 (satu) kali.

Sedangkan alat yang digunakan adalah perangkat lunak MOBOTSIM Versi 1.0.03 dari Mobotsoft yang terdapat dalam situs www.mobotsoft.com dan diciptakan oleh Gonzalo Rondriquez Mir dengan bahasa pemrogramannya yang telah terintegrasi dalam MOBOTSIM adalah Sax Basic Versi 6.4.50/32 dari Polar Engineering. Perangkat lunak ini akan digunakan dalam metode penelitian pada tahap verifikasi prototipe mobile robot. Selain itu digunakan pula komputer dengan prosesor minimal setara Intel Pentium III, memori 128 Mbytes, Harddisk 10 Mbytes, dan sistem operasi minimal Microsoft Windows 98 (Tm) sebagai alat untuk dapat menjalankan perangkat lunak MOBOTSIM tersebut di atas.

3.3 Waktu dan Tempat Penelitian

(37)

4

HASIL DAN PEMBAHASAN

4.1 Deskripsi Informal Sistem

Telah dijelaskan dalam Bab 2 sebelumnya mobile robot atau mobot

adalah robot yang memiliki mekanisme penggerak (actuators) berupa roda (wheel) atau kaki (leg), untuk dapat berpindah tempat dari suatu tempat ke tempat yang lain. Dalam beroperasi mobot sering harus bergerak dalam

rangka menjelajahi lingkungannya.

Navigasi mobot adalah sistem yang dibuat untuk memandu mobot

agar tidak tersesat ketika menjelajahi lingkungannya. Melalui sistem ini

mobot dapat mengetahui posisi kedudukan pada peta lingkungannya serta

arah hadap mobot saat itu (sudut azimuth atau bearing) berdasarkan arah mata angin. Deskripsi informal sistem navigasi mobot dibuat berdasarkan

hal-hal sebagai berikut :

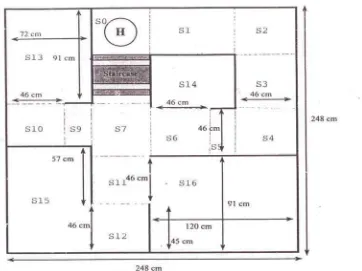
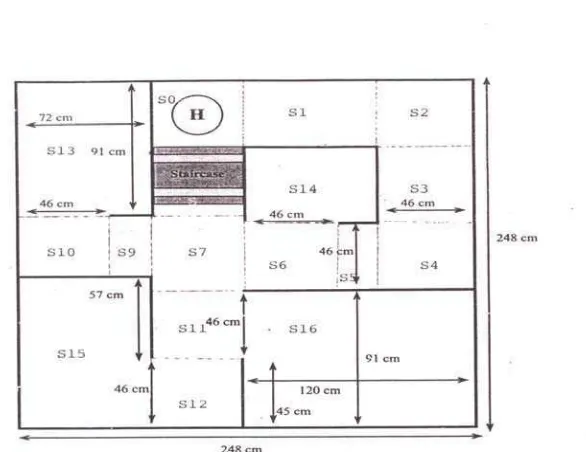
a. Peta Lingkungan Mobot

Peta lingkungan mobot yang digunakan dalam penelitian

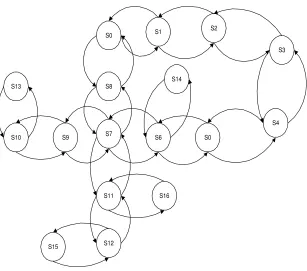
[image:37.612.187.480.452.678.2]

ini adalah peta lingkungan (environment map) mobot dalam KRCI 2006 sebagaimana digambarkan dalam Gambar 4.1.

(38)

Peta lingkungan di atas diasumsikan membentang dari barat

hingga ke timur, artinya atas adalah utara (arah 90), kanan adalah

timur (arah 0), bawah adalah selatan (arah 270), dan kiri adalah

barat (arah 180). Derajat arah mata angin ini agak berbeda,

disesuaikan dengan yang berlaku dalam program navigasi, dapat

dilihat penjelasannya nanti pada bagian deskripsi kompas program

navigasi.

b. Posisi Start dan Finish Mobot

Sesuai dengan persyaratan KRCI 2006, bahwa mobot harus

dapat start maupun finish di posisi s0, sedangkan persyaratan KRCI

2005 yang mungkin akan diberlakukan kembali pada KRCI

mendatang, mobot harus dapat start maupun finish di posisi s4.

Untuk itu dalam penelitian diasumsikan start dan finish di s0

maupun s4.

c. Tujuan (Goal) yang Ingin dicapai

KRCI mensyaratkan mobot start dari tempat yang telah ditentukan (misalnya s0), mengunjungi (visiting) ke-empat ruangan

(s13, s14, s15, dan s16) di mana setiap ruangan dikunjungi tepat 1

(satu) kali, dan kembali ke tempat semula (s0).

d. Komponen Pendukung Navigasi

KRCI pada dasarnya tidak membatasi komponen yang

digunakan dalam mobot, khususnya komponen pendukung

navigasi. Berdasarkan komponen yang umumnya terpasang pada

mobot KRCI, terdapat 2 komponen penting pendukung navigasi

yaitu :

Sensor Penghalang

(39)

19

dihindari oleh mobot (obstacle avoidance). Sensor dapat berupa sensor proximity (sensor yang hanya mampu mendeteksi keberadaan penghalang tanpa mampu

mendeteksi jarak mobot ke penghalang) maupun sensor

range (sensor yang mampu mendeteksi jarak mobot ke penghalang).

Selain bertujuan untuk menghindari penghalang,

beberapa sensor ini secara bersama-sama dapat digunakan

pula untuk menghasilkan ciri lingkungan robot sehingga

dapat dilakukan abstraksi posisi mobot pada peta

lingkungannya. Contoh untuk perempatan s7 akan memiliki

ciri sebelah kiri, kanan, dan depan tidak ada penghalang.

Sensor Posisi Mobot

Sensor posisi mobot yang dimaksud di sini adalah

kompas. Melalui kompas mobot dapat mengetahui arah

hadapnya (berupa sudut azimuth atau bearing) berdasarkan arah mata angin.

4.2 Pra-Spesifikasi Sistem

Peta lingkungan mobotKRCI 2006 sebagaimana tergambar dalam

Gambar 4.1 merupakan bentuk abstraksi kontinu, sedangkan spesifikasi

sistem secara formal dilakukan pada trajectory yang baik dari abstraksi diskrit, untuk itu pra-spesifikasi sistem bertujuan melakukan transformasi

lingkungan mobot kontinu ke diskrit, dan menentukan trajectory yang baik.

a. Transformasi Lingkungan Kontinu ke Diskrit

Sebagaimana telah diuraikan dalam bab 2, transformasi

lingkungan kontinu ke diskret dilakukan dengan cara

(40)

map dibagi menjadi s0, s1, s2, …, s12. Sedangkan untuk s13, s14, …,

s16 adalah status tujuan (ruang yang harus dikunjungi).

b. Transformasi Lingkungan Diskrit ke Graf

Transformasi lingkungan diskrit ke graf dilakukan dengan

[image:40.612.235.512.265.603.2]

membuat model graf dalam bentuk tuple Mobotenv = (S, I, F, T, G, P) di mana penjelasan tuple diuraikan dalam Tabel 4.1 dan sedangkan graf diilustrasikan dalam Gambar 4.2

Tabel 4.1 Penjelasan Tuple Mobotenv Variabel Keterangan

S Himpunan seluruh status di mana berlaku siЄ S jika dan

hanya jika 0 < i < 16

I Himpunan status awal (Initial state) di mana berlaku I = {s0, s4} dan I C S. Terdapat pula fungsi i(t) adalah

fungsi i : T Æ I atau dengan kata lain fungsi i memetakkan trajectory t ke status awal si Є I

s0 jika t Є {0,1}

i(t) =

s4 jika t Є {2}

F Status akhir (Finish state) di mana berlaku F = {s0, s4} dan

F C S. Terdapat pula fungsi f(t) adalah fungsi f : T Æ F atau dengan kata lain fungsi f memetakkan trajectory t ke status akhir si Є F

s0 jika t Є {0,1}

f(t) =

s4 jika t Є {2}

T Himpunan trajectory yang baik di mana berlaku tiЄ T dan

i = 0,1,2, …ti ditentukan melalui penelusuran (walk) secara

heuristik.

G Himpunan status tujuan (goal) di mana berlaku G C S dan siЄ G jika dan hanya jika maxvisited(si) = 1, dan bila ~(si Є G) maka maxvisited(si) = ∞ (tak terhingga). Dalam

kasus ini G = {s13, s14, s15, s16}

(41)

21

c. Menentukan Trajectory yang Baik

Untuk menentukan trajectory yang baik dilakukan dalam 2 (dua) tahap sebagai berikut :

Pembobotan Edge Berdasarkan Matriks w(si,sj)

Pembobotan edge berdasarkan matriks w(si,sj)

dilakukan dengan membuat tabel atau matriks 2 dimensi

dengan ukuran ordo 6 x 6. Angka 6 ditentukan dari jumlah

status tujuan yaitu ada 4 status tujuan dan 2 initial state

(finish state adalah sama dengan initial state). Pada setiap sel matriks tersebut berisi nilai bobot terkecil dalam jumlah

hop (ruang yang dilompati) dari si ke sj. Tabel 4.2

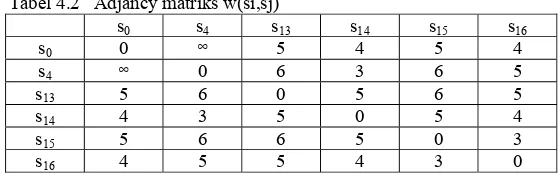
menjelaskan bobot edge dalam adjancy matrix.

S0

S8

S7 S9

S10 S13

S3 S2

S1

S4

S6 S0 S14

S11

S12

S16

[image:41.612.167.474.97.368.2]

S15

(42)

[image:42.612.230.510.84.171.2]

Tabel 4.2 Adjancy matriks w(si,sj)

s0 s4 s13 s14 s15 s16

s0 0 ∞ 5 4 5 4

s4 ∞ 0 6 3 6 5

s13 5 6 0 5 6 5

s14 4 3 5 0 5 4

s15 5 6 6 5 0 3

s16 4 5 5 4 3 0

Pendekatan Heuristik Untuk Menentukan Trajectory yang Baik

Telah dijelaskan dalam bab 2 bahwa melalui

pendekatan heuristik dapat dihasilkan (good trajectory)

trajectory yang baik dengan cara memberi nilai sekecil mungkin pada matriks yang merepresentasikan jarak

terdekat atau rute terpendek antara 2 status tujuan (misal si

dan sj dimana si dan sj Є G) yang belum pernah dikunjungi

(unvisited) dan terhubung (adjacent) dengan status sekarang (current state). Dengan demikian diharapkan merupakan trajectory optimal, dan akan lebih cepat daripada mencoba seluruh kemungkinan secara permutasi.

Akhirnya trajectory yang baik dapat yang diperoleh dapat dilihat pada Tabel 4.3.

Tabel 4.3 Trajectory Yang Baik Nomor

Trajectory

( t )

Trajectory Nilai Path (Dihitung dengan w(si,sj))

0 s0-s14-s16-s15-s13-s0 4+4+3+6+5 = 22

1 s0-s16-s15-s14-s13-s0 4+3+5+5+5 = 22

2 s4-s14-s16-s15-s13-s4 3+4+3+6+6 = 22

4.3 Spesifikasi Sistem

Spesifikasi sistem dilakukan dalam 2 (dua) tahap yaitu spesifikasi

fungsi proposisi dan spesifikasi formula proposisinya. Hasil akhir dari

spesifikasi sistem adalah formula proposisi untuk setiap trajectory t, yang merepresentasikan pergerakan robot. Berikut ini adalah uraian setiap

[image:42.612.234.514.480.555.2]

(43)

23

a. Fungsi Proposisi p(t,s)

Bila {┬, ┴} adalah himpunan nilai logika yang memiliki

keanggotaan ┬ (true) dan ┴ (false), maka fungsi proposisi p(t,s) dengan t Є T dan s Є G adalah fungsi p : T,G Æ {┬, ┴} atau dengan kata lain fungsi yang memetakkan T,G ke suatu nilai logika

┬ (true) atau ┴ (false) dalam himpunan nilai logika tersebut. Fungsi proposisi ini merepresentasikan pergerakan robot ke status

si dari sembarang status sj yang adjacent dengan si pada trajectory

t, dan akan menghasilkan nilai logika ┬ bila berhasil atau ┴ bila

gagal.

b. Formula Proposisi Ø.

Hasil akhir dari spesifikasi model formal ini adalah formula

proposisi. Formula proposisi dalam penelitian ini berupa suatu

persamaan matematika yang disusun dari beberapa fungsi proposisi

dengan menggunakan operator logika.

Agar pergerakan robot sesuai dengan trajectory yang optimal, maka formula proposisi untuk setiap trajectory disusun dalam bentuk sequencing atau keterurutan sebagaimana telah dijelaskan dalam Bab 2. Untuk itu Tabel 4.4 mengilustrasikan

[image:43.612.198.511.519.610.2]

fungsi proposisi untuk setiap trajectory t adalah sebagai berikut :

Tabel 4.4 Formula Proposisi Untuk Trajectory Yang Baik

Trajectory

( t )

Trajectory Formula Proposisi Ø

0 s0-s14-s16-s15-s13-s0 Ø = ◊(p(0,s14) ^ ◊(p(0,s16) ^ ◊(p(0,s15) ^ ◊(p(0,s13) ^ ◊p(0,s0)))))

4.4 Prototipe Mobot

Verifikasi sistem dilakukan untuk memeriksa kebenaran

(44)

langsung pada prototipenya. Untuk itu sebelumnya perlu dilakukan

disain prototipe mobot yang merupakan pra-kegiatan sebelum

melaksanakan verifikasi sistem.

Prototipe mobot diwujudkan dalam pemrograman simulator

dengan menggunakan MOBOTSIM versi 1.1.03. Sebelum memprogram

dalam simulator, perlu ditetapkan terlebih dahulu property prototipe melalui disain aktuator, kerangka dan penempatan sensor, serta kompas.

Akhirnya sebagai inti dari prototipe ditetapkan pula disain fungsi

proposisi, dan formula proposisi dalam perangkat lunak simulasi ini yang

merupakan implementasi dari fungsi proposisi dan formula proposisi

dalam model formal. Untuk lebih jelasnya, dapat dijelaskan sebagai

berikut :

a. Disain Aktuator

Aktuator adalah bagian yang dikendalikan dalam sistem

kendali (system control). Atau dapat dikatakan aktuator merupakan keluaran dari sistem kendali. Mobot ini didisain

untuk menggunakan sistem kemudi (steering system) diferensial. Untuk itu aktuator adalah berupa perilaku roda kiri dan kanan serta

pengaruhnya terhadap arah gerakan. Untuk lebih jelasnya

diuraikan dalam Tabel 4.5 di bawah ini.

Tabel 4.5 Perilaku Roda dan Pengaruh Arah Gerakan

Roda Kiri Roda Kanan Efek (Arah Gerakan)

Clockwise Clockwise Maju

Clockwise Counterclockwise Kiri

Counterclockwise Clockwise Kanan

Counterclockwise Counterclockwise Mundur

Disain aktuator berkaitan erat dengan disain kinematik

yaitu disain gerakan mobot dengan mengabaikan pengaruh

dinamikanya atau pengaruh gaya-gaya yang bekerja pada sistem

tersebut. Kelebihan perangkat lunak MOBOTSIM ini adalah

terdapat sarana disain kinematik dengan cara mengendalikan

keluaran langsung pada gerakan robotnya dan mengabaikan

gerakan roda mobot. Hal ini dapat dilakukan melalui penggunaan

(45)

25

RotationalSpeed). Untuk kesederhanaan, dalam penelitian ini menggunakan fungsi SetSteering dengan harapan dapat dipelajari pengaruhnya secara langsung pada gerakannya. Sebagai ilustrasi

[image:45.612.185.510.174.285.2]

parameter fungsi SetSteering terdapat dalam Tabel 4.6 yaitu :

Tabel 4.6 Penjelasan parameter fungsi SetSteering

Parameter Penjelasan

mobot: index or name of mobot to set the steering

Nomor indeks mobole robot

CenterSpeed: displacement speed at the center point of the mobot in m/sec

Kecepatan mobile robot terhadap titik pusat robot (karena bentuk robot adalah lingkaran) dalam mater per detik

RotaionalSpeed: steering rate in degrees/sec

Kecepatan putar atau belokan (angular) dalam derajat per detik

b. Disain Kerangka dan Sensor

Disain kerangka tampak atas robot ini berbentuk lingkaran,

dan disain ini mempengaruhi pula penempatan sensor yang optimal,

sehingga abstraksi lingkungan robot berdasarkan penerimaan sensor

tersebut akan optimal pula.

Dari cara abstraksinya terdapat 2 macam sensor robot yaitu

sensor proximity adalah sensor yang hanya mendeteksi penghalang (obstacle) tanpa mengetahui jaraknya, dan sensor jarak (range) adalah sensor yang dapat mendeteksi penghalang serta jarak antara

sensor dan penghalang tersebut. Program simulasi ini telah

menyediakan sensor simulasi jarak, sehingga abstraksi lingkungan

robot dapat lebih baik lagi. Tabel 4.7 berikut ini menjelaskan

bagaimana karakteristik bentuk kerangka dan sensornya.

Tabel 4.7 Karakteritik Kerangka dan Sensor

Karakteristik Keterangan Bentuk Kerangka Bentuk kerangka berupa lingkaran (tampak atas)

Jenis sensor Berupa sensor pengukur jarak (range sensor) Jumlah sensor 7 buah (sensor0, sensor1, …, sensor6)

Penjelasan penempatan posisi sensor

s0 adalah sensor kanan, berturut-turut berlawanan arah

jarum jam, s3 adalah sensor depan dan s6 adalah sensor

kiri

Sudut antara 2 sensor 30o _{(30 derajat)}

[image:45.612.192.514.576.688.2]

(46)

c. Kompas Robot

Dalam program simulasi ini terdapat kompas robot untuk

mengetahui arah gerakan robot. Sesuai dengan kompas pada

umumnya, derajat arah adalah dalam modulo 360 derajat. Artinya

untuk satu putaran 360 derajat, sudut arah akan kembali ke 0.

Sedangkan perbedaannya kalau pada kompas umumnya memiliki

derajat arah yang mengacu pada utara = 0 derajat, maka kompas ini

justru mengacu pada arah timur = 0 derajat. Untuk lebih jelasnya

karakteristik kompas robot ini dan perbedaannya dengan kompas

[image:46.612.190.513.305.460.2]

umumnya diuraikan dalam Tabel 4.8 berikut ini.

Tabel 4.8 Karakteritik Kompas Robot dan Perbedaan Dengan Kompas Umumnya Keterangan

Karakteristik

Kompas Umumnya Kompas Robot Simulasi

Derajat Arah Utara : 0 Timur : 90 Selatan : 180 Barat : 270

Utara : 90 Timur : 0 Selatan : 270 Barat : 180

Putaran Dilihat dari derajat arah

di atas maka untuk putaran (belok) ke kiri akan memiliki sudut putar negatif dan sebaliknya untuk putaran (belok) ke kanan memiliki sudut putar positif

Dilihat dari derajat arah di atas maka untuk putaran (belok) ke kiri akan memiliki sudut putar positif dan sebaliknya untuk putaran (belok) ke kanan memiliki sudut putar negatif

d. Disain Proses

Proses perilaku pergerakan robot berdasarkan navigasi yang

telah ditetapkan dalam spesifikasi sistem formal dilakukan dengan

cara mengeksekusi formula proposisinya, yang selanjutnya akan

mengeksekusi fungsi proposisi yang terlibat dalam formula proposisi

tersebut.

Disain Fungsi Proposisi

Dalam spesifikasi sistem formal telah jelaskan

bahwa fungsi proposisi memiliki bentuk umum p(t,s) di

(47)

27

gerakan robot pada trajectory t ke status s dari sembarang status yang terhubung dengan status s, dan mengembalikan

nilai logika true bila berhasil mengunjungi status s dan akan mengembalikan nilai logika false bila gagal.

Bentuk fungsi proposisi yang mengakomodasi

trajectory t = 0,1,2 dengan berbagai status tujuan untuk setiap trajectory t dalam bahasa pemrograman SaxBasic adalah sebagai berikut :

Function P(t,s)

' Fungsi proposisi yang memetakkan trajectory

dan state goal ke nilai proposisi true atau false

' Fungsi akan true bila trajectory reachcable

(berhasil dieksekusi)

'Debug.Print "Starting P(";t;",";s;")" 'Stop

If t = 0 Then

' Trajectory 0 --> s0-s14-s16-s15-s13-s0 If s=14 Then

ElseIf s=16 Then

ElseIf s=15 Then

ElseIf s=13 Then

ElseIf s=0 Then

End If

P=True

ElseIf t = 1 Then

ElseIf s=15 Then

ElseIf s=14 Then

ElseIf s=13 Then

ElseIf s=0 Then

End If

P=True

ElseIf t = 2 Then

(48)

ElseIf s=15 Then

ElseIf s=13 Then

ElseIf s=4 Then

End If

P=True Else

P = False

End If

EraseTrajectories End Function

Disain Formula Proposisi

Formula proposisi yang disusun sebagai

representasi trajectory berupa suatu persamaan matematika logika dari beberapa fungsi proposisi yang dioperasikan

dengan operator logika. Sebagai contoh dalam spesifikasi

sistem formal untuk trajectory t = 0, bentuk formula proposisinya adalah :

Ø = ◊(p(0,s14) ^ ◊(p(0,s16) ^ ◊(p(0,s15) ^ ◊(p(0,s13) ^ ◊p(0,s0)))))

Maka dalam bahasa pemrograman SaxBasic bentuk

formula proposisinya dapat digeneralisasikan menjadi :

proposisi = ((((P(t,cqget) And P(t,cqget)) And P(t,cqget)) And

P(t,cqget)) And P(t,cqget))

di mana :

proposisi Variabel logika penampung nilai boolean

hasil operasi logika pada formula

proposisi

t Trajectory ke-t

cqget Antrian status (queue of state) pada

trajectory ke-t

tanda () Digunakan untuk menjamin bahwa

(49)

29

kiri ke kanan, sesuai dengan semantik

formula proposisi dalam spesifikasi

sistem formal

4.5 Verifikasi Sistem

Verifikasi sistem dilakukan melalui pengamatan langsung pada

perilaku prototipenya, bila perilaku prototipe sesuai dengan yang

diharapkan maka spesifikasi sistem formal tersebut telah valid. Untuk menjelaskan verifikasi sistem berikut ini dijelaskan karakteristik untuk

setiap trajectory dan pembahasan simulasi trajectory untuk setiap

trajectory t di mana t = 0, 1, 2 adalah sebagai berikut :

a. Karakteristik Trajectory t = 0,1,2

[image:49.612.187.514.337.714.2]

Karakteristik setiap trajectory untuk trajectory t = 0,1,2 diilustrasikan dalam Tabel 4.9 adalah sebagai berikut :

Tabel 4.9 Karakteristik trajectory t = 0,1,2

Karakteristik Trajectory t = 0 Trajectory t = 1 Trajectory t = 2 Status Asal (Initial

State)

s0 s0 s4

Status Akhir (Finish State)

s0 s0 s4

Trajectory s0-s14-s16-s15-s13

-s0

s0-s16-s15-s14-s13

-s0

s4-s14-s16-s15-s13

-s4

Fungsi Proposisi ◊p(0,s14) :

Fungsi

proposisi untuk

trajectory 0 dan akan bernilai benar setelah mobot

mengunjungi status 14

◊p(0,s16) :

Fungsi

proposisi untuk

◊p(0,s15) :

Fungsi

proposisi untuk

◊p(1,s16) :

Fungsi

proposisi untuk

◊p(1,s15) :

Fungsi

proposisi untuk

◊p(1,s14) :

Fungsi

proposisi untuk

◊p(2,s14) :

Fungsi

proposisi untuk

◊p(2,s16) :

Fungsi

proposisi untuk

◊p(2,s15) :

Fungsi

(50)

trajectory 0 dan akan bernilai benar setelah mobot mengunjungi status 15

◊p(0,s13) :

Fungsi

proposisi untuk

◊p(0,s0) :

Fungsi

proposisi untuk

◊p(1,s13) :

Fungsi

proposisi untuk

◊p(1,s0) :

Fungsi

proposisi untuk

◊p(2,s13) :

Fungsi

proposisi untuk

◊p(2,s4) :

Fungsi

proposisi untuk

mengunjungi status 0 Formula Proposisi Ø = ◊(p(0,s14) ^

◊(p(0,s16) ^

◊(p(0,s15) ^

◊(p(0,s13) ^

◊p(0,s0)))))

Ø = ◊(p(1,s16) ^

◊(p(1,s15) ^

◊(p(1,s14) ^

◊(p(1,s13) ^

◊p(1,s0)))))

Ø = ◊(p(2,s14) ^

◊(p(2,s16) ^

◊(p(2,s15) ^

◊(p(2,s13) ^

◊p(2,s4)))))

Jumlah Hop 5 5 5

b. Simulasi Trajectory.

1. Eksekusi Trajectory t=0

Eksekusi trajectory t=0 dapat dijelaskan pada setiap fungsi proposisi yang terdapat dalam formula proposisi

Ø = ◊(p(0,s14) ^ ◊(p(0,s16) ^ ◊(p(0,s15) ^ ◊(p(0,s13) ^ ◊p(0,s0)))))

Status Awal : Sebelum eksekusi fungsi proposisi, mobot berada pada status awal (initial state), telah dijelaskan status awal mobot ini adalah s0. Pada status ini mobot

memeriksa kompas yang menunjukkan arah hadapnya, dan

selanjutnya akan berbelok ke arah hadap 270 derajat atau

menghadap selatan. Di bawah ini adalah cuplikan 2

(51)

31

SetMobotPosition(0,20,5,sdt) ‘Menempatkan

posisi mobot pada ‘status 0, dengan sudut hadap awal sdt bernilai sembarang

belok 270 ‘Robot menghadap

ke arah selatan atau 270 derajat pada kompas.

Proposisi ◊p(0,s14) : Eksekusi proposisi status 14 untuk trajectory t = 0 adalah maju hingga persimpangan, belok ke timur menuju ke depan gerbang status 14, setelah tiba di

depan gerbang status 14, belok ke utara hingga tiba di

mulut gerbang. Lebih jelasnya, dijelaskan logika

penggalan program di bawah ini.

' Maju sampai persimpangan

Do

bacasensor

selisih = jarak(6) -jarak(0)

If selisih > 0 Then

SetSteering(0,10,10) ElseIf selisih < 0 Then SetSteering(0,10,-10) Else SetSteering(0,10,0) End If StepForward

Loop Until (jarak(6) = maxjarak) And (jarak(0) =maxjarak)

belok 0

Maju hingga persimpangan, dimana bila sensor 6 dan sensor 0 tidak mendeteksi adanya dinding tembok, maka telah mencapai persimpangan tersebut.

Selanjutnya mobot akan belok menuju arah 0 derajat atau ke arah timur

' Maju sampai gerbang status 14

Do

bacasensor

SetSteering(0,10,0)

(52)

StepForward

Loop Until (jarak(0) < maxjarak) And

(jarak(6) = maxjarak)

belok 90

gerbang status 14.

Selanjutnya mobot belok ke arah 90 derajat atau utara.

Do

bacasensor

If jarak(4) > 3 Then

SetSteering(0,10,10) ElseIf jarak(4) < 3 Then SetSteering(0,10,-10) Else SetSteering(0,10,0) End If StepForward

Loop Until jarak(6) < maxjarak

visiting 14

Mobot berjalan lurus ke depan, bila sensor 6 mendeteksi adanya tembok, maka mobot telah tiba di mulut gerbang 14

Untuk selanjutnya mobot berjalan mengelilingi ruangan status 14 sebagai hasil eksekusi visiting 14

Akhirnya bila berhasil maka nilai proposisi ◊p(0,s14) akan

bernilai true atau benar.

Proposisi ◊p(0,s16) : Mula-mula mobot di gerbang status 14

menghadap selatan (arah 270), dan telah siap berjalan ke status

16.

Do

SetSteering(0,10,0) StepForward

bacasensor

Loop Until jarak(3) < 3

Mobot berjalan menghadap selatan (arah

270) keluar dari status

14, menuju hallway atau

(53)

33

belok 180 Selanjutnya mobot akan

belok ke arah timur (arah 180) dan siap

berjalan menuju perempatan. Do SetSteering(0,10,0) StepForward bacasensor

Loop Until jarak(6) = maxjarak

belok 270

Mobot berjalan lurus menuju perempatan. Bila sensor 6 tidak mendeteksi dinding, maka mobot telah tiba di perempatan.

Selanjutnya mobot akan belok ke arah selatan (arah 270).

Do

bacasensor

Loop Until (jarak(6) = maxjarak) And (jarak(4) < maxjarak)

belok 0 visiting 16

Mobot berjalan lurus ke arah selatan hingga tiba di depan gerbang status 16, bila sensor 4 mendeteksi adanya dinding dan sensor 6 tidak mendeteksi adanya dinding, maka telah tiba di depan gerbang 14.

Mobot belok ke arah timur (arah 0) untuk siap masuk (visiting) ke ruangan status 16.

Proposisi ◊p(0,s15) : Posisi mobot ada di gerbang status 16,

dengan arah hadap ke barat (arah 180) dan siap untuk

melangkah keluar.

Do

bacasensor

Mobot berjalan lurus ke arah barat (arah 180) ke luar status 16. Bila sensor depan (sensor 3)

(54)

belok 270

Do

bacasensor

belok 180

visiting 15

telah tiba di hallway.

Mobot membelok ke arah selatan (270) untuk menuju status 15

Mobot berjalan lurus ke selatan hingga sensor depan mendeteksi adanya dinding, yang menandakan mobot telah tiba di depan gerbang status 15.

Mobot belok ke arah barat (arah 180) untuk siap masuk ke ruang status 15

Mobot mengunjungi status 15

Proposisi ◊p(0,s13) : Posisi mobot berada di gerbang status 15

menghadap ke arah timur (arah 0) dan siap keluar status 15.

Do

bacasensor

belok 90

Do

bacasensor

SetSteering(0,10,10) ElseIf jarak(6) < 7 Then

Mobot berjalan lurus ke timur (arah 0) hingga

ke hallway, bila sensor

depan (sensor 3) mendetaksi adanya dinding, maka mobot telah sampai di hall way

Mobot belok ke arah utara (arah 90)

(55)

35 SetSteering(0,10,-10) Else SetSteering(0,10,0) End If StepForward

Loop Until (jarak(0) =

maxjarak) And (jarak(6) = maxjarak)

belok 180

Do

bacasensor

Loop Until (jarak(3) < 4) And (jarak(0) > 4)

belok 90 visiting 13

perempatan.

Mobot belok ke arah barat (arah 180) untuk siap menuju ke status 13

Mobot berjalan lurus ke timur hingga tiba di depan gerbang status 13, bila sensor kanan mendeteksi dinding dalam jarak > 4 meter dan sensor depan mendeteksi adanya dinding, maka mobot telah tiba di gerbang 13.

Mobot belok ke utara (arah 90) dan segera mengunjungi status 13.

Proposisi ◊p(0,s0) : Mobot berada di gerbang status 13

menghadap arah selatan (arah 270) dan siap keluar status 13.

Do

bacasensor

belok 0

Do

bacasensor

Loop Until (jarak(0) > 7) And (jarak(6) > 7)

Mobot berjalan lurus ke

selatan menuju hallway.

Bila sensor depan mendeteksi adanya dinding, maka mobot telah tiba di hall way Mobot belok ke arah timur (arah 0)

(56)

belok 90

Do

bacasensor

SetSteering(0,10,10)

ElseIf jarak(4) < 4 Then

SetSteering(0,10,-10) Else

SetSteering(0,10,0) End If

StepForward

Loop Until (jarak(0) > 7) And (jarak(3) < 4)

belok 0 belok 270

maka telah tiba di perempatan.

Mobot belok ke arah utara menuju status 0 (home).

Mobot berjalan lurus ke utara, hingga tiba di home, bila sensor kanan (sensor 0) tidak mendeteksi dinding, dan sensor depan (sensor 3) mendeteksi dinding, maka mobot telah tiba di home.

Mobot mengembalikan

arah hadapnya sebagaimana arah hadap

saat start yaitu ke arah selatan (arah 270) dengan cara putar (balik) kanan.

Akhirnya formula proposisi untuk trajectory t = 0

Ø = ◊(p(0,s14) ^ ◊(p(0,s16) ^ ◊(p(0,s15) ^ ◊(p(0,s13) ^ ◊p(0,s0)))))

yang diprogram dengan bahasa pemrograman SaxBasic

memiliki bentuk :

proposisi = ((((P(t,cqget) And P(t,cqget)) And P(t,cqget)) And P(t,cqget))

And P(t,cqget))

(57)

37

3. Eksekusi Trajectory t = 1

Eksekusi trajectory t=1 dapat dijelaskan pada setiap fungsi proposisi yang terdapat dalam formula proposisi

Ø = ◊(p(1,s16) ^ ◊(p(1,s15) ^ ◊(p(1,s14) ^ ◊(p(1,s13) ^ ◊p(1,s0)))))

Status Awal : Sebelum eksekusi fungsi proposisi, mobot berada pada status awal (initial state) yaitu s0, dan perilaku

mobot ini sama dengan perilaku mobot di status awal s0

pada trajectory t=0 yang telah dijelaskan di atas.

Proposisi ◊p(1,s16) : Mobot berada pada s0 dalam kondisi

menghadap ke selatan (arah 270). Langkah selanjutnya

dijelaskan dalam fungsi proposisi berikut ini :

Do

bacasensor

selisih = jarak(6) -jarak(0)

If selisih > 0 Then

SetSteering(0,10,10) ElseIf selisih < 0 Then

SetSteering(0,10,-10) Else

SetSteering(0,10,0)

End If

StepForward

Loop Until (jarak(6) = maxjarak) And (jarak(0) =maxjarak) belok 270 Do SetSteering(0,10,0) StepForward bacasensor Loop Until Abs(jarak(0)+jarak(6)) <= 11

Do

bacasensor

Mobot bergerak maju dari status 0 menuju status 8, dan akan tiba dipersimpangan (status 7) dengan ciri sensor 6 dan sensor 0 tidak mendeteksi adanya dinding atau sensor = maxjarak.

Mobot tiba dipersimpangan

(status 7) dan memantapkan arah ke selatan (arah 270) hingga tiba di dekat pintu status 16 yang dicirikan dengan salah satu dari sensor 0 atau 6 mengenai dinding.

(58)

Loop Until Abs(jarak(0)+jarak(6)) > 11

belok 0 Do

bacasensor

Loop Until (jarak(6) < maxjarak)

visiting 16

status 11 atau tepat di depan pintu status 16 yang dicirikan dengan salah satu sensor 0 atau 6 tidak mendeteksi adanya