METODE NUMERIK UNTUK MENENTUKAN HARGA OPSI
DENGAN MODEL VOLATILITAS LELAND
ARSYAD L
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa tesis berjudul Metode Numerik untuk Menentukan Harga Opsi dengan Model Volatilitas Lelandadalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, November 2015
Arsyad L
RINGKASAN
ARSYAD L. Metode Numerik untuk Menentukan Harga Opsi dengan Model Volatilitas Leland. Dibimbing oleh DONNY CITRA LESMANA dan ENDAR HASAFAH NUGRAHANI
Salah satu hal penting dalam perdagangan opsi adalah penentuan harga jual yang optimal. Teori penentuan harga opsi telah dikembangkan pada tahun 1973 oleh Fisher Black dan Myron Scholes yang berhasil merumuskan masalah penentuan harga opsi ke dalam bentuk persamaan diferensial parsial (PDP) Black Scholes. Model Black scholes menggunakan beberapa asumsi, yang salah satunya adalah tidak terdapat biaya transaksi. Model Black scholes tidak relevan sebab pada kenyataannya terdapat biaya transaksi di pasar saham. Dengan memasukkan biaya transaksi ke dalam model, Leland menunjukkan bahwa persaman diferensial parsial (PDP) Black Scholes berubah menjadi persamaan diferensial parsial taklinear. Selanjutnya dengan mengasumsikan biaya transaksi proporsional dengan nilai uang dari aset yang dijual atau dibeli, Leland memodifikasi persamaan diferensial parsial (PDP) Black Scholes standar menjadi persamaan diferensial parsial (PDP) Black Scholes taklinear.
PDP tak linier tersebut tidak mempunyai solusi analitik sehingga dibutuhkan pendekatan metode numerik untuk menentukan solusi hampirannya. Pada penelitian ini digunakan metode beda hingga upwind untuk diskretisasi ruang (harga saham) serta diskretisasi eksplisit dan implisit untuk diskretisasi waktu.
Pada penelitian ini dapat terlihat bahwa penggunaan metode beda hingga
upwind akan konvergen ketika menggunakan skema diskretisasi implisit terhadap waktu. Skema diskretisasi ini terbukti monoton, konsisten dan stabil. Berdasarkan hasil dari simulasi numerik, telah ditunjukkan bahwa orde kekonvergenan untuk metode beda hingga upwind dengan model volatilitas Leland adalah sekitar 1.80 untuk opsi Call, 1.80 untuk opsi Put , 1.35 opsi Cash or Nothing, serta 1.84 untuk opsi Butterfly.
SUMMARY
ARSYAD L. Metode Numerical Method for Determining The Price Of Option With Leland Volatility Model. Supervised by DONNY CITRA LESMANA and ENDAR HASAFAH NUGRAHANI
One of the most important things in options trading is the determination of the optimal sales price. Option pricing theory was developed in 1973 by Fisher Black and Myron Scholes. They successfully formulated option pricing problems into partial differential equations (PDE) form that called Black Scholes equation. Black Scholes model uses several assumptions, one of which is there is no transaction fee. Black-Scholes model is irrelevant because there is in fact the cost of transactions in the stock market. Furthermore, assuming that the transaction costs are proportionate to the value of money from assets being sold or purchased, Leland modifies the standard equation into a nonlinear partial differential equation (PDE).
Nonlinear PDE is hardly to solve by analytic method. Therefore Numerical methods may be needed to determine the solutions. In this study we use upwind finite difference method for discretizing space (stock price) and the implicit discretization for discretizing time.
In this study, it can be seen that the use of upwind finite difference method will converge when using implicit discretization scheme. The convergence is shown by proving that the discretization is monotone, consistent and stable. Using numerical simulations, it can be seen that the order of convergence for this methode is about 1.80 for a call option and put option, 1.35 for cash or nothing option, and 1.84 for butterfly option.
© Hak Cipta Milik IPB, Tahun 2015
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Matematika Terapan
METODE NUMERIK UNTUK MENENTUKAN HARGA OPSI
DENGAN MODEL VOLATILITAS LELAND
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
Judul Tesis : Metode Numerik untuk Menentukan Nilai Opsi dengan Model Volatilitas Leland
Nama : Arsyad L NIM : G551130131
Program Studi : Matematika Terapan
Disetujui oleh Komisi Pembimbing
Dr. Donny C. Lesmana MFinMath Ketua
Dr. Ir. Endar H. Nugrahani MS Anggota
Diketahui oleh
Ketua Program Studi Matematika Terapan
Dr Jaharuddin, MS
Dekan Sekolah Pascasarjana
Dr Ir Dahrul Syah, MScAgr
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan januari 2015 ini ialah keuangan, dengan judul Metode Numerik untuk Menentukan Harga Opsi dengan Model Volatilitas Leland
Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis juga menyampaikan terima kasih kepada:
1. Bapak Lahmuddin dan Ibu Baeyana selaku orang tua penulis.
2. Dr Donny C. Lesmana MFinMath selaku Ketua Komisi Pembimbing. 3. Dr Ir Endar H. Nugrahani MS selaku Anggota Komisi Pembimbing. 4. Dr Dr Ir IGP Purnaba, DEA selaku Penguji Luar Komisi Pembimbing. 5. Dr Jaharuddin, MS selaku Ketua Program Studi Matematika Terapan.
6. Direktorat Jendral Pendidikan Tinggi (DIKTI) sebagai sponsor Beasiswa Pendidikan Pascasarjana dalam Negeri (BPP-DN).
7. Seluruh keluarga yang selalu memberi dorongan dan doa untuk keberhasilan studi penulis.
8. Seluruh mahasiswa Departemen Matematika khususnya teman-teman angkatan tahun 2013 di Program Studi S2 Matematika Terapan.
9. Sahabat-sahabat yang tidak dapat disebutkan satu persatu yang telah banyak membantu penulis dalam penyelesaian tesis ini.
Semoga semua bantuan, bimbingan dan motivasi yang telah diberikan kepada penulis senantiasa mendapatkan balasan dari Allah subhanahu wa ta’ala.
Akhirnya, semoga penulisan tesis ini dapat memperkaya pengalaman belajar dan wawasan kita semua.
Bogor, November 2015
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
2 TINJAUAN PUSTAKA 2
Sekuritas 2
Teori Tentang Opsi 2
Faktor-faktor yang Memengaruhi Harga Opsi 3
Lemma Ito’ 4
Proses Harga Saham 5
Persamaan Black-Scholes Standar 5
Model Volatilitas Leland 7
Metode Beda Hingga Upwind 7
Metode Iterasi Newton-Raphson 8
Matriks M 8
Solusi Viskositas 9
3 METODE PENELITIAN 9
4 HASIL DAN PEMBAHASAN 9
Syarat Awal dan Syarat Batas 9
Diskretisasi Implisit 10
Kekonvergenan dari Skema Numerik 12
Solusi Sistem Taklinear Skema Diskretisasi 15
Simulasi Numerik 17
5 SIMPULAN 23
DAFTAR PUSTAKA 23
LAMPIRAN 25
DAFTAR TABEL
1 Hasil perhitungan norma dan rasio untuk opsi call 22 2 Hasil perhitungan norma dan rasio untuk opsi put 22 3 Hasil perhitungan norma dan rasio untuk opsi cash or nothing 22 4 Hasil perhitungan norma dan rasio untuk opsi butterfly 23
DAFTAR GAMBAR
1 Harga dari opsi call Eropa dengan M = dan N = . 18 2 Harga dari opsi call Eropa dengan M = dan N = . 18 3 Harga dari opsi put Eropa dengan M = dan N = . 19 4 Harga dari opsi put Eropa dengan M = dan N = . 19 5 Harga dari opsi cash or nothing Eropa dengan M = dan N = . 20 6 Harga dari opsi cash or nothing Eropa dengan M = dan N = . 20 7 Harga dari opsi butterfly Eropa dengan M = dan N = . 21 8 Harga dari opsi butterfly Eropa dengan M = dan N = . 21
DAFTAR LAMPIRAN
1 Sintaks programuntuk diskretisasi eksplisit 25
1. PENDAHULUAN
Latar Belakang
Pasar modal memiliki peran penting bagi perekonomian suatu negara karena menjalankan dua fungsi. Fungsi yang pertama adalah sebagai sarana bagi pendanaan usaha atau sebagai sarana bagi perusahaan untuk mendapatkan dana dari masyarakat pemodal (investor). Dana yang diperoleh dari pasar modal dapat digunakan untuk pengembangan usaha, ekspansi, penambahan modal kerja dan lain sebagainya. Kemudian, fungsi yang kedua adalah menjadi sarana bagi masyarakat untuk berinvestasi pada instrumen keuangan seperti saham, obligasi, reksa dana, dan lain-lain. Dengan demikian, masyarakat dapat menempatkan dana yang dimilikinya sesuai dengan karakteristik keuntungan dan risiko masing-masing instrumen.
Peran pasar modal dalam pembangunan perekonomian bangsa ataupun pembangunan nasional dapat membawa keuntungan yang sangat besar jika dilakukan dalam koridor yang baik, adil, benar, dan efisien. Keikutsertaan masyarakat investor melalui instrumen pasar modal menjadi harapan bersama untuk memberikan sumbangan bagi pembangunan ekonomi secara nasional.
Produk-produk yang diperdagangkan pada industri pasar modal mengalami perkembangan yang sangat pesat. Jika dulu hanya ada produk dasar seperti saham dan obligasi, sekarang juga meliputi produk turunannya (derivatif). Salah satu produk derivatif yang sering diperdagangkan adalah opsi.Opsi adalah suatu kontrak antara dua pihak di mana pemegang opsi mempunyai hak untuk membeli atau menjual suatu aset tertentu dengan harga dan waktu yang telah ditentukan (Zhao 2007).
Hal terpenting dalam perdagangan opsi adalah penentuan harga jual yang optimal. Teori penentuan harga opsi telah dikembangkan pada tahun 1973 oleh Fisher Black dan Myron Scholes yang berhasil merumuskan masalah penentuan harga opsi ke dalam bentuk persamaan diferensial parsial (PDP) Black Scholes. Model ini menggunakan beberapa asumsi, yang salah satunya adalah tidak terdapat biaya transaksi (Black & Scholes 1973).
Model Black Scholes standar tidak relevan sebab pada kenyataannya terdapat biaya transaksi di pasar saham. Adanya biaya transaksi akan memengaruhi harga suatu opsi (Company et al. 2008). Dengan memasukkan biaya transaksi ke dalam model, Leland (1985) menunjukkan bahwa persaman diferensial parsial (PDP) Black Scholes berubah menjadi persamaan diferensial parsial tak linear.
Akibat adanya biaya transaksi, volatililitas dari harga saham menjadi tidak konstan dan merupakan fungsi dari turunan kedua opsi terhadap harga saham. Hal itu menyebabkan PDP menjadi tidak linear. PDP tak linear tersebut tidak mempunyai solusi analitik sehingga dibutuhkan pendekatan metode numerik untuk menentukan solusi hampirannya.
Beberapa pendekatan secara numerik dapat dilakukan untuk menentukan harga opsi yaitu dengan metode beda hingga (finite difference method), metode elemen hingga, metode volume hingga (finite volume method) (Zhang & Wang 2009), dan lain-lain. Pada penelitian ini akan dikembangkan metode beda hingga
2
Tujuan Penelitian Adapun tujuan dalam penelitian ini adalah:
1. mengembangkan metode numerik untuk mencari harga opsi ketika terdapat biaya transaksi. Metode tersebut didasarkan pada metode implisit untuk diskretisasi waktu, serta metode beda hingga upwind untuk diskretisasi ruang (harga saham).
2. menentukan orde kekonvergenan dari metode beda hingga upwind.
2. TINJAUAN PUSTAKA
Sekuritas Definisi 2.1 Sekuritas Primitif
Sekuritas primitif (primitive security) adalah instrumen seperti saham atau obligasi yang pembayarannya hanya bergantung pada status keuangan pihak penerbit (Bodie et al. 2003).
Definisi 2.2 Sekuritas Derivatif
Sekuritas derivatif (derivative security) dibentuk dari perangkat sekuritas primitif yang menghasilkan imbal hasil yang bergantung pada faktor-faktor di luar karakteristik pihak penerbit dan mungkin dikaitkan dengan harga aset lain (Bodie
et al. 2003).
Teori Tentang Opsi Definisi 2.3 Opsi
Opsi pada suatu aset adalah suatu kontrak antara dua pihak, yang memberikan hak, tetapi bukan kewajiban, untuk melakukan jual atau beli aset pada harga tertentu yang disebut strike price atau exercise price dan dalam jangka waktu tertentu (jatuh tempo).
Berdasarkan jenisnya opsi dibagi menjadi dua yaitu opsi call dan opsi put.
Definisi 2.4 Opsi Call
Opsi call memberikan hak kepada pemegangnya untuk membeli suatu aset pada harga eksekusi pada saat atau sebelum tanggal jatuh tempo (maturity) yang ditentukan.
Definisi 2.5 Opsi Put
Opsi put memberikan hak kepada pemegangnya untuk menjual suatu aset dengan harga eksekusi tertentu pada saat atau sebelum tanggal jatuh temponya.
3
Definisi 2.6 Opsi Eropa
Opsi Eropa (European option) adalah opsi yang memberikan hak kepada pemegangnya untuk membeli atau menjual underlying asset dengan harga tertentu hanya pada waktu jatuh tempo.
Definisi 2.7 Opsi Amerika
Opsi Amerika (American option) memberikan hak kepada pemegangnya untuk membeli atau menjual underlying asset pada harga tertentu pada saat atau sebelum waktu jatuh tempo.
Faktor-faktor yang Memengaruhi Harga Opsi
Harga opsi dipengaruhi oleh berbagai faktor, di antaranya adalah harga aset yang mendasari, harga eksekusi, waktu jatuh tempo, volatilitas, dan suku bunga bebas risiko.
a. Harga aset yang mendasari dan harga eksekusi
Harga aset yang mendasari (saham) adalah harga jual atau beli yang berlaku pada pasar dari perdagangan aset yang mendasari (saham). Harga eksekusi merupakan harga jual atau beli saham yang tercantum dalam kontrak opsi, biasa juga disebut sebagai harga exercise atau harga strike.
b. Tanggal jatuh tempo besar nilai waktunya. Nilai waktu akan menurun ketika mendekati waktu jatuh tempo, oleh karena itu harga opsi put akan turun nilainya ketika mendekati waktu jatuh tempo.
c. Volatilitas
Volatilitas atas aset yang mendasari adalah sebuah ukuran tingkat ketidakpastian mengenai penyimpangan harga aset dari nilai harapan aset yang mendasari tersebut di masa datang. Jika volatilitas meningkat maka akan meningkat pula peluang aset yang mendasari untuk mengalami peningkatan atau penurunan terhadap suatu opsi.
d. Suku Bunga Bebas Risiko (Risk Free Interest Rate)
Suku bunga bebas risiko memengaruhi harga suatu opsi. Jika tingkat suku bunga dalam perekonomian mengalami kenaikan, maka akan mempengaruhi harapan kenaikan harga aset yang mendasari (dalam hal ini saham). Dengan mengasumsikan bahwa semua peubah tetap, maka harga opsi
put akan menurun jika suku bunga bebas risiko mengalami peningkatan. Begitu pula sebaliknya, harga opsi call akan selalu meningkat seiring dengan peningkatan suku bunga bebas risiko.
4
Proses Wiener adalah gerak Brown dengan rataan 0 dan variansi 1 (Niwiga 2005). Definisi 2.11 Proses Wiener Umum
Proses Wiener Umum (Generalized Wiener Process) untuk suatu peubah acak S
dapat dinyatakan sebagai berikut (Hull 2006):
= +
(1) disebut sebagai komponen deterministik dan menyatakan komponen stokastik, serta adalah proses Wiener, sedangkan dan masing-masing menyatakan rataan dan standar deviasi dari S.
Definisi 2.12 Proses Ito’
Proses Ito’ adalah proses Wiener umum dengan dan menyatakan suatu fungsi
dari peubah acak S dan waktu t. Secara aljabar proses Ito’ dapat dinyatakan
�� ada. Selanjutnya didefinisikan persamaan
differensial stokastik dari variabel � dengan drift rate �, dan variansi rate �, ,
� = �, + �,
5
= {��� �, +�� + �, ��� } + �, ��� (4)
Proses Harga Saham
Harga saham merupakan variabel stokastik, karena harga saham pada waktu yang akan datang tidak bisa ditentukan sekarang. Harga saham dapat dipengaruhi oleh faktor-faktor yang tidak dapat ditentukan secara pasti. Faktor-faktor ini dipandang sebagai komponen stokastik yang tidak dapat ditentukan sebelumnya. Oleh karena itu, perubahan harga saham dapat dipandang sebagai persamaan diferensial stokastik berikut:
= � + � .
(5) dengan � dan � sebagai konstanta yang berturut-turut menyatakan ekspektasi dari
return dan volatilitas saham. Persamaan ini juga dikenal sebagai model
Solusi dari persamaan (5) adalah:
= exp { � − � + � }. (7)
dengan , , �, �, dan T berturut-turut adalah harga saham pada awal kontrak, harga saham pada akhir kontrak, tingkat suku bunga bebas resiko, volatilitas harga saham dan waktu sampai dengan jatuh tempo.
Persamaan Black-Scholes Standar
Fischer Black dan Myron Scholes (1973) dalam merumuskan nilai suatu opsi mendasarkan pada beberapa asumsi, yaitu:
1. Suku bunga bebas risiko r adalah konstan dan sama untuk semua waktu jatuh tempo.
2. Dimungkinkan adanya short selling terhadap aset (saham) yaitu menjual aset tanpa harus memiliki aset terlebih dahulu.
3. Perdagangan dari aset yang mendasari bersifat kontinu. 4. Tidak terdapat peluang arbitrage.
5. Tidak ada pembayaran dividen selama opsi berlaku.
6
Versi diskret dari persamaan (5) dan (9) adalah
∆ = � ∆ + � ∆ (9) (9) dan (10) adalah sama. Selanjutnya dipilih sebuah portofolio dari saham S dan opsi U sehingga proses Wiener ∆ dapat dihilangkan.Portofolio tersebut adalah − opsi dan + �
Perubahan nilai portfolio ∆�, dalam selang waktu ∆ adalah
∆� = −∆ + �� ∆ . (12)
Substitusi (9) dan (10) ke dalam (12), menghasilkan
∆� = −�� − � �� ∆ . (13)
Portofolio ini dikatakan tidak berisiko karena tidak ada faktor ketidakpastian. portofolio ini mempunyai pendapatan yang sama dengan aset yang bebas risiko.
Perubahan nilai portofolio bebas risiko dapat dinyatakan dengan ∆� = �∆ , dengan r adalah suku bunga bebas risiko. Dengan menggunakan persamaan (11) dan ∆� =
�∆ ke persamaan (13) diperoleh
( − �� ) ∆ = �� + � �� ∆ (14)
� �� + �� +�� − = . (15)
Persamaan (15) ini dikenal sebagai persamaan Black-Scholes standar. Dengan melakukan transformasi � = − , maka
7
Seperti yang dijelaskan sebelumnya volatilitas menyatakan tingkat risiko penyimpangan harga suatu aset dari nilai harapannya. Semakin besar nilai volatilitas, semakin tak terduga pergerakan harga saham. Sebaliknya, semakin kecil volatilitas, semakin mudah untuk menduga harga saham tersebut (Morgenson dan Harvey 2002).
Volatilitas harga saham bisa berupa konstanta atau merupakan sebuah fungsi. Pada saat terdapat biaya transaksi, volatilitas harga saham tidak konstan tapi merupakan fungsi dari turunan kedua harga opsi terhadap harga saham.
Selanjutnya dengan mengasumsikan biaya transaksi proporsional dengan nilai uang dari aset yang dijual atau dibeli, Leland memodifikasi persamaan diferensial parsial (PDP) Black Scholes menjadi persamaan diferensial parsial (PDP) Black Scholes tak linear
� = � + − , (19)
dengan �= − dan volatitas termodifikasi sebagai berikut
� = � + √� � √� Sign , (20) di mana σ adalah volatilitas termodifikasi, k adalah biaya transaksi dan adalah periode transaksi (Leland 1985).
Metode Beda Hingga Upwind
Metode beda hingga upwind adalah suatu metode numerik untuk menyelesaikan persamaan diferensial parsial taklinear dengan cara mengkombinasikan metode beda hingga maju dan beda hingga mundur untuk diskretisasi ruang (harga saham).
Persamaan Black-Scholes taklinear akan diaproksimasi dengan diskretisasi harga dan waktu. Untuk diskretisasi harga, misalkan = , �� dibagi menjadi
sub-interval, di mana
= , + , = , , … . , −
dengan = < < < = ��, dan untuk setiap = , , … . , − dimisalkan ℎ = + − . Untuk diskretisasi waktu, misalkan � = , dibagi menjadi sub-interval, di mana
� = � , � + , = , , … . , −
dengan = � < � < < � = dan untuk setiap = , , … . , − dimisalkan ∆�= � + − � .
8
Untuk sembarang = , , … , ′ dan = , , … , ′
dengan = , , … . , dan = , , … . , , didefinisikan turunan pertama dan turunan kedua mengikuti operator beda hingga berikut
� = �
Metode Newton-Raphson (umumnya disebut dengan metode Newton) merupakan metode penyelesaian persamaan taklinear yang sering digunakan di antara metode lainnnya, karena metode ini memberikan konvergensi yang lebih cepat dibandingkan dengan metode lainnya. Metode Newton sering konvergen dengan cepat, terutama bila iterasi dimulai "cukup dekat" dengan akar yang diinginkan. Namun bila iterasi dimulai jauh dari akar yang dicari, metode ini dapat meleset tanpa peringatan. Implementasi metode ini biasanya mendeteksi dan mengatasi kegagalan konvergensi.
Metode Newton Raphson merupakan metode yang paling dikenal untuk mencari hampiran terhadap akar fungsi real dan dapat memecahkan persamaan
f(x)=0, dengan f diasumsikan mempunyai turunan kontinu. Metode ini menggunakan suatu garis lurus sebagai hampiran fungsi. Garis tersebut adalah garis singgung pada kurva. Dengan menggunakan suatu nilai awal x0 dan awalnya dipilih oleh Alexander Ostrowski mengacu pada nama Hermann Minkowski, yang membuktikan bahwa jika suatu matriks Z yang memiliki semua baris jumlah yang positif, maka determinan matriks yang bernilai positif (Bermon
et al. 1994). Matriks M sendiri didefisikan sebagai berikut Definisi 2.13
9
Menurut teorema Perron Frobenius, untuk matriks tak-singular A, maka nilai , dan untuk matriks-M tak-singular, elemen-elemen diagonal utama
dari matriks A haruslah bernilai positif. Solusi Viskositas
Misalkan diberikan PDP orde-2 sebagai berikut
�, , , = . (24)
Solusi viskositas diberikan pada definisi berikut Definisi 7 (Solusi Viskositas)
Misalkan Ω ⊆ adalah himpunan terbuka dan kontinu di Ω.
i. Dikatakan bahwa adalah subsolusi viskositas persamaan (24) pada titik � ∈ Ω, jika dan hanya jika, untuk setiap fungsi uji � ∈ Ω sedemikian sehingga − � mencapai maksimum lokal di � , dan
� , � , � � , � � , (25)
ii. Dikatakan bahwa adalah supersolusi viskositas persamaan (24) pada titik � ∈ Ω, jika dan hanya jika, untuk setiap fungsi uji � ∈ Ω sedemikian sehingga − � yang mencapai minimum lokal di � , dan
� , � , � � , � � , (26)
iii. Dikatakan bahwa adalah solusi viskositas pada himpunan terbuka jika adalah subsolusi viskositas dan supersolusi viskositas, pada setiap titik � ∈ Ω
(Dragoni 2009).
3. METODE PENELITIAN
Adapun langkah-langkah yang akan dilakukan dalam penelitian ini adalah: 1. melakukan diskretisasi untuk model Black-Scholes taklinear dengan
diskretisasi beda hingga upwind untuk diskretisasi ruang (harga saham) serta diskretisasi implisit untuk diskretisasi waktu.
2. memeriksa kekonvergenan skema numerik metode beda hingga upwind. 3. melakukan simulasi numerik untuk menunjukkan akurasi dari metode
diskretisasi beda hingga upwind.
4.
HASIL DAN PEMBAHASAN
Untuk menyelesaikan suatu permasalahan persamaan diferensial parsial dengan menggunakan metode beda hingga upwind ada beberapa hal yang perlu diperhatikan, yaitu kondisi syarat awal dan syarat batas, diskretisasi persamaan tersebut, serta kekonvergenan dari skema beda hingga upwind.
Syarat Awal dan Syarat Batas
Sebelum membahas skema diskretisasi untuk metode beda hingga upwind
10
diferensial parsial Black-Scholes taklinear. Karena persamaaan Black-Scholes taklinear mempunyai domain ∈ , ∞ maka untuk perhitungan komputasi perlu dibatasi menjadi ∈ , �� , dengan �� merupakan nilai yang cukup besar yang menjamin akurasi dari solusi.
Syarat batas untuk persamaaan Black-Scholes taklinear adalah sebagai berikut:
, = � , ∈ , �� , (27)
Dengan menggunakan diskretisasi skema implisit terhadap waktu, persamaan Black-Scholes taklinear (19) diaproksimasi mengikuti bentuk metode beda hingga upwind menggunakan operator (21-23) menjadi seperti berikut:
� − � + + − persamaan di atas dapat ditulis menjadi:
11
Untuk penyederhanaan, persamaan (32) dapat dituliskan menjadi bentuk berikut
Berdasarkan syarat batas (27-29), didefinisikan syarat awal dan syarat batas untuk persamaan (33) adalah sebagai berikut
= � = � � = � � (37)
untuk = , , … . , − dan = , … . , , sehingga persamaan (33) dapat dituliskan menjadi bentuk matriks berikut
+ + ̂ + =
Untuk membuktikan Teorema 4.1, harus ditunjukkan bahwa untuk = , , … , − :
< , > , < (39)
| | + | | (40)
Untuk matriks + , dari persamaan (34) - (36) dapat dilihat bahwa syarat (39) terpenuhi. Selanjutnya syarat (40), karena dan
∆�� maka:
12
| + | + | + | (41)
Dari definisi = ( ) dan berdasarkan (41), diperoleh: , ≠ , > , > ∑| |
−
=
Dengan demikian, merupakan matriks-M karena matriks tridiagonal memiliki diagonal utama yang bernilai positif dan dua diagonal di atas dan di bawah diagonal utama bernilai negatif.
Kekonvergenan dari Skema Numerik
Barles (1997) telah menunjukkan bahwa metode numerik dikatakan konvergen ke solusi viskositas jika metode tersebut terbukti konsisten, stabil dan monoton. Pada bagian ini akan ditunjukkan bahwa skema diskretisasi metode beda hingga upwind yang digunakan memenuhi syarat konvergen tersebut.
Untuk − dan − didefinisikan suatu fungsi +
Skema diskretisasi (33) akan ditunjukkan monoton melalui Lemma 4.1. Lemma 4.1
Skema diskretisasi pada persamaan (33) monoton yaitu untuk sembarang > dan = , , … , − ,
ruas kanan dari persamaan (42) secara berturut-turut taknaik terhadap ++ , naik terhadap + dan turun terhadap .
Misalkan = , , … , ⏟ , , … ,
′
adalah suatu matriks berukuran − × . Berdasarkan definisi , diperoleh
( + +
− + + ) = ℎ ( −+ + ) − ℎ ( + ) + ℎ ( ++ + )
13
Lebih lanjut diperiksa tanda pada bagian taklinear − � Γ + Γ + , dimana � Γ didefinisikan sebagai model gabungan bagian linear dan bagian taklinear dari persamaan (50) sebagai berikut:
+ + ,
dengan cara yang sama diperoleh
+ + + ,
++ , −+ ,
14
− � + √
� √ sign ( + − ℎ )
+ + , ++ , −+ , .∎
Kestabilan
Skema diskretisasi (33) akan ditunjukkan stabil melalui Lemma 4.2 Lemma 4.2
Dari bentuk di atas diperoleh:
+ | + | − + | persamaan (28), (29) dan (37) dapat dilihat bahwa:
∥ + ∥
∞ �{| + |, | + | } �{∥ � ∥∞, ∥ � ∥∞} (49)
Dengan menggabungkan (36) dan (37), diperoleh:
∥ + ∥
∞ �{∥ ∥∞, | + |, | + |}
�{∥ � ∥∞, ∥ � ∥∞, ∥ � ∥∞}. ∎
15
Kekonsistenan
Skema diskretisasi (33) akan ditunjukkan konsisten melalui Lemma 4.3. Lemma 4.3
Skema diskretisasi (33) konsisten. Bukti:
Teorema ekuivalensi Lax menyatakan bahwa metode beda hingga konsisten untuk masalah nilai awal yang diberikan (Strikwerda 1989). ∎
Teorema 4.2 Kekonvergenan
Skema diskretisasi (33) konvergen ke solusi (19) dengan syarat batas (27) - (29) ketika ℎ, ∆� → .
Bukti:
Barles (1997) membuktikan bahwa jika suatu diksretisasi dari PDP taklinear orde-2 konsisten, stabil dan monoton, maka konvergen ke solusi viskositas. Karena diksretisasi (33) terbukti konsisten, stabil dan monoton, maka diskretisasi (33) konvergen. Teorema 4.5 merupakan akibat dari Teorema 4.2, 4.3 dan 4.4. ∎
Solusi Sistem Taklinear Skema Diskretisasi
Untuk menyelesaikan sistem taklinear skema diskretisasi (38) disusun sebuah metode iterasi pada setiap langkah waktu. Diketahui diskretisasi (38) berbentuk dinotasikan sebagai + + , dengan
16
di mana + = ���+
� �+ untuk semua dan . Dengan menggunakan persamaan
(21) - (23), dan (20), serta menggunakan notasi Lemma 4.1, diperoleh persamaan untuk turunan berikut
Dengan cara yang serupa, diperoleh
,+ = + langkah 2. Jika sebaliknya berhenti.
Dengan menggunakan matriks Jacobi + , diperoleh Teorema 3 berikut. Teorema 4.3
Untuk sembarang + dengan = , , . , − , + adalah matriks M.
Bukti:
Untuk membuktikan Teorema 3, harus ditunjukkan bahwa
, − < , , > , , + < , (50)
, | , − | + | , + |. (51)
Untuk matriks + , diperoleh
, − = + = −�ℎ + √
� √ Sign < .
17
, = +
= ∆� + ℎ + +�ℎ + √ � √ Sign > .
, + = +
= − ℎ −�ℎ + √� � √� Sign < .
Selanjutnya karena > dan
∆�� > maka
,+ = | , −+ | + | , ++ | + + ∆� ,
| , −+ | + | , ++ |.
untuk sembarang = , , … , − dengan ketentuan bahwa ,+ = =
− ,
+ . Oleh karena itu, matriks + adalah matriks M. ∎
Sistem linear pada langkah 3 dari Algoritma 1 biasanya berskala besar dan teorema di atas menjamin bahwa sistem linear tersebut memiliki solusi khusus. Solusi untuk sistem linear dengan dekomposisi LU atau metode iteratif akan stabil secara numerik.
Simulasi Numerik
Pada bagian ini akan disajikan hasil pendekatan numerik dari empat jenis harga opsi tipe Eropa untuk melihat perilaku dan kekonvergenan dari metode beda hingga upwind baik dengan skema eksplisit maupun implisit. Pada simulasi numerik ini akan ditentukan derajat kekonvergenan dari metode iteratif untuk penyelesaian persamaan taklinear dengan memilih serangkaian mesh yang dibangkitkan dengan membagi-dua parameter mesh pada iterasi sebelumnya. a) Opsi call
1. Perhitungan harga opsi call menggunakan parameter = , , � = , , = , = , �� = , k = 0,01, = 0,02, = dan =
. Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 1.
18
(a) Skema eksplisit (b) Skema implisit
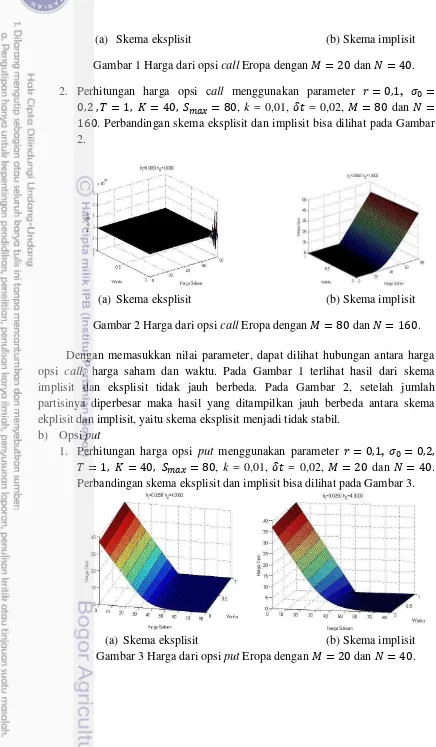
Gambar 1 Harga dari opsi call Eropa dengan = dan = . 2. Perhitungan harga opsi call menggunakan parameter = , , � =
, , = , = , �� = , k = 0,01, = 0,02, = dan =
. Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 2.
(a) Skema eksplisit (b) Skema implisit
Gambar 2 Harga dari opsi call Eropa dengan = dan = . Dengan memasukkan nilai parameter, dapat dilihat hubungan antara harga opsi call, harga saham dan waktu. Pada Gambar 1 terlihat hasil dari skema implisit dan eksplisit tidak jauh berbeda. Pada Gambar 2, setelah jumlah partisinya diperbesar maka hasil yang ditampilkan jauh berbeda antara skema ekplisit dan implisit, yaitu skema eksplisit menjadi tidak stabil.
b) Opsi put
1. Perhitungan harga opsi put menggunakan parameter = , , � = , , = , = , �� = , k = 0,01, = 0,02, = dan = .
Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 3.
(a) Skema eksplisit (b) Skema implisit
19
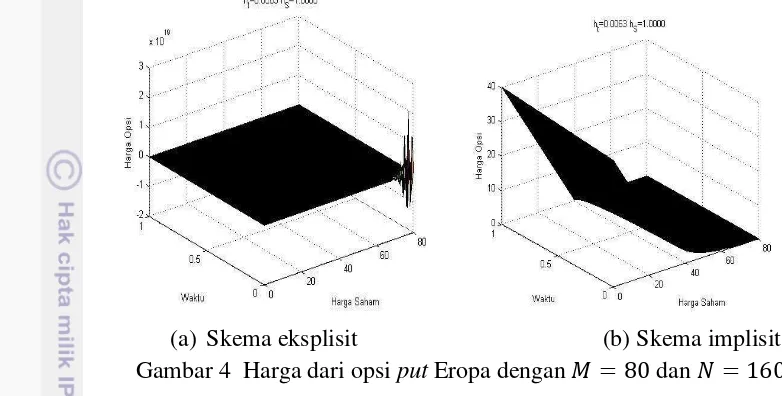
2. Perhitungan harga opsi put menggunakan parameter = , , � = , , = , = , �� = , k = 0,01, = 0,02, = dan = .
Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 4.
(a) Skema eksplisit (b) Skema implisit
Gambar 4 Harga dari opsi put Eropa dengan = dan = . Gambar 3 dan 4 memperlihatkan hubungan antara harga opsi put, harga saham dan waktu dengan menggunakan parameter yang sama pada perhitungn opsi call. Seperti yang terjadi pada opsi call dari Gambar 3 dapat dilihat untuk opsi put perbedaan yang terjadi pada kedua skema yang digunakan tidak signifikan. Pada Gambar 4, karena metode eksplisit tidak stabil maka hasilnya memiliki pola yang tidak beraturan.
c) Opsi cash or nothing
1. Perhitungan harga opsi cash or nothing menggunakan parameter = , , � = , , = , = , �� = , k = 0,01 , = 0,02, = dan
= . Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 5.
(a) Skema eksplisit (b) Skema implisit
20
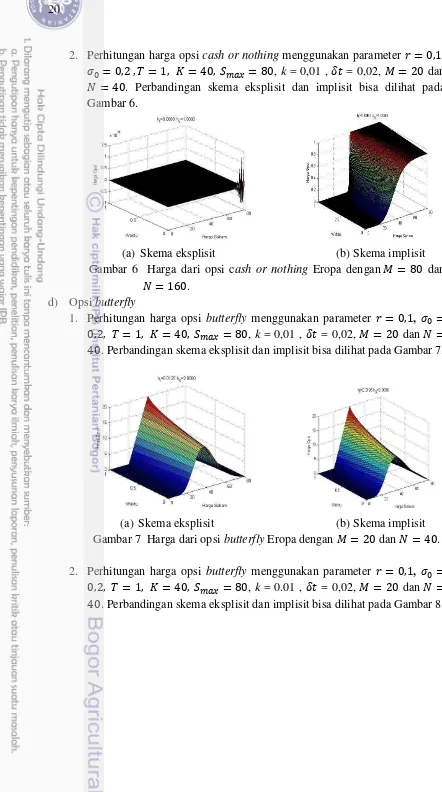
2. Perhitungan harga opsi cash or nothing menggunakan parameter = , , � = , , = , = , �� = , k = 0,01 , = 0,02, = dan
= . Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 6.
(a) Skema eksplisit (b) Skema implisit
Gambar 6 Harga dari opsi cash or nothing Eropa dengan = dan
= .
d) Opsi butterfly
1. Perhitungan harga opsi butterfly menggunakan parameter = , , � = , , = , = , �� = , k = 0,01 , = 0,02, = dan =
. Perbandingan skema eksplisit dan implisit bisa dilihat pada Gambar 7.
(a) Skema eksplisit (b) Skema implisit
Gambar 7 Harga dari opsi butterfly Eropa dengan = dan = . 2. Perhitungan harga opsi butterfly menggunakan parameter = , , � = , , = , = , �� = , k = 0.01 , = 0,02, = dan =
21
(a) Skema eksplisit (b) Skema implisit
Gambar 8 Harga dari opsi butterfly dengan = dan = . Dari Gambar 1-8 dapat dilihat untuk semua jenis opsi call. put, cash or nothing dan butterfly pada saat = = hasil yang diperlihatkan metode eksplisit dan implisit tidak jauh berbeda. Namun ketika jumlah partisinya diperbesar menjadi = = perbedaan yang terjadi antara kedua metode tersebut sangat signifikan, hal ini di sebabkan karena metode ekplisit tidak stabil sehingga polanya tidak beraturan untuk partisi yang lebih besar.
Selanjutnya akan dihitung orde kekonvergenan metode tersebut dengan membandingkan solusi eksaknya. Dalam menghitung orde kekonverenan metode tersebut, dipilih serangkaian mesh yang dibangkitkan secara berurutan dengan membagi dua ukuran mesh sebelumnya. Karena solusi eksak tidak diketahui, maka digunakan solusi numerik dari mesh seragam dengan ℎ = , , =
dan ∆� = , , = sebagai solusi “eksak”, dilambangkan dengan � � . Selanjutnya dengan menggunakan solusi “eksak” tersebut, dihitung rasio dari solusi numerik dari mesh yang berurutan dengan
Rasio = ‖ h
Untuk orde kekonvergenan metode numeriknya dihitung dengan Orde kekonvergenan = rata-rata rasio
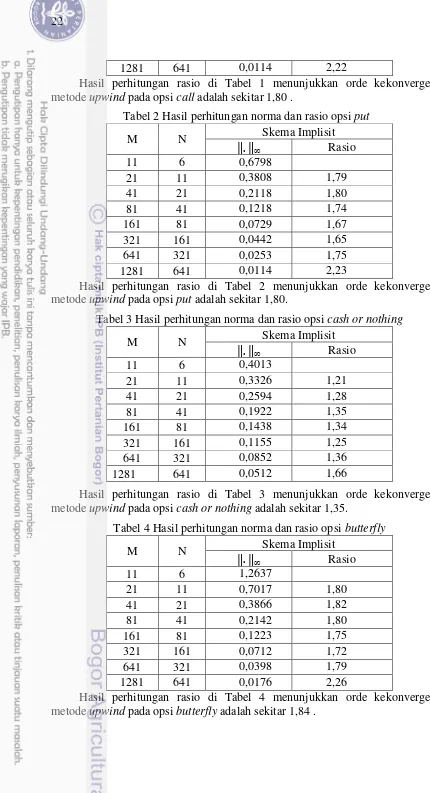
Tabel 1 Hasil perhitungan norma dan rasio untuk opsi call
22
1281 641 0,0114 2,22
Hasil perhitungan rasio di Tabel 1 menunjukkan orde kekonvergenan metode upwind pada opsi call adalah sekitar 1,80 .
Tabel 2 Hasil perhitungan norma dan rasio opsi put
M N Skema Implisit
Hasil perhitungan rasio di Tabel 2 menunjukkan orde kekonvergenan metode upwind pada opsi put adalah sekitar 1,80.
Tabel 3 Hasil perhitungan norma dan rasio opsi cash or nothing
M N Skema Implisit
Hasil perhitungan rasio di Tabel 3 menunjukkan orde kekonvergenan metode upwind pada opsi cash or nothing adalah sekitar 1,35.
Tabel 4 Hasil perhitungan norma dan rasio opsi butterfly
M N Skema Implisit
23
5.
SIMPULAN
Pada penelitian ini dapat dilihat bahwa penggunaan metode beda hingga
upwind akan konvergen ketika menggunakan skema diskretisasi implisit terhadap waktu. Skema diskretisasi ini terbukti monoton, konsisten dan stabil. Berdasarkan hasil dari simulasi numerik, dapat ditunjukkan bahwa orde kekonvergenan untuk metode beda hingga upwind dengan model volatilitas Leland adalah sekitar 1,80 untuk opsi call dan opsi put, 1,35 opsi cash or nothing, serta 1,84 untuk opsi
butterfly.
DAFTAR PUSTAKA
Bermon A, Robert J & Plemmons. 1994. Nonnegative Matrices in the Mathematical Sciences, Philadelphia: Society for Industrial and Applied Mathematics.
Barles G. 1997. Convergence of Numerical Schemes for Degenerate Parabolic Equations Arising in Finance, in: L.C.G. Rogers, D. Talay (Eds.), Numerical Methods in Finance. Cambridge: Cambridge University Press. Black F, Scholes M. 1973. The Pricing of Option and Corporate Liabilities. J.
Political Economy. 81: 637-659.
Bodie Z, Kane A, Marcus AJ. 2003. Invesment. United State of America: The McGraw-Hill.
Company R, Navarro E, Pintos JR. 2008. Numerical solution of linear and nonlinear Black–Scholes option pricing equations. J. Computers and Mathematics with Applications. 56 :813–821.
Dragoni F. 2009. Introduction to Viscosity Solutions for Nonlinear PDEs. London: Notes Imperial College London.
Fujimoto T, Ranade R. 2004. Two characterizations of inverse-positive matrices: the Hawkins-Simon condition and the Le Chatelier-Braun principle.
Electronic Journal of Linear Algebra 11: 59–65.
Hull J, White A. 2006. Option. Future. and Other Derivatives. 6th edition. New Jersey: Prentice – Hall.
Hull J, White A. 1987. The pricing of option on asset with stochastic volatilities. J. Finance. 42:281-300.
Leland HE. 1985. Option pricing and replication with transaction costs. J. Finance. 40: 1283-1301.
Lesmana DC, Wang S. 2013. An upwind finite difference for a taklinear Black-Scholes equation governing European option valuation under transaction costs. J. Applied Mathematics and Computation. 219: 8811-8828
Niwiga DB. 2005. Numerical method for valuation of financial derivatives. [Thesis]. South Africa : University of Werstern Cape.
Morgenson G, Harvey CR. 2002. The New York Times Dictionary of Money and Investing: The Essential A-to-Z Guide to The Language of The New Market. New York: Times Book.
24
Strikwerda JC. 1989. Finite Difference Schemes and Partial Differential Equations. 1st Ed. Madison: Wadsworth & Brooks.
Zhang K, Wang S. 2009. A Computational scheme for options under jump diffusion processes. J. Numerical Analysis and Modeling 6 : 110-123. Zhao Jichao. 2007. Compact finite difference method for American option pricing.
J.Computational and Applied Mathematics 206 : 306–321.
LAMPIRAN
1. Sintaks program untuk diskretisasi eksplisit
function D=ExplisitAr(u0,g1,g2,S_end,T,nS,nt) format long
nS1 = nS + 1; %% jumlah titik S nt1 = nt + 1; %% jumlah titik t
hS = S_end/nS; %% panjang sub-interval S hS2 = hS*hS;
ht = T/nt; %% panjang sub-interval t sigma0 = 0.2;
r = 0.08; %% tingkat suku bunga bebas risiko
%k = 0.01; %% biaya transaksi %dt = 0.02; %% periode transaksi
26
s1=sprintf('h_t=%6.4f h_S=%6.4f', ht, hS); title(s1);
end
2. Sintaks program untuk diskretisasi implisit
function V=BedaHinggaUP(u0,g1,g2,S_end,T,nS,nt)
%%%% Mendefenisiakan Nilai Opsi
27
28
%%%% Menyelesaikan Tridiagonal Solvers Ja*Z=-F dgn Crout Factorization
29
s1=sprintf('h_t=%6.4f h_S=%6.4f', ht, hS); title(s1);
RIWAYAT HIDUP
Penulis dilahirkan di Ketulungan, Luwu Utara, Sulawesi Selatan pada tanggal 20 juli 1988, sebagai anak ketiga dari pasangan Lahmuddin dan Baeyana. Pendidikan sekolah menengah ditempuh di SMA Negeri 1 Sukamaju, Luwu Utara, Sulawesi Selatan Program IPA, lulus pada tahun 2006. Pada tahun yang sama penulis diterima di program studi Matematika Universitas Negeri Makassar, dan menyelesaikannya tahun 2011. Pada tahun 2013 Penulis diterima di program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor (IPB) dengan sponsor Beasiswa Pendidikan Pascasarjana dalam Negeri (BPP-DN) dari Direktorat Jendral Pendidikan Tinggi (DIKTI).
30
Sebuah artikel dengan judul “Numerical method for determining option price with Leland volatility model” telah diterima untuk diterbitkan di jurnal Applied Mathematical Sciences (AMS), Hikari Ltd, Bulgaria. Karya ilmiah tersebut merupakan bagian dari penelitian S-2 penulis.