Harvesting models in fishery management

MODEL PEMANENAN DALAM MANAJEMEN PERIKANAN

DIAN LESTARI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

DIAN LESTARI. Model Pemanenan dalam Manajemen Perikanan. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

Pemanenan merupakan salah satu kegiatan yang umum dilakukan dalam pemanfaatan sumber daya alam, seperti pemanenan sumber daya kelautan. Dalam manajemen perikanan, ada beberapa strategi pemanenan yang dapat dilakukan yaitu pemanenan konstan, proporsional, threshold proporsional dan musiman. Usaha pemanenan didefinisikan sebagai peubah kontrol dalam strategi pemanenan. Hal itu penting untuk menemukan usaha pemanenan optimal yang dapat memberikan hasil pemanenan maksimum yang berkelanjutan, sehingga kepunahan populasi ikan tidak terjadi.

ABSTRACT

DIAN LESTARI. Harvesting Models in Fishery Management. Supervised by ENDAR HASAFAH NUGRAHANI and ALI KUSNANTO.

Harvesting is one of the common activities in using natural resources, such as harvesting of marine resources. In fishery management, there are several harvesting strategies which can be applied, i.e. constant, proportional, proportional with threshold, and seasonal harvesting. Fishing effort is defined as a control variable in the harvesting strategies. It is important to be able to find an optimal fishing effort that gives maximum sustainable yield, so that extinction of fish population does not happen.

MODEL PEMANENAN DALAM MANAJEMEN PERIKANAN

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

DIAN LESTARI

G54050769

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Nama : Model Pemanenan dalam Manajemen Perikanan

Nama : Dian Lestari

NRP : G54050769

Menyetujui,

Pembimbing I

Pembimbing II

Dr. Ir. Endar Hasafah Nugrahani, M.S.

Drs. Ali Kusnanto, M.Si.

NIP. 19631228 198903 2 001

NIP. 19650820 199003 1 001

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP. 19610328 198601 1 002

RIWAYAT HIDUP

Penulis dilahirkan di Bandung pada tanggal 24 Mei 1988 sebagai anak pertama dari dua bersaudara, anak dari pasangan Wawan dan Berty.

Tahun 2005 penulis lulus dari SMU Negeri 1 Margahayu Bandung dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI). Tahun 2006 masuk di Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Dr. Ir. Endar Hasafah Nugrahani, M.S. selaku dosen pembimbing I (terima kasih atas semua ilmu, kesabaran, motivasi, dan bantuannya selama penulisan skripsi ini).

2. Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing II (terima kasih atas semua ilmu, kesabaran, saran, motivasi, dan bantuannya selama penulisan skripsi ini).

3. Dr. Hadi Sumarno, M.S. selaku dosen penguji (terima kasih atas semua ilmu dan sarannya).

4. Semua dosen Departemen Matematika (terima kasih atas semua ilmu yang telah diberikan).

5. Pa Yono, Bu Susi, Bu Ade, Bu Marisi, Mas Bono, Mas Heri, Mas Deni.

6. Keluargaku tercinta: Papah (terima kasih atas doa dan dukungannya), Mamah (terima kasih banyak atas semua doa, dukungan, kerja keras dan kasih sayangnya), Ade ku Widya (makasih atas doa, semangat dan dukungannya).

7. Teman-teman : Mba ik, Mba Rie, Bundo, Mba Vino, Agem, Uni, Fence, Atieh, Yie2, Utie, Nida, Noviar (makasih atas doa,dorongan, saran, dan semangat yang kalian berikan selama ini).

8. Teman-teman Math 42 : Ayank Nur Vita, Senior Jane, Niken, Hikmeh, Otong, Tasya, Ryu, Ida, Iput, Yusep, Ardy, Kaisar Dendy, Eko, Mas Warno, Awie, Mocco, Djawa, Bude Tie2, Acuy, Mira, Facrie, Sapto, Mas Ayep, Achi, Hapsari, Ilie, Pp, Lisda, Gita, Riken, Ocoy, Bima, Eyyi, Ridu, Nyoman, Ayu, Agnes, K’Mukhtar, Lela, Rima, Herry, Yuni, Oby, Zil, Yudi, Danuradi, Erlin, Acuy, Sima, Pipit, Rendy, Boy dan lainnya (makasih buat doa, bantuan, saran, semangat, dan dukungannya).

9. Tema-teman PF : Kudung, Agus, Poye, Sars dan lainnya (terima kasih semangat, bantuan, dan dukungannya).

10. Adik-adik 43: (makasih atas doa, semangat dan dukungannya). 11. Adik-adik 44: (makasih atas doa, semangat dan dukungannya). 12. Adik-adik 45 : (makasih atas doa dan semangatnya).

13. Teman – teman sman_387 : 8-an (Desay, Umie, Dara, Holiday, Sitay, Dinay, Wie2), Echo, Vlma, Ch, Jaka, Yanuar, Heri dan lainnya (makasih atas doa dan semangat yang kalian berikan).

Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Juli 2009

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II LANDASAN TEORI 2.1 Persamaan Diferensial Biasa ... ` 1

2.2 Persamaan Diferensial Terpisahkan ... 1

2.3 Teknik Mencari Solusi Persamaan Diferensial Terpisahkan ... 1

2.4 Persamaan Bernoulli... 2

2.5 Masalah Kontrol Optimum ... 2

2.6 Kestabilan PD Orde Satu ... 2

2.7 Digram Fase ... 3

III MODEL – MODEL DASAR 3.1 Model Logistik ... 3

3.2 Model Umum Pemanenan ... 4

3.3 Model Usaha Pemanenan ... 4

3.4 Model Keuntungan Maksimum ... 5

3.5 Teori Modal ... 5

IV MODEL PEMANENAN PERIKANAN 4.1 Model Pemanenan Ikan ... 5

4.1.1 Pemanenan Konstan ... 5

4.1.2 Pemanenan Proporsional ... 6

4.1.3 Pemanenan Threshold Proporsional ... 6

4.1.4 Pemanenan Musiman ... 6

4.2 Maksimum Sustainable Yield ... 6

4.2.1 Level Usaha Pemanenan ... 7

4.2.2 Hasil Pemanenan Maksimum ... 13

V KEBIJAKAN PEMANENAN OPTIMAL 5.1 Penentuan Solusi Optimal Usaha Pemanenan ... 16

5.1.1 Pemanenan Konstan yang Optimal ... 16

5.1.2 Penentuan Pemanenan Proporsional yang Optimal ... 16

5.2 Contoh Penerapan dalam Manajemen Perikanan ... 17

KESIMPULAN ... 18

DAFTAR PUSTAKA ... 19

DAFTAR TABEL

Halaman

1 Dinamika populasi pemanenan konstan ... 7

2 Dinamika populasi dengan beberapa nilai awal ... 8

3 Dinamika populasi pemanenan proporsional ... 9

DAFTAR GAMBAR

Halaman 1 Bidang fase . ( ) x f x ... 3

2 Kurva pertumbuhan logistik ... 4

3 Dinamika pemanenan konstan ... 8

4 Dinamika populasi pemanenan konstan q0.2 dengan nilai awal ... 8

5 Dinamika populasi pemanenan proporsional ... 9

6 Pengaruh nilai β terhadap dinamika populasi ... 9

7 Bidang fase pemanenan threshold ... 10

8 Pengaruh nilai β = 1 ... `11

9 Pengaruh nilai β = 2.5 ... 11

10 Pengaruh nilai  2.5 10 4 ... 11

11 Dinamika populasi dengan  q 0.80.5, 1 ... 11

12 Dinamika populasi pemanenan musiman ... 12

13 Pengaruh nilai β untuk αq = 0.49 ... 12

14 Pengaruh nilai β untuk αq = 0.04 ... 13

15 Kurva saha pemanenan konstan ... 13

16 Kurva usaha pemanenan proporsional ... 14

17 Kurva usaha pemanenan proporsional threshold ... 15

18 Kurva usaha pemanenan musiman ... 15

19 Kurva keuntungan ... 17

DAFTAR LAMPIRAN

Halaman 1 Solusi Pemanenan Konstan ... 21

2 Solusi Pemanenan Proporsional ... 22

3 Waktu Awal Pemanenan Proporsional ... 23

I PENDAHULUAN

1.1 Latar Belakang

Perikanan merupakan salah satu sumber daya alam yang dapat diperbaharui, tetapi kepunahan mungkin dapat terjadi. Hal ini disebabkan karena kecanggihan alat penangkapan ikan dan peningkatan penangkapan ikan yang dilakukan manusia. Untuk menghindari kepunahan, ada beberapa strategi pemanenan yang dapat dilakukan.

Pemanenan merupakan salah satu kegiatan yang dipilih masyarakat untuk memanfaatkan sumber daya perikanan. Di dalam melakukan pemanenan diperlukan berbagai sarana sebagai input yang biasa disebut sebagai usaha pemanenan.

Hal yang sangat penting dalam manajemen perikanan adalah diperolehnya keuntungan maksimum yang dapat berkelanjutan. Hal penting lainnya adalah usaha pemanenan tanpa menggerakkan sistem lingkungannya menuju kepunahan (Brauer & Soudack, 1981).

Strategi pemanenan yang dapat diterapkan dalam manajemen perikanan, diantaranya pemanenan yang dilakukan secara konstan, proporsional, threshold proporsional, dan musiman.

Model persamaan diferensial dapat digunakan untuk memperoleh berbagai model

pemanenan. Dengan melakukan analisis terhadap model pemanenan tersebut dapat dilihat dinamika populasi dan pengaruh peubah kontrol (usaha pemanenan) terhadap nilai kestabilan dan dinamika populasinya.

Karya ilmiah ini menjelaskan pemanenan-pemanenan yang dapat diterapkan dalam manajemen perikanan dan pengaruh dari usaha pemanenan terhadap dinamika populasinya. Sebagai contoh penerapannya dibahas pula pemanenan optimal yang memberikan keuntungan maksimum dan berkelanjutan (sustainable). Pembahasan pemanenan optimal hanya dibatasi untuk pemanenan yang dilakukan secara konstan dan proporsional.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini meliputi:

1. memodelkan dinamika populasi ikan dan analisis kestabilannya;

2. menganalisis pengaruh peubah kontrol terhadap nilai kestabilan dan dinamika populasinya;

3. menganalisis model kebijakan pemanenan optimal yang memberikan keuntungan maksimum dan berkelanjutan.

II LANDASAN TEORI

2.1 Persamaan Diferensial Biasa (PDB)

Persamaan diferensial biasa merupakan suatu persamaan yang melibatkan turunan pertama atau lebih dari fungsi sebarang peubah tak bebas terhadap peubah bebas

.

Suatu persamaan diferensial biasa orde I dapat dinyatakan sebagai berikut

'

( ) ( ) ( ). g x x t  f t

dengan g x( ) adalah fungsi dalam x dan x merupakan peubah tak bebas (xx t( )) dan

( )

f t adalah fungsi dalam t, dengan t peubah bebas.

(Farlow, 1994)

2.2 Persamaan Diferensial Terpisahkan

Persamaan diferensial (PD) terpisahkan adalah persamaan yang dapat ditulis sebagai

.

( , ) atau ( , ). dx

F x t x F x t

dt  

dengan F x t( , ) merupakan persamaan yang ditulis sebagai F x t( , ) f x g t( ) ( ), f x( ) merupakan fungsi dari x dan g t( ) merupakan fungsi dari t. Kemudian persamaan tersebut dapat terpisahkan menjadi

( ) . ( )

dx

g t dt f x 

(Bajpai & Hyslop, 1970)

2.3 Teknik Mencari Solusi PD Terpisahkan (i) Menuliskan persamaan diferensial dengan terpisah

( ) . ( )

dx

g t dt f x 

MODEL PEMANENAN DALAM MANAJEMEN PERIKANAN

DIAN LESTARI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

DIAN LESTARI. Model Pemanenan dalam Manajemen Perikanan. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

Pemanenan merupakan salah satu kegiatan yang umum dilakukan dalam pemanfaatan sumber daya alam, seperti pemanenan sumber daya kelautan. Dalam manajemen perikanan, ada beberapa strategi pemanenan yang dapat dilakukan yaitu pemanenan konstan, proporsional, threshold proporsional dan musiman. Usaha pemanenan didefinisikan sebagai peubah kontrol dalam strategi pemanenan. Hal itu penting untuk menemukan usaha pemanenan optimal yang dapat memberikan hasil pemanenan maksimum yang berkelanjutan, sehingga kepunahan populasi ikan tidak terjadi.

ABSTRACT

DIAN LESTARI. Harvesting Models in Fishery Management. Supervised by ENDAR HASAFAH NUGRAHANI and ALI KUSNANTO.

Harvesting is one of the common activities in using natural resources, such as harvesting of marine resources. In fishery management, there are several harvesting strategies which can be applied, i.e. constant, proportional, proportional with threshold, and seasonal harvesting. Fishing effort is defined as a control variable in the harvesting strategies. It is important to be able to find an optimal fishing effort that gives maximum sustainable yield, so that extinction of fish population does not happen.

MODEL PEMANENAN DALAM MANAJEMEN PERIKANAN

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

DIAN LESTARI

G54050769

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Nama : Model Pemanenan dalam Manajemen Perikanan

Nama : Dian Lestari

NRP : G54050769

Menyetujui,

Pembimbing I

Pembimbing II

Dr. Ir. Endar Hasafah Nugrahani, M.S.

Drs. Ali Kusnanto, M.Si.

NIP. 19631228 198903 2 001

NIP. 19650820 199003 1 001

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP. 19610328 198601 1 002

RIWAYAT HIDUP

Penulis dilahirkan di Bandung pada tanggal 24 Mei 1988 sebagai anak pertama dari dua bersaudara, anak dari pasangan Wawan dan Berty.

Tahun 2005 penulis lulus dari SMU Negeri 1 Margahayu Bandung dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI). Tahun 2006 masuk di Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Dr. Ir. Endar Hasafah Nugrahani, M.S. selaku dosen pembimbing I (terima kasih atas semua ilmu, kesabaran, motivasi, dan bantuannya selama penulisan skripsi ini).

2. Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing II (terima kasih atas semua ilmu, kesabaran, saran, motivasi, dan bantuannya selama penulisan skripsi ini).

3. Dr. Hadi Sumarno, M.S. selaku dosen penguji (terima kasih atas semua ilmu dan sarannya).

4. Semua dosen Departemen Matematika (terima kasih atas semua ilmu yang telah diberikan).

5. Pa Yono, Bu Susi, Bu Ade, Bu Marisi, Mas Bono, Mas Heri, Mas Deni.

6. Keluargaku tercinta: Papah (terima kasih atas doa dan dukungannya), Mamah (terima kasih banyak atas semua doa, dukungan, kerja keras dan kasih sayangnya), Ade ku Widya (makasih atas doa, semangat dan dukungannya).

7. Teman-teman : Mba ik, Mba Rie, Bundo, Mba Vino, Agem, Uni, Fence, Atieh, Yie2, Utie, Nida, Noviar (makasih atas doa,dorongan, saran, dan semangat yang kalian berikan selama ini).

8. Teman-teman Math 42 : Ayank Nur Vita, Senior Jane, Niken, Hikmeh, Otong, Tasya, Ryu, Ida, Iput, Yusep, Ardy, Kaisar Dendy, Eko, Mas Warno, Awie, Mocco, Djawa, Bude Tie2, Acuy, Mira, Facrie, Sapto, Mas Ayep, Achi, Hapsari, Ilie, Pp, Lisda, Gita, Riken, Ocoy, Bima, Eyyi, Ridu, Nyoman, Ayu, Agnes, K’Mukhtar, Lela, Rima, Herry, Yuni, Oby, Zil, Yudi, Danuradi, Erlin, Acuy, Sima, Pipit, Rendy, Boy dan lainnya (makasih buat doa, bantuan, saran, semangat, dan dukungannya).

9. Tema-teman PF : Kudung, Agus, Poye, Sars dan lainnya (terima kasih semangat, bantuan, dan dukungannya).

10. Adik-adik 43: (makasih atas doa, semangat dan dukungannya). 11. Adik-adik 44: (makasih atas doa, semangat dan dukungannya). 12. Adik-adik 45 : (makasih atas doa dan semangatnya).

13. Teman – teman sman_387 : 8-an (Desay, Umie, Dara, Holiday, Sitay, Dinay, Wie2), Echo, Vlma, Ch, Jaka, Yanuar, Heri dan lainnya (makasih atas doa dan semangat yang kalian berikan).

Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Juli 2009

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II LANDASAN TEORI 2.1 Persamaan Diferensial Biasa ... ` 1

2.2 Persamaan Diferensial Terpisahkan ... 1

2.3 Teknik Mencari Solusi Persamaan Diferensial Terpisahkan ... 1

2.4 Persamaan Bernoulli... 2

2.5 Masalah Kontrol Optimum ... 2

2.6 Kestabilan PD Orde Satu ... 2

2.7 Digram Fase ... 3

III MODEL – MODEL DASAR 3.1 Model Logistik ... 3

3.2 Model Umum Pemanenan ... 4

3.3 Model Usaha Pemanenan ... 4

3.4 Model Keuntungan Maksimum ... 5

3.5 Teori Modal ... 5

IV MODEL PEMANENAN PERIKANAN 4.1 Model Pemanenan Ikan ... 5

4.1.1 Pemanenan Konstan ... 5

4.1.2 Pemanenan Proporsional ... 6

4.1.3 Pemanenan Threshold Proporsional ... 6

4.1.4 Pemanenan Musiman ... 6

4.2 Maksimum Sustainable Yield ... 6

4.2.1 Level Usaha Pemanenan ... 7

4.2.2 Hasil Pemanenan Maksimum ... 13

V KEBIJAKAN PEMANENAN OPTIMAL 5.1 Penentuan Solusi Optimal Usaha Pemanenan ... 16

5.1.1 Pemanenan Konstan yang Optimal ... 16

5.1.2 Penentuan Pemanenan Proporsional yang Optimal ... 16

5.2 Contoh Penerapan dalam Manajemen Perikanan ... 17

KESIMPULAN ... 18

DAFTAR PUSTAKA ... 19

DAFTAR TABEL

Halaman

1 Dinamika populasi pemanenan konstan ... 7

2 Dinamika populasi dengan beberapa nilai awal ... 8

3 Dinamika populasi pemanenan proporsional ... 9

DAFTAR GAMBAR

Halaman 1 Bidang fase . ( ) x f x ... 3

2 Kurva pertumbuhan logistik ... 4

3 Dinamika pemanenan konstan ... 8

4 Dinamika populasi pemanenan konstan q0.2 dengan nilai awal ... 8

5 Dinamika populasi pemanenan proporsional ... 9

6 Pengaruh nilai β terhadap dinamika populasi ... 9

7 Bidang fase pemanenan threshold ... 10

8 Pengaruh nilai β = 1 ... `11

9 Pengaruh nilai β = 2.5 ... 11

10 Pengaruh nilai  2.5 10 4 ... 11

11 Dinamika populasi dengan  q 0.80.5, 1 ... 11

12 Dinamika populasi pemanenan musiman ... 12

13 Pengaruh nilai β untuk αq = 0.49 ... 12

14 Pengaruh nilai β untuk αq = 0.04 ... 13

15 Kurva saha pemanenan konstan ... 13

16 Kurva usaha pemanenan proporsional ... 14

17 Kurva usaha pemanenan proporsional threshold ... 15

18 Kurva usaha pemanenan musiman ... 15

19 Kurva keuntungan ... 17

DAFTAR LAMPIRAN

Halaman 1 Solusi Pemanenan Konstan ... 21

2 Solusi Pemanenan Proporsional ... 22

3 Waktu Awal Pemanenan Proporsional ... 23

I PENDAHULUAN

1.1 Latar Belakang

Perikanan merupakan salah satu sumber daya alam yang dapat diperbaharui, tetapi kepunahan mungkin dapat terjadi. Hal ini disebabkan karena kecanggihan alat penangkapan ikan dan peningkatan penangkapan ikan yang dilakukan manusia. Untuk menghindari kepunahan, ada beberapa strategi pemanenan yang dapat dilakukan.

Pemanenan merupakan salah satu kegiatan yang dipilih masyarakat untuk memanfaatkan sumber daya perikanan. Di dalam melakukan pemanenan diperlukan berbagai sarana sebagai input yang biasa disebut sebagai usaha pemanenan.

Hal yang sangat penting dalam manajemen perikanan adalah diperolehnya keuntungan maksimum yang dapat berkelanjutan. Hal penting lainnya adalah usaha pemanenan tanpa menggerakkan sistem lingkungannya menuju kepunahan (Brauer & Soudack, 1981).

Strategi pemanenan yang dapat diterapkan dalam manajemen perikanan, diantaranya pemanenan yang dilakukan secara konstan, proporsional, threshold proporsional, dan musiman.

Model persamaan diferensial dapat digunakan untuk memperoleh berbagai model

pemanenan. Dengan melakukan analisis terhadap model pemanenan tersebut dapat dilihat dinamika populasi dan pengaruh peubah kontrol (usaha pemanenan) terhadap nilai kestabilan dan dinamika populasinya.

Karya ilmiah ini menjelaskan pemanenan-pemanenan yang dapat diterapkan dalam manajemen perikanan dan pengaruh dari usaha pemanenan terhadap dinamika populasinya. Sebagai contoh penerapannya dibahas pula pemanenan optimal yang memberikan keuntungan maksimum dan berkelanjutan (sustainable). Pembahasan pemanenan optimal hanya dibatasi untuk pemanenan yang dilakukan secara konstan dan proporsional.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini meliputi:

1. memodelkan dinamika populasi ikan dan analisis kestabilannya;

2. menganalisis pengaruh peubah kontrol terhadap nilai kestabilan dan dinamika populasinya;

3. menganalisis model kebijakan pemanenan optimal yang memberikan keuntungan maksimum dan berkelanjutan.

II LANDASAN TEORI

2.1 Persamaan Diferensial Biasa (PDB)

Persamaan diferensial biasa merupakan suatu persamaan yang melibatkan turunan pertama atau lebih dari fungsi sebarang peubah tak bebas terhadap peubah bebas

.

Suatu persamaan diferensial biasa orde I dapat dinyatakan sebagai berikut

'

( ) ( ) ( ). g x x t  f t

dengan g x( ) adalah fungsi dalam x dan x merupakan peubah tak bebas (xx t( )) dan

( )

f t adalah fungsi dalam t, dengan t peubah bebas.

(Farlow, 1994)

2.2 Persamaan Diferensial Terpisahkan

Persamaan diferensial (PD) terpisahkan adalah persamaan yang dapat ditulis sebagai

.

( , ) atau ( , ). dx

F x t x F x t

dt  

dengan F x t( , ) merupakan persamaan yang ditulis sebagai F x t( , ) f x g t( ) ( ), f x( ) merupakan fungsi dari x dan g t( ) merupakan fungsi dari t. Kemudian persamaan tersebut dapat terpisahkan menjadi

( ) . ( )

dx

g t dt f x 

(Bajpai & Hyslop, 1970)

2.3 Teknik Mencari Solusi PD Terpisahkan (i) Menuliskan persamaan diferensial dengan terpisah

( ) . ( )

dx

g t dt f x 

diperoleh

.

( ) ( ) dx

g t dt A

f x  

 

dengan A merupakan konstanta pengintegralan yang merupakan hasil penggabungan dua konstanta pengintegralan yaitu A₁ dan A₂ dari

.

( )

1 2

( ) dx

A g t dt A

f x   

 

(iii) Melakukansubstitusi sederhana untuk mereduksi persamaan yang peubahnya tidak dapat dipisahkan.

(Bajpai & Hyslop, 1970)

2.4 Persamaan Bernoulli

PDB linear orde satu tak homogen dapat dinyatakan dengan

( ) ( ).

dx

P t x Q t

dt   (2.1)

.

( ) ( )

dx _n

P t x Q t x

dt   _(2.2) (i) Persamaan (2.1) dapat disederhanakan menjadi



P t x Q t( )  ( )



dtdx0.

yang merupakan PDB tak eksak karena



( ) ( )



(1)

. P t x Q t

x y

  



 

dengan memilih faktor integrasi yang hanya tergantung pada t, yaitu ( )t

,

maka persamaan (2.1) dapat dituliskan

( ( ) ( ) t P t x( ) ( ))t Q t dt( )t dx0. yang merupakan PDB eksak, sehingga harus memenuhi

.

( ( ) ( )t P t x ( ) ( ))t Q t ( )t

x t          dan diperoleh ( ) P t dt e

  dengan 0.

selanjutnya dengan mengalikan  pada persamaan (2.1) diperoleh solusi berikut

( ) ( ) ( )

( ) ( )

dx

P t dt P t dt P t dt

e e P t x Q t e

dt

 _  _ 



( )



( )

( )

d P t dt P t dt

e x Q t e

dt

 _ 

( ) ( )

( )

P t dt P t dt

e xe Q t dtc

.

( ) ( ) ( ) P t dt P t dt

xe e Q t dtc

(ii) Persamaan (2.2) dapat disederhanakan

menjadi

1

( ) ( ).

ndx n

x P t x Q t

dt

 _  _

(2.3) dipilih

1

maka (1 )

. (1 )

n n

n

dv dx

v x n x

dt dt

dx x dv

dt n dt

 

  

 

(2.4)

dengan mensubstitusikan persamaan (2.4) ke persamaan (2.3) diperoleh

1

( ) ( ) (1 )

(1 ) ( ) (1 ) ( ). dv

P t v Q t n dt

dv

n P t v n Q t dt        (2.5) dengan memisalkan ( ) (1 ) ( ). ( ) (1 ) ( ).

Pp t n P t

Qq t n Q t

   

sehingga persamaan (2.5) dapat dituliskan menjadi

( ) ( ). dv

Pp t v Qq t

dt   (2.6) persamaan (2.6) memiliki bentuk persamaan yang sama dengan persamaan (2.1) sehingga diperoleh solusi

( 0 ( )

( ) Pp t dt Pp t dt ( ) v t e e Qq t dtc

1 1 1 ( ) . ( ) n x t v t         (Farlow, 1994)

2.5 Masalah Kontrol Optimum

Masalah kontrol optimum terdiri atas pemilihan semua peubah kontrol U t( ) yang mungkin, yang membawa sistem dinamik (dalam hal ini sistem satu dimensi) dari suatu keadaan awal x t( )₀ pada waktu t₀ ke keadaan akhir x T( ) pada waktu T , sedemikian sehingga menghasilkan fungsi tujuan yang maksimum, yaitu

Maks

 

0

0( ( ), ( ), ) .

T

J U f x t u t t dt

t

 

dengan f₀( , , )x u t diberikan dan merupakan fungsi bernilai real.

(Tu, 1993)

2.6 Kestabilan PD Orde Satu

Suatu persamaan diferensial linear orde satu berbentuk

.

0 dengan 0.

x ax  a (2.7)

memiliki nilai ..

x a yang bersifat stabil jika 0

a dan bersifat tidak stabil jikaa0.

Bukti :

Tuliskan persamaan (2.7) sebagai /

dx x adt, kemudian kedua sisi diintegralkan sehingga diperoleh

0

( ) at

x t x e

.

Jika a0, maka solusi akan meningkat secara eksponensial. Jika a0, maka solusi akan menuju nol. Solusi ekuilibrium adalah

( ) 0. x t 

Jika a0 maka solusi bersifat tak stabil, karena

0

lim_t| ( )x t  0 | lim_t|x |eat  . Jika a 0 maka solusi bersifat stabil, karena

0

lim_t| ( )x t  0 | lim_t|x |eat 0.

(Tu, 1994)

2.7 Diagram Fase

Suatu persamaan diferensial .

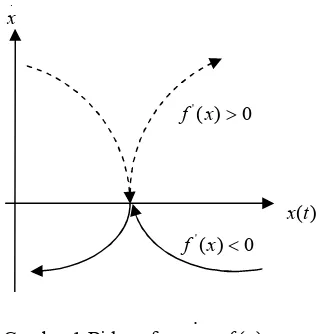
( ) x f x tidak semuanya dapat diselesaikan secara kuantitatif. Jika hal ini terjadi maka diperlukan solusi kualitatif dalam bentuk diagram fase. Diagram fase akan menggambarkan perubahan kecepatan

. ( )x terhadap x (Lihat pada Gambar 1).

Jika .

0

x maka kurva berada di atas

sumbu horizontal, yaitu x meningkat sepanjang waktu yang ditunjukkan oleh panah dari arah kiri ke kanan. Jika

. 0 x maka kurva berada di bawah sumbu horizontal, yaitu

x

menurun sepanjang waktu ditunjukkan oleh panah dari arah kanan ke kiri. Pada sumbu horizontal,

. 0

x yaitu tidak berubah, merupakan titik ekuilibrium atau titik tetap.

Jika f'( )x 0 maka ( )f x adalah fungsi turun, sehingga ekuilibrium stabil. Jika

' ( ) 0

f x  maka f x( ) adalah fungsi naik, sehingga ekuilibrium tak stabil.

(Tu, 1994)

. x

'

( ) 0 f x 

x t( ) '

( ) 0 f x 

Gambar 1 Bidang fase .

( ) x f x

III MODEL - MODEL DASAR

3.1 Model Logistik

Menurut Clark (1976), Murray (1993) dan Kreyszig (1993), jika dimisalkan x t( ) adalah populasi ikan pada waktu t, maka tingkat pertumbuhan populasi ikan terhadap waktu t pada suatu daerah tertentu dapat dituliskan sebagai berikut

dx dt/ = kelahiran- kematian + migrasi. Model sederhana tingkat pertumbuhan populasi tanpa migrasi dapat dituliskan seperti berikut

/ ( ) .

dx dt  nm x Rx

dengan n m, adalah konstanta positif yang masing-masing menyatakan tingkat kelahiran dan kematian populasi ikan dan R adalah

parameter yang menyatakan pertumbuhan alamiah ikan (kelahiran dikurangi kematian) dan diasumsikan positif.

Adanya persaingan antar individu, keterbatasan ruang, keterbatasan makanan dan keterbatasan sumber daya lainnya akan mempengaruhi pertumbuhan populasi ikan. Untuk itu model yang lebih baik adalah model pertumbuhan logistik yang diperkenalkan oleh P.F. Velhurst, yaitu

2

/

dalam populasi per satuan waktu.

Misalkan dalam populasi ada x individu, dan daya dukung lingkungan K dimasukkan ke dalam model, maka lingkungan masih dapat mendukung Kx individu. Jadi masih ada bagian lingkungan yang masih bisa diisi sebesar K x

K



.

Bagian inilah yang sebanding dengan pertumbuhan populasi. Oleh karena itu persamaan pertumbuhan menjadi

.

( ) ( ) ( ) 1

dx x t

F x Rx t

dt K

 















(3.1)

Persamaan (3.1) disebut model pertumbuhan logistik.

Sebagai keterangan K R a/ menyatakan daya dukung lingkungan atau titik maksimum dimana laju pertumbuhan akan menurun bahkan berhenti.

Dari persamaan matematis (3.1) terlihat bahwa dalam keadaan seimbang dx 0

dt 













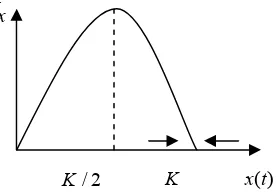
populasi akan sama dengan daya dukung lingkungan, sedangkan maksimum pertumbuhan akan terjadi pada kondisi setengah daya dukung lingkungan. Kurva pertumbuhan logistik dapat dilihat pada gambar di bawah ini

. x

K/ 2 K ( )x t

Gambar 2 Kurva pertumbuhan logistik Solusi persamaan (3.1) menggunakan masalah nilai awal (0)x K N/ , dimana N suatu konstanta positif tak nol N 1 dapat diselesaikan dengan pengintegralan terpisahkan, yaitu

.

( )

1 ( 1) Rt K x t

N e



  (3.2)

3.2 Model Umum Pemanenan

Persamaan pertumbuhan logistik (3.1) menunjukkan bahwa model perikanan tersebut belum mengalami eksploitasi atau

faktor penangkapan belum dimasukkan ke dalam model. Dalam usaha penangkapan ikan dibutuhkan berbagai sarana sebagai faktor masukkan atau input yang biasa disebut sebagai usaha pemanenan.

Hubungan antara tingkat pertumbuhan alamiah dengan usaha pemanenan merupakan dinamika populasi persediaan ikan. Laju pertumbuhan persediaan ikan (dx dt/ ) ditentukan oleh kemampuan reproduksi alamiah dan hasil ikan yang dipanen dari persediaan ikan tersebut.

Hasil pemanenan dapat dituliskan sebagai ( )

h t yang merupakan fungsi produksi yang diasumsikan menggambarkan dua kuantitas, yaitu ukuran persediaan populasi ikan saat t dan tingkat usaha pemanenan (0U 1) sehingga

( ) ( ) .

h t qx t U (3.3) dengan 0 q 1 adalah konstanta yang menyatakan catchability (kemampuan tangkap) .

Menurut Clark (1979), jika usaha pemanenan dilakukan dengan ukuran h t( ), maka persamaan (3.1) menjadi

( ) ( ) dx

F x h t

dt  

Rx t( )(1x t( ) /K)qx( ) .t U (3.4) dengan peubah tak bebas x t( )0, peubah kontrol U t( )0yang tergantung pada strategi pemanenan yang dilakukan. Populasi awal (0)x diasumsikan diketahui, sedangkan

( )

h t

diasumsikan 0h t( )h_maks, dengan h_maks hasil maksimum ikan yang dipanen setiap waktu.

3.3 Model Usaha Pemanenan

Diasumsikan usaha pemanenan konstan yaitu

( , ) . U t x U

Sedangkan usaha pemanenan tak konstan diasumsikan sebagai berikut

.

1

( , ) ( ) ( ) dx

U t x t t

x dt

 

  (3.5)

dengan  0 dan  0 adalah fungsi kontinu terhadap t

,

akan tetapi dalam pembahasan selanjutnya dandiasumsikan konstan.

(Idels & Wang, 2008)

3.4 Model Keuntungan Maksimum

Dalam kegiatan penangkapan ikan, perusahaan menjual tingkat output tertentu

( )

h t dengan harga pasar p per unit output yang dijual. Maka penerimaan total per unit waktu dapat dituliskan

( ) ( ). P_rev t  ph t

Dalam memproduksi h t( ) total biaya ekonomi per unit usaha yang ditanggung dapat dinyatakan dengan cU dan dituliskan sebagai berikut

. B

cU c UnwU dengan

B

c : biaya overhead untuk pemeliharaan satu perahu per unit waktu t, dengan

0. c

n : rata-rata jumlah pemancing per perahu.

p : harga jual per unit ikan, p0. w : gaji satu pemancing per unit waktu.

Sehingga keuntungan per unit waktu yang dapat berkelanjutan dituliskan

( ) ( ) .

P U  pqUx t cU (3.6) Dalam pembahasan ini c_B, n, p dan wdiasumsikan bernilai konstan. Kondisi yang diperlukan untuk nilai U konstan yang memaksimumkan keuntungan ditentukan dengan P U'( )0.

3.5 Teori Modal

Apabila modal awal P diinvestasikan pada suku bunga tahunan  dan dimajemukkan k kali per tahun, maka setelah t

t

ahun nilainya akan bertambah secara eksponensial seperti berikut

.

( ) 1

kt

B t P

k



















(3.7)

Jika suku bunga dimajemukkan secara kontinu (bukan tahunan, bulanan, atau harian, tetapi setiap saat) dengan kata lain k , maka rumus (3.7) akan berubah dengan perhitungan sebagai berikut

Misalkan n k



 maka n  dan kn sehingga

1

1 1

kt n t

P P k n     

























1 1 .

t n P n  































karena n , maka

.

1

( ) lim 1

n t t

B t _n P Pe

n

 

 _

















(3.8)

dengan B t( ) adalah future value, waktu 0

t dan e2.718.

Present value dari penerimaan sebesar B di masa yang akan datang adalah

.

( ) t

PB t e (3.9) Total present value yang kontinu dari deretan pendapatan P0, dengan 0 t T dapat dirumuskan sebagai berikut

0

.

( ) T

t

P B t edt (3.10) Untuk kasus T  , persamaan (3.10) menjadi

0

lim ( )

T

t T

P _B t e dt

0

.

( ) t P B t e  dt

 _

  (3.11) (Hoftmann & Bradley, 1989)

IV MODEL PEMANENAN PERIKANAN

4.1 Model Pemanenan Ikan

4.1.1 Pemanenan Konstan

Pemanenan konstan yaitu pemanenan dengan hasil panen yang tetap setiap tahunnya. Diasumsikan usaha pemanenan

( , )

U t x U adalah fungsi konstan dan hasil pemanenan h t( ) dijaga tetap konstan, sehingga model pemanenan konstan, yaitu

( )

( ) 1 ( ).

dx x t

Rx t qUx t

dt   K 













(4.1)

Solusi persamaan (4.1) diperoleh dengan menggunakan persamaan Bernoulli (Lihat pada Lampiran 1), yaitu

( ) .

( )

( )

( ) t R qU

K R qU

x t

CK R qU e  R

 

 

(4.2

)

4.1.2 Pemanenan Proporsional

Pemanenan proporsional yaitu pemanenan dengan hasil panen yang meningkat secara proporsional setiap tahunnya. Diasumsikan usaha pemanenan tak konstan.

Dengan mensubstitusikan persamaan (3.5) ke persamaan (3.4) diperoleh model pemanenan proporsional, yaitu

( ) 1

( ) 1 ( ) ( ) ( ) .

dx x t dx

Rx t qx t t t

dt K x dt

  

































(4.3)

0 1 merupakan konstanta yang menyatakan ukuran proporsional. Persamaan (4.3) dapat disederhanakan menjadi

( )

( ) 1 ( ).

1 1

dx R x t q

x t x t

dt q K q

          













(4.4) dengan  q 1.

Solusi persamaan (4.4) diperoleh dengan menggunakan persamaan Bernoulli (Lihat pada Lampiran 2), yaitu

.

( )

( )

1

( )

K R q

x t

R q t

q

CK R q e R

               _  _   (4.5) dengan C suatu konstanta.

4.1.3 Pemanenan Threshold Proporsional

Pemanenan threshold adalah pemanenan proporsional dengan batasan harus ada populasi yang dipertahankan. Diasumsikan usaha pemanenan tak konstan serta ada besaran populasi yang harus dipertahankan yaitu x_thre

.

Dengan mensubstitusikan persamaan (3.5) ke persamaan (3.4) diperoleh model pemanenan threshold proporsional, yaitu

(i) jika ( )x t x_thre maka



( )



( )

( ) 1 x t _xthre

dx x t

Rx t q

dt   K  













.

1 ( )t ( )t dx

x dt

 













_(4.6)

(ii) jika

x t

( )



x

thre, maka

.

( ) ( ) 1

dx x t

Rx t

dt   K













0

x_thre  , 0  1 merupakan konstanta yang menyatakan ukuran proporsional. Persamaan (4.6) dapat disederhanakan menjadi

.

( )

( ) 1 0 1 ( ( ) )

1 1

( ) x t

Rx t q x t x

thre dx K x dt _thre q x t            





































(4.7) . 1 ( ) 1 x_thre x t

q

 

















4.1.4 Pemanenan Musiman

Pemanenan dengan hasil panen yang berubah setiap tahunnya, ada saat hasil panennya meningkat dan ada saat hasil panennya menurun. Hal ini dikarenakan adanya pengaruh musim yang dirumuskan dengan fungsi periodik ( ( )) t . Selanjutnya diasumsikan usaha pemanenan tak konstan.

Dengan mensubstitusikan persamaan (3.5) ke persamaan (3.4) diperoleh model pemanenan musiman, yaitu

( )

( ) 1 x t ( ) ( )

dx _{Rx t t qx t}

dt   _K 













.

1 ( )t ( )t dx

x dt

 













(4.8)

( )t

 merupakan fungsi periodik dengan periode satu tahun. Persamaan (4.8) dapat disederhanakan menjadi

.

( )

( ) 1 ( ) ( )

1 ( )

x t

Rx t t qx t

dx K

dt t q

       













(4.9) dengan ( )t q 1.

4.2 Maximum Sustainable Yield

Menurut Clark (1976), manajemen sumber daya yang dapat diperbaharui (perikanan) didasarkan pada konsep maximum sustainable yield (MSY) atau hasil pemanenan maksimum yang berkelanjutan. Konsep tersebut didasarkan pada model pertumbuhan biologi yang mengasumsikan jika banyaknya persediaan dalam populasi lebih rendah dibandingkan dengan suatu level persediaan

K, maka akan terdapat surplus produksi

yang dapat dipanen. Jika surplus tersebut tidak dipanen maka akan menyebabkan peningkatan level atau menuju daya dukung lingkungan

K.

Untuk memperlihatkan perilaku dinamika dari populasi yang berhubungan dengan kesimbangan dan kestabilan ekuilibrium biologis dalam perikanan, akan ditinjau dua hal berikut, yaitu

4.2.1 Level Usaha Pemanenanan

(1) Pemanenan Konstan

Untuk level usaha pemanenan konstan, maka persamaan (4.1) akan memiliki ekuilibrium stabil pada x0, yang diberikan oleh

* *

1 x qU 0

Rx K R   













* 0 xu  dan

*

1 qU .

x_s K

R 















Kondisi kestabilan dari titik tetap x_u*

,

*

s

x diperoleh dengan memeriksa turunan pertama model pertumbuhannya, kemudian disesuaikan dengan kondisi kestabilan pada sub bab 2.6.

2 ( ) .

dF Rx t

R qU

dx K

   (4.10)

a. Kestabilan Titik Tetap x_u*

Dengan mensubstitusi x_u* 0 ke persamaan (4.10) diperoleh

. dF

R qU

dx  

Agar sistem di titik x_u*stabil, maka harus dipenuhi syarat dF 0

dx 

0 .

dF

R qU

dx   

Pada keadaan x_u* 0 tidak dapat dilakukan pemanenan, karena populasi akan menuju kepunahan.

b. Kestabilan Titik Tetap x_s* Dengan mensubstitusikan

*

1 qU

x_s K

R 















ke persamaan (4.10) diperoleh dF

dx , yaitu

( ) .

dF

R qU K

dx   

Agar sistem di titik s* 1 qU

x K

R 















stabil,

maka harus dipenuhi dF 0 dx 

0 ( )

dF

R qU

dx    

RqU.

Pada keadaan x_s* 1 qU K R 















dapat

dilakukan pemanenan, karena kepunahan tidak akan terjadi.

Sehingga dapat disimpulkan

* 1 ; jika R>qU

0 ; selainnya

qU K x R           Misalkan

1, 0.3, 0.10 / 0.20 / 0.36 / 0.42 / 1.00

K  R q

danU 1.15

,

sehingga diperoleh _xs*0.617 untukq0.15danxs*0.233 untukq0.20

, sedangkan untuk qlainnya populasi akan menuju kepunahaan.

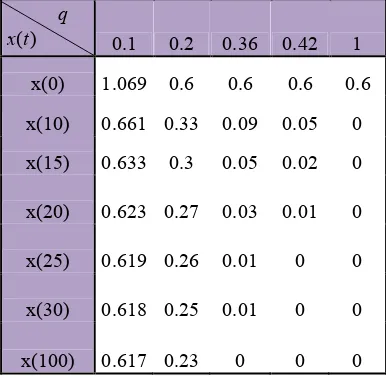
Tabel 1 Dinamika populasi pemanenan konstan

q ( )

x t _{0.1 0.2 0.36 0.42 1} x(0) 1.069 0.6 0.6 0.6 0.6 x(10) 0.661 0.33 0.09 0.05 0 x(15) 0.633 0.3 0.05 0.02 0

x(20) 0.623 0.27 0.03 0.01 0

x(25) 0.619 0.26 0.01 0 0

x(30) 0.618 0.25 0.01 0 0

x(100) 0.617 0.23 0 0 0

Tabel 2 Dinamika populasi dengan beberapa nilai awal

x(t) q 0.2

x(0) 0.1 0.2 0.3 0.6 x(10) 0.14 0.22 0.26 0.3 x(15) 0.16 0.22 0.25 0.3 x(20) 0.18 0.22 0.24 0.3 x(25) 0.19 0.23 0.24 0.3 x(30) 0.2 0.23 0.24 0.3 x(100) 0.23 0.23 0.23 0.2

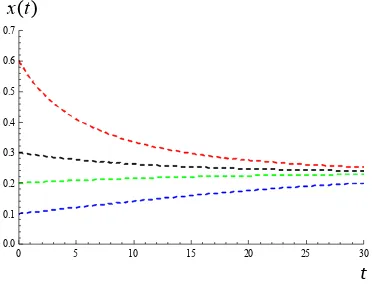
Kenaikan q dengan U tetap yang menyebabkan qU R maka populasi menuju nol (kepunahan), tetapi jika qU R maka populasi menuju nilai kestabilannya untuk sembarang nilai awal.

( ) x t

0 5 10 15 20 25 30

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

t

Gambar 3 Dinamika populasi pemanenan konstan

Keterangan : Kuning : q = 0.10 Merah : q

=

0.20 Ungu : q = 0.36 Hijau : q = 0.42 Hitam : q = 1.00

( ) x t

0 5 10 15 20 25 30

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

t

Gambar 4 Dinamika populasi pemanenan konstanq0.2 dengan nilai awal

(2) Pemanenan Proporsional

Untuk level usaha pemanenan proporsional, maka persamaan (4.4) akan memiliki ekuilibrium stabil pada x0, yang diberikan oleh

* _*

* 1

1 1

R x q

x x

q K q

 

   

 

 

 

  

 

*

0

u

x  dan * 1 q K.

s _R

x _  _

Kondisi kestabilan dari titik tetap x_u*,x_s* diperoleh dengan memeriksa turunan pertama model pertumbuhannya, kemudian disesuaikan dengan kondisi kestabilan pada sub bab 2.6.

.

2

1 (1 ) 1

dF R Rx q

dx q K q q



     

 _  _  _

a. Kestabilan Titik Tetap *

u

x

Dengan mensubstitusikan * 0

u

x  ke

persamaan (4.11) diperoleh dF

dx

,

yaitu

.

1

dF R q

dx q

    

 _

Agar sistem di titik x_u*0 stabil, maka harus dipenuhi syarat dF 0

dx  0

1

dF q R

dx q

     



 R  q .

Pada keadaan x_u*0 tidak dapat dilakukan pemanenan, karena populasi akan menuju kepunahan.

b. Kestabilan Titik Tetap * s x Dengan mensubstitusikan * 1 s q x K R          

ke persamaan (4.1.1) diperoleh dF

dx , yaitu

.

1

dF q R

dx q

   

 _

Agar sistem di titik * 1

s q x K R        

  stabil, maka harus dipenuhi dF 0

dx 

0 0

1

dF q R

dx q

   

  



 R  q .

Pada keadaan x_s* 1 q K R

 

 

 

 

  dapat dilakukan pemanenan, karena kepunahan tidak akan terjadi.

Sehingga dapat disimpulkan

1 ; jika

0 ; selainnya

* q K R q

R x_s   _{ }  _  _       

Selanjutnya akan diperlihatkan pengaruh peubah kontrol  terhadap dinamika populasi menuju nilai kestabilannya. Kenaikan  menyebabkan populasi lebih cepat menuju nilai kestabilannya.

Misalkan

0.5, 0.5, 0.8, 1.0, 1.0, 1

R  q    K 

dan  q 0.40.5

,

sehingga diperoleh

* 0.2

s

x  . Kenaikan  sehingga  q 0.5 menyebabkan populasi menuju nol (kepunahan).

Tabel 3 Dinamika populasi pemanenan proporsional

x(0) β x(5) x(20) x(50) x(100)

0.6

1 0.28 0.21 0.2 0.2 0.5 0.31 0.21 0.2 0.2 0.3 0.32 0.21 0.2 0.2

0.1

1 0.14 0.19 0.19 0.2 0.5 0.13 0.18 0.2 0.2 0.3 0.13 0.18 0.2 0.2

Perubahan nilai  tidak mempengaruhi nilai kestabilan, tetapi kenaikan  menyebabkan populasi lebih cepat menuju nilai kestabilannya.

( ) x t

0 5 10 15 20 25 30

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 _t

Gambar 5 Dinamika populasi pemanenan proporsional

Keterangan :

Merah :  0.5;q0.6 Hijau :  0.5;q0.1 Ungu :  0.7;q0.6

( ) x t

0 5 10 15 20 25 30

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 t

Gambar 6 Pengaruh nilai  terhadap dinamika populasi Keterangan :

Merah :  1 Hijau :  0.5 Ungu :  0.3

(3) Pemanenan Threshold Proporsioanal

Untuk level pemanenan threshold proporsional, maka persamaan (4.7) akan memiliki ekuilibrium stabil pada x0, yang diberikan oleh









0

*

* ₁ *

* 1

* x

Rx q x x_thre

K q

x x_thre x

 

  

  

 

















2 2

( ) ( ) 4 ( )

*

0 2

K q R q R K RK _{q xthre}

xu

R

     

      

dan

2 2

( ) ( ) 4 ( )

*

0 2

K q R q R K RK _{q xthre}

x s

R

     

    

 

a. Kestabilan Titik Tetap *

u

x

*

0

u

x  menunjukkan populasi ikan punah.

b. Kestabilan Titik Tetap *

s

x Jikax t( ) x

thre

 dengan 0 x K

thre

 

maka pemanenan dapat dilakukan dan populasi menuju titik tetap stabil dengan nilai x_s* lebih kecil dari K pemanenan threshold proporsional tidak menyebabkan populasi menuju kepunahan (Lihat pada Gambar 7).

Suatu persamaan diferensial tidak semuanya dapat diselesaikan secara kuantitatif. Dinamika populasi dan pengaruh

peubah kontrol β akan diperlihatkan dengan

solusi kualitatif.

Misalkan

1.0,K 1.0,x_thre 0.2 1,R 0.5, 0.5

      

0.8, 1.0,

q   dan  q 0.40.5, sehingga diperoleh x_u*  0.312 dan

*

0.512 s

x  .

.

x

0.1 0.2 0.3 0.4 0.5 0.02

0.04 0.06 0.08

x

Gambar 7 Bidang fase pemanenan threshold

Akan diperlihatkan pengaruh nilai  terhadap dinamika populasipada Gambar 8, 9, 10. Pada gambar tersebut dapat terlihat bahwa perubahan nilai  tidak mempengaruhi nilai kestabilannya, akan tetapi kenaikan  menyebabkan populasi lebih cepat menuju nilai kestabilannya. Pada pemanenan threshold proporsional, meskipun

q R

   populasi tidak akan menuju nol atau kepunahan (Lihat pada Gambar 11) .

(4) Pemanenan Musiman

Untuk level usaha pemanenan musiman, maka persamaan (4.9) akan memiliki ekuilibrium stabil pada x(0)0, yang diberikan oleh

*

* *

1 ( )

0 1 ( )

x

Rx t qx

K t q

 

 

 

 

















* 0

u

x 

dan

( ) *

1 t q K.

s _R

x  _  _

Kondisi kestabilan dari titik tetap

* * ,

u s

x x diperoleh dengan memeriksa turunan pertama model pertumbuhannya, kemudian disesuaikan dengan kondisi kestabilan pada sub bab 2.6, yaitu

.

2

( )

1 ( )

Rx

R t q

dF _K

dx t q

 

 

 



 _(4.12)

a. Kestabilan Titik Tetap

Dengan mensubstitusi * 0

u

x  ke

persamaan (4.12) diperoleh dF

dx , yaitu

.

( ) 1 ( )

dF R t q

dx t q

 

 

 



Agar sistem di titik x_u*0 stabil, maka harus dipenuhi syarat dF 0

dx  ( )

0 0

1 ( )

dF R t q

dx t q

 

 



  _ 

 R ( )t q.

Dengan demikian x_u* merupakan titik tetap tak stabil dan pada keadaan _xu*0 tidak dapat dilakukan pemanenan, karena populasi akan menuju kepunahan.

11

Gambar 8 Pengaruh nilai  1 Gambar 9 Pengaruh nilai  2.5

Gambar 10 Pengaruh nilai Gambar 11 Dinamika populasi dengan

4

2.5 10

   

b. Kestabilan Titik Tetap * s x Dengan mensubstitusikan ( ) *

1 t q K

x_s R          

ke persamaan (4.12) diperoleh

.

( ) 1 ( )

dF t q R

dx t q

 

  



Agar sistem di titik x* 1 ( )t q K

s _R           stabil, maka harus dipenuhi dF 0

dx  ( )

0 0 ( ) .

1 ( )

dF t q R

R t q

dx t q

  _{ }

 

  _   

Dengan demikian *

s

x merupakan titik tetap stabil dan pada keadaan

( ) *

1 t q

x_s K

R

 

 

 

 

  dapat dilakukan

pemanenan, karena kepunahan tidak akan terjadi.

Sehingga dapat disimpulkan ( )

1 ; jika R>λ(t)qα *

0 ; selainnya

t q K x R            

Misalkan 1 sin(2 )

4

( )t t

   akan maksimum pada saat (0.25n)0.5 dan minimum pada saat (0.75 n)0 untukn=0, 1, 2, … karena ( )t bersifat periodik menyebabkan nilai x_s* berubah-rubah.

Misalkan diberikan data seperti berikut 0.3, 4, 0.04 / 0.30 / 0.49, 1

R   q K 

( ) x t

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6

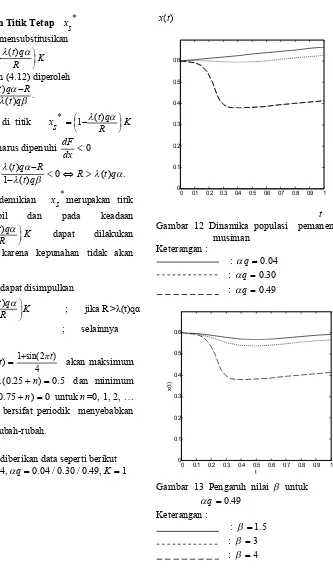
t Gambar 12 Dinamika populasi pemanenan

musiman Keterangan :

: q0.04 : q0.30 : q0.49

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 t x (t )

Gambar 13 Pengaruh nilai  untuk 0.49

q

  Keterangan :

:  1.5 :  3

:  4

[image:31.595.167.500.74.661.2]

[image:32.595.117.293.99.362.2]

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 t x (t )

Gambar 14 Pengaruh nilai  untuk 0.04

q

  Keterangan :

:  0 :  1.5

:  4

Dari Gambar 13 dan 14 terlihat bahwa nilai  mempengaruhi *

s

x , jika x(0) di atas *

xs maka penurunan nilai  akan menyebabkan kenaikan pada x_s*. Tetapi jika

(0)

x di bawah x_s* maka perubahan nilai  tidak menyebabkan perubahan pada *

s

x . Pada pemanenan ini, populasi tidak akan menuju kepunahan.

4.2.2 Hasil Pemanenan Maksimum

1. Pemanenan Konstan

Ekuilibrium hasil pemanenan (sustainable yield)

,

diperoleh dengan mensubstitusikan persamaan _xs* ke persamaan (3.3), sehingga diperoleh persamaan berikut

* ( )

h U qx U_s

( )h U q 1 qU KU. R 















(4.13)

Persamaan (4.13) merupakan persamaan kuadrat yang memiliki grafik berbentuk parabola. Nilai U yang memaksimumkan h

diperoleh dengan menentukan dh 0

dU 

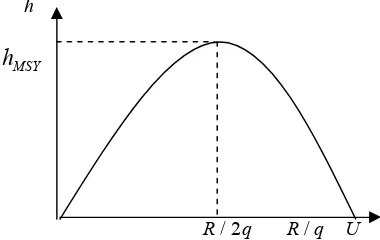
sehingga diperoleh U* R/ 2q pada saat ( ) / 2

x t K . Solusi inilah yang dikenal dengan maximum sustainable yield (MSY).

h

MSY

h

[image:32.595.324.514.174.294.2]

R/ 2q R q/ U Gambar 15 Kurva usaha pemanenan konstan

Gambar 15 menyatakan hubungan antara U dan h, kenaikan U akan meningkatkan hasil pemanenan hingga sampai pada level pemanenan maksimum yaitu pada

/ 2

U R q dan x t( )K/ 2

,

untuk / 2

U R q hasil pemanenan akan menurun menuju nol. Untuk U R q/ hasil pemanenan adalah nol. Usaha pemanenan yang cukup besar dapat menyebabkan populasi punah dan hasil panen menjadi nol.

Level pemanenan h konstan ( ) .

dx

F x h

dt   (4.14) Sehingga hasil pemanenan maksimum (maximum sustainable yield ) diperoleh pada saat dx 0

dt  yaitu

( ) 0

F x h

dx

dt  



h F x( )

MSY 

( ) ( ) 1 x t Rx t K         /2 1 2 RK K K        

. 4 RK

 (4.15) Misalkan K 1,R0.5,q0.8 sehingga

diperoleh h_MSY 0.125 dengan U*0.3125 pada saat persediaan populasi ikan

( ) 0.5.

x t  Jika dipilihU 0.25U*maka hasil panen sebesar h0.12, sehingga usaha

[image:32.595.325.510.500.747.2]

pemanenan masih dapat ditingkatkan sampai mencapai hasil panen yang maksimum.

2. Pemanenan Proporsional

Ekuilibrium hasil pemanenan (sustainable yield) h, diperoleh dengan mensubstitusikan persamaan x_s* dan persamaan (3.5) ke persamaan (3.3), sehingga diperoleh persamaan berikut

* ( )

h  q x s

.

( ) 1 q

h q K

R

 

   _  _ (4.16) Persamaan (4.16) merupakan persamaan

kuadrat yang memiliki grafik berbentuk parabola. Nilai  yang memaksimumkan

( )

h diperoleh dengan menentukan

/ 0,

dh d  sehingga diperoleh 2

R q

  _

dengan ( )x t K/ 2.Solusi inilah yang dikenal dengan maximum sustainable yield (MSY).

Dengan mensubstitusikan nilai

*

2 R q

  _ ke persamaan (4.16), maka akan

diperoleh hasil pemanenan maksimum dalam keadaan seimbang tanpa kepunahan h* yaitu

MSY 4 . RK

h  (4.17)

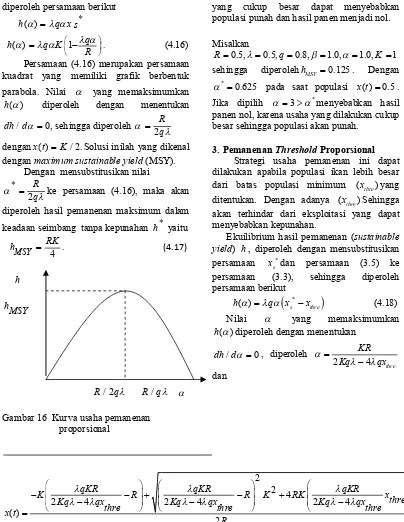
h

h_MSY

[image:33.595.111.515.188.710.2]

R/ 2q R q/  

Gambar 16 Kurva usaha pemanenan proporsional

Dari Gambar 16 dapat dilihat hubungan antara  dan h, kenaikan  akan meningkatkan hasil pemanenan hingga sampai pada level pemanenan maksimum yaitu pada

/ 2

R q

  dan x t( )K/ 2, untuk / 2

R q

 hasil pemanenan akan menurun menuju nol, sedangkan untuk R q/ hasil pemanenan adalah nol. Usaha pemanenan yang cukup besar dapat menyebabkan populasi punah dan hasil panen menjadi nol.

Misalkan

0.5, 0.5, 0.8, 1.0, 1.0, 1

R  q    K 

sehingga diperolehh_MSY 0.125. Dengan *

0.625

  _{pada saat populasi} x t( )0.5. Jika dipilih *

3

  menyebabkan hasil panen nol, karena usaha yang dilakukan cukup besar sehingga populasi akan punah.

3. Pemanenan Threshold Proporsional

Strategi usaha pemanenan ini dapat dilakukan apabila populasi ikan lebih besar dari batas populasi minimum (x_thre)yang ditentukan. Dengan adanya (xthre)Sehingga akan terhindar dari eksploitasi yang dapat menyebabkan kepunahan.

Ekuilibrium hasil pemanenan (sustainable yield) h, diperoleh dengan mensubstitusikan persamaan *

s

x dan persamaan (3.5) ke persamaan (3.3), sehingga diperoleh persamaan berikut



*



( ) _{s thre}

h  q x x (4.18) Nilai  yang memaksimumkan ( )

h diperoleh dengan menentukan

/ 0

dh d  , diperoleh

2 4 _thre

KR Kq qx      dan 2 2 ₄

2 4 2 4 2 4

( )

2

qKR qKR qKR

K R R K RK x

thre

Kq qx Kq qx Kq qx

thre thre thre

Solusi inilah yang dikenal dengan maximum sustainable yield (MSY).









( )

( ) .

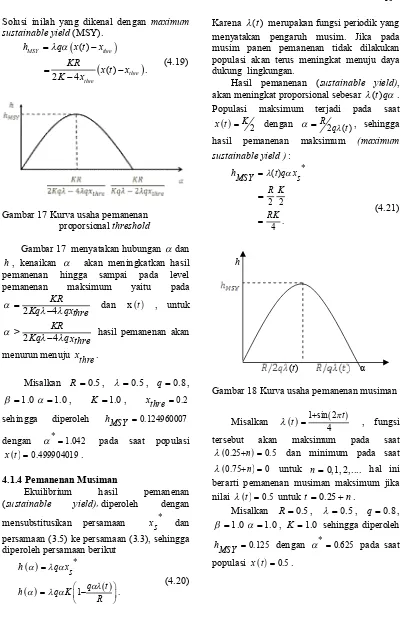
2 4

MSY thre

thre thre

h q x t x

KR

x t x

K x

 

 

 



[image:34.595.111.516.69.706.2]

(4.