PERBANDINGAN ANALISIS RAGAM KLASIFIKASI SATU ARAH METODE KONVENSIONAL DENGAN METODE ANOM

PERBANDINGAN ANALISIS RAGAM KLASIFIKASI SATU ARAH METODE KONVENSIONAL DENGAN METODE ANOM

(Skripsi)

Oleh

Latusiania Oktamia 0817031005

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

ABSTRAK

PERBANDINGAN ANALISIS RAGAM KLASIFIKASI SATU ARAH METODE KONVENSIONAL DENGAN METODE ANOM

Oleh

LATUSIANIA OKTAMIA

Untuk melihat apakah ada perbedaan antar rata-rata perlakuan umumnya

digunakan analisis ragam. Pada penelitian ini akan dibahas penggunaan analisis ragam klasifikasi satu arah metode konvensional dengan metode ANOM. Pembahasan dikhususkan pada analisis ragam klasifikasi satu arah, dan dilanjutkan dengan perbandingan nilai tengah dengan menggunakan metode SANOM dan ProsedurTukey w. Dari hasil penelitian diperoleh kesimpulan bahwa ANOM dan SANOM merupakan prosedur alternatif analisis ragam dalam membandingkan rata-rata dan pasangan nilai tengah yang dapat diterapkan dengan lebih mudah dan efisien serta ANOM juga menghasilkan grafik yang

menunjukkan letak perbedaan rata-rata yang tidak ditunjukkan pada Anara dengan metode konvensional.

ABSTRACT

COMPARATIVE STUDY OF ONE-WAY ANALYSIS OF VARIANCE USING CONVENTIONAL METHODS WITH ANOM

By

LATUSIANIA OKTAMIA

Analysis of variance (ANOVA) is a common way to compare the difference of treatments effect. In this study, we showed the use of conventional ANOVA compare with ANOM. We also tried to elaborate SANOM method and Tukey to see the difference between the two method. The results showed that ANOM and SANOM can be applied more easily and efficiently and produces a graph that shows the location of the average of treatment effect which is not shown in conventional method.

MENGESAHKAN

1. Tim Penguji

Ketua : Netti Herawati, Ph.D. ………

Sekretaris : Eri Setiawan, M.Si. ………

Penguji

Bukan Pembimbing : Mustofa Usman, Ph.D. ………

2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Prof. Suharso, Ph.D.

NIP. 19690530 199512 1 001

RIWAYAT HIDUP

Penulis dilahirkan pada 21 Oktober 1991 di Sukaratu kecamatan Kalianda kabupaten Lampung Selatan, dan adalah anak ketiga dari tiga bersaudara, dari pasangan Bapak Harudin dan Ibu Mursida.

Penulis memulai pendidikan dari SD Negeri 1 Padan pada tahun 1996 dan diselesaikan pada tahun 2002. Kemudian pendidikan sekolah lanjut tingkat menengah diselesaikan di SMP Negeri 1 Kalianda pada tahun 2005 dan sekolah lanjutan tingkat atas di SMA Negeri 1 Kalianda pada tahun 2008. Pada masa sekolah lanjutan tingkat atas penulis menorehkan prestasi di berbagai kejuaraan karate tingkat kabupaten dan propinsi.

MOTTO

Dan apabila hamba-hambaKu bertanya kepadamu tentang Aku, maka (jawablah) bahwasanya Aku adalah dekat, Aku mengabulkan permohonan orang

yang berdoa apabila ia memohon kepadaKu (QS. Al-Baqarah : 186)

Jangan takut jatuh, karena yang tidak pernah memanjatlah yang tidak pernah jatuh. Jangan takut gagal, karena yang tidak pernah gagal hanyalah

orang-orang yang tidak pernah melangkah. Jangan takut salah, karena dengan kesalahan yang pertama kita dapat menambah pengetahuan untuk mencari jalan

yang benar pada langkah yang kedua (Buya Hamka)

PERSEMBAHAN

Satu persembahan kecil yang mampu diselesaikan atas izin Allah SWT untuk kedua orang tua, Bapak Harudin dan Ibu Mursida, kakak dan abang, Nurhayani

SANWACANA

Alhamdulillahi robbil ‘alamin_{, puji dan syukur penulis kepada Allah SWT atas} izin ridho-Nya dalam menyelesaikan skripsi ini. Shalawat juga salam atas Nabi Muhammad SAW, tuntunan dan tauladan utama.

Pada proses penyusunan skripsi ini, penulis memperoleh banyak dukungan, kritik, dan saran yang membangun sehingga skripsi ini mampu penulis selesaikan. Untuk itu penulis ingin mengucapkan terima kasih kepada :

1. Ibu Netti Herawati, Ph.D., selaku dosen pembimbing utama yang telah meluangkan waktu dari padatnya kesibukan beliau untuk membimbing dan mengoreksi, hingga skripsi ini selesai.

2. Bapak Eri Setiawan, M.Si., selaku dosen pembimbing pembantu yang telah banyak membantu dan memberikan pengarahan dalam proses penyusunan skripsi ini.

3. Bapak Mustofa Usman, Ph.D., selaku dosen penguji bukan pembimbing yang memberi penulis masukan dan saran.

4. Ibu Fitriani, M.Sc., selaku pembimbing akademik.

5. Bapak Tiryono Ruby, Ph.D., selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.

7. Dosen, staf dan karyawan Jurusan Matematika FMIPA UNILA yang telah memberikan ilmu pengetahuan dan bantuan kepada penulis.

8. Ayah, Emak, Kak Ani dan Bang Bian, yang telah memberikan dukungan secara finansial dan moril, mengirimkan doa, nasihat dan semangat yang sangat membantu selama penyusunan skripsi.

9. Keluarga besar Kajong Hi. Jaya dan Keluarga besar Kajong A. Roni untuk semangat yang dikirim lewat doa dan perhatian.

10. Keluarga besar LEMKARI Lampung, terutama Sensei Mahyudin Bayas selaku Ketua Majelis Sabuk Hitam LEMKARI Lampung serta Senpai Zulkifli dan Senpai Gana selaku pelatih yang telah memberikan dukungan kepada penulis.

11. Viptiana, Wiwid, Wiwik, Achi, Ida, Cepy, Ichi, Recan, Eflin, Jihan, Lucky, Tiyas, Noven, Yayat, Toro, Edo, Edi, dan teman–teman Exoters lainnya, serta Akma, Kak Gayoh, Bang Zul, Adit, Angkatan 2009 dan Kaliawers terimakasih atas saran, dukungan dan semangat kebersamaannya.

12. Teman–teman Jurusan Matematika yang telah sama–sama tersesat di jalan yang benar, dan pengurus HIMATIKA FMIPA atas kerjasama dan

persaudaraan yang terjalin.

13. Semua pihak yang telah membantu selama ini, yang tidak dapat disebutkan satu persatu.

Bandar Lampung, Nopember 2012 Penulis

I. PENDAHULUAN

1.1 Latar Belakang dan Masalah

Tujuan dari analisis data statistik adalah untuk mendapatkan dan

mengkomunikasikan pengetahuan tentang proses dan fenomena dengan

menggunakan data. Membandingkan rata-rata sering menjadi bagian dari analisis untuk data statistik. Metode yang paling umum digunakan untuk membandingkan rata-rata dari perlakuan yang berbeda (kelompok yang timbul dari stratifikasi) adalah analisis ragam (Anara). Anara dengan satu kriteria untuk pengklasifikasian data disebut analisis ragam klasifikasi satu arah.

ANOM merupakan teknik yang dikembangkan oleh Ott (1967) untuk

membandingkan rata-rata kelompok perlakuan untuk memastikan apakah salah satu diantaranya berbeda dari keseluruhan rata-rata pada tingkat signifikan tertentu. Ott menggunakan perkiraan nilai kritis dalam melakukan prosedur ANOM. Nelson (1983) memberikan nilai kritis hαuntuk ANOM dengan tingkat signifikansi α= .10, .05, .01, .001 ketika ukuran sampel sama. ANOM

2 Hipotesis uji Anara dan ANOM tidak identik, Anara menguji apakah terdapat rata-rata perlakuan berbeda satu sama lain. Sedangkan ANOM menguji apakah ada rata-rata yang berbeda dari keseluruhan rata-rata. Dalam Anara yang signifikan, hanya menunjukkan bahwa adanya perbedaan pengaruh perlakuan, tetapi tidak mengungkapkan di mana letak perbedaan berasal. Meskipun ANOM tidak dapat digunakan dalam pengaturan yang sama seperti Anara tersebut, ANOM memiliki keuntungan menjadi lebih intuitif dan memberikan hasil grafik yang mudah dipahami, yang menunjukkan rata-rata yang berbeda dari rata-rata keseluruhan dan memungkinkan untuk mempermudah penilaian praktis serta signifikansi statistik.

1.2 Tujuan Penelitian

II. TINJAUAN PUSTAKA

2.1 Analisis Ragam Klasifikasi Satu Arah

Untuk menguji kesamaan dari beberapa nilai tengah secara sekaligus diperlukan sebuah teknik yang disebut analisis ragam. Analisis ragam adalah suatu metode untuk menguraikan keragaman total data menjadi komponen-komponen yang mengukur berbagai komponen keragaman. Analisis ragam klasifikasi satu arah adalah analisis ragam dengan satu kriteria untuk pengklasifikasian data

(Montgomery, 1991).

Model nilai tengah,

= +

= +

sehingga didapat model pengaruh,

= + +

dimana,

= nilai pengamatan pada perlakuan ke-i dan ulangan ke-j i = 1, 2, ... , k; j = 1, 2, ... , n

4 = pengaruh galat percobaan pada perlakuan ke-i ulangan ke-j dengan asumsi

galat menyebar normal dengan nilai tengah 0 dan ragam σ

= rata-rata percobaan faktor ke-i (Moser, 1994).

Asumsi-asumsi yang mendasari Anara adalah:

1) Pengaruh perlakuan dan pengaruh lingkungan bersifat aditif

Yang dimaksud dengan bersifat aditif artinya dapat dijumlahkan sesuai dengan model. Adanya ketidakaditifan dalam model akan mengakibatkan keheterogenan ragam galat. Model aditif linier adalah sebuah model yang umumnya digunakan untuk menjelaskan komponen sebuah pengamatan yang tersusun atas nilai tengah dan galat. Komponen nilai tengah terdiri dari satu atau lebih parameter( ). Model umum adalah sebagai berikut:

= +

Bila asumsi tidak terpenuhi maka perlu dilakukan tranformasi data. Apabila tidak dilakukan transformasi data, ragam galat gabungan yang diperoleh sedikit tidak efisien untuk selang kepercayaan pengaruh perlakuan dan dapat memberikan tingkat nyata yang palsu untuk perbandingan nilai tengah perlakuan tertentu.

2) Galat percobaan memiliki ragam yang homogen

5 tertentu. Bila nilai tengah satu atau dua perlakuan lebih tinggi dari yang lainnya dan keragamannya juga lebih tinggi dari yang lainnya, akan mengakibatkan keragaman galat yang tidak homogen. Untuk menguji homogenitas ragam digunakan ujiBartlett’s_.

Prosedur pada ujiBartlett’s_{diperoleh dengan menggunakan pendekatan}

sebaran khi-kuadrat dengan (k-1) derajat bebas.

Untuk menguji hipotesis: : = =

:paling sedikit satu ragam yang tidak sama

UjiBartlett’s_{diperoleh dengan memisalkan sebagai penduga bagi}

yang diperoleh dari m pengulangan dengan 1derajat bebas.

= [ ( 1)] ( ) ( 1) ( )

dimana,

=

1

= ( )

1

= ( ) 1

= 1

6 = ragam dari tiap perlakuan

= banyaknya ulangan tiap perlakuan = nilai sampel sari perlakuan tiap ulangan = rata-rata perlakuan tiap ulangan

=0, 1, 2, ….n

Maka diperoleh,

= ( 1) ( 1)

= ( 1) dimana,

= jumlah ragam tiap perlakuan = banyaknya satuan percobaan = banyaknya perlakuan

Dengan nilai C sebagai berikut:

= 1 + ( 1) ( ( 1)) 3( 1)

dengan,

= banyaknya ulangan tiap perlakuan = banyaknya perlakuan.

7 3) Galat percobaan yang saling bebas

Asumsi mengenai faktor untuk Anara adalah ~ (0, ). Peluang bahwa galat dari salah satu pengamatan yang mempunyai nilai tertentu haruslah tidak bergantung dari nilai-nilai galat untuk pengamatan yang lain. Atau dapat dikatakan bahwa tidak ada korelasi antar galat. Jika galat percobaan tidak saling bebas akan mengakibatkan uji nyata yang

dilakukan akan mengecoh. Salah satu cara untuk mencapai sifat saling bebas adalah dengan melakukan pengacakan terhadap pengamatan.

4) Galat percobaan menyebar normal

Asumsi ini berlaku terutama untuk pengujian hipotesis, dan tidak diperlukan pada pendugaan komponen ragam. Jika galat percobaan ternyata menjulur ke kanan atau ke kiri, komponen galat dari perlakuan cenderung merupakan fungsi nilai tengah perlakuan. Ini akan

mengakibatkan ragam tidak homogen. Jika hubungan fungsional diketahui, maka transformasi dapat ditentukan sehingga akan membuat galat tersebut menyebar mendekati sebaran normal. Dengan demikian analisis ragam dapat dilakukan pada data transformasi (Mattjik dan Sumertajaya, 2000).

2.2 Pengujian Hipotesis Analisis Ragam Klasifikasi Satu Arah

8 Hipotesisnya:

0: 1= 2 = = 5

[image:18.595.119.507.227.335.2]

1: sekurang-kurangnya satu perlakuan tidak sama dengan lainnya.

Tabel 1. Analisis Ragam Klasifikasi Satu Arah.

Sumber Keragaman Jumlah Kuadrat Derajat Bebas Kuadrat

Tengah F hitung

Perlakuan JKP k–1 KTP

Galat JKG k (n-1) KTG

Total JKT nk–1

Faktor koreksi (C) adalah jumlah semua pengamatan dikuadratkan dan dibagi dengan jumlah pengamatan.

= . . = ,

Jumlah kuadrat total (JKT) dapat diperoleh dari rumus:

= ,

Jumlah kuadrat yang berasal dari peubah klasifikasi, yaitu perlakuan disebut jumlah kuadrat perlakuan (JKP) yang diperoleh dengan rumus:

= . + .+ + .

Jumlah kuadrat antar individu yang diperlakukan sama juga disebut jumlah kuadrat galat (JKG) yang diperoleh melalui pengurangan jumlah kuadrat perlakuan dari jumlah kuadrat total, seperti dalam persamaan berikut:

9 JKG juga dapat diperoleh melalui penggabungan jumlah kuadrat dalam perlakuan, seperti yang ditunjukkan dalam persamaan berikut:

= .

Kuadrat tengah perlakuan (KTP) dan kuadrat tengah galat (KTG) diperoleh dari membagi jumlah kuadrat dengan derajat bebasnya, seperti yang ditunjukkan dalam persamaan berikut:

= 1

= / ( 1)

Nilai diperoleh dari membagi kuadrat tengah perlakuan dengan kuadrat tengah galat, seperti dalam persamaan berikut:

= /

(Steel dan Torrie, 1995).

2.3 Analisis Rata-rata (ANOM)

Analisis rata-rata (ANOM) adalah prosedur grafis yang digunakan untuk mengukur perbedaan antara kelompok perlakuan dalam berbagai desain eksperimental dan situasi penelitian observasional.

ANOM didasarkan pada dua asumsi: 1. Galat mendekati distribusi normal

2. Untuk semua perlakuan memiliki ragam yang homogen. Dapat dinotasikan sebagai:

10 dengan,

= +

dimana,

= nilai tengah dari setiap perlakuan = galat terkait dengan ,

dan kedua asumsi tersebut menyiratkan ~ (0, ). adalah variabel acak, kita dapat menghitung kesalahan spesifik yang terkait dengan pengamatan . dapat diduga dengan rata-rata sampel.

= .

sehingga,

= .

disebut residual. Residual tidak lebih dari perubahan pengamatan asli, sehingga setiap himpunan nilai perlakuan berpusat pada nol. Untuk menguji asumsi kenormalan dari residual data dan kehomogenan ragam digunakanNormal Probability Plot. Jika data terletak pada garis lurus maka kedua asumsi tersebut

terpenuhi.

Hipotesis untuk ANOM sama dengan metode konvensional yaitu: 0: ₁ = ₂= =

11 ANOM didasarkan pada perhitunganupper decision lines(UDL) danlower

decision lines(LDL) untuk k perlakuan adalah sebagai berikut:

= . . + ( ; , )

= . . ( ; , )

dimana,

Mean square error( ) dari Anom adalah : = =

yang hanya memiliki satu faktor dan derajat bebas (db) N–k. Rata-rata keseluruhan : _.. = _.

Rata-rata tiap perlakuan : _.= , = 1,2, , = 1, 2, . . . ,

Ragam dari tiap perlakuan: = _{( ) .}

Daerah kritis ( ; , )tergantung pada : = tingkat signifikan yang diinginkan = jumlah perlakuan yang dibandingkan = derajat bebas untuk

Nilai kritis untuk jumlah perlakuan rata-rata (k) dan derajat bebas = untukα= 0,01;α= 0,1 danα= 0,05 dapat dilihat pada tabel Nelson (Nelson, Wludyka, dan Copeland, 2005).

12 Ketika melakukan ANOM, pertama-tama menentukan batas keputusan atas dan bawah. Jika semua sampel rata-rata berada dalam batas-batas itu, dapat dikatakan bahwa dengan 100 (1 -α) persen keyakinan tidak ada dasar untuk menolak

hipotesis nol, yaitu tidak ada perbedaan yang signifikan di antara sampel. Jika setidaknya satu rata-rata berada di luar batas, maka hipotesis nol ditolak. Batas-batas keputusan atas dan bawah tergantung pada beberapa faktor, yaitu : rata-rata sampel, rata-rata secara keseluruhan rata-rata sampel, standar deviasi, tingkat signifikansi, jumlah sampel, dan ukuran sampel untuk menentukan derajat kebebasan (Oyeyemi dan Adeleke, 2004).

2.4 ProsedurTukey w

Prosedur Tukey diterapkan untuk membandingkan pasangan nilai tengah.

Prosedur ini memerlukan satu nilai tunggal untuk menentukan nyata atau tidaknya semua beda pasangan nilai tengah. Prosedur ini menghitung nilai kritik dan menerapkannya pada beda antara semua pasangan nilai tengah.

Nilai kritik :

= ( , )

dimana = , r adalah banyaknya ulangan.

13 mempunyai satu atau lebih pernyataan kesimpulan yang salah dan dalam 95 persen kumpulan itu tidak ada yang dinyatakan berbeda (Steel dan Torrie, 1995).

2.5 Sekuensial Analisis Rata-rata (SANOM)

Prosedur ini merupakan analisis lanjutan dari ANOM untuk membandingkan pasangan nilai tengah. Prosedur SANOM menghasilkan kelompok rata-rata homogen yangnon-overlapping. Dengan menggunakan LDL dan UDL pada grafik ANOM, dibangun beberapa tahap. Pada tahap pertama, diasumsikan bahwa rata-rata yang jatuh antara LDL dan UDL membentuk kelompok pertama. Sedangkan rata-rata yang jatuh di atas UDL membentuk kelompok kedua dan rata-rata yang jatuh di bawah LDL sebagai kelompok ketiga. Prosedur ANOM kemudian diulang pada kelompok kedua dan ketiga. Adapun tahapan dalam melakukan prosedur SANOM adalah sebagai berikut:

1. Tahap pertama dilakukan prosedur ANOM untuk menentukan nilai LDL dan UDL.

2. Pada tahap pertama didapatkan grafik _., = 1,2, , terhadap garis keputusan.

a. Jika semua rata-rata jatuh di antara LDL dan UDL maka dapat disimpulkan bahwa secara signifikan tidak ada perbedaan di antara rata-rata. Dalam hal ini analisis dihentikan.

14 homogen dan yang di luar garis keputusan tidak termasuk dalam

kelompok tersebut.

3. Perhatikan rata-rata perlakuan(2 < ) yang jatuh di atas UDL dan akan selidiki apakah rata-rata tersebut membentuk kelompok homogen atau tidak. Selanjutnya menghitung garis keputusan sebagai:

= . . + ( ; , )

= . . ( ; , )

..dan dihitung dari rata-rata dan = . Jika rata-rata jatuh antara dan maka dapat disimpulkan bahwa

membentuk kelompok homogen II. Jika = 1, maka tahap 3 tidak perlu dilakukan dan diasumsikan bahwa rata-rata ini milik kelompok homogen II.

4. Perhatikan rata-rata perlakuan(2 < ) yang jatuh di atas UDL dan akan selidiki apakah rata-rata tersebut membentuk kelompok homogen atau tidak. Selanjutnya menghitung garis keputusan sebagai:

= . . + ( ; , )

= . . ( ; , )

..dan dihitung dari rata-rata dan = . Jika rata-rata jatuh antara dan maka dapat disimpulkan bahwa

15 5. Jika beberapa rata-rata (minimal 2) pada langkah 3 dan beberapa

III. METODOLOGI PENELITIAN

3.1 Metode Penelitian

Langkah-langkah untuk membandingkan Anara konvensional dengan metode ANOM dilakukan dengan beberapa tahapan yaitu:

1. Melakukan pengujian asumsi Anara pada data jumlah buah tomat pertanaman dibawah pengaruh lama pemaparan medan magnet. 2. Melakukan analisis ragam klasifikasi satu arah denganmetode

konvensional untuk data jumlah buah tomat pertanaman dibawah pengaruh lama pemaparan medan magnet.

3. Melakukan analisis ragam dengan metode ANOM pada data jumlah buah tomat pertanaman dibawah pengaruh lama pemaparan medan magnet dengan menggunakan perangkat lunak (software) SAS versi 9.0.

4. Melakukan analisis perbandingan nilai tengah dengan metode Tukey dan SANOM.

[image:27.595.120.507.183.315.2]

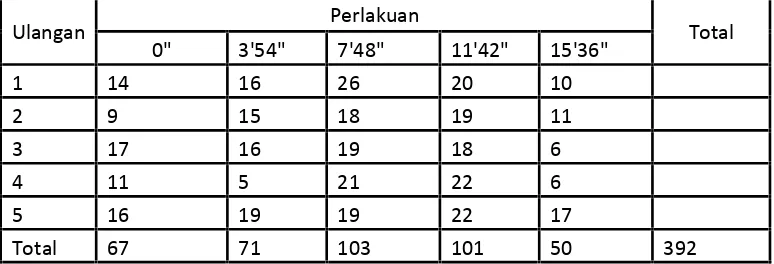
17 3.2 Data Penelitian

Tabel 2. Data jumlah buah tomat pertanaman dibawah pengaruh lama pemaparan medan magnet.

Ulangan Perlakuan Total

0" 3'54" 7'48" 11'42" 15'36"

1 14 16 26 20 10

2 9 15 18 19 11

3 17 16 19 18 6

4 11 5 21 22 6

5 16 19 19 22 17

V. KESIMPULAN

Dari hasil penelitian membandingkan analisis ragam klasifikasi satu arah metode konvensional dengan metode ANOM serta membandingkan prosedur Tukey dengan SANOM maka dapat disimpulkan sebagai berikut:

1. ANOM dan SANOM merupakan prosedur alternatif analisis ragam dalam membandingkan rata-rata dan pasangan nilai tengah yang dapat diterapkan dengan lebih mudah dan efisien.