Sharper Analysis Of Upper Bound For The Iteration Complexity Of An Interior-Point Method Using Primal-Dual Full-Newton Step Algorithm

.I

ｾ＠

..

,

ｾ＠

,/.

,.:. ...

ﾷ ｾ＠

/

...

/

',•

This tJtle · •• • ·

·-

:,..,,

ｩ ｳ ＱＱ､ｦＬ ｾｴＺＺ＠

• • '

in Scopus ·: • ,. _ｾﾷ＠

• / ;. :.. • Ｚｾ＠ ,• ../ r :. '

--:- -

.

.

--

,.

..

:""

SC:JPU• ,. , ... ｾＭ 1,.

,, . . ! · '

ｒ･ｰｲｩｾｴ

Ｏ･ｾ ｾ ｦｩＺｯｭ＠

ｴｨ ﾷ･ ｾﾷ Ｍ

.. :·.

·:

:.

J • •

,,

.,

<· _,

·•

($t·

•

.

, /

ｾ＠ ..

.. , ,. :I,. ,

:

• r . . / r

Fal·East

Jpurrial

of·

.

Mathern.atical Sciences (FJMS) ··

/ Volu.me 95, Nu·mbe-r 1

/ 2014,

PP'

ＶＹｾＸＰ＠

/

, / .

..

, ,; ,

.

,

. / ' ,; Ｌｉ Ｍｾ＠ , . /

,,,, . ..

'""·'

ｾｈｾｒｐｅｒ＠

_,1'

ANALYSIS '(j'F

_.

ｕｐｾ ﾷｅｒ＠

_•.

8'ouNo'

_{. .}

FORtTHE

.... ... /

/

ITERATION COMPLEXITY .OF AN INTERIOR-POIN..T.

. ... ,, , / ,.,

.

.. _,,,,,,..

...

. .

.

.I' .. • • ,- '

.. ｾ＠ ,

....

,,.

,,

" ,

. -

METHOD USING PRIMAL-DUAL FULL-NE.WJ"ON .

/

r'·"'

.

· ...

,

..

/

/'

,

,

....

·

STE,P AtGO_RITHM

,r

,·

'

...:

b •

Y.,,

.r. _,'

.

,.

/

/

.

Bib Paruhum

ｓｩｬ｡

ｬ ｡ｨｾ＠

.I ...

·'

! '· , ,...

J ii""

' .

, , ,. I

,.

, _{, , ,} •.· "'

, I

..

.•

I ｾﾷＭ

·'

Pustlpa l>(.blishing

Hou$e · ;

··

VIJaya Ntwas, 198 MumfordganJ Allahabad 211002, INDIA

..

ｴＧＮｬＧＢＢ Ｇ ｭＭＱ［ｩ［ ＱｲＮＱｾ＠•

.,-ff,.i;.,

ｾﾷ＠ http://pphmJ.com!Joumals/flms.htm

fjmsOpphmj.com & arun@pphm).com . :.

..

-,·

.•

.

'· ｾ＠

... , .

,

.

•

. lnfonnat1gn for Authors

Alms and ｾｯｰ･ Ｚ＠

The

Far East Journal of Mathematical Scie.J&1i/f JMS) is devoted to publishing

origlnll research papers and critical survey articles In the field of Pure and Applied Mathematics,

ｾａｰｰｬｩ｣｡ｴｩｯｮｳ＠ and Sta6stics. The FJMS is a fottnightty journal published in twelve volumes

annuttly II/Id each volume comprises of two issues.

ｾＱＱＹ Ｎ＠ Indexing and Reviews: Global Impact Factor : 0.692, Scopus, M athematical Reviews,

MalhSciNet. ProOuest, lndexCopemicus, EBSCOhost. Zentralblatt MATH, Ulridl's web, Indian

Sdence AbslractS. SCIRUS, OCLC, Google Scholar, Exoellence in Research for Australia (ERA), .k8demlcl<eys.

Submlalon of Manuscripts: Authors may submit their papers ror consideration in the Far East

Joumel of Mathematical Sciences (FJMS) by the following modes:

1. Online 1ubmluton: Please visltjoumal's homepage at http://www.pphmj.comfJOUmalslfjms.htm

2. Elec1ronalty: At the &-mail address: tjms@pphmj.oom or kkazad@pphmj.oom

S. turd copies: Papers in duplicate with a lette< of submission at the address of the publisher.

The ｾ＠ must be typed only on one side in double spacing wi1h a generous margin all round. Ari

elb1 II made to pubfish a paper duty recommended by a refereG within a period of three months. One

Mt ol galley proofs of a paper will be sent to the author submitting the paper. unless requested

ollelwt9e. without the original manuscript, for cooectioos.

ｾ｡ｮ､＠ Refennce1: Authors are requested to provide an abstract of not moni than 250 WOl'ds --' 18test Mathematics Subject Classification. Statements of Lemmas. Propositions and Th80fems ｾ＠ be set in itafics and references should be arranged in alphabetical Of'der by the surname of the

lr'ltalthor.

Pege Charges and ｾｰｲｩｮｴｳ Ｚ＠ Authors are requested to arrange page charges of their papers @ USO

40.00 per page for USA and Canada. and EUR 30.00 per page for rest of the worid from their

lns1ilutions/researcti grants, if any. However. for authors in India this charge Is Rs. 800.00 per page.

No eldra charges for colour figures. Twenty-five reprints in print version and a copy in soft version are

provided to the COfT'espooding authof ex-gratis. Additional sets of reprints may be ordered at the time

°'proof comtdion.

Copynght It is assumed that the submitted manuscript has not been published and will not be

ｾｳｴｹ＠ submitted or published elsewhere. By submitting a manuscript, the authors agree that

h copyright for their artides is transferred to the Pushpa Publishing House. Allahabad, India, if and

when. the paper Is accepted for publication. The pubfisher cannot take the responsibility of any loss of

nwnusa1pt. Therefore. authors are requested to maintain a copy at their end.

Subscription Information for 2014

lnstllutloNI Price for all countries except India

Eledronlc Subscription € 720.00

Print Subscription includes Online Access € 1195.00

USS995.00 USS 1695.00

,., - . . . ＨＩ＾ｾ｡＠ lcel'M b ｾｳＩ＠ ol lie F• &st_,,,,, ol ....,__ s... ｃｆＮｉｍｓｾ＠ ... lacillly ｉｏｾ＠

... h ｾ＠ loll be ...,.,, fvough ... lnsVlulioNI 9 digits II' eddr9u 10 be prcMcled by Iha ｾ＠ -...ly The

. . . "' _..., _ . ..,,.,.,. bl ... lfld o1 ... neJCI ｾ＠ )4W ll'Om 111t last ia-ol Ille \l()lume ""'9cribed. F0< ｾ＠

ＮＮＮＮＮＮＬｾ ｉｏＢＭｴｬＱ･ｾｯｬ＠ ... ｟ＬＬＮｾＭＮＮＮＮＮＱｯｲＭｩＭＭＭｾｉｔ｜ＹＩＧ｢･ｨ｡､ｯｮ｡ｾ＠

...

Price In Indian Rs. (For Indian Institutions 1n India only)

( Print Subscription Only

I

Rs. 15000.00

I

The IUbecription year runs from January 1. 2014 through December 31, 2014.

lnfonnatlon: The journals published by the "Pushpa Publishing House· are solely distributed by the ｾ＠ Boolts and Jourmil• Dl1tributors·.

Cone.ct Person: Subscription Manager. Vijaya Books and Journals Distributors. Vijaya Niwas, 198 ｍｵｭｦｯｲ､ｧ｡ｾ Ｎ＠Allahabad 211002. India; sub@pphmj.com : arun@pphmj.com

Far East Journ1I of M1them1tle1f Sciences (FJMS) C> 2014 Pushpa Publishing House, Allahabad, India Available online at http://pphmj.com/joumals/fjms.htm Volume 95, Number I, 2014, Pages 69-80

SHARPER ANALYSIS OF UPPER BOUND FOR THE

ITERATION COMPLEXITY OF AN INTERIOR-POINT

METHOD USING PRIMAL-DUAL FULL-NEWTON

STEP ALGORITHM

Bib Paruhum Silalabi Department of Mathematics

Faculty of Mathematics and Natural Sciences Bogor Agricultural University

JI. Meranti, Kampus IPB Dannaga Bogor, 16680, Indonesia

e-mail: bibparuhum!@yahoo.com

Abstract

The use of interior-point methods to solve linear optimizarion problems has become a great attention to the researchers. The most important thing is that the interior-point methods have the best complexiry compared to other methods and also efficient in practice. The worst upper bound for the iteration complexiry of this method is polynomial. Roos, Terlaky and Vial presented an interior-point method using primal-dual full-Newton step algorithm that requires the best known upper bound for the iteration complexiry of an interior. point method. In Lhis paper, we present their method with a slightly better iteration bound .

1. Introduction

Recently, the use of interior-point methods (IPMs) for solving linear

ｒ･｣･Ｑｶ｣､ｾｊｵｬｹ＠

8, 2014; Revised: August 20, 2014; Accepted: September J. 2014 20 I 0 Mathemaiics Subject C lassificaiion: 90COS. 90C5 I.

70 • Bib Paruhum Silalahi

· optimization (I:.0) problems has become a major concern of the optimization researchers. This happens mainly due to the fact that interior-point methods have polynomjaJ complexity, which is the best compared to other methods and these methods are also efficient in practice.

Interior-point method first appeared in 1984, when Karmarkar [4] proposed a polynorrual-time method for LO problems. In the worst-<:ase, for a problem with

n

inequalities and L bits of input data, Karmarkar's algorithm requires O(n3·5

L)

arithmetic operations on numbers with O(L) bits.

In [8], Renegar improved the number of iterations to

0(

,/;

L) iterations. Other variants of IPMs, called potential reduction methods, require also only

o(.J;iL)

iterations. This was shown by Ye [13], Freund [I], Todd and Ye [12] and Kojima et al. [5].

Sonnevend [ 11] and Meggido [ 6] introduced a class of IP Ms which uses the so-<:alled central path as a guide line to the set of optimal solutions. These methods are called path-following methods. A variant of path-following methods was presented by Gonzaga (3], Monteiro and Adler [7] and Roos and Vial [I 0). Their methods require 0(

..In

l) iterations, which is the best known upper bound for the iteration complexity of an IPM. Roos et al. in their book (9) obtained the same upper bound by using an algorithm which is a so-called primal-dual full-Newton step algorithm. Their upper bound for the number of iterations is

ｲｅｮＱｮｮｾ

Ｐ

ｩＮ＠

(I.I)

where t is the absolute accuracy of the objective function and µ0 > 0

denotes the initial value of the so-called barrier parameter.

In this paper, by careful analysis, we reduce the upper bound by a factor

ｾ Ｎ＠ The iteration upper bound that we obtained is

r

..r;;

log

ｮｾｯ＠

l

ﾷ ｾ＠

Sharper Analysis of Upper Bound for the Iteration Complexity

2. Primal-dual IPM with Full-Newton Steps

The standard fonn of an LO problem is as follows: min{cT x : Ax == b, x

ｾ＠

O},

71

(P)

where c, x e '.Rn, b

e

'.Rm and A e '.J?.mxn. Any LO problem can be transfonned into standard form, by introducing additional variables (2). The problem (P) is often called the primal problem. Associated with any LO problem is another LO problem called the dual problem, which consists of the same data {A, b,

c)

arranged in a different way. The dual of (P) is

max{bT y : AT y

+

s

=

c, s

ｾ＠

0},

(D)

where s e J<n and y e '.Rm; (D) is called the dual problem.

The feasible regions of (P) and (D) are denoted by P and V,

respectively. The (relative) interiors of P and V are denoted by P0 _and V0 •

Finding an optimal solution of (P) and (D) is equivalent to solving the following system (9):

Ax== b, x ｾ＠ 0,

T

A y +

s

=

c, s

ｾ＠ 0,

xs=O, (2. 1)

where xs is the component-wise (or Hadamard) product of the vectors x ands

and 0 denotes the zero vector. The first line in (2. 1) is s imply the feasibility constraint for the primal problem (P) and the second line represents the feasibility constraint for the dual problem (D) . The last equation is the so-called complementarity condition.

72· Bib Paruhum Silalahi respect to µ . The resulting system is

Ax= b, x ｾ＠ 0,

T

A y +

s

=

c, s

ｾ＠ 0,

XS= µe. (2.2)

If system (2.2) has a solution for some µ > 0, then a solution exists for every µ > 0 [9). This happens if and only if interior point condition (IPC) is satisfied. The solutions are denoted as x(µ), y(µ) and s{µ). We call x(µ)

the µ-center of(P) and (y(µ), s(µ)) the µ-center of(D).

When µ runs through (0,

oo),

then x{µ) runs through a curve in

P

0

which is called the central path of (P). Similarly, the set {(y(µ), s(µ)) : µ e

(O, oo)}

is called the central path of(D).

Ifµ-+

0, then x(µ), y(µ) and s(µ) converge to a solution of (2.1 ), which means that the central path converges to the set of optimal solutions of (P) and (D). On the other hand, if

µ --. oo, then x(µ) and (y(µ), s(µ)) converge to the so-called analytic center

of (P) and (0), respectively.

Next, it will describe how Newton 's method can be used to obtain an approximate solution of system (2.2), for fixed µ . Given a primal-dual feasible pair (x, (y, s )}, we want to define search direction

tu,

fly and t:.s

such that (x

+

flx , y +fly, s +

t:.s)

satisfy (2.2).

Since Ax = b and Ary+

s

=

c,

system (2.2) is equivalent to the following system:

ａｾｸ＠

=

0,

AT fly

+

t:.s

=

0,

stu

+ xt:.s +

tu!:Js

=

µe - xs.

Sharper Analysis of Upper Bound for the Iteration Complexity 73 The third equation is nonlinear, due to the quadratic tenn

t:.xt:.s.

By neglecting this quadratic tenn, according to Newton's method for solving nonlinear equations, we obtain the linear system

Atu

=

0,

AT fly + t:.s

=

0,

stu

+ xt:.s

=

µ e - xs. (2.3)

The resulting directions of (2.3) are known as the primal-dual Newton directions. By taking a step along these directions, one finds new iterates

(x +, (y +, s + )) such that x + and s + are positive. The new iterates are given

by

+ + +

x

=

x +tu,

y

=

y

+

fly ,

s

=

s

+

t:.s.

In the process of following the central path to the optimal solution, by using Newton steps, we generate a sequence of points within the neighborhood of central path. We need a quantity to measure the proximity

of (x, (y, s)) to the µ-center.

Before defining this proximity measure, we refonnulate the linear system

(2.3), by scaling

tu,

fly and t:.s to d.x, d .₁• and ds as follows:

d _x -_{- - -}

vt:.x

x '

where

fly

dy

=

-iµ·

v=J!f.

d _s -_{- - -}vt:.s

s

'

lfwe define D

=

diag(J;/S), then system (2.3) is equivalent to

ADd.x

=

0,

(AD)T d y

+

ds

=

0,

74 Bib Paruhum Silalahi

The first two equations of system (2.4) show that the vectors dx and ds

belong to the null space and the row space of the matrix AD, respectively. These two spaces are orthogonal, therefore, d x and ds are orthogonal. The orthogonality of dx and d5 implies

II

dx

ｾ

Ｒ＠

+II

ds

ｾ

Ｒ＠

=II

dx + ds

11

2

=llv-

1

-vf

Note that dx , ds (and also dy) are zero if and only if v-1 - v

=

0, which happens only if v = e, and then x, y and s coincide with the respective µ-centers. Therefore, to measure the 'distance' of (x, (y, s )) to the µ-center, we use the quantity

O{x,

s; µ) defined by

o(x, s;

µ)

:=

o{v)

:=

ｴｾ＠

v -1 - v

f

(2.5)

For any t ｾ＠ 0, the t-neighborhood of the µ-center is given by the set

{{x,

y,

s): x E 'P,

(y.

s) EV,

o(x.

s; µ) :5

<}.

After a full-Newton step, the duality gap at the new iterates always assumes the same value as at the µ-centers, i.e., (x +)Ts+

=

nµ (cf. [9, Theorem 11.47]). An IPM with full-Newton steps can be described as in Figure 1.

Primal-dual IPM with full-Newton steps Input:

an accuracy parameter E > O; a proximity parameter t, 0 :5 t

<

I;

strictly feasible

(x

0•

yo,

s0) with

(x

0 )r

s

0

=

nµ0 and o(x0,

s

0; µ 0)::;; r : a barrier update parameter 0, 0

<

0

<

I .

Sharper Analysis of Upper Bound for the Iteration Complexity

begin

x

:=

xo; s :=so; Y

=yo; µ:= µo ;

while nµ ｾ＠ E do µ := (1 - 0)µ;

x := x

+

6x;

y := y

+

6y;

s

:=

s

+

65;

end while

end

Figure 1. Primal-dual IPM with full-Newton steps.

3.

Analysis of the Primal-dual

IPM

with Full-Newton Steps

We first deal with the effect of a full-Newton step on the proximity measure. The next lemma implies that when

o(x,

s;

µ)

is small enough then the primal-dual Newton step is quadratically convergent, as stated in Corollary 3.1.

Lemma 3.1 (cf. (9, Theorem 11.50]).

If

o

:= O(x, s;

µ)

:5 I, then the

primal-dual Newton step is feasible, i.e., x+ and s• are nonnegative.

Moreover,

if

o

<

I, then x + and s + are positive and

52

S(x+ • s+; µ) :5

ｾＲＨＱ＠

-

o

2 )

Corollary 3.1.

If

o

:=

O{x,

s;

µ)

s

*,

then o(x+, s•;

µ)

s

o

2 .

76 _{Bib Paruhum Silalahi}

Lemma 3.2 (cf. (9, Lemma 11.17]). After at most

r

t

nµo1

9log7

iterations, the algorithm stops and we have nµ s; &.

We have the following lemma that will be used in proving the next two theorems.

Lemma 3.3 (cf. [9, Lemma 11.54]). Let (x,

s)

be a positive primal-dual pair and µ

>

0 such that xr s = nµ. Moreover, let

o

:= S{x, s;

µ)

and let

µ+ =(I - 9)µ. Then

+ )2 ( 2 92n

O(x, s;

µ

=

I - 9)o

+

4(1 _a)"

The next theorems present iteration bound of the primal-dual IPM with full-Newton steps.

Theorem 3.1.

If

t =

1/.Ji

and 9

］ ｉＯｾＮ＠

then the algorithm

requires at most

r

Fn+i

log

ｮｾｯＱ＠

terations. The output is a primal-dual pair (x, s) such that x Ts s; &.

Proof. Let us take t =

If.Ji.

By using Corollary 3.1, since we have

5(x, s;

µ)<;If.Ji,

after the primal-dual Newton step we have o(x+, s+;

µ)

S 1/2. Then, after the update of the barrier parameter to µ + = (I - 9)µ with

} =

1/Fn+I, by using Lemma 3.3, we get the following upper bound of

>(x+, s+; µ + )2:

+ + 2 I - 9 92 n

=

_!. .

O(x•, s

;

µ ) s -4- + 4(1-9) 2

Sharper Analysis of Upper Bound for the Iteration Complexity 77

The last equality follows by substituting 0 =

t/..r;;+T.

Hence, we obtain

o(x+, s+; µ+) s;

1/./2

=

t . This means that the property o(x, s;

µ)

s; t

is maintained after each iteration. Therefore, combining this with Lemma 3.2, we obtain the theorem. 0 Note that Theorem 3.1 holds for every n ｾ＠ 1. In practice, n is much larger. For such cases it is worth mentioning that slightly bcner iteration bounds can be obtained, as the following theorem.

T heorem 3.2.

If

t

e

[0.6687, 0.6773] and 9

=

1/Fn, then for n ｾ＠ 47,

the algorithm requires at most

r

Fntog

ｮｾ

Ｐ

Ｑ＠

iterations.

Pr oof. Let us take 0 =

1/Fn.

By using Lemma 3.1 and Lemma 3.3, we can verify that if

(I - l/Fn)'t4 ₊ 1 _<t 2

2(1 -

t2 ) 4(1 - 1/Fn) - •

(3.1)

then o(x, s;

µ)

s; t is maintained. The region in the ( t , n )-space defined by (3 .1) is depicted in Figure 2, where the smallest value of n is around 46.6274 at t

=

0.6731. Therefore, n = 47 is the smallest integer value of n which satisfies (3.1 ). We can find out that for n ｾ＠ 47, the inequality (3. 1) holds for

Bib Paruhum Silalahi

to

j

.

(1-1/v'ii}iA 1

I

1

n

I

2(1 - T2)

+

4(1 - l/ Jn} $

TJ

10•

.l

i

sof.

"

/

1

I

..,

___._

- - __j

oc: OM OM _{O• 01}

o.n

[image:7.1024.129.788.11.597.2]

t

Figure 2. The region defined by (3. 1 ).

The value of n in Theorem 3.2 can be improved to n

ｾ＠

6, as stated in the following theorem.

Theorem 3.3.

If

't E [0.7433, 0.8289) and

e

=

1/../n,

then for n

ｾ＠

6,

the algorithm requires at most

rJniog

nn

iterations.

Proof. We use (9, Theorem 11.52], a sharper quadratic convergence result of a primal-dual Newton step. This theorem states that if

o

:= O(x, s;

µ)

< I,

then

52

o(x•,s•;µ)S

J1(t-04)·

Then,

by

using Lemma 3.3, we obtain that for

e

=

t/../n

the propeny

O(x, s;

µ )

ｾ＠ 't is maintained if

Sharper Analysis of Upper Bound for the Iteration Complexity 79

(1 - l /

fn)-r

4 I 2

2(1 - 't4 ) + 4(1 - 1/Tn) $ 't .

(3.2)

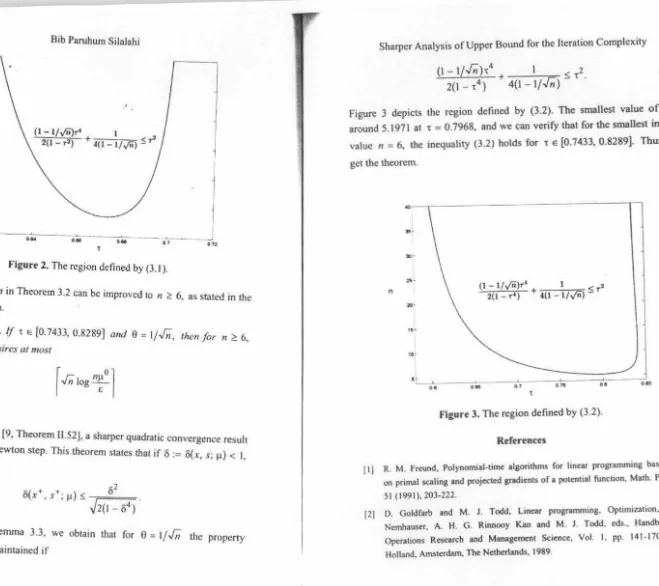
Figure 3 depicts the region defined by (3.2). The smallest value

of

n is around 5.1971 at 't

=

0.7968, and we can verify that for the smallest integer

value n = 6, the inequality (3 .2) holds for 't

e

[0.7433, 0.8289]. Thus, we

get the theorem. 0

..,

35 ·

:io

25

-n ( l - l /y'ii)r

4

l <

TJ

2(1 - r4)

+ 4(1 1/Jii)

20

-IS •

10 •

51..

ｌｾ＠

o• OM ,...,___ 07 on 0 1

D

ｯｾ＠

t

Figure 3. The region defined by (3.2).

References

(I] R. M. Freund, Polynomial-time algorithms for linear programming based only on primal scaling and projected gradients of a potential function, Math. Program. 51 ( 1991 ), 203-222.

[2] D. Goldfarb and M. J. Todd, Linear programming. Optimization. G. L.

[image:7.1024.74.415.44.287.2]

80

.

Bib Paruhum Silalahi

f3) C. C. Gonzaga, An algorithm for solving linear programming problems in

O(n3L) operations, Progress in Mathematical Programming: Interior Point and Related Methods, N. Meggido, ed., pp. 1-28, Springer-Verlag, New York, 1989.

[4) N. Karmar'kar, A new polynomial-time algorithm for linear programming, Combinatorica 4(4) (1984). 373-395.

[5) M. Kojima, S. Mizuno and A. Yoshise, An O(../nL) iteration potential reduction a.lgorithrn for linear complementarity problems, Math. Pro&f31!1., Series A 50

( 1991), 331-342.

[6) N. Meggido, Pathways 10 the optimal set in linear programming, Progress in

Mathematical Programming: lnterior Point and Related Methods, N. Meggido, ed., pp. 13 1-158, Springer Verlag, New York, 1989. Identical version in: Proceedings

of the 6th Mathematical Programming Symposium of Japan, Nagoya, Japan, 1986, pp. 1-35.

[7] R. D. C. Monteiro and I. Adler, Interior-path following primal-dual algorithms. Part I: Linear programming, Math. Program. 44 ( 1989). 27-41.

(8] J. Renegar, A polynomial-time algorithm, based on Newton's method, for linear programming, Math. Program. 40 ( 1988), 59-93.

f9] C. Roos, T. Terla.ky and J.-Ph. Vial, Interior Point Methods for Li near

Optimization, Springer, New York, 2006. Second Edition of Theory and Algorithms for Linear Optimization, Wiley, Chichester, 1997.

f IO) C. Roos and J.-Ph. Vial, A polynomial method of approximate centers for the linear programming problem, Math. Program. 54 (1992), 295-306.

r

11) G. Son.nevend, An "analytic center" for polyhedrons and new classes of global algorithms for linear (smooth, convex} programming. A. Prckopa, J. Szelezsan and B. Strazicky, eds., System Modelling and Optimization· Proceedings of the 12th IFIP-Confercncc held in Budapest, Hungary, September 1985, Vol. 84 of Lccrure

Notes in Control and Information Sciences, pp. 866-876, Springer-Verlag , Berlin, West Germany, 1986.

{ 12) M. J. Todd and Y. Ye, A centered projective algorithm for ltnear programming, Math. Oper. Res. 15 (1990), 508-529.

(13) Y. Ye, A class of potential functions for linear programming. Management Science Working Paper 88-13, Dept. of Management Science, University of Iowa, Iowa City, IA 52242, USA, 1988.

FAR EAST JOURNAL OF MATHEMATICAL SCIENCES (FJMS)

Editorial Board

Gunjan Agrawal, lndia

Natig M. Atakishiyev, Mexico

Antonio Carbone, Italy

Hasan Coskun, USA

Zhenlu Cui, USA

Manav Das, USA

Sbusheng Fu, China

Wei Dong Gao, China

Toshio Horiuchi, Japan

Lisa M. James, USA

Koji Kikuchi, Japan

Victor N. Krivtsov, Russian Federation

Alison Marr, USA

Jong Seo Park, South Korea

Alexandre J. Santana, Brazil

A.

L.

Smimov, Russian Federation

Chun-Lei Tang, China

Carl A. Toews, USA

Vladimir Tulovsky, USA

Qing-Wen Wang, China

Peter Wong, USA

Pu Zhang, China

George S. Androulakis, Greece

Carlo Bardaro, Italy

Yong Gao Chen, China

Claudio Cuevas, Brazil

Maslina Daros, Malaysia

Massimiliano Ferrara, Italy

Salvatore Ganci, Italy

Demetris P. K. Ghikas, Greece

Jay M. Jahangiri, USA

Young Bae Jun, South Korea

Hideo Kojima, Japan

Yangming Li, China

Manouchehr Misaghian, USA

Cheon Seoung Ryoo, South Korea

K. P. Shum, China

Ashish K. Srivastava, USA

E. Thandapani, India

B. C. Tripathy, India

Mitsuru Uchiyama, Japan

G . Brock Williams, USA

Chaohui Zhang, USA

Kewen Zhao, China

!:

"·

...

r!'

I J' • ; ' .. • 7 ＢＧＧﾷＧｾ＠ , •

-

r

· ""·

/'

·.

· ·

M}·

r"

i"

ｬ ｾＺ＠ ｾ､ｾ｣･ｳ＠

ｾａｭｊｩｾｯｾｾｾ｣ｾＧＨｾＺ＠

Ｅ＿Ｗｾ

ＭＭｾＧ＠

. _:,_.

I._

'1-;'lJ

:,,

2:

Ｑｾｾｾ＠

ａｰｰｾｾｯｯｳ＠

..

in

ａｷ､

ﾷ ｾｾｾｻｇｉｆＺ＠

ｯＮｾｾ［＠

ｓｏｏｾｵ＠

..

s) _ ,.

ｾＭ

3.

ＬＬ ａｩｦｶｾ＠

aod(Applicatioos

ftt-Staff.stics

ＨｾＮｳＡ･ｦ＠

. " ,

p;-

·J,

ｾ＠

r:

•J/ 4., _'"

ｾＬｪｮｃｯｭｰｵｴＶｪＮＭｓ｣ｩ｣ｮ｣･ＢＢＧｾｧ

_{ｾ＠ - ..,-:,7 •}

ﾷ Ｈｯｉｆ

Ｚ Ｐ Ｎ Ｗｬｋｬ

_/

--v

Ｎ＠

,

/ · ·

-

..%?.:

_;z.

•/

.I _,) '

Sr

AdvaiaS

iii

Diffcn!iiQal Equations ｡ｮ､ｾｬ＠ ｾｳ｣ｳ＠ (GIP

:..O.<i07) · ,_;__ -'..

;j

-ｾ＠ ｾ＠ .I i" • ·< ;,r • - •

,.

ｾＮｾｖｩｵｸＺ･ｳ＠ in Fuzzy Sefs-and Sntems ( : u.703) .. ·.,... .

t/· , · • -._

£

t-. ,..rn /, . ,,.

·-:{: ＷＮ ﾷ ｾｾｾｉｄｾＨｾＱｲＺｾＸＷｴ Ｌ＠ f-/·,..,-·· ＬＬ｟＿ＬＺｾＭＮＬＬ＠

8. Far

ｅ｡ｳｴ｟ｊｾ｡ｬ＠

ＮｯＶｷｬｩｾｾｇｕＺ

ＬＺ＠

0.7Z7) .)

ｾＭ Ｍ

_

#.

-

.

ｾｪ＠ , . . l·:.·

"!i!, 9. ｆ｡ｲｅＮＮＬｕｯｵｮｪｾｵ＾ｦｬ＾ｹ｡｡ｭｩ｣｡ｴ＠ ｳｾ＠ ＨｇｩＺ･ＮＮ［ｊ＾ＮＶＸＵｽ ｾ＠ ( ..• ｾＮＮＬ＠ ｾ＠

...

'··-:... 10.', Far

ｅ｡ｳｴｊｾ＠

ｯｦｾｾｾｾ＠

ｾｾｇｗ＠

Ｚ ＰＮＱＰＡＬ

Ａ ｾｳｾ

Ｎ＠

11.

ｆ｡ｲｅ｡ｦｴＧｊｯｵｭ｡ｬｑｦｾｯｲｴＨｴｊｷＺＰ

Ｎ ＶＹＴＩ

ｾ

Ｎ＠

r.

ｾ ＭＮ＠

0

. i;.{_:/lr2.

ｆｾ＠ ｾ＠ ｾ＠

＿ｾｭ｡ｴｩｾ

Ｍ ｾ･ｬｊｉＣ＠

Ｈｆｾｾ＠

Ｈｇｾ Ｚ＠ ｾＮｾＧｻ＠

ｾ

ﾷ＠

..

ｾﾷ＠

.•

ｾ＠

./ 1Y.

ｆ｡ｲｅ｡ｳｴｊｯｵｭ｡ｬ

Ｇ ｯｦＧｾﾵ｣｡ｬ＠

Statistics (GIEdU67) _, • . ,__ ·.

·

ｾ｜ Ｎ ＱＴ ［ ＧＮＺＧＮＺ Ｍｮ［＠ ｾｾｯｦ＠

ａｬｾ

ｾ ｾｭｾｾｦｯ＠

ＢｴｙＮｐｬｩ｣ｾｾＧｇｉｆ＠

ｾＮ ＶＸＩ Ｇｽ Ｍｓ｣ｰｫｲｾ

ｦＧ＠

·

ｾＬＮＮ＠

"ts.,

JP ff"l'"'•l _""?:·- ofBiostiti.stics Ｈｇｲｆ ｾ Ｚ＠ O.S8l) ₇ .. _. I, • ' · {/ .

/_.cql ; ｾ＠

16.

ｊ ｾ ｦｯｵｾｾｾｾ

ｾｐｯｩ､

ｦ ｾ

ｴＮ ｾ＠ ａｰｰｬｩｾｯｩＡｪＢＨｇｉｆＺ＠

ＰＮＶｾ＠

;f:;..

ｾｾ＠

,, , · .-17 . •

ｊｐｊｾｾｦｾｾＬｏｏｔｯｾＨｏｉｆ

ｩＬ｟ ｾＮＡＩｓ［ｾｐｕｓＩ＠

;

r...

,.

ＺＮ ｾ＠

18.

ｊｐ Ｍｊｏｵ｝ｩｲ｡ｬｯｦｈ･｡ｴ｡ｮ､ｾＧｬＧｾｳｦ｣ｲＨｇｾｾｾ［ｾｐｕｓＩ＠

·J··;.

,_ .·

19.

ｨｕ･ｭ｡ｴｩｏｮｦｬＩｾ＠ of

Punctionit

AW

_··;s.

Ope:ritQtlfheory

1¢

ApplicafiOns

'•·1 .A "lh •

r.

rf'> I

z./'!P,'7' .

r .

.

;i;

{GIP: 0.597) ｾﾫＮＧﾷ＠ • ' ()1· , ., • • ｾ＠

20 . .

ｉｮｾｾ＠

ｾ｡ｦ｟ｱｾｲｴ｡ｨ＠

ｅｮｾ

Ｎ＠

g

｡ｮｳｬＭｊ･｣ｾｬｯｧｪ＠

(GIF.i

ｏＮｾＩ＠

- 2J.

ｾＮｊｏｯｭ｡ｬ＠

QtNumeri.cat

ｍｾ＠

add

A ·" ucadons;(GJF:

ｯＮｾｰｊ＠

/ ./ .:-::n_

ｕｲｵｖｾｬｏｵｭ｡ｬｦＺＧｦｾｰｴｴｾ｡ｮ､

Ｌ＠

M"athematr:

ｓ｣ｩｾｾＺ＠

ｏｾＩ＠

Ｇ ＧＮｾ＠

ｾ Ｍ ｓｊｬｦｖｾｩｦｩｍｊｴ｢｣Ｎｩｩ｣ｳ＠

ｾｾ＠

ｓ｣ｩ･Ｐ

｣ｲ･ＤＨｾ

ｊＡ［ＵＡＸ

ｴ［｟＠

_

¥,

·- ·

1Ai1

ｾｾ＠

Joomal of Nutrition aOctf)jetetics

1?-;

' ·

7--

1

f ., , ｾ Ｍ . ,_.r -

;?

Ｎｲｾ＠

. / ,.

ｾﾷ Ｎ＠ r?;,L I , . J:- / , ｾ＠ • • ｾ Ｇﾷｾ＠ ｾ＠ ./r>

ｾＺＭ ｎ･ｷＭＴｱｵｲｮ｡ｊｳｬＧｲｯＡｩＱＲＰＱＮ｟Ｍ

ｾｾ

Ｑ

ﾷ＠ ｾ＠

i

' ···.

y.' .. ,

• _{1. • i I} .l·/' _{-"j , / ,-,•} "-' 7 _. · ' ₍ • _{ｾ＠ - ' ?} •. _{_,} ?-' r ₍ I' _•

ＮＭｾＮ＠

r'.

2SY

ｾｴｮ､ｩ｣ｳ＠

in

A.rtificia'i

ＱＮｮｾＺｍｮ｣･＠

,.,.,, ,, • .. . /

·.

ｾ＠ ｾ ＨＮ＠ ｪＮｾｾｾ＠

ki:i

ａｰｰｬｩｾｾｩ

ｴ ｭ＠ ﾧ＼＾ｙＢｾｆＯｓｩｮ･･ｮ

｟＠

·•

·rig

.:/,-".I·

' ..

r;:

•

_,....-J

'21.i 'J-.2.J; ...

_{, uuu•r v .,} f

ｬｩＮｾ＼Ｉｶ＠

_Ｍｾ＠

·

ｾ＠ ･ｵ､ｩ｣｡ｾ

_{,"$ • ｾ＠}

Ｍ ･ｴｾｵｮｩ｣ｬｬｬｯｯｬＮ

_{ｾ＠ • _ ) ' 1'!'}

ＮＧＬＮＮＭ

'

v ·

1

,,, .

_{, ,,,, I- ﾷ ｾ}

ｾ ＺＭ ｬｊ｡ｩｶ｣ｲｳ｡ｬ＠

_{ｌＧ ﾷ ｾ＠ ,, / "} J ·• , _{( ｾ＠}

ｯｦｾ

Ｇ＠ Ｇ ｬｩ･､ ｾ＠

sics

｡ｮ､ Ｎｾ･､ｩｮｯｬｯｧｹ＠

r

,I

ｾＭＭ ｾ ＮＺ Ｚ ｾｾｊｯｵｭＸＱＹ｟Ａ

ＮＮ＠

,.

ｭｩｦＺＧＮＮ｡ｮ､ｂｵｾｃｓＢ

ＱＮ ＬｍｾｧＫｴ＠

. , 30

.-;/"u ...

ＱａｾＭ］ＭＱ＠ P( :it:2 , .

En .

. ,

and ｲＭｾ＠

. • ,

' ' ·,,. • 1 ｾ＠

ruv ..

ｾ Ｍ ｾ＠

... o

Electfi

gmpenng

.

ｷｯｮｮ｡ｴｩ ｣｡ＮＺＬＮ ｾＭＨﾷＮ＠

,..

Ｎｾ＠

ｾ＠

ｩＧ ｾ ｊ＠ ＮﾷｾＮ ｬｬｦ＠

_{. I} versal

ｬｾ＠

_,, 9f M . 1iCal Stieoces

and

ｔｾｊｭｯｬｰｧｹ＠

.&·

ｾ＠

_,,-ｾ＠ ... ,.._"7f . • /· ...

..

ｾ＠

. . . .

ｾｾｾ

Ｎ ｾｾＱＡＱＱｬ

Ｇ ｾｾＲｴｴｩ＠

. . '·'

, •• ｾ＠ ,..,. .. ＬＮ ｾ＠ ;,:r',. ｾ＠ ,; t" 1.

r._.. __ " ,... _ , ... ｾＮ＠ ｾ＠ ' ｾ＠ J

'· • - · •l ..• _,. -.._,J - ｾ ＭＧ Ｍ ｾ Ｏﾷ＠ • ,-;"'

/

.

-l

v

'.<

.

Ｇｾ＠

'}·

.. •

-

I '

. ,.,

ｾ＠ .

-

J ' _{-,f. ;} • #

..

.

,.. __ ,. '- "1 i--!..C . 4 f . .

)

..

, ,._., /

r.- .. r ; " ｾＺ＠ ＭＭｾ＠ •. r """, -,,,, ｲｾＺ＠

/_,,,,.

• -"....:! • ' ,..., , ｾ＠ . , • , ,

, /_ .. . . ,,. .. - _fi_°"" Ｍ ｾ＠ ｾ＠ . . ... -:.. •

· - ＬｾＭ Ｎ Ｏ［ＮＮ＠ :;y,· .. - Ｚｾ＠ ｾ＠ • ｾ＠

., c;

/'1 ,. ..

, .

,.._, --:-<.

Jr . ,

··-:'f""'.'."-'

''" . f , ,.

··'ff / - -;,

:.,--,... ,,_">_ ,__ ....