SIMULASI PENCARIAN JALUR TERPENDEK
MENGGUNAKAN ALGORITMA DIJKSTRA
TUGAS AKHIR
Disusun untuk memenuhi syarat kelulusan
Pada Program Studi Sistem Komputer Strata Satu di Jurusan Teknik Komputer
Oleh :
Giri Mega Gentara
10204096
Pembimbing : Wendi Zarman, M.Si
Sri Nurhayati, M.T
JURUSAN TEKNIK KOMPUTER
FAKULTAS TEKNIK DAN ILMU KOMPUTER
UNIVERSITAS KOMPUTER INDONESIA
i
ABSTRAK
Algoritma dijkstra merupakan salah satu metode pencarian jalur terpendek untuk menemukan sebuah jalur antara dua node dengan jumlah bobot minimal. Pada implementasi pencarian jalur tercepat antara dua lokasi yang berbeda dalam sebuah peta, node akan merepresentasikan lokasi pada peta dan bobot merepresentasikan efisiensi waktu yang dibutuhkan untuk melakukan perjalanan antara dua lokasi tersebut. Beberapa kasus yang membutuhkan tingkat efisiensi waktu tinggi yaitu pengiriman barang, pencarian lokasi dan sebagainya.
Aplikasi algoritma dijkstra untuk pencarian jalur terpendek dibangun dengan mengggunakan lingkungan pengembangan perangkat lunak Borland Delphi 7. Aplikasi ini akan melakukan pencarian jalur terpendek dari node awal ke node tujuan dengan jumlah bobot terkecil. Pada aplikasi ini posisi node, jumlah node, node awal dan node tujuan ditentukan oleh pengguna dengan besar bobot yang ditentukan secara otomatis sesuai dengan jarak tiap node yang tersambung atau edge.
Aplikasi ini juga akan memberikan informasi lamanya waktu proses pecarian jalur terpendek. Aplikasi ini dapat melakukan pencarian jalur terpendek dari node awal ke node tujuan dengan menggunakan algoritma djikstra melalui node-node yang tersambung. Lamanya waktu pencarian tergantung pada banyaknya jumlah node dan jumlah edge. Pertambahan jumlah node akan berpengaruh secara signifikan terhadap waktu pencarian dibandingkan dengan penambahan jumlah edge.
ii
ABSTRACT
Dijkstra algorithm is one of the shortest path problem method for finding a path between two nodes with a minimal amount of weight. an example is finding the quickest way between two different locations in a road map, the node will represent a location on the map and the weights represent the efficiency of the time it takes to travel between two locations. some cases requiring a high degree of time efficiency such as delivery service, location search and so on.
The application of dijkstra algorithm is developed by using Borland Delphi 7 IDE. This application will find the shortest path from the initial node to the destination node that the sum of the weight of its constituent edges is minimized. the node positions, the number of nodes, the initial node, and the destination node on this application is determined by user, but the weight of its constituent edges is automatically determined according to the distance between nodes.
This application will also provide the information of time needed for searching the shortest path. This application can search the shortest path from initial node to destination node using dijkstra algorithm through the connected nodes or edges. the search time depends on the number of nodes and the number of edges. The number of nodes will significantly affect the search time compared with the addition of the number of edges.
iii
KATA PENGANTAR
Assalamualaikum Wr, Wb.
Segala puji dan syukur kehadirat Allah SWT, yang telah memberikan karunia dan hidayah-Nya kepada penulis sehingga dapat menyelesaikan tugas akhir dengan judul : “Simulasi Pencarian Jalur Terpendek Menggunakan Algoritma Dijkstra”. Tugas akhir ini disusun untuk memenuhi syarat dalam meraih gelar kesarjanaan pada Jurusan Teknik Komputer Fakultas Teknik dan Ilmu Komputer di Universitas Komputer Indonesia.
Segala usaha tersebut tidak akan berhasil tanpa dorongan serta bimbingan dari semua pihak terutama dari pihak keluarga, dosen pembimbing dan rekan-rekan mahasiswa, sehingga penyusun dapat menyelesaikan tugas akhir ini. Oleh karena itu, perkenankan penyusun mengucapkan terima kasih dan penghargaan yang sebesar-besarnya kepada:
1. Allah SWT atas segala nikmat dan karunia tanpa batas.
2. Kedua orang tua, Bapak dan Ibu yang telah memberikan semangat, dukungan dan doa demi kelancaran pengerjaan tugas akhir ini
3. Ibu Sri Nurhayati, M.T. Selaku Ketua Jurusan Teknik Komputer dan sebagai Dosen Pembimbing II yang telah memberikan banyak waktu dan inspirasi selama proses bimbingan.
4. Bapak Wendi Zarman, M.Si. Selaku Dosen Pembimbing I yang telah meluangkan waktu dan tenaga untuk memberikan bimbingan dan masukan yang sangat berharga bagi terselesaikannya tugas akhir ini.
iv
7. Seluruh pihak yang tidak bisa disebutkan satu persatu, yang telah membantu dalam penyelesaian tugas akhir ini.
Penulis menyadari bahwa masih terdapat kekurangan di dalam tugas akhir ini. Oleh karena itu, penulis mengharapkan saran dan kritik yang bersifat membangun dan semoga tugas akhir ini bermanfaat dalam pengembangan wawasan ilmu pengetahuan bagi pembaca pada umumnya dan penulis pada khususnya.
Kesempurnaan hanya milik Allah SWT, dan kita hanyalah manusia yang tak luput dari salah dan dosa. Semoga apa yang disampaikan bermanfaat bagi semua pihak.
Wassalamualaikum Wr, Wb.
Bandung, Juli 2011
1
BAB I
PENDAHULUAN
1.1 Latar Belakang Masalah
Dalam kehidupan ini permasalahan pencarian jalur terpendek merupakan sebuah kajian yang menarik, terutama dalam hal efisiensi waktu perjalanan antara satu lokasi ke lokasi lainnya. Hal ini akan sangat berguna untuk diimplementasikan pada beberapa kasus yang membutuhkan tingkat efisiensi waktu tinggi seperti pengiriman barang, pencarian lokasi, dan sebagainya. Dengan memperoleh jalur terpendek antara dua lokasi, maka tingkat efisiensi waktu yang dibutuhkan untuk melakukan perjalanan antara dua lokasi tersebut akan semakin baik.
Pencarian jalur terpendek merupakan suatu permasalahan untuk menemukan sebuah jalur antara dua node dengan jumlah bobot minimal. Pada kasus pencarian jalur tercepat antara dua lokasi yang berbeda dalam sebuah peta, node akan merepresentasikan lokasi pada peta dan bobot merepresentasikan waktu yang dibutuhkan untuk melakukan perjalanan antara dua lokasi tersebut. Salah satu metode yang dapat digunakan untuk menyelesaikan permasalahan pencarian jalur terpendek yaitu dengan menggunakan algoritma dijkstra.
Algoritma dijkstra akan mencari jalur terpendek mulai dari node awal sampai node tujuan. Algoritma ini akan membandingkan bobot terkecil dari node awal sampai ke node tujuan untuk menemukan jalur paling efisien.
Berdasarkan latar belakang ini penulis mengangkat tugas akhir dengan judul
2
1.2 Maksud dan Tujuan
Maksud tugas akhir ini adalah membuat Simulasi pencarian jalur terpendek menggunakan algoritma dijkstra. Tujuan tugas akhir ini dapat memberi informasi tentang jalur terpendek yang dapat ditempuh.
1.3 Batasan Masalah
Pada tugas akhir ini terdapat batasan masalah sebagai berikut: 1. Graf yang digunakan adalah graf tidak berarah dan berbobot.
2. Rute antara satu node dengan node lain hanya dapat dilewati satu kali. 3. Bahasa pemrograman yang dipakai menggunakan bahasa pemrograman
Pascal, dan lingkungan pengembangan perangkat lunak Borland Delphi 7.
1.4 Metode Penelitian
Dalam penelitian ini menggunakan metodologi penelitian experimental. Tahap-tahap yang dilakukan penulis pada penelitian ini antara lain :
1. Studi literatur
2. Perancangan dan pengujian sistem 3. Analisis kinerja sistem pada simulasi 4. Kesimpulan
1.5 Sistematika Penulisan
Sistematik penulisan pada tugas akhir ini adalah :
BAB I PENDAHULUAN
Dalam bab ini mengulas latar belakang masalah, rumusan masalah, batasan masalah, metode penelitian dan sistematika penulisan.
BAB II LANDASAN TEORI
3
BAB III PERANCANGAN SISTEM
Dalam bab ini akan dipaparkan mengenai bagaimana mencari solusi pada persoalan pencarian jalur terpendek dengan menggunakan algoritma Dijkstra.
BAB IV ANALISIS MASALAH
Dalam bab ini membahas implementasi dari perancangan program, menguji keberhasilan algoritma Dijkstra dalam mencari solusi pada masalah pencarian jalur terpendek.
BAB V KESIMPULAN DAN SARAN
4
BAB II
LANDASAN TEORI
2.1 Definisi Graf
Graf adalah himpunan benda-benda yang disebut simpul (vertex atau node) yang terhubung oleh sisi (edge) atau busur (arc). Biasanya graf digambarkan sebagai kumpulan titik-titik (melambangkan simpul) yang dihubungkan oleh garis-garis (melambangkan sisi) atau garis berpanah (melambangkan busur). Suatu graf G didefenisikan sebagai pasangan himpunan (V,E), di mana V = himpunan yang berisikan simpul pada graf tersebut { , } dan E adalah himpunan sisi yang menghubungkan simpul-simpul { , } atau dapat ditulis dengan notasi G = (V,E) . [2] [6]
Berdasarkan orientasi arah pada sisi, graf dapat dibedakan atas dua jenis yaitu : 1. Graf Berarah
2. Graf Tidak Berarah
2.1.1 Graf Berarah (directed graf)
Graf G disebut graf berarah (directed graf) jika setiap sisinya berarah. titik awal dari suatu sisi disebut simpul awal (initial vertex) sedangkan titik akhir dari suatu sisi disebut simpul akhir (terminal vertex). Loop pada graf adalah sisi yang simpul awal dan simpul akhirnya sama.
5 Digraf pada Gambar 2.1 menunjukkan graf berarah dengan himpunan simpul, V(G) = { , } dan himpunan busur A(G) = {a1,a2, a3, a4, a5, a6} yaitu pasangan terurut dari {(v1,v2), (v2,v3), (v3,v4), (v4,v5), (v5,v1), (v2,v5)}.
2.1.2 Graf Tidak Berarah
Graf Tak Berarah (Undirected Graph) Graf G disebut graf tak berarah jika setiap sisinya tidak berarah.
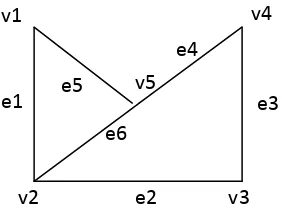
Gambar 2.2 GrafTidak Berarah
Graf pada gambar 2.2 menunjukkan graf tidak berarah dengan himpunan simpul, V(G) = { , } dan himpunan sisi E(G) {e1, e2, e3, e4, e5, e6} yaitu pasangan terurut dari {(v1,v2), (v2,v3), (v3,v4), (v4,v5), (v5,v1), (v5,v2)}.
2.1.3 Graf Berbobot
Di dalam model graf, ada informasi yang ditambahkan pada busur graf. Misalnya pada graf yang menggambarkan antara kota-kota, dapat ditambahkan sebuah bilangan pada setiap busur untuk menujukkan jalur antara kedua kota yang dibutuhkan oleh busur tersebut.
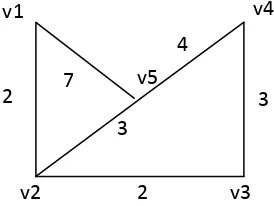
6 Graf pada gambar 2.3 adalah grafberbobot dan tidakberarah yang terdiri dari lima node yaitu node 1, 2, 3, 4, 5.
Gambar 2.3 Grafberbobot dan tidakberarah
2.1.4 Representasi Grafdalam Matriks
Matriks dapat digunakan untuk menyatakan suatu graf, graf yang direpresentasikan pada matriks, dapat dibedakan sebagai berikut :
1. Matriks Adjacency
Misalkan G adalah graf yang tidak berarah yang terdiri dari n node tanpa edge paralel. Matriks Adjacency pada graf G adalah matriks bujursangkar n x n, A= ( dengan
Matriks adjacency dari graf pada gambar 2.2 adalah:
A =
Jika graf yang diberikan adalah graf berbobot, maka elemen matriks yang terhubung antara verteks adalah bobot graf. [6]
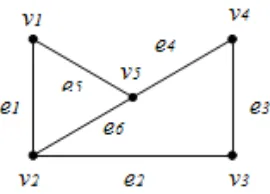
7 2. Matriks Incidency atau matriks bersisian adalah matriks yang merepresentasikan hubungan antara node dan edge. Misalkan B adalah matriks dengan m baris untuk setiap node dan n kolom untuk setiap edge. Jika node terhubung dengan edge, maka elemen matriks bernilai 1. Sebaliknya, jika node tidak terhubung dengan edge, maka elemen matriks bernilai 0.
Gambar 2.4 Graf dengan 5 node dan 6 edge
Matriks bersisian dari graf padagambar 2.4 adalah:
A
=
2.2 Definisi Lintasan (Path)
Lintasan adalah hubungan antar titik atau node dalam sebuah graf. Suatu lintasan yang berawal dan berakhir pada node yang sama, maka disebut lintasan tertutup (close path), jika node awal dan node akhir dari lintasan tersebut berbeda, disebut lintasan terbuka (open path). [3] [7]
8
2.2.1 Lintasan Terpendek (Shortest Path)
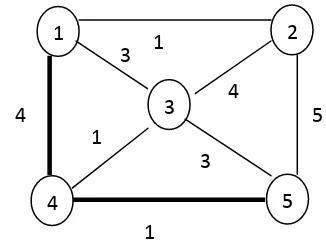
Lintasan terpendek adalah lintasan yang memiliki total bobot minimum untuk mencapai suatu tempat dari tempat tertentu. Lintasan terpendek dapat dicari dengan menggunakan graf. Graf yang digunakan adalah graf yang berbobot, yaitu graf yang setiap sisinya diberikan suatu nilai atau bobot. Bobot pada sisi graf dapat menyatakan, waktu, biaya dan sebagainya. [3]
Gambar 2.5 Shortest Path (garis tebal)
Gambar 2.5 menunjukkan lintasan terpendek (garis tebal) dari node 1 ke node 5 dengan jalur 1-4-5 dengan jumlah bobot lima (5).
2.3 Algoritma Dijkstra
2.3.1 Sejarah Algoritma Dijkstra
Algoritma Dijkstra ditemukan oleh seorang ilmuwan asal Belanda, Edger Wybe Dijkstra. Algoritma ini digunakan untuk mencari lintasan terpendek pada graf berarah, tetapi algoritma ini juga bisa diterapkan pada graf tak berarah.
Algoritma Dijkstra adalah sebuah algoritma untuk memecahkan permasalahan jalur terpendek (shortest path problem) pada sebuah graf berarah (directed graf) atau graf tidak berarah (undirected graf) dengan bobot-bobot sisi (edge weights) yang bernilai tidak negatif. Bila node dari sebuah graf melambangkan kota-kota dan bobot sisi (edge weights) melambangkan jalur antara kota-kota tersebut, maka algoritma Dijkstra dapat digunakan untuk menemukan jalur terpendek antara dua kota.
9 Dalam menentukan jalur terpendek dari suatu graf oleh algoritma dijkstra akan didapatkan jalur yang terbaik, karena pada waktu penentuan jalur yang akan dipilih, akan dianalisis bobot dari node yang belum terpilih, lalu dipilih node dengan bobot yang terkecil. Jika ternyata ada bobot yang lebih kecil melalui node tertentu maka bobot akan dapat berubah. Algoritma dijkstra akan berhenti ketika semua node sudah terpilih. Sehingga akan ditemukan jalur terpendek dari seluruh node, tidak hanya untuk node dari asal dan node tujuan tertentu saja. [5]
2.3.2 Cara Kerja Algoritma Dijkstra
Algoritma ini mencari panjang lintasan terpendek dari node asal ke node tujuan dalam sebuah graf.
Langkah-langkah dalam menentukan lintasan terpendek pada algoritma Dijkstra yaitu :
1. Pada awalnya inisialisasikan node asal (V1) dan node tujuan (V2).
2. Buat 2 buah list, open list dan closed list. Keduanya tidak ada data atau kosong, dan formatnya {node, bobot, node induk}.
3. Masukkan V1 ke open list.
4. Pilih 1 node dengan bobot terkecil pada open list, tambahkan kedalam closed list.
5. Cari node yang bertetangga langsung dari node sebelumnya, yang masuk terakhir dalam closed list. Tambahkan bobot dengan node yang terkait, apabila sudah ada dalam closed list abaikan.
6. Apabila dalam open list terdapat node yang sudah ada bandingkan, lalu cari yang terkecil, dan perbaharui. Bila ternyata jumlah bobotnya sama dalam node yang sama, maka abaikan.
10 8. Dalam closed list cari V2, telusuri jalur berdasarkan node induk sampai
mengacu ke node asal (V1), dan balikkan urutan node. 9. Lintasan terpendek ditemukan bersama bobotnya.
Algoritma dijkstra digunakan untuk pencarian jalur terpendek dari suatu graf, sehingga akan didapatkan jalur yang akan ditempuh. [5]
2.3.3 Penerapan Cara Kerja Algoritma Dijkstra
Gambar 2.6 Sebelum pencarian jalur terpendek
Gambar 2.6 menunjukkan pencarian jalur terpendek dari graf yang memiliki enam buah node dan sembilan edge yang saling terhubung, pencarian dimulai dari node satu (1) ke node enam (6) sebagai node yang dituju.
Langkah awalnya inisialisasikan node 1 sebagai node awal (V1) dan node 6 sebagai node tujuan (V2), buat 2 buah list, open list dan closed list.
Tabel 2.1 Hasil Iterasi Ke-1
Open List Closed List
{1,0,null} -
Dari tabel 2.1 masukkan node 1 ke dalam open list, node 1 memiliki bobot 0, dan node induknya null karena sebagai awal proses pencarian.
Tabel 2.2 Hasil Iterasi Ke-2
11 {2,9,1} {1,0,null}
{3,8,1}
Dari tabel 2.2 Proses dari bobot terkecil lebih dahulu, dikarenakan ada satu yaitu, node 1 maka masukkan kedalam closed list. Node yang bertetangga dengan node 1 adalah, node 2 dan node 3, lalu masukkan ke dalam open list, node 2 memiliki bobot 9, dan node induknya node 1, node 3 memiliki bobot 8, dan node induknya node 1.
Tabel 2.3 Hasil Iterasi Ke-3
Open List Closed List
{2,9,1} {1,0,null} {4,18,3} {3,8,1}
Dari tabel 2.3 Proses dari bobot terkecil lebih dahulu yaitu, node 3 dan masukkan kedalam closed list, node yang bertetangga dengan node 3 adalah node 1 dan node 4, lalu masukkan ke dalam open list, karena node 1 sudah masuk ke dalam closed list diabaikan dan node 4 memiliki bobot 18, dan node induknya node 3.
Tabel 2.4 Hasil Iterasi Ke-4
Open List Closed List
{4,18,3} {1,0,null} {5,19,2} {3,8,1} {6,25,2} {2,9,1}
12 18, dan node induknya node 3. Node 5 memiliki bobot 19, dan node induknya node 2, dan node 6 memiliki bobot 25, dan node induknya node 2.
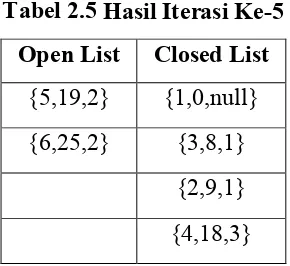
Tabel 2.5 Hasil Iterasi Ke-5
Open List Closed List
{5,19,2} {1,0,null} {6,25,2} {3,8,1}
{2,9,1} {4,18,3}
Dari tabel 2.5 Proses dari bobot terkecil lebih dahulu yaitu, node 4 dan masukkan kedalam closed list, node yang bertetangga dengan node 4 adalah node 2, node 3, node 5 dan node 6, lalu masukkan ke dalam open list, karena node 2, dan node 3 sudah masuk ke dalam closed list diabaikan, karena node 5 dan node 6 sudah ada dalam open list bandingkan bobotnya, ambil yang terkecil. Sehingga node 5 memiliki bobot 19, dan node induknya node 2. Node 6 memiliki bobot 25, dan node induknya node 2.
Tabel 2.6 Hasil Iterasi Ke-6
Open List Closed List
13 open list bandingkan bobotnya, ambil yang terkecil. Sehingga node 6 memiliki bobot 25, dan node induknya node 2.
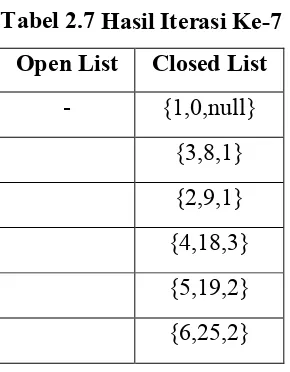
Tabel 2.7 Hasil Iterasi Ke-7
Open List Closed List
- {1,0,null} {3,8,1} {2,9,1} {4,18,3} {5,19,2} {6,25,2}
Dari tabel 2.7 Proses dari bobot terkecil lebih dahulu, karena tinggal 1 maka node 6 masukkan kedalam closed list, node yang bertetangga dengan node 6 adalah node 2, node 4 dan node 5, lalu masukkan ke dalam open list, karena node 2, node 4 dan node 5 sudah masuk ke dalam closed list diabaikan.
Pencarian akan berhenti dikarenakan open list sudah kosong, didalam closed list telusuri V2 atau node tujuan dengan mengacu pada node induk, dan balikkan urutan nodenya, sehingga pencarian jalur terpendek dari graf yang dimulai dari node satu (1) ke node enam (6) diperoleh jalur 1-2-6 dengan jumlah bobot 25. Dapat dilihat pada gambar 2.6.
15
2.4 DFD (Data Flow Diagram)
Data Flow Diagram (DFD) adalah alat pembuatan model yang memungkinkan professional sistem untuk menggambarkan sistem sebagai suatu jaringan proses fungsional yang dihubungkan satu sama lain dengan alur data, baik secara manual maupun komputerisasi. DFD ini sering disebut juga dengan nama Bubble chart, Bubble diagram, model proses, atau model fungsi. DFD ini adalah salah satu alat pembuatan model yang sering digunakan, khususnya bila fungsi-fungsi sistem merupakan bagian yang lebih penting dan kompleks dari pada data yang dimanipulasi oleh sistem.
Dengan kata lain, DFD adalah alat perancangan sistem yang berorientasi pada alur data dengan konsep dekomposisi dapat digunakan untuk penggambaran analisa maupun rancangan sistem yang mudah dikomunikasikan oleh professional sistem kepada pemakai maupun pembuat program.
2.4.1 Penggambaran DFD
Tidak ada aturan baku untuk menggambarkan DFD. Tapi dari berbagai referensi yang ada, secara garis besar langkah untuk membuat DFD adalah : 1. Identifikasai terlebih dahulu semua entitas luar yang terlibat di sistem. 2. Identifikasi semua input dan output yang terlibat dengan entitas luar. 3. Buat diagram konteks, disebut juga diagram level tertinggi dari DFD yang
menggambarkan hubungan sistem dengan lingkungan luarnya. Caranya dengan tentukan nama sistemnya, tentukan batasan sistemnya, tentukan terminator apa saja yang ada dalam sistem, lalu tentukan apa yang diterima/diberikan terminator dari/ke sistem, dan gambarkan diagram konteks.
16 5. Buat diagram Level Satu, diagram ini merupakan dekomposisi dari level zero. Caranya tentukan proses yang lebih kecil dari proses utama yang ada di level zero, tentukan apa yang diberikan/diterima masing-masing proses ke/dari sistem sambil memperhatikan konsep keseimbangan, apabila diperlukan muculkan data store (transaksi) sebagai sumber maupun tujuan alur data dan gambarkan diagram Level Satu.
6. DFD Level Dua, Tiga, ..
Diagram ini merupakan dekomposisi dari level sebelumnya. Proses dekomposisi dilakukan sampai dengan proses siap dituangkan ke dalam program. Aturan yang digunakan sama dengan level satu.
2.5 Pemrograman Borland Delphi
2.5.1 Pengenalan Borland Delphi
Delphi adalah sebuah IDE COMPILER untuk bahasa pemrograman Pascal dan lingkungan pengembangan perangkat lunak. Produk ini dikembangkan oleh CodeGear sebagai divisi pengembangan perangkat lunak milik Embarcadero, divisi tersebut sebelumnya adalah milik Borland. Bahasa Delphi, atau dikenal pula sebagai object pascal (pascal dengan ekstensi pemrograman berorientasi objek (PBO/OOP)) pada mulanya ditujukan hanya untuk Microsoft Windows, namun saat ini telah mampu digunakan untuk mengembangkan aplikasi untuk Linux dan Microsoft .NET framework.
17
2.5.2 Bagian Umum Lingkungan Borland Delphi 7
Lingkungan pengembangan terpadu atau Integrated Development Environment (IDE) dalam program Delphi terbagi menjadi delapan bagian umum, yaitu Main Menu, ToolBar, Component Palette, Form Designer, Code Editor,Object Inspector, Exploring, dan Object Tree View. Untuk lebih jelasnya ditunjukkan pada gambar 2.5.
Gambar 2.7 Lembar Kerja Borland Delphi
IDE merupakan sebuah lingkungan di mana semua tombol perintah yang diperlukan untuk mendesain aplikasi, menjalankan dan menguji sebuah aplikasi disajikan dengan baik untuk memudahkan pengembangan program. [1] [8]
Lingkungan pengembangan terpadu dalam program delphi terdiri dari: (1) Main Menu
Menu utama pada Delphi memiliki kegunaan yang sama seperti program aplikasi windows lainnya. Dengan mengunakan fasilitas menu, program dapat dipanggil atau disimpan. Pada dasarnya semua perintah yang diberikan dapat ditemukan pada bagian menu utama ini.
(2) Tool bar
18 (3) Component Palette
Component palette berisi kumpulan ikon yang melambangkan komponen-komponen yang terdapat pada VCL (Visual Component Library). Pada komponen palette dapat ditemukan beberapa page control, seperti standard, additional, win 32, system, data access dan lain-lain.
(4) Form Designer
Form designer merupakan suatu obyek yang dapat dipakai sebagai tempat untuk merancang program aplikasi. Dalam sebuah form terdapat titik-titik yang disebut grid yang berguna untuk membantu pengaturan tata letak obyek yang dimasukkan dalam form.
(5) Object Inspector
Object inspector digunakan untuk mengubah properti atau karakteristik dari sebuah komponen. Object inspector terdiri dari dua tab yaitu properties dan event.
(6) Code Editor
Code editor merupakan tempat kode program dituliskan. Keuntungan bagi pemakai Delphi adalah tidak perlu menuliskan kode- kode sumber, karena Delphi telah menyediakan kerangka penulisan sebuah program. Code editor dilengkapi dengan fasilitas highlight yang memudahkan pemakai menemukan kesalahan.
(7) Code Explorer
Jendela pada code explorer adalah lembar kerja baru yang terdapat di dalam Delphi 7 yang tidak ditemukan pada versi-versi sebelumnya. Code explorer digunakan untuk memudahkan pemakai berpindah antar file unit yang terdapat di dalam jendela code editor.
(8) Object Tree View
18
BAB III
PERANCANGAN SISTEM
3.1 Deskripsi Sistem Pencarian Jalur Terpendek
Pencarian jalur terpendek menggunakan algoritma dijkstra menjadi permasalahan yang akan dipecahkan dan dibahas pada tugas akhir ini, aplikasi pencarian jalur terpendek berdasarkan bobot atau panjanganya jalur yang dilewati dari node asal ke node tujuan, dan tidak tergantung dari berapa jumlah node atau titik yang dilewati.
3.2 Perancangan Sistem
Pada perancangan sistem akan dibuat suatu program yang dapat dijalankan pada PC maupun laptop, yang dapat digunakan untuk mencari jalur yang paling efisien dilihat dari segi panjang jalur yang hendak ditempuh.
Kebutuhan untuk membangun sistem tersebut adalah sebagai berikut : 1. Hardware
Kebutuhan hardware untuk sistem ini adalah : a. Processor : 400 MHz atau lebih baik b. Memory : 256 MB SDRAM atau lebih baik c. 475 MB ruang harddisk (setelah instalasi)
d. 800 x 600 atau resolusi yang lebih tinggi dengan 256 warna. e. Keyboard dan mouse.
2. Software
Kebutuhan software dari aplikasi untuk sistem ini adalah : a. OS : Windows 98 atau lebih baik
19
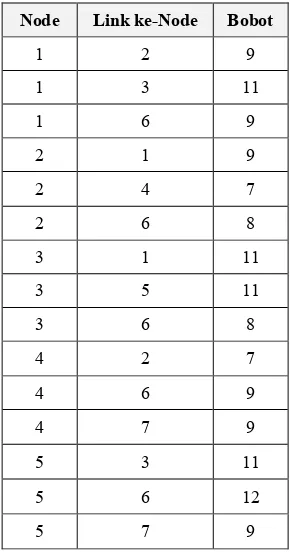
3.2.1 Data dalam Graf
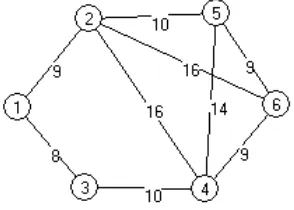
Gambar 3.1 menunjukkan contoh dari penempatan node beserta bobotnya.
Gambar 3.1 Graf dengan 7 node yang tidak berarah dan berbobot
Dalam tabel 3.1 menunjukkan bobot antar node yang tersambung ke node lainnya dengan mengacu pada graf dalam gambar 3.1.
20
3.2.2 Diagram Konteks
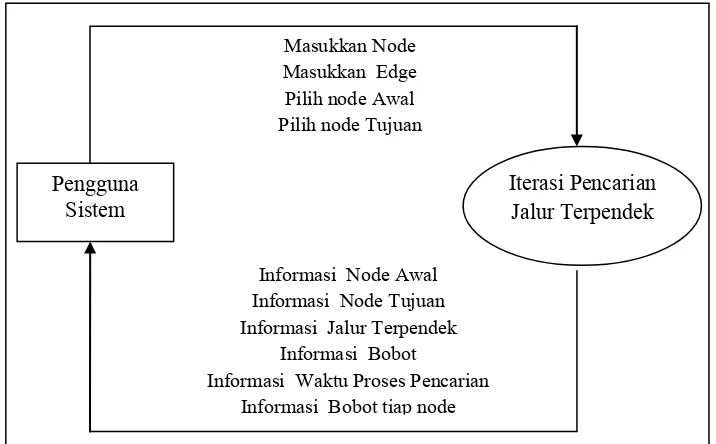
Diagram Konteks merupakan suatu model yang menjelaskan secara global bagaimana data digunakan dan diinformasikan untuk proses, atau dengan kata lain merupakan gambaran umum mengenai sistem yang menggambarkan aliran data kedalam dan keluar sistem. Berikut ini adalah diagram dari sistem yang akan dibangun.
Gambar 3.2 Diagram konteks
3.2.3 Diagram Alir Data
Setelah diagram konteks terbentuk, tahapan selanjutnya adalah membuat diagram alir data (Data Flow Diagram/DFD) untuk menjelaskan proses input data sistem pencarian jalur terpendek yang telah terbentuk.
Pengguna
21
Dari DFD Level 1 terdapat dua tahapan, yaitu :
1. Pada proses penempatan data, pengguna diharuskan untuk memasukkan node dan menyambungkan dengan edge pada node lainnya dan data berupa gambar graf.
22
3.2.4 Perancangan Input/Output Sistem
Perancangan T01
1. Jika Node di klik maka akan keluar node yang mulai dari node ke-1 2. Jika garis (\) di klik maka dapat
menghubungkan antar node.
3. Jika Node Sumber di klik, lalu pilih node dan akan tampil di Node Awal (V1)
4. Jika Node Tujuan di klik, lalu pilih node dan akan tampil di Node Akhir (V2)
5. Jika Mulai Pencarian di klik, menghasilkan data untuk Jalur yang ditempuh beserta Bobot juga data antar node yang berkaitan dan waktu yang ditempuh. Dapat dilihat pada T02
Perancangan T02
23
3.2.5 Perancangan Prosedural
A. Prosedur Program Utama
Pada bagian ini akan dibuat deskripsi rinci dari perangkat lunak, yaitu algoritma yang akan digunakan pada sistem yang akan dibuat, perancangan terlihat pada gambar 3.5.
djikstra(count)
Selesai
Type TJarak = array[1 ... max, 1 ... max] of integer; TPath = record
nodeke : byte
arraypath : array[1 ... max] of byte Jarak : integer
initdata(count)
Gambar 3.4 Prosedur Program Utama
B. Prosedur Initdata
Prosedur ini berfungsi untuk menginisialisasikan data dalam pencarian jalur terpendek.
24
Gambar 3.5 Prosedur Initdata
C. Prosedur Dijkstra
Prosedur ini berfungsi untuk memulai pencarian jalur terpendek dengan cara algoritma dijkstra.
Gambar 3.6 Prosedur Dijkstra
D. Prosedur Lessthen
25
jauh[i] := a path[i] := path[x] path[i].nodeke := path[i] + 1 path[i].arraypath[path[i].nodeke] := i
path[i].Jarak := path[i].Jarak+Data[path[i].arraypath[path[i].nodeke - 1], path[i].arraypath[path[i].nodeke]] count : byte
Gambar 3.7 Prosedur Lessthen
E. Prosedur Update
Prosedur ini berfungsi mencari jalur terpendek dengan cara memasukkan node ke dalam closed list.
Mulai
closed:=path[Tujuan]
Selesai Closed : TPath
26
F. Prosedur Open
Prosedur ini berfungsi untuk mencari jalur terpendek dengan cara menentukkan node mana yang terlebih dahulu diproses dalam open list, proses dilakukan berdasarkan bobot yang paling minimum diantara node lainnya.
Mulai
i>count
jauh[i] < minimum dan open[i] = 0
minimum:=jauh[i] j:=i successor:=j
Selesai minimum:=9999
count : byte i : byte j : byte minimum : real
Y T
Y
T
27
BAB IV
ANALISIS MASALAH
4.1 Spesifikasi PC
Analisis pada implementasi algoritma dijkstra menggunakan dua PC, dengan spesifikasi sebagai berikut:
1) PC-1
Processor : Intel Core 2 duo 1,66 GHz Memory : 1 GB
2) PC-2
Processor : Intel Pentium 4 1,8D GHz Memory : 2,5 GB
Perancangan pencarian jalur terpendek ini menggunakan dua PC dengan jumlah node sebanyak 10 node dengan 20 edge, 10 node dengan 30 edge, 10 node dengan 40 edge, 20 node dengan 40 edge, 20 node dengan 50 edge, 20 node dengan 60 edge, 30 node dengan 50 edge, 30 node dengan 70 edge, 30 node dengan 90 edge.
4.2 Kasus 10 node
4.2.1 Kasus 10 node dengan 20 edge
28
Gambar 4.1 Tampilan jalur sebanyak 10 node dengan 20 edge
4.2.2 Kasus 10 node dengan 30 edge
Pada gambar 4.2 menampilkan suatu jalur dari node sumber, node 6 ke node 2, sebagai node yang dituju. Program akan mencari jalur dari node awal ke setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
29
4.2.3 Kasus 10 node dengan 40 edge
Pada gambar 4.3 menampilkan suatu jalur dari node sumber, node 1 ke node 10, sebagai node yang dituju. Program akan mencari jalur dari node awal ke setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
Gambar 4.3 Tampilan jalur sebanyak 10 node dengan 40 edge
4.3 Kasus 20 node
4.3.1 Kasus 20 node dengan 40 edge
30
Gambar 4.4 Tampilan jalur sebanyak 20 node dengan 40 edge
4.3.2 Kasus 20 node dengan 50 edge
Pada gambar 4.5 menampilkan suatu jalur dari node sumber, node 13 ke node 7, sebagai node yang dituju. Program akan mencari jalur dari node awal ke setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
Gambar 4.5 Tampilan jalur sebanyak 20 node dengan 50 edge
4.3.3 Kasus 20 node dengan 60 edge
31 setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
Gambar 4.6 Tampilan jalur sebanyak 20 node dengan 60 edge
4.4 Kasus 30 node
4.4.1 Kasus 30 node dengan 50 edge
Pada gambar 4.7 menampilkan suatu jalur dari node sumber, node 1 ke node 15, sebagai node yang dituju. Program akan mencari jalur dari node awal ke setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
32
4.4.2 Kasus 30 node dengan 70 edge
Pada gambar 4.8 menampilkan suatu jalur dari node sumber, node 2 ke node 25, sebagai node yang dituju. Program akan mencari jalur dari node awal ke setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
Gambar 4.8 Tampilan jalur sebanyak 30 node dengan 70 edge
4.4.3 Kasus 30 node dengan 90 edge
Pada gambar 4.9 menampilkan suatu jalur dari node sumber, node 25 ke node 3, sebagai node yang dituju. Program akan mencari jalur dari node awal ke setiap node yang lain sampai menemukan solusi jalur terpendek pada node yang menjadi tujuan.
33
4.5 Total kasus pada PC 1
Gambar 4.10 menggambarkan total kasus pada PC 1 yang dilakukan proses run sebanyak tiga kali, dalam pengujian dengan 10 node yang berbeda edge mempunyai perubahan waktu yang tidak terlalu signifikan selama proses run, ketika pengujian dengan 20 node dan 30 node yang berbeda edge juga, perubahan waktu mulai terlihat signifikan, atau dapat dikatakan dengan pertambahan node akan menyebabkan waktu terlihat signifikan dibanding dengan pertambahan edge. Dalam total kasus pada pengujian PC 1, proses rata-rata run masih dibawah 1 detik, dapat dilihat pada tabel 4.1.
Gambar 4.10 Tampilan total kasus pada PC 1
Tabel 4.1 Total waktu pada PC 1
4.6 Total kasus pada PC 2
Gambar 4.11 menggambarkan total kasus pada PC 2 yang dilakukan proses run sebanyak tiga kali, dalam pengujian dengan 10 node yang berbeda edge mempunyai perubahan waktu yang tidak terlalu signifikan selama proses run,
Node 10 20 30
Edge 20 30 40 40 50 60 50 70 90
Run 1 (detik) 0.03 0.03 0.03 0.14 0.18 0.29 0.31 0.29 0.29 Run 2 (detik) 0.04 0.03 0.03 0.15 0.25 0.31 0.14 0.34 0.31
Run 3 (detik) 0.05 0.03 0.03 0.12 0.17 0.28 0.32 0.33 0.3
Rata-rata (detik) 0.04 0.03 0.03 0.14 0.20 0.29 0.26 0.32 0.30 Waktu (detik)
34 ketika pengujian dengan 20 node dan 30 node yang berbeda edge juga, perubahan waktu mulai terlihat signifikan, atau dapat dikatakan dengan pertambahan node akan menyebabkan waktu terlihat signifikan dibanding dengan pertambahan edge. Dalam total kasus pada pengujian PC 2, proses rata-rata run masih dibawah 1 detik sampai dengan pengujian menggunakan 20 node, ketika pengujian dengan 30 node waktu proses mulai diatas 1 detik, dapat dilihat pada tabel 4.2.
Gambar 4.11 Tampilan total kasus pada PC 2
Tabel 4.2 Total waktu pada PC 2
4.7 Perbandingan pada PC 1 dan PC 2
Gambar 4.12 Perbandingan PC1 dan PC2 dengan 10 node dan 20 edge
Node 10 20 30
Edge 20 30 40 40 50 60 50 70 90
Run 1 (detik) 0.12 0.15 0.14 0.56 0.48 0.53 1.12 1.22 1.24 Run 2 detik) 0.13 0.13 0.13 0.47 0.48 0.44 1.15 1.22 1.22 Run 3 (detik) 0.12 0.14 0.13 0.54 0.49 0.44 1.16 1.28 1.32 Rata-rata ( detik) 0.12 0.14 0.13 0.52 0.48 0.47 1.14 1.24 1.26 Waktu (detik)
35 Gambar 4.12 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 10 node dan 20 edge. PC 1 mempunyai waktu rata-rata 0.04 detik dan PC 2 mempunyai waktu rata-rata 0.12 detik.
Gambar 4.13 Perbandingan PC1 dan PC2 dengan 10 node dan 30 edge
Gambar 4.13 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 10 node dan 30 edge. PC 1 mempunyai waktu rata-rata 0.03 detik dan PC 2 mempunyai waktu rata-rata 0.14 detik.
36 Gambar 4.14 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 10 node dan 40 edge. PC 1 mempunyai waktu rata-rata 0.03 detik dan PC 2 mempunyai waktu rata-rata 0.13 detik.
Gambar 4.15 Perbandingan PC1 dan PC2 dengan 20 node dan 40 edge
Gambar 4.15 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 20 node dan 40 edge. PC 1 mempunyai waktu rata-rata 0.13 detik dan PC 2 mempunyai waktu rata-rata 0.50 detik.
37 Gambar 4.16 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 20 node dan 50 edge. PC 1 mempunyai waktu rata-rata 0.20 detik dan PC 2 mempunyai waktu rata-rata 0.48 detik.
Gambar 4.17 Perbandingan PC1 dan PC2 dengan 20 node dan 60 edge
Gambar 4.17 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 20 node dan 60 edge. PC 1 mempunyai waktu rata-rata 0.29 detik dan PC 2 mempunyai waktu rata-rata 0.47 detik.
38 Gambar 4.18 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 30 node dan 50 edge. PC 1 mempunyai waktu rata-rata 0.26 detik dan PC 2 mempunyai waktu rata-rata 1.14 detik.
Gambar 4.19 Perbandingan PC1 dan PC2 dengan 30 node dan 70 edge
Gambar 4.19 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 30 node dan 70 edge. PC 1 mempunyai waktu rata-rata 0.32 detik dan PC 2 mempunyai waktu rata-rata 1.24 detik.
39 Gambar 4.20 menggambarkan perbandingan proses run sebanyak tiga kali pada PC 1 dan PC 2 dengan menggunakan 30 node dan 90 edge. PC 1 mempunyai waktu rata-rata 0.30 detik dan PC 2 mempunyai waktu rata-rata 1.26 detik.
Tabel 4.3 Tampilan perbandingan dengan 2 PC
Node Edge
PC
Solusi Jalur Terpendek
1 2
Waktu Proses (detik) Waktu Proses (detik)
40
BAB V
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Dari hasil pengujian penulis dapat membuat kesimpulan sebagai berikut :
1. Telah berhasil dibuat suatu aplikasi simulasi untuk mencari jalur terpendek dengan menggunakan algoritma dijkstra.
2. Jumlah node dan edge berpengaruh pada proses waktu untuk mencari solusi dalam pencarian jalur terpendek.
3. Pertambahan node akan menambah proses waktu yang cukup signifikan dalam pencarian jalur terpendek dibandingkan dengan pertambahan edge.
5.2 Saran
Adapun saran-saran untuk pengembangan lebih lanjut:
1. Rute antara satu node dengan node lain dapat dilewati lebih dari satu kali.
2. Mengimplementasikan aplikasi ini pada kondisi sebenarnya atau peta. 3. Menerapkan aplikasi ini pada system berbasis web pada layanan peta
DAFTAR PUSTAKA
[1] Cantu, Marco, Mastering Delphi 7, Sybex, California, 2002.
[2] Joyner, David and Minh Van Nguyen, Algorithmic Graph Theory Version 03, GNU Free Documentation License, 2010.
[3] Wibisono, Samuel, Matematika Diskrit, Graha Ilmu, Yogyakarta, 2008. [4] Wibisono, Yudi, Handout Program Delphi:Pengantar Fasilitas Grafik
dalam Delphi, Jurdikmat UPI.
[5] Algoritma Dijkstra, (http://tech-algorithm.com/articles/dijkstra-algorithm/, diakses 10 Mei 2011).
[6] Dwi, Yuni, Teori graf, (http://yuni_dwi.staff.gunadarma.ac.id/Downloads /files/12671/Bab+1+-+Dasar+Teori+Graf.pdf, diakses 14 Mei 2011).
[7] Informatika. Lintasan terpendek, (http://www.informatika.org/~rinaldi /Matdis/2009-2010/Makalah0910/MakalahStrukdis0910-075.pdf, diakses 11 Mei 2011).
Giri Mega Gentara lahir di Bandung pada 5 Juli 1985.
Anak ke-3 dari 3 bersaudara memiliki tinggi badan 172 cm.
Alamat sekarang Jl. Tera no 20 RT/RW. 06/05 Kota.
Bandung Jawa Barat. Lulus SDN Merdeka V pada tahun
1997, SLTP Negeri 3 Bandung pada tahun 2000, SMA
Negeri 7 pada tahun 2003, dan Gelar Sarjana Teknik
Komputer diperoleh dari Program Studi Teknik Komputer
Fakultas Teknik dan Ilmu Komputer UNIKOM tahun 2011. Pengalaman kerja
praktek di Dinas Tata Ruang dan Pemukiman bagian Administrator Jaringan pada