Least Squares Predictions and Mean Varia

_______________________________________________

FINANCIAL MARKETS GROUP

AN ESRC RESEARCH CENTRE

_______________________________________________

LONDON SCHOOL OF ECONOMICS

Any opinions expressed are those of the author and not necessarily those of the Financial Markets Group.

Least Squares Predictions and

Mean-Variance Analysis

By

Enrique Sentana

DISCUSSION PAPER 312

L east Squar es P r edict ions and

M ean-Var iance A nalysis

1

Enr ique Sent ana

(

C

E

M F

I

,

C

E

P

R

a

n d

L

S

E

F

M G )

R

e

v

i

s

e

d

:

D

e

c

e

m

b

e

r

1 9

9

8

1 _{Iwouldliketothan kM an uelArellan o,G aryChamberlain ,Ian Domowitz ,Lars}

Han sen ,JorgePadilla,Ign acioPeñ a,Raf aelRepullo,SushilW adhwan i,an daudien ces

atCEM FI,LSEan dtheIIISpan ishM eetin gon Fin an cialEcon omicsf orveryusef ul commen tsan ddiscussion s. Of course,theusualcaveatapplies. Addressf orcorrespon

A bst r act

W ecomparetheSharperatiosof in vestmen tf un dswhichcombin eon eriskless an don eriskyassetf ollowin g:i) timin gstrategieswhichf orecastexcessreturn s

usin gsimpleregression s;ii) astrategywhichusesmultipleregression in stead;an d iii) apassiveallocation whichcombin esthef un dsin i) withcon stan tweightin gs.

W eshowthatiii) domin atesi) an dii) ,asitimplicitlyusesthelin earf orecastin g

rulethatmaximiz estheSharperatioof activelytradedportf olios,buttherelative ran kin gof i) an dii) isgen erallyun clear. W ealsodiscussun derwhatcircumstan ces

1

I nt r oduct ion

Fromaf ormalpoin tof view,mean -varian cean alysisan dleastsquarespre -diction sareverycloselyrelated,asbotharetheresultof themin imisation of a

mean squaren ormoveraclosedlin earsubspaceof thesetof allran domvari -ableswith…n itesecon dmomen ts(seee. g. Han sen an dSargen t(1 991 ) ) . Froma

practicalpoin tof view,theyarealsocloselycon n ected,sin ceman y…n an cialmar -ketpractition erscombin etheprediction sf romtheirregression equation switha

mean -varian ceoptimiserin ordertomakedyn amicportf olioallocation decision s. In f act,given asetof variableswhichhelppredictstockmarketreturn sorother …n an cialassets,on ewouldthin kapriorithatthisisarathern aturalwaytotime themarket.

T hepurposeof thispaperistodetermin etowhatexten tthisin tuition iscor

-rect. W ean alyz etheportf olioallocation between asaf eassetan dariskyon e, an dderiveclosed-f orman alyticalsolution s. W econ sideraltern ativeprediction rules,an dran kthemin termsof theSharperatiosof theassociatedmarkettim

-in gstrategies. In particular,wecomparetheperf orman ceof in vestmen tf un ds thatf ollow:i) dyn amicportf olioallocation swhichusesimpleregression stof ore

-castexcessreturn s;ii) an activestrategywhichusesmultipleregression in stead; an diii) apassiveportf olioallocation whichcombin esthef un dsin i) withcon

-stan tweightin gsimpliedbystan dardmean -varian cean alysis. Furthermore,we obtain an expression f orthelin earf orecastin grulethatmaximisestheSharpera -tioof an activelytradedportf olio,an ddiscussun derwhichcircumstan cessuchan

“ optimal” f orecastcoin cides(uptoaproportion alityf actor) withthecon dition al expectation .

T herestof thispaperisorgan isedasf ollows. W ein troducethetheoretical set-upin section 2 ,derivetheactivean dpassiveportf oliostrategiesmen tion ed

wemakeassumption saboutthejoin tdistribution of thesign als,an dan alyz ein detailseveralspecialcases. Fin ally,section 4 con tain sadiscussion of ourresultsin relation toseveralareasof curren tresearchin terestin the…n an cean decon ometrics

literatures. Proof sof ourmain proposition s,togetherwithsomeauxiliaryresults, aregatheredin theappen dix.

2

I nvest m ent St r at egies and Shar pe R at ios

Let’scon sideraworldwithasaf eassetan dariskyon e. Letr betheexcess

return on theriskyasset,an dsupposethattherearek in dicatorvariables,or

sign als,x= (x₁; : : : ; x_{k )}0,whichhelppredictr.

T omakethecomparison ssimpler,weassumethatthe(un con dition al) ex -pectedreturn on theriskyassetequalsthesaf ereturn . Sin cethisimpliessecon d

orderstochasticdomin an cein theabsen ceof in f ormation (ourben chmarkcase) , riskaverseun in f ormedin vestorswillon lyholdcash.

Let’sn owsupposethattherearek f un dman agers,eachen dowedwithprivate

in f ormation on asin glein dicatorvariable,x_j ,j _{= 1}; : : : ; k,whopursueactive

portf oliostrategies. Speci…cally,wemakethestan dardassumption in thelit -eraturethatthef raction of theirwealthin vestedin theriskyassetislin earin theirin f ormation . On ef ormalwayof ration aliz in gsuchabehaviouristhrough con dition almean -varian cean alysis,un derthemain tain edassumption thatthe

con dition alexpectation sof return sarelin earin (somein stan tan eoustran sf orma -tion of ) thesign als,an dthecorrespon din gcon dition alvarian cescon stan t. M ore precisely,if weassumethattheoptimisation problemof aman ageren dowedwith in f ormation I can beexpressedas

max

w r (I )

n

w _{r (}I₎E ₍r _jI_)¡ ® 2w

2

r (I)V (r jI)

o

(1 )

strategywillbe

w ¤

r (I) =

1 ®

E ₍r_jI₎ V ₍r_jI₎ (2 )

In thecaseof man agerj,in particular,w ¤

r (xj ) willbeproportion altothede

-mean edvalueof thejt h predictorvariable,x_{~j =} x_{j ¡} º_j ,asstated.

Importan tly,weassumethattherearen otran saction costsorotherimpedi -men tstotrade,an din particular,thatshort-salesareallowed. W ealsoassume

thatthesiz esof thein vestmen tf un dsaresuchthattheirbehaviourdoesn otalter thedistribution of return s.

T okeepthen otation simple,de…n e±_{j =} ¾_{j r} = ¾_{j j} asthecoe¢cien tin the

(theoretical) simpleregression of r on x_j ; "_{j =} r_{j ¡} ±_j x_~j astheassociatedprediction

error,¾_"

j" j = ¾r r ¡ ¾

2

j r = ¾j j asitsvarian ce,an d½j r = ¾j r =p¾r r ¾j j asthetheoretical

correlation coe¢cien tbetween r an dx_j . T hen ,theexcessreturn son eachf un d

willbe

r_{j =} 1

® ¢ ±_j x_~j

¾_"

j " j

¢r (3 )

sothat

E ₍r_{j ) =} 1

® ¢ ±_j ¾_{j r}

¾_"

j " j

= 1

® ¢ ½2_{j r}

1_¡ ½2_{j r} ¸0 (4 )

withequalityif an don lyif thejt h in dicatorvariablehasn opredictivepoweratall.

T heref ore,r_j isn oton lymorepro…tableon averagethan theben chmarkstrategy

of holdin gcash,butalsoitspro…tabilityin creaseswiththepredictivepowerof x_j .

However,suchatimin gstrategyisalsoriskier,sin ceobviously

V ₍r_{j ) =} 1 ®2

±2_j ¸_{j j} ¾2

" j " j

¸0 (5 )

where¸_{j j =} V _{( ~}x_j r₎.

Let’sn owcon sideran otherf un dman ager,a say,whoalsof ollowsan active

kn owin gthewholeof x.1 Let¯= _§ ¡1

x x ¾x r bethecoe¢cien tsof the(theoretical)

multipleregression of return son thein dicators,r^₌ E ₍r_{) + ¾}0

x r § ¡x x1(x¡ º) = ¯0~x

the…ttedvaluesf romthatregression ,u ₌ r _{¡ ¯}0_x~theprediction errors,¾_{r^r^ =}

¾0_{x r} § ¡_{x x}1¾x r thevarian ceof thepredictedvalues,¾u u = ¾r r ¡ ¾0x r § ¡x x1¾x r the

varian ceof theresiduals,an d…n allyR 2_{= (}¾_{^r ^r} = ¾_{r r )} thetheoreticalmultiplecor

-relation coe¢cien t. Suchadyn amicportf oliostrategyproducesexcessreturn s

of

r_{a =} 1 ®

¯0x~

¾_{u u} ¢r (6 )

T hen ,sin ceE _(~xr_{) = ¾x r} E ₍r_{a ) =} 1

® ¾_r^r^ ¾_{u u} =

1

® ¢ R 2

1¡ R 2 ¸0 (7 )

sothatE ₍r_{j ) ·}E ₍r_{a )} f orj _{= 1}; : : : ; k,asR 2

¸½2

j r . Butagain ,suchastrategyis

risky,sin ce

V ₍r_{a ) =} 1 ®2

¯0¤ ¯

¾2

u u ¸

0 (8 )

where¤ = V _(~xr₎.

Fin ally,let’sin troduceyetan otherman ager,p say,whodoesn otobserve_xat

all,butf ree-rideson theotherman agersbycon structin gan “ umbrella” f un dof the

k in dividualf un dsan dthesaf eassetwithcon stan tweightin gs,accordin gtothe

rulesof un con dition almean -varian cean alysis. Let’scall¹= E _(r) an d_-= V _(r),

whereristhevectorof excessreturn son eachf un d,i. e. r= (r₁; : : : ; r_{k )}0. Let_©

beak _£ k diagon almatrixwithtypicalelemen tÁ

j j = ±j = ¾" j" j ,sothatin matrix

n otation ,wecan write

r= 1

® ©x~r (9)

1 _{W ithin acon dition almean -varian cef ramework,thisassumption implicitlyimposesrestric}

-tion son thejoin tdistribution of thesign als,becausewewouldbesimultan eouslyassumin gthat

thedistribution of return scon dition alon thewholeof xan deachof itselemen tshasalin ear

mean an dacon stan tvarian ce. In thisrespect,itisimportan ttomen tion thatalltheexamples

¹= 1

® ©¾x r (1 0 )

-= 1

®2©¤ © (1 1 )

Asiswellkn own ,theoptimalproportion sof man agerp’sresourcesin vested

in eachf un dwillbegiven bythevector

w¤p =

1

® -¡1

¹= _©¡1

¤ ¡1¾x r

Hen ce,theexcessreturn sf romherstaticportf olioallocation willbe

r_{p = w}¤0

p r=

1 ® ¾

0

x r ¤ ¡1~xr (1 2 )

Fromhere,itisstraightf orwardtoseethat

E ₍r_{p ) =} 1 ® ¾

0

x r ¤ ¡1¾x r ¸0 (1 3 )

an d

V ₍r_{p ) =} 1 ® 2¾

0

x r ¤ ¡1¾x r ¸0 (1 4 )

G iven thattheorigin alsign als,ortheirtran sf ormation s,maywellbeprivate in f ormation ,in lin ewithstan dardpracticeweshallcomputetheun con dition al risk-return trade-o¤,orSharperatio,of thedi¤eren tportf oliostoevaluatetheir perf orman cetakin gin toaccoun ttheirrisk.

Lets₍r_{j )},s₍r_{a )} an ds₍r_{p )} den otetheSharperatiosof man agersj,a an dp

respectively. In viewof (4 ) -(5 ) ,(7 ) -(8 ) ,an d(1 3 ) -(1 4 ) wehavethat

s₍r_{j ) = p}E (rj ) V ₍r_{j )} =

j¾_{j r j} p

¸_{j j} (1 5 )

s₍r_{a ) = p}E (ra ) V ₍r_{a )} =

¾_{^r ^r}

p

¯0¤ ¯ (1 6 )

an d

s₍r_{p ) = p}E (rp ) V ₍r_{p )} =

p

¾0

In ordertocompares₍r_{j )},s₍r_{a )} an ds₍r_{p )},wecouldmakef urtherassumption s

on thejoin tdistribution of thesign als. W eshallexplorethisaven uein then ext section ,butbef ore,wecan statethef ollowin ggen eralresult:

P r op osit ion 1 s₍r_{p ) ¸}s₍r_{a ) w i t h e q u a l i t y i f a n d o n l y i f ¤ §} ¡_{x x}1_{¾x r i s p r o p o r t i o n a l}

t o _{¾x r} .

T heref ore,in termsof un con dition alrisk-return trade-o¤s,man agerp,who

pursuesapassiveportf oliostrategy,doesalwaysatleastaswellas,an dof ten betterthan ,man agera,whopursuesan activeportf oliostrategy.

In ordertogain somein tuition on thisresult,itiscon ven ien ttoun derstan d

whatthebehaviourof man agera lookslikef romman agerp’sperspective. In this

respect,itisimportan ttorealiz ethatman agera isin di¤eren tbetween astrategy

basedon theun derlyin griskyassetalon e,oron ebasedon someof thek f un ds,

asshecan alwaysun win dtheirposition s. In f act,itistrivialtoseethaton ecan replicateherorigin alactivestrategywiththepassivestrategy¾¡1

u u ¾0x r § ¡x x1©¡1r.

T heref ore,f romthepoin tof viewof p,man agera isobservation allyequivalen t

toapassiveportf olioman agerwhoissuboptimallyallocatin gherwealthbetween

thek f un dsan dthesaf easset. Sin cewekn owf romthetheoryof mean -varian ce

an alysiswitharisklessassetthattheSharperatioof theoptimalportf oliowillbe higherthan theSharperatioof an yotherportf olio,in cludin gtheorigin alassets, itisn otsurprisin gthattheSharperatioof r_p ,willbeatleastashighasthe

Sharperatioof r_a ,an din deedan yr_j .

In con trast,f roma’svan tagepoin t,man agerp iscon ductin gasuboptimal

activein vestmen tstrategy,in whichthef raction of herwealthin vestedin therisky assetis®¡1

¾0x r ¤ ¡1~xasopposedto®¡1¾¡u u1¾0x r § ¡x x1x~. T heref ore,herbehaviour

isobservation allyequivalen ttothatof an activeportf olioman agerwhoused

(¾_{u u )¾}0

x r ¤ ¡1~xin steadof ¾0x r § ¡x x1~xasherlin earprediction rule. G iven thatthe

somepassivestrategywhichcombin esr₁; : : : ; r_k an dtherisklessasset,in viewof

ourpreviousdiscussion ,itisn otsurprisin gthatwecan characteriz etheoptimality of man agerp’sf orecastin gruleasf ollows:

P r op osit ion 2 _¾0

x r ¤ ¡1~xi s ( p r o p o r t i o n a l t o ) t h e l i n e a r f o r e c a s t i n g r u l e , °¤0~xs a y ,

t h a t m a x i m i s e s t h e r a t i o o f e x c e s s m e a n r e t u r n t o s t a n d a r d d e v i a t i o n o f a n a c t i v e l y t r a d e d p o r t f o l i o .

NotethatProposition 2 isstron gerthan Proposition 1 ,asitsaysthatp is

n oton lybetterthan a in termsof Sharperatios,butalsobetterthan an yother

tradin gstrategywhichislin earin thesign als.

However,wecan n otran kin gen erals₍r_{a )} an ds₍r_{j )},sothatman agera,who

usesin f ormation on theen tirevectorx,maydobetterorworsethan aman ager

whoon lyusesin f ormation on aparticularx_j ,despitethef actthatexpectedexcess

return sf ora arealwayshigher. In prin ciple,wewouldexpects₍r_{p ) ¸}s₍r_{a ) ¸}s₍r_{j )}

f orallj. Nevertheless,itispossibletocon structexamplesin whichs₍r_{a )} < s₍r_{j )} < s₍r_{p )} f orsomej (seesection 3 . 4 below) .

Our…n alproposition makestherelation shipbetween s₍r_{p )} an ds₍r_{j )} precise: P r op osit ion 3 T h e S h a r p e r a t i o o f t h e o p t i m a l p o r t f o l i o ( i n t h e u n c o n d i t i o n a l

m e a n - v a r i a n c e s e n s e ) , s₍r_{p ), d e p e n d s o n l y o n t h e v e c t o r o f S h a r p e r a t i o s o f t h e}

k _{u n d e r l y i n g f u n d s ,} s_{(r), a n d t h e i r c o r r e l a t i o n m a t r i x , ¦, t h r o u g h t h e f o l l o w i n g}

q u a d r a t i c f o r m :

s2₍r_{p ) =} s_(r)0_¦¡1_s

(r)

T heaboveexpression ,whichf orthecaseof k _{= 2} adoptstheparticularly

simplef orm:

s2₍r_{p ) =} 1 1_¡ ¼2₁₂

£

s2₍r_{1) +} s2₍r_{2)¡ 2}¼₁₂s₍r₁₎s₍r₂₎¤

where¼_{12 =} co r₍r₁; r₂₎,turn souttoberemarkablysimilartothef ormulathat

relatestheR 2 of themultipleregression of r on (acon stan tan d) _xwiththe

correlation sof thesimpleregression s. Speci…cally,

R 2_{= ½}0

T hesimilarityisn otmerelycoin ciden tal. Fromthemathematicsof themean

-varian cef ron tier,wekn owthatE ₍r_{j ) =} co v₍r_j ; r_{p )}E ₍r_{p )}= V ₍r_{p )},an dtheref ore,

thats₍r_{j ) =} co r₍r_p ; r_{j )}s₍r_{p )}. In otherwords,thecorrelation coe¢cien tbetween r_p an dr_j istheratioof Sharperatioss₍r_{j )}= s₍r_{p )}. T hen ,theresultin Proposition 3

f ollowsf rom(1 8 ) an dthef actthatthecoe¢cien tof determin ation in themultiple regression of r_p on allk r0

j s willbe1 .

3

Examples

3.1

T wo bi nar y si gnals

Let’san alyz ein detailthecaseof twobin arysign als,whosejoin tdistribution

isgiven by:

x_2Â x_{1 1 ¡ 1} 1 1₄(1 + ½₁₂₎ 1

4(1¡ ½12) 12

¡ 1 1₄(1¡ ½₁₂₎ 1

4(1 + ½12) 12 1

2

1 2

(1 9)

sothatE ₍x_{1) =} E ₍x_{2) = 0},V ₍x_{1) =} V ₍x_{2) = 1}an dco v₍x₁; x_{2) =} ½₁₂.

Itisstraightf orwardtoprovethatf orthef ourpossiblecombin ation sof the sign alswewillhave

x₁ x₂ E ₍r_jx₁₎ E ₍r_jx₂₎ E ₍r_jx₁; x₂₎ 1 1 ¾_1r ¾_{2r (}¾_{1r +} ¾_{2r )}=_{(1 +} ½₁₂₎

1 ¡ 1 ¾_{1r ¡} ¾_{2r (}¾_{1r ¡} ¾_{2r )}=_(1¡ ½₁₂₎

¡ 1 1 _¡ ¾_1r ¾_{2r ¡ (}¾_{1r ¡} ¾_{2r )}=_(1¡ ½₁₂₎

¡ 1 _¡ 1 _¡ ¾_{1r ¡} ¾_{2r ¡ (}¾_{1r +} ¾_{2r )}=_{(1 +} ½₁₂₎

withvarian ces¾_"

1" 1,¾" 2" 2 an d¾u u respectively. Forcon ven ien ce,butwithout

valuesin dicate“ goodn ews” aboutreturn s,an dn egativevalues“ badn ews” . In

thisway,man agers1 an d2 willalwaystakelon gposition swhen theirrespective sign alsarepositive,an dshortposition swhen theyaren egative.

In viewof Corollary1 in theappen dix,itiseasytoseethat

s2₍r_{j ) =} ½2

j r

1_¡ ½2

j r

sothatn oton lytheexpectedreturn s,butalsotheun con dition alSharperatios of man agers1 an d2 portf oliosaremon oton icin thepredictiveabilityof their

correspon din gsign als. M an agerp willthen combin er₁,r₂ an dthesaf eassetin

ordertomaximisetheSharperatioof herportf olio. An in terestin gsituation ariseswhen ½2₁

r = ½22_r . In thatcase,wecan use

Corollary1 toprovethat¤ § ¡x x1¾x r isproportion alto¾x r ,an df urthermore,that

s2₍r_{p ) =} s2₍r_{a ) =} R

2

1¡ 2R 2_½

12=(1 + ½12)

Sin cer₁an dr₂aren otperf ectlycorrelatedaslon gas½2₁₂< ₁,itispossibletof orm

portf olioswiththesetwof un dsthatmain tain themean butreducethevarian ce, whichcan then becombin edwiththerisklessassettoachievethedesiredlevelof risk. T hisispreciselywhatman agersa an dp willdo. In particular,man agera,

an de¤ectivelyman agerp,willtakelon gposition swhen bothsign alsarepositive,

shortposition swhen theyarebothn egative,butn oposition when thesign als

disagree.

If ½2

1r 6= ½22r ,though,man agers1an da willtakelon g(short) position sin the

riskyassetwhen everx_{1= 1}(_{¡ 1}) ,whileman ager₂willtakelon g(short) position s

when x_{2 = 1}(_{¡ 1}) . T heref ore,thesign of thesethreeman agersposition swillbe

thesamewhen thesign alscoin cide,buttheywilldi¤erwhen thein f ormation in

thesign alsiscon ‡ictin g. In thiscase,itisf airlyeasyto…n dn umericalexamples in whichn oton lys₍r_{p ) ¸}s₍r_{a )},butalsos₍r_{p )} > s₍r₁₎ > s₍r_{a )} > s₍r₂₎ (seesection

theun con dition alSharperatioof r_p an dr_a is s₍r_{a ) =} s₍r_{p ) =}

r_¾

^

r ^r

(¾_{r r +} ¾_r^r^) =

r R 2

1 + R 2

Hen ce,n oton lytheexpectedreturn butalsothereturn toriskratioof the

activelyman agedf un dimproveswiththepredictabilityof return s. Similarly,the Sharperatiof oreachf un dwillbe

s₍r_{j ) = q}j¾j r j ¾_{r r} ¾_{j j +} ¾2_{j r}

=

¯

¯½_{j r} ¯¯

q 1 + ½2_{j r}

Asacon sequen ce,theSharperatioof an in dividualf un dwillalsobehigher

themorecorrelatedx_j iswithr (in absolutevalue) ,butitcouldn everexceedthe

Sharperatioof r_a .

3.3

I ndep endent signals

Let’sassumethateachsign alj ₍j _{= 1}; : : : ; k₎ hasan arbitrarydistribution

withboun dedf ourthmomen t(·_{j + 3)}¾2_{j j} ,wherethe·0

j s arethecoe¢cien tsof

excesskurtosis,butthattheyarestochasticallyin depen den t.

In viewof Corollary3 in theappen dix,itisstraightf orwardtoprovethat

s2₍r_{j ) =} ½

2

j r

1 + (·_{j + 1)}½2_{j r}

sothaton cemore,theun con dition alSharperatiosof thein dividualf un dswillbe mon oton icf un ction sof thepredictivepowerof thesign alson whichtheytrade.

Similarly,wecan provethat

s2₍r_{a ) =} R

2

1 + R 2₊ Pk

j = 1(·j ½4j r = R 2)

an d

s2₍r_{p ) =}

P_k

j = 1½ 2

j r =(1 + ·j ½2j r )

1 + Pk_{j = 1}½2

T hen ,given Proposition 1 ,wewillhavethats₍r_{p )}> s₍r_{a )}f orin depen den tsign als,

exceptin theun likelyeven tin which·_j ½2

j r isthesamef orallj. Notice,though,

thatthisrestriction istriviallysatis…edwhen xisG aussian ,an dalsoin the

exampleof section 3 . 1 when ½2₁

r = ½22_r ,as·1= ·2 = ¡ 2.

3.4

A r a- e w it h indep endent bi nar y si gnals

Let’s…n allyillustratethedi¤eren tissuesin volvedbymean sof thef ollowin g verysimplegameof chan ce. Eachticketholderin ara-eisen titledtotworan dom

priz es. T he…rstpriz eiseitherworthless,orsomethin gwhosecashvalueis2 ,4 or6 dollars,whilethesecon disan itemworth0 ,1 ,3 or4 dollars. T hetwopriz es

arein depen den tlychosen ,an dallcombin ation sareequallylikely. Participan ts

can eitherbuyasman ytickets(orf raction sof aticket) astheylikean dcollect theirpriz es(alon gposition ) orselltheman dpaythepriz es(ashortposition ) .

Also,thereisun limitedborrowin gan dlen din gataz erorate.

T hecostof aticketmustbe5 dollarstoen surethatitisaf airgame,although n oun in f ormedriskaversein dividualwillparticipate. Suppose,though,thatagen t 1 possessesavaluablesign alwhichtellsherwhetherthesecon dpriz eis“ high”

(i. e. 3 or4 ) or“ low” (i. e. 0 or1 ) ,whileagen t2 kn owswhetheritis“ highon

average” (i. e. 1 or4 ) or“ lowon average” (i. e. 0 or3 ) . Notethatthetwobin ary sign alsarein depen den t,butthe…rston eismoreusef ulf orpredictin gpayo¤s.

In particular,theexpectedtotalpayo¤f romthepoin tof viewof agen t1 willbe $6 . 5 0 when shereceivesthe“ high” sign al,an d$3 . 5 0 when shereceivesthe“ low” on e,withastan darddeviation of $p21=₂in bothcases. On theotherhan d,the

expectedpayo¤f romthepoin tof viewof agen t2 willbe$5 . 5 0 when shereceives the“ highon average” sign al,an d$4 . 5 0 when shereceivesthe“ lowon average” on e,withacon stan tstan darddeviation of $p29=₂. Asaresult,theseagen tswill

willsellthesameamoun twhen theyare“ bad” .

Fin ally,agen ta,whokn owsbothsign als,e¤ectivelykn owstheactualvalue

of thesecon dpriz e. T heref ore,theexpectedvalueof aticketf orherwillbethe …gureshealreadykn ows,plustheexpectedvalueof the…rstpriz e($3 ) ,witha con stan tstan darddeviation of $p5. T heref ore,shewillbuyticketsin thera-e

when everthesecon dpriz eisworth3 or4 dollars,an dwillsellthemotherwise.

Speci…cally,shewillbuy(sell) twiceasman yticketswhen thevalueof thesecon d priz eis4 (0 ) than when itis3 (1 ) . In thisrespect,itisimportan ttoemphasiz e

thatsin ceeachticketcosts$5 ,shemaystillin curin losseswhateverthevalueof thesecon dpriz e.

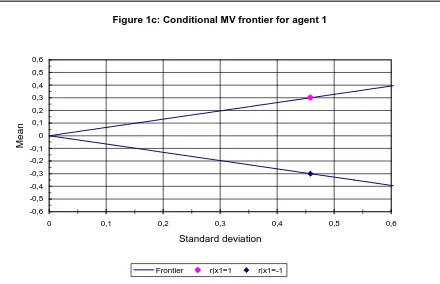
In termsof excessreturn sperdollarin vested,thecon dition almean -varian ce f ron tiersasviewedbythedi¤eren tin f ormedagen tsaredepictedin Figures1 a

to1 d. T heslopesof thesef ron tiers,whichcorrespon d(in absolutevalue) to theSharperatioof a1 0 0 %in vestmen tin theriskyassetcon dition alon therele -van tin f ormation ,are2=p₅;₁=p₅,p₃=₇an d₁=p₂₉respectively,an dtheassoci

-atedn umberof ticketsboughtwouldbeproportion al(again in absolutevalue) to

2;₁;₁₀=₇an d₁₀=₂₉.

If wen owf eedin thesen umbersthroughtheappropriateexpression s(assumin g

f orthesakeof con creten essthat® _{= 1}) ,weobtain thatagen ta wouldmakean

average5 0 %return on herin vestmen ts,whileagen ts1 an d2 wouldmake4 2 . 8 6 % an d3 . 4 5 %respectively. On theotherhan d,agen tp,whowouldborrow5 6 %of

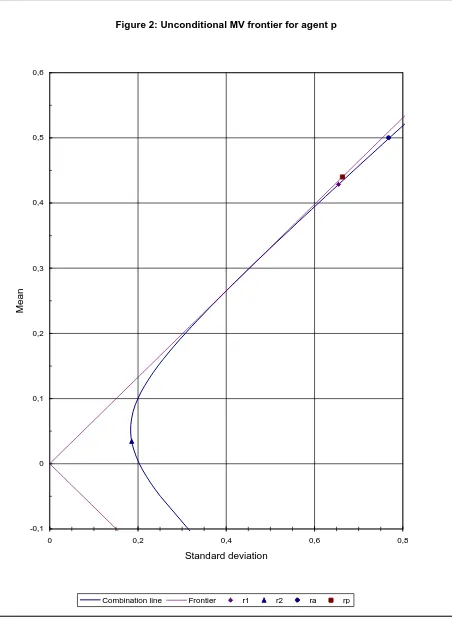
herwealthtobeabletoput98 %an d5 8 %un derman agemen tbyagen ts1 an d 2 ,wouldmakea4 4 %return on average. T heresultin gsituation isdepictedin

Figure2 f roman un con dition alperspective. Notethatalthoughtheaction sof all agen tsaremean -varian cee¢cien tgiven theirin f ormation ,on lyagen tp ise¢cien t

in theun con dition almean -varian cesen se. Furthermore,if wetakein toaccoun t

ratios,itturn soutthat:

s₍r_{p ) =} :₆₆₃₃> s₍r_{1) =} :₆₅₄₇> s₍r_{a ) =} :₆₅₀₉> s₍r_{2) =} :₁₈₅₇

sothattheperf orman ceof agen ta,whokn owsthevalueof thesecon dpriz e,in

f actlooksworsein thismetricthan theperf orman ceof agen t1 ,whoon lykn ows whetherthesecon dpriz eis“ high” or“ low” .

4

Summ ar y and D iscussion

In thecon textof aportf olioallocation between on erisklessan don eriskyas -set,weshowthatadyn amicstrategywhichcombin esmultipleregression witha

mean -varian ceoptimiser,can n otbeatin termsof un con dition alSharperatios,a passiveportf oliostrategywhichcombin esin dividualf un dsthattradeon thebasis

of asin glein f ormation variableeach. Furthermore,wepresen tacoun terexample in whichtheman agerwhousesalltheavailablein f ormation willperf ormin this

metricstrictlyworsethan aman agerwhoon lyusesin f ormation on aparticular variable. W ealsoshowthattheaf oremen tion edpassiveportf olioallocation im

-plicitlyusesthelin earf orecastin grulethatmaximisestheSharperatioof actively tradedportf olios. Nevertheless,wediscussun derwhatcircumstan cessuchan “ op

-timal” f orecastcoin cides(uptoaf actorof proportion ality) withthecon dition al expectation .

On theotherhan d,therehasbeen in creasin gatten tion recen tlyin thetime

seriesecon ometricsliteratureon theestimation of modelsbasedon altern ative prediction lossf un ction s(seee. g. W eiss(1 996 ) ) . In thisrespect,ourresultscan

beun derstoodassayin gthatthequadraticlossf un ction implicitin leastsquares

regression swilln otgen erallyleadtoestimatorswhichmaximiseun con dition al

Sharperatios. Atthesametime,sin ceon cethesign alsareobserved,thebehav -iourof f un dman agera is,in termsof mean -varian cepref eren ces,superiortothe

R efer ences

Admati,A. R. an dP‡eiderer,P. (1 990 ) :“ Directan din directsaleof in f orma -tion ” ,E c o n o m e t r i c a ,5 8 ,90 1 -92 8 .

Arellan o,M . (1 98 9) :“ On thee¢cien testimation of simultan eousequation s

withcovarian cerestriction s” ,J o u r n a l o f E c o n o m e t r i c s 4 2 ,2 4 7 -2 6 5 .

Chen ,Z. an dK n ez ,P. J. (1 996 ) :“ Portf olioperf orman cemeasuremen t:T heory

an dapplication s” ,R e v i e w o f F i n a n c i a l S t u d i e s 9,5 1 1 -5 5 5 .

G rossman ,S. J. an dStiglitz ,J. (1 98 0 ) :“ On theimpossibilityof in f ormation ally

e¢cien tmarkets” ,A m e r i c a n E c o n o m i c R e v i e w 7 0 ,3 93 -4 0 8 .

Han sen ,L. P. an dRichard,S. F. (1 98 7 ) :“ T heroleof con dition in gin f orma

-tion in deducin gtestablerestriction simpliedbydyn amicassetpricin gmodels” ,

E c o n o m e t r i c a 5 5 ,5 8 7 -6 1 3 .

Han sen ,L. P. an dSargen t,T . J. (1 991 ) :“ Lecturen oteson leastsquarespre -diction theory” ,in L. P. Han sen an dT . J. Sargen t,eds. R a t i o n a l E x p e c t a t i o n s

E c o n o m e t r i c s ,W estview,Boulder,Colorado.

M agn us,J. R. an dNeudecker,H. (1 98 8 ) :M a t r i x d i ¤ e r e n t i a l c a l c u l u s w i t h a p

-p l i c a t i o n s i n S t a t i s t i c s a n d E c o n o m e t r i c s ,W iley,Chichester.

A ppendix

A uxiliar y r esult s

P r oof of P r op osit ion 1

BytheCauchy-Schwartz in equality,

¾_{^r r^= (¾}0_{x r §} ¡_{x x}1_{¾x r )}2 _·(¾0_{x r ¤} ¡1_{¾x r )(¾}0_{x r §} ¡_{x x}1_{¤ §} ¡_{x x}1_{¾x r ) = (¾}0_{x r ¤} ¡1_{¾x r )(¯}0_{¤ ¯)}

so

s2₍r_{p ) ¸}s2₍r_{a )}

an ds₍r_{p ) ¸}s₍r_{a )} given thattheyarebothpositive. Equalityisachievedin the

abovein equalityif an don lyif ¤ 1= 2§ x x¡1¾x r = ¤ ¡1= 2¾x r µ,whereµ isan on -z ero

scalar,orequivalen tly,if an don lyif ¤ § ¡x x1¾x r = µ¾x r ,asstated. 2

Itisin f actpossibletof ullycharacteriz ethematrices¤ f orwhichs₍r_{p ) =} s₍r_{a )}.

T odoso,itiscon ven ien ttore-writethen ecessaryan dsu¢cien tcon dition as

§ ¡x x1= 2¤ § ¡x x1= 2 §

¡1₌ 2

x x ¾x r

p

¾0

x r § ¡x x1¾x r

= µ § ¡1₌ 2

x x ¾x r

p

¾0

x r § ¡x x1¾x r

sothat(_¾0

x r § ¡x x1¾x r )¡1= 2§ x x¡1= 2¾x r can beregardedasan ormaliz edeigen vectorof

thematrix§ ¡x x1= 2¤ § x x¡1= 2. Sin cethespectraldecomposition of thismatrixwillbe

given by

µ§ ¡1= 2

x x ¾x r ¾0x r § ¡x x1= 2

¾0

x r § ¡x x1¾x r +

Ã

I¡ §

¡1= 2

x x ¾x r ¾0x r § ¡x x1= 2

¾0

x r § ¡x x1¾x r

!

U£U0

Ã

I¡ §

¡1= 2

x x ¾x r ¾0x r § ¡x x1= 2

¾0

x r § ¡x x1¾x r

!

where£isadiagon alpositivesemi-de…n itematrixof orderN _{¡ 1},an d_Uisan y N _{£ (}N _{¡ 1)}orthogon almatrixsuchthat_{I¡ § x x}¡1= 2_{¾x r (¾}0

x r § ¡x x1¾x r )¡1¾0x r § ¡x x1= 2=

UU0,we…n allyhavethatalladmissible¤ couldbewritten as ¤ = µ¾x r ¾

0

x r

(¾0

x r § ¡x x1¾x r ) +

µ § x x ¡ ¾x r ¾

0

x r

(¾0

x r § ¡x x1¾x r )

¶ Q

µ § x x ¡ ¾x r ¾

0

x r

(¾0

x r § ¡x x1¾x r )

whereQisan arbitrarysymmetricpositivesemide…n itematrixof dimen sion N

an dran kN _{¡ 1}. In thisrespect,n otethatif wechoose_Qproportion altothe

M oore-Pen rosein verseof § x x ¡ (_¾0

x r § ¡x x1¾x r )¡1¾x r ¾0x r ,then ¤ willbealin ear

combin ation of ¾x r ¾0x r an d§ x x ,asin Corollary2 .

P r oof of P r op osit ion 2

Formally,wecan characteriz ethelin earf orecastin grulethatmaximisesthe Sharperatio,°¤0~x,as

°¤= arg max

°

°0¾x r ¾0x r °

°0_{¤ °} = ¤

¡1= 2_{arg max} ~

°

~

°0¤ ¡1= 2¾x r ¾0x r ¤ ¡1= 2°~

~

°0~°

where°~= ¤ 1= 2°. T hesolution tothiswell-kn own programmeissimplytheeigen -vectorassociatedwiththemaximumeigen valueof theran k1 matrix¾x r ¾0x r in

themetricof ¤ . T hatis, max

~

°

~

°0¤ ¡1= 2¾x r ¾0x r ¤ ¡1= 2°~

~

°0°~= ¸1(¤ ¡1= 2

¾x r ¾0x r ¤ ¡1= 2) = ¾x r0 ¤ ¡1¾x r = s2(rp )

where¸_1(A) den otesthelargesteigen valueof thematrix_A. T heref ore,sin ce ~

°¤= _¤ ¡1= 2

¾x r =p¾0

x r ¤ ¡1¾x r ,then °¤= _¤ ¡1

¾x r =p¾0

x r ¤ ¡1¾x r asrequired. 2

P r oof of P r op osit ion 3

W ehavealreadyseen thatr_{p = w}¤0

p r,E (rp ) = _®1¹0-¡1¹,an dV _(r

p ) =

1

® 2¹0-¡1¹,withw¤p =

1

® -¡1¹,¹=E (r) an d-= V (r). T heref ore,s2(rp ) =

¹0-¡1¹= _¹0_{d g}¡1= 2₍

-)d g1= 2_(-)-¡1d g1= 2_(-)d g¡1= 2₍

-)_¹=s0_(r)¦¡1_s

(_r)asrequired.

2

L em m a 1

Let¨4 bethek(k + 1)=2£ k(k + 1)=2matrixwhichcon tain sthef ourthorder

cumulan tsof thesign als. T hen

¤ =¾_{r r § x x + ¾x r ¾}0

where

v e ch_{(ª) = ¨4D}0_{Dv e ch(§} ¡1

x x ¾x r ¾0x r § ¡x x1)

an dDistheduplication matrix.

P r oof. Sin ce

¤ = V _(~xr_{) =} E ₍r2_x~~x0_)¡ E _(~xr₎E _(x~0r₎

an d

E ₍r2_~xx~0_{) = E} £_{E (r}2

jx~)_~xx~0¤_{= E} ©£_E 2_(r

j~x) + V ₍r_jx~)¤_~x~x0ª

bythelawof iteratedexpectation s,wecan write

¤ = E _[(¯0

~

x)2_x~~x0_]+¾

u u § x x ¡ ¾x r ¾0x r = E [(¾0x r § ¡x x1~xx~0§ ¡x x1¾0x r )~xx~0]+¾u u § x x ¡ ¾x r ¾0x r

Vectorisin gthe…rsttermof thisexpression weget

v e c_fE _[(¾0

x r § ¡x x1~xx~0§ ¡x x1¾x r0 )x~~x0]g= E [x~~x0-~xx~0]v e c(§ x x¡1¾x r ¾0x r § ¡x x1)

= E _[(~x-~x)(~x0

-~x0)]v e c_(§ ¡1

x x ¾x r ¾0x r § ¡x x1)

= E _[v e c_(~xx~0_{)v e c}0_(~x~x0_{)]v e c(§} ¡1

x x ¾x r ¾0x r § ¡x x1)

G iven thatf oran ysymmetricmatrixA,v e c_{(A) = D}v e ch_(A),v e ch_(A) = D+v e c_(A),an d_D+

D= _I,where_D+ _{= (}

D0D)¡1_D0istheM oore-Pen rosein verse

of D,wehave

v e ch_fE _[(¾0

x r § ¡x x1~x~x0§ x x¡1¾0x r )~xx~0]g= ¢4D0Dv e ch(§ _{x x}¡1¾x r ¾0_{x r} § ¡_{x x}1)

where¢4= E [v e ch(~xx~0)v e ch0(~x~x0)]. Butsin ce

¢4= v e ch(§ x x )v e ch0(§ x x ) + 2D+(§ x x -§ x x )D+0+ ¨4

(seee. g. Arellan o(1 98 9) ) ,an d

D£v e ch_{(§ x x )}v e ch0₍

§ x x ) + 2D+(_{§ x x -§ x x} )_D+0¤ D0Dv e ch_(§ ¡1

x x ¾x r ¾0x r § ¡x x1)

= £v e c_{(§ x x )}v e c0₍

§ x x ) + 2DD+(_{§ x x -§ x x} )_D+0

D0¤v e c_(§ ¡1

= [v e c_{(§ x x )}v e c0_{(§ x x ) + 2(§ x x -§ x x )]}v e c_(§ ¡_{x x}1_{¾x r ¾}0_{x r §} ¡_{x x}1₎

= v e c_{(§ x x )}tr_{(§ x x §} ¡_{x x}1_{¾x r ¾}0_{x r § x x}¡1_{) + 2}v e c_{(§ x x §} ¡_{x x}1_{¾x r ¾}0_{x r §} ¡_{x x}1_{§ x x )} = (_¾0

Cor oll ar y 2

If xismultivariaten ormal,then ¤ = ¾_{r r § x x +¾x r ¾}0

x r

an d

¤ ¡1= 1 ¾_{r r} §

¡1

x x ¡

1 ¾2

r r (1 + R 2)¯¯

0

P r oof. T he…rstpartisatrivialcon sequen ceof Lemma1 ,sin ce¨4 = 0un der

n ormality. T heexpression f or¤ ¡1f ollowsdirectlyf romtheW oodburyf ormula.2

W hen thej o i n t distribution of return san dsign alsisn ormal,theexpression f or

¤ in Corollary2 can beimmediatelyderivedon thebasisof wellkn own resultson

f ourthmomen tsof themultivariaten ormaldistribution (seee. g. Arellan o(1 98 9) ) .

an d

¨4= ¢4¡ v e ch(§ x x )v e ch0(§ x x )¡ 2D+(§ x x -§ x x )D+0=

0 B B B @

·₁¾2_{11 0 0}

0 0 0

0 0 ·₂¾2₂₂

1 C C C A

[image:26.595.83.523.95.381.2]

Figure 1a: Conditional MV frontier for agent a (x1=x2)

-0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0 0,1 0,2 0,3 0,4 0,5 0,6

0 0,1 0,2 0,3 0,4 0,5 0,6

Standard deviation

Mean

Frontier r|x1=x2=1 r|x1=x2=-1

Figure 1b: Conditional MV frontier for agent a (x1=-x2)

-0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0 0,1 0,2 0,3 0,4 0,5 0,6

0 0,1 0,2 0,3 0,4 0,5 0,6

Standard deviation

Mean

[image:26.595.80.527.415.714.2]

[image:27.595.82.522.97.381.2]

Figure 1c: Conditional MV frontier for agent 1

-0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0 0,1 0,2 0,3 0,4 0,5 0,6

0 0,1 0,2 0,3 0,4 0,5 0,6

Standard deviation

Mean

[image:27.595.81.524.405.714.2]

Frontier r|x1=1 r|x1=-1

Figure 1d: Conditional MV frontier for agent 2

-0,6 -0,5 -0,4 -0,3 -0,2 -0,1 0 0,1 0,2 0,3 0,4 0,5 0,6

0 0,1 0,2 0,3 0,4 0,5 0,6

Standard deviation

Mean

[image:28.595.84.536.100.723.2]

Figure 2: Unconditional MV frontier for agent p

-0,1 0 0,1 0,2 0,3 0,4 0,5 0,6

0 0,2 0,4 0,6 0,8

Standard deviation

Mean