PREDIKSI KECEPATAN PHASE
GELOMBANG SOLITER TERGANGGU
AHMAD HAKIM
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis dengan judul Prediksi Kecepatan Phase Gelombang soliter terganggu adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Juli 2009
Ahmad Hakim
Under supervision of JAHARUDDIN and ALI KUSNANTO.
The Ocean can be considered to be inviscid and incompressible fluid (ideal fluid) which consist of some layers, where each layer has different constant density. Internal waves are waves occurred under sea surface. One of internal waves is internal solitary wave.
One of formulations that can describe solitary wave movement is Korteweg-de Vries (KdV) equation. This research studies a solution of the slowly varying solitary wave using asymtotic solution of the perturbed KdV equation. Some variations of the solitary wave amplitude and the accompanying trailing tail are recovered. Here, the analysis is carried out through second order asymtotic expansion to determine a general expression for the first order phase speed.
Two cases of example for the prediction of the first order phase speed are given. By using Mathematica 6 Software, the variation of the undisturbed solitary wave amplitude is shown to be influenced by some disturbance factors and . The first case shows that as amplitude increases, the tail decreases. Furthermore the first order phase speed increases as time increases for both positive and negative . On the other hand, the second case shows that as amplitude decreases, the tail decreases. Finally the first order phase speed increases as time increases for positive .
RINGKASAN
AHMAD HAKIM. Prediksi Kecepatan Phase Gelombang Soliter Terganggu. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.
Gelombang tak linier yang dikaji dalam penelitian ini adalah gelombang soliter. Gelombang soliter adalah gelombang yang memiliki satu puncak, dimana dalam perambatannya mempertahankan bentuk dan kecepatannya. Selain itu, gelombang soliter juga memiliki sifat seperti partikel, yakni stabil melawan tumbukan.
Persamaan gerak yang dapat menggambarkan gerak gelombang soliter adalah persamaan Korteweg-de Vries (KdV). Dalam bentuk standar, gelombang soliter persamaan KdV tidak mengalami gangguan. Dalam penelitian ini dikaji penyelesaian gelombang soliter persamaan KdV yang melibatkan faktor gangguan (perturbasi).
Penyelesaian persamaan KdV yang melibatkan parameter perturbasi. diselesaikan dengan menggunakan metode asimtotik, dengan uraian asimtotik dilakukan hingga orde kedua. Metode ini banyak digunakan untuk menyelesaikan berbagai masalah tak linier.
Dalam metode asimtotik, persamaan KdV diselesaikan dengan memisalkan peubah-peubah tak bebasnya dalam bentuk uraian asimtotik. Dari uraian asimtotik, dengan memperhatikan orde persamaan, maka pada orde rendah diperoleh persamaan KdV standar. Penyelesaian persamaan ini dilakukan dengan menggunakan asumsi bahwa penyelesaiannya berupa gelombang soliter. Diperoleh tiga parameter gelombang soliter tak terganggu, yaitu , dan , dengan menyatakan amplitudo gelombang, menyatakan kecepatan phase gelombang dan memberikan panjang gelombang soliter tak terganggu. Ketiga parameter ini saling berkaitan dan bergantung pada waktu, sehingga jika salah satu parameter diketahui, maka dua parameter lainnya dapat ditentukan.
Untuk orde selanjutnya pada uraian asimtotik, pada kondisi terselesaikan diperoleh suatu persamaan yang secara ekplisit menggambarkan perilaku koreksi kecepatan phase bagi gelombang soliter terganggu. Persamaan bagi konsisten dengan hukum konservasi.
Selanjutnya, diberikan dua studi kasus untuk memprediksi kecepatan phase . Pada dua studi kasus tersebut dikaji perubahan amplitudo ekor-ekor gelombang soliter terganggu dan kecepatan phase gelombang soliter terganggu. Dengan software Mathematica6, pada kasus pertama didapatkan hasil bahwa perubahan amplitudo gelombang soliter tak terganggu dipengaruhi oleh faktor gangguan (delta) yang diberikan. Untuk delta positif, perubahan amplitudo gelombang soliter tak terganggu meningkat dan sebaliknya menurun untuk delta negatif. Sementara itu, perubahan amplitudo gelombang soliter tak terganggu tidak berpengaruh secara signifikan terhadap perubahan amplitudo ekor gelombang soliter terganggu dan kecepatan phase gelombang soliter terganggu. Amplitudo ekor gelombang soliter terganggu menurun sedangkan kecepatan phase meningkat untuk delta positif dan negatif.
gelombang itu merambat, dimana dalam perambatannya gelombang soliter terganggu disertai ekor (tail) gelombang dengan kecepatan phase yang meningkat dan amplitudo ekor gelombang yang menurun. Selanjutnya gelombang soliter tak terganggu merambat dengan kecepatan phase meningkat, tetapi relatif tidak mengalami perubahan simpangan gelombang untuk waktu yang cukup lama.
Kata kunci : Gelombang soliter, persamaan KdV, faktor gangguan, metode asimtotik
.
@ Hak Cipta Milik IPB, tahun 2009 Hak Cipta dilindungi Undang-undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber
a. Pengutipan hanya boleh untuk kepentingan pendidikan penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah,
b. Pengutipan tidak merugikan kepentingan yang wajar IPB
AHMAD HAKIM
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Program Studi Matematika Terapan
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
NIM : G551070641
Disetujui Komisi Pembimbing
Dr. Jaharuddin, M.S. Drs. Ali Kusnanto, M.Si.
Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana
Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2008 ini adalah gelombang soliter, dengan judul Prediksi Kecepatan Phase Gelombang Soliter Terganggu.
Terima kasih penulis ucapkan kepada Bapak Dr. Jaharuddin, MS dan Drs. Ali Kusnanto, M.Si. selaku Pembimbing, serta Dr. Ir. Endar H. Nugrahani, M.S selaku penguji luar komisi dan selaku Ketua Program Studi Matematika Terapan yang telah membimbing dan banyak memberikan saran. Ucapan terima kasih juga disampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB. Ucapan terima kasih yang tiada hingga kepada kedua Orangtua, Istri dan dua anak tercinta serta seluruh keluarga, atas segala do’a dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Juli 2009
PREDIKSI KECEPATAN PHASE
GELOMBANG SOLITER TERGANGGU
AHMAD HAKIM
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis dengan judul Prediksi Kecepatan Phase Gelombang soliter terganggu adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Juli 2009
Ahmad Hakim
Under supervision of JAHARUDDIN and ALI KUSNANTO.
The Ocean can be considered to be inviscid and incompressible fluid (ideal fluid) which consist of some layers, where each layer has different constant density. Internal waves are waves occurred under sea surface. One of internal waves is internal solitary wave.
One of formulations that can describe solitary wave movement is Korteweg-de Vries (KdV) equation. This research studies a solution of the slowly varying solitary wave using asymtotic solution of the perturbed KdV equation. Some variations of the solitary wave amplitude and the accompanying trailing tail are recovered. Here, the analysis is carried out through second order asymtotic expansion to determine a general expression for the first order phase speed.
Two cases of example for the prediction of the first order phase speed are given. By using Mathematica 6 Software, the variation of the undisturbed solitary wave amplitude is shown to be influenced by some disturbance factors and . The first case shows that as amplitude increases, the tail decreases. Furthermore the first order phase speed increases as time increases for both positive and negative . On the other hand, the second case shows that as amplitude decreases, the tail decreases. Finally the first order phase speed increases as time increases for positive .
RINGKASAN
AHMAD HAKIM. Prediksi Kecepatan Phase Gelombang Soliter Terganggu. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.
Gelombang tak linier yang dikaji dalam penelitian ini adalah gelombang soliter. Gelombang soliter adalah gelombang yang memiliki satu puncak, dimana dalam perambatannya mempertahankan bentuk dan kecepatannya. Selain itu, gelombang soliter juga memiliki sifat seperti partikel, yakni stabil melawan tumbukan.
Persamaan gerak yang dapat menggambarkan gerak gelombang soliter adalah persamaan Korteweg-de Vries (KdV). Dalam bentuk standar, gelombang soliter persamaan KdV tidak mengalami gangguan. Dalam penelitian ini dikaji penyelesaian gelombang soliter persamaan KdV yang melibatkan faktor gangguan (perturbasi).
Penyelesaian persamaan KdV yang melibatkan parameter perturbasi. diselesaikan dengan menggunakan metode asimtotik, dengan uraian asimtotik dilakukan hingga orde kedua. Metode ini banyak digunakan untuk menyelesaikan berbagai masalah tak linier.
Dalam metode asimtotik, persamaan KdV diselesaikan dengan memisalkan peubah-peubah tak bebasnya dalam bentuk uraian asimtotik. Dari uraian asimtotik, dengan memperhatikan orde persamaan, maka pada orde rendah diperoleh persamaan KdV standar. Penyelesaian persamaan ini dilakukan dengan menggunakan asumsi bahwa penyelesaiannya berupa gelombang soliter. Diperoleh tiga parameter gelombang soliter tak terganggu, yaitu , dan , dengan menyatakan amplitudo gelombang, menyatakan kecepatan phase gelombang dan memberikan panjang gelombang soliter tak terganggu. Ketiga parameter ini saling berkaitan dan bergantung pada waktu, sehingga jika salah satu parameter diketahui, maka dua parameter lainnya dapat ditentukan.
Untuk orde selanjutnya pada uraian asimtotik, pada kondisi terselesaikan diperoleh suatu persamaan yang secara ekplisit menggambarkan perilaku koreksi kecepatan phase bagi gelombang soliter terganggu. Persamaan bagi konsisten dengan hukum konservasi.
Selanjutnya, diberikan dua studi kasus untuk memprediksi kecepatan phase . Pada dua studi kasus tersebut dikaji perubahan amplitudo ekor-ekor gelombang soliter terganggu dan kecepatan phase gelombang soliter terganggu. Dengan software Mathematica6, pada kasus pertama didapatkan hasil bahwa perubahan amplitudo gelombang soliter tak terganggu dipengaruhi oleh faktor gangguan (delta) yang diberikan. Untuk delta positif, perubahan amplitudo gelombang soliter tak terganggu meningkat dan sebaliknya menurun untuk delta negatif. Sementara itu, perubahan amplitudo gelombang soliter tak terganggu tidak berpengaruh secara signifikan terhadap perubahan amplitudo ekor gelombang soliter terganggu dan kecepatan phase gelombang soliter terganggu. Amplitudo ekor gelombang soliter terganggu menurun sedangkan kecepatan phase meningkat untuk delta positif dan negatif.
gelombang itu merambat, dimana dalam perambatannya gelombang soliter terganggu disertai ekor (tail) gelombang dengan kecepatan phase yang meningkat dan amplitudo ekor gelombang yang menurun. Selanjutnya gelombang soliter tak terganggu merambat dengan kecepatan phase meningkat, tetapi relatif tidak mengalami perubahan simpangan gelombang untuk waktu yang cukup lama.
Kata kunci : Gelombang soliter, persamaan KdV, faktor gangguan, metode asimtotik
.
@ Hak Cipta Milik IPB, tahun 2009 Hak Cipta dilindungi Undang-undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber
a. Pengutipan hanya boleh untuk kepentingan pendidikan penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah,
b. Pengutipan tidak merugikan kepentingan yang wajar IPB
AHMAD HAKIM
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Program Studi Matematika Terapan
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
NIM : G551070641
Disetujui Komisi Pembimbing
Dr. Jaharuddin, M.S. Drs. Ali Kusnanto, M.Si.
Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana
Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2008 ini adalah gelombang soliter, dengan judul Prediksi Kecepatan Phase Gelombang Soliter Terganggu.
Terima kasih penulis ucapkan kepada Bapak Dr. Jaharuddin, MS dan Drs. Ali Kusnanto, M.Si. selaku Pembimbing, serta Dr. Ir. Endar H. Nugrahani, M.S selaku penguji luar komisi dan selaku Ketua Program Studi Matematika Terapan yang telah membimbing dan banyak memberikan saran. Ucapan terima kasih juga disampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa kepada penulis selama menempuh pendidikan di IPB. Ucapan terima kasih yang tiada hingga kepada kedua Orangtua, Istri dan dua anak tercinta serta seluruh keluarga, atas segala do’a dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Juli 2009
Halaman
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... x
I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan Penelitian ... 2
II LANDASAN TEORI ... 3
2.1 Konsep Metode Asimtotik ... 3
2.2 Persamaan Dasar Fluida Ideal ... 5
2.3 Penurunan Persamaan KdV... 6
2.4 Konsep Hukum Konservasi ... 10
III METODE PENELITIAN……… 12
IV HASIL DAN PEMBAHASAN ... 14
4.1 Analisis Asimtotik ………... 14
4.2 Gelombang Soliter Tak Terganggu ... 15
4.3 Gelombang Soliter Terganggu... 16
4.4 Studi Kasus……… 20
4.4.1 Kasus Pertama………..……. 20
4.4.2 Kasus Kedua………. 25
V KESIMPULAN DAN SARAN ... 30
DAFTAR PUSTAKA ... 31
DAFTAR GAMBAR
Halaman
1 Grafik penyelesaian MNA dengan metode asimtotik (garis penuh) dan penyelesaian eksak (garis putus-putus) ... 4 2 Grafik perubahan amplitudo gelombang soliter tak terganggu
dengan K , dan . ... 22 3 Grafik M dan kecepatan phase gelombang soliter terganggu
dengan K , dan . ... 22 4 Grafik perubahan amplitudo gelombang soliter tak terganggu
dengan K , dan . ……… 22
5 Grafik M dan kecepatan phase gelombang soliter terganggu dengan K , dan . ... 23 6 Simpangan gelombang soliter tak terganggu dengan K ,
dan . ... 24 7 Simpangan gelombang soliter terganggu dengan K ,
dan . ... 25 8 Grafik perubahan amplitudo gelombang soliter tak terganggu
dengan K , v dan . ……….………... 27
9 Grafik M dan kecepatan phase gelombang soliter terganggu dengan K , v dan . ... 27 10 Simpangan gelombang soliter tak terganggu dengan K dan
v …………... 28 11 Simpangan gelombang soliter terganggu dengan K dan
DAFTAR LAMPIRAN
Halaman
1
I PENDAHULUAN
1.1 Latar belakang
Gelombang internal merupakan gelombang yang terjadi di bawah permukaan laut. Gelombang internal terjadi karena adanya perbedaan rapat massa pada setiap lapisan air laut. Perbedaan rapat massa ini disebabkan antara lain oleh adanya perbedaan kadar garam ataupun perbedaan temperatur. Akibat perbedaan rapat massa menjadikan air laut berlapis-lapis, dimana air dengan rapat massa yang lebih besar akan berada di bawah dan air dengan rapat massa yang lebih kecil berada di atas. Berdasarkan perbedaan rapat massa di setiap lapisan, kemudian muncul aliran partikel dari suatu tempat ke tempat yang lain di setiap lapisan air laut. Garis arus dari gerak partikel inilah yang merupakan gelombang internal.
Salah satu jenis gelombang internal yang menarik untuk diamati adalah gelombang yang hanya memiliki satu puncak yang disebut gelombang soliter. Gelombang soliter internal adalah suatu gelombang berjalan yang dalam perambatannya mempertahankan bentuk dan kecepatannya.
Gelombang soliter internal dapat menjadi masalah bagi lingkungan, seperti robohnya tiang pancang penyangga bangunan yang dibangun di lepas pantai, atau naiknya polutan dari dasar laut ke permukaan yang dapat mempengaruhi kehidupan habitat laut. Masalah tersebut dapat diantisipasi apabila diketahui sifat dan kekuatan gelombang tersebut. Pengetahuan mengenai sifat gelombang internal tersebut akan bermanfaat antara lain sebagai bahan pertimbangan dalam merencanakan bangunan lepas pantai atau menentukan lokasi pembuangan limbah bagi perusahaan tambang yang biasanya dibuang di dasar laut. Manfaat lainnya adalah pada navigasi bawah laut, dimana gelombang internal berpengaruh terhadap keselamatan pelayaran kapal selam.
Salah satu sifat yang menarik dari persamaan KdV adalah berlakunya hukum konservasi massa dan energi, serta memiliki penyelesaian dalam bentuk gelombang soliter.
Salah satu penelitian mengenai perilaku penyelesaian persamaan KdV yang melibatkan parameter perturbasi dengan menggunakan pendekatan metode perturbasi multiskala (multiscale perturbation expansion) dilakukan oleh Johnson [1]. Kemudian dikembangkan oleh Ko dan Koehl [2] dan Grimshaw [5]. Kapman dan Maslov [3], Kaup dan Newell [4], melakukan hal yang sama yakni untuk mengetahui perilaku penyelesaian persamaan KdV, tetapi dengan metode yang berbeda, yaitu dengan menggunakan teknik transformasi hamburan terbalik (the techniques of the inverse scattering transform).
Berdasarkan kedua pendekatan yang dilakukan di atas diperoleh hasil yang
sama untuk perubahan amplitudo gelombang soliter terhadap besaran yang sama. Keduanya konsisten dengan hukum konservasi massa dan energi. Tetapi prediksi
terhadap kecepatan phase gelombang soliternya belum disajikan. Penelitian ini akan mencakup prediksi terhadap kecepatan phase gelombang soliter, khususnya gelombang soliter terganggu (pada persamaan KdV yang melibatkan parameter perturbasi).
1.2 Tujuan Penelitian
Berdasarkan uraian di atas, maka tujuan dari penelitian ini adalah :
1.2.1 Menurunkan suatu persamaan bagi kecepatan phase gelombang soliter terganggu dengan menggunakan metode asimtotik.
3
II LANDASAN TEORI
Pada bagian ini akan dibahas konsep-konsep yang mendasari penelitian, yakni konsep metode asimtotik yang disajikan dari [6] dan [7], persamaan dasar fluida dan penurunan persamaan KdV yang dirangkum dari [8] dan [9], serta konsep hukum konservasi dari pustaka [10] dan [11].
2.1 Konsep Metode Asimtotik
Metode asimtotik adalah suatu teknik yang digunakan untuk menentukan suatu fungsi yang merupakan penyelesaian dari suatu masalah nilai awal/batas, dimana fungsi tersebut dinyatakan dalam deret pangkat terhadap suatu parameter kecil. Deret pangkat tersebut dapat berupa deret yang konvergen atau divergen. Berikut ini adalah konsep dasar metode asimtotik.
Misalkan f(t ,x, : R x R nx R kontinu terhadap dan x , dan merupakan parameter kecil. Fungsi f mempunyai uraian terhadap . Untuk kasus yang khusus f mempunyai uraian Taylor terhadap , yaitu : masalah di atas dengan menggunakan metode asimtotik.
Misalkan penyelesaian persamaan tersebut dalam bentuk uraian asimtotik
.
Jika pemisalan penyelesaian di atas disubstitusikan ke dalam persamaan (2.2), maka koefisien untuk memberikan persamaan
dan seterusnya, untuk , , , … memberikan
Penyelesaian eksak dari persamaan differensial (2.2) dengan syarat awal , , , adalah
√ t)
√ √ t).
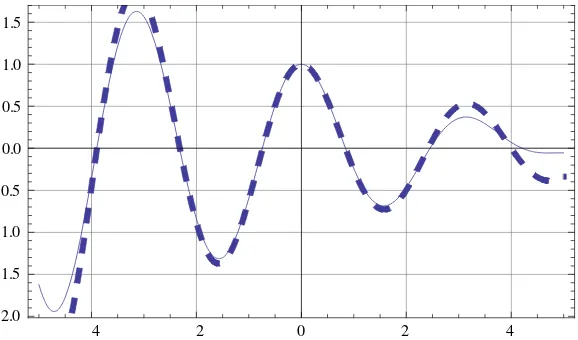
Perbandingan penyelesaian MNA pada persamaan (2.2), baik penyelesaian dengan pendekatan metode asimtotik maupun penyelesaian eksaknya untuk = 0.1, diberikan pada Gambar 1 berikut.
Gambar 1 Grafik penyelesaian MNA dengan metode asimtotik (garis penuh) dan penyelesaian eksak (garis putus-putus).
5
2.2 Persamaan Dasar Fluida Ideal
Dalam menurunkan persamaan dasar fluida, yaitu fluida yang tak mampat (incompressiable) dan tak kental (inviscid) diperlukan hukum kekekalan massa dan hukum kekekalan momentum. Hukum kekekalan massa pada suatu sistem dinyatakan secara sederhana sebagai laju perubahan massa dalam elemen luas, yaitu selisih antara massa yang masuk dengan massa yang keluar pada elemen luas tersebut. Hukum kekekalan momentum dinyatakan sebagai laju perubahan momentum yaitu momentum yang keluar ditambah gaya-gaya yang bekerja pada elemen luas tersebut.
Misalkan gerak partikel fluida dinyatakan dalam dua dimensi dengan kecepatan partikel dalam arah horizontal dan vertikal berturut-turut adalah dan . Fluida memiliki rapat massa , , dengan , dan berturut-turut dan hukum kekekalan momentum memberikan persamaan Euler berikut :
(2.5)
(2.6)
dengan dan berturut-turut menyatakan tekanan dan percepatan gravitasi.
Berdasarkan asumsi fluida tak berotasi (irrotational), diperoleh adanya suatu fungsi skalar Ф yang disebut kecepatan potensial, sehingga Ф Ф ,Ф . Jadi persamaan (2.4) dapat ditulis
Ф Ф .
sedangkan syarat batas dinamik terjadi karena adanya gaya-gaya yang bekerja pada fluida. Misalkan , adalah kurva yang membatasi air dan udara dan dinyatakan oleh persamaan permukaan , , , , sehingga diperoleh syarat batas kinematik pada permukaan fluida adalah
di z = , ,
sedangkan syarat batas kinematik di dasar fluida yang tidak rata adalah
di z = -h(x).
Syarat batas dinamik hanya berlaku pada permukaan saja, diturunkan berdasarkan persamaan Euler dengan asumsi fluida tak kental (invicid) dan tekanan di permukaan sama dengan tekanan udara, misalnya nol. Jadi syarat batas dinamik adalah Asimtotik. Metode ini merupakan cara penurunan persamaan KdV yang diperkenalkan oleh Newell dengan menskalakan peubah berikut :
;
7
Jika peubah-peubah tersebut di atas disubstitusikan ke persamaan (2.7), (2.8), (2.9) dan (2.10), maka diperoleh
di Ω(η); (2.11)
di z = -h(x); (2.12)
√ di z = (2.13)
di z = (2.14) Selanjutnya untuk penyederhanaan, tanda ( ) dapat diabaikan.
Misalkan penyelesaian persamaan (2.11) – (2.14) berbentuk
Φ(x, z, t) = (x,z,t)+ , , , , … (2.15) Jika persamaan (2.15) disubstitusikan kedalam persamaan (2.11), maka diperoleh
. (2.16)
Koefisien dari , dan memberikan persamaan berikut
(2.17) (2.18) . (2.19) Jika persamaan (2.15) disubstitusikan ke persamaan (2.12), maka diperoleh :
, di (2.20)
Koefisien dari , dan memberikan persamaan berikut
di (2.21) , di (2.22)
, di (2.23)
Karena , maka diperoleh
, ,
sehingga fungsi tidak bergantung pada peubah . Jadi dapat dimisalkan , , (2.24) Dari persamaan (2.18) dan persamaan (2.24) diperoleh
,
dan integralkan dari ke , diperoleh
,
Karena , maka setelah diintegralkan dari ke diperoleh
. (2.25)
Dengan cara yang sama, dimana h = O( ), diperoleh berbentuk
. (2.26)
Jika persamaan (2.24), (2.25) dan (2.26) disubstitusikan kembali ke persamaan (2.15), maka diperoleh
, , ,
. (2.27)
Dengan memisalkan pada persamaan (2.27), maka persamaan (2.13) dan (2.14) berturut –turut memberikan persamaan berikut
(2.28)
dan
9 Jika persamaan (2.31) disubstitusikan ke persamaan (2.28) dan (2.29), maka diperoleh
. (2.32)
Kemudian dimisalkan
∆ ; (2.33)
U , (2.34) maka persamaan (2.32) dapat dinyatakan oleh persamaan berikut
. (2.35)
Penurunan persamaan (2.35) diberikan pada lampiran 1.
Jika batas bawah berupa dasar yang bervariasi dengan sangat lambat ( kecil), maka dari persamaan (2.35) diperoleh
(2.36)
dengan suatu parameter kecil. Dalam tulisan ini akan dikaji persamaan KdV yang melibatkan parameter perturbasi yang dinyatakan oleh persamaan berikut
(2.37)
dengan suatu fungsi yang bergantung pada dan turunan-turunan .
(2.38)
yang merupakan persamaan KdV standar. Persamaan KdV standar memenuhi hukum konservasi massa dan energi yang dibahas dalam subbab berikut.
2.4 Konsep Hukum Konservasi
Misalkan E dan F fungsi yang bergantung pada , dan memenuhi [ . (2.39) Jika terdapat fungsi E dan F yang memenuhi persamaan (2.39), maka dikatakan berlaku hukum konservasi.
merupakan konstanta terhadap t, dan dikenal sebagai hukum konservasi massa.
Selanjutnya, jika persamaan (2.40) diturunkan terhadapx, diperoleh
= 0,
sehingga
11
Jika dipilih E =
F = ,
maka diperoleh bentuk
yang merupakan konstanta terhadap t, dan dikenal dengan hukum konservasi
III METODE PENELITIAN
Pada penelitian ini, dibahas tinjauan matematis mengenai gelombang internal. Salah satu persamaan yang dapat menggambarkan perilaku gerak gelombang internal adalah persamaan KdV. Persamaan KdV ini diturunkan dari persamaan dasar fluida ideal, yaitu fluida yang tak mampat (incompressible) dan tak kental (inviscid). Persamaan KdV adalah suatu persamaan bagi gelombang yang panjang gelombangnya jauh lebih besar dari pada amplitudonya.
Untuk menentukan penyelesaian persamaan KdV yang melibatkan parameter perturbasi secara eksak, dengan menggunakan metode standar, penyelesaian persamaan differensial parsial tersebut sulit dilakukan. Oleh karena itu dalam tulisan ini penyelesaiannya ditentukan dengan menggunakan metode asimtotik. Metode ini banyak digunakan dan tepat untuk menyelesaikan berbagai masalah tak linier.
Dalam metode asimtotik, persamaan KdV diselesaikan dengan memisalkan peubah-peubah tak bebasnya dalam bentuk uraian asimtotik, sebagaimana yang dilakukan oleh Grimshaw dan Mitsudera [12].
Dari uraian asimtotik, jika orde persamaan diperhatikan, maka pada orde pertama diperoleh persamaan KdV standar. Penyelesaian persamaan KdV standar dilakukan dengan menggunakan asumsi bahwa penyelesaiannya berupa gelombang berjalan yang berupa gelombang soliter, yaitu suatu gelombang yang dalam perambatannya mempertahankan bentuk dan kecepatannya. Asumsi ini diperlukan karena dalam observasi di laut dan di selat, gelombang soliter internal terdeteksi di permukaan lewat foto satelit melalui pola gelap terang. Dimana pola gelap terang tersebut berkaitan dengan panjang gelombang soliter internal.
13
Besaran-besaran yang diperoleh dari penyelesaian persamaan KdV standar yang berupa gelombang soliter tak tergangu, digunakan untuk memprediksi kecepatan phase gelombang soliter terganggu.
Aplikasi dari metode yang telah diuraikan ini, dilakukan dengan mengkaji dua contoh kasus. Berdasarkan kedua contoh kasus ini dibahas perubahan amplitudo dan kecepatan phase gelombang soliter terganggu. Selain itu, dibahas juga perubahan ekor-ekor dari gelombang soliter terganggu. Hasil numerik diperoleh dengan bantuan software Mathematica6.
IV PEMBAHASAN DAN HASIL
4.1 Analisis Asimtotik
Pada bagian ini akan dibahas penurunan persamaan kecepatan phase gelombang soliter dengan menggunakan metode asimtotik. Untuk itu, tinjau persamaan Korteweg-de Vries (KdV) yang melibatkan parameter perturbasi berikut
Ut + 6UUx + Uxxx = R(U) (4.1)
dengan suatu parameter kecil, dan R(U) merupakan fungsi yang tidak hanya bergantung pada U(x,t) tetapi juga pada turunan-turunan U. Selanjutnya, sebagaimana yang dilakukan oleh Grimshaw dan Mitsudera [12], peubah waktu dan koordinat horizontal masing-masing dimisalkan sebagai berikut :
T = . (4.2)
, .
dengan C suatu fungsi yang bergantung pada waktu, dan diinterpretasikan sebagai besaran kecepatan.
Dengan menggunakan metode asimtotik, diasumsikan bahwa peubah tak bebas dan peubah C memiliki uraian asimtotik sebagai berikut :
, …. (4.4) (4.5) Substitusikan persamaan (4.2), (4.3), (4.4) dan (4.5) ke persamaan (4.1), maka koefisien untuk memberikan persamaan
. (4.6) Untuk koefisien memberikan persamaan
, (4.7)
sedangkan untuk koefisien memberikan persamaan
= . (4.8) Persamaan (4.6) merupakan persamaan KdV standar untuk , sedangkan dan
15
persamaan (4.6), (4.7) dan (4.8) diberikan pada lampiran 2.
4.2 Gelombang Soliter Tak Terganggu
Berikut ini akan ditentukan penyelesaian dari persamaan KdV (4.6) yang diasumsikan berupa gelombang soliter, yaitu gelombang berjalan yang dalam perambatannya mempertahankan bentuk dan kecepatannya.
Jika persamaan (4.6) diintegralkan terhadap , maka diperoleh
(4.9) dengan K konstanta pengintegralan. Misalkan gelombang berjalan yang ditinjau berupa gelombang soliter, dimana simpangan gelombang dan semua turunannya menuju 0 di ∞, maka K = 0, sehingga persamaan (4.9) menjadi . (4.10) Jika persamaan (4.10) dikalikan dengan , kemudian diintegralkan terhadap , diperoleh
= . (4.11) Karena diasumsikan penyelesaian berupa gelombang soliter, maka , sehingga persamaan (4.11) menjadi
= , (4.12) atau
=
√
. (4.13)Kemudian kedua ruas pada persamaan (4.13) diintegralkan, diperoleh
√ tanh √ (4.14) Fungsi , yang diberikan pada persamaan (4.16) merupakan simpangan gelombang soliter dalam kondisi tak terganggu (tanpa perturbasi).
gelombang soliter untuk persamaan KdV (4.6), yaitu a, γ dan C0 yang semuanya
bergantung pada T. Jika salah satu parameter diketahui, maka dua parameter lainnya dapat ditentukan. Parameter C0 menyatakan kecepatan phase gelombang
soliter tak terganggu, parameter a menyatakan amplitudo gelombang, sedangkan parameter γ memberikan panjang gelombang soliter tak terganggu.
4.3 Gelombang Soliter Terganggu
Dari Grimshaw dan Mitsudera [12], adjoint dari bentuk homogen persamaan (4.18) adalah
, .
dengan ketika ∞. Dapat ditunjukan bahwa penyelesaian persamaan (4.20) adalah U0 pada persamaan (4.16), V = 1 dan dengan
.
dimana
, . .
Bukti diberikan pada lampiran 3. Selanjutnya, persamaan (4.18) memiliki penyelesaian, jika memenuhi kondisi terselesaikan berikut
. .
Jika pada persamaan (4.19) disubstitusikan ke persamaan (4.23), maka diperoleh
. .
Persamaan (4.24) yang diperoleh di atas merupakan rata-rata perubahan energi bagi gelombang soliter pada dasar yang bervariasi dengan sangat lambat (slowly
varying). Jika persamaan (4.16) disubstitusikan ke persamaan (4.24), maka
diperoleh
17
Jika pada persamaan (4.16) disubstitusikan ke persamaan (4.28), maka diperoleh
. .
Penurunan persamaan (4.29) diberikan pada lampiran 4.
Penyelesaian persamaan (4.26) dan (4.27) dapat diperoleh dari penyelesaian persamaan homogen dan tak homogennya. Penyelesaian persamaan homogen ( untuk pada persamaan (4.26) adalah dan w pada persamaan (4.21). Bukti untuk ini dapat dilihat pada lampiran 5. Adapun Wronskian dari dan w adalah
. .
Selanjutnya, penyelesaian tak homogen persamaan (4.26) dan (4.27) akan ditentukan dengan metode variasi parameter. Untuk itu, misalkan
dipisahkan kedalam penjumlahan dua fungsi, yaitu dan yang masing-masing merupakan fungsi genap dan fungsi ganjil dalam . Karena fungsi
genap, maka persamaan (4.28) terpenuhi bila = . Dengan demikian penyelesaian umum dari persamaan (4.26) dan (4.27) dimisalkan dalam bentuk
.
dengan dan untuk ∞.
.
Penurunan persamaan (4.32) - (4.35) diberikan pada lampiran 6. Bentuk pada persamaaan (4.16) memenuhi
. . sehingga penyelesaian tak homogen persamaan (4.32) adalah
. kajian ini tidak ditentukan. Hal ini dapat dikembangkan pada kajian lebih lanjut dalam menentukan koreksi kecepatan phase orde kedua ( . , sehingga tanpa mengurangi perumumanbentuk dapat diabaikan.
Selanjutnya, persamaan (4.8) yang merupakan persamaan orde kedua dari hampiran asimtotik, akan digunakan untuk menurunkan suatu persamaan bagi kecepatan phase gelombang soliter terganggu. Untuk itu, tinjau persamaan (4.8) yang ditulis kembali sebagai berikut :
, .
dengan
. .
19
Jika pada persamaan (4.41) disubstitusikan ke persamaan (4.43), maka diperoleh
. .
Jika metode integral parsial digunakan pada persamaan (4.44) dengan pada ∞ dan di ∞, maka diperoleh
. .
Persamaan (4.45) menyatakan rata-rata perubahan energi bagi gelombang soliter terganggu, sedangkan rata-rata perubahan energi bagi gelombang soliter tak terganggu diberikan oleh persamaan (4.24). Bukti untuk ini diberikan pada lampiran 7. Selain itu, persamaan (4.45) bergantung pada , sedangkan
bergantung yang merupakan koreksi kecepatan phase gelombang soliter terganggu, yang secara ekplisit termuat dalam persamaan (4.44).
.
Ruas kiri dan kanan dari persamaan (4.46) bergantung pada , dan berupa persamaan diferensial dengan fungsi dari T yang akan ditentukan. Penurunan persamaan (4.46) – (4.49) diberikan pada lampiran 8. Selanjutnya, bila diasumsikan , maka dari persamaan (4.34) diperoleh = 0, sehingga dari persamaan (4.38) = 0 dan G = 0. Dengan demikian bentuk integral sebelah kiri persamaan (4.46) juga sama dengan nol. Jadi berdasarkan persamaan (4.46), diperoleh
.
Secara ringkas prosedur untuk memperoleh dilakukan sebagai berikut. Misalkan diberikan , yaitu suatu fungsi yang bergantung pada U. Fungsi di digunakan pada persamaan (4.25), (4.29), (4.47) dan (4.48) yang masing-masing memberikan persamaan untuk , , dan . Nilai-nilai , , dan digunakan pada persamaan (4.50) untuk memperoleh persamaan bagi . Besaran diperoleh sebagai penyelesaian dari suatu persamaan differensial.
4.4 Studi Kasus
4.4.1 Kasus pertama
Misalkan
. (4.51) Jika persamaan (4.51) disubstitusikan ke persamaan (2.25), maka diperoleh . . Kemudian dari persamaan (4.29) diperoleh
, .
21
. . . Pada kasus ini, , sehingga G . Jika persamaan (4.52-4.55) disubstitusikan ke persamaan (4.50), maka diperoleh persamaan untuk berikut
. .
Penurunan persamaan (4.52) – (4.56) diberikan pada lampiran 9.
Khususnya, Jika suatu konstanta, yaitu , maka penyelesaian persamaan (4.52) adalah
, . dengan K konstanta pengintegralan. Berdasarkan persamaan (4.17), diperoleh nilai dan berikut :
, .
dan
. .
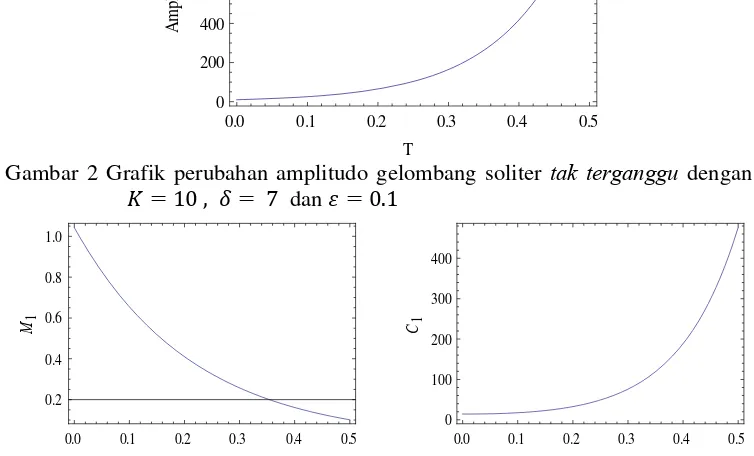
terganggu didasarkan masing-masing pada persamaan (4.57), (4.60) dan persamaan (4.62). Dengan menggunakan software Mathematica6, diperoleh grafik perubahan amplitudo, tail dan kecepatan phase gelombang untuk positif dan negatif yang masing-masing diberikan pada Gambar 2, 3, 4 dan Gambar 5 berikut :
Gambar 2 Grafik perubahan amplitudo gelombang soliter tak terganggu dengan
, dan .
Gambar 3 Grafik dan kecepatan phase gelombang soliter terganggu dengan , dan .
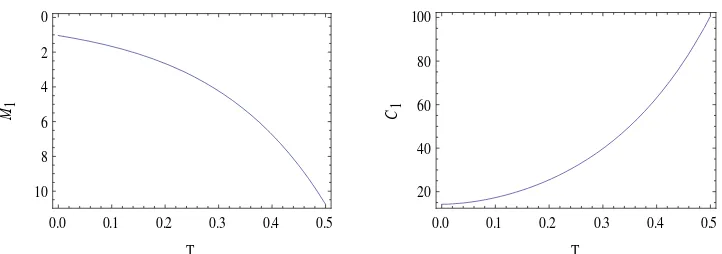
Gambar 4 Grafik perubahan amplitudo gelombang soliter takterganggu dengan
23
Gambar 5 Grafik dan kecepatan phase gelombang soliter terganggu dengan
, dan .
Pada Gambar 2 dengan positif teramati bahwa perubahan amplitudo gelombang soliter tak terganggu grafiknya naik (increases) sedangkan untuk negatif seperti pada Gambar 4, perubahan amplitudo gelombang soliter tak terganggu grafiknya turun (decreases). Selain itu, turun (decreases) baik positif maupun negatif, sedangkan kecepatan phase seperti diberikan pada Gambar 3 dan 5, nilai naik (increases) untuk positif dan negatif. Dengan demikian turun dan naik, ketika T naik baik positif maupun negatif. Berikut ini akan digambarkan simpangan gelombang soliter internal baik terganggu maupun tak terganggu. Untuk itu substitusikan nilai dan yang masing-masing diberikan pada persamaan (4.57) dan (4.58) ke dalam persamaan (4.16) sehingga diperoleh simpangan gelombang soliter tak terganggu berikut
, . .
Simpangan gelombang soliter terganggu diperoleh berdasarkan persamaan (4.4), yang ditulis ulang berikut
, , .
dengan diberikan pada persamaan (4.63). Persamaan untuk diperoleh dari persamaan (4.37) dan (4.38) dan diperoleh
, (4.65)
ditulis dalam bentuk
, , (4.66)
Selanjutnya, persamaan (4.64) dapat dinyatakan berikut :
.
dengan
, dan (4.68)
dimana , , dan masing-masing diberikan pada persamaan (4.57), (4.58), (4.59) dan (4.62). Persamaan (4.63) diinterpretasikan sebagai gelombang soliter tak terganggu yang identik dengan persamaan (4.67) pada saat . Selain itu, persamaan (4.67) menyatakan bahwa perambatan gelombang soliter memenuhi konservasi energi.
Grafik simpangan gelombang soliter tak terganggu dan terganggu masing-masing diperoleh berdasarkan persamaan (4.63) dan (4.66).
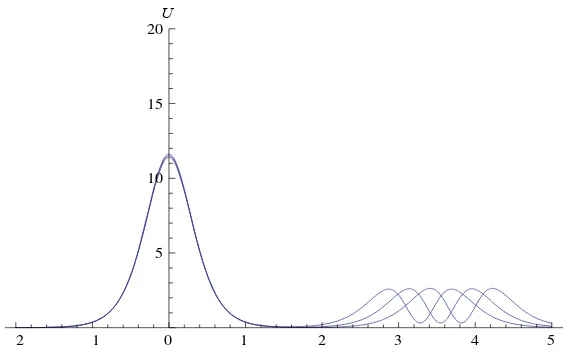
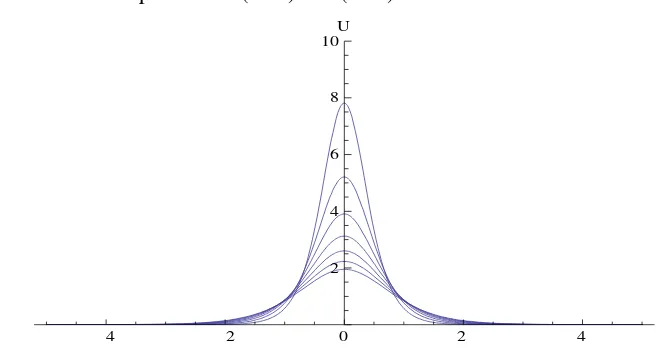
Gambar 6 Simpangan gelombang soliter tak terganggu dengan , , dan .
2 1 0 1 2 3
25
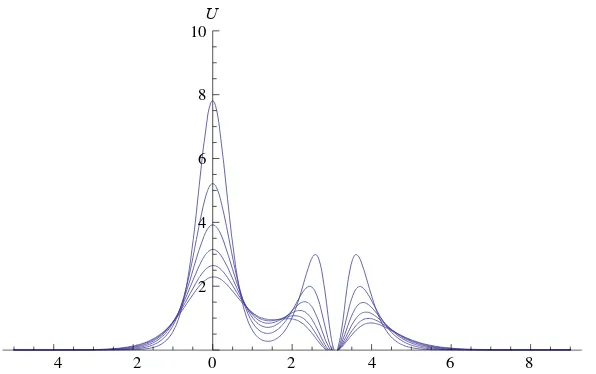
Gambar 7 Simpangan gelombang soliter terganggu dengan , dan .
Pada Gambar 6 dan 7 teramati bahwa gelombang soliter terganggu tampak dalam perambatannya mengalami perubahan bentuk pada simpangan gelombangnya, yakni adanya gelombang dengan amplitudo yang lebih kecil yang menyertai gelombang soliter utama, yang disebut dengan ekor (tail) gelombang soliter terganggu dengan amplitudo ekor yang menurun (decreases) dan kecepatan phase meningkat (increases) di . Pada gelombang soliter tak terganggu tampak dalam perambatannya, bentuk simpangan gelombangnya relatif tidak berubah dalam waktu yang cukup lama. Untuk lebih jelas, berikut ini diberikan studi kasus yang lain.
4.4.2 Kasus kedua
Misalkan
, (4.69) Jika persamaan (4.69) disubstitusikan ke persamaan (4.25), maka diperoleh . . Kemudian dari persamaan (4.29), diperoleh
dan
. . Sama dengan pada kasus pertama, pada kasus ini juga , sehingga
. Dengan mensubstitusikan persamaan (4.70) – (4.73) ke persamaan (4.50) diperoleh persamaan untuk berikut
. .
Penurunan persamaan (4.70) – (4.73) diberikan pada lampiran 10.
Selanjutnya, jika merupakan suatu konstanta, maka penyelesaian persamaan (4.70) berbentuk
. .
Berdasarkan persamaan (4.17), diperoleh nilai dan masing-masing sebagai berikut :
, . dan
27
Berikut ini akan dibahas perubahan amplitudo gelombang soliter tak terganggu, tail dan kecepatan phase gelombang soliter terganggu pada saat gelombang tersebut merambat. Perubahan amplitudo, tail dan didasarkan masing-masing pada persamaan (4.75), (4.78) dan persamaan (4.80). Dengan menggunakan software Mathematica6 diperoleh grafik perubahan amplitudo gelombang soliter tak terganggu, seperti pada Gambar 8 berikut :
Gambar 8 Grafik perubahan amplitudo gelombang soliter takterganggu dengan
, dan .
Perubahan tail dan kecepatan phase gelombang soliter terganggu diberikan pada Gambar 9 berikut.
Gambar 9 Grafik dan kecepatan phase gelombang soliter terganggu dengan
, dan .
Selanjutnya, dengan proses yang sama pada kasus pertama, diperoleh simpangan gelombang soliter tak terganggu berikut
, . .
dengan dan masing-masing diberikan pada persamaan (4.75) dan (4.76). Simpangan gelombang soliter terganggu diperoleh
, , (4.82)
dengan diberikan pada persamaan (4.81) dan diperoleh dari persamaan berikut
, (4.83)
dengan pada persamaan (4.80).
Sama halnya dengan kasus pertama, pada kasus ini , juga identik dengan , pada persamaan (4.67) dan (4.68) di , dengan , , dan masing-masing diberikan pada persamaan (4.75), (4.76), (4.77) dan (4.80) yang merupakan gelombang soliter tak terganggu yang dalam perambatannya memenuhi konservasi energi
Simpangan gelombang soliter tak terganggu dan terganggu masing-masing diperoleh berdasarkan persamaan (4.81) dan (4.82).
Gambar 10 Simpangan gelombang soliter Tak terganggu dengan ,
29
Gambar 11 Simpangan gelombang soliter terganggu dengan , dan .
Pada Gambar 10 dan 11 teramati bahwa simpangan gelombang soliter tak terganggu dalam perambatanya relatif tidak berubah, hal yang berbeda dengan gelombang soliter terganggu dimana dalam perambatannya mengalami perubahan bentuk simpangan gelombangnya, yakni adanya ekor (tail) gelombang yang menyertai gelombang utama dengan kecepatan phase dan amplitudo ekor gelombang yang turun di .
4 2 0 2 4 6 8
2 4 6 8 10
V KESIMPULAN DAN SARAN
5.1 Kesimpulan
Banyak model persamaan tak linier yang diturunkan dari pengamatan terhadap gelombang internal. Salah satunya adalah persamaan Korteweg-de Vries (KdV). Persamaan KdV ini memiliki sifat berlakunya hukum konservasi.
Penyelesaian persamaan KdV yang melibatkan parameter perturbasi diselesaikan dengan menggunakan metode asimtotik. Dari uraian asimtotik, jika orde diperhatikan, maka diperoleh persamaan KdV standar. Penyelesaian persamaan KdV standar menggunakan asumsi bahwa penyelesaiannya berupa gelombang soliter. Gelombang soliter yang diperoleh memiliki tiga parameter gelombang, yaitu amplitudo gelombang, panjang gelombang dan kecepatan phase gelombang yang saling berkaitan dan semuanya bergantung pada waktu.
Kemudian, untuk orde selanjutnya, pada kondisi terselesaikan diperoleh suatu persamaan yang secara ekplisit menggambarkan perubahan kecepatan phase gelombang soliter terganggu dan konsisten dengan hukum konservasi energi. Perubahan amplitudo gelombang soliter tak terganggu dipengaruhi oleh faktor ganguan (delta) yang diberikan, dimana perubahan amplitudo gelombang soliter tak terganggu meningkat untuk delta positif dan sebaliknya turun untuk delta negatif. Namun demikian, perubahan amplitudo tidak berpengaruh secara signifikan terhadap amplitudo ekor gelombang dan kecepatan phase gelombang soliter terganggu. Amplitudo ekor gelombang yang menurun dan kecepatan phase meningkat, jika delta positif maupun negatif.
5.2 Saran
31
DAFTAR PUSTAKA
[1] Johnson R. On an Asymtotic solution of the Korteweg-de Vries equation with slowly varying coefficients. J. Fluid. Mec 1973; 86: 415-431.
[2] Ko K and Kuehl H H. Korteweg-de Vries soliton in a slowly varying medium.
Phys. Rev. Lett;1978; 40: 233-236.
[3] Grimshaw R. Slowly varying solitary wave.I Korteweg-de Vries equation,
Proc. Roy. Soc. Ser. A;1979; 368: 359-375.
[4] Karpman V I and Maslov E M. Structure of tails produced under the action of perturbation on solitons. Sov. Phy. JETP; 1978; 48; 252-259.
[5] Kaup D J and Newell A C. Solitons as Paricles, Oscillators, and in Slowly Changing Media: A Singular Perturbation Theory,Proc. Roy. Soc. Ser. A 1978; 361, 412-446.
[6] Tuwankotta JM. Pengantar Analisis Asimtotik. Seminar Matematika Kelompok Bidang Analisis Jurusan Matematika ITB 1997; Bandung, 31 Oktober 1997. Bandung:Jurusan Matematika,FMIPA ITB.hlm1-6
[7] Jaharuddin. Gelombang Soliter di Selat Lombok dan Simulasi Numerik Fenomena Morning Glory [Disertasi]. Bandung: Program Pascasarjana, Institut Tehnologi Bandung;2004
[8] Ihsanudin. Kekonsistenan Hamiltonian pada Gerak Gelombang Interfacial [Tesis]. Bogor: Program Pascasarjana, Institut Pertanian Bogor;2008 [9] Ramayanti T. Data Hamburan pada Persamaan Korteweg-De Vries (KdV)
dengan Perturbasi [Skripsi]. Bogor: Fakultas MIPA, Institut Pertanian Bogor;1999
[10] Gerd Baumann. Classical Mechanics and Nonlinier Dynamics, Mathematica for Theoretical Physics, Edisi ke-2, Springer;2004; 505-508.
[11] Grimshaw R. Solitary Waves in Fluids. WIT Press 2007; 20-51
[12] Grimshaw R & Mitsudera H. Slowly varying solitary wave solutions of the perturbed Korteweg-de Vries equation revisited, Stud. Appl.Math,1993;
33
Lampiran 1.
Penurunan Persamaan (2.26)
Dari persamaan (2.25) berikut
Ф ,
Jika persamaan di atas diturunkankan terhadap x, maka turunan pertama dan kedua berurut-turut diperoleh :
Selanjutnya, berdasarkan persamaan (2.20) diperoleh
. (6.4)
Jika persamaan (6.4) diintegralkan terhadap ,maka
35
Jika persamaan (2.28) diturunkan terhadap dan persamaan (2.29) diturunkan terhadap x, kamudian mengurangkan kedua persamaan tersebut, maka diperoleh persamaan berikut
. (6.26)
Perhatikan kembali persamaan (6.26) berikut
. (6.27) Jika persamaan (6.16), (6.17) dan (6.21) disubstitusikan secara bersama-sama ke ruas kanan persamaan (6.27), maka didapat ruas kanan persamaan (6.27) berikut
atau
atau
(6.28) Kemudian dari ruas kanan persamaan (6.26) ditulis kembali dalam bentuk
. (6.29)
secara bersama-sama, substitusikan persamaan (6.14 – 6.25) ke persamaan (6.29) sehingga diperoleh
atau
atau
. (6.30)
Selanjutnya, dari penyetaraan persamaan (6.28) dan (6.30) diperoleh atau
37
Sehingga didapat persamaan (2.32) berikut
Penurunan Persamaan (2.35)
Kemudian, tinjau persamaan (2.33) berikut ∆ , maka diperoleh
. . Selain itu diperoleh pula
. Dari persamaan (2.34) berikut
atau (6.33) diperoleh persamaan-persamaan berikut
Jika persamaan-persamaan di atas disubstitusikan ke persamaan (2.32) yang ditulis ulang dalam bentuk
,
maka diperoleh
atau
.
Selanjutnya, jika kedua ruas persamaan (6.34) dibagi dengan , maka diperoleh
atau
atau
.
Jika peubah diganti dengan , maka diperoleh persamaan (2.35) berikut
.
…
…
(7.7)
Substitusikan persamaan (4.5) ke persamaan (7.7), diperoleh
…
Jadi koefisien memberikan persamaan (4.6) berikut :
, Koefisien memberikan persamaan (4.7) berikut :
,
41
dan untuk koefisien memberikan persamaan (4.8) berikut :
.
Lampiran 3.
Pembuktian persamaan (4.20)
Dari persamaan (4.15) berikut
(8.1)
diturunkan terhadap , maka turunan pertama, kedua dan ketiga berturut-turut adalah
.
.
=
(8.4)
Kemudian dari persamaaan (4.21) yang ditulis ulang dalam bentuk berikut ini
w =
(8.5)
diturunkan terhadap , maka turunan pertama, kedua dan ketiga berturut-turut adalah
=
43
(8.6)
(8.7)
. (8.8)
Persamaan adjoint (4.20) memiliki penyelesaian untuk V adalah 1, dan w,
dengan dan w masing-masing diberikan persamaan (4.16) dan persamaan (4.21). Bukti untuk ini menggunakan persamaan (8.1) – (8.8) yang detilnya diberikan berikut
Untuk V = 1
Jika V = 1 disubstitusikan ke persamaan (4.20) diperoleh
0
Untuk V =
Jika V = disubstitusikan ke persamaan (4.20) diperoleh
(8.9)
Substitusikan persamaan (8.2) dan (8.4) ke persamaan (8.9) diperoleh berikut
45
Untuk V= w
Jika V= w disubstitusikan ke persamaan (4.20), maka diperoleh
(8.10)
Dengan cara yang sama, jika persamaan (4.16), (8.6) dan persamaan (8.8) disubstitusikan ke persamaan (8.10) diperoleh
Lampiran 4. Jika persamaan (4.16) dan . disubstitusikan ke persamaan . , maka diperoleh
} Sehingga
=
} =
atau
(9.3)
Jika persamaan (4.25) disubstitusikan ke persamaan (9.3), maka diperoleh persamaan (4.29) berikut
=
=
atau
49
Lampiran 5.
Pembuktian Persamaan (4.30).
Dari persamaan homogen (4.26) berikut
(10.1)
diperoleh penyelesaiannya sebagai berikut w dan , dengan demikian
Wronskian dari w dan adalah sebagai berikut :
W(w, = (10.2)
Bukti diberikan sebagai berikut.
Jika persamaan (8.3) dan (8.5) disubstitusikan ke persamaan (10.2) diperoleh uraian berikut
(10.3)
Jika persamaan (8.2) dan persamaan (8.6) disubstitusikan ke uraian persamaan (10.2) diperoleh uraian berikut
51
Kemudian jika uraian persamaan (10.3) dan (10.4) disubstitusikan ke persamaan (10.2), maka diperoleh
=
+
= (
-
+
= (
+
= (
=
53
Karena W(w, , maka w dan merupakan penyelesaian homogen persamaan (4.26).
Jika disubstitusikan ke persamaan (4.26), maka diperoleh
.
Substitusikan persamaan . dan . ke persamaan . diperoleh
.
Jika disubstitusiakan ke persamaan . , maka diperoleh
.
Selanjutnya, substitusikan persamaan . dan . ke persamaan . ,
diperoleh
+
55
atau
atau
Sehingga diperoleh berturut-turut persamaan (4.32), (4.33), (4.34) dan (4.35) berikut
,
dan
,
dengan
. dan
59
Selanjutnya, substitusikan persamaan (7.4) dan (7.5) ke persamaan (11.1), diperoleh
, atau
. . Dengan menggunakan metode asimtotik, diasumsikan bahwa peubah tak bebas dan peubah E memiliki uraian asimtotik sebagai berikut :
F = F0 + (11.3)
E (11.4) Substitusikan persamaan (11.3) dan (11.4) ke persamaan (11.2) maka diperoleh
Sehingga koefisien memberikan persamaan terhadap , maka persamaan (11.6) memberikan
61
Substitusikan persamaan (11.8) dan (11.9) ke persamaan (11.11), dan perhatikan bahwa di ∞, dan atau , maka diperoleh
atau
Jadi diperoleh persamaan (4.24) berikut
Kemudian dengan cara yang sama, substitusikan persamaan (11.8) – (11.10) ke persamaan (11.12), dan perhatikan bahwa daripersamaan (4.40) dan (4.41) dapat ditunjukan bahwa atau ketika ∞, maka diperoleh :
atau
atau
Karena pada saat ∞, diperoleh persamaan (4.45) berikut
63
∞
∞ +
atau
∞
∞ + ∞∞
∞
∞ ∞∞ ∞∞
∞ ∞
atau
+
∞
∞ (12.2)
Jika persamaan (4.16), (4.17) dan (4.29) disubstitusikan ke persamaan (12.2), maka diperoleh berturut-turut persamaan (4.46), (4.47), (4.48) dan persamaan (4.49) berikut
dengan
dan
Lampiran 9.
Penurunan Persamaan (4.52) – (4.56)
Dari persamaan (4.25 ) berikut
,
disubstitusikan persamaan (4.16), (4.17) dan (4.51), maka diperoleh
65
Dari persamaan (4.48), diperoleh
Jika persamaan (4.51) – (4.55) disubstitusikan ke persamaan (4.50) maka diperoleh
=
atau
atau
atau
atau
Lampiran 10.
Penurunan Persamaan (4.70) – (4.73)
Sama halnya dengan penurunan persamaan pada kasus pertama, pada kasus ini yang dimisalkan dalam bentuk persamaan (4.69) berikut
. dengan
(13.1)
dan
. (13.2)
Selanjutnya, persamaan (4.70)diperoleh dengan cara mensubstitusikan persamaan (13.2) ke persamaan (4.25), diperoleh
67
Persamaan (4.71) untuk , diperoleh dari persamaan (4.29) berikut
. cara mensubstitusikan persamaan (13.2) ke persamaan (4.47) dan (4.48) berikut
Untuk diperoleh