PEMODELAN FREKUENSI PETIR DI BOGOR
MENGGUNAKAN PENDEKATAN LOGIKA
FUZZY
NURLAELA ROSDIYANA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa skripsi berjudul Pemodelan Frekuensi Petir di Bogor Menggunakan Pendekatan Logika Fuzzy adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, November 2014
Nurlaela Rosdiyana
ABSTRAK
NURLAELA ROSDIYANA. Pemodelan Frekuensi Petir di Bogor Menggunakan Pendekatan Logika Fuzzy. Dibimbing oleh SRI NURDIATI dan ELIS KHATIZAH.
Guinness Book of Record pada tahun 1989 dalam artikel Antara News (2013) menunjukkan bahwa Bogor adalah salah satu daerah yang memiliki potensi petir tertinggi di dunia. Namun, alat pencatat frekuensi petir yaitu
lightning counter sering mengalami kerusakan sehingga data frekuensi petir tidak tercatat dengan baik. Penelitian ini dilakukan untuk membuat model frekuensi petir di Bogor menggunakan pendekatan logika fuzzy. Metode yang digunakan adalah metode Mamdani yang terdiri atas empat tahapan yaitu fuzzifikasi, aplikasi fungsi implikasi, agregasi semua aturan, dan defuzzifikasi. Model yang terbentuk mengambil input berupa suhu udara, kelembaban udara, kecepatan angin, curah hujan dan penguapan. Output dari model ini adalah frekuensi petir. Hasil penelitian menunjukkan bahwa terdapat 81 aturan model frekuensi petir. Keakuratan pemodelan fuzzy dapat dilihat dari nilai mean percentage absolute
error (MAPE) sebesar 17.2%.
Kata kunci: Petir, Pemodelan Fuzzy, MAPE
ABSTRACT
NURLAELA ROSDIYANA. Modelling the Frequency of Lightning in Bogor Using Fuzzy Logic Approach. Supervised by SRI NURDIATI and ELIS KHATIZAH.
Guinness Book of Records in 1989 as indicated in the Antara News article (2013) showed that Bogor is one of the areas with the highest potential for lightning in the world. However, the recording devices that count frequency lightning are repeatedly damaged. Hence, the records are badly documented. This study was conducted to model the frequency of lightning in Bogor using fuzzy logic approach. The method used is the Mamdani method consists of four stages: fuzzification, implication function application, aggregation of rules, and defuzzification. The formed model took the following inputs: air temperature, air humidity, wind speed, rainfall and evaporation. The output data of this model is the frequency of lightning. The results indicate 81 rules model of lightning frequency. Fuzzy modelling accuracy could be indicated by the mean value of the absolute percentage error (MAPE) of 17.2%.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PEMODELAN FREKUENSI PETIR DI BOGOR
MENGGUNAKAN PENDEKATAN LOGIKA
FUZZY
NURLAELA ROSDIYANA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi : Pemodelan Frekuensi Petir di Bogor Menggunakan Pendekatan Logika Fuzzy
Nama : Nurlaela Rosdiyana NIM : G54090050
Disetujui oleh
Dr Ir Sri Nurdiati, MSc Pembimbing I
Elis Khatizah, MSi Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga karya ilmiah yang berjudul Pemodelan Frekuensi Petir di Bogor Menggunakan Pendekatan Logika Fuzzy berhasil diselesaikan.
Terima kasih penulis ucapkan kepada Ibu Dr Ir Sri Nurdiati, MSc dan Ibu Elis Khatizah, MSi selaku dosen pembimbing serta Bapak Dr Ir Fahren Bukhari, MSc selaku dosen penguji yang telah memberikan bimbingan, motivasi, dan saran selama penulisan karya ilmiah ini. Ungkapan terima kasih juga disampaikan kepada Bapak Riyadi, Ibu Siti Rohmah, Renny Yanti, Abdul Azis Maulana, Kholifah Azzula Oktaviyani, Hafizah Risty Febrari, serta seluruh keluarga atas doa dan kasih sayangnya. Selain itu, terimakasih juga diberikan kepada BMKG Dramaga Bogor, Karya Salemba Empat, LAWALATA IPB, teman-teman Matematika 46, serta semua pihak terkait yang telah membantu dalam proses penyusunan karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat.
Bogor, November 2014
DAFTAR ISI
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
METODOLOGI 2
Data 2
Pengambilan Data 2
Pemodelan Fuzzy 4
Ukuran Kesalahan 5
HASIL DAN PEMBAHASAN 6
Pembentukan Himpunan Fuzzy 6
Aplikasi Fungsi Implikasi 11
Agregasi Semua Aturan 12
Defuzzifikasi 12
Ukuran Kesalahan 13
SIMPULAN DAN SARAN 13
Simpulan 13
Saran 13
DAFTAR PUSTAKA 13
LAMPIRAN 15
DAFTAR GAMBAR
Gambar 1 Histogram Suhu Udara Rata-Rata di Bogor Tahun 2012 6 Gambar 2 Representasi Suhu Udara Rata-Rata di Bogor Tahun 2012 7 Gambar 3 Histogram Kelembaban Udara di Bogor Tahun 2012 8 Gambar 4 Representasi Kelembaban Udara di Bogor Tahun 2012 8 Gambar 5 Histogram Kecepatan Angin di Bogor Tahun 2012 9 Gambar 6 Representasi Kecepatan Angin di Bogor Tahun 2012 9 Gambar 7 Histogram Curah Hujan di Bogor Tahun 2012 9 Gambar 8 Representasi Curah Hujan di Bogor Tahun 2012 10 Gambar 9 Histogram Penguapan di Bogor Tahun 2012 10 Gambar 10 Representasi Penguapan di Bogor Tahun 2012 10 Gambar 11 Histogram Frekuensi Petir di Bogor Tahun 2012 11 Gambar 12 Representasi Frekuensi Petir di Bogor Tahun 2012 11 Gambar 13 Hasil Perhitungan dari Agregasi Semua Aturan Model Frekuensi
Petir 12
DAFTAR LAMPIRAN
Lampiran 1 Data iklim dan data frekuensi petir 15 Lampiran 2 Fungsi keanggotaan data iklim dan frekuensi petir 20 Lampiran 3 Aturan model frekuensi petir dengan menggunakan pendekatan 26
logika fuzzy
Lampiran 4 Contoh proses penggunaan fungsi implikasi 28 Lampiran 5 Proses agregasi semua aturan model frekuensi petir 31 Lampiran 6 Hasil pemodelan frekuensi petir di Bogor menggunakan
pendekatan logika fuzzy dan nilai MAPE 33
PENDAHULUAN
Latar Belakang
Bogor merupakan salah satu daerah yang berpotensi rawan petir karena memiliki topografi yang memungkinkan tumbuhnya awan-awan konvektif di sekitar lereng pegunungan. Sejumlah pegunungan yang mengelilingi Bogor dengan ketinggian mencapai ribuan kaki dapat mengalihkan awan menuju ketinggian yang potensial menimbulkan terjadinya petir (Suharsono 1982). Daerah yang dikenal dengan julukan kota hujan ini memiliki curah hujan yang sangat tinggi sehingga berpotensi menghasilkan petir dengan frekuensi yang besar. Petir merupakan pelepasan muatan elektrostatis yang berasal dari badai guntur (Hidayat 2008). Artikel Antara News (2013) menyebutkan bahwa Bogor adalah salah satu daerah yang memiliki potensi petir sangat tinggi di dunia, tercatat dalam Guinness Book of Record pada tahun 1989.
Petir sering terjadi pada saat hujan karena kadar air dalam udara lebih tinggi dan mengakibatkan daya isolasi udara menurun sehingga arus menjadi lebih mudah mengalir. Selain curah hujan, faktor yang menyebabkan terjadinya petir adalah ketakstabilan udara, mekanisme pengangkatan masa udara (lifting), pertumbuhan awan, kecepatan angin, suhu udara, kelembaban udara, tekanan udara, dan penguapan (Bayong 2004). Keberadaan petir memberikan beberapa manfaat antara lain sebagai sumber energi, pemicu terjadinya reaksi kimia dalam pembentukan lapisan ozon, dan pembentukan NH4 untuk kesuburan tanah.
Namun, serangan petir dapat menjadi bencana. Serangan petir dapat mengganggu transmisi listrik, menimbulkan tegangan tinggi, dan merenggut nyawa manusia yang terkena serangan secara langsung. Bahaya yang ditimbulkan dari sambaran petir ini sangat merugikan manusia sehingga kita perlu waspada dan hati-hati pada saat hujan yang disertai petir (Husni 2002).
2
Pada karya ilmiah ini dilakukan pemodelan frekuensi petir menggunakan pendekatan logika fuzzy yang mengadopsi pengetahuan manusia ke komputer dan dapat menyelesaikan masalah seperti yang dilakukan para ahli. Beberapa penelitian yang terkait dengan karya ilmiah ini adalah penelitian Akhmad Akbar (2012) tentang Pruning pada Fuzzy Decision Tree dalam Klasifikasi Data Iklim dan Titik Api di Daerah Tjilik Riwut, Palangkaraya, Kalimantan Selatan dan Penelitian tentang Karakteristik Petir Terkait Curah Hujan Lebat di Wilayah Bandung, Jawa Barat oleh Deni Septiadi (2012). Diharapkan dengan pendekatan ini pengambilan keputusan dapat dilakukan secara tepat mendekati hasil pengetahuan para ahli. Pada karya ilmiah ini, pemodelan frekuensi petir di Bogor menggunakan pendekatan logika fuzzy dilakukan dengan bantuan software
matematika.
Tujuan Penelitian
Tujuan dari karya ilmiah ini adalah:
1. Membuat model frekuensi petir di Bogor menggunakan pendekatan logika
fuzzy.
2. Menghitung ukuran kesalahan dari model frekuensi petir.
METODOLOGI
Data
Data yang digunakan adalah data frekuensi petir dan data iklim hasil pengamatan tahun 2012 di Stasiun Klimatologi Kelas 1 BMKG Dramaga, Bogor.
Pengambilan Data
Suhu Udara
Suhu dapat didefinisikan sebagai tingkat panas suatu benda yang dapat berubah sesuai tempat dan waktu (Bayong 2004). Pengukuran suhu udara hanya memperoleh satu nilai yang menyatakan nilai rata-rata suhu udara. Suhu udara harian rata-rata didefinisikan sebagai rata-rata pengamatan selama 24 jam yang dilakukan setiap jam. Suhu harian rata-rata di Indonesia dapat dihitung dengan persamaan:
dengan - adalah suhu harian rata-rata, adalah pengamatan suhu
udara pada pukul 07.00, pukul 13.00 dan pukul 18.00 waktu setempat.
3 Kelembaban Udara
Besaran yang dipakai untuk menyatakan kelembaban udara adalah kelembaban relatif. Kelembaban relatif adalah perbandingan nisbah pencampuran (r) dengan nilai jenuhnya (rs) dan dinyatakan dalam persen (Bayong 2004). Alat yang digunakan untuk mengukur kelembaban adalah psikrometer. Cara pengukurannya, dengan memutar psikrometer di luar sangkar meteorologi selama 1-2 menit kemudian dapat dibaca suhu dari termometer bola basah dan bola kering. Kelembaban udara dapat dinyatakan dengan persamaan:
dengan RH adalah kelembaban relatif, e adalah tekanan uap air jenuh, dan es adalah tekanan uap air suhu bola basah.
Tekanan uap air merupakan jumlah tekanan parsial dari uap air yang berada di udara. Berikut persamaan dari tekanan uap air:
( )
dengan esadalah tekanan uap air suhu bola basah dan To adalah suhu bola kering. Tekanan uap air jenuh merupakan jumlah tekanan dari uap air yang berada di udara saat jenuh. Tekanan uap air jenuh dapat dinyatakan dengan persamaan:
dengan e adalah tekanan uap air jenuh, Twadalah suhu bola basah dan Pqfe adalah tekanan udara stasiun pengamatan.
Kecepatan Angin
Gerak udara yang sejajar dengan permukaan bumi disebut angin. Udara bergerak dari daerah yang bertekanan tinggi ke daerah yang bertekanan rendah. Kecepatan angin tergantung pada ketinggiannya dari permukaan tanah. Dalam hal ini, semakin tinggi posisi angin semakin cepat lajunya (Bayong 2004). Angin diukur dengan satuan mil laut per jam atau disebut juga knot (kn) dengan 1 kn = 1.85 km jam-1 = 1.151 mil jam-1 = 0.514 m det-1 atau 1 m det-1 = 2.237 mil jam-1 = 1.944 kn. Anemometer merupakan alat yang digunakan untuk mengukur kecepatan angin. Berbentuk seperti cup, anemometer terhubung dengan anemograf yang berfungsi sebagai pencatat kecepatan angin. Pengukuran angin dilakukan di puncak menara setinggi 10 m dari permukaan tanah.
Curah Hujan
4
Alat untuk mengukur jumlah curah hujan disebut penakar curah hujan biasa. Pada alat tersebut terdapat kran untuk mengeluarkan air hujan yang akan diukur dengan menggunakan gelas ukuran. Pengamatan dilakukan setiap pukul 07.00 waktu setempat.
Penguapan
Proses perubahan fase air atau es menjadi fase uap yang naik ke udara disebut dengan penguapan. Besarnya penguapan tergantung pada suhu udara, kelembaban udara, tekanan udara, dan kecepatan angin (Bayong 2004). Alat untuk mengukur besarnya penguapan disebut evaporimeter panci. Pengamatan dilakukan setiap pukul 07.00 waktu setempat
Frekuensi Petir
Pelepasan muatan elektrolisis yang berasal dari badai guntur dapat disebut dengan petir. Pelepasan muatan ini disertai dengan pancaran cahaya dan radiasi elektromagnetik. Energi pelepasan petir sangat besar sehingga menimbulkan rentetan cahaya, panas, dan bunyi menggelegar yang disebut geluduk atau geledek. Sedemikian besarnya energi petir itu sampai-sampai langit menjadi terang (Byers 1997). Alat penghitung frekuensi petir adalah lightning counter
yang terhubung dengan alat digital untuk mencatat banyaknya frekuensi petir. Proses kerjanya adalah sambaran petir yang sampai di bumi dapat tersensor dengan lightning counter yang terhubung pada alat digital. Dari alat digital ini dapat terlihat berapa frekuensi petir yang terjadi dalam satu hari.
Pemodelan Fuzzy
Logika fuzzy digunakan sebagai cara untuk memetakan permasalahan dari input menuju ke output. Model logika fuzzy memungkinkan pembuatan keputusan yang relatif dalam suatu lingkungan ketidaktentuan dan ketidakteraturan (Zadeh 1996). Hal yang harus dipahami dalam logika fuzzy adalah variabel dan himpunan
fuzzy. Salah satu aplikasi dari logika fuzzy adalah sistem inferensi fuzzy (Fuzzy Inference Sytem/ FIS), yaitu sistem komputasi yang bekerja atas dasar prinsip penalaran fuzzy. Metode yang digunakan dalam karya ilmiah ini adalah metode Mamdani atau dikenal dengan metode maximum-minimum yang dapat menerima masukan dari manusia, intuitif, dan berdasarkan penalaran manusia (Kusumadewi dan Purnomo 2010). Ebrahim Mamdani memperkenalkan metode tersebut pada tahun 1975. Tahapan mendapatkan output, yaitu:
1. Pembentukan himpunan fuzzy
Fuzzifikasi merupakan proses mengubah variabel tegas menjadi variabel
fuzzy (Frans Susilo 2006). Variabel ditentukan berdasarkan proses yang akan dilakukan. Data dari masing-masing variabel dibuat histogram untuk melihat
trend data. Himpunan fuzzy pada metode Mamdani dibagi menjadi satu atau lebih himpunan. Fungsi keanggotaan adalah suatu bentuk untuk mencari nilai keanggotaan. Nilai keanggotaan pada himpunan fuzzy terletak pada rentang 0 sampai 1. Nilai keanggotaan diperlukan untuk memberikan bobot pada suatu variabel, sehingga variabel tersebut dapat dinyatakan dengan nilai.
5 Penyusunan basis aturan berupa implikasi fuzzy yang menyatakan relasi antara variabel input dan output. Fungsi implikasi yang digunakan dalam metode Mamdani adalah min dengan operator and pada setiap aturan. Metode ini mengambil nilai keanggotaan terkecil antarelemen pada himpunan yang sesuai. Persamaan dari setiap aturan dalam fungsi implikasi, yaitu:
IF (x1is A1) and (x2is A2) THENyis B
dengan A dan B adalah himpunan fuzzy, sedangkan x dan y merupakan variabel
fuzzy. Proposisi yang mengikuti IF disebut anteseden, sedangkan proposisi yang mengikuti THEN disebut konsekuen (Kusumadewi dan Purnomo 2010). 3. Agregasi semua aturan
Agregasi semua aturan menggunakan metode max. Solusi himpunan fuzzy
dapat diperoleh dengan cara mengambil nilai maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy, dan mengaplikasikannya ke output dengan menggunakan operator or. Secara umum dituliskan:
dengan adalah nilai keanggotaan solusi fuzzy sampai aturan ke-i dan
adalah nilai keanggotaan konsekuen fuzzy aturan ke-i (Kusumadewi
dan Purnomo 2010). 4. Defuzzifikasi
Defuzzifikasi adalah proses pengubahan output fuzzy ke output crisp
(Marimin, 2002). Input dari proses defuzzifikasi adalah suatu himpunan fuzzy
yang diperoleh dari agregasi semua aturan fuzzy, sedangkan output yang dihasilkan berupa bilangan pada domain himpunan fuzzy tersebut (Kusumadewi dan Purnomo 2010). Proses defuzzifikasi menggunakan metode
centroid (composite moment) dengan output diperoleh mengambil titik pusat daerah fuzzy. Secara umum dituliskan:
∫
∫
∑ ( )
∑ ( )
dengan adalah titik pusat, z adalah domain himpunan fuzzy, dan µ adalah derajat keanggotaan.
Ukuran Kesalahan
6
periode tersebut (Makridakis et.al 1995). MAPE dapat digunakan untuk membandingkan metode dan ramalan terbaik dalam menyusun model kontinu. MAPE mengindikasi seberapa besar kesalahan dalam hasil ramalan bila dibandingkan dengan nilai nyata. MAPE mengukur ketepatan nilai dugaan model yang dinyatakan dalam bentuk persentase absolut kesalahan. Persamaan MAPE dapat dituliskan:
E ∑ dengan E -
dimana Fi adalah data aktual pada periode ke-i, Fi* adalah nilai ramalan pada periode ke-i, dan n adalah banyaknya periode waktu.
HASIL DAN PEMBAHASAN
Pada penelitian ini, faktor-faktor terjadinya petir hanya dibatasi sampai data iklim saja seperti: suhu udara rata-rata, penguapan, kecepatan angin, kelembaban udara, dan curah hujan, sedangkan untuk data petir menggunakan data frekuensi petir. Data dapat dilihat pada Lampiran 1.
Pemodelan Fuzzy
1. Pembentukan Himpunan Fuzzy
Variabel input berupa suhu udara rata-rata, kelembaban udara, kecepatan angin, penguapan, curah hujan, dan variabel output berupa frekuensi petir.
Suhu Udara
Data tegas dari suhu udara rata-rata dibuat histogram sehingga dapat terlihat
trend datanya. Penentuan fungsi keanggotaan dapat dilakukan setelah melihat
trend data suhu udara rata-rata.
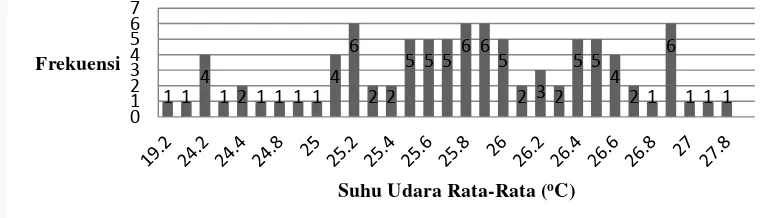
Gambar 1 Histogram Suhu Udara Rata-Rata di Bogor Tahun 2012
Langkah fuzzifikasi selanjutnya adalah mengubah nilai tegas suhu udara rata-rata menjadi nilai samar. Nilai fuzzy diubah dengan cara mengklasifikasi nilai tegas suhu udara rata-rata berdasarkan histogramnya. Dengan demikian didapatkan variabel input berupa suhu udara rata-rata (T). Jika x menyatakan suhu udara rata-rata, maka himpunan fuzzy yang terbentuk terdiri atas: Sangat Rendah
7 (SRe) dengan x < 25.1 oC, Rendah (Re) dengan 25.1 oC ≤x < 25.5 oC, Normal (N) dengan 25.5 oC ≤ x < 26.4 oC, Sedang (S) dengan 26.4 oC ≤ x < 26.9 oC, dan Tinggi (T) dengan x≥ 26.9 oC.
Suhu udara rata-rata (T) memiliki fungsi keanggotaan dengan bentuk trapesium sebagai berikut:
Representasi untuk variabel suhu udara diperlihatkan pada Gambar 2.
Gambar 2 Representasi Variabel Suhu Udara Rata-Rata di Bogor Tahun 2012
8
Kelembaban Udara
Histogram variabel input kelembaban udara sebagai berikut.
Gambar 3 Histogram Kelembaban Udara di Bogor Tahun 2012
Variabel input berupa kelembaban udara (RH). Jika x menyatakan kelembaban udara, maka himpunan fuzzy yang terbentuk terdiri atas: Rendah (Re) dengan x < 83 %, Sedang (S) dengan 83 % ≤x < 94 %, dan Tinggi (T) dengan x≥
94%.
Kelembaban udara (RH) memiliki fungsi keanggotaan dengan bentuk trapesium sebagai berikut:
Representasi variabel kelembaban udara diperlihatkan pada Gambar 4.
Gambar 4 Representasi Kelembaban Udara di Bogor Tahun 2012
9 Kecepatan Angin
Histogram untuk variabel input kecepatan angin sebagai berikut.
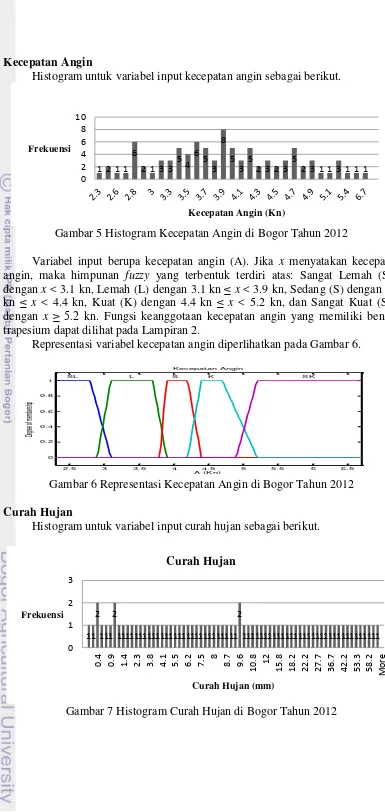
Gambar 5 Histogram Kecepatan Angin di Bogor Tahun 2012
Variabel input berupa kecepatan angin (A). Jika x menyatakan kecepatan angin, maka himpunan fuzzy yang terbentuk terdiri atas: Sangat Lemah (SL) dengan x < 3.1 kn, Lemah (L) dengan 3.1 kn ≤x < 3.9 kn, Sedang (S) dengan 3.9 kn ≤ x < 4.4 kn, Kuat (K) dengan 4.4 kn ≤ x < 5.2 kn, dan Sangat Kuat (SK) dengan x ≥ kn. Fungsi keanggotaan kecepatan angin yang memiliki bentuk trapesium dapat dilihat pada Lampiran 2.
Representasi variabel kecepatan angin diperlihatkan pada Gambar 6.
Gambar 6 Representasi Kecepatan Angin di Bogor Tahun 2012 Curah Hujan
Histogram untuk variabel input curah hujan sebagai berikut.
Gambar 7 Histogram Curah Hujan di Bogor Tahun 2012
10
Variabel input berupa curah hujan (CH). Jika x menyatakan curah hujan, maka himpunan fuzzy yang terbentuk terdiri atas: Sangat Ringan (SRi) dengan x < 1 mm, Ringan (Ri) dengan 1 mm ≤ x < 9.6 mm, Sedang (S) dengan 9.6 mm ≤ x < 34.5 mm, dan Lebat (Le) dengan x ≥ mm Fungsi keanggotaan curah hujan yang memiliki bentuk trapesium dapat dilihat pada Lampiran 2.
Representasi variabel curah hujan diperlihatkan pada Gambar 8.
Gambar 8 Representasi Curah Hujan di Bogor Tahun 2012 Penguapan
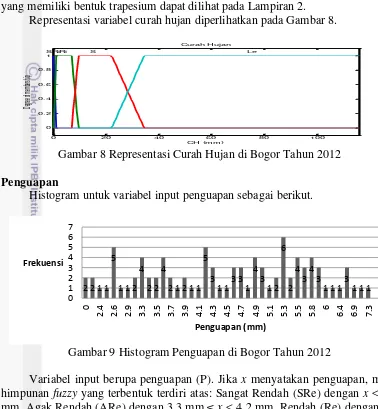
Histogram untuk variabel input penguapan sebagai berikut.
Gambar 9 Histogram Penguapan di Bogor Tahun 2012
Variabel input berupa penguapan (P). Jika x menyatakan penguapan, maka himpunan fuzzy yang terbentuk terdiri atas: Sangat Rendah (SRe) dengan x < 3.3 mm, Agak Rendah (ARe) dengan 3.3 mm ≤ x < 4.2 mm, Rendah (Re) dengan 4.2 mm ≤ x < 4.6 mm, Sedang (S) dengan 3.3 mm ≤ x < 4.6 mm, dan Lebat (Le) dengan x ≥ mm Fungsi keanggotaan penguapan yang memiliki bentuk trapesium dapat dilihat pada Lampiran 2.
Representasi variabel penguapan diperlihatkan pada Gambar 10.
Gambar 10 Representasi Penguapan di Bogor Tahun 2012
11 Frekuensi Petir
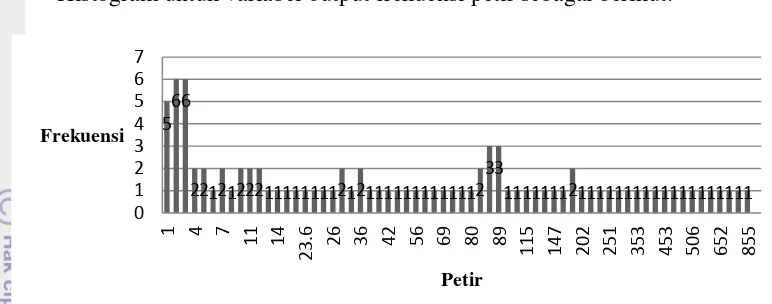
Histogram untuk variabel output frekuensi petir sebagai berikut.
Gambar 11 Histogram Frekuensi Petir di Bogor Tahun 2012
Variabel input berupa frekuensi petir (PETIR). Jika x menyatakan frekuensi petir, maka himpunan fuzzy yang terbentuk terdiri atas: A dengan x < 4, B1 keanggotaan frekuensi petir yang memiliki bentuk trapesium dapat dilihat pada Lampiran 2.
Representasi variabel frekuensi petir diperlihatkan pada Gambar 12.
Gambar 12 Representasi Frekuensi Petir di Bogor Tahun 2012 2. Aplikasi Fungsi Implikasi
Basis aturan disusun berupa implikasi fuzzy yang menyatakan relasi antara variabel input dengan variabel output. Banyaknya aturan dapat ditentukan dari banyaknya nilai linguistik untuk masing-masing variabel input fuzzy (Frans Susilo 2006). Artinya jumlah maksimum aturan yang terbentuk dapat ditentukan dengan jumlah himpunan fuzzy pada variabel input. Variabel input pada karya ilmiah ini seperti suhu udara rata-rata memiliki lima himpunan fuzzy, kelembaban udara
5
100 200 300 400 500 600 700 800
12
memiliki tiga himpunan fuzzy, kecepatan angin memiliki lima himpunan fuzzy, curah hujan memiliki empat himpunan fuzzy, dan penguapan memiliki tujuh himpunan fuzzy, maka akan terdapat 2 100 aturan. Namun, aturan yang mungkin dan sesuai dengan basis pengetahuan ada 81 aturan (Lampiran 3).
Himpunan fuzzy pada setiap variebel diawali dengan mengaplikasikan fungsi implikasi untuk setiap aturan. Aplikasi fungsi implikasi ini berfungsi untuk mencari suatu nilai fuzzy output dari fuzzy input. Prosesnya adalah suatu nilai
fuzzy yang berasal dari tahap fuzzifikasi dimasukkan ke dalam sebuah aturan yang telah dibuat untuk dijadikan sebuah fuzzy output. Pada metode Mamdani, fungsi implikasi yang digunakan adalah metode min dengan operator fuzzy and, oleh karena metode min yang digunakan maka input terkecil yang akan diambil. Contoh proses penggunaan fungsi implikasi dapat dilihat pada Lampiran 4.
3. Agregasi Semua Aturan
Suatu keputusan didasarkan pada pengujian semua aturan, maka aturan harus dikombinasikan dalam beberapa cara untuk membuat keputusan. Agregasi adalah proses dimana himpunan fuzzy yang mewakili output dari setiap aturan digabungkan ke dalam himpunan fuzzy tunggal. Agregasi hanya terjadi sekali untuk setiap output variabel. Output dari proses agregasi adalah salah satu himpunan fuzzy untuk setiap variabel output.
Agregasi semua aturan menggunakan metode max dengan operator fuzzy or.
Dengan demikian, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum aturan. Setelah itu, output didapatkan dengan cara defuzzifikasi. Agregasi semua aturan dilakukan dengan menggunakan bantuan toolbox yang terdapat pada software matematika. Proses agregasi semua aturan dapat dilihat pada Lampiran 5.
4. Defuzzifikasi
Hasil agregasi semua aturan berupa himpunan fuzzy, oleh karena itu perlu dilakukan proses defuzzifikasi untuk memperoleh nilai berupa anggota himpunan
crisp (tegas). Metode yang digunakan pada kasus ini adalah metode centroid, yaitu dengan mengambil titik pusat himpunan fuzzy tersebut.
Gambar 13 Hasil Perhitungan dari Agregasi Semua Aturan Model Frekuensi Petir Dengan demikian dihasilkan bila T (suhu udara) sebesar 25.2 0C dan RH (kelembaban udara) sebesar 84 % dan A (kecepatan angin) sebesar 3.9 kn dan CH (curah hujan) sebear 26.3 mm dan P (penguapan) sebesar 7.3 mm, maka diperoleh prediksi frekuensi petir yang terjadi adalah 75.
13 Ukuran kesalahan
Nilai MAPE berdasarkan data dan model yang digunakan pada karya ilmiah ini adalah sebesar 17.2%. Nilai MAPE tersebut dapat mengindikasi seberapa besar kesalahan dalam menyusun model frekuensi petir. Ukuran kesalahan sebesar 17.2% merupakan dugaan model yang dinyatakan dalam bentuk persentase absolut kesalahan. Nilai keakuratan tersebut belum dapat dikatakan baik atau buruk dari suatu model karena belum ada acuan dari peneliti sebelumnya mengenai model frekuensi petir. Hasil perhitungan nilai MAPE dapat dilihat pada Lampiran 6.
SIMPULAN DAN SARAN
Simpulan
Logika fuzzy dapat digunakan dalam membuat model frekuensi petir, sehingga memungkinkan untuk memprediksi frekuensi petir ketika lightning counter mengalami gangguan. Pada karya ilmiah ini, didapatkan nilai MAPE sebesar 17.2% berdasarkan dengan data dan model frekuensi petir pada tahun 2012.
Saran
Pemodelan frekuensi petir yang lebih baik dapat menggunakan data lebih dari satu tahun agar dapat memperkecil ukuran kesalahan.
DAFTAR PUSTAKA
Akbar Akhmad. 2012. Pruning pada Fuzzy Decision Tree dalam Klasifikasi Data Iklim dan Titik Api di Daerah Tjilik Riwut, Palangkaraya, Kalimantan Selatan [skripsi]. Bogor (ID): Institut Pertanian Bogor.
Asdak C. 1995. Hidrologi dan Pengelolaan Daerah Aliran Sungai. Yogyakarta (ID): Gajah Muda University Press.
Byers JR. 1997. Element of Cloud Physics. Chicago (US): The University of Chicago Press.
Susilo Frans SJ. 2003. Himpunan dan Logika Kabur Serta Aplikasinya. Yogyakarta (ID): Graha Ilmu Yogyakarta.
Hidayat S. 2008. Ketika Petir Menyambar Tower BTS [internet]. [diacu 2013 November 10]. Tersedia pada: http://www.wordpress.com/2008/04/10/html. Husni M. 2002. Mengenal Bahaya Petir. Jurnal Meteorologi dan Geofisika Vol 3
No. 4 Oktober - Desember 2002. Jakarta (ID).
Kusumadewi S, Purnomo H. 2010. Analisis Logika Fuzzy untuk Mendukung Keputusan. Yogyakarta (ID): Graha Ilmu.
14
Marimin. 2002. Teori dan Aplikasi Sistem Pakar dalam Teknologi Manajerial. Bogor (ID): IPB Press – Pascasarjana IPB.
Maryati. 2013. Periset Jepang Teliti Petir di Bogor. Antara News. D0-18.
Septiadi Deni. 2012. Karakteristik Petir Terkait Curah Hujan Lebat di Wilayah Bandung, Jawa Barat [Skripsi]. Bogor (ID): Institut Pertanian Bogor.
Suharsono H. 1982. Beberapa Aspek Iklim Bogor [Skripsi]. Bogor (ID): Jurusan Agrometeorologi Departemen Ilmu Pengetahuan Alam Fakultas Pertanian Institut Pertanian Bogor.
Tjasyono Bayong HK. 2004. Klimatologi Edisi Ke-2. Bandung (ID): ITB Press. Zadeh L. 1996. Fuzzy Logic: Computing with words, IEEE Transactions on Fuzzy
20
Lampiran 1 Data iklim dan data frekuensi petir
DATA IKLIM 2012
Lokasi Stasiun Klimatologi Dramaga Bogor
Lintang 06o 31' LS
Bujur 106o 44' BT Elevasi 207 m
TGL
TEMPERATUR (0C)
RH (%)
ANGIN RATA-RATA CURAH
PENGUAPAN (mm)
CUACA KHUSUS
RATA-RATA MAX MIN
ARAH ANGIN
KEC. ANGIN (kn)
HUJAN
(mm) CUACA F. PETIR
Januari 6 24.1 29.4 22.4 94 NW 3.5 18.3 4.2 RA+TS 89
10 24.3 29.8 23 88 W 4.8 8 3.3 RA+TS 69
18 26 31.4 23.4 85 W 4 18.2 3.6 RA+TS 3
19 25.5 31.8 21.8 85 N 3.8 0 5 RA+TS 10
23 25.3 28.4 24.4 81 W 5.4 8.7 5.3 RA+TS 4
26 26.8 29.6 23.4 79 NW 2.5 7.5 2.4 RA+TS 174
Februari 1 25.5 30.2 22 88 N 2.5 8.8 4.4 RA+TS 13
3 24.2 30.2 22.5 91 NW 3.3 2.8 3.5 RA+TS 2
4 25.2 30.2 22.2 69 N 3.4 4.5 2.7 RA+TS 55
5 26 32.2 22.3 85 NW 3.7 - 2.5 TS 14
6 25.5 30.2 21.3 85 W 4.6 - 6.9 TS 3
8 26.6 33.4 22.8 86 N 4.2 6 6 RA+TS 1
10 25.3 32.6 22.2 84 N 4.1 29.5 5.3 RA+TS 88
11 25.2 32.6 21.9 84 N 3.9 26.3 7.3 RA+TS 76
12 26.5 31.4 22.8 86 N 4.1 53.3 6.7 RA+TS 6
TGL
TEMPERATUR (0C)
RH (%)
ANGIN RATA-RATA CURAH PENGUAPAN (mm)
CUACA KHUSUS
RATA-RATA MAX MIN
ARAH ANGIN
KEC. ANGIN (kn)
HUJAN
(mm) CUACA F. PETIR
16 26.2 31.4 23.8 85 N 4.7 1 5.3 RA+TS 155
19 24.4 28 22.4 92 NW 2.9 44.5 5.4 RA+TS 251
20 24.9 32 22.2 86 N 2.3 11 4.1 RA+TS 3
21 25.9 32 22.2 86 W 4.2 18.5 4.6 RA+TS 174
22 25.8 31.4 23.6 91 NW 2.8 0.2 5 RA+TS 7
23 26.6 32 23.2 87 N 3.9 42.2 5.9 RA+TS 725
24 26.7 32.2 23.6 88 N 3.3 9.8 4.9 RA+TS 41
25 26.3 33.4 23.8 87 N 3.6 - 5.6 TS 147
26 24.4 32 23.1 94 E 5.7 27.7 5.5 RA+TS 523
27 25.6 30.4 22 85 N 4.3 56.2 5.6 RA+TS 453
28 25.9 32.1 23.8 87 W 3.1 2.3 3.7 RA+TS 58
29 24.2 29.5 23.2 98 NW 3.5 10.8 3.6 RA+TS 855
Maret 1 19.2 29.8 23 89 N 3.4 34.5 3.9 RA+TS 88
2 26.1 32.4 22.6 81 NW 2.8 8.4 4 RA+TS 2
3 27.2 33.4 22.8 74 W 4.9 0.4 5.5 RA+TS 1
5 26.6 31.4 23.2 78 W 2.8 6.2 1.7 RA+TS 1
6 26.9 32 23.4 81 N 6.7 1.2 7.2 RA+TS 89
28 26.5 33 21.2 83 N 3.9 15.8 3.2 RA+TS 56
29 25.7 33 22.7 86 NW 3.8 3.8 5.1 RA+TS 2
30 25.8 31 23.4 87 N 3.5 8.5 4.9 RA+TS 136
31 25.7 32.4 22.4 88 N 3.9 - 3.9 TS 17
April 1 25.8 32.5 23 89 N 3.3 1 5.3 RA+TS 36
17
TGL
TEMPERATUR (0C)
RH (%)
19
TGL
TEMPERATUR (0C)
RH (%)
ANGIN RATA-RATA CURAH PENGUAPAN (mm)
CUACA KHUSUS
RATA-RATA MAX MIN
ARAH ANGIN
KEC. ANGIN (kn)
HUJAN
(mm) CUACA F. PETIR
10 25.4 34.6 22.2 80 N 4.9 - 5.8 TS 1
16 26.9 34 21.6 75 N 4.8 - 5.8 TS 7
Sumber: Stasiun Klimatologi Kelas 1 BMKG Dramaga, Bogor.
20
25
{
≤ ≥ 0
≤ ≤ ≤ ≤ 00 0
≤ ≤ 0
{
≤ 00 ≥ 00
≤ ≤ 0 ≤ ≤ 0
≤ ≤
{
≤ 0 ≥ 0
≤ ≤ ≤ ≤ 0
≤ ≤ 0
{
≤ ≥
≤ ≤ 0 ≤ ≤
≤ ≤
{
≤
≤ ≤
26
20
Lampiran 4 Contoh proses penggunaan fungsi implikasi
Aturan 6
Jika T (suhu udara) Sangat Rendah dan RH (kelembaban udara) Sedang dan A (kecepatan angin) Kuat dan CH (curah hujan) Sedang dan P (penguapan) Agak Rendah, maka PETIR F2 dengan frekuensi petir antara 55 sampai 70.
C
( C )
0 0 0 0 0
81 : µT SRe (25.2)=0 dan 82 : µRH S (84)=1 dan 83 : µA K (3.9)=0 dan 84 : µCH S (26.3)=0 dan 85 : µP ARe (7.3)=0 maka g : µPETIR F2 (76)=0
Aturan 23
Jika T (suhu udara) Rendah dan RH (kelembaban udara) Sedang dan A (kecepatan angin) Sedang dan CH (curah hujan) Sedang dan P (penguapan) Sangat Tinggi, maka PETIR F3 dengan frekuensi petir antara 70 sampai 85.
- C
( C )
0 0
3
81 : µT Re (25.2)=1 dan 82 : µRH S (84)=1 dan 83 : µA S (3.9)=1 dan 84 : µCH S (26.3)=0.67 dan 85 : µP ST (7.3)=1 maka g : µPETIR F3 (76)=0.67
Aturan 48
Jika T (suhu udara) Normal dan RH (kelembaban udara) Sedang dan A (kecepatan angin) Sedang dan CH (curah hujan) Sangat Ringan dan P (penguapan) Sedang, maka PETIR g ≤ x < 132.
C
( C )
0 0
81 : µT N (25.2)=0 dan 82 : µRH S (84)=0 dan 83 : µA S (3.9)=0 dan 84 : µCH SRi (26.3)=0 dan 85 : µP S (7.3)=1 maka g : µPETIR H1 (76)=0
4
Aturan 79
Jika T (suhu udara) Tinggi dan RH (kelembaban udara) Rendah dan A (kecepatan angin) Sangat Kuat dan CH (curah hujan) Ringan dan P (penguapan) Sangat Tinggi, maka PETIR G dengan frekuensi petir antara 85 sampai 99.
- C
( K C )
0 0 0 0 0
81 : µT T (25.2)=0 dan 82 : µRH Re (84)=0 dan 83 : µA SK (3.9)=0 dan 84 : µCH Ri (26.3)=0 dan 85 : µP ST (7.3)=1 maka g : µPETIR G (76)=0
5
Lampiran 5 Proses agregasi semua aturan model frekuensi petir
Input fuzzy Aplikasi fungsi implikasi (min)
6
Seluruh aturan sebanyak 81 diagregasi, maka hasil agregasi semua aturan (max) model frekuensi petir sebagai berikut.
7
RIWAYAT HIDUP
Penulis dilahirkan di Lamongan pada tanggal 23 Juli 1991 sebagai anak kedua dari lima bersaudara dari pasangan bapak Riyadi dan Ibu Siti Rohmah. Tahun 2009 penulis lulus dari SMAN 75 Jakarta dan pada tahun yang sama penulis diterima di Institut Pertanian Bogor melalui jalur USMI dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan di IPB, penulis aktif di salah satu Unit Kegiatan Mahasiswa (UKM) yang bergerak dalam bidang lingkungan hidup dan Adventural LAWALATA-IPB dan Himpunan Profesi GUMATIKA. Penulis pernah melakukan ekspedisi tentang Studi Pelestarian Kakatua Seram di Sekitar Kawasan Taman Nasional Manusela, Maluku Tengah pada tahun 2010 dan Studi Interaksi Masyarakat dengan Tumbuhan Hutan di Cagar Alam Biak Utara, Papua pada tahun 2011. Penulis juga pernah mengikuti PKM-P tentang Studi Karakteristik Habitat Penyu Hijau (Cheloniamydas) di Suaka Margasatwa Cikepuh, Sukabumi pada tahun 2012 dan Kajian Bioekologi Rafflesia rochussenii