Kriteria Laplace Pada Pencarian Solusi Program Linier Fuzzy

(1)

Elisabeth Aritonang : Kriteria Laplace Pada Pencarian Solusi Program Linier Fuzzy, 2009.

KRITERIA LAPLACE PADA PENCARIAN SOLUSI

PROGRAM LINIER FUZZY

SKRIPSI

ELISABETH ARITONANG

050803067

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(2)

KRITERIA LAPLACE PADA PENCARIAN SOLUSI

PROGRAM LINIER FUZZY

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

ELISABETH ARITONANG

050803067

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(3)

PERSETUJUAN

Judul : KRITERIA LAPLACE PADA PENCARIAN SOLUSI

PROGRAM LINIER FUZZY

Kategori : SKRIPSI

Nama : ELISABETH ARITONANG

Nomor Induk Mahasiswa : 050803067

Program Studi : SARJANA (S-1) MATEMATIKA

Diluluskan di

Medan, September 2009

Komisi Pembimbing:

Pembimbing I Pembimbing II

Dra. Esther S. M. Nababan, M.Sc Drs. Henry Rany Sitepu, M.Si NIP. 19610318 198711 2001 NIP. 19530303 198303 1002

Diketahui/Disetujui oleh:

Departemen Matematika FMIPA USU

(4)

PERNYATAAN

KRITERIA LAPLACE PADA PENCARIAN SOLUSI PROGRAM LINIER FUZZY

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan langsung yang masing-masing disebutkan sumbernya.

Medan, September 2009

(5)

PENGHARGAAN

Terima kasih kepada Yesus Kristus atas anugerah terindah dan kasih yang melimpah yang telah diberikan-Nya kepada penulis sehingga skripsi ini dapat diselesaikan sebaik mungkin.

(6)

ABSTRAK

Model pemrograman linier yang memiliki fungsi objektif fuzzy maupun kendala fuzzy dikenal sebagai pemrograman linier fuzzy. Pencarian solusi program linier fuzzy memerlukan langkah-langkah dimana pengambilan keputusan kriteria Laplace yaitu suatu kriteria pengambilan keputusan dibawah ketidakpastian akan digunakan dalam perumusan tujuan yang bersifat multiobjektif menjadi tujuan tunggal dan pada akhirnya menyelesaikannya dengan metode simpleks. Pada tulisan ini kriteria keputusan Laplace memberikan rata-rata nilai keanggotaan yang cukup besar pada persoalan program linier fuzzy yaitu sebesar µ = 0,72.

(7)

KRITERIA LAPLACE PADA PENCARIAN SOLUSI PROGRAM LINIER FUZZY

ABSTRACT

Linear programming model which has fuzzy objective function or fuzzy constraints are known as fuzzy linear programming model. In the case to find the solution of fuzzy linear programming (FLP) needs some steps where the decision criterion of Laplace will be used to formulate the multiobjective function to be single objective function, and then solve it with Simpleks method. In this research, Laplace decision criterion gives a large number of expected membership value in fuzzy linear programming problem that is µ = 0,72.

(8)

DAFTAR ISI

Halaman

Persetujuan ii

Penyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar x

BAB I PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 2

1.3 Pembatasan Masalah 2

1.4 Maksud dan Tujuan Penelitian 2

1.5 Metodologi Penelitian 3

1.6 Tinjauan Pustaka 3

BAB II LANDASAN TEORI 5

2.1 Program Linier 5

2.2 Metode Simpleks 8

2.3 Teori Himpunan Fuzzy 20

2.4 Fungsi Keanggotaan Fuzzy 21

2.4.1 Bilangan Fuzzy Triangular 21

2.4.2 Bilangan Fuzzy Trapezoidal 22

2.5 Himpunan Penyokong (Support set) 23

2.6 Nilai Alfa-Cut 24

2.7 Operasi-operasi pada Himpunan Fuzzy 25

2.7.1 Interseksi Himpunan Fuzzy 25

(9)

2.7.3 Komplemen (Negasi) 26

2.8 Masalah Keputusan 27

2.8.1 Kriteria Maximin Wald 28

2.8.2 Kriteria Optimis-pesimis Hurwicz 28

2.8.3 Kriteria Minimax Savage 29

2.8.4 Kriteria Prinsip ketidakcukupan Laplace 29

BAB III PEMBAHASAN 31

3.1 Program Linier Fuzzy 31

3.2 Fungsi Objektif Fuzzy dan Batasan Crisp 32 3.3 Usulan Langkah-langkah Pencarian Solusi Program Linier

Fuzzy dengan Pengambilan Keputusan Kriteria Laplace 34

3.4 Ilustrasi Numerik 36

BAB IV KESIMPULAN DAN SARAN 43

4.1 Kesimpulan 43

4.2 Saran 43

DAFTAR PUSTAKA

(10)

DAFTAR TABEL

TABEL Halaman

2.1 Bentuk tabel simpleks 8

2.2 Bentuk tabel awal simpleks sebelum pivoting 10

2.3 Bentuk tabel simpleks sesudah pivoting 13

2.4 Tabel simpleks untuk solusi awal 15

2.5 Tabel simpleks untuk solusi yang baru 16

2.6 Tabel simpleks untuk solusi akhir 17

2.7 Tabel simpleks untuk solusi awal 18

2.8 Tabel simpleks untuk solusi akhir 19

2.9 Bentuk umum tabel keputusan 27

3.1 Tabel simpleks awal 39

3.2 Tabel simpleks untuk solusi yang baru 40

3.3 Tabel simpleks untuk solusi yang baru-2 41

3.4 Tabel simpleks untuk solusi yang baru-3 41

(11)

DAFTAR GAMBAR

GAMBAR Halaman

2.1 Flowchart penyelesaian program linier

dengan metode simpleks 14

2.2 Bilangan fuzzy Triangular 21

2.3 Himpunan fuzzy : BERAT (kurva triangular) 22

2.4 Bilangan fuzzy Trapezoidal 23

2.5 Himpunan fuzzy : BERAT (kurva trapezoidal) 23

2.6 Support set untuk himpunan fuzzy BERAT 24

(12)

(13)

BAB I

PENDAHULUAN

1.1 Latar Belakang

Semua masalah dalam dunia nyata erat hubungannya dengan masalah manusia yang mengandung ketidakpastian. Dari kebutuhan untuk menggambarkan keadaan dunia nyata yang tidak pasti inilah muncul istilah fuzzy, yang pertama kali dikemukakan oleh Zadeh (1962). Teori ini dapat digunakan untuk menangani ketidakpastian dalam masalah dunia nyata. Teori ini memperkenalkan himpunan yang keanggotaannya dinyatakan dengan derajat keanggotaan tertentu dalam selang tertutup antara nol dan satu [0,1].

Program Linier Fuzzy adalah Program Linier yang dinyatakan dengan fungsi objektif dan fungsi kendala yang memiliki parameter fuzzy dan ketidaksamaan fuzzy. Tujuan dari program linier fuzzy adalah mencari solusi yang dapat diterima berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala.

Program linier fuzzy membutuhkan langkah-langkah dalam pencarian solusinya dimana pada pendekatan program linier fuzzy menjadi program linier biasa dengan fungsi objektif tunggal, digunakan kriteria Maximin.

Pada tulisan ini akan digunakan kriteria Laplace of insufficient reason criterion pada langkah pencarian solusinya untuk menggantikan kriteria Maximin, dimana kriteria Laplace dan kriteria Maximin sama-sama kriteria pengambilan keputusan dibawah ketidakpastian. Hanya saja kriteria Laplace mengasumsikan bahwa setiap kejadian memiliki nilai peluang untuk terjadi namun apabila informasi untuk kejadian itu tidak mencukupi maka peluang untuk setiap kejadian diasumsikan sama.

Kriteria Laplace ini dapat dituliskan sebagai berikut :

Jika peluang akan keadaan sesungguhnya/keadaan masa depan tidak

diketahui, asumsikan bahwa mereka memiliki kesempatan yang sama untuk muncul

atau terjadi.

Nilai peluang untuk kejadian dari s1, s2, s3, ...,sn tidak diketahui, maka tidak diperoleh

(14)

kejadian-Elisabeth Aritonang : Kriteria Laplace Pada Pencarian Solusi Program Linier Fuzzy, 2009.

kejadian tersebut akan berbeda. Sehingga kesimpulannya nilai peluang setiap state dianggap sama, dimana P{s1}=P{s2}=. . . = P{sn}=

n

1

. Diberikan v

( )

a_i,s_j yang menyatakan perolehan, maka pilihan terbaik dapat didefinisikan sebagai berikut :

i a

max

( )

   





∑

= n

j vai sj

n 1 ,

1

Dimana

n

1

adalah peluang bahwa s_j (j = 1,2,3,...,n) terjadi.

1.2 Perumusan Masalah

Permasalahan dalam penelitian ini adalah bagaimana menyelesaikan suatu masalah program linier fuzzy dengan mentransformasikan kriteria pengambilan keputusan Laplace pada langkah-langkah pencarian solusinya.

1.3 Pembatasan Masalah

Tulisan ini dibatasi untuk masalah program linier fuzzy dengan fungsi objektif fuzzy dan kendala crisp. Sedangkan fungsi keanggotaannya dibatasi pada bilangan fuzzy triangular untuk parameter fuzzy yang terdapat pada fungsi objektif.

1.4 Maksud dan Tujuan Penelitian

(15)

1.5 Metodologi Penelitian

Penelitian ini dilakukan dalam bentuk studi literatur dari berbagai buku teks dan jurnal. Usulan langkah-langkah pencarian solusi bagi program linier fuzzy adalah sebagai berikut :

Langkah 1 : Menentukan nilai-nilai berikut :

z1min = min (c*-c-) x

z1max = max (c*-c-) x

z2min = min c* x

z2max = max c* x

z3min = min (c+- c*)x

z3max = max (c+- c*)x

Langkah 2 : Mendefinisikan fungsi keanggotaan segitiga dengan menggunakan fungsi-fungsi objektif diatas.

Langkah 3 : Mendefinisikan ketiga fungsi keanggotaan diatas dengan pengambilan keputusan kriteria Laplace.

Langkah 4 : Mendefinisikan fungsi tujuan dengan kendala adalah penggabungan dari langkah-3 dengan kendala awal permasalahan.

Langkah 5 : Penyelesaian dengan menggunakan Metode Simpleks (Big M Method).

1.6 Tinjauan Pustaka

Zimmerman (1991), dalam tulisannya mengemukakan tujuan dan batasan-batasan dipresentasikan dengan himpunan fuzzy dan pembuat keputusan dapat menetapkan sebuah tingkat ide untuk nilai dari fungsi objektif yang ingin dicapai. Selain itu dibicarakan juga tentang bentuk umum model program linier fuzzy.

(16)

Sri Kusumadewi (2002), dalam tulisannya mengemukakan jika diasumsikan bahwa keputusan linier programming akan dibuat pada lingkungan fuzzy maka model program linier klasik akan mengalami sedikit perubahan yaitu :

1. Bentuk imperatif pada fungsi objektif tidak lagi benar-benar “maksimum” atau “minimum”, karena adanya beberapa hal yang perlu mendapat pertimbangan dalam suatu sistem.

(17)

BAB II

LANDASAN TEORI

Pada bab ini akan dibicarakan beberapa konsep dan teorema tanpa bukti yang akan digunakan pada bab pembahasan.

2.1 Program Linier

Program linier merupakan model umum yang dapat digunakan dalam pemecahan masalah pengalokasian sumber-sumber yang terbatas secara optimal. Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau menentukan tingkat setiap kegiatan yang akan dilakukannya, dimana masing-masing kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas.

Secara sederhana dapat diambil contoh bagian produksi suatu perusahaan yang dihadapkan pada masalah penentuan tingkat produksi masing-masing jenis produk dengan memperhatikan batasan faktor-faktor produksi : mesin, tenaga kerja, bahan mentah, dan sebagainya untuk memperoleh tingkat keuntungan maksimal atau biaya yang minimal.

Dalam memecahkan masalah diatas, program linier menggu nakan model matematis. Sebutan " linier " berarti bahwa semua fungsi matematis yang disajikan dalam model ini haruslah fungsi-fungsi linier.

(18)

Menurut Nasendi ( 1985, p13-14 ), agar dapat merumuskan suatu permasalahan ke dalam program linier, maka ada syarat-syarat yang harus dipenuhi yaitu :

1. Tujuan

Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut Fungsi tujuan.

Fungsi tujuan tersebut dapat berupa dampak positif, manfaat-manfaat, keuntungan-keuntungan, dan kebaikan-kebaikan yang ingin dimaksimumkan, atau dampak negatif, kerugian-kerugian, risiko-risiko, biaya-biaya, jarak, waktu, dan sebagainya yang ingin diminimumkan.

2. Alternatif Perbandingan

Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan ; misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu terlambat dan biaya terendah; atau antara alternatif padat modal dengan padat karya; atau antara kebijakan A dengan B; atau antara proyeksi permintaan tinggi dengan rendah; dan seterusnya.

3. Sumber Daya

Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas. Misalnya keterbatasan waktu, keterbatasan biaya, keterbatasan tenaga, keterbatasan luas tanah, keterbatasan ruangan, dan lain-lain. Keterbatasan dalam sumber daya tersebut dinamakan sebagai kendala atau syarat ikatan.

4. Perumusan Kuantitatif

Fungsi tujuan dan kendala tersebut harus dapat dirumuskan secara kuantitatif dalam apa yang disebut model matematika.

5. Keterkaitan Peubah

(19)

Model Dasar

Model dasar atau model baku PL (Program Linier) dapat dirumuskan sebagai berikut :

Fungsi tujuan :

Maksimalkan atau minimalkan : n nx

c x

c x c

Z = ₁ ₁+ ₂ ₂ +...+ (2.1)

Kendala :

1 1

2 12 1

11x a x ... a x atau b

a + + + n n ≤ ≥

2 2

2 22 1

21x a x ... a x atau b

a + + + _n _n ≤ ≥

. . . . (2.2)

. . . .

m n

mn m

m x a x a x atau b

a ₁ ₁ + ₂ ₂ +...+ ≤ ≥

, 0 ≥ j

x untuk j =1,2,...,n (syarat non-negatif) (2.3)

Bentuk diatas dapat juga ditulis sebagai berikut : Fungsi tujuan :

Maksimumkan atau minimumkan :

∑

₌

= n

j j jx

c Z

1

(2.4)

Kendala :

i n

j j

ijx atau b

a ≤ ≥

∑

₌₁ untuk i=1,2,...,m (2.5) Dan x_j ≥0 , j =1,2,...,n (2.6)

Untuk : j

c = Parameter yang dijadikan kriteria optimisasi, atau koefisien peubah pengambilan keputusan dalam fungsi tujuan.

j

x = Peubah pengambilan keputusan atau kegiatan (yang ingin dicari; yang tidak diketahui).

ij

(20)

i

b = Sumber daya yang terbatas, yang membatasi kegiatan atau usaha yang bersangkutan; disebut konstanta atau ‘ nilai sebelah kanan ‘ dari kendala ke-i.

Z = Nilai skalar kriteria pengambilan keputusan; suatu fungsi tujuan .

Model dasar yang dirumuskan dalam (2.1)-(2.3) atau (2.4)-(2.6) dapat diformulasikan lagi dalam notasi matriks, yaitu :

Fungsi tujuan :

Maksimumkan atau minimumkan :

X C'

=

Z (2.7)

Kendala :

b

AX≤atau≥ (2.8)

Dan X≥0

Dengan C,X,0∈Rn,b∈Rm,A∈Rmxn (2.9)

2.2 Metode Simpleks

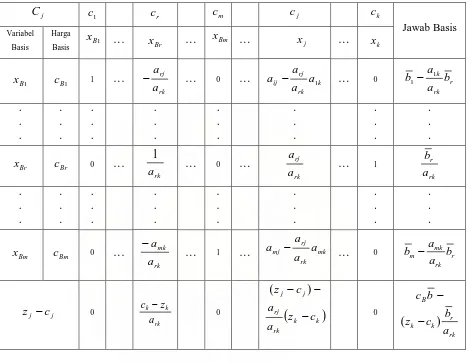
Tabel 2.1 Bentuk tabel simpleks

j

C c1 . . . ck . . . cn

Jawab Basis Variabel Basis Harga Basis 1 B

x . . . x_k . . . x_n

1 B

x c_B₁ a₁₁ . . . a₁_k . . . a₁_n b₁

. . . . . . . . . . . . . . . . . . Br

x c_Br a_r₁ . . .

rk

a . . .

rn

a b_r

. . . . . . . . . . . . . . . . . . Bm

x c_Bm a_m₁ . . .

mk

a . . .

mn

a b_m

j j c

(21)

Sebelum menyelesaikan suatu tabel simpleks terlebih dahulu menginisialisasikan dan merumuskan suatu persoalan keputusan ke dalam model matematik persamaan linier, caranya adalah sebagai berikut :

1. Konversikan semua ketidaksamaan menjadi persamaan.

Agar persamaan garis batasan memenuhi persyaratan penyelesaian pada daerah kelayakan (feasible) maka untuk model program linier diubah menjadi suatu model yang sama dengan menambahkan variabel slack, surplus dan variabel buatan (artificial variable) pada tiap batasan (constraint) serta memberi harga nol kepada tiap koefisien

c -nya. Batasan dapat dimodifikasi sebagai berikut :

1) Untuk batasan bernotasi (≤) dapat dimodifikasi kepada bentuk persamaan dengan menambahkan variabel slack kedalamnya.

2) Untuk batasan bernotasi (≥) dapat dimodifikasi kepada bentuk persamaan dengan mengurangkan variabel surplus dan kemudian menambahkan variabel buatan (artificial variabel) kedalamnya.

3) Untuk batasan bernotasi (=) diselesaikan dengan menambahkan variabel buatan (artificial variabel) kedalamnya.

Dengan penambahan variabel buatan ini akan merusak sistem batasan, hal ini dapat diatasi dengan membuat suatu bilangan besar M sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Jika persoalan maksimal maka dibuat – M sebagai harga, dan jika persoalan minimal dibuat +M sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M method).

Penambahan variabel slack dan variabel buatan (artificial variable) pada tiap batasan (constraint) untuk persoalan maksimal dapat dirumuskan sebagai berikut :

Maksimalkan :

∑

₌ − ₌ ₊

= m

m i

i n

j j

jx M B

c Z

1

1 ₁

(2.10)

Dengan batasan :

i i n

j j

ijx x b

a + =

∑

₌₁ , i=1,2,...,m₁ (untuk batasan bernotasi ≤) (2.11)

i i n

j j

ijx B b

a + =

(22)

Elisabeth Aritonang : Kriteria Laplace Pada Pencarian Solusi Program Linier Fuzzy, 2009. i i j n j j

ijx x B b

a − + =

∑

₌₁ , i=m₁ +m₂ +1,...,m (untuk batasan bernotasi ≥)(2.13) 0 , 0 , 0 ,

0 ≥ ≥ ≥

≥ i i i

j x B b

x untuk semua harga idan j

m m i b B m i b x n j x i i i i j ,..., 1 , ,..., 2 , 1 , ,..., 2 , 1 , 0 1 1 + = = = = = =

2. Menyusun persamaan-persamaan di dalam tabel awal simpleks

Tabel 2.2 Bentuk tabel awal simpleks sebelum pivoting

j

C c₁ c_r c_m c_j c_k Jawab

Basis Variabel Basis Harga Basis 1 B x ... Br x ... Bm

x ... xj ... xk

1 B

x cB1

1 ... 0 ... 0 ...

j

a₁ ...

k

a₁ b₁

. . . . . . . . . . . . . . . . . . . . . . . . Br

x c_Br 0 ... 1. ... 0 ... a_rj ... a_rk b_r

. . . . . . . . . . . . . . . . . . . . . . . . Bm

x cBm 0 ... 0 ... 1 ... amj ... amk bm

j j c

z − 0 0 0 z_j −c_j z_k −c_k c_Bb

Langkah-langkah yang digunakan untuk menyelesaikan suatu tabel simpleks adalah sebagai berikut :

Langkah 1 : Mengecek nilai optimal imbalan.

(23)

* Untuk persoalan minimal : z_k −c_k = maksimal{zj −cj:j∈R}

Jika zk −ck ≤0 maka selesai, berarti jawab atau solusi sudah optimal.

Harga-harga imbalan (z_j −c_j) dapat diperoleh dengan rumus :

j j c

z − = _j

m j

ij Bia c

c −

∑

₌₁ (2.14)

Untuk : c_j = Harga dari semua variabel dalam z .

ij

a = Koefisien dari semua variabel dalam sistem batasan.

Bi

c = Harga dari variabel basis.

Langkah 2 : Menentukan variabel yang akan masuk dalam basis.

Untuk persoalan maksimalkan jika terdapat beberapa z_j −c_j ≤0 maka kolom yang menjadi kolom pivot adalah kolom dengan z_j −c_j terkecil, dan variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk ke dalam basis. Untuk persoalan minimal jika terdapat beberapa zj −cj ≥0 maka kolom yang menjadi kolom pivot adalah kolom dengan zj −cj terbesar, dan variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk ke dalam basis.

Jika pada baris z_j −c_j terdapat lebih dari satu kolom yang mempunyai nilai negatif yang angkanya terbesar dan sama pada persoalan maksimal atau terdapat lebih dari satu kolom yang mempunyai nilai positif terbesar dan sama pada persoalan minimal maka terdapat dua kolom yang bisa terpilih menjadi kolom pivot. Untuk mengatasi hal ini, dapat dipilih salah satu dari zj −cj secara sembarang.

Langkah 3 : Menentukan variabel yang akan keluar dari basis.

Menetapkan variabel yang keluar dari basis yaitu :

   



 _>

=min : ik 0

ik i rk

r

a a

b imum a

(24)

Variabel yang sehubungan dengan baris pivot yang demikian adalah variabel yang keluar dari basis.

Jika terdapat dua baris atau lebih nilai rk

r

a b

maka ada beberapa baris yang dapat terpilih sebagai baris pivot. Dapat dipilih baris pivot secara bebas diantara keduanya dan hasilnya akan sama.

Langkah 4 : Menyusun tabel simpleks baru .

Untuk menyusun tabel simpleks yang baru, maka harus mencari koefisien elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat dicari dengan menghubungkan kolom pivot dengan baris pivot sedemikian rupa sehingga titik potong kedua pivot ini menunjukkan koefisien, yang disebut elemen pivot.

Koefisien-koefisien baris pivot baru dapat dicari dengan menggunakan rumus sebagai berikut :

rk rj

a a

(2.15) Untuk menghitung nilai baris baru lainnya dilakukan dengan menggunakan rumus sebagai berikut :

ik rk rj ij a

a a

a − (2.16)

Langkah 5 : Mengecek nilai optimal imbalan dari tabel simpleks yang baru.

(25)

Tabel 2.3 Bentuk tabel simpleks sesudah pivoting

j

C c₁ c_r c_m cj ck

Jawab Basis Variabel Basis Harga Basis 1 B

x _{. . .}

Br

x . . . xBm _{. . .}

j

x . . . x_k

1 B

x cB1 1 . . .

rk rj

a a

− . . . 0 . . . _k

rk rj ij a

a a

a − ₁ . . . 0 _r

rk k b a a b 1 1− . . . . . . . . . . . . . . . . . . . . . . . . Br

x cBr 0 . . .

rk

a

1

. . . 0 . . .

rk rj

a a

. . . 1

rk r a b . . . . . . . . . . . . . . . . . . . . . . . . Bm

x c_Bm 0 . . .

rk mk

a a −

. . . 1 . . . mk rk rj

mj a

a a

a − _{. . .} ₀

r rk mk m b a a b − j j c

z − 0

rk k k a z c − 0 − − )

(z_j c_j

(26)

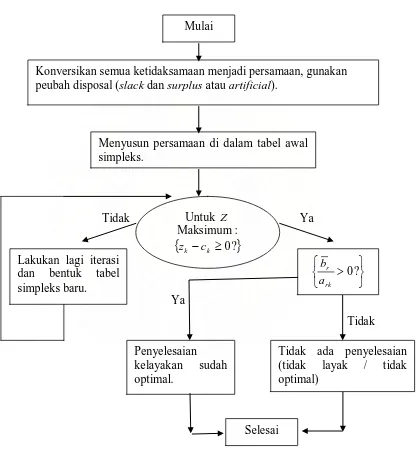
Langkah-langkah penyelesaian Program Linier dengan metode simpleks dapat digambarkan dalam bentuk flowchart berikut :

Tidak Ya

Ya

Tidak

Gambar 2.1 Flowchart penyelesaian Program Linier dengan metode simpleks

Mulai

Konversikan semua ketidaksamaan menjadi persamaan, gunakan peubah disposal (slack dan surplus atau artificial).

Menyusun persamaan di dalam tabel awal simpleks.

Untuk Z

Maksimum :

{

z_k −c_k ≥0?

}

Lakukan lagi iterasi

dan bentuk tabel

simpleks baru. 

  

  _>

? 0 rk

r

a b

Penyelesaian

kelayakan sudah optimal.

Tidak ada penyelesaian (tidak layak / tidak optimal)

(27)

Contoh 2.1 :

Maksimumkan : Z =8x₁+9x₂ +4x₃

Kendala : x₁ +x₂ +2x₃ ≤2 3 2

1 3 4

2x + x + x ≤3 3 2

1 6 2

7x + x + x ≤8 0 , , 2 3 1 x x ≥

x

Agar persamaan diatas memenuhi persyaratan penyelesaian dalam daerah kelayakan (feasible), maka pada sisi kiri persamaan batasan ditambahkan variabel slack. Sehingga bentuk bakunya sebagai berikut :

Maksimumkan : Z =8x₁+9x₂ +4x₃ +0x₄ +0x₅ +0x₆

Kendala : x₁ +x₂ +2x₃+x₄ = 2

3 2

1 3 4

2x + x + x +x5 = 3 3

2

1 6 2

7x + x + x +x₆ = 8 0 , , , ,

, 2 3 4 5 6 1 x x x x x ≥

x

Model diatas dapat dibawa ke dalam tabel simpleks sebagai berikut :

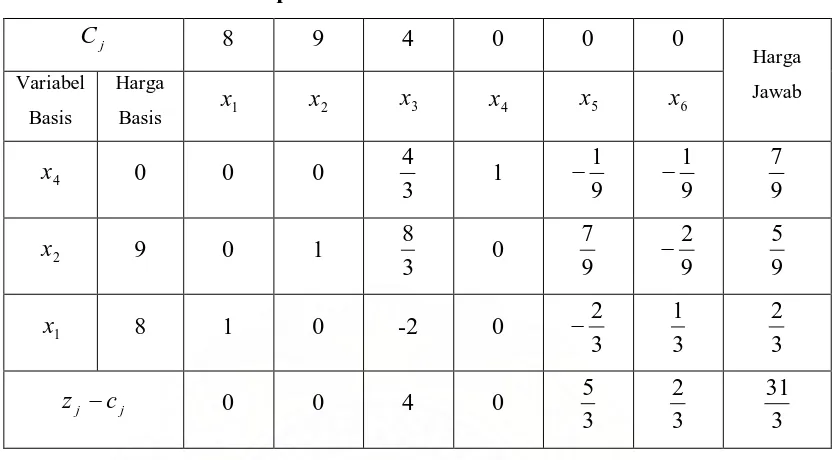
Tabel 2.4 Tabel simpleks untuk solusi awal

j

C 8 9 4 0 0 0

Harga

Jawab Variabel

Basis

Harga

Basis

1

x x ₂ x ₃ x ₄ x ₅ x ₆

4

x 0 1 1 2 1 0 0 2

5

x 0 2 3 4 0 1 0 3

6

x 0 7 6 2 0 0 1 8

j j c

(28)

Dari tabel 2.4 diatas, tampak bahwa penyelesaian optimal belum dicapai dimana harga j

j c

z − terkecil dari tabel diatas adalah -9, sehingga variabel yang masuk basis adalah variabel x . Kolom variabel 2 x menjadi kolom pivot dan perhitungan untuk indeks 2 (I) adalah :

      ₌ ₌ ₌

= 1,33

6 8 , 1 3 3 , 2 1 2 min I

Diperoleh I_min=1, maka variabel yang meninggalkan basis adalah variabel x ₅

kemudian digantikan dengan variabel x . Angka kunci (elemen pivot) yang diperoleh ₂

= 3, maka tabel simpleks yang baru adalah :

Tabel 2.5 Tabel simpleks untuk solusi yang baru

j

C 8 9 4 0 0 0 Harga

Jawab Variabel Basis Harga Basis 1

x x 2 x 3 x 4 x 5 x 6

4

x 0

3 1 0 3 2 1 3 1

− 0 1

2

x 9

3

2 1

3

4 0

3

1 0 1

6

x 0 3 0 -6 0 -2 1 2

j j c

z − -2 0 8 0 3 0 9

Dari tabel 2.5 diatas tampak bahwa penyelesaian optimal belum tercapai dimana harga j

j c

z − terkecil dari tabel diatas adalah -2, sehingga variabel yang masuk basis adalah variabel x . Kolom variabel ₁ x menjadi kolom pivot dan perhitungan untuk indeks (I) ₁

adalah :           = = =

= 0,67

3 2 ; 5 , 1 3 2 1 ; 3 3 1 1 min I

Diperoleh I_min= 0,67 maka variabel yang meninggalkan basis adalah variabel x ₆

(29)

Tabel 2.6 Tabel simpleks untuk solusi akhir

j

C 8 9 4 0 0 0

Harga

Jawab Variabel

Basis

Harga

Basis x 1 x 2 x 3 x 4 x 5 x 6

4

x 0 0 0

3 4 1 9 1 − 9 1 − 9 7 2

x 9 0 1

3 8 0 9 7 9 2 − 9 5 1

x 8 1 0 -2 0

3 2 − 3 1 3 2 j j c

z − 0 0 4 0

3 5 3 2 3 31

Dari tabel 2.6 tidak ada lagi z_j −c_j<0, dengan demikian telah dicapai penyelesaian optimal yaitu :

0 56 , 0 9 5 67 , 0 3 2 3 2 1 = = = = = x x x

( )

0 4 9 5 9 3 2

8 +

     +       =

(30)

Contoh 2.2 :

Maksimumkan : Z =3x₁+2x₂ +x₃

Kendala : 3x₁ +4x₂ +5x₃≥5 3 2 1 6

2x + x +x ≤6 3 2

1 x 5x

x + + ≥7

0 , , 2 3 1 x x ≥

x

Agar persamaan diatas memenuhi persyaratan penyelesaian dalam daerah kelayakan (feasible), maka pada sisi kiri persamaan batasan ≤ ditambahkan variabel slack sedangkan untuk persamaan batasan ≥ dikurangkan dengan variabel surplus dan ditambah dengan variabel buatan (artificial variable). Sehingga bentuk bakunya sebagai berikut :

Maksimumkan : Z =3x₁+2x₂ +x₃ +0x₄ +0x₅ +0x₆ −Mx₇ −Mx₈

Kendala : 3x₁+4x₂ +5x₃ −x₄ +x₇ = 5 3

2 1 6

2x + x +x +x6 = 6 8

5 3 2

1 x 5x x x

x + + − + = 7 x1,x2,x3,x4,x5,x6,x7,x8 ≥0

[image:30.595.109.499.275.494.2]

Model diatas dapat dibawa ke dalam tabel simpleks sebagai berikut :

Tabel 2.7 Tabel simpleks untuk solusi awal

j

C 3 2 1 0 0 0 -M -M

Harga

Jawab Variabel

Basis

Harga

Basis x 1 x 2 3

x x ₄ x 5 x 6 x 7 x 8

6

x 0 3 4 5 -1 0 0 1 0 5

7

x -M 2 6 1 0 0 1 0 0 6

8

x -M 1 1 5 0 -1 0 0 1 7

j j c

(31)

[image:31.595.108.524.146.560.2]

Cara perhitungan tabel simpleks ini sama dengan cara perhitungan tabel simpleks pada contoh 2.1.

Tabel 2.8 Tabel simpleks untuk solusi akhir

j

C 3 2 1 0 0 0 -M -M

Harga

Jawab Variabel

Basis

Harga

Basis x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8

3

x 1 3,24 6,05 1 0 0 1,01 0 0 6,45

5

x 0 5,35 29,41 0 0 1 5,08 0 -1 23,38

4

x 0 3,72 26,35 0 1 0 -4,04 -1 0 25,33

j j c

z − 0,24 4,05 0 0 0 1,01 M M 6,44

Dari tabel 2.8 tidak ada lagi z_j −c_j<0, dengan demikian telah dicapai penyelesaian optimal yaitu :

45 , 6 3 =

x

38 , 23 5 =

x

33 , 25 4 =

x

0 8 7 6 2

1 =x = x =x = x =

x

) 45 , 6 ( 1 ) 0 ( 2 ) 0 (

3 + +

=

(32)

2.3 Teori Himpunan Fuzzy

Himpunan A dikatakan crisp jika sebarang anggota-anggota yang ada pada himpunan A tersebut dikenakan suatu fungsi, akan bernilai 1 yakni jika a∈A maka fungsi a=1. Namun jika a∉A, maka nilai fungsi yang dikenakan pada a adalah 0. Nilai fungsi yang dikenakan pada sebarang anggota himpunan A dikatakan sebagai nilai keangotaan. Jadi pada himpunan crisp, hanya mempunyai 2 nilai keanggotaan yaitu 0 atau 1. Tetapi pada himpunan fuzzy, nilai keanggotaan dari anggota-anggota nya tidak hanya 1 dan 0 saja. Tapi berada pada interval tertutup [0,1]. Dengan kata lain himpunan A dikatakan fuzzy selama fungsi µ:A→

[ ]

0,1.

Misalkan diketahui klasifikasi dari harga sebuah barang sebagai berikut : MURAH harga < 35.000

STANDARD 35.000 ≤ harga ≤ 55.000 MAHAL harga > 55.000

(33)

2.4 Fungsi Keanggotaan Fuzzy

Sebuah himpunan fuzzy A dari bilangan riil ℜ didefinisikan oleh fungsi keanggotaannya (dinotasikan oleh A)

A

µ : ℜ [ 0,1 ]

Jika x∈ℜ maka µA( x ) dikatakan sebagai derajat keanggotaan x dalam A. Himpunan fuzzy dalam ℜ disebut normal jika terdapat x∈ℜ sehingga µA ( x ) =1. Himpunan fuzzy A adalah himpunan fuzzy dari bilangan riil dengan normal, (fuzzy) convex dan fungsi keanggotaan yang kontinu dari penyokong yang terbatas.

2.4.1 Bilangan Fuzzy Triangular

Sebuah himpunan fuzzy A disebut bilangan fuzzy triangular dengan nilai tengah a , sebelah kiri α > 0, dalam ℜ disebut convex jika A adalah unimodal (sebagai sebuah fungsi). Bilangan fuzzy dan sebelah kanan β > 0.

Fungsi keanggotaannya adalah sebagai berikut :

( )

  

   

 

− −

=

0 1 1

β α

µ x a

x a

x

A jika,

lainnya a x a

a x a

β α

+ ≤ ≤

≤ ≤ −

(2.17)

Penyokong A adalah (a−α,a+β). Bilangan fuzzy triangular dengan nilai tengah a dilihat sebagai nilai kwantitas fuzzy.

“ x dekat terhadap a “ atau “ x hampir sama dengan a “.

(34)

[image:34.595.122.449.212.542.2]

a−α a a+β x

Gambar 2.2 Bilangan Fuzzy Triangular

Contoh 2.2 :

Fungsi keanggotaan triangular untuk himpunan BERAT pada variabel berat badan (kg) seperti terlihat pada gambar 2.3.

BERAT

µ [23] = (23-15)/(25-15) = 8/10

= 0,8

BERAT µ

[ ]

x 1

0,8

0 15 23 25 35 x

Gambar 2.3 Himpunan fuzzy : BERAT (kurva triangular)

2.4.2 Bilangan Fuzzy Trapezoidal

Sebuah himpunan fuzzy A disebut bilangan fuzzy trapezoidal dengan interval toleransi [ a, ], sebelah kiri b α dan kanan β.

Fungsi keanggotaannya adalah sebagai berikut :

( )

  

   

 

− −

=

0 1 1 1

β α µ

b x

x a

x

A jika,

lainnya b x a

b x a

a x a

β α

+ ≤ ≤

≤ ≤

≤ ≤ −

[image:34.595.184.394.632.743.2]

(35)

Penyokong A adalah ( a−α,b+β ). Bilangan fuzzy trapezoidal dapat dilihat sebagai kwantitas fuzzy.

“ x mendekati pada interval [ a, ] “. b

µ(x) 1

a−α a b b+β x Gambar 2.4 Bilangan Fuzzy Trapezoidal Contoh 2.3 :

Fungsi keanggotaan trapezoidal untuk himpunan BERAT pada variabel berat badan (kg) terlihat seperti gambar 2.5.

BERAT

µ [32] = (35-32)/(35-27) = 3/8

= 0,375

µ(x) BERAT

1

0,375

[image:35.595.152.397.134.277.2]

0 15 24 27 32 35 x

Gambar 2.5 Himpunan fuzzy : BERAT (kurva trapezoidal)

2.5 Himpunan Penyokong ( Support Set )

[image:35.595.144.439.342.568.2]

(36)

disebut dengan himpunan penyokong (support set). Hal ini penting untuk menginterpretasikan dan mengatur daerah fuzzy yang dinamis.

BERAT 1

µ(x)

30 35 40 45 50 x

[image:36.595.116.446.186.434.2]

Support set

Gambar 2.6 Support set untuk himpunan fuzzy BERAT

2.6 Nilai Alfa – Cut

Salah satu teknik yang erat hubungannya dengan himpunan penyokong adalah himpunan level-alfa (α-cut). Level-alfa ini merupakan nilai ambang batas domain yang didasarkan pada nilai keanggotaan untuk tiap-tiap domain. Himpunan ini berisi semua nilai domain yang merupakan bagian dari himpunan fuzzy dengan nilai keanggotaan lebih besar atau sama dengan α .

BERAT µ(x)

1

α =0,5

30 34 40 45 50 x

[image:36.595.150.431.565.723.2]

(37)

α - cut lemah dapat dinyatakan sebagai : µ_A

( )

x ≥α α -cut kuat dapat dinyatakan sebagai : µ_A

( )

x >α

2.7 Operasi – operasi Pada Himpunan Fuzzy

Seperti halnya himpunan biasa, ada beberapa operasi yang didefinisikan secara khusus untuk mengkombinasi dan memodifikasi himpunan fuzzy. Berikut ini beberapa operasi logika fuzzy yang didefinisikan oleh Zadeh :

Interseksi : µ_A_∩_B =min

(

µ_A

[ ] [ ]

x,µ_B y

)

Union : µ_A_∪_B =max

(

µ_A

[ ] [ ]

x,µ_B y

)

(2.19) Komplemen : µ_A'

( )

x =1−µA

( )

x

Karena himpunan fuzzy tidak dapat dibagi dengan tepat, seperti halnya pada himpunan crisp, maka operasi-operasi ini diaplikasikan pada tingkat keanggotaan. Suatu elemen dikatakan menjadi anggota himpunan fuzzy jika :

1. Berada pada domain himpunan tersebut. 2. Nilai kebenaran keanggotaannya ≥0 3. Berada diatas α - cut yang berlaku.

2.7.1 Interseksi Himpunan Fuzzy

Pada himpunan crisp, interseksi antara dua himpunan berisi elemen-elemen yang berada pada kedua himpunan. Hal ini ekivalen dengan operasi aritmatik atau logika AND.

Pada logika fuzzy konvensional, operator AND diperlihatkan dengan derajat keanggotaan minimal antar kedua himpunan. Berikut adalah aturan dasar Zadeh untuk interseksi fuzzy, daerah diantara dua himpunan ditentukan oleh aplikasi operasi tersebut :

[ ] [ ]

(

A x B y

)

B

A µ µ

(38)

2.7.2 Union Himpunan Fuzzy

Union dari dua himpunan dibentuk dengan menggunakan operator OR. Pada logika fuzzy konvensional, operator OR diperlihatkan dengan derajat keanggotaan minimal antar kedua himpunan. Operator fuzzy OR jarang sekali digunakan dalam pemodelan sistem, karena operasi OR pada dasarnya dapat dibentuk sebagai gabungan dari 2 proposisi fuzzy.

Sebagai contoh :

If x is A OR y is B then z is C

Dapat dibentuk :

If x is A then z is C If y is B then z is C

Pada kedua kasus, kekuatan nilai keanggotaan antara konsekuen z dan daerah fuzzy

C oleh max

(

µA

[ ] [ ]

x,µB y

)

. Seperti halnya pada operator AND, dapat juga

memvisualisasikan proses ini sebagai peng-OR-an bit pada vector Boolean yang merepresentasikan kebenaran dari ekspresi himpunan karakteristik untuk tiap-tiap kategori.Untuk membangun himpunan fuzzy menggunakan union dari dua himpunan berikut digunakan aturan Zadeh dasar untuk union fuzzy, ditentukan oleh operasi sebagai berikut :

[ ] [ ]

(

A x B y

)

B

A µ µ

µ _∪ =max , (2.21)

2.7.3 Komplemen (Negasi)

Komplemen atau negasi suatu himpunan A berisi semua elemen yang tidak berada di A dan direpresentasikan dengan :

( )

x A

( )

x

A µ

(39)

Pada logika fuzzy, komplemen dihasilkan dengan cara menginversikan fungsi kebenaran untuk tiap-tiap titik pada himpunan fuzzy tersebut.

2.8 Masalah Keputusan

Banyak masalah keputusan dapat disajikan dalam bentuk tabel keputusan seperti dibawah ini:

Tabel 2.9 Bentuk umum tabel keputusan Akibat

Kondisi Masa Depan 1

S S ₂ . . . S _n

Tindakan

1

a x ₁₁ x ₁₂ . . . x₁_n

2

a x ₂₁ x ₂₂ . . . x₂_n

. .

m

a x _m₁ x_m₂ . . . x_mn

Ide yang mendasari hal ini adalah akibat dari sebarang tindakan ditentukan tidak hanya oleh tindakan itu sendiri tetapi juga oleh jumlah faktor-faktor luar.Faktor-faktor luar ini adalah diluar kendali dari pembuat keputusan dan tidak diketahui oleh mereka pada waktu membuat keputusan.

Dengan kondisi masa depan (state of nature), maka akan diperoleh gambaran yang lengkap dari faktor-faktor luar ini. Sehingga jika pembuat keputusan mengetahui kondisi masa depan yang harus dipegang, maka orang tersebut dapat memprediksikan konsekuensi dari sebarang tindakan dengan penuh kepastian. Namun bagaimana halnya apabila pembuat keputusan tidak dapat berkata apa pun tentang kondisi masa depan yang sebenarnya karena informasi yang diperolehnya tidak mencukupi untuk membuat keputusan yang optimal. Ini artinya pembuat keputusan dihadapkan pada suatu pengambilan keputusan dibawah ketidakpastian.

[image:39.595.107.527.285.450.2]

(40)

1. Kriteria Maximin Wald

2. Kriteria optimis-pesimis Hurwicz

3. Kriteria minimax Savage

4. Kriteria prinsip ketidakcukupan Laplace

2.8.1 Kriteria maximin Wald

Dibawah tindakan a akibat buruk yang mungkin terjadi memiliki nilai kepada _i

pembuat keputusan dari ; ij n j

i x

S

,..., 2 , 1 min =

= (2.22)

i

S dapat disebut sebagai level keamanan dari a , contohnya _i a menjamin pembuat _i

keputusan dalam pengembalian paling sedikit S . _i

Wald (1950) menyarankan bahwa pembuat keputusan seharusnya memilih a _k

sehingga mempunyai level keamanan sebesar mungkin. Sehingga kriteria pengembalian maximin Wald adalah :

Pilih a sehingga _k s = k i m imax=1,..., S

= _ij

j i minx

max (2.23) Kriteria ini adalah kriteria pemilihan yang sangat pesimis, dimana filsafat umumnya adalah mengasumsikan bahwa yang terburuklah yang akan terjadi.

2.8.2 Kriteria optimis-pesimis Hurwicz

Definisikan tingkat optimis dari a menjadi ; i ij

n j

i x

O

,..., 1 max

=

Sehingga O merupakan nilai dari konsekuensi terbaik yang diperoleh jika i a diambil. i Kriteria pengembalian maximax adalah ; memilih a sedemikian hingga _k

ij j i i n j

k O x

O max maxmax

,...,

1 =

(41)

Hurwicz (1951) menganjurkan bahwa pembuat keputusan seharusnya memberi rank pada tindakan menurut rata-rata pembobotan dari level keamanan dan level optimis :

i

i O

S (1 α)

α + − , dimana 0≤α ≤1, adalah indeks optimis-pesimis dari pembuat keputusan.

Hurwicz merekomendasikan aturan dalam keputusan; memilih a sedemikian hingga _k

{

i i

}

i k

k O S O

S (1 α) maxα (1 α)

α + − = + − (2.25)

2.8.3 Kriteria minimax Savage

Savage mendefinisikan penyesalan dari sebuah akibat yaitu :

{ }

lj ij m

l

ij x x

r = −

=1,...,

max (2.26) Bahwa perbedaan diantara nilai berdasarkan dari tindakan terbaik yang diberikan dimana S_j adalah kondisi masa depan yang sebenarnya dan memperoleh nilai dari a _i

dibawah S_j.

Savage menyarankan bahwa rij seharusnya memindahkan xij dalam tabel keputusan dan pada tabel regret yang baru, pembuat keputusan seharusnya memilih dengan mengikuti pendekatan pesimis Wald, tetapi dengan mengingat bahwa penyesalan adalah 'kehilangan' bukan 'perolehan'. Setiap tindakan diberikan indeks :

ij n j

i r

,.., 1 max

=

ρ (2.27) Bahwa penyesalan terburuk dapat terjadi dari tindakan a dan sebuah tindakan _i

seharusnya dipilih untuk meminimisasi ρ_i, contohnya memilih a sedemikian _k

hingga;

ij j i i m j

k min minmaxr ,..,

1 =

= ₌ ρ

ρ (2.28)

2.8.4 Kriteria prinsip ketidakcukupan Laplace

(42)

Jika tindakan a dipilih dan jika semua state memiliki peluang yang sama, maka _i

pengambil keputusan memperoleh nilai rata-rata dari akibat yang tidak pasti sehingga dia seharusnya memaksimasi nilai rata-rata dari pilihannya.

Aturan keputusan Laplace :

1. Menetapkan

( )

n S

P

pj = j = 1 untuk j = 1, 2, . . . , n

2. Untuk setiap A (matriks baris payoff), hitung nilai rata-ratanya : _i

( )

Ai =

∑

jpj

( )

xij = pj

∑

j

( )

xij

E (2.29) 3. Pilih tindakan dari E

( )

A_i yang memberikan nilai terbaik sebagai keputusan

yang optimal sehingga ;

( )

∑

( )

= =

= n

j

ij m

i

i _n x

A E

1 ,..., 1

1

(43)

(44)

BAB III

PEMBAHASAN

3.1 Program Linier Fuzzy

Model Program linier adalah suatu hal khusus dari model keputusan, dalam hal ini daerah keputusan didefinisikan oleh :

1. Batasan-batasan

2. Maksud dari fungsi tujuan

3. Jenis keputusan yaitu pengambilan keputusan dibawah ketentuan.

Dari bab landasan teori dikatakan bahwa model program linier biasa untuk persoalan maksimum dinyatakan sebagai berikut :

Maksimumkan : Z =C'X (3.1)

Dengan batasan : AX≤b (3.2)

X≥0 (3.3)

Dengan C,X∈Rn,b∈Rm,A∈Rmxn

Jika model program linier klasik diatas dibuat ke dalam himpunan fuzzy maka bentuk model klasik dari program linier akan mengalami sedikit modifikasi (perubahan) yaitu

1. Batasan-batasan mungkin saja menjadi tidak jelas, yaitu notasi “≤” dalam kasus maksimasi tidak diartikan secara matematik, tetapi pelanggaran lebih kecil dapat diterima. Dengan kata lain jika batasan-batasan menunjukkan kebutuhan yang diukur dengan perasaan berarti tidak bisa dikemukakan secara tepat oleh batasan crisp. Dalam hal ini koefisien dari A, b dan c bersifat fuzzy.

(45)

Masalah program linier fuzzy tidak didefinisikan secara unik. Masalah fuzzy tergantung pada jenis-jenis fuzzy yang diberikan dan ditetapkan oleh pembuat keputusan. Secara garis besar masalah program linier fuzzy dapat diklasifikasikan sebagai berikut :

1. Masalah program linier fuzzy dengan fungsi objektif crisp dan batasan fuzzy. 2. Masalah program linier fuzzy dengan fungsi objektif fuzzy dan batasan crisp. 3. Masalah program linier dengan fungsi objektif fuzzy dan batasan fuzzy.

Dalam skripsi ini penulis hanya membahas masalah program linier dengan fungsi objektif fuzzy dan batasan crisp.

3.2 Fungsi Objektif Fuzzy dan Batasan Crisp

Bentuk umum dari program linier dengan fungsi objektif fuzzy dan batasan crisp adalah sebagai berikut :

Maksimumkan : z=c~1x1 +c~2x2 +...+~cnxn (3.4) Kendala : a_i₁x₁+a_i₂x₂ +...+a_inx_n ≤b_i (3.5) x_j ≥0, j=1,2,...,n , i=1,2,...,m (3.6) Bilangan fuzzy triangular c~ adalah sebuah himpunan fuzzy dengan batas bawah a dan batas atas d serta fungsi keanggotaan triangular yang didefinisikan sebagai :

(

)

        − − − − = 0 ) ( ) ( ) ( ) ( , , ; c d x d a c a x d c a x µ jika jika jika d x d x c c x a > ≤ ≤ ≤ ≤

atau x<a

(3.7)

Bilangan fuzzy triangular c~ pada (3.4) dilambangkan dengan c~=(c−,c0,c+) atau )

, , ( ~ _a _c _d

c = dalam hal ini c− =a,c0 =c, dan c+ =d.

Bilangan fuzzy c~ dicirikan oleh fungsi keanggotaan (3.7) yang menggambarkan derajat keanggotaan suatu bilangan terhadap himpunan bilangan yang nilainya "sekitar

j

(46)

Berikut ini adalah langkah-langkah pembentukan program linier fuzzy untuk kasus dengan fungsi objektif fuzzy berbentuk maksimasi :

Langkah-1 : Tentukan model program linier yang akan diubah ke dalam model

program linier fuzzy.

Langkah-2 : Tentukan jenis bilangan fuzzy bagi setiap koefisien fungsi objektif

(yaitu bilangan fuzzy triangular (3.7)).

Langkah-3 : Tentukan :

a). c* =c=(c₁...c_j...c_n), yaitu vektor koefisien fungsi objektif yang komponen ke-j nya adalah koefisien fungsi objektif variabel xj.

b). ( 1... ... ) − − − − ₌

n j c

c c

c , yaitu vektor yang komponen ke-j nya

adalah batas bawah dari bilangan kabur c_j. c.) ( 1... ... )

+ + + + ₌

n j c

c c

c , yaitu vektor yang komponen ke-j nya

adalah batas atas dari bilangan kabur c_j.

Langkah 4 : Rumuskan pemrograman linier yang multiobjektif berfungsi objektif

memaksimumkan nilai bilangan fuzzy triangular sebagai berikut :

x c−

(47)

3.3 Usulan langkah-langkah pencarian solusi program linier fuzzy dengan

pengambilan keputusan kriteria Laplace

Langkah-1 : Menentukan nilai-nilai berikut :

z1min = min (c*-c-) x

z1max = max (c*-c-) x

z2min = min c* x

z2max = max c* x

z3min = min (c+- c*)x

z3max = max (c+- c*)x

Langkah-2 : Mendefinisikan ketiga fungsi keanggotaan berikut :

      − − − = − 0 ) ( 1 ) ( _min 1 max 1 * max 1 1 z z x c c z x Z

µ jika,

max 1 * max 1 * min 1 min 1 * ) ( ) ( ) ( z x c c z x c c z z x c c ≥ − ≤ − ≤ ≤ − − − − (3.8)       − − = 0 1 ) ( _min 2 max 2 min 2 * 2 z z z x c x Z

µ jika,

min 2 * max 2 * min 2 max 2 * z x c z x c z z x c ≤ ≤ ≤ ≥ (3.9)       − − − = + 0 ) ( 1 ) ( _min 3 max 3 min 3 * 3 z z z x c c x Z

µ jika,

min 3 * max 3 * min 3 max 3 * ) ( ) ( ) ( z x c c z x c c z z x c c ≤ − ≤ − ≤ ≥ − + + + (3.10)

Langkah-3 : Mendefinisikan ketiga fungsi keanggotaan diatas dengan

pengambilan keputusan kriteria Laplace yaitu :

( )

∑

₌ = n i zi x n x 1 1 ) ( µ µ )) ( ... ) ( ) ( ( 1 )

( 1 x 2 x x

n

x µz µz µzn

µ = + + +

Persamaan diatas adalah ekivalen dengan persamaan berikut : )) ( ... ) ( ) ( ( ) ( )

(x n x z1 x z2 x zn 1 x

zn = µ − µ +µ + +µ −

(48)

Langkah-4 : Mendefinisikan fungsi tujuan dengan kendala adalah

penggabungan dari (3.12) dengan (3.5)-(3.6) yaitu : Maksimumkan : µ

( )

x

Kendala : nµ(x)−(µ_z₁(x)+µ_z₂(x)+...+µ_zn₋₁(x))= µ_zn(x) n

in i

i x a x a x

a₁ ₁ + ₂ ₂ +...+ ≤b_i

0

≥

j

x , j =1,2,...,n , i=1,...,m

(49)

3.4 Ilustrasi Numerik

Sebagai ilustrasi numerik bagi Model Program Linier Fuzzy, diambil kasus berikut :

[image:49.595.113.522.284.380.2]

PT.X memproduksi tiga macam produk, yaitu bangku, meja, dan kursi. Pembuatan ketiga jenis produk tersebut membutuhkan bahan dasar berupa kayu, jam kerja untuk proses finishing serta jam kerja untuk proses carpentry. Kebutuhan ketiga jenis sumber daya per unit produk disajikan pada tabel berikut :

Tabel. Kebutuhan Sumber Daya untuk Kasus PT. X

Sumber Daya Bangku Meja Kursi

Kayu 8 Lembar 6 Lembar 1 Lembar

Jam finishing 4 Jam 2 Jam 1,5 Jam

Jam carpentry 2 Jam 1,5 Jam 0.5 Jam

Saat ini PT.X memiliki persediaan kayu 48 lembar kayu, 20 jam kerja finishing, dan 8 jam kerja carpentry. Bangku, meja, dan kursi berturut-turut dapat dijual seharga Rp 60, Rp 30, dan Rp 20. PT. X bermaksud memaksimasi pendapatannya.

Masalah PT. X dapat dimodelkan sebagai berikut : - Definisikan variable-variabel keputusan berikut :

X1 = banyaknya bangku yang diproduksi

X2 = banyaknya meja yang diproduksi

X3 = banyaknya kursi yang diproduksi

- Merumuskan fungsi tujuan sebagai berikut :

Max Z = 60 x1 + 30 x2 + 20 x3 (3.13)

- Merumuskan kendala-kendala sebagai berikut : Ketersediaan kayu : 8x1 +6x2 +x3 ≤48 (3.14) Ketersediaan jam finishing : 4x₁+2x₂ +1,5x₃ ≤20 (3.15) Ketersediaan jam carpentry : 2x₁+1,5x₂ +0,5x₃ ≤8 (3.16)

0 ,

, ₂ ₃

1 x x ≥

(50)

Misalkan selanjutnya didapatkan informasi tambahan dari PT. X bahwa sebenarnya : - Harga jual bangku tidaklah tepat sebesar c1* = Rp60, melainkan berada pada

rentang antara c1 = Rp55 −

sebagai batas bawahnya, dan c1 =Rp62 +

sebagai batas atasnya.

- Harga jual meja tidaklah tepat sebesar c2* =Rp30, melainkan berada pada rentang antara c₂− =Rp28 sebagai batas bawahnya, dan c₂+ = Rp35 sebagai batas atasnya.

- Harga jual kursi tidaklah tepat sebesar c3* =Rp20, melainkan berada pada rentang antara c₃− = Rp17 sebagai batas bawahnya, dan c₃+ =Rp22 sebagai batas atasnya.

Informasi tambahan ini, menuntut perumusan model yang baru, dengan catatan bahwa hanya fungsi objektifnya sajalah yang berbentuk fuzzy (kabur).

Langkah 1 :

(3.16)) -(3.14) (Kendala 3 2 1 min

1 =min5x +2x +3x =0

z (3.16)) -(3.14) (Kendala 3 2 1 max

1 =max5x +2x +3x =40

z (3.16)) -(3.14) (Kendala 3 2 1 min

2 =min60x +30x +20x =0

z (3.16)) -(3.14) (Kendala 3 2 1 max

2 =max60 +30x +20x =280

z (3.16)) -(3.14) (Kendala 3 2 1 min

3 =min2x +5x +2x =0

z (3.16)) -(3.14) (Kendala 3 2 1 max

3 =max2x +5x +2x =30,4

z

Langkah 2 : Ketiga fungsi keanggotaannya ;

      − + + − = 0 0 40 ) 3 2 5 ( 40 1 )

( 1 2 3

(51)

Elisabeth Aritonang : Kriteria Laplace Pada Pencarian Solusi Program Linier Fuzzy, 2009.       − − + + = 0 0 280 0 ) 20 30 60 ( 1 )

( 1 2 3

2 x x x x z µ 0 20 30 60 , 280 20 30 60 0 , 280 20 30 60 , 3 2 1 3 2 1 3 2 1 < + + < + + < ≥ + + x x x jika x x x jika x x x jika       − − + + = 0 0 4 , 30 0 ) 2 5 2 ( 1 )

( 1 2 3

3 x x x x z µ 0 2 5 2 , 4 , 30 2 5 2 0 , 4 , 30 2 5 2 , 3 2 1 3 2 1 3 2 1 ≤ + + < + + < ≥ + + x x x jika x x x jika x x x jika

Langkah 3 : Ketiga fungsi keanggotaan diatas akan dirumuskan ke dalam pengambilan keputusan Kriteria Laplace yaitu :

∑

₌ = 3 1 ) ( 3 1 ) ( i zi x x µ µ )) ( ) ( ) ( ( 3 1 )

(x µz1 x µz2 x µz3 x

µ = + +

Persamaan diatas adalah ekivalen dengan relasi berikut :

1 062 , 0 221 , 0 155 , 0 ) ( 3 ) ( ) ( ) ( 3 ) ( 3 2 1 3 2 1 = − − − − − = x x x x x x x

x _z _z

z

µ µ µ µ

µ _(3.17)

Langkah 4 : Definisikan fungsi dengan kendala adalah penggabungan dari (3.17) dengan (3.14)-(3.16) yaitu :

Max µ

S.t : 3 µ(x)−0,155x1−0,221x2−0,062x3 =1

(52)

Untuk menyelesaikan persamaan diatas maka diperlukan penambahan variabel slack dan variabel buatan, sehingga program linier akan berbentuk sebagai berikut :

Max µ

S.t : µ(x)−0,155x1−0,221x2−0,062x3+x7 =1 4

3 2 1 6

8x + x +x +x =48

4x₁+2x₂+1,5x₃ +x ₅ =20 3

2 1 1,5 0,5

2x + x + x +x =8 6 0 , , , , , ,

, ₂ ₃ ₄ ₅ ₆ ₇ 1 x x x x x x µ ≥

x

Program Linier ini akan diselesaikan dengan Metode M besar (Big M Method) karena persoalannya adalah memaksimalkan. Jika persoalan meminimalkan dan terdapat variabel buatan pada persamaan pembatasnya, maka lebih baik diselesaikan dengan metode dua fase dengan tujuan untuk menghindari tingkat error yang besar akibat dari nilai M.

[image:52.595.109.524.401.619.2]

Sehingga model diatas dapat dibawa ke bentuk tabel simpleks sebagai berikut :

Tabel 3.1 Tabel simpleks awal

Basis Cj

1 0 0 0 0 0 0 -M

NK

µ x 1 x 2 x 3 x 4 x 5 x 6 x 7

4

x 0 0 8 6 1 1 0 0 0 48

5

x 0 0 4 2 1,5 0 1 0 0 20

6

x 0 0 2 1,5 0,5 0 0 1 0 8

7

x -M 3 -0,155 -0,221 -0,062 0 0 0 1 1

j j c

z − -3M-1 0,155M 0,22M 0,062M 0 0 0 0 -M

Dari tabel awal diatas tampak bahwa penyelesaian optimal belum dicapai, karena nilai j

j c

z − < 0 (bernilai negatif). Harga z_j −c_j terkecil dari tabel awal diatas adalah -3M-1, sehingga variabel yang masuk dalam basis adalah variabel µ, kolom variabel

µ menjadi kolom pivot, dan perhitungan untuk indeks (I) adalah :

   

  =

= 0,33

3 1 min

(53)

Untuk nilai kolom kunci yang berharga negatif atau nol, maka pembagian NK terhadap nilai kolom kunci tersebut tidak diikut sertakan dalam I_min.

Dari I_min=0,33, maka variabel yang meninggalkan basis adalah x , kemudian ₇

[image:53.595.108.524.228.434.2]

digantikan oleh variabel µ, selanjutnya baris µ menjadi baris pivot, diperoleh angka kunci (elemen pivot) = 3, maka tabel simpleks yang baru adalah :

Tabel 3.2 Tabel simpleks untuk solusi yang baru

Basis Cj

1 0 0 0 0 0 0 -M

NK

µ x 1 x 2 x 3 x 4 x 5 x 6 x 7

4

x 0 0 8 6 1 1 0 0 0 48

5

x 0 0 4 2 1,5 0 1 0 0 20

6

x 0 0 2 1,5 0,5 0 0 1 0 8

µ 1 1 -0,05 -0,074 -0,021 0 0 0 0,33 0,33

j j c

z − 0 -0,05 -0,074 -0,021 0 0 0 0,33+M 0,33

Dari tabel diatas penyelesaian optimal belum dicapai, karena nilai z_j −c_j < 0 (bernilai negatif). Harga z_j −c_j terkecil dari tabel awal diatas a