PERBANDINGAN KRITERIA KEPUTUSAN MAXIMIN DENGAN
KRITERIA KEPUTUSAN LAPLACE PADA PENCARIAN SOLUSI
PROGRAM LINIER FUZZY
SKRIPSI
MELVA YETTI SIHOTANG
070803024
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERBANDINGAN KRITERIA KEPUTUSAN MAXIMIN DENGAN KRITERIA KEPUTUSAN LAPLACE PADA PENCARIAN SOLUSI PROGRAM LINIER
FUZZY
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MELVA YETTI SIHOTANG
070803024
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : PERBANDINGAN KRITERIA KEPUTUSAN MAXIMIN DENGAN KRITERIA LAPLACE PADA PENCARIAN SOLUSI PROGRAM LINIER FUZZY
Pembimbing 2 Pembimbing 1
Drs. Djakaria Sebayang, M.Si Dra. Esther S M Nababan, M.Sc NIP 19511227 198503 1 002 NIP 19511227 198503 1 002 Diketahui/ Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
PERBANDINGAN KRITERIA KEPUTUSAN MAXIMIN DENGAN KRITERIA KEPUTUSAN LAPLACE PADA PENCARIAN SOLUSI PROGRAM LINIER
FUZZY
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan,
PENGHARGAAN
Dengan segala kerendahan hati penulis memanjatkan puji dan syukur kepada Tuhan Yesus Kristus atas kasih, kekuatan, dan perlindunganNya, yang memampukan penulis dalam mengerjakan dan menyelesaikan penulisan skripsi ini.
Ucapan terima kasih penulis sampaikan kepada Dra. Esther S M Nababan, M.Sc dan Drs. Djakaria Sebayang, M.Si sebagai dosen pembimbing yang telah banyak memberikan panduan ilmu pengetahuan serta atas nasehat, motivasi, dan bimbingan yang diberikan kepada penulis dalam mengerjakan skripsi ini. Ucapan terima kasih juga disampaikan kepada Drs. Gim Tarigan, M.Si dan Drs. Djenda Djudjur Ginting, MS sebagai dosen pembanding yang banyak memberikan saran dan masukan dalam penyelesaian skripsi ini. Ucapan terima kasih juga penulis sampaikan kepada kepada Prof.Dr.Tulus, M.Si dan Dra. Mardiningsih, M.Si sebagai Ketua dan Sekretaris Departemen Matematika FMIPA USU, Dr. Sutarman, M.Sc sebagi Dekan FMIPA USU, Bapak dan Ibu Dosen di Departemen Matematika FMIPA USU, dan Staf administrasi Departemen Matematika FMIPA USU. Terima kasih kepada teman-teman mahasiswa matematika stambuk 2007, buat persahabatan, kebersamaan, dukungan, dan motivasinya bagi penulis selama perkuliahan dan penulisan skripsi ini. terkhusus buat Riris, Jojor, Siska, Magda, Zetty, Enrico, Falen dan Leo buat doa, motivasi dan teguran kepada penulis dalam mengerjakan skripsi. Penulis juga berterimakasih untuk Florence (K‟Tiur, Rolina, Dewi, Anita, Desri) untuk doa dan dukungannya selama ini.
Akhirnya, penulis juga mengucapkan banyak terima kasih kepada kedua orang tua yang sangat saya cintai dan mencintai saya Alm Ayahanda H. Sihotang dan. Ibunda P.br. Saragi atas doa, kepercayaan, nasehat dan dukungan moril dan materil, yang menjadi sumber inspirasi dan motivasi bagi penulis untuk tetap semangat dalam perkuliahan dan penulisan skripsi ini. Terima kasih juga kepada Bang Harryanto, Bang Irfan, Kak Erdita dan Adik Junremon buat doa, nasehat, masukan dan dukungannya selama perkuliahan sampai penyelesaian skripsi ini. Semoga Tuhan membalas segala kebaikan yang sudah diberikan dan biarlah kasih dan kemurahan Tuhan yang senantiasa menyertai kita.
ABSTRAK
Permasalahan program linier adalah asumsi kepastian (deterministik), dimana setiap parameter yaitu data-data dalam pemodelan program linier yang terdiri dari koefisien fungsi tujuan, konstanta sebelah kanan dan koefisien teknologis diketahui secara pasti. Tetapi dalam dunia nyata sering terjadi ketidakpastian, dari keadaaan ini lah muncul istilah fuzzy. Program linier fuzzy adalah program linier yang dinyatakan dengan fungsi objektif dan fungsi kendala yang memiliki parameter fuzzy dan ketidaksamaaan fuzzy. Tujuan program linier adalah mencari solusi yang dapat diterima berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala. Program linier fuzzy membutuhkan langkah-langkah dalam pencarian solusinya di mana pada pendekatan program linier fuzzy menjadi program linier biasa dengan fungsi objektif tunggal, digunakan kriteria maximin. Kriteria pengambilan keputusan maximin dikenal dengan pandangan yang pesimis (berlaku penghindar resiko) untuk suatu hasil yang akan dicapai diwaktu yang akan datang. Dalam tulisan ini penulis membandingkan kriteria maximin dengan kriteria Laplace pada pencarian solusi program linier fuzzy. Kriteria laplace mengasumsikan bahwa setiap kejadian memiliki nilai peluang untuk terjadi tetapi jika informasi untuk kejadian itu tidak mencukupi maka peluang untuk setiap kejadian dianggap sama. Dari hasil pembahasan diperoleh bahwa kriteria laplace memberikan nilai keuntungan opitimal (Z opitimal) dan nilai
ABSTRACT
DAFTAR ISI
2.2.1 Bilangan Fuzzy Triangular 8
2.2.2 Bilangan Fuzzy Trapezoidal 9 2.3 Himpunan Penyokong (Support Set) 10
2.4 Nilai Alfa-Cut 10
2.5.1 Metode Simpleks 14
3.2 Usulan Langkah-langkah Pencarian Solusi Program Linier Fuzzy Dengan Kriteria Keputusan Maximin 34 3.3 Usulan Langkah-langkah Pencarian Solusi Program Linier Fuzzy
Dengan Kriteria Keputusan Laplace 35
3.4 Ilustasi Numerik 37
3.4.1 Pencarian Solusi Program Linier Fuzzy dengan
Kriteria Keputusan Maximin 38
3.4.2 Pencarian Solusi Program Linier Fuzzy dengan
Kriteria Keputusan Laplace 41
DAFTAR TABEL
Halaman
Tabel 2.1 Bentuk Tabel Simpleks 14
Tabel 2.2 Bentuk Tabel Awal Simpleks 16
Tabel 2.3 Bentuk Tabel Simpleks Sesudah Pivoting 19 Tabel 2.4 Tabel Simpleks untuk Solusi Awal 20 Tabel 2.5 Tabel Simpleks untuk Solusi yang Baru 21 Tabel 2.6 Tabel Simpleks untuk Solusi yang Baru 22 Tabel 2.7 Tabel Simpleks untuk Solusi Akhir 23 Tabel 2.8 Tabel Simpleks untuk Solusi Awal 24 Tabel 2.9 Tabel Simpleks untuk Solusi Akhir 25 Tabel 2.10 Bentuk Umum Tabel Keputusan ` 26 Tabel 3.1 Kebutuhan Sumber Daya untuk Kasus PT.X 37 Tabel 3.2 Perbandingan Kriteria keputusan Maximin dengan Kriteria
DAFTAR GAMBAR
Halaman
Gambar 2.1 Fungsi Keanggotaan Segitiga 9
Gambar 2.2 Fungsi Keanggotaan Trapesium 9
ABSTRAK
Permasalahan program linier adalah asumsi kepastian (deterministik), dimana setiap parameter yaitu data-data dalam pemodelan program linier yang terdiri dari koefisien fungsi tujuan, konstanta sebelah kanan dan koefisien teknologis diketahui secara pasti. Tetapi dalam dunia nyata sering terjadi ketidakpastian, dari keadaaan ini lah muncul istilah fuzzy. Program linier fuzzy adalah program linier yang dinyatakan dengan fungsi objektif dan fungsi kendala yang memiliki parameter fuzzy dan ketidaksamaaan fuzzy. Tujuan program linier adalah mencari solusi yang dapat diterima berdasarkan kriteria yang dinyatakan dalam fungsi objektif dan kendala. Program linier fuzzy membutuhkan langkah-langkah dalam pencarian solusinya di mana pada pendekatan program linier fuzzy menjadi program linier biasa dengan fungsi objektif tunggal, digunakan kriteria maximin. Kriteria pengambilan keputusan maximin dikenal dengan pandangan yang pesimis (berlaku penghindar resiko) untuk suatu hasil yang akan dicapai diwaktu yang akan datang. Dalam tulisan ini penulis membandingkan kriteria maximin dengan kriteria Laplace pada pencarian solusi program linier fuzzy. Kriteria laplace mengasumsikan bahwa setiap kejadian memiliki nilai peluang untuk terjadi tetapi jika informasi untuk kejadian itu tidak mencukupi maka peluang untuk setiap kejadian dianggap sama. Dari hasil pembahasan diperoleh bahwa kriteria laplace memberikan nilai keuntungan opitimal (Z opitimal) dan nilai
ABSTRACT
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Konsep program linier (linear programming) ditemukan dan diperkenalkan seorang ahli matematika bangsa Amerika, Dr.George Dantzig yaitu dengan dikembangkannya metode simplex pada tahun 1947. Dantzig pada waktu itu merupakan salah seorang teknokrat yang tergabung dalam Kelompok Riset Operasi dari Angkatan Udara Amerika Serikat. Penerapan program linier untuk pertama kalinya adalah di bidang perencanaan militer khususnya dalam Perang Dunia II oleh angkatan bersenjata Amerika Serikat dan Inggris. Sejak itulah seiring dengan berjalannya waktu, pembangunan dan teknologi, teknik-teknik analisis program linier semakin berkembang dan diterapkan dalam berbagai bidang dan disiplin ilmu untuk memecahkan berbagai permasalahan yang dihadapi.
Salah satu asumsi dasar dalam permasalahan program linier adalah asumsi kepastian (deterministik), di mana setiap parameter yaitu data-data dalam pemodelan program linier yang terdiri dari koefisien-koefisien fungsi tujuan, konstanta-konstanta sebelah kanan dan koefisien-koefisien teknologis diketahui secara pasti. Tetapi dalam kehidupan nyata asumsi ini jarang dipenuhi. Dalam dunia nyata sering terjadi ketidakpastian, dari keadaan inilah muncul istilah fuzzy. Fuzzy pertama kali dikemukakan oleh Zadeh (1962), teori ini dapat digunakan untuk mengatasi masalah ketidakpastian dalam dunia nyata. Teori ini memperkenalkan himpunan yang keanggotaannya dinyatakan dengan derajat keanggotaan tertentudalam selang tertutup antara nol dan satu [0,1].
pendekatan program linier fuzzy menjadi program linier biasa dengan fungsi objektif tunggal, digunakan kriteria maximin. Kriteria pengambilan keputusan Maximin dikenal dengan pandangan yang pesimis (berlaku penghindar resiko) untuk suatu hasil yang akan dicapai diwaktu yang akan datang. .Dengan kata lain, kita harus menerima keadaan terburuk. Pada tulisan ini akan dibandingkan penyelesaian program linier fuzzy dengan menggunakan kriteria pengambilan keputusan Maximin dan penyelesaian program linier fuzzy dengan menggunakan kriteria pengambilan keputusan laplace. Kriteria laplace dan maximin sama-sama kriteria pengambilan keputusan di bawah ketidakpastian. Kriteria laplace mengasumsikan bahwa setiap kejadian memiliki nilai peluang untuk terjadi tetapi jika informasi untuk kejadian itu tidak mencukupi maka peluang untuk setiap kejadian diasumsikan sama. Nilai peluang untuk kejadian dari dianggap sama, dimana
Berdasarkan latar belakang permasalahan di atas, penulis memilih judul untuk skripsi ini, yaitu “ Perbandingan Kriteria Keputusan Maximin Dengan Kriteria Keputusan Laplace Pada Pencarian Solusi Program Linier Fuzzy”.
1.2 Perumusan Masalah
Permasalahan dalam tulisan ini adalah membandingkan bagaimana suatu permasalahan program linier fuzzy diselesaikan dengan mentransformasikan kriteria pengambilan keputusan maximin pada langkah-langkah pencarian solusinya dan program linier fuzzy diselesaikan dengan mentransformasikan kriteria pengambilan keputusan laplace pada langkah-langkah pencarian solusinya.
1.3 Batasan Masalah
1.4 Tinjauan Pustaka
B.D. Nasendi (1984) dalam bukunya „ Program Linear dan Variansinya‟ mengatakan
bahwa program linear merupakan suatu teknik perencanaan yang bersifat analitis yang analisis-analisisnya memakai model matematika dengan tujuan menemukan beberapa kombinasi alternatif pemecahan masalah, kemudian dipilih mana yang terbaik di antaranya dalam rangka menyusun strategi dan langkah-langkah kebijakan lebih lanjut tentang alokasi sumber daya dan dana yang terbatas guna mencapai tujuan atau sasaran yang diinginkan secara optimal.
Zimmerman (1991) dalam tulisannya mengemukakan tujuan dan batasan-batasan yang dipresentasikan dengan himpunan fuzzy dan pembuat keputusan dapat menetapkan sebuah tingkat ide untuk nilai dari fungsi objektif yang ingin dicapai.
Sri Kusumadewi dan Hari Purnomo (2004) dalam bukunya „Aplikasi Logika Fuzzy Untuk pendukung Keputusan‟ mengemukakan jika apabila persoalan program
linier akan dibuat pada lingkungan fuzzy maka model program linier klasik akan mengalami sedikit perubahan yaitu:
1. Bentuk imperatif pada fungsi objektif tidak lagi benar-benar “maksimum”
atau “minimum”, karena ada beberapa hal yang perlu mendapat pertimbangan
dalam suatu sistem.
2. Tanda (pada batasan dalam kasus maksimasi) dan tanda (pada batasan dalam kasus minimasi) tidak lagi bermakna crisp secara matematis, namunsedikit mengalami pelanggaran makna. Hal ini juga disebabkan karena adanya beberapa hal yang perlu dipertimbangkan dalam sistem yang mengakibatkan batasan tidak dapat didekati secara tegas.
Bentuk umum dari program linier fuzzy adalah
Maksimumkan :
Kendala
di mana dan semuanya adalah bilangan fuzzy (kabur).
= Parameter yang dijadikan kriteria optimisasi, atau koefisien peubah pengambilan keputusan dalam fungsi tujuan.
= Peubah pengambilan keputusan atau kegiatan (yang ingin dicari; yang tidak diketahui).
Koefisien teknologi peubah pengambilan keputusan (kegiatan yang bersangkutan) dalam kendala ke- i.
= Sumber daya yang terbatas, yang membatasi kegiatan atau usaha yang bersangkutan disebut pula konstanta atau nilai sebelah kanan dari kendala
ke-i.
Z = Nilai skalar kriteria pengambilan keputusan suatu fungsi tujuan.
Operasi penambahan dan perkalian adalah operasi-operasi aritmatika fuzzy, dengan tanda dan menyatakan urutan bilangan fuzzy. Pada umumnya, pemecahan permasalahan program linier fuzzy diawali dengan mengkonversikan permasalahan tersebut ke dalam bentuk program linier. Hasil akhirnya diperoleh dalam bentuk bilangan nyata yang menggambarkan kompromi dari bilangan-bilangan fuzzy yang diproses di dalamnya.
1.5 Tujuan Penelitian
1.6 Kontribusi Penelitian
Tulisan ini diharapkan dapat digunakan sebagai bahan referensi dalam penyelesaian permasalahan program linier dengan kondisi parameter-parameter yang tidak pasti di masa yang akan datang.
1.7 Metodologi Penelitian
Metode penelitian ini dilakukan dengan studi literatur dari berbagai jurnal dan buku teks. Usulan langkah-langkah pencarian solusi bagi program linier fuzzy dengan menggunakan kriteria maximin adalah sebagai berikut:
Langkah 1: Menentukan nilai-nilai berikut
Langkah 2 : Mendefinisikan fungsi keanggotaan segitiga dengan menggunakan fungsi-fungsi objektif di atas.
Langkah 3 : Mendefinisikan ketiga fungsi di atas dengan pengambilan keputusan maximin.
Langkah 4 : Mendefinisikan fungsi tujuan dengan kendala dari langkah 3 .
Usulan langkah-langkah pencarian solusi bagi program linier fuzzy dengan menggunakan kriteria laplace adalah sebagai berikut:
Langkah 1: Menentukan nilai-nilai berikut
Langkah 2 : Mendefinisikan fungsi keanggotaan segitiga dengan menggunakan fungsi-fungsi objektif di atas.
Langkah 3 : Mendefinisikan ketiga fungsi di atas dengan kriteria pengambilan keputusan laplace.
Langkah 4 : Mendefinisikan fungsi tujuan dengan kendala dari langkah 3 .
Langkah 5 : Penyelesaian dengan metode simpleks.
Untuk :
a. , yaitu vektor koefisien fungsi objektif yang komponen ke-j nya adalah koefisien fungsi objektif variabel .
b. , yaitu vektor yang komponen ke-j nya adalah batas bawah dari bilangan kabur .
BAB 2
LANDASAN TEORI
2.1Teori Himpunan Fuzzy
Pada himpunan tegas (crisp), nilai keanggotaan suatu item x dalam himpunan A, yang sering ditulis dengan memiliki dua kemungkinan, yaitu:
1. Nol (0), yang berarti bahwa suatu item tidak menjadi anggota dalam suatu himpunan.
2. Satu (1), yang berarti bahwa suatu item menjadi anggota dalam suatu himpunan
Sri Kusumadewi (2002) dalam bukunya yang berjudul “Analisis Desain Fuzzy Menggunakan Tool Box Matlab” menyatakan bahwa himpunan Fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi karakteristik sedemikian hingga fungsi tersebut akan mencakup bilangan real pada interval [0, 1]. Nilai keanggotaannya menunjukkan bahwa suatu item dalam semesta pembicaraan tidak hanya berada pada 0 atau 1, namun juga nilai yang berada diantaranya.
Misalkan diketahui klasifikasi sebagai berikut:
MUDA umur < 35 tahun
SETENGAH BAYA 35 ≤ umur ≤ 55 tahun TUA umur > 55 tahun
umur 45 tahun, kemudian perlahan menurun menuju ke 0 untuk umur dibawah 35 tahun dan diatas 55 tahun.
2.2Fungsi Keanggotaan Fuzzy
Sebuah himpunan fuzzy A dari bilangan riil didefenisikan oleh fungsi keanggotaannya (dinotasikan oleh A)
:
Jika maka dikatakan sebagai derajat keanggotaan x dalam A. Himpunan fuzzy dalam disebut normal jika terdapat sehingga . Himpunan fuzzy A adalah himpunan fuzzy dari bilangan riil dengan normal, (fuzzy) convex dan fungsi keanggotaan yang kontinu dari penyokong yang tebatas.
2.2.1 Bilangan Fuzzy Triangular
Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan segitiga (triangular) jika mempunyai tiga buah parameter, yaitu a, b, c dengan . Fungsi keanggotaannya adalah sebagai berikut:
1
b c
Gambar 2.1 Fungsi Keanggotaa segitiga
2.2.2 Bilangan Fuzzy trapezoidal
Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan trapesium (trapezoidal) jika mempunyai empat parameter yaitu a, b, c, d dengan
.
Fungsi keanggotaannya adalah sebagai berikut:
(2.2)
a b c d
2.3Himpunan Penyokong ( Support Set)
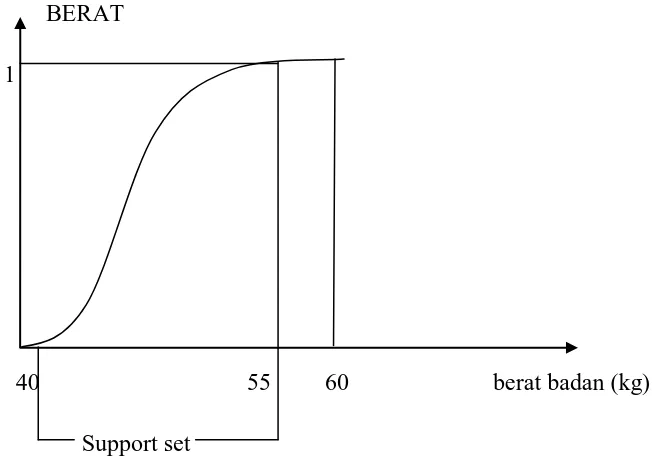
Terkadang bagian tidak nol dari suatu himpunan fuzzy tidak ditampilkan dalam domain. Sebagai contoh, domain untuk BERAT adalah 40 kg hingga 60 kg, namun kurva yang ada dimulai dari 42 kg hingga 52 kg (gambar 2.3)
BERAT 1
40 55 60 berat badan (kg) Support set
Gambar 2.3 Himpunan penyokong untuk himpunan fuzzy BERAT
2.4Nilai Alfa-Cut
BERAT 1
0 45 60 berat badan (kg) Ganbar 2.4 Nilai ambang -cut untuk himpunan fuzzy berat. Ada dua alasan -cut begitu berguna, yaitu:
1. -cut di nol (0) merupakan himpunan penyokong bagi suatu himpunan fuzzy 2. -cut di nol (0) menunjukkan tenaga atau fungsi kekuatan yang digunakan
oleh suatu model fuzzy untuk memutuskan ada tidaknya suatu nilai kebenaran yang harus dipertimbangkan.
2.5 Program Linier
Program linier memakai suatu model matematis dalam untuk menggambarkan
masalah yang dihadapi. Kata „linier‟ berarti bahwa semua fungsi matematis dalam
model ini harus menggunakan fungsi- fungsi linier.
Dalam program linier dikenal dua jenis fungsi, yaitu fungsi objektif (fungsi tujuan) dan fungsi- fungsi batasan (kendala). Fungsi tujuan adalah fungsi yang menggambarkan tujuan / sasaran di dalam permasalahan program linier yang berkaitan dengan pengaturan secara optimal sumber daya untuk mendapatkan keuntungan yang maksimal atau biaya minimal. Pada umumnya nilai optimal dinyatakan dengan Z. Fungsi batasan (kendala) merupakan bentuk penyajian secara matematis batasan- batasan kapasitas yang tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.
Menurut Parlin Sitorus (1997, 2), syarat- syarat yang harus dipenuhi dalam merumuskan suatu problema ke dalam model matematik persamaan linier sebagai berikut:
1. Memiliki kriteria tujuan
2. Sumber daya yang tersedia bersifat terbatas
3. Semua variabel dalam model memilki hubungan matematis bersifat linier 4. Koefisien model diketahui dengan pasti
MODEL UMUM MATEMATIK
Model umum program linier dapat dirumuskan ke dalam bentuk matematik sebagai berikut:
Fungsi tujuan :
Maksimalkan atau Minimalkan:
Z = (2.7) Kendala :
+ ... +
+ ... + (2.8)
. . . . .
. . . . .
+ ... +
untuk j = 1, 2, ..., n (2.9)
(syarat non-negatif)
Bentuk di atas dapat juga ditulis sebagai berikut : Fungsi tujuan :
Memaksimalkan atau Meminimalkan:
, untuk j= 1, 2, ..., n (2.10)
Kendala :
(2.11)
untuk i= 1, 2,....,m
Untuk :
= Parameter yang dijadikan kriteria optimisasi, atau koefisien peubah pengambilankeputusan dalam fungsi tujuan.
= Peubah pengambilan keputusan atau kegiatan (yang ingin dicari yang tidak diketahui).
Koefisien teknologi peubah pengambilan keputusan (kegiatan yang bersangkutan) dalam kendala ke- i.
= Sumber daya yang terbatas, yang membatasi kegiatan atau usaha yang bersangkutan disebut pula konstanta atau nilai sebelah kanan dari kendala
ke-i.
Z = Nilai skalar kriteria pengambilan keputusan suatu fungsi tujuan.
Sebelum menyelesaikan suatu tabel simpleks pertama kali menginisialisasikan dan merumuskan suatu persoalan keputusan ke dalam model matematik persamaan linier, yaitu sebagai berikut:
1. Konversikan semua ketidaksamaan menjadi persamaan.
Agar persamaan garis batasan memenuhi persyaratan pada daerah kelayakan (feasible) maka untuk model program linier diubah menjadi model yang sama dengan menambahkan variabel slack, surplus, variabel buatan (artificial variable) pada tiap batasan serta memberi harga nol kepada tiap koefisien c- nya. Batasan dapat dimodifikasi dengan cara berikut:
1. Untuk batasan bernotasi (≥) dapat dimodifikasi ke dalam bentuk persamaan dengan mengurangkan variabel surplus dan kemudian menambahkan variabel buatan ke dalamnya.
2. Untuk batasan (≤) dapat dimodifikasi ke dalam bentuk persamaan dengan menambahlan variabel slack ke dalamnya.
3. Untuk batasan (=) dapat diselesaikan dengan menambahkan variabel buatan ke dalamnya.
Dengan menambahkan variabel buatan akan merusak sistem batasan, hal ini dapat diatasi dengan membuat suatu bilangan besar M sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Jika persoalan maksimasi maka dibuat –M sebagai harga variabel buatan, apabila persoalan minimasi maka dibuat +M sebagai harga variabel buatan. Metode ini dikenal dengan metode M besar (Big M Method).
; ; ≥ 0 untuk semua harga i dan j (2.17)
; j = 1, 2,...., n ; i = 1, 2,...,
; i = , ..., m
2. Menyusun persamaan- persamaan ke dalam tabel awal simpleks
Tabel 2.2 Bentuk Tabel Awal simpleks
Jawab
Langkah- langkah yang digunakan untuk menyelesaikan suatu tabel simpleks adalah sebagai berikut:
Langkah 1: Mengecek nilai optimal imbalan
a. Untuk persoalan maksimal: = minimal { - }
Jika ≥ 0 maka selesai. Artinya solusi sudah optimal b. Untuk persoalan minimal : = maksimal { - }
Harga imbalan ) dapat diperoleh dengan rumus:
= (2.18)
Untuk : = harga semua variabel dalam z.
= koefisien dari semua variabel dalam sistem batasan.
= Harga dari variabel basis.
Langkah 2: Menentukan variabel yang masuk dalam basis.
Untuk persoalan maksimal jika terdapat beberapa ≤ 0 maka kolom yang menjadi kolom pivot adalah kolom dengan terkecil, dan variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk ke dalam basis. Untuk persoalan minimal jika terdapat beberapa ≥ 0 maka kolom yang menjadi kolom pivot adalah kolom dengan terbesar, dan variabel yang sehubungan dengan kolom pivot adalah variabel yang masuk ke dalam basis. Jika pada baris terdapat lebih dari satu kolom yang mempunyai nilai negatif yang angkanya terbesar dan sama pada persoalan maksimal atau terdapat lebih dari satu kolom yang mempunyai nilai positif terbesar dan sama pada persoalan minimal maka terdapat dua kolom yang bisa terpilih menjadi kolom pivot. Hal ini dapat diatasi dengan memilih salah satu dari
secara sembarang
Langkah 3: Menentukan variabel yang akan keluar dari basis.
Menetapkan variabel yang akan keluar dari basis yaitu:
= minimum { : > o } (2.19)
Langkah 4: Menyusun tabel simpleks yang baru
Untuk menyusun tabel simpleks yang baru, maka harus dicari koefisien elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat dicari dengan menghubungkan kolom pivot dengan baris pivot sedemikian rupa sehingga titik potong kedua pivot ini menunjukkan koefisien, yang disebut elemen pivot.
Koefisien baris pivot yang baru dapat dicari dengan menggunakan rumus sebagai berikut:
(2.20)
Untuk menghitung nilai baris baru lainnya dapat dilakukan dengan menggunakan rumus sebagai berikut :
(2.21)
Langkah 5 : Mengecek nilai optimal imbalan dari tabel simpleks yang baru.
Agar persamaan di atas memenuhi persamaan penyelesaian dalam daerah kelayakan (feasible), maka pada sisi persamaan batasan ditambahkan variabel slack sehingga bentuk bakunya sebagai berikut:
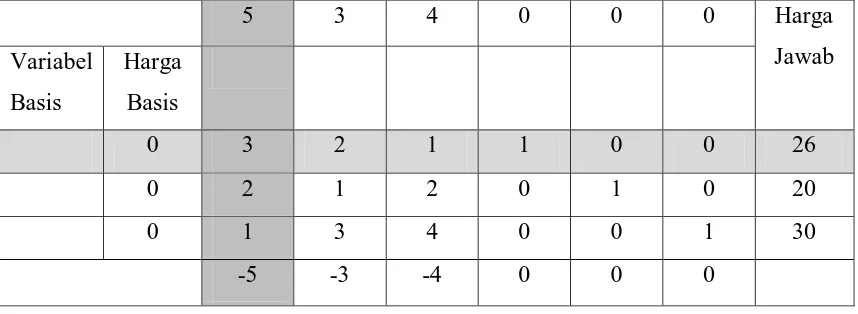
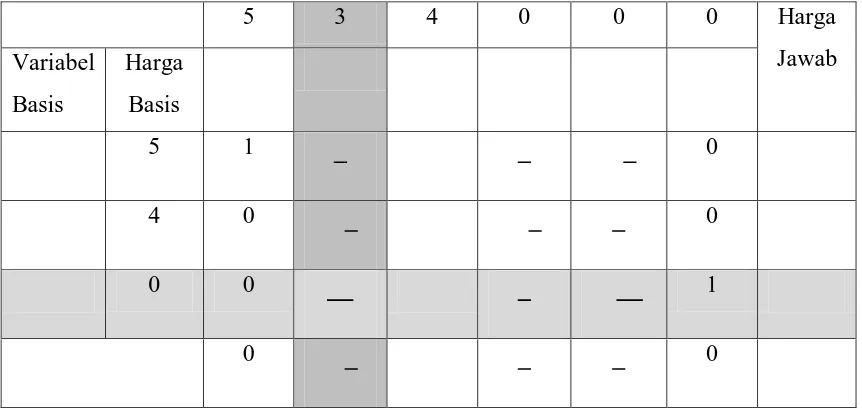
Model di atas dapat dibuat dalam tabel simpleks sebagai berikut: Tabel 2.4 Tabel Simpleks untuk solusi awal
5 3 4 0 0 0 Harga terkecil dari tabel di atas adalah -5, sehingga variabel yang masuk dalam basis adalah
. Kolom variabel menjadi kolom pivot dan perhitungan untuk indeks I adalah:
= { ; ; }
Tabel 2.5 Tabel simpleks untuk solusi yang baru
5 3 4 0 0 0 Harga
Jawab Variabel
Basis
Harga Basis
5 1 0 0
0 0 1 0
0 0 0 1
0 0 0
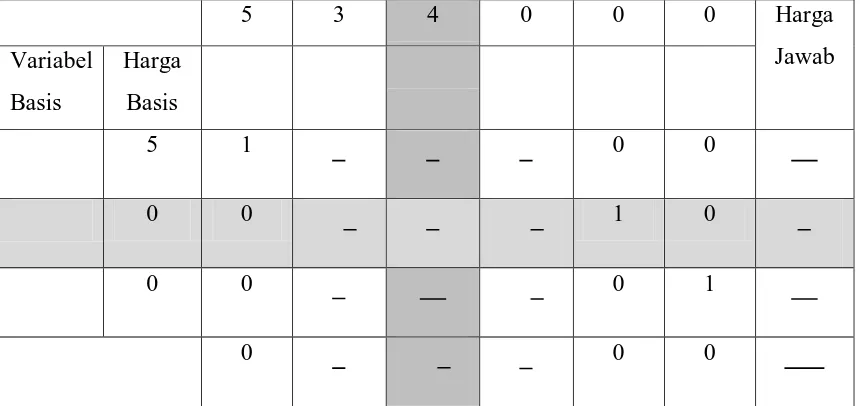
Dari tabel 2.5 tampak bahwa penyelesaian belum optimal yaitu harga terkecil dari tabel di atas adalah , sehingga variabel yang masuk dalam basis adalah . Kolom variabel menjadi kolom pivot dan perhitungan untuk indeks I adalah:
=
Tabel 2.6 Tabel simpleks untuk solusi yang baru
5 3 4 0 0 0 Harga
Jawab Variabel
Basis
Harga Basis
5 1 0
4 0 0
0 0 1
0 0
Dari tabel 2.6 tampak bahwa penyelesaian belum optimal yaitu harga terkecil dari tabel di atas adalah , sehingga variabel yang masuk dalam basis adalah . Kolom variabel menjadi kolom pivot dan perhitungan untuk indeks I adalah:
=
Agar persamaan di atas memenuhi persyaratan penyelesaian dalam daerah kelayakan
(feasible), maka pada sisi kiri persamaan batasan ≤ ditambahkan variabel slack sedangkan untuk sebelah kiri persamaan batasan ≥ dikurangkan dengan variabel
surplus dan ditambahkan dengan variabel buatan. Persamaan di atas diselesaikan dengan tehnik M. Sehingga bentuk bakunya sebagai berikut :
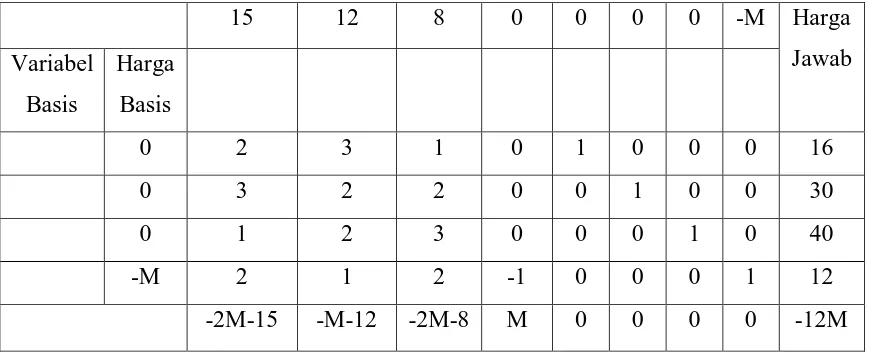
Maksimumkan : Z = 1 5 + 12 + 8 + 0 + 0 + 0 + 0 - M Kendala : 2 + 3 + + = 16
3 + 2 + 2 = 30 + 2 +3 + = 40 2 + + 2 - + 12
Dari model di atas dapat dibentuk tabel simpleks berikut : Tabel 2.8 Tabel simpleks untuk solusi awal
15 12 8 0 0 0 0 -M Harga
Tabel 2.9 Tabel simpleks untuk solusi akhir
Pada dasarnya asa empat kategori keputusan yaitu:
1. Keputusan dalam keadaan ada kepastian (certainty) 2. Keputusan dalam keadaan risiko (risk)
3. Keputusan dalam keadaan ketidakpastian (uncertainty) 4. Keputusan dalam keadaan ada konflik (conflict)
Banyak masalah keputusan dapat disajikan dalam bentuk tabel keputusan seperti di bawah ini:
Tabel 2.10 Bentuk umum tabel keputusan
Ada lima kriteria yang dipergunakan dalam pengambilan keputusan dibawah ketidakpastian (uncertainty), yaitu:
1. Kriteria Laplace 2. Kriteria Hurwicz
3. Kriteria Maximin dari Wald 4. Kriteria Minimax
5. Kriteria Maximax
2.6.1 Kriteria Laplace
Laplace (1825) menyarankan bahwa “dengan tidak mengetahui apa- apa tentang
kondisi masa depan yang sebenarnya” adalah ekivalen dengan “ setiap state memiliki peluang yang sama untuk terjadi”. Jika tindakan dipilih dan jika semua state memiliki peluang yang sama, maka pengambil keputusan memperoleh nilai rata- rata dari akibat yang tidak pasti sehingga dia seharusnya memaksimasi nilai rata- rata dari pilihannya.
Aturan keputusan Laplace:
1. Menetapkan ; untuk j = 1, 2, 3,..., n
2. Untuk setiap matriks baris pay off), hitung nilai rata-ratanya:
2.6.2 Kriteria Hurwicz
Kriteria Hurwicz diusulkan oleh Leonid Hurwicz, merupakan hasil kompromi antara kriteria maximin dan maximax. Di dalam prakteknya jarang seorang pengambil keputusan sangat pesimis atau optimis.
Didefenisikan tingkat optimis dari menjadi:
Sehingga merupakan nilai dari konsekuensi terbaik yang diperoleh jika diambil. Kriteria pengambilan maximax adalah memilih sedemikian hingga
Hurwicz (1951) menganjurkan bahwa pembuat keputusan seharusnya memberi rank pada tindakan menurut rata-rata pembobotan pada level keamanan dan level optimis : , dimana , adalah indeks optimis-pesimis dari
pembuat keputusan.
Hurwicz merekomendasikan aturan dalam keputusan memilih sedemikian hingga
2.6.3 Kriteria Maximin
Kriteria maximin didasarkan pada pandangan yang sangat pesimis (berperilaku penghindar resiko). Dengan demikian kita harus mengharapkan hasil terjelek bagi setiap alternatif tindakan yang dipilih.
dapat disebut sebagai level keamanan dari , contohnya menjamin pembuat keputusan dalam pengembalian paling sedikit .
Wald (1950) menyarankan bahwa pembuat keputusan seharusnya memilih sehingga mempunyai level keamanan sebesar mungkin. Sehingga kriteria maximin wald adalah:
Pilih sehingga =
2.6.4 Kriteria Minimax
Kriteria minimax sering disebut regret criterian didasarkan atas konsep kehilangan kesempatan (opportunity loss). Ide dasar dari kriteria ini diusulkan oleh L.J.Savage. Menurut Savage pengambil keputusan akan mengalami kehilangan kesempatan (penyesalan) apabila menghadapi kejadian tak pasti yang terjadi dan alternatif yang terpilih menghasilkan pay off yang lebih kecil dari pay off maksimum yang mungkin bisa dicapai untuk kejadian tak pasti tersebut.
Savage mendefenisikan penyesalan dari sebuah akibat yaitu:
Bahwa perbedaan diantara nilai berdasarkan dari tindakan terbaik yang diberikan dimana adalah kondisi masa depan yang sebenarnya dan memperoleh nilai dari dibawah . Savage menyarankan bahwa seharusnya memindahkan dalam tabel keputusan dan pada tabel regret yang baru, pembuat keputusan seharusnya memilih dengan mengikuti pendekatan pesimis Wald, tetapi dengan mengingat bahwa
penyesalan adalah „kehilangan‟ bukan „perolehan‟. Setiap tindakan diberikan indeks:
2.6.5 Kriteria maximax
Kriteria maximax didasarkan pada pandangan yang sangat optimis, sikap yang agresif, optimis mengenai hasil yang akan dicapai diwaktu terbesar (maximum) diantara yang terbesar.
Dibawah tindakan hasil terbaik yang mungkin terjadi memiliki nilai kepada pembuat keputusan dari:
dapat disebut sebagai hasil terbaik dari , artinya menjamin pembuat keputusan dalam perolehan hasil terbaik . Kriteria maximax menyarankan bahwa pembuat keputusan seharusnya memilih sehingga mempunyai hasil yang paling tinggi. Sehingga kriteria maximax adalah:
BAB 3
PEMBAHASAN
3.1 Program Linier Fuzzy
Model program linier adalah salah satu model matematika yang digunakan untuk menyelesaikan masalah optimisasi, yaitu memaksimumkan atau meminimumkan fungsi tujuan yang bergantung pada sejumlah variabel input. Model program linier didefinisikan oleh:
1. Batasan –batasan
2. Maksud dari fungsi tujuan
3. Jenis keputusan yaitu pengambilan keputusan dibawah ketentuan Dari bab landasan teori dikatakan bahwa model program linier biasa untuk persoalan maksimum dinyatakan sebagai berikut:
Maksimumkan : , untuk j= 1, 2, ..., n (3.1)
Kendala : (3.2)
untuk i= 1, 2,....,m
dan ≥ 0 (3.3)
Dalam banyak aplikasi, fungsi objektif maupun kendala-kendalanya seringkali tidak dapat dinyatakan dengan formula tegas (crisp). Oleh karena itu, program linier (tegas) dikembangkan menjadi program linier kabur dengan bentuk yang paling umum adalah sebagai berikut:
Maksimumkan : (3.4)
Kendala (3.5)
(3.6)
Jika model program linier klasik di atas dibuat ke dalam himpunan fuzzy maka bentuk model klasik dari program linier akan mengalami sedikit modifikasi, yaitu:
1. Batasan- batasan mungkin saja menjadi tidak jelas, yaitu notasi „ ‟ dalam kasus maksimasi tidak diartikan secara matematik, tetapi pelanggaran lebih kecil dapat diterima. Dengan kata lain jika batasan-batasan menunjukkan kebutuhan yang diukur dengan perasaan berarti tidak bisa dikemukakan secara tepat oleh batasan crisp (tegas). Dalam hal ini koefisien a, b,c bersifat fuzzy. 2. Pembuat keputusan mungkin tidak benar-benar ingin memaksimumkan atau
meminimumkan fungsi tujuan melainkan ingin mencapai beberapa tingkat ide yang bisa didefinisikan secara tegas (crisp).
Masalah program linier fuzzy tergantung pada jenis-jenis fuzzy yang diberikan dan ditetapkan oleh pembuat keputusan. Secara garis besar masalah program linier fuzzy dapat diklasifikasikan sebagai berikut:
1. Masalah program linier fuzzy dengan fungsi objektif fuzzy dan kendala crisp. 2. Masalah program linier dengan fungsi objektif crisp dan kendala fuzzy. 3. Masalah program linier fuzzy dengan fungsi objektif fuzzy dan kendala fuzzy. Dalam skripsi ini penulis hanya membahas masalah program linier dengan fungsi objektif fuzzy dan kendala crisp.
Bentuk umum program linier dengan fungsi objektif fuzzy dan kendala crisp
(3.10)
Bilangan fuzzy triangular dilambanhkan dengan = ( ) atau dalam hal ini , ,
Bilangan fuzzy triangular dicirikan oleh fungsi keanggotaan triangular yang menggambarkan derajat keanggotaan suatu bilangan terhadap himpunan bilangan
yang nilainya „sekitar ‟ atau „kurang lebih ‟.
Berikut adalah langkah-langkah pembentukan program linier fuzzy untuk kasus dengan fungsi objektif fuzzy berbentuk maksimasi:
Langkah 1 : Tentukan model program linier yang akan diubah ke dalam model program linier fuzzy.
Langkah 2 : Tentukan jenis bilangan fuzzy bagi setiap koefisien fungsi objektif (dalam tulisan ini bilangan fuzzy triangular).
Langkah 3 : Tentukan:
a. , yaitu vektor koefisien fungsi objektif yang komponen ke-j nya adalah koefisien fungsi objektif variabel . b. , yaitu vektor yang komponen ke-j nya adalah
batas bawah dari bilangan kabur .
c. , yaitu vektor yang komponen ke-j nya adalah batas atas dari bilangan kabur .
Langkah 4 : Rumuskan pemrograman linier yang multiobjektif berfungsi objektif memaksimumkan nilai bilangan fuzzy triangular sebagai berikut:
3.2 Usulan Langkah-langkah Pencarian Solusi Program Linier Fuzzy Dengan Kriteria Keputusan Maximin
Langkah 1 : Menentukan nilai-nilai berikut:
Langkah 2 : Mendefinisikan ketiga fungsi keanggotaan berikut:
(3.11)
(3.12)
Langkah 3 : Mendefinisikan ketiga fungsi keanggotaan di atas dengan kriteria pengambilan keputusan maximin yaitu:
1. Definisikan fungsi berikut:
(3.14)
Yang ekivalen dengan ketiga relasi berikut:
(3.15)
(3.16)
(3.17)
Langkah 4 : Definisikan masalah optimasi :
(3.18) Dengan kendala (3.15)- (3.17) dan ≥ 0
3.3 Usulan Langkah-langkah Pencarian Solusi Program Linier Fuzzy Dengan Kriteria Keputusan Laplace
Langkah 2 : Mendefinisikan ketiga fungsi keanggotaan berikut:
(3.19)
(3.20)
(3.21)
Langkah 3 : Mendefinisikan ketiga fungsi keanggotaan di atas dengan pengambilan keputusan laplace yaitu:
Persamaan di atas ekivalen dengan persamaan berikut:
(3.22)
Langkah 4 : Mendefinisikan fungsi tujuan dengan kendala penggabungan dari (3.22) dengan (3.8)-(3.9) :
Maksimumkan : Kendala :
3.4 Ilustrasi Numerik
Sebagai ilustrasi numerik bagi model program linier fuzzy, diambil kasus berikut:
PT.X memproduksi tiga macam produk, yaitu bangku, meja, dan kursi. Pembuatan ketiga jenis produk tersebut membutuhkan bahan dasar berupa kayu, jam kerja untuk proses finishing serta jam kerja untuk proses carpentery. Kebutuhan ketiga jenis sumber daya per unit produk disajikan pada tabel berikut:
Tabel 3.1 Kebutuhan Sumber Daya Untuk Kasus PT.X
Sumber Daya
Saat ini PT.X memiliki persediaan kayu 58 lembar kayu, 24 jam kerja finishing, dan 10 jam kerja carpentery. Meja, bangku, dan kursi dapat dijual seharga $70, $40, $30. PT.X memperoleh informasi bahwa semua bangku dan kursi yang diproduksi pasti terjual, sementara meja paling banyak hanya akan terjual 8 meja. PT.X bermaksud memaksimasi pendapatannya dari ketiga jenis produk tersebut.
Dari keterangan di atas permasalahan yang dihadapi PT.X dapat dimodelkan sebagai berikut:
a. Definisikan variabel-variabel keputusan berikut: = banyaknya meja yang diproduksi = banyaknya bangku yang diproduksi = banyaknya kursi yang diproduksi b. Merumuskan fungsi tujuan sebagai berikut:
c. Merumuskan kendala sebagai berikut:
ketersediaan kayu : (3.23) ketersediaan jam carpentery : (3.24) ketersediaan jam finishing : (3.25) penjualan meja : (3.26)
(kendala non-negatif variabel)
Serta didapat informasi tambahan dari PT.X sebagai berikut:
a. Harga jual meja tidaklah tepat sebesar , melainkan berada pada rentang antara sebagai batas bawahnya dan sebagai batas atasnya.
b. Harga jual bangku tidak lah tepat sebesar , melainkan berada pada rentang antara sebagai batas bawahnya dan sebagai batas atasnya.
c. Harga jual kursi tidak lah tepat sebesar , melainkan berada pada rentang antara sebagai batas bawahnya dan sebagai batas atasnya.
Informasi tambahan di atas bila ingin diakomodasikan ke bentuk program linier fuzzy membutuhkan perumusan model yang baru, dengan catatan hanya koefisien fungsi objektifnya yang berbentuk kabur.
3.4.1 Pencarian Solusi Program Linier Fuzzy Dengan Kriteria Keputusan Maximin
Langkah 1 : Menentukan nilai berikut
b.
Solusi dapat dilihat pada lampiran 1
c.
d.
Solusi dapat dilihat pada lampiran 2
e.
f.
Solusi dapat dilihat pada lampiran 3
Langkah 2 : Definisikan ketiga fungsi keanggotaan berikut
(3.27)
(3.29)
Langkah 3 : Definisikan fungsi
(3.30)
Yang ekivalen dengan ketiga relasi berikut:
atau
atau
atau
Langkah 4 : Definisikan masalah optimasi
Dengan kendala:
≥ 0
Solusi dapat dilihat pada lampiran 4
Dari permasalahan yang dihadapi PT.X maka keputusan terbaik yang akan diambil dengan menggunakan kriteria keputusan Maximin adalah memproduksi unit bangku, unit meja, unit kursi, . Bila keputusan ini diambil maka:
yang menggambarkan perbedaan nilai antara fungsi objektif semula dengan fungsi objektif berkoefisien batas bawah kabur . Nilai tertinggi dari adalah 1 yang tercapai jika nilai lebih kecil atau sama dengan 0. Nilai terendah adalah 0 yang tercapai jika nilai lebih besar dari 16,28.
b. Dari persamaan (3.28) didapat nilai , nilai ini mencerminkan tingkat kepuasan terhadap nilai yang dicapai oleh fungsi yaitu fungsi objektif semula. Nilai tertinggi dari adalah 1 yang tercapai jika nilai lebih besar atau sama dengan 240. Nilai terendah adalah 0 yang tercapai jika nilai lebih kecil atau sama dengan 0.
c. Dari persamaan (3.29) didapat nilai , nilai ini mencerminkan tingkat kepuasan terhadap nilai yang dicapai oleh fungsi yang menggambarkan perbedaan nilai antara fungsi objektif berkoefisien batas atas bilangan kabur dengan fungsi objektif semula . Nilai tertinggi dari adalah 1 yang tercapai jika nilai lebih besar atau sama dengan 25. Nilai terendah adalah 0 yang tercapai jika nilai lebih kecil atau dama dengan 0.
d. Dari persamaan (3.30) nilai =
3.4.2 Pencarian Solusi Program Linier Fuzzy Dengan Kriteria Keputusan Laplace
Langkah 1 : Menentukan nilai berikut
b.
Solusi dapat dilihat pada lampiran 1
c.
d.
Solusi dapat dilihat pada lampiran 2
e.
f.
Solusi dapat dilihat pada lampiran 3
Langkah 2 : Definisikan ketiga fungsi keanggotaan berikut
(3.31)
(3.32)
Langkah 3 : Mendefinisikan ketiga fungsi keanggotaan di atas dengan pengambilan keputusan kriteria Laplace yaitu:
(3.34)
Persamaan di atas ekivalen dengan relasi berikut:
Langkah 4 : Definisikan fungsi dengan kendala ri penggabungan(3.35) dengan (3.23)-(3.26) yaitu:
Max
Kendala :
Solusi dapat dilihat pada lampiran 5
Dari permasalahan yang dihadapi PT.X maka keputusan terbaik yang akan diambil dengan menggunakan kriteria laplace adalah memproduksi unit bangku, unit meja, unit kursi, . Bila keputusan ini di ambil maka:
nilai lebih kecil atau sama dengan 0. Nilai terendah adalah 0 yang tercapai jika nilai lebih besar dari 16,28.
b. Dari persamaan (3.32) didapat nilai , nilai ini mencerminkan tingkat kepuasan terhadap nilai yang dicapai oleh fungsi yaitu fungsi objektif semula. Nilai tertinggi dari adalah 1 yang tercapai jika nilai lebih besar atau sama dengan 240. Nilai terendah adalah 0 yang tercapai jika nilai lebih kecil atau sama dengan 0.
c. Dari persamaan (3.33) didapat nilai , nilai ini mencerminkan tingkat kepuasan terhadap nilai yang dicapai oleh fungsi
yang menggambarkan perbedaan nilai antara fungsi objektif berkoefisien batas atas bilangan kabur dengan fungsi objektif semula . Nilai terendah adalah 0 yang tercapai jika nilai lebih
Tabel 3.2 Perbandingan Kriteria keputusan Maximin dengan Kriteria Keputusan Laplace Pada Permasalahan PT.X
Pembanding Kriteria Maximin Kriteria Laplace
BAB 4
KESIMPULAN DAN SARAN
4.1 KESIMPULAN
Berdasarkan pembahasan pada bab 3 dapat disimpulkan bahwa Masalah pemrograman linier dengan Koefisien Fungsi Objektif kabur dan Kendala Crisp dapat didekati menjadi masalah pemrograman Linier biasa dengan fungsi objektif tungggal dengan menggunakan kriteria pengambilan keputusan maximin dan menggunakan kriteria pengambilan keputusan laplace. Dari pembahasan bab 3 didapat:
1. Kriteria Laplace memberikan nilai yang lebih besar dari kriteria maximin, yaitu kriteria Laplace.
2. Kriteria Laplace memberikan nilai keuntungan optimal (Z) yang lebih besar dibandingkan dari nilai keuntungan optimal (Z) yang didapat dengan menggunakan kriteria maximin.
Hal ini hanya berlaku untuk permasalahan PT.X.
4.2 SARAN
1. Perlu dilakukan lebih lanjut mengenai penerapan kriteria maximin dan laplace secara tepat dalam pengambilan keputusan pada langkah-langkah penyelesaian program linier fuzzy.
DAFTAR PUSTAKA
Kusumadewi, Sri. 2002. Analisis Desain Sistem Fuzzy Menggunakan Tool Box Matlab. Jogjakarta: Graha Ilmu.
Lieberman, G. J. dan F. S. Hittler. 1990. Introduction to Operation Research. Fifth Edition, Mc Graw – Hill.
Mulyono, Sri. 2004. Riset Operasi. Jakarta: Fakultas Ekonomi Universitas Indonesia. Nasendi, B. D. Dan Efendi Anwar. 1984. Program Linier dan Variansinya. Jakarta:
Gramedia.
Siagian, P. 1987. Penelitian Operasional. Jakarta: Universitas Indonesia.
Sitorus, Parlin. 1997. Program Linier. Jakarta: Universitas Trisakti.
Sri, K. dan Hari, P. 2004. Aplikasi Logika Fuzzy Untuk Pendukung Keputusan.
Yogyakarta: Graha Ilmu.
Supranto, J. 1983. Linear Progra mming. Jakarta: Fakultas Ekonomi Universitas Indonesia.
Supranto, Johannes.1991. Teknik Pengambilan Keputusan. Jakarta: Rineka Cipta. Susanto, S., et al., Pemodelan Pemrograman Linier dengan Koefisien Fungsi Objektif
Berbentuk Bilangan Kabur Segitiga dan Kendala Kabur Beserta Usulan Solusinya. Jurnal Teknik Industri Vol.8, No.1, Juni 2006: 14-27.
Susilo, Frans. 2006. Himpunan dan Logika Kabur Serta Aplikasinya. Yogyakarta: Graha Ilmu.
LAMPIRAN
Lampiran 4 : Penyelesaian dengan kendala :
Lampiran 5: Penyelesaian Max Dengan kendala: