Metode Penyelesaian Program Fuzzy Integer Linier Dengan Fungsi Keanggotaan Linier

(1)

SKRIPSI

NURUL FEBRINA TAMBUNAN

050803005

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

ii

PERSETUJUAN

Judul : METODE PENYELESAIAN PROGRAM FUZZY

INTEGER LINIER DENGAN FUNGSI KEANGGOTAAN LINIER.

Kategori : SKRIPSI

Nama : NURUL FEBRINA TAMBUNAN

Nomor Induk Mahasiswa : 050803005

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA

UTARA

Medan, Oktober 2009

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Djakaria Sebayang Prof. Dr. Herman Mawengkang NIP 19511227 198031 002 NIP 19461128 1974031 001

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua.

(3)

PERNYATAAN

METODE PENYELESAIAN PROGRAM FUZZY INTEGER LINIER DENGAN FUNGSI KEANGGOTAAN LINIER

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Oktober 2009-

(4)

iv

PENGHARGAAN

Puji dan syukur penulis ucapkan kehadirat Allah SWT yang telah melimpahkan karunia-Nya, sehingga penulis berhasil menyelesaikan skripsi ini dalam waktu yang telah ditetapkan.

Dalam kesempatan ini, penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada semua pihak yang telah membantu dan membimbing penulis dalam penyusunan skripsi ini, ucapan terima kasih saya sampaikan kepada :

1. Bapak Prof. Dr. Herman Mawengkang. selaku pembimbing I dan Bapak Drs. Djakaria Sebayang selaku pembimbing II yang telah memberikan bimbingan dan pengarahan kepada saya sehingga skripsi ini dapat saya selesaikan.

2. Ibu Dra. Elly Rosmaini, M.Si. dan Bapak Drs. H. Haludin Panjaitan selaku dosen penguji saya.

3. Bapak Dr. Saib Suwilo, M.Sc. dan Bapak Drs. Henry Rani Sitepu, M.Sc. selaku Ketua dan Sekretaris Departemen Matematika.

4. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

5. Semua Dosen pada Departemen Matematika FMIPA USU, pegawai di FMIPA USU

6. Seluruh teman di jurusan Matematika khususnya stambuk 2005, serta sahabat– sahabatku: Devi, Lia, Nenna, Rima, Yuni, Sundari, Radhi, Santri dan terutama Andika yang selama ini telah memberikan semangat, dorongan dan saran dalam pengerjaan skripsi ini.

7. Kedua orang tua serta adik-adik saya yang selama ini memberikan bantuan dan dorongan yang diperlukan.

(5)

ABSTRAK

(6)

vi

ABSTRACT

(7)

DAFTAR ISI

Halaman

PERSETUJUAN ii

PERNYATAAN iii

PENGHARGAAN iv

ABSTRAK v

ABSTRACT vi

DAFTAR ISI vii

DAFTAR TABEL viii

DAFTAR GAMBAR ix

Bab 1 PENDAHULUAN 1

1.1Latar Belakang 1

1.2Perumusan Masalah 2

1.3Tinjauan Pustaka 2

1.4Tujuan Penelitian 4

1.5Kontribusi Penelitian 4

1.6Metode Penelitian 4

Bab 2 LANDASAN TEORI 5

2.1 Teori Himpunan Fuzzy 5

2.2 Fuzzy Set 7

2.3 Fuzzy Set Operation 8

2.4 Sistem Fuzzy 9

2.5 Fungsi Keanggotaan (Membership Function) 10

2.6 Program Linier 14

2.7 Fuzzy Linier Programming 25

2.8 Permasalahan Linier Fuzzy 27

Bab 3 PEMBAHASAN 29

3.1 Program Integer 29

3.2 Model Dasar 29

3.3 Percabangan (Branching) 30

3.4 Pembatasan (Bounding) 30

3.5 Fuzzy Integer Linier Programming 33

3.6 Contoh Numerik 34

Bab 4 KESIMPULAN DAN SARAN 43

4.1 Kesimpulan 43

4.2 Saran 44

(8)

viii

DAFTAR TABEL

Halaman

Tabel 2.1 Bentuk Tabel Simpleks 18

Tabel 2.2 Bentuk tabel awal simpleks sebelum pivoting 20 Tabel 2.3 Bentuk tabel simpleks sesudah pivoting 22

Tabel 2.4 Tabel simpleks untuk iterasi 1 23

(9)

DAFTAR GAMBAR

Halaman Gambar : Nilai keanggotaan muda, parobaya, dan tua 6

Gambar : Representasi linier naik 11

Gambar : Representasi linier turun 12

Gambar : Representasi kurva segitiga 12

(10)

v

ABSTRAK

(11)

ABSTRACT

(12)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Dalam pemodelan program linier (PL) salah satu asumsi dasar adalah asumsi

kepastian, yaitu setiap parameter, data-data dalam pemodelan PL, yang terdiri dari

koefisisen-koefisien fungsi tujuan , konstanta-konstanta sebelah kanan dan

koefisien-koefisien teknologis, diketahui secara pasti, Liebermann. Tetapi dalam praktek,

asumsi ini jarang dipenuhi. Sebab, kebanyakan model PL dirumuskan untuk memilih

suatu tindakan atau keputusan di waktu yang akan datang. Jadi, parameter-parameter

yang akan dipakai didasarkan atas suatu prediksi mengenai kondisi masa datang.

Karena ketidakpastian tersebut, biasanya dilakukan analisa kepekaan setelah didapat

penyelesaian optimal. Tujuannya adalah untuk mengetahui parameter-parameter yang

sensitif, untuk mencoba mengestimasinya dengan lebih baik, dan kemudian memilih

suatu pemecahan yang tetap atau lebih baik untuk nilai-nilai yang mungkin dimiliki

oleh parameter-parameter sensitif tersebut. Untuk pengambilan keputusan dari

permasalahan yang semakin kompleks, kadang-kadang tingkat ketidakpastian yang

timbul terlalu kompleks untuk dapat dilakukan analisa kepekaan. Misalnya adalah

ketidakpastian yang disebabkan oleh kekurang-jelasan dalam penentuan nilai-nilai

parameter, hal ini terutama dipengaruhi oleh faktor subjektif dan intuitif yang domain.

Teori himpunan fuzzy, yang dikembangkan oleh L. Zadeh pada pertengahan

tahun 60-an, telah banyak berhasil dalam menangani masalah pengambilan keputusan

dalam lingkungan kabur atau tidak pasti karena faktor subjektif ataupun karena

(13)

Dalam pengambilan keputusan dengan model PL, ketidakpastian karena faktor

subjektif dapat diakomodasi dan dipecahkan dengan teori himpunan fuzzy. Persoalan

program linier fuzzy yang timbul secara alami pada aplikasi-aplikasi dunia nyata,

banyak diantaranya yang menginginkan variabel keputusannya hanya berupa

bilangan cacah, sebagai contoh diterapkan dalam studi kelayakan pada pabrik-pabrik

dan bidang produksi material. Dengan adanya syarat cacah untuk nilai variabel

keputusan, maka permasalahan ini disebut Fuzzy Integer Linier Programming

(program integer linier fuzzy) yang dapat digunakan untuk menyelesaikan kasus pada

fungsi keanggotaan linier.

Dengan latar belakang inilah maka penulis memilih judul “ Metode

Penyelesaian Program Fuzzy Integer Linier dengan Fungsi Keanggotaan Linier ”.

1.2 Perumusan Masalah

Yang menjadi permasalahan dalam penelitian ini adalah bagaimana menyelesaikan

permasalahan dalam program fuzzy integer linier dengan fungsi keanggotaan linier,

dalam hal ini dibatasi pada bilangan kabur segitiga (triangular fuzzy number).

1.3 Tinjauan Pustaka

Sebagai sumber pendukung teori dalam penulisan ini, maka penulis mengggunakan

beberapa pustaka antara lain :

Winston, W.L, 2003. Operations Research: Applications and Algorithms,

menyatakan bahwa bentuk umum model program linier adalah sebagai berikut:

Maksimumkan : Z =c₁x₁+c₂x₂+...+c_jx_j

(minimumkan)

Kendala : a₁₁x₁+a₁₂x₂+...+a₁_ix_j ≤b₁

2 2

2 22 1

21x a x ... a x b

(14)

3 ⋮ ⋮ ⋮ j j ij i

i x a x a x b a₁ ₁+ ₂ ₂ +...+ ≤

x_i ≥0 (i=1,2,...,n)

Dimana:

j

x = Variabel keputusan ke-j.

j

c = Koefisien fungsi objektif (KFO) dari variabel

keputusan ke-j.

ij

a = Koefisien teknologi dari variabel keputusan

ke-j pada kendala ke-i.

i

b = Koefisien ruas kanan pada kendala ke-i

i = 1,2,…,m (m = jumlah variabel keputusan) dan j = 1,2,…,n

(n = jumlah kendala).

Sri Kusumadewi, 2002. Analisa & desain sistem fuzzy menggunakan toolbox

matlab menyatakan bahwa bentuk umum fuzzy linier programming adalah:

Maksimumkan _j

n j jx c Z

∑

= = 1 ~

Kendala _j _i

n

j

ijx b a~ ~ 1

≤

∑

=

( i = 1,2,…,m)

0 ≥ j

x ( j = 1,2,…,n)

Dimana c~ , _j a~ dan _ij b~_j semuanya adalah bilangan fuzzy.

International Journal Of Contemporary Mathematical Sciences, Fuzzy

Integer Linier Programming.(diakses 10 Maret 2009) menyatakan

bahwa bentuk umum dari program integer linier fuzzy adalah sebagai

berikut:

Min C X~

t

s. AX~ =H

( ) (

T = −b+br,b−br

)

_X~* ≥₀_,_X~∈_I_._S⌢_._Tn

Dimana A∈ℜmxn,C∈ℜn dan T STm

⌢ ⌢

.

(15)

Itu berarti bahwa, jika

( )

c;w adalah solusi maka w adalah bilangan integer.

1.4 Tujuan Penelitian.

Secara umum tujuan dari penelitian ini adalah untuk menyelesaikan masalah program

fuzzy integer linier dengan fungsi keanggotaan linier.

1.5 Kontribusi Penelitian.

Dengan mengadakan penulisan ini, penulis berharap dapat menambah referensi bagi

pembaca dan pengambil keputusan dalam menyelesaikan program fuzzy integer linier

dengan fungsi keanggotaan linier.

1.6 Metode Penelitian.

Penelitian ini bersifat studi literatur yang disusun berdasarkan rujukan pustaka dengan

langkah-langkah sebagai berikut:

Langkah-1 : Menjelaskan definisi fungsi keanggotaan linier pada fuzzy

Langkah-2 : Menjelaskan prosedur untuk mereduksi program integer linier fuzzy

menjadi dua problema yang singkat dalam program integer linier

(16)

BAB 2

LANDASAN TEORI

2.1 Teori Himpunan Fuzzy

Dalam kebanyakan jenis pemikiran setiap harinya, orang – orang menggunakan crisp

set untuk mengelompokan sesuatu. Menjadi anggota dari crisp set adalah seluruhnya

berhubungan atau tidak sama sekali. Seorang wanita dikatakan hamil ataupun tidak, ia

tidak pernah “hamil sebagian” atau “sedikit hamil”.

Berpikir dengan crisp set menjadikan segala sesuatunya lebih sederhana,

karena sesuatu bisa merupakan anggota dari suatu crisp set atau tidak. Crisp set dapat

digunakan untuk merepresentasikan gambaran pengertian hitam dan putih. Seringkali

juga, saat sesuatu itu merupakan anggota dari sebuah crisp set maka ia kemudian

(pada waktu yang sama) bukan merupakan anggota dari crisp set manapun. Kembali

hal ini menyederhanakan penggunaan logika dengan proses pemikiran semacam ini.

Konstruksi linguistik yang menggambarkan jenis pemikiran ini dapat benar – benar

berguna, terutama saat kategori crisp digunakan.

Pada himpunan tegas (crisp), nilai keanggotaan suatu item x dalam suatu

himpunan A, yang sering ditulis dengan µ A[x], memiliki 2 kemungkinan, yaitu :

• µA[1], yang berarti bahwa suatu item menjadi anggota dalam suatu himpunan,

atau

• µA[0], yang berarti bahwa suatu item tidak menjadi anggota dalam suatu

(17)

Untuk lebih jelasnya, bisa dilihat dari contoh dibawah ini :

Dari gambar diatas dapat dijelaskan bahwa:

• Apabila seseorang berusia 34 tahun, maka ia dikatakan MUDA (µMUDA[34]=1);

• Apabila seseorang berusia 35 tahun, maka ia dikatakan TIDAK MUDA (µMUDA[35]=0);

• Apabila seseorang berusia 35 tahun kurang 1 hari, maka ia dikatakan TIDAK MUDA (µMUDA[35-1hr]=0);

• Apabila seseorang berusia 35 tahun, maka ia dikatakan PAROBAYA (µPAROBAYA[35]=1);

• Apabila seseorang berusia 34 tahun, maka ia dikatakan TIDAK PAROBAYA (µPAROBAYA[34]=0);

• Apabila seseorang berusia 55 tahun, maka ia dikatakan PAROBAYA (µPAROBAYA[55]=1);

• Apabila seseorang berusia 35 tahun kurang 1 hari, maka ia dikatakan TIDAK PAROBAYA (µPAROBAYA[35-1hr]=0);

Dari sini bisa dikatakan bahwa pemakaian himpunan crisp untuk menyatakan umur

sangat tidak adil, adanya perubahan kecil saja pada suatu nilai mengakibatkan

perbedaan kategori yang cukup signifikan. Oleh karena itu digunakanlah himpunan

(18)

7

2.2 Fuzzy Set

Logika fuzzy lahir berdasarkan fenomena – fenomena alam yang serba tidak tepat dan

samar ditinjau dari cara berpikir manusia, dimana pada kenyataannya tidak ada suatu

kondisi atau pernyataan yang tepat 100% benar atau 100% salah. Untuk

mempresentasikan nilai ketidakpastian, Prof. Lotfi A. Zadeh mengembangkan suatu

teori berdasarkan conventional set yang disebut fuzzy set (himpunan fuzzy). Logika

fuzzy memberikan nilai yang spesifik pada setiap nilai dengan menentukan fungsi

keanggotaan (membership function) bagi tiap nilai input dari proses fuzzy (crisp

input) dan derajat keanggotaan (degree of membership) yaitu menyatakan derajat dari

crisp input sesuai membership function antara 0 sampai 1.

Menurut Prof. Lotfi A Zadeh, fuzzy set adalah sebuah kelas dari obyek dengan

serangkaian kesatuan dari grades of membership (nilai keanggotaan). Sebuah set

dikarakterisasikan oleh sebuah fungsi keanggotaan (karakteristik) yang memberikan

tiap obyek sebuah nilai keanggotaan yang rentang nilainya antara 0 dan 1. Gagasan

pencantuman (inclusion), penyatuan (union), persimpangan (intersection), pelengkap

(complement), hubungan (relation), kecembungan (convexity), dan sebagainya

diberikan pada set tersebut, dan berbagai macam sifat dari pemikiran ini dalam

konteks dari fuzzy set dibangun. Secara khusus, dalil untuk fuzzy set cembung

dibuktikan tanpa perlu fuzzy set terputus.

Aturan umum untuk teori fuzzy set dituliskan sebagai berikut:

dimana n merupakan jumlah kemungkinan.

Untuk lebih jelasnya mengenai himpunan fuzzy dapat dilihat pada contoh persoalan

(19)

Dengan adanya himpunan fuzzy memungkinkan seseorang untuk dapat masuk

kedalam 2 himpunan yang berbeda, MUDA dan PAROBAYA, PAROBAYA dan

TUA, dan sebagainya. Seberapa besar eksistensinya dalam himpunan tersebut dapat

dilihat pada nilai keanggotaannya. Dari gambar diatas, dapat dilihat bahwa :

• Seseorang yang berumur 40 tahun, termasuk dalam himpunan MUDA dengan µMUDA[40] = 0,25; namun dia juga termasuk dalam himpunan PAROBAYA

dengan µPAROBAYA[40] = 0,5.

• Seseorang yang berumur 50 tahun, termasuk dalam himpunan MUDA dengan µMUDA[50] = 0,25; namun dia juga termasuk dalam himpunan PAROBAYA

dengan µPAROBAYA[50] = 0,5.

Kalau pada himpunan crisp, nilai keanggotaan hanya ada 2 kemungkinan,

yaitu 0 atau 1, pada himpunan fuzzy nilai keanggotaan terletak pada rentang 0 sampai

1. apabila x memiliki nilai keanggotaan fuzzy µA[x] = 0 berarti x tidak menjadi

anggota himpunan A, demikian pula apabila x memiliki nilai keanggotaan fuzzy

µA[x] = 1 berarti x menjadi anggota penuh pada himpunan A.

2.3 Fuzzy Set Operation

Fuzzy set operation adalah operasi yang dilakukan pada fuzzy set. Operasi – operasi

ini merupakan generalisasi dari operasi crisp set. Terdapat lebih dari satu generalisasi

yang mungkin. Operasi – operasi yang paling banyak digunakan secara luas disebut

standard fuzzy set operations. Terdapat tiga operasi yaitu :

a) Fuzzy Union.

Fungsi keanggotaan dari Union dari dua fuzzy set A dan B dengan fungsi

keanggotaan µA dan µB berturut – turut ditetapkan sebagai maksimum dari

dua fungsi keanggotaan tersendiri. Ini disebut standar maksimum.

(

)

max ,

A B A B

(20)

9

b) Fuzzy Intersection.

Fungsi keanggotaan dari Intersection dari dua fuzzy set A dan B dengan fungsi

keanggotaan µA dan µB berturut – turut ditetapkan sebagai minimum dari dua

fungsi keanggotaan tersendiri. Ini disebut standar minimum.

(

)

min ,

A B A B

µ _∩ = µ µ .

c) Fuzzy Complements.

Fungsi keanggotaan dari Intersection dari sebuah fuzzy set A dengan fungsi

keanggotaan µ_A ditetapkan sebagai negasi dari fungsi keanggotaan yang

ditentukan. Ini disebut standar negasi.

A

A µ

µ _' =1− .

2.4 Sistem Fuzzy

Ada beberapa hal yang perlu diketahui dalam memahami system fuzzy, yaitu:

a. Variabel fuzzy

Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu system

fuzzy. Contoh : umur, temperature, permintaan, dsb.

b. Himpunan fuzzy

Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau

keadaan tertentu dalam suatu variabel fuzzy.

c. Semesta Pembicaraan

Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk

dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan

himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari

kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif

maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi

(21)

Contoh:

• Semesta pembicaraan untuk variabel umur: [0, +∞) • Semesta pembicaraan untuk variabel temperature : [0, 40]

d. Domain

Domain himpunan fuzzy adalah keseluruhan nilai yang di ijinkan dalam

semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy.

Seperti halnya semesta pembicaraan, domain merupakan himpunan bilangan

real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai

domain dapat berupa bilangan positif maupun negatif.

Contoh domain himpunan fuzzy:

• MUDA = [0, 45] • PAROBAYA = [35, 55] • TUA = [45, +∞).

2.5 Fungsi Keanggotaan (Membership Function).

Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukan

pemetaan titik – titik input data kedalam nilai keanggotaannya (sering juga disebut

dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1. Salah satu cara

yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah dengan melalui

pendekatan fungsi. Ada beberapa fungsi yang bisa digunakan.

Representasi Linier

Pada representasi linier, pemetaan input ke derajat keanggotaannya digambarkan

sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik

(22)

11

Ada 2 keadaaan himpunan fuzzy yang linier. Pertama, kenaikan himpunan

dimulai pada nilai domain yang memiliki derajat keanggotaan nol [0] bergerak ke

kanan menuju ke nilai domain yang memiliki derajat keanggotaan lebih tinggi.

Representasi Linier Naik :

Fungsi keanggotaan :

[ ]

( ) ( )

b

x

b

x

a

x

b

x

a

x

≥

≤











=

−

=

;

1

/

0

µ

Kedua, merupakan kebalikan yang pertama. Garis lurus dimulai dari nilai domain

dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak menurun ke

(23)

Representasi linier Turun :

[ ]

(

) (

)

b

x

b

x

a

b

x

b

x

≥

≤







=

−

=

;

0

/

µ

Representasi Kurva Segitiga

Kurva Segitiga pada dasarnya merupakan gabungan antara 2 garis (linier) seperti

(24)

13

[ ]

(

) (

)

(

) (

)

c x atau c x b b x a a x b c x b a b a x x ≥      ≤ ≤ ≤ ≤ ≤ − − = − − = = ; / ; / ; 0 µ

Representasi Kurva Trapesium

Kurva Trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa titik

yang memiliki nilai keanggotaan 1 ( Gambar ).

(25)

2.6 Program linier

Sebelum mengarah pada bagaimana fuzzy dibuat untuk kekurangan pada linier

programming, sebaiknya terlebih dahulu mengetahui apa itu optimasi.

Optimasi.

Optimasi adalah sarana untuk mengekspresikan model matematika yang

bertujuan memecahkan masalah dengan cara terbaik. Untuk tujuan bisnis, hal ini

berarti memaksimalkan keuntungan dan efisiensi serta meminimalkan kerugian, biaya

atau resiko. Hal ini juga berarti merancang sesuatu untuk meminimalisasi bahan baku

atau memaksimalisasi keuntungan. Adapun keinginan untuk memecahkan masalah

dengan model optimasi secara umum sudah digunakan pada banyak aplikasi.

Program Linier.

Program linier merupakan model umum yang dapat digunakan dalam

pemecahan masalah pengalokasian sumber-sumber yang terbatas secara optimal.

Masalah tersebut timbul apabila seseorang diharuskan untuk memilih atau

menentukan tingkat setiap kegiatan yang akan dilakukannya, di mana masing-masing

kegiatan membutuhkan sumber yang sama sedangkan jumlahnya terbatas. Secara

sederhana, dapat diambil contoh bagian produksi suatu perusahaan yang dihadapkan

pada masalah penentuan tingkat produksi masing-masing jenis produk dengan

memperhatikan batasan faktor-faktor produksi: mesin, tenaga kerja, bahan mentah,

dan sebagainya untuk memperoleh tingkat keuntungan maksimal atau biaya yang

minimal.

Pada masa modern sekarang, program linier masih menjadi pilihan dalam

upaya untuk memperoleh tingkat keuntungan maksimal atau biaya yang minimal.

Dalam memecahkan masalah di atas, Program linier menggunakan model matematis.

Sebutan “linier” berarti bahwa semua fungsi matematis yang disajikan dalam model

ini haruslah fungsi-fungsi linier. Dalam Program linier dikenal dua macam fungsi,

yaitu fungsi tujuan (objective function) dan fungsi-fungsi batasan (constraint

function). Fungsi tujuan adalah fungsi yang menggambarkan tujuan/sasaran di dalam

permasalahan program linier yang berkaitan dengan pengaturan secara optimal

(26)

15

minimal. Pada umumnya nilai yang akan dioptimalkan dinyatakan sebagai Z. Fungsi

batasan merupakan bentuk penyajian secara matematis batasan-batasan kapasitas yang

tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.

Agar dapat menyusun dan merumuskan suatu persoalan atau permasalahan

yang dihadapi ke dalam model program linier, maka ada lima syarat yang harus

dipenuhi:

1. Tujuan

Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dipecahkan

dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi

tujuan.

2. Alternatif perbandingan

Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan;

misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu

terlambat dan biaya terendah.

3. Sumber daya

Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas

4. Perumusan kuantitatif

Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif dalam

apa yang disebut model matematika.

5. Keterkaitan peubah

Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut harus

(27)

Model Dasar

Model dasar program linier dapat dirumuskan sebagai berikut:

Carilah nilai-nilai X₁,X₂,…,X_n_{yang dapat menghasilkan berbagai} kombinasi optimum (maksimum atau minimum) dari:

) . ( 2 2 1 1 tujuan fungsi X C X C X C

Z = + +…+ _n _n

(2.1)

Dengan syarat bahwa fungsi tujuan tersebut memenuhi kendala-kendala atau syarat-syarat ikatan sebagai berikut:

1 1

2 12 1

11X a X a X atau b

a + +…+ _n _n ≤ ≥

2 2

2 22 1

21X a X a X atau b

a + +…+ _n _n ≤ ≥

⋮ ⋮ ⋮ ⋮⋮

m n

mn m

m X a X a X atau b

a + +…+ ≤ ≥

2 2 1

1 (2.2)

dan bahwa: X_j ≥0,untuk j=1,2,…,n _(2.3)

Keterangan:

=

j

C Parameter yang dijadikan kriteria optimisasi, atau koefisien peubah

pengambilan keputusan dalam funsi tujuan.

= j

X Peubah pengambilan keputusan atau kegiatan (yang ingin dicari; yang

tidak diketahui).

= ij

a Koefisien teknologi peubah pengambilan keputusan (kegiatan yang

bersangkutan) dalam kendala ke-i.

=

i

b Sumber daya yang terbatas, yang membatasi kegiatan atau usaha yang bersangkutan; disebut pula konstanta atau “nilai sebelah kanan” dari kendala ke-i.

=

Z Nilai skalar kriteria pengambilan keputusan; suatu fungsi tujuan.

(28)

17

Asumsi – asumsi program linier

1. Linieritas

Asumsi ini menginginkan agar perbandingan antara input yang satu dengan

input lainnya, atau untuk suatu input dengan output besarnya tetap dan terlepas

(tidak tergantung) pada tingkat produksi.

2. Proposionalitas

Asumsi ini menyatakan bahwa jika peubah pengambilan keputusan, X _j

berubah maka dampak perubahannya akan menyebar dalm proposi yang sama

terhadap fungsi tujuan, C_jX_j, dan juga pada kendalanya, a_ijX_j.

3. Aditivitas

Asumsi ini menyatakan bahwa nilai parameter suatu kriteria optimisasi

(koefisien peubah pengambilan keputusan dalam fungsi tujuan) merupakan jumlah

dari nilai individu-individu C dalam model PL tersebut. _j

4. Divisibilitas

Asumsi ini menyatakan bahwa peubah-peubah pengambilan keputusan X_j,

jika diperlukan dapat dibagi ke dalam pecahan-pecahan.

5. Deterministik

Asumsi ini menghendaki agar semua parameter dalam PL (yaitu nilai – nilai

j

C , a , dan ij bi) tetap dan dikehendaki atau ditentukan secara pasti.

Metode Simpleks

Apabila suatu masalah Linier Programming hanya mengandung dua kegiatan

(variabel-variabel keputusan) saja, maka dapat diselesaikan dengan metode grafik.

(29)

sehingga diperlukan metode simpleks. Metode ini lazim dipakai untuk menentukan

kombinasi dari tiga variabel atau lebih.

Masalah Program linier yang melibatkan banyak variabel keputusan dapat

dengan cepat dipecahkan dengan bantuan komputer. Bila variabel keputusan yang

dikandung tidak terlalu banyak, masalah tersebut dapat diselesaikan dengan suatu

algoritma yang biasanya sering disebut metode tabel simpleks. Disebut demikian

karena kombinasi variabel keputusan yang optimal dicari dengan menggunakan

tabel-tabel.

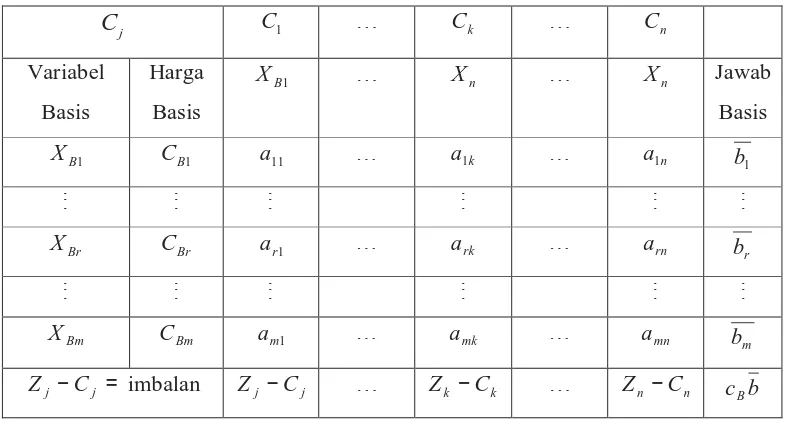
Tabel 2.1 Bentuk tabel simpleks

j

C

C1 … Ck … Cn

Variabel

Basis

Harga

Basis

1 B

X …

n

X …

n

X Jawab

Basis

1 B

X C_B₁ a₁₁ …

k

a1 … a1n b ₁

⋮ ⋮ ⋮ ⋮ ⋮ ⋮

Br

X C_Br a_r₁ …

rk

a …

rn

a _b_r

⋮ ⋮ ⋮ ⋮ ⋮ ⋮

Bm

X C_Bm a_m₁ …

mk

a …

mn a

m b

= − j j C

Z imbalan Zj −Cj … Zk −Ck … Zn −Cn cBb

Sebelum menyelesaikan suatu tabel simpleks terlebih dahulu menginisialisasikan dan

merumuskan suatu persoalan keputusan kedalam model matematik persamaan linier,

caranya sebagai berikut:

1. Konversikan semua ketidaksamaan menjadi persamaan.

Agar persamaan garis batasan memenuhi persyaratan penyelesaian pada daerah

kelayakan (feasible) maka model program linier diubah menjadi suatu model yang

(30)

19

variabel) pada tiap batasan (constraint) serta memberi harga nol kepada setiap

koefisien C nya. Batasan dapat di modifikasi sebagai berikut:

a. Untuk batasan bernotasi

( )

≤ dapat dimodifikasikan kepada bentuk persamaan dengan menambahkan variabel slack ke dalam nya.

b. Untuk batasan bernotasi ≥ atau

( )

= diselesaikan dengan menambahkan variabel surplus dan variabel buatan. Dengan penambahan variabel buatan

ini akan merusak sistem batasan, hal ini dapat diatasi dengan membuat suatu

bilangan besar M sebagai harga dari variabel buatan tersebut dalam fungsi

tujuan. Jika persoalan maksimal maka dibuat –M sebagai harga, dan jika

persoalan minimal dibuat +M sebagai harga dari variabel buatan. Cara

pendekatan ini dikenal dengan metode M besar (Big M method).

Penambahan variabel slack dan variabel buatan (artificial variabel) pada tiap batasan

(constrain) untuk persoalan maksimal dapat dirumuskan sebagai berikut:

Maksimalkan:

∑

+ = = − = m m i i j n j

jx M B c

Z

1

1 1

(2.4)

Dengan batasan :

1 1 , , 2 , 1

,i m

b x x

a _j _i _i n

j

ij + = = …

∑

=

(untuk batasan bernotasi ≤ ) (2.5)

2 1 1 1 , , 1

,i m m m

b B x

a _j _i _i n

j

ij + = = + +

∑

=

… _{(untuk batasan bernotasi = )} _(2.6)

m m m i b B x x

a _j _i _i _i n

j

ij , 1 2 1 ,

1 … + + = = + −

∑

=

(untuk batasan bernotasi ≥ ) (2.7)

0 ≥ j

x , xi ≥0, Bi ≥0, bi ≥0 untuk semua harga i dan j

n j

(31)

[image:31.612.133.531.132.352.2]

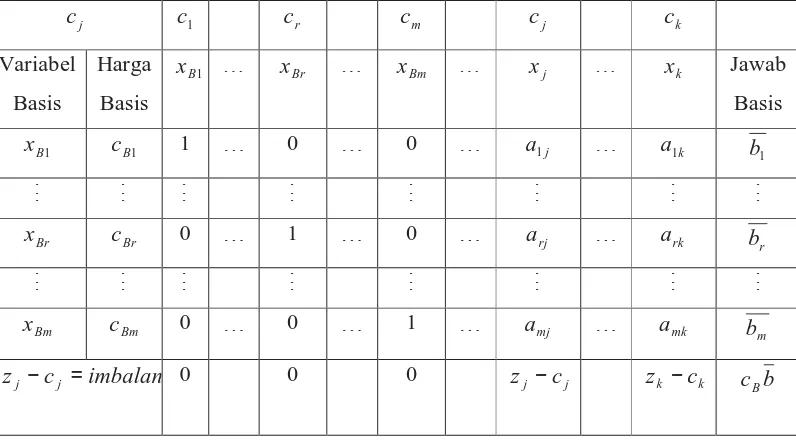
2. Menyusun persamaan – persamaan di dalam tabel awal simpleks.

Tabel 2.2 Bentuk tabel awal simpleks sebelum pivoting

j

c c₁ c_r c_m c_j c_k

Variabel Basis Harga Basis 1 B x … Br

x …

Bm

x …

j

x …

k

x Jawab

Basis

1 B

x c_B₁ 1 … ₀ … ₀ …

j

a₁ …

k a₁ 1 b ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ Br

x c_Br 0 … 1 … 0 … rj a … rk a r b ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ Bm

x c_Bm 0 … 0 … 1 …

mj a … mk a m b imbalan c

z_j − _j = 0 0 0 z_j −c_j z_k −c_k _c _b B

Langkah – langkah yang digunakan untuk menyelesaikan suatu tabel simpleks

adalah sebagai berikut:

Langkah 1 : Mengecek nilai optimal imbalan.

Untuk persoalan maksimal : z_k −c_k = minimal {z_j −c_j : j∈R}. Jika

k k c

z − ≥0 maka selesai, berarti jawab atau solusi sudah optimal.

Untuk persoalan minimal : z_k −c_k = maksimal {z_j −c_j : j∈R}. Jika

k k c

z − ≤0 maka selesai, berarti jawab atau solusi sudah optimal.

Harga – harga imbalan (zj −cj) dapat diperoleh dengan rumus :

j ij m j Bi j

j

c

a

c

z

−

=

∑

−

=1

(32)

21

Untuk : c_j = Harga dari semua variabel dalam z .

= ij

a Koefisien dari semua variabel dalam sistem batasan.

= Bi

c Harga dari variabel.

Langkah 2 : Menentukan variabel yang akan masuk dalam basis.

Untuk persoalan maksimal jika terdapat beberapa z_j−c_j ≤0 maka

kolom yang menjadi kolom pivot adalah kolom dengan z_j −c_j terkecil, dan variabel

yang sehubungan dengan kolom pivot adalah variabel yang masuk kedalam basis.

Untuk persoalan minimal jika terdapat beberapa z_j −c_j ≥0 maka kolom yang

menjadi kolom pivot adalah kolom dengan z_j−c_j terbesar, dan variabel yang

sehubungan dengan kolom pivot adalah variabel yang masuk ke dalam basis.

Langkah 3 : Menentukan variabel yang akan keluar dari basis.

Menetapkan variabel yang keluar dari basis yaitu :

imum

m i rk

r a

b

min

1≤≤ =

  

  

>0 : _ik ik

a a

b

Variabel yang sehubungan dengan baris pivot

yang demikian adalah variabel yang keluar dari basis.

Langkah 4 : Menyusun tabel simpleks baru.

Untuk menyusun tabel simpleks yang baru, maka harus mencari

koefisien elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat

dicari dengan menghubungkan kolom pivot dengan baris pivot sedemikian rupa

sehingga titik potong kedua pivot ini menunjukkan koefisien, yang disebut elemen

pivot, Koefisien – koefisien baris pivot baru dapat dicari dengan menggunakan rumus

sebagai berikut :

rk rj a a

(33)

Untuk menghitung nilai baris baru lainnya dilakukan dengan menggunakan rumus

sebagai berikut :

ik rk rj ij a a a

a − − (2.10)

Langkah 5 : Mengecek nilai optimal imbalan dari tabel simpleks yang baru.

Jika imbalan sudah optimal maka tafsirkan hasil penyelesaian, jika

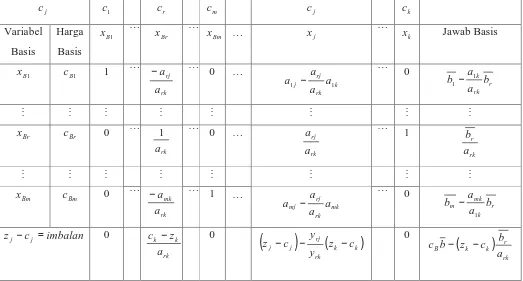
[image:33.612.46.569.290.571.2]

belum optimal maka kembali kepada langkah 2.

Tabel 2.3 Bentuk tabel simpleks sesudah pivoting

j

c c₁ c_r c_m c_j c_k

Variabel Basis Harga Basis 1 B

x … x _Br … x_Bm …

j

x … x _k Jawab Basis

1 B

x c_B₁ 1 …

rk rj a

a

− … 0 …

k rk rj j a a a a₁ − ₁

… 0 r rk k _b a a b 1 1− ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ Br

x c_Br 0 …

rk a

1 … 0 …

rk rj a

a … 1

rk r a b ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ Bm

x cBm 0

…

rk mk a

a

− … 1 …

mk rk rj mj a a a a − … 0 r k mk m b a a b 1 − imbalan c

z_j− _j = 0

rk k k

a z

c − 0

(

)

(

k k

)

rk rj j

j z c

y y c

z − − − 0

(

)

rk r k k B a b c z b

(34)

23

Contoh 2.1

Maksimumkan : z=3x₁+4x₂

Kendala 2x1+x2 ≤6

9 3 2x₁+ x₂ ≤

1

x , x2≥0

Solusi :

Maksimumkan z=3x₁+4x₂+0x₃+0x₄

Kendala 2x₁+x₂ +x₃+0x₄ =6

9 0

3

2x1+ x2+ x3 +x4 =

0 , , , ₂ ₃ ₄ 1 x x x ≥ x

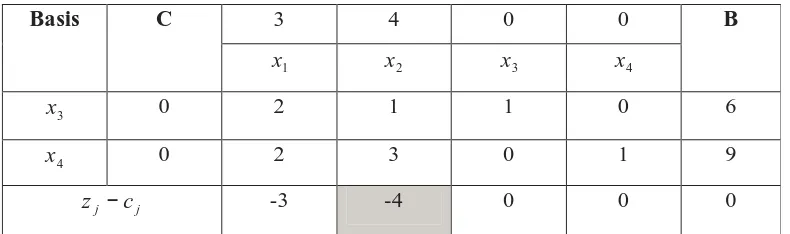
[image:34.612.126.521.484.601.2]

Model diatas dapat dibawa ke bentuk tabel simpleks sebagai berikut :

Tabel 2.4 Tabel simpleks untuk iterasi 1

Basis C 3 4 0 0 B

1

x x 2 x 3 x 4

3

x 0 2 1 1 0 6

4

x 0 2 3 0 1 9

j j c

z − -3 -4 0 0 0

Dari tabel 2.4 diatas, tampak bahwa penyelesaian optimal belum dicapai, karena nilai

j j c

z − masih bernilai < 0 (masih mengandung harga negatif). Harga z_j−c_j terkecil

dari tabel diatas adalah -4, sehingga variabel yang masuk dalam basis adalah variabel

2

x , kolom variabel x₂ menjadi kolom pivot, harga x₂ maksimal yang diperkenankan

(35)

      = = = 3 3 9 ; 6 1 6 2 Min x

Harga x₂ =3 adalah nilai terkecil (positif) sehubungan dengan variabel x₄, sehingga

variabel yang meninggalkan basis ialah x₄, kemudian digantikan dengan variabel x₂,

[image:35.612.128.517.227.346.2]

maka tabel simpleks yang baru adalah :

Tabel 2.5 Tabel simpleks untuk iterasi 2

Basis C 3 4 0 0 B

1

x x₂ x₃ x₄

3

x 0 1,3333 0 1 -0,3333 3

2

x 4 0,6667 1 0 0,3333 3

j j c

z − -0,3333 0 0 1,3333 12

Dari tabel 2.5 diatas, maka tampak bahwa penyelesaian optimal belum dicapai, karena

nilai zj−cj masih bernilai < 0 (masih mengandung harga negatif). Harga zj−cj

terkecil dari tabel diatas adalah -0,3333, sehingga variabel yang masuk dalam basis

adalah variabel x , kolom variabel ₁ x menjadi kolom pivot, harga ₁ x maksimal yang ₁

diperkenankan adalah :

      = =

= 4,5

6667 , 0 3 ; 25 , 2 333 , 1 3 1 Min x

Harga x₁ =2,25 adalah nilai terkecil (positif) sehubungan dengan variabel x , ₃

sehingga variabel yang meninggalkan basis ialah x₃, kemudian digantikan dengan

variabel x₁, maka tabel simpleks yang baru adalah :

Tabel 2.6 Tabel simpleks untuk iterasi 3

Basis C 3 4 0 0 B

1

[image:35.612.130.519.676.722.2]

(36)

25

1

x 3 1 0 0,75 -0,25 2,25

2

x 4 0 1 -0,5 0,5 1,5

j j c

z − 0 0 0,25 1,25 12,75

Dari tabel 2.6 tidak ada lagi z_j −c_j<0, dengan demikian telah dicapai penyelesaian

optimal:

25 , 2 1=

x ; x₂ =1,5 ; z=12,75

2.7 Fuzzy Linier Programming.

Pada Fuzzy Linier Programming, bentuk persamaan akan mengalami sedikit

perubahan sebagai berikut :

• Bentuk imperatif pada fungsi obyektif tidak lagi benar-benar “maksimum” atau “minimum”, karena adanya beberapa hal yang perlu mendapat

pertimbangan dalam suatu sistem.

• Tanda ≤ (pada batasan) dalam kasus maksimasi dan tanda ≥ (pada batasan) dalam kasus minimasi tidak lagi bermakna crisp secara matematis, namun

sedikit mengalami pelanggaran makna. Hal ini juga disebabkan karena adanya

beberapa yang perlu dipertimbangkan dalam sistem yang mengakibatkan

(37)

Defenisi 3.1

Sepasang fungsi T =

(

u

( ) ( )

r,u r

)

, 0≤r≤1, disebut fuzzy number jika dan hanya jika mengikuti kebutuhan :

(1). u

( )

r adalah batas kontinu sebelah kiri fungsi tidak turun

[ ]

0,1

(2). u

( )

r adalah batas kontinu sebelah kiri fungsi tidak naik

[ ]

0,1

(3). u

( )

r dan u

( )

r kontinu kanan pada 0

(4). u

( ) ( )

r ≤u r , 0≤r ≤1

dimanau

( )

r =wr+

(

c−w

)

dan u

( )

r =−wr +

(

c+w

)

, 0≤r ≤1. yang mana

( )

T Core c

R w

c, ∈ , = dan w=W

( )

T ≥0.

( )

c w

T = , disebut Symmetric Triangular Fuzzy Number (STFN). Andaikan ST menjadi

himpunan dari STFN. Bilangan crisp direpresentasikan dengan u

( ) ( )

r =u r =α, 1

0≤r≤

Teorema 3.1

Jika T =

(

c₁,w₁

)

,U =

(

c₂,w₂

)

adalah STFNs, k∈R,X ∈STdan A adalah sebuah matrik maka :

1. T =Ujika dan hanya jika c₁ =c₂dan w₁ =w₂

2. T +U =

(

c₁+c₂,w₁+w₂

)

3. kT =

(

kc₁,kw₁

)

(38)

27

Defenisi 3.2

Andaikan T =

(

c₁,w₁

)

,U =

(

c₂,w₂

)

anggota SFTNs. katakan T <~Ujika dan hanya jika:

1. c₁ <c₂ atau

2. c₁ =c₂ dan w₁ <w₂

Dan T ≤~Ujika dan hanya jika T <~U atau T =U.

2.8 Permasalahan Linier Fuzzy.

Berdasarkan program linier fuzzy :

Min CX~

Kendala AX~ =b~

0 ~ ~ , ~

≥ ∈ST X

X (2.11)

Yang mana m n n

C

A∈ℜ × , ∈ℜ dan b~ adalah sebuah vektor fuzzy triangular. Sekarang

bagi persoalan (2.11) menjadi 2 permasalahan.

Min CX~

Kendala AX =Core(b)

0 ≥

X (2.12)

(39)

Min CY

Kendala AY =W(b)

0 ≥ Y

Dimana , _i.

i ij

ij a C c

A = = (2.13)

Teorema 3.2

X~ adalah solusi yang layak dari permasalahan (2.11) jika dan hanya jika

( )

X

Core

X = ~ adalah solusi yang layak dari permasalahan (2.12) dan Y =W

( )

X~

adalah solusi dari permasalahan (2.13).

Teorema 3.3

* ~

X adalah solusi optimal dari permasalahan (2.11) jika dan hanya jika

( )

~*

* ~

X Core

X = adalah solusi optimal dari permasalahan (2.12) dan Y*=W

( )

X~*

adalah solusi optimal dari permasalahan (2.13).

Teorema 3.4

Permasalahan (2.11) adalah tidak layak jika dan hanya jika permasalahan (2.12)

adalah tidak layak atau permasalahan (2.13) adalah tidak layak.

Teorema 3.5

(40)

Bab 3

PEMBAHASAN

3.1 Program Integer.

Program integer atau dikenal dalam bahasa Inggris dengan integer programming

merupakan bentuk khusus atau variasi dari program linier atau program nonlinier, di

mana satu atau lebih dari peubah – peubahnya dalam vektor penyelesaiannya memiliki

nilai – nilai bukan pecahan atau angka bulat yang disebut integer

Suatu peubah disebut integer, jika peubah tersebut hanya diperkenankan

memiliki nilai – nilai integer yang terletak di antara batas yang tetap (fixed bounds).

Misalnya, jika peubah X hanya dapat memiliki nilai – nilai -1, 0, 1, dan 2; maka

disebut nilai – nilai integer yang terletak di antara selang -1 dan +2.

3.2 Model Dasar

Model umum dari suatu program integer adalah sebagai berikut :

Optimumkan (maksimumkan atau minimumkan)

j n

i jX C Z

∑

=

1

(3.1)

Syarat ikatan :

j n

i ijX a

∑

=1

≤ atau ≥b_i (3.2)

Dan Xj ≥0 i=1,2, ,m (3.4)

j

(41)

3.3 Percabangan (Branching)

Jika aproksimasi pertama mengandung variabel yang tidak bulat, katakanlahx_j*,

maka i₁< x_j*<i₂, di mana i₁ dan i₂ adalah dua bilangan bulat tak negatif yang

berturutan. Dari sini kemudian dibentuk dua program bilangan bulat yang baru dengan

cara memperluas program bilangan bulat semula dengan kendala x_j ≤i₁ atau kendala

2 i

x_j ≥ . Proses ini disebut pencabangan (branching), yang mempunyai efek

mempersempit daerah layak sedemikian rupa sehingga mengeliminasi pemecahan

bilangan tak bulat bagi x dari tinjauan selanjutnya tetapi masih tetap _j

mempertahankan semua pemecahan bilangan bulat yang mungkin terhadap persoalan

yang semula.

3.4 Pembatasan (Bounding)

Anggaplah bahwa fungsi obyektifnya akan dimaksimumkan. Proses pencabangan akan

terus dilakukan hingga diperoleh sebuah pendekatan pertama yang bulat (yang mana

adalah suatu pemecahan bilangan bulat). Nilai dari obyektif bagi pemecahan bilangan

bulat yang pertama ini menjadi suatu batas terbawah bagi persoalan ini dan semua

program yang aproksimasi pertamanya, bulat atau pun tidak, menghasilakan nilai –

nilai dari fungsi obyektif yang lebih kecil daripada batas terbawah ini diabaikan.

Pencabangan ini terus berlanjut dari program – program yang memiliki

aproksimasi pertama tak bulat yang memberikan nilai – nilai fungsi obyektif yang

lebih besar daripada batas terbawah. Jika dalam proses percabangan ini, ditemukan

sebuah pemecahan bilangan bulat baru, yang nilai fungsi obyektifnya lebih besar

daripada batas terbawah yang ditinjau, maka nilai dari fungsi obyektif itu menjadi

batas terbawah yang baru. Program yang menghasilkan batas terbawah yang lama

selanjutnya diabaikan, begitu pula program – program yang pendekatan – pendekatan

pertamanya memberikan nilai – nilai fungsi obyektif yang lebih kecil daripada batas

terbawah yang baru ini. Proses pencabangan ini terus berlanjut hingga tidak ada bagi

program – program dengan pendekatan pertama tak-bulat yang ditinjau. Pada tahap

(42)

31

bulat yang sama. Jika fungsi obyektifnya hendak diminimumkan, maka prosedurnya

tetap sama, kecuali bahwa yang digunakan adalah batas teratas (upper bounds).

Contoh 3.1:

Maksimumkan : z=3x₁+4x₂

Kendala 2x₁+x₂ ≤6

9 3 2x₁+ x₂ ≤

1

x dan x₂ bulat tak negatif

Dengan mengabaikan persyaratan bilangan bulat, diperoleh

5 , 1 , 25 , 2 ₂* *

1 = x =

x dengan _z* =12,75

sebagai pemecahan program linier yang

bersangkutan. Karena x lebih jauh menyimpang dibandingkan dengan ₂* x , maka ₁*

yang akan digunakan untuk membentuk cabang – cabang adalah x2 ≤1 dan x2 ≥2.

Program 2 Program 3

Maksimumkan: z=3x₁+4x₂ maksimumkan: z=3x₁+4x₂

Kendala: 2x₁+x₂ ≤6 kendala: 2x₁+x₂ ≤6

2x₁+3x₂ ≤9 2x₁+3x₂ ≤9

1 2 ≤

x x₂ ≥2

1

x dan x₂ bulat tak negatif x₁ dan x₂ bulat tak negatif

Aproksimasi pertama bagi program 2 adalah x₁* =2,5, x₂* =1 dengan

5 , 11 * ₌

z . Aproksimasi pertama program 3 adalah x₁* =1,5, x₂* =2 dengan

5 , 12 * =

z . Karena program 2 dan 3 memiliki aproksimasi pertama yang tak-bulat,

(43)

harga fungsi obyektif yang terbesar (mendekati optimal). Disini 1<x₁* <2 sehingga

program – program yang barunya adalah:

Program 4 Program 5

2x₁+3x₂ ≤9 2x₁+3x₂ ≤9

2 2 ≥

x x₂ ≥2

1 1 ≤

x x₁ ≥2

1

x dan x bulat tak negatif ₂ x dan ₁ x bulat tak negatif ₂

Ternyata tidak ada pemecahan bagi program 5, sedangkan program 4 adalah

1 * 1 =

x ,

3 7 * 2 =

x , dengan z* =12,33. Percabangan dapat dilanjutkan dari program 2

ataupun program 4. Dipilih program 4 karena memiliki nilai z yang terbesar. Disini

3

2< x₂* < maka program yang barunya adalah

Program 6 program 7

2x₁+3x₂ ≤9 2x₁+3x₂ ≤9

2 2 ≥

x x₂ ≥2

1 1 ≤

x , x₂ ≤2 x₁ ≤1, x₂ ≥3

1

(44)

33

Pemecahan bagi program 6 adalah x₁* =1, x₂* =2 dengan z* =11. Karena ini

berbentuk pemecahan bilangan bulat, maka z = 11 menjadi suatu batas terbawah bagi

persoalan ini. Dengan demikian, setiap program yang menghasilkan suatu nilai-z yang

lebih kecil daripada 11 akan dikesampingkan. Pendekatan pertama bagi program 7

adalah x₁* =0, x₂* =3 dengan z* =12. Karena hasil ini berbentuk pemecahan

bilangan bulat dengan nilai-z yang lebih besar daripada batas terbawah sebelumnya,

maka z* =12 menjadi batas terbawah baru, dan program 6 dikesampingkan. Dengan

demikian, cabang ini memberikan pemecahan optimal bagi program 1 : x₁* =0,

3 * 2 =

x dengan z* =12.

3.5 Fuzzy integer linier programming

Pada bagian ini Fuzzy Integer Linier Programming (FILP) akan dibagi menjadi dua

Integer Linier Programmng (ILP).

n T S I X b X A X C X Kendala Min . . ~ ~ ~ , 0 ~ * ∈ =      ≥ (3.6)

dimana A∈ℜm×n,C∈ℜn dan b~ adalah sebarang vektor bilangan fuzzy.

Persamaan FILP yang baru:

n T S I X T X A X C X Kendala Min . . ~ ~ ~ , 0 ~ * ∈ =      ≥ (3.7)

(45)

Persamaan (3.6) mengurangi persamaan (3.7), berdasarkan dua permasalahan tersebut maka :

( )

n T S I X T Core X A X C X Kendala Min . . ~ ~ ~ , 0 ~ * ∈ =      ≥ (3.8)

Dimana _A∈ℜm×n_,_C∈ℜn_dan_T∈_S_._Tm_{dan elemen ke t}_Core

( )

_T _{adalah inti dari} elemen ke i dari T.

Dan

( ) (

)

n T S I X br b br b T H X A X C X Kendala Min . . ~ , ~ ~ , 0 ~ * ∈ − + − = =      ≥ (3.9)

Dimana A∈ℜm×n,C∈ℜn dan T∈S.Tm dan H

( )

T =T−Core

( )

T . Ini berarti bahwa, jika

( )

c;w adalah solusi dari (3.9) maka w adalah bilangan integer.

Catatan bahwa :

( )

(

H T

)

=Core

( )

T −Core

(

Core

( )

T

)

=Core

( )

T −Core

( )

T =0

Core .

3.6 Contoh Numerik :

Untuk memudahkan pemahaman prinsip penyelesaian program fuzzy integer linier

dengan menggunakan teknik branch and bound, diambil contoh sebagai berikut :

Max 7~x₁+9~x₂

Kendala −x~₁+3~x₂ +~x₃ =

(

1+5r,11−5r

)

+

+ 2 1 ~ ~

7x x x~4 =

(

30+5r,40−5r

)

0 ~ , ~ , ~ , ~ 4 3 2

1 x x x ≥ x

Z x x x

(46)

35

Solusi :

Terlebih dahulu persoalan diatas dibagi menjadi dua Program linier yaitu :

Permasalahan 1

Max 7x₁+9x₂

Kendala −x₁+3x₂ +x₃ =6

+ + 2 1

7x x x₄ =35

0 , , , ₂ ₃ ₄ 1 x x x ≥ x

Z x x x

x₁, ₂, ₃, ₄∈

Dengan menggunakan metode simpleks persoalan tersebut dapat di selesaikan

[image:46.612.127.519.317.435.2]

sebagai berikut :

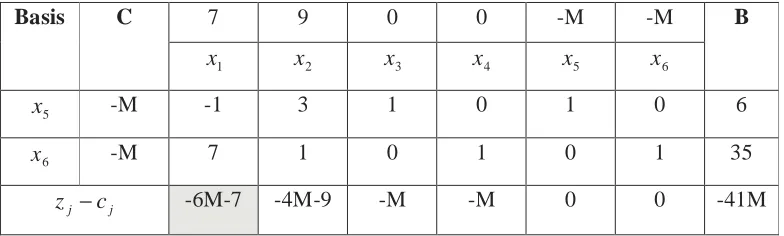
Tabel 3.1 Tabel simpleks untuk iterasi 1

Basis C 7 9 0 0 -M -M B

1

x x₂ x₃ x₄ x₅ x₆

5

x -M -1 3 1 0 1 0 6

6

x -M 7 1 0 1 0 1 35

j j c

z − -6M-7 -4M-9 -M -M 0 0 -41M

j j c

z − masih bernilai < 0 (masih mengandung harga negatif). Harga zj−cj terkecil

dari tabel diatas adalah -6M-7, sehingga variabel yang masuk dalam basis adalah

variabel x₁, kolom variabel x₁ menjadi kolom pivot, harga x₁ maksimal yang

      = − = − = 5 7 35 ; 6 1 6 1 Min x

Harga x₁ =5 adalah nilai positif terkecil sehubungan dengan variabel x , sehingga ₆

variabel yang meninggalkan basis ialah x , kemudian digantikan dengan variabel ₆ x , ₁

(47)

[image:47.612.87.568.104.224.2]

Tabel 3.2 Tabel simpleks untuk iterasi 2

Basis C 7 9 0 0 -M -M B

1

x x2 x3 x4 x5 x6

5

x -M 0 3,1429 1 0,1429 1 0,1429 11

1

x 7 1 0,1429 0 0,1429 0 0,1429 5

j j c

z − 0 -3,1429M-7,9997 -M -0,1429M+1,0003 0 0,8571M+1,0003 -11M+5

j j c

dari tabel diatas adalah -3,1429M-7,9997 , sehingga variabel yang masuk dalam basis

adalah variabel x₂, kolom variabel x₂ menjadi kolom pivot, harga x₂ maksimal yang

   

 

= =

= 35

1429 , 0

5 ; 5 , 3 1429 , 3

11 2 Min x

Harga x₂ =3,5 adalah nilai positif terkecil sehubungan dengan variabel x₅, sehingga

variabel yang meninggalkan basis ialah x₅, kemudian digantikan dengan variabel x₂,

maka tabel simpleks yang baru adalah :

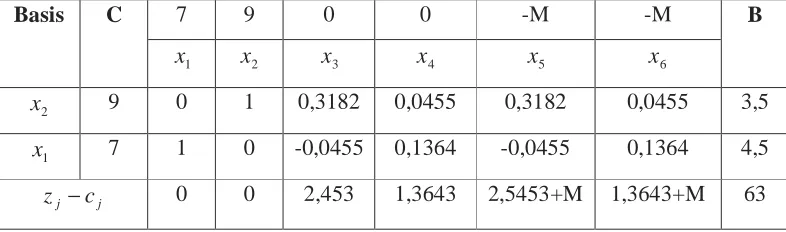
Tabel 3.3 Tabel simpleks untuk iterasi 3

Basis C 7 9 0 0 -M -M B

1

x x2 x3 x4 x5 x6

2

x 9 0 1 0,3182 0,0455 0,3182 0,0455 3,5

1

x 7 1 0 -0,0455 0,1364 -0,0455 0,1364 4,5

j j c

z − 0 0 2,453 1,3643 2,5453+M 1,3643+M 63

Dari tabel 3.3 tidak ada lagi z_j −c_j<0, dengan demikian telah dicapai penyelesaian

[image:47.612.128.521.525.641.2]

(48)

37

Agar permasalahan fuzzy ini mempunyai solusi yang bernilai integer, maka akan

digunakan metode branch and bound :

Maksimumkan : 7x₁+9x₂

Kendala −x₁+3x₂ +x₃ =6

+ + 2 1

7x x x4 =35

1

x , x , ₂ x dan ₃ x bulat tak negatif ₄

Dengan mengabaikan persyaratan bilangan bulat, diperoleh x₁* =4,5;

5 , 3 * 2 =

x ; 6* 0

* 5 * 4 *

3 =x =x =x =

x dengan z=63 sebagai pemecahan program linier

yang bersangkutan. Karena x lebih jauh menyimpang dibandingkan dengan ₂* x , ₁*

maka yang akan digunakan untuk membentuk cabang – cabang adalah 3<x*2 <4

Program 2 Program 3

Maksimumkan: 7x₁+9x₂ maksimumkan: 7x₁+9x₂

Kendala: −x₁+3x₂+x₃ =6 kendala: −x₁+3x₂+x₃ =6

7x₁+x₂ + x₄ =35 7x₁+x₂ + x₄ =35

3 * 2 ≤

x x2* ≥4

1

x , x , ₂ x dan ₃ x bulat tak negatif ₄ x , ₁ x , ₂ x dan ₃ x bulat tak negatif ₄

Aproksimasi pertama bagi program 2 adalah x₁* =4,5714; x₂* =3;

5714 , 1 * 3 =

x ; x₄* =x₅* =x₆* =0 dengan z=59. Aproksimasi pertama program 3

adalah tidak mempunyai solusi yang layak. Karena program 2 memiliki aproksimasi

pertama yang tak-bulat, maka dapat dibentuk percabangan yang baru.. Disini

2

(49)

Program 4 Program 5

Maksimumkan: 7x₁+9x₂ maksimumkan: 7x₁+9x₂

Kendala: −x₁+3x₂+x₃ =6 kendala: −x₁+3x₂+x₃ =6

7x₁+x₂ + x₄ =35 7x₁+x₂ + x₄ =35

3 * 2 ≤

x x₂* ≥4

1 * 3 ≤

x x₃* ≥2

1

x , x , ₂ x dan ₃ x bulat tak negatif ₄ x , ₁ x , ₂ x dan ₃ x bulat tak negatif ₄

Ternyata tidak ada pemecahan bagi program 5, sedangkan program 4 adalah

4 * 1 =

x ; x₂* =3; x₃* =1; x₄* =4dengan z* =55. Karena ini berbentuk pemecahan

bilangan bulat, maka z = 55 menjadi suatu batas terbawah bagi persoalan ini. Dengan

demikian, setiap program yang menghasilkan suatu nilai-z yang lebih kecil daripada

55 akan dikesampingkan. Dengan demikian, cabang ini memberikan pemecahan

optimal bagi program 1 : x1* =4; 3 * 2 =

x ; x3* =1; 4 * 4 =

x dengan z* =55. Dengan

menggunakan metode branch and bound di dapat solusi integer 4

3

1

4 X

      =_{ }    

Permasalahan 2

Max 7y₁+9y₂

Kendala y₁+3y₂ +y₃ =5

+ + 2 1

7y y y₄ =5

0 , , , ₂ ₃ ₄ 1 y y y ≥ y

Z y y y

(50)

39

Dengan menggunakan metode simpleks persoalan tersebut dapat di selesaikan sebagai

[image:50.612.127.519.144.262.2]

berikut :

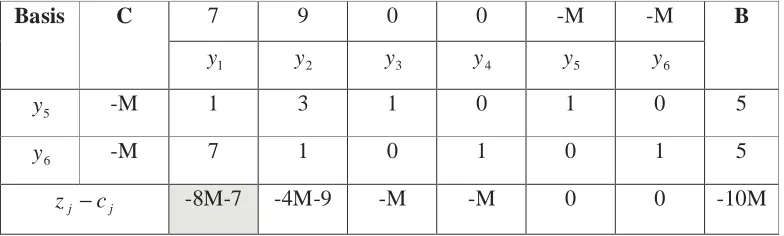
Tabel 3.4 Tabel simpleks untuk iterasi 1

Basis C 7 9 0 0 -M -M B

1

y y 2 y 3 y 4 y 5 y 6

5

y -M 1 3 1 0 1 0 5

6

y -M 7 1 0 1 0 1 5

j j c

z − -8M-7 -4M-9 -M -M 0 0 -10M

j j c

dari tabel diatas adalah -8M-7, sehingga variabel yang masuk dalam basis adalah

variabel y , kolom variabel ₁ y menjadi kolom pivot, harga ₁ y maksimal yang ₁

   

 

= =

= 0,7143

7 5 ; 5 1 5 1 Min y

Harga y₁ =0,7143 adalah nilai positif terkecil sehubungan dengan variabel y , ₆

sehingga variabel yang meninggalkan basis ialah y , kemudian digantikan dengan ₆

[image:50.612.43.564.586.703.2]

variabel y , maka tabel simpleks yang baru adalah : ₁

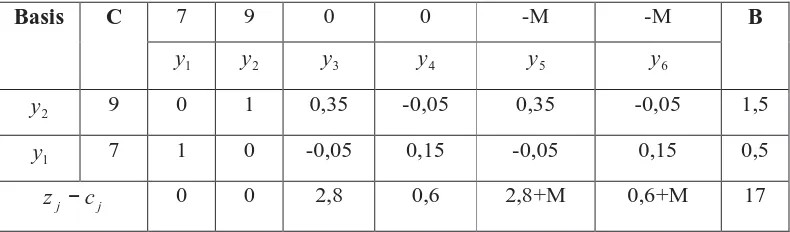
Tabel 3.5 Tabel simpleks untuk iterasi 2

Basis C 7 9 0 0 -M -M B

1

y y ₂ y ₃ y ₄ y ₅ y ₆

5

y -M 0 2,8571 1 -0,1429 1 -0,1429 4,2857

1

y 7 1 0,1429 0 0,1429 0 0,1429 0,7143

j j c

(51)

j j c

dari tabel diatas adalah 2,8571M-7,9997, sehingga variabel yang masuk dalam basis

adalah variabel