BAB 2
LANDASAN TEORI
2.1 Matriks
2.1.1 Definisi Matriks
Matriks adalah suatu kumpulan angka-angka (elemen-elemen) yang disusun menurut baris dan kolom sehingga berbentuk empat persegi panjang, di mana panjang dan lebarnya ditunjukkan oleh banyaknya kolom-kolom dan baris-baris. Matriks pada dasarnya merupakan alat yang ampuh di dalam pemecahan persoalan-persoalan yang terdiri dari lebih dari dua persamaan dengan beberapa variabel dan memudahkan di dalam pembuatan analisis-analisis yang mencakup hubungan antara variabel-variabel.
Pada awalnya matriks ditemukan dalam sebuah studi yang dilakukan oleh seorang ilmuan yang berasal dari Inggris yang bernama Arthur Cayley (1821-1895) yang mana studi yang dilakukan untuk meneliti persamaan linier dan transformasi linier awal dari semua ini matriks dianggap sebagai sebuah permainan karena matriks dapat diaplikasikan, sedangkan pada tahun 1925 matriks digunakan sebagai kuantum dan pada perkembangannya matriks digunakan dalam berbagai bidang. Di dalam memecahkan persoalan operation research atau linier programming, matriks memegang peranan penting terutama
sebagai landasan yang kuat untuk memahami pengertian-pengertian pemecahan dasar, metode simpleks dan lain sebagainya.
Keterangan :
A = , i = 1, 2, ..., m dan j = 1, 2, ..., n.
merupakan elemen matriks A dari baris i dan kolom j, i dan j dinamakan indeks (subcript), yaitu petunjuk letak (posisi) bagi setiap elemen. Elemen-elemen: , , ..., , ..., disebut diagonal pokok (main diagonal).
Matriks tereduksi adalah matriks yang tiap kolom dan tiap barisnya mengandung atau memiliki paling sedikit satu buah angka 0 dan elemen-elemen lainnya bernilai non-negatif. Untuk mendapatkan matriks tereduksi, maka tiap baris atau kolom yang belum mengandung angka 0 dikurangi dengan nilai terkecil pada baris atau kolom tersebut.
2.1.2 Jenis-jenis Matriks
Beberapa jenis matriks sebagai berikut: 1. Matriks kuadrat
2. Matriks diagonal
Matriks kuadrat dinamakan matriks diagonal jika semua elemen di luar diagonal utama adalah nol, untuk dan paling tidak satu elemen pada diagonal pokok untuk . Jumlah elemen-elemen diagonal utama suatu matriks kuadrat disebut trace ditulis .
3. Matriks Identitas
Matriks disebut matriks identitas dan biasa diberi symbol
4. Matriks singular
Matriks kuadrat dikatakan singular jika semua elemen pada salah satu baris atau kolom adalah nol atau jika semua kofaktor dari elemen suatu baris atau kolom sama dengan nol. Untuk melihat kesingularan suatu matriks adalah dengan menghitung determinan matriks tersebut. Apabila determinannya sama dengan nol maka matriks tersebut singular.
5. Matriks orthogonal
Matriks kuadrat dikatakan dapat didiagonalisasi secara orthogonal jika terdapat matriks orthogonal sehingga berlaku . Matriks orthogonal didefinisikan sebagai matriks kuadrat yang inversnya sama dengan transposenya, sehingga dan adalah matriks orthogonal.
Ada beberapa operasi dalam matriks, yaitu : 1. Perkalian matriks dengan skalar
Jika adalah matriks dan adalah suatu skalar, maka hasil kali
dengan adalah matriks
dengan .
2. Perkalian matriks dengan matriks
Jika adalah matriks dan adalah matriks maka hasil kali dari matriks dan matriks ditulis dengan adalah matriks
.
3. Penjumlahan matriks
Jika adalah matriks dan adalah matriks maka penjumlahan matriks dan matriks yang ditulis dengan dengan:
(2.1)
4. Transpose matriks
Jika adalah matriks maka matriks dengan dan disebut dengan transpose dari matriks
Matriks yang umum dapat ditulis:
5. Invers matriks
Jika matriks disebut non singular apabila terdapat matriks maka Matriks disebut invers dari matriks . Jika tidak terdapat matriks maka matriks disebut singular. Secara umum invers matriks adalah:
Sifat-sifat invers:
a. Jika matriks non singular, maka adalah non singular dan
b. Jika dan adalah matriks non singular, maka adalah non singular dan
c. Jika adalah matriks non singular, maka .
2.2 Program Linier
Pemrograman linier adalah salah satu model yang umum digunakan dalam masalah pengalokasian sumber daya secara optimal. Pemrograman linier meliputi kegiatan untuk mencapai hasil yang optimal dari antara alternatif-alternatif yang mungkin menggunakan model matematis berbentuk fungsi linier. Program linier disusun oleh George B. Dantzig tahun 1947 pada saat memimpin Air Force Statistical Control’s Combat Analysis Branch di Pentagon. Saat Dantzig menganalisis masalah perencanaan Air Force dia menyadari dapat merumuskan sistem ketidaksamaan linier. Hal di atas merupakan awal pemberian nama untuk teknik “program dan struktur linier” yang belakangan ini disederhanakan menjadi program linier (Taylor, 2001).
Program linier merupakan model matematika untuk mendapatkan alternatif penggunaan terbaik atas sumber-sumber organisasi. Kata sifat linier digunakan untuk menunjukkan fungsi-fungsi matematika yang digunakan dalam bentuk linier dalam arti hubungan langsung dan proporsional. Program menyatakan penggunaan teknik matematika tertentu. Jadi, program linier adalah suatu teknik perencanaan yang bersifat analitis menggunakan model matematis dengan tujuan menemukan beberapa kombinasi alternatif pemecahan optimum terhadap persoalan (Aminuddin, 2005).
Program linier adalah suatu teknik penyelesaian optimal atas suatu problema keputusan dengan cara menentukan terlebih dahulu fungsi tujuan (memaksimalkan atau meminimalkan) dan kendala-kendala yang ada ke dalam model matematik persamaan linier. Program linier sering digunakan dalam penyelesaian problema-problema alokasi sumber daya, seperti dalam bidang manufacturing, pemasaran, keuangan, personalia, administrasi, dan lain
sebagainya (Parlin Sitorus, 1997).
Program linier adalah suatu cara untuk menyelesaikan persoalan pengalokasian sumber-sumber yang terbatas di antara beberapa aktivitas yang bersaing, dengan cara terbaik yang mungkin dilakukan. Pokok pikiran utama dalam menggunakan program linier adalah merumuskan masalah dengan jelas dengan menggunakan sejumlah informasi yang tersedia. Sesudah masalah terumuskan dengan baik, maka langkah berikut ialah menerjemahkan masalah ke dalam bentuk model matematika (P. Siagian, 2006).
2.2.1 Persyaratan Penyelesaian Program Linier
Syarat-syarat yang harus dipenuhi dalam merumuskan suatu problema keputusan ke dalam model matematik persamaan linier adalah sebagai berikut (Parlin Sitorus, 1997):
1. Tujuan
Apa yang menjadi tujuan permsasalahan yang dihadapi yang ingin dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi tujuan.
2. Alternatif Perbandingan
Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan, misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu terlambat dan biaya terendah.
3. Sumber Daya
Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas. 4. Perumusan Kuantitatif
Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif sesuai dengan yang disebut dalam model matematika.
5. Keterkaitan Peubah
2.2.2 Model Umum Matematik Program Linier
Model umum program linier dapat dirumuskan ke dalam bentuk matematik sebagai berikut (Parlin Sitorus, 1997):
Dengan kendala:
dan
Keterangan:
= Fungsi tujuan = Variabel keputusan
= Nilai kontribusi dari variabel keputusan
= Koefisien teknologi dari variabel keputusan dalam kendala
ke-= Sumber daya yang tersedia dalam kendala ke-
2.2.3Karakteristik Program Linier
Karakteristik-karakteristik dalam program linier yang biasa digunakan untuk memodelkan suatu masalah dan memformulasikannya secara matematik, yaitu (Siswanto, 2006):
1. Variabel Keputusan
Variabel keputusan adalah variabel yang secara lengkap menguraikan keputusan-keputusan yang akan dibuat.
2. Fungsi Tujuan
Fungsi tujuan merupakan suatu hubungan linier dari variabel keputusan yang berupa fungsi maksimum atau minimum.
3. Fungsi Kendala
Fungsi kendala merupakan batasan-batasan dalam penyelesaian program linier yang harus diperhatikan. Kendala diekspresikan dalam persamaan dan
pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumber daya dalam suatu masalah.
2.2.4 Asumsi dalam Program Linier
Dalam membangun model dari formulasi suatu persoalan akan digunakan karakteristik-karakteristik yang biasa digunakan dalam persoalan program linier, yaitu (Syahputra, 2012):
1. Linieritas (Linierity)
Fungsi tujuan (objective function) dan fungsi kendala (constraint) dibuat dalam fungsi linier. Sifat linieritas suatu kasus dapat ditentukan dengan menggunakan beberapa cara, misalnya dengan menggunakan grafik.
2. Kesetaraan (Propotionality)
a. Kontribusi setiap variabel keputusan terhadap fungsi tujuan adalah sebanding dengan nilai variabel keputusan.
b. Kontribusi suatu variabel keputusan terhadap ruas kiri dari setiap pembatas juga sebanding dengan nilai variabel keputusan itu.
3. Penambahan (Addivity)
Sifat penambahan mengasumsikan bahwa tidak terdapat bentuk perkalian silang pada model, baik bagi fungsi tujuan maupun fungsi kendala. 4. Pembagian (Divisibility)
Nilai variabel keputusan harus lebih besar atau sama dengan nol. 6. Kepastian (Certainty)
Koefisien pada fungsi tujuan ataupun fungsi kendala merupakan suatu nilai pasti, bukan merupakan suatu nilai dengan peluang tertentu.
Asumsi-asumsi tersebut harus dipenuhi apabila ingin menyelesaikan masalah model program linier. Jika asumsi-asumsi tersebut tidak dapat terpenuhi, persoalan dapat diselesaikan dengan program matematika lain seperti integer programming nonlinier programming, goal programming dan dynamic programming.
Suatu masalah dapat mempunyai banyak algoritma penyelesaian. Algoritma yang digunakan tidak saja harus benar tetapi harus efisien. Efisiensi suatu algoritma dari waktu eksekusi algoritma dan kebutuhan ruang memori. Algoritma yang efisien adalah algoritma yang meminimumkan kebutuhan waktu dan ruang. Dengan menganalisis beberapa algoritma untuk suatu masalah, dapat diidentifikasi satu algoritma yang paling efisien. Besaran yang digunakan untuk menjelaskan model pengukuran waktu dan ruang ini adalah kompleksitas algoritma.
2.3 Metode Grafik
Metode grafik merupakan salah satu metode yang dapat digunakan untuk memecahkan permasalahan program linier. Metode ini menggunakan pendekatan grafik dalam pengambilan keputusan dengan seluruh fungsi kendala dibuat dalam satu bagian gambar kemudian diambil keputusan melalui grafik tersebut untuk menentukan nilai variabel keputusan yang optimum. Metode ini hanya dapat menyelesaikan dua variabel keputusan, apabila memiliki lebih dari dua variabel keputusan maka metode ini tidak dapat digunakan (Parlin Sitorus, 1997).
Langkah-langkah metode grafik (Andi wijaya 2012):
1. Mengidentifikasi variabel keputusan dan memformulasikan dalam simbol matematis.
2. Mengidentifikasikan tujuan yang akan dicapai dan kendala-kendala. 3. Memformulasikan tujuan dan kendala ke dalam fungsi matematik.
4. Membuat grafik untuk kendala-kendala yang ada dalam satu bagian. Untuk membuat grafik fungsi kendala yang berbentuk pertidaksamaan ( dan diubah terlebih dahulu ke dalam bentuk persamaan (
5. Menentukan daerah layak pada grafik. Daerah layak dapat dilihat dari pertidaksamaan pada kendala. Apabila kendala berbentuk maka daerah arsiran terjadi pada bagian kiri atau bawah atau kiri bawah, tetapi apabila kendala berbentuk , maka daerah arsiran dilakukan di kanan atau kanan atas. Apabila berbentuk persamaan ( maka daerah layak terjadi di sepanjang grafik atau garis.
6. Menentukan titik-titik variabel keputusan pada daerah layak.
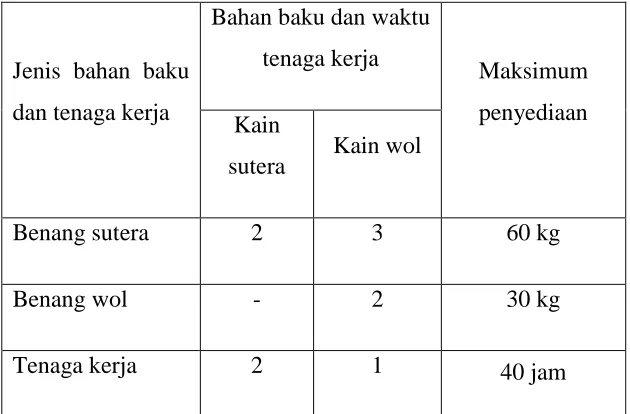
Contoh 2.1
, b.
c.
,
Gambar 2.1 Fungsi Kendala
5. Menentukan daerah layak pada grafik.
Gambar 2.2 Daerah Layak
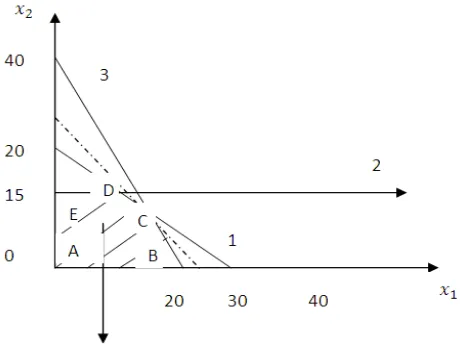
Gambar 2.3 Himpunan Penyelesaian a. Titik A:
b. Titik B:
c. Titik C:
d. Titik D:
e. Titik E:
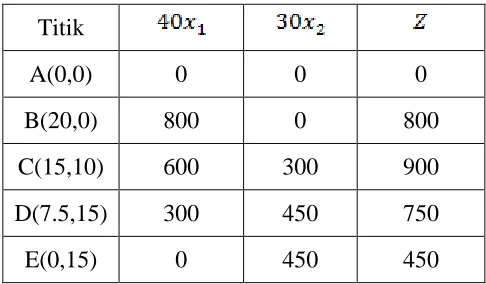
Hasil perhitungan disajikan dalam Tabel 2.2 sebagai berikut:
Tabel 2.2 Hasil Perhitungan
Titik
A(0,0) 0 0 0
B(20,0) 800 0 800
C(15,10) 600 300 900
D(7.5,15) 300 450 750
E(0,15) 0 450 450
Jadi berdasarkan hasil perhitungan pada tabel 2.2 diperoleh nilai berada pada titik C dengan dan
2.4 Metode Simpleks
Metode simpleks merupakan prosedur aljabar yang bersifat iteratif yang secara sistematis dimulai dari suatu pemecahan dasar yang fisibel ke pemecahan dasar fisibel lainnnya, dilakukan secara berulang-ulang sehingga tercapai suatu
pemecahan dasar yang optimum dan setiap langkah menghasilkan suatu nilai dari fungsi tujuan yang selalu lebih besar atau sama dari iterasi sebelumnya (Parlin Sitorus, 1997).
mengajukan suatu metode yang tepat untuk menyelesaikan permasalahan program linier yang disebut metode simpleks. Metode simpleks merupakan prosedur aljabar yang bersifat iteratif yang bergerak selangkah demi selangkah, dimulai dari titik ekstrim pada daerah feasible (ruang sousi) menuju titik ekstrem yang optimum (Aminuddin 2005).
Dalam menyelesaikan permasalahan program linier dengan metode simpleks, bentuk dasar yang digunakan haruslah merupakan bentuk standar, yaitu bentuk formulasi yang memenuhi ketentuan berikut ini (Mustafa dan Parkhan, 1999).
1. Seluruh pembatas linier harus berbentuk persamaan dengan ruas kanan yang nonnegatif.
2. Seluruh peubah keputusan harus merupakan peubah nonnegatif. 3. Fungsi tujuannya dapat berupa maksimasi atau minimasi.
Beberapa hal yang dapat dilakukan untuk mengubah bentuk permasalahan program linier yang belum standar ke dalam bentuk standar permasalahan program linier sesuai dengan ketentuan Pembatas linier (linier constraint) yang terdiri dari:
a. Pembatas linier bertanda ”≤” dapat dijadikan suatu persamaan ”=” dengan cara menambahkan ruas kiri dari pembatas linier itu dengan slack variable (peubah penambah). Slack variabel pada umumnya digunakan
untuk mewakili jumlah kelebihan ruas kanan pembatas linier dibandingkan dengan ruas kirinya. Pada pembatas linier bertanda ”≤”, ruas kanan umumnya mewakili batas ketersediaan sumber daya sedangkan ruas kiri umumnya mewakili penggunaan sumber daya tersebut yang dibatasi oleh berbagai kegiatan yang berbeda (peubah) dari suatu model program linier sehingga slack variable dapat diartikan untuk mewakili jumlah sumber daya yang tidak dipergunakan.
ruas kanan umumnya mewakili penetapan persyaratan spesifikasi minimum, sehingga surplus variabel dapat diartikan untuk mewakili jumlah kelebihan sesuatu dibandingkan spesifikasi minimumnya.
c. Ruas kanan dari suatu persamaan dapat dijadikan bilangan nonnegatif dengan cara mengalikan kedua ruas dengan -1.
d. Arah pertidaksamaan berubah apabila kedua ruas dikalikan dengan -1.
e. Pembatas linier dengan pertidaksamaan yang ruas kirinya berada dalam tanda mutlak dapat diubah menjadi dua pertidaksamaan.
Berikut langkah-langkah dalam menyelesaikan permasalahan program linier dengan metode simpleks (Handayani, 2014):
1. Konversikan formulasi persoalan ke dalam bentuk standar.
Agar persamaan garis batasan memenuhi persyaratan penyelesaian daerah kelayakan (feasible) maka semua pertidaksamaan diubah menjadi persamaan dengan cara menambahkan variabel slack, surplus dan variabel buatan (artifisial variabel) pada tiap batasan (constraint) serta memberi harga nol pada setiap koefisien tujuannya. Batasan dapat dimodifikasi sebagai berikut:
a. Untuk batasan bernotasi diubah ke dalam bentuk persamaan dengan menambahkan variabel slack.
b. Untuk batasan bernotasi atau diselesaikan dengan menambahkan variabel surplus dan variabel buatan. Dengan penambahan variabel buatan ini akan merusak sistem batasan, hal ini dapat diatasi dengan membuat suatu bilangan penalty M (M bilangan positif yang sangan besar) sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Untuk kasus maksimasi maka dibuat –M sebagai harga dari variabel buatan dan untuk kasus minimasi dibuat +M sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M method).
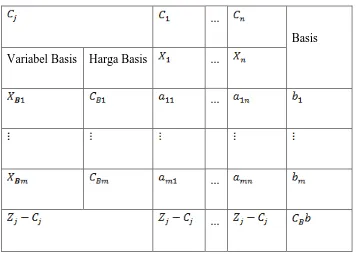
Tabel 2.3 Bentuk Tabel Simpleks
...
Basis Variabel Basis Harga Basis ...
...
...
...
3. Pilih kolom kunci, yaitu kolom yang memiliki nilai yang paling positif untuk kasus maksimasi atau yang memiliki nilai yang paling negatif untuk kasus minimasi.
4. Pilih baris kunci yang memiliki nilai indeks terkecil. Nilai indeks adalah perbandingan nilai kanan dengan kolom kunci,
5. Tentukan nilai elemen cell, yaitu nilai perpotongan antara kolom kunci dan baris kunci.
6. Lakukan iterasi dengan menentukan baris kunci baru, baris Z baru, dan baris variabel-variabel slack baru.
a. Baris kunci baru ditentukan dengan membagi baris kunci lama dengan elemen cell.
b. Baris Z baru dan baris-baris lainnya ditentukan dengan cara:
Baris lama – (nilai kolom kunci baris yang sesuai × baris kunci baru) c. Letakkan nilai-nilai baris yang baru diperoleh ke dalam tabel.
ada lagi yang bernilai negatif (untuk kasus minimasi) berarti sudah optimal. Jika kriteria belum terpenuhi, diulangi dari langkah 3.
2.5 Algoritma Titik Interior
Titik interior merupakan titik-titik yang beradadi dalam daerah layak. ada dua langkah yang diperlukan dari metode titik interior, yaitu mencarik arah layak yang memperbaiki nilai fungsi sasaran pada titik tertentu dari setiap iterasi dan menentukan besar langkah yang menghasilkan titik baru yang berada pada daerah layak yang memperbaiki nilai fungsi sasaran. Algoritma titik interior di bagi dalam empat kelas utama yaitu, affine scaling methods, metode proyektif atau dikenal dengan metode Karmarkar, path following methods dan potential reduction methods.
Algoritma titik interior pertama kali diperkenalkan oleh Narendra Karmarkar (1984) dari Laboratorium AT & T mengenai algoritma baru untuk menyelesaikan masalah-masalah pemrograman linier yang besar. Algoritma titik interior merupakan metode untuk menyelesaikan masalah pemrograman linier yang memotong atau menembus interior dari daerah fisibel untuk mencapai suatu solusi optimal. Titik interior merupakan titik-titik yang berada di dalam daerah fisibel (Hillier & Lieberman, 1990). Dasar teori algoritma ini menggunakan konsep gradien dan proyeksi.
Algoritma titik interior dalam menyelesaikan persoalan program linier secara fundamental berbeda dari metode simpleks. Langkah awal dalam algoritma titik interior yaitu menentukan titik awal pemecahan masalah. Titik awal algoritma titik interior dari dalam himpunan fisibel dan bergerak menuju verteks optimal. Algoritma titik interior berhenti menemukan solusi yang memiliki nilai fungsi tujuan lebih kecil atau sama dengan nilai berhenti yang telah ditentukan pertama kali. Gagasan dasar dari algoritma titik interior dapat dilihat dalam permasalahan program linier berikut:
Agar masalah program linier menjadi bentuk standar, maka ditambahkan variabel pengetat pada masalah program linier di atas, sehingga menjadi:
Maksimumkan dengan kendala
dengan adalah variabel slack.
Gambar 3.1 Permasalahan untuk Memaksimalkan Nilai
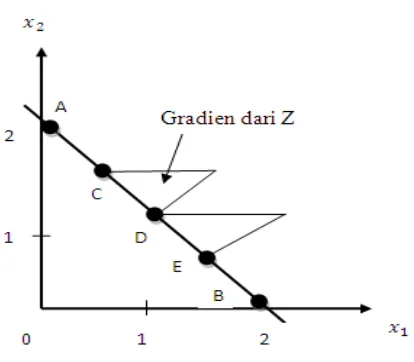
Gambar 3.1 menggambarkan permasalahan untuk memaksimalkan nilai . Ruang pemecahan diketahui dengan ruas dan arah kenaikan adalah arah postif . Iterasi dimulai dari titik interior C dalam ruang penyelesaian (garis AB). gradien fungsi tujuan ( di C adalah arah yang membuat fungsi tujan meningkat dengan cepat. Jika satu titik sembarang ditempatkan di sepanjang gradien itu dan kemudian memproyeksikannya secara tegak lurus terhadap ruang penyelesaian (garis ), maka diperoleh titik baru . Dari sudut pandang nilai , titik yang baru ini lebih baik dari titik awal .
yang lebih dekat dengan titik optimum. Dapat diperkirakan jika bergerak dengan sangat hati-hati dalam arah gradien terproyeksikan, maka akan dicapai titik optimum . Langkah-langkah yang dihasilkan di sepanjang gradien terproyeksi tidak akan meleset dari titik optimum di dan dalam kasus dimensi pada umumnya. Arah yang diciptakan oleh gradien terproyeksi tidak akan menyebabkan terjebaknya algoritma tersebut di titik yang bukan optimum. Prosedur gradien yang diproyeksikan akan menjauh dari titik ke arah optimum di (
Penggunaan algoritma titik interior untuk menyelesaikan masalah program linier harus diubah terlebih dahulu kedalam bentuk kanonik karmarkar dan memenuhi beberapa asumsi metode karmarkar (Bazaraa, 2010). Bentuk kanonik dari karmarkar adalah:
= koefisien variabel fungsi tujuan = vector kolom berukuran m dari 0
Semua batasan kendala merupakan persamaan homogen kecuali untuk kendala 1 yang merupakan kendala untuk mendefinisikan sebuah simpleks n dimensi. Algoritma titik interior memiliki konsep atau pemikiran dasar sebagai berikut:
1. Bergerak melalui daerah fisibel menuju suatu penyelesaian optimal.
3. Mengubah daerah layak tersebut untuk menempatkan penyelesaian percobaan yang sedekat mungkin pada titik pusatnya dan dengan demikian memungkunkan peningkatan yang besar bilamana melaksanakan konsep yang pertama.
2.6Langkah-langkah Algoritma Titik Interior
Langkah–langkah pengerjaan algoritma titik interior:
1. Mengidentifikasi variabel keputusan, fungsi tujuan, dan fungsi kendala.
2. Memformulasikan variabel keputusan, fungsi tujuan, dan fungsi kendala ke dalam bentuk program linier.
3. Diubah dalam bentuk maximize (diperluas) dengan menambahkan variabel slack pada fungsi kendala.
4. Jika program linier sudah dalam bentuk minimize (diperluas), maka permasalahan dapat diselesaikan dengan algoritma titik interior dengan langkah sebagai berikut:
Langkah 1: Diketahui penyelesaian percobaan awal ( yang di ambil dari fungsi kendala D adalah matriks diagonal dari percobaan awal.
Langkah 2: Hitung nilai Langkah 3: Hitung nilai
Langkah 4: Hitung nilai ,
Langkah 5: Hitung nilai
Langkah 7: Hitung ,
Langkah 8: Hitung , jika penyelesaian percobaan ini tidak berubah dari percobaan sebelumnya maka algoritma telah memuat suatu penyelesaian optimal.
Keterangan:
= Matriks koefisien kendala
= Perkalian antara matriks kofisien kendala dan matriks diagonal dari percobaan awal
= Vektor kolom dari koefisien fungsi tujuan = Tingkat kemiringan
= Matriks proyeksi
= Tingkat kemiringan yang diproyeksikan = Penyelesaian percobaan awal baru