Informasi Dokumen
- Sekolah: Universitas Indonesia
- Mata Pelajaran: Program Linier
- Topik: Perbandingan Metode Simpleks Dengan Algoritma Titik Interior Dalam Penyelesaian Masalah Program Linier
- Tipe: thesis
- Tahun: 2023
- Kota: Jakarta
Ringkasan Dokumen
I. Introduction
The introduction discusses the importance of linear programming in optimizing resource allocation in various fields, particularly in business and economics. It highlights the historical context of linear programming, introduced by George Dantzig in 1947, and its applications in decision-making processes. The objective of the study is to compare the efficiency of the Simplex method and the Interior Point algorithm in solving linear programming problems, emphasizing the relevance of these methods in educational settings for teaching optimization techniques.
II. Theoretical Framework
This section provides foundational knowledge about matrices and linear programming. It defines matrices, their types, and operations, which are crucial for understanding linear programming formulations. The significance of linear programming is outlined, including its role in optimal resource allocation and decision-making. The section also covers the requirements and characteristics of linear programming models, emphasizing the importance of clearly defined objectives and constraints for effective problem-solving.
2.1 Matrices
Matrices are defined as collections of numbers arranged in rows and columns, serving as essential tools in solving linear equations. This subsection discusses various types of matrices, such as square, diagonal, and identity matrices, along with their operations, which are fundamental in the formulation of linear programming problems.
2.2 Linear Programming
Linear programming is introduced as a mathematical model for optimal resource allocation, focusing on maximizing or minimizing a linear objective function subject to constraints. The historical development of linear programming and its applications in various sectors are discussed, reinforcing its relevance in academic curricula for operations research.
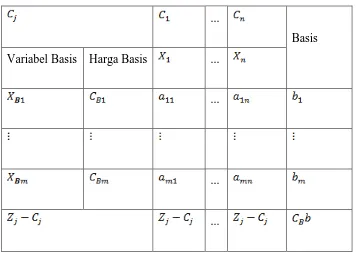
2.3 Simplex Method
The Simplex method is described as an iterative algorithm used to solve linear programming problems by moving from one feasible solution to another until the optimal solution is found. The steps involved in implementing the Simplex method are outlined, providing students with a practical understanding of how to apply this technique in real-world scenarios.
2.4 Interior Point Algorithm
This subsection introduces the Interior Point algorithm, developed by Narendra Karmarkar, as an alternative to the Simplex method. The algorithm's approach of moving through the feasible region towards an optimal solution is explained, highlighting its efficiency in handling larger problems. The comparison of both methods sets the stage for understanding their respective advantages in educational contexts.
III. Results and Discussion
The results section presents a case study involving a small company producing multiple products with limited resources. The application of both the Simplex method and the Interior Point algorithm is demonstrated through detailed calculations and iterations. The outcomes of each method are compared, focusing on the number of iterations required to reach the optimal solution, thus illustrating the practical implications of each approach in educational settings.
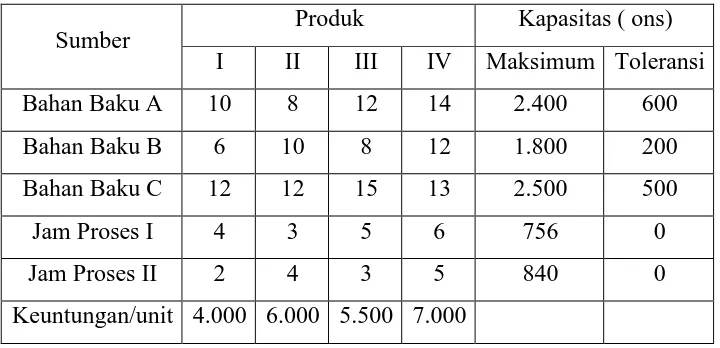
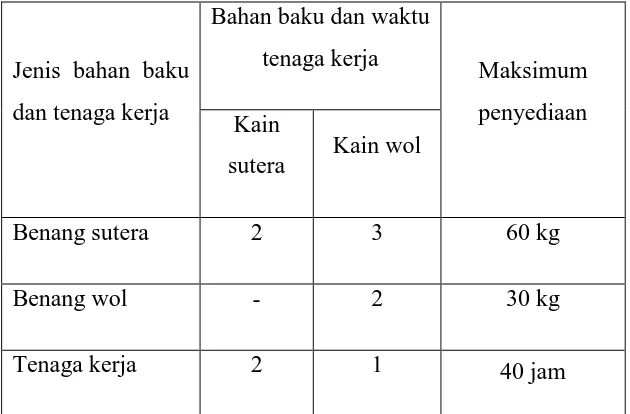
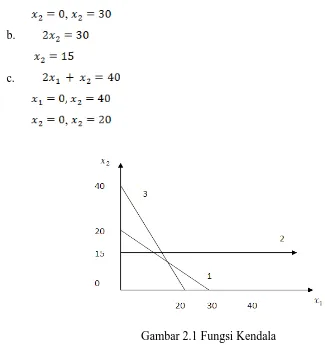
3.1 Problem Formulation
This subsection outlines the linear programming problem faced by the company, including the constraints related to raw materials and labor. The formulation of the objective function and constraints is presented, providing a clear example for students to understand the application of theoretical concepts in practical scenarios.
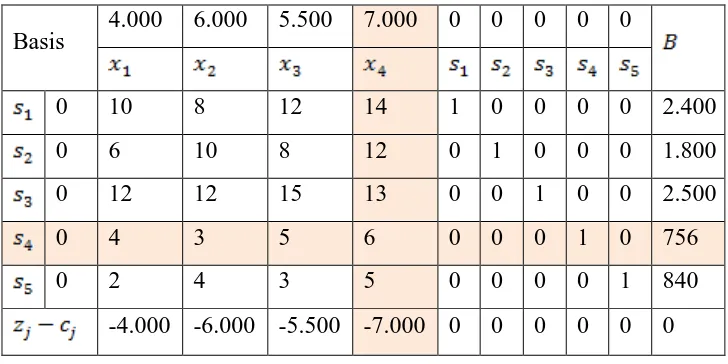
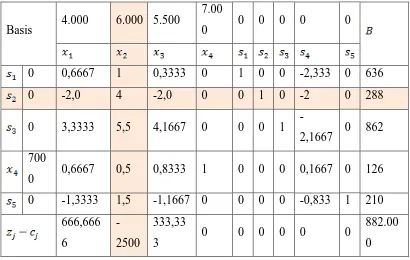
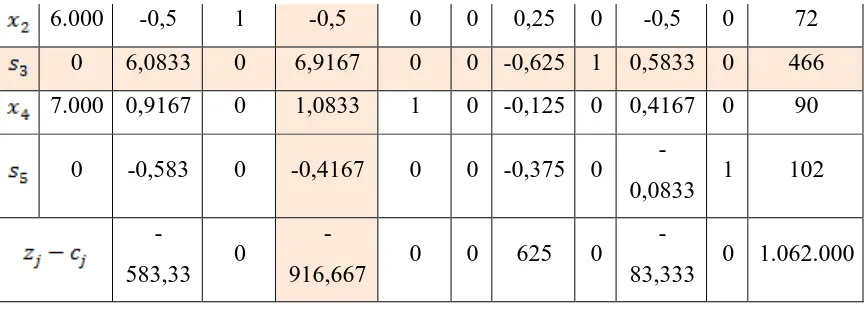
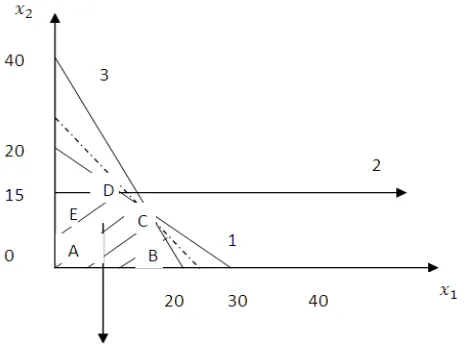
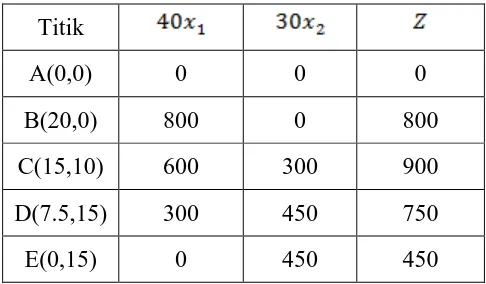
3.2 Solution Using Simplex Method
The Simplex method is applied to the formulated problem, with a detailed tabulation of the steps taken to arrive at the optimal solution. This practical demonstration reinforces the learning outcomes by showing students how to systematically approach linear programming problems using the Simplex method.
3.3 Solution Using Interior Point Algorithm
Similar to the Simplex method, the Interior Point algorithm is applied to the same problem. The iterative process and calculations are presented, allowing for a direct comparison of the efficiency and outcomes of both methods. This comparison is crucial for students to grasp the nuances of different optimization techniques.
IV. Conclusion and Recommendations
The conclusion summarizes the findings of the study, stating that both the Simplex method and the Interior Point algorithm yield the same optimal solution for the given problem, but differ in their computational efficiency. Recommendations for future research are provided, including the need for studies involving larger variable sets and alternative optimization methods. This section emphasizes the importance of continuous learning and adaptation in the field of operations research.
4.1 Conclusion
The study concludes that both methods are effective for solving linear programming problems, but the Simplex method is generally more efficient in terms of iterations required for smaller problems. This insight is valuable for students and practitioners in selecting the appropriate method based on problem size.
4.2 Recommendations
Future research should explore the application of these methods in more complex scenarios with multiple variables. Additionally, integrating computational tools into the curriculum can enhance students' understanding of these algorithms and their practical applications in real-world situations.