METODE BOUND AND DECOMPOSITION UNTUK MENYELESAIKAN PERMASALAHAN PROGRAM LINIER FUZZY PENUH
SKRIPSI
MILA HANDAYANI
100803008
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN
ALAM UNIVERSITAS SUMATERA UTARA
METODE BOUND AND DECOMPOSITION UNTUK MENYELESAIKAN PERMASALAHAN PROGRAM LINIER FUZZY PENUH
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat untuk mencapai gelar
sarjana sains
MILA HANDAYANI 100803008
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul :Metode Bound and Decomposition Untuk
Menyelesaikan Permasalahan Program Linier Fuzzy
Penuh
Kategori : Skripsi
Nama : Mila Handayani
Nomor Induk Mahasiswa : 100803008
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam (FMIPA)
Universitas Sumatera Utara
Diluluskan di
Medan, Juli 2014
Komisi pembimbing :
Pembimbing 2, Pembimbing 1,
Drs. Partano Siagian, M.Sc. Prof. Dr. Drs. Iryanto, M.Si. NIP. 19511227 198003 1 001 NIP. 19460404 197107 1 001
Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
METODE BOUND AND DECOMPOSITION UNTUK MENYELESAIKAN PERMASALAHAN PROGRAM LINIER FUZZY PENUH
SKRIPSI
Saya mengaku bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing–masing disebutkan sumbernya.
Medan, Juli 2014
PENGHARGAAN
Assalamu’alaikum Wr.Wb
Puji dan syukur penulis ucapkan kepada Allah SWT Yang Maha Esa dan Kuasa atas limpahan rahmat dan karuniaNYA sehingga skripsi ini dapat diselesaikan.Pada skripsi ini, penulis mengambil judul Metode Bound and Decomposition Untuk Menyelesaikan Permasalahn Program Linier Fuzzy Penuh.
Dalam penyusunan skripsi ini banyak pihak yang membantu, sehingga dengan segala rasa hormat penulis mengucapkan terima kasih kepada:
1. Bapak Prof. Dr. Drs. Iryanto, M.Si.selaku dosen pembimbing 1 yang berkenan dan rela mengorbankan waktu, tenaga, dan fikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.
2. Bapak Drs. Partano Siagian, M.Sc. selaku dosen pembimbing 2 yang juga berkenan dan rela mengorbankan waktu, tenaga, dan fikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.
3. Bapak Syahriol Sitorus, S.Si., M.IT dan Bapak Drs. Sawaluddin, M.IT selaku komisi penguji atas saran yang telah diberikan demi perbaikan skripsi ini.
4. Bapak Dr. Sutarman, M.Sc selaku dekan FMIPA USU
5. Bapak Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si selaku ketua dan sekretaris Departemen Matematika FMIPA USU.
6. Ibunda tercinta Yetri, S.Pd., Ayahanda tercinta Masni, S.Pd., serta adik-adikku tersayang Reza Dwi Rahmi dan Fitri Latifa atas segala perhatian, pengertian, kesabaran, do’a, dukungan dan kasih sayang yang telah diberikan kepada penulis selama di bangku perkuliahan hingga akhirnya menyelesaikan skripsi ini.
7. Untuk orang–orang tersayang khususnya Imel, Wewen, Nita, Zati, Yundi, Lita, Ade, Eti, Vela, Sharah dan Komutatif 2010 yang telah membantu penulis dengan memberikan semangat dan do’a dalam menyelesaikan skripsi ini.
Penulis juga menyadari masih banyak kekurangan dalam skripsi ini, baik dalam teori maupun penulisannya. Oleh karena itu, penulis mengharapkan saran dari pembaca demi perbaikan bagi penulis. Semoga segala bentuk bantuan yang telah diberikan kepada penulis mendapatkan balasan yang lebih baik dari Allah SWT. Akhir kata penulis berharap semoga tulisan ini bermanfaat bagi para pembaca.
Medan, Juli 2014 Penulis,
METODE BOUND AND DECOMPOSITION UNTUK MENYELESAIKAN PERMASALAHAN PROGRAM LINIER FUZZY PENUH
ABSTRAK
Asumsi kepastian tentang nilai-nilai parameter pada masalah pengambilan keputusan yang dimodelkan dengan program linier dalam praktek kenyataannya sering sulit untuk dipenuhi. Untuk mengatasi ketidakpastian tersebut diterapkanlah teori himpunan fuzzy pada program linier yang selanjutanya disebut Program Linier Fuzzy. Model Program Linier Fuzzy ini terus dikembangkan hingga terbentuklah model Program Linier Fuzzy Penuh yang semua nilai-nilai parameternya berupa bilngan fuzzy. Dalam tulisan ini dekemukakan sebuah metode untuk mencari solusi optimal dari permasalahan Program Linier Fuzzy Penuh untuk bilangan trapezoidal fuzzy yaitu Metode Bound andDecomposition. Program Linier Fuzzy Penuh akan diuraikan ke dalam empat Crisp Linier Programming (CLP) atau bentuk program linier tegas dengan dibatasi oleh variabel-variabel kendala. Keempat permasalahan CLP tersebut akan diselesaikan secara terpisah dengan metode simplek dan solusi optimal yang diperoleh menjadi solusi optimal dari permasalahan Program Linier Fuzzy Penuh.
BOUND AND DECOMPOSITION METHOD TO SOLVING FULLY FUZZY LINEAR PROGRAMMING PROBLEM
ABSTRACT
The assumption of certainty about the values of the parameters in the decision making problem which is modeled with linear programming in real world systems are too complex to be defined. Then to overcome this uncertainty applied the fuzzy set theory on linear programming that called as Fuzzy Linear Programming. This Fuzzy Linear Programming is continue to be developed till formed Fully Fuzzy Linear Programming that all values of the parameters are fuzzy numbers. In this paper told a method to finding an optimal solution to Fully Fuzzy Linear Programming for trapezoidal fuzzy is Bound and Decomposition Method. The Fully Fuzzy Linear Programming problem is decomposed into four Crisp Linear programming (CLP) problems with bounded variabels constraints. The four CLP problems are solved separately using simplex method and the optimal solution which obtained becoming an optimal solution for Fully Fuzzy Liner Programming problem.
DAFTAR ISI
Daftar Tabel viii
Daftar gambar ix
Bab 1 Pendahuluan 1
1.1Latar Belakang Masalah 1
1.2Rumusan Masalah 3
1.3Batasan Masalah 3
1.4Tinjauan Pustaka 3
1.5Tujuan Penelitian 5
1.6Kontribusi Penelitian 5
1.7Metodologi Penelitian 5
Bab 2 Landasan Teori 7
2.1 Program Linier 7
2.1.1 Syarat Utama Program Linier 7
2.1.2 Asumsi dalam Model Program Linier 8
2.1.3 Karakteristik Program Linier 9
2.2 Metode Simpleks 10
2.3 Himpunan Fuzzy 12
2.4 Fungsi Keanggotaan Fuzzy 13
2.5 Bilangan Fuzzy 14
2.6 Program Linier Fuzzy 15
2.7 Program Linier Fuzzy Penuh 16
Bab 3 Analisis 17
Bab 4 Pembahasan 21
Bab 5 Kesimpulan dan Saran 28
5.1 Kesimpulan 28
5.2 Saran 28
DAFTAR TABEL
Nomor Judul Halaman
Tabel
2.1 Bentuk Tabel Simpleks 11
3.1 Tabel Simpleks Awal 22
3.2 Tabel Simpleks Iterasi 1 23
3.3 Tabel Simpleks Iterasi 2 23
3.4 Tabel Optimal Simpleks MLP II 24
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
METODE BOUND AND DECOMPOSITION UNTUK MENYELESAIKAN PERMASALAHAN PROGRAM LINIER FUZZY PENUH
ABSTRAK
Asumsi kepastian tentang nilai-nilai parameter pada masalah pengambilan keputusan yang dimodelkan dengan program linier dalam praktek kenyataannya sering sulit untuk dipenuhi. Untuk mengatasi ketidakpastian tersebut diterapkanlah teori himpunan fuzzy pada program linier yang selanjutanya disebut Program Linier Fuzzy. Model Program Linier Fuzzy ini terus dikembangkan hingga terbentuklah model Program Linier Fuzzy Penuh yang semua nilai-nilai parameternya berupa bilngan fuzzy. Dalam tulisan ini dekemukakan sebuah metode untuk mencari solusi optimal dari permasalahan Program Linier Fuzzy Penuh untuk bilangan trapezoidal fuzzy yaitu Metode Bound andDecomposition. Program Linier Fuzzy Penuh akan diuraikan ke dalam empat Crisp Linier Programming (CLP) atau bentuk program linier tegas dengan dibatasi oleh variabel-variabel kendala. Keempat permasalahan CLP tersebut akan diselesaikan secara terpisah dengan metode simplek dan solusi optimal yang diperoleh menjadi solusi optimal dari permasalahan Program Linier Fuzzy Penuh.
BOUND AND DECOMPOSITION METHOD TO SOLVING FULLY FUZZY LINEAR PROGRAMMING PROBLEM
ABSTRACT
The assumption of certainty about the values of the parameters in the decision making problem which is modeled with linear programming in real world systems are too complex to be defined. Then to overcome this uncertainty applied the fuzzy set theory on linear programming that called as Fuzzy Linear Programming. This Fuzzy Linear Programming is continue to be developed till formed Fully Fuzzy Linear Programming that all values of the parameters are fuzzy numbers. In this paper told a method to finding an optimal solution to Fully Fuzzy Linear Programming for trapezoidal fuzzy is Bound and Decomposition Method. The Fully Fuzzy Linear Programming problem is decomposed into four Crisp Linear programming (CLP) problems with bounded variabels constraints. The four CLP problems are solved separately using simplex method and the optimal solution which obtained becoming an optimal solution for Fully Fuzzy Liner Programming problem.
BAB 1 PENDAHULUAN
1.1 Latar Belakang Masalah
Program linear merupakan model umum yang dapat digunakan dalam pemecahan
masalah pengalokasian sumber yang terbatas secara optimal yaitu
memaksimumkan keuntungan atau meminimumkan biaya. Ide mengenai program
linier pertama kali dicetuskan oleh seorang ahli matematika asal Rusia bernama
L.V. Kantorivich dalam bukunya yang berjudul Mathematical Method in The
Organization and Planning of Production. Pada buku ini, beliau telah
merumuskan pertama kalinya permasalahn program linier. Namun, cara-cara
pemecahan persoalan ini di Rusia tidak berkembang dengan baik dan ternyata
para ahli di negara Barat dan AS yang menggunakan cara ini dan dimanfaatkan
dengan baik.
Pada tahun 1947, seorang ahli matematika dari AS yang bernama George
B. Dantzig menemukan suatu metode untuk memecahkan persoalan-persoalan
program linier. Metode pemecahan ini dinamakan metode simpleks, yang
diuraikan dalam bukunya Linear Programming and Extention. Selanjutnya teori
ini berkembang pesat sekali terutama dibidang kemiliteran yang menyangkut
optimisasi dalam strategi perang dan di bidang-bidang lainnya.
Salah satu asumsi dasar dalam program linier adalah asumsi kepastian,
yaitu setiap parameter, data dalam pemodelan program linier, yang terdiri dari
koefisisen-koefisien fungsi tujuan, konstanta-konstanta sebelah kanan dan
koefisien-koefisien fungsi kendala, diketahui secara pasti. Namun dalam
prakteknya asumsi tersebut sulit untuk dipenuhi, karena banyak dari informasi
bukanlah data yang deterministik. Untuk mengatasi persoalan ketidakpastian
dikenalkan pertama kali oleh L. A. Zadeh pada tahun 1965. Zadeh memodifikasi
teori himpunan dimana setiap anggotanya memiliki derajat keanggotaan yang
bernilai kontinu antara 0 dan 1. Penerapan teori himpunan fuzzy pada program
linier kemudian disebut program linier fuzzy.
Program linier fuzzy merupakan program linier yang dinyatakan dengan
fungsi objektif dan fungsi kendala yang mengandung parameter fuzzy dan
ketidaksamaan fuzzy. Rumusan mengenai program linier fuzzy pertamakali
diajukan oleh Zimmerman (1978). Sejak saat itu, para peneliti terus
mengembangkan jenis-jenis yang berbeda dari permasalahan program linier fuzzy
dan mengajukan beberapa pendekatan sebagai solusi dari permasalahan tersebut.
Hingga dikemukakan bentuk permasalahan program linier fuzzy dimana semua
parameter dan variabel baik dalam fungsi objektif, fungsi kendala dan
ketidaksamaan merupakan bilangan fuzzy. Persoalan seperti ini disebut persoalan
program linier fuzzy penuh.
T. Allahviranloo et al (2008) menyelesaiakan permasalahan program linier
fuzzy penuh menggunakan fungsi rangking. A. Kumar et al(2010) mengajukan
sebuah metode untuk menyelesaikan permasalahan program linier fuzzy penuh
dengan ketidaksamaan fungsi kendala. S.H. Nasseri et al(2010) memperkenalkan
teori dualitas pada program linier fuzzy dengan bilangan symetric trapezoidal
fuzzy. A. Kumar dan J. Kaur (2011) memperkenalkan sebuah metode baru yang
diberi nama Mehar’s Method untuk menyelesaiakan permasalahan program linier
fuzzy. A.T. Afriani dkk (2012) menyelesaiakan permasalahn program linierr fuzzy
dengan variabel trapezoidal fuzzy dengan metode SimpleksFuzzy.Jayalakshmi dan
Pandian (2012) mengajukan sebuah metode baru untuk solusi permasalahan
program linier fuzzy penuh yaitu metode Bound and Decomposition. Metode ini
diterapkan pada program linier fuzzy penuh bilangan triangular fuzzy.
Penyelesaian didapat secara tepat untuk semua kendala dengan perhitungan yang
lebih sederhana. Dalam tulisan ini penulis akan menerapkan metode Bound and
Decompositionuntuk permasalahan program linier fuzzy penuh untuk trapezoidal
Kendala
1.2 Rumusan Masalah
Bagaimana penerapan metode Bound and Decomposition untuk menentukan
penyelesaian permasalahan program linier fuzzy penuh.
1.3 Batasan Masalah
Dalam tulisan ini yang akan dibahas hanya program linier fuzzy penuh yang mana
semua parameter dan variabel yang terdapat dalam fungsi objektif, fungsi kendala
dan ketidaksamaannya adalah bilangan trapezoidal fuzzy.
1.4 Tinjauan Pustaka
P. Siagian (2006) dalam bukunya “Penelitian Operasional: Teori dan Praktek”
menyatakan bahwa pokok pikiran yang utama dalam menggunkan program linier
ialah merumuskan masalah dengan jelas dengan menggunakan sejumlah informasi
yang tersedia. Sesudah masalah terumuskan dengan baik, maka langkah
berikutnya adalah menerjemahkan masalah ini ke dalam bentuk model
matematika yang terang mempunyai cara pemecahan yang lebih mudah dan rapi
guna menemukan jawaban terhadap masalah yang dihadapai.
Siringoringo, Hotniar. 2005. “Seri Teknik Operasional”, menyatakan
bahwa bentuk umum model program linier adalah sebagai berikut:
Kendala
Kendala
�� = koefisien fungsi tujuan ��� = koefisien fungsi kendala
�� = jumlah masing-masing sumber daya yang ada
L.A. Zadeh (1965, hal: 338) menyatakan bahwa suatu himpunan fuzzy
merupakansebuah kelas dari objek – objek dengan suatu rangkaian kesatuan dari
nilai keanggotaan. Demikian sebuah himpunan digolongkan oleh sebuah fungsi
(karakteristik) keanggotaan yang memberikan setiap objek sebuah nilai
keanggotaanyang berkisar antara 0 dan 1.
Sri Kusumadewi, 2002. “Analisa & Desain Sistem Fuzzy menggunakan Toolbox Mathlab” menyatakan bahwa bentuk umum fuzzy linier programming adalah:
�=� �̃���
Jayalakshmi dan Pandian (2012) dalam tulisannya menyatakan bahwa
bentuk umum program linier fuzzy penuh adalah:
dengan����,�̃�,���,���adalah bagian dari himpunan semua bilangan fuzzy yang terdefinisi dalam himpunan bilangan rill.
1.5 Tujuan Penelitian
Tujuan dari penelitian ini adalah menentukan penyelesaian dari
permasalahanprogram linier fuzzy penuh untuk trapezodal fuzzy dengan metode
Bound and Decomposition.
1.6 Kontribusi Penelitian
Dengan adanya tulisan ini, penulis berharap dapat menambah referensi bagi
pembaca dan pengambil keputusan dalam menyelesaikan program linier fuzzy
penuh untuk trapezoidal fuzzy.
1.7 Metodologi Penelitian
Penelitian ini bersifat literatur yang disusun berdasarkan rujukan pustaka dengan
langkah-langkah sebagai berikut:
Langkah-1 : Memaparkan konsep bilangan fuzzy terutama trapezoidal
fuzzydanprosedur perhitungan aritmatikanya.
Langkah-2 : Menjelaskan konsep program linear fuzzy penuh untuk
trapezoidal fuzzy.
Langkah-3 : Menjelaskan prosedur metode Bound and Decompositionuntuk
pencarian solusi permasalahan program linier fuzzy penuh untuk
trapezoidal fuzzy.
Langkah-4 : Menyelesaikan contoh numerik permasalahan dalam program
linier fuzzy penuh untuk trapezoidal fuzzy dengan metode Bound
Langkah-5 : Menyimpulkan dari penerapan metode terhadap contoh numerik
sekaligus memberikan saran untuk pengembangan penelitian
BAB 2
LANDASAN TEORI
2.1 Program Linier
Program linier merupakan model umum yang dapat digunakan untuk
menyelesaikan persoalan pengalokasian sumber-sumber yang terbatas di antara
beberapa aktivitas yang bersaing secara optimal, dengan cara yang terbaik yang
mungkin dilakukan. Sebagai contoh sederhana sebuah bank hendak
mengalokasikan dananya untuk mencapai kemungkinan hasil tertinggi.Dalam hal
ini bank tersebut harus beroperasi dalam peraturan likuiditas yang dibuat oleh
pemerintah dan harus mampu menjaga fleksibilitas yang memadai untuk
memenuhi permintaan pinjaman dari para nasabah.
Dalam penerapannya program linier menggunakan model matematis
dalam pemecahan berbagai persoalan.Kata sifat linier digunakan untuk
menggambarkan hubungan antara dua atau lebih variabel, hubungan yang
berlangsung haruslah berupa fungsi yang linier.Sedangkan kata program
menyatakan penggunaan teknik matematika tertentu untuk mendapatkan
kemungkinan pemecahan terbaik dari persolan yang melibatkan sumber yang
serba terbatas.memiliki hubungan fungsional atau hubungan keterkaitan.
2.1.1 Syarat Utama Program Linier
Agar dapat menyusun dan merumuskan suatu persoalan atau permasalahanyang
dihadapi ke dalam model program linier, maka ada lima syarat yang harus
1. Tujuan
Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin
dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas
yang disebut fungsitujuan.
2. Alternatif perbandingan
Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan,
misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan
waktuterlambat dan biaya terendah.
3. Sumber daya
Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas.
4. Perumusan kuantitatif
Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif
dalamapa yang disebut model matematika.
5. Keterkaitan peubah
Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut
harusmemiliki hubungan fungsional atau hubungan keterkaitan.
2.1.2 Asumsi dalam Model Program Linier
Dalam menggunakan model program linear, diperlukan beberapa asumsi sebagai
berikut:
1. Asumsi kesebandingan (proportionality)
a. Konstribusi setiap variabel keputusan terhadap fungsi tujuan adalah
sebanding dengan nilai variabel keputusan.
b. Konstribusi suatu variabel keputusan terhadap ruas kiri dari setiap
pembatas linier juga sebanding dengan nilai keputusan itu.
2. Asumsi penambahan (additivity)
a. Konstribusi setiap variabel keputusan terhadap fungsi keputusan
bersifat bergantung pada nilai dari variabel keputusan yang lain.
b. Konstribusi suatu variabel keputusan pada nilai dari variabel keputusan
ruas kiri dari setiap pembatas linier bersifat tidak bergantung pada nilai
3. Asumsi pembagian(divisiblity)
Dalam persoalan program linier, variabel keputusan boleh diasumsikan
berupa pecahan.
4. Asumsi kepastian (certainty)
Setiap parameter, yaitu koefisien fungsi tujuan, ruas kanan, dan koefisien
fungsi kendala diasumsikan dapat diketahui secara pasti.
2.1.3 Karakteristik Program Linier
Dalam membangun model dari formulasi suatu persoalan akan digunakan
karakteristik-karakteristik yang biasa digunakan dalam persoalan program linier,
yaitu:
1. Peubah keputusan
Peubah keputusan adalah peubah yang menguraikan secara lengkap
keputusan-keputusan yang akan dibuat.
2. Fungsi tujuan (objective function)
Fungsi tujuan merupakan fungsi dari peubah keputusan yang akan
dimaksimumkan (untuk pendapatan) atau diminimumkan (untuk ongkos).
Untuk menyatakan fungsi tujuan biasanya digunakan peubah z sehingga
fungsi tujuan dapat dinyatakan:
�= �(�) 3. Pembatas Linier (linier constraints)
Pembatas linear merupakan kendala yang dihadapi sehingga kita tidak
dapat menentukan harga-harga variabel keputusan secara sembarang.
Koefisien dari variabel keputusan pada pembatas linear dinamakan
koefisien fungsi kendala, sedangkan bilangan yang ada di sisi (ruas) kanan
setiap pembatas linear dinamakan ruas kanan pembatas.
4. Pembatas tanda / kondisi pengetat
Pembatas tanda adalah pembatas yang menjelaskan apakah variabel
keputusannya diasumsikan hanya berharga nonnegatif atau variabel
Secara umum model program linier dapat dirumuskan sebagai berikut:
�� = jumlah masing-masing sumber daya yang ada (ruas kanan pembatas)
2.2 Metode Simpleks
Cara yang paling sederhana unrtuk menyelesaikan permasalahan program linier
adalah dengan pendekatan grafikal. Namun cara tersebut hanya bisa diterapkan
untuk program linier dengan dua variabel keputusan. Pada kenyataannya sebagian
besar permasalahan program linier mempunyai lebih dari dua variabel
keputusan.Hal ini tentu sulit untuk menerapkan pendekatan grafikal untuk
memperoleh penyelesaian dari permasalahan tersebut.
Oleh karen itu, pada tahun 1947 George Dantzig mengajukan suatu
metode yang tepat untuk menyelesaiakn permasalahan program linier yang
disebut metode simpleks. Metode simpleks merupakan prosedur aljabar yang
bersifat iteratif yang bergerak selangkah demi selangkah, dimulai dari titik
ekstrim pada daerah feasible (ruang sousi) menuju titik ekstrim yang optimum.
Berikut langkah-langkah dalam menyelesaikan permasalahan program
linier dengan metode simpleks:
Agar persamaan garis batasan memenuhi persyaratan penyelesaian daerah
kelayakan (feasible) maka semua pertidaksamaan diubah menjadi
persamaan dengan cara menambahkan variabel slack, surplus dan variabel
buatan (artifisial variabel) pada tiap batasan (constraint) serta memberi
harga nol pada setiap koefisien tujuannya. Batasan dapat dimodifikasi
sebagai berikut:
a. Untuk batasan bernotasi (≤) diubah ke dalam bentuk persamaan
dengan menambahkan variabel slack.
b. Untuk batsan bernotasi (≥) atau (=) deselesaikan dengan
menambahkan variabel surplus dan variabel buatan. Dengan
penambahan variabel buatan ini akan merusak sistem batasan, hal ini
dapat diatasi dengan membuat suatu bilangan penalty M (M bilangan
positif yang sangan besar) sebagai harga dari variabel buatan tersebut
dalam fungsi tujuan. Untuk kasus maksimasi maka dibuat –M sebagai
harga dari variabel buatan dan untuk kasus minimasi dibuat +M
sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan
metode M besar (Big M method).
2. Susun persamaan-persamaan ke dalam tabel simpleks
Tabel 2.1. Bentuk Tabel Simpleks
3. Pilih kolom kunci, yaitu kolom yang memiliki nilai ��� − ��� yang paling positif untuk kasus maksimasi atau yang memiliki nilai ��� − ��� yang paling negatif untuk kasus minimasi.
4. Pilih baris kunci yang memiliki nilai indeks terkecil. Nilai indeks adalah
perbandingan nilai kanan dengan kolom kunci,
5. Tentukan nilai elemen cell, yaitu nilai perpotongan antara kolom kunci
dan baris kunci.
6. Lakukan iterasi dengan menentukan baris kunci baru, baris Z baru, dan
baris variabel-variabel slack baru.
a. Baris kunci baru ditentukan dengan membagi baris kunci lama dengan
elemen cell.
b. Baris Z baru dan baris-baris lainnya ditentukan dengan cara:
Baris lama – (nilai kolom kunci baris yang sesuai × baris kunci baru)
c. Letakkan nilai-nilai baris yang baru diperoleh ke dalam tabel.
7. Lakukan uji optimalisasi. Jika semua koefisien pada baris ��� − ��� sudah tidak ada lagi yang bernilai positif (untuk kasus maksimasi) atau sudah
tidak ada lagi yang bernilai negatif (untuk kasus minimasi) berarti sudah
optiamal. Jika kriteria belum terpenuhi, diulangi dari langkah 3.
2.3 HimpunanFuzzy
Istilah fuzzylahir dari gagasan seorang guru besar pada University of California,
Berkeley, Amerika Serikat, Prof. Lotfi Asker Zadeh.Sejak tahun 1960 Zadeh telah
merasa bahwa sistem analisis matematika tradisional yang dikenal sampai saat itu
bersifat terlalu eksak sehingga tidak dapat berfungsi dalam banyak masalah dunia
nyata yang seringkali amat kompleks.Pada akhirnya di tahun 1965 Zadeh
mempublikasikan karangan ilmiahnya berjudul “Fuzzy Set”. Terobosan baru yang
deperkenalkan oleh Zadeh ini telah memperluas konsep himpunan klasik menjadi
himpunan fuzzy yang dapat mempresentasikan nilai-nilai ketidakpastian yang
Menurut Zadeh, himpunan fuzzy (fuzzy set) adalah sebuah kelas dari obyek
denganserangkaian kesatuan dari nilai keanggotaan. Sebuah set dikarakterisasikan
oleh sebuah fungsi keanggotaan yang memberikan tiap obyek sebuah nilai
keanggotaan yang rentang nilainya antara 0 dan 1.
2.4 Fungsi Keanggotaan Fuzzy
Sebuah himpunan fuzzy �̃ pada X ditandai oleh fungsi keanggotaan ���(�) yang berhubungan dengan setiap titik di X, sebuah bilangan riilpada interval [0,1]
dengan nilai dari ���(�) pada x mewakili derajat keanggotaan x pada �̃. Maka, semakin dekat nilai ���(�)ke semesta pembicaraan, semakin tinggi derajat keanggotaan x pada �̃. Fungsi keanggotaan (membership function) adalah suatu
kurva yang menunjukkan pemetaan titik – titik input data ke dalam nilai
keanggotaan yang mempunyai interval antara 0 sampai 1.
Definisi 2.1: X adalah sebuah himpunan tak kosong. Sebuah himpunan fuzzy �̃pada X ditandai oleh fungsi keanggotaannya:
�̃:� →[0,1]
Dan �̃(�)diinterpretasikan sebagai derajat keanggotaan dari
elemen x pada himpunan fuzzy�̃.untuk setiap � ∈ �.
Nilai 0 digunakan untuk mewakili bukan anggota, nilai 1 digunakan
untukmewakili keanggotaan penuh, dan nilai – nilai di antaranya digunakan untuk
mewakili derajat keanggotaan menengah. Pemetaan �̃juga disebut sebagai fungsi
keanggotaan dari himpunan fuzzy�̃.
2.5 Bilangan Fuzzy
Konsep bilangan fuzzy muncul dalam kehidupan sehari-hari maupun dalam
aplikasi teori fuzzy dalam bentuk besaran yang dinyatakan dengan bilangan yang
tidak tepat, misalnya “kurang lebih 10 orang”, kira-kira 3 jam”, “sekitar 5 km”,
dan lain sebagainya. Secara intuitif dapat diterima bahwa ungkapan “kurang lebih
10” dapat dinyatakan dengan suatu himpunan kaburpada semesta bilangan riil, di
mana bilangan 10 mempunyai derajat keanggotaan kurang dari 1, dan semakin
jauh bilangan itu dari derajat keanggotaanya semakin mendekati 0.
Definisi 2.3: Sebuah bilangan fuzzy �̃ adalah himpunan fuzzy dalam semesta bilangan riil yang memenuhi kondisi normal dan konveks.
Definisi 2.4: Sebuah bilangan fuzzy �̃ = (�,�,�,�)disebut bilanga trapezoidal fuzzy jika fungsi keanggotaanya diberikan oleh:
���(�) =
Fungsi keanggotaan trapezoidalfuzzy �̃= (�,�,�,�)digambarkan sebagai berikut:
Gambar 2.1Grafikfungsikeanggotaantrapezoidal fuzzy (Sumber: Sri Kusumadewi, 2002)
�(�)
1
0
Definisi 2.5: Misalkan �̃ = (�,�,�,�) dan ��= (�,�,�,ℎ) adalah dua bilangan himpunan dari semua bilangan fuzzy yang terdefinisi dalam himpunan bilngan rill,
adalah pemetaan setiap bilangan fuzzy ke dalam himpunan bilangan rill. Untuk
bilngan trapezoidal fuzzy�̃ = (�,�,�,�), maka fungsi rangkingnya adalah:
ℜ��̃�= 1
4(�+�+�+�)
2.6 Program Linier Fuzzy
Program Linier Fuzzy adalah sebuah aplikasi dari teori himpunan fuzzy pada
masalah proses pengambilan keputusan linear, di mana sebagian besar dari
masalah tersebut terkait dengan permasalahan program linear dengan variabel
fuzzy.
Secara umum model program linier fuzzy dinyatakan oleh:
�=� �����
�
Kendala � �
����� ≤ℜ��� �
�=1
(�= 1, 2, … ,�)
��� ≥ℜ0� (�= 1, 2, … ,�)
di mana koefisien fungsi tujuan (��) dan koefisien fungsi kendala (���) adalah koefisien crisp dan ��� adalah konstanta fuzzyserta ��� adalah variabel keputusan fuzzy.
2.7 Program Linier Fuzzy Penuh
Program Linier Fuzzy adalah sebuah aplikasi dari teori himpunan fuzzy pada
masalah proses pengambilan keputusan linear, di mana semua parameter yaitu
koefisien, variabel maupun konstanta dalam model berupa bilangan fuzzy.
Bentuk umum program linier fuzzy penuh dengan � buah kendala
pertidaksamaan fuzzy dan � buah variabel fuzzy:
Maksimumkan atau Minimumkan �=� �̃����
�
�=1
Kendala � ������� ≤ℜ��� �
�=1
(�= 1, 2, … ,�)
��� ≥ℜ 0� (� = 1, 2, … ,�)
BAB 3 ANALISIS
Ambil sebuah permasalahan program linier fuzzy penuh sebagai berikut:
Maksimumkan atau Minimumkan �̃=� �̃����
�
�=1
Kendala � ������� ≤ℜ��� �
�=1
(�= 1, 2, … ,�)
��� ≥ℜ 0� (� = 1, 2, … ,�)
Dengan ����,�̃�,���,��� adalah bagian dari himpunan semua bilangan fuzzy secara berurut (���,���,���,ℎ��),���,��,��,���,���,��,��,���, (��,��,��,��)yang
terdefinisi dalam himpunan bilangan rill.
Maka permasalahan tersebut dapat ditulis sebagai berikut:
Maks (Min)��1,�2,�3,�4� =�(��,��,��,��)⨂( �
�=1
��,��,��,��)
Kendala�����,���,���,ℎ���⨂���,��,��,��� ≤ℜ���,��,��,���; � = 1,2, … ,� �
�=1
���,��,��,��� ≥ℜ 0� ; �= 1,2, … ,�
Artinya ���,��,��,��� merupakan bilangan fuzzy dari variabel keputusan ���yang nilainya haruslah besar sama dengan nol (non-negative) yang terdefinisi dalam
bilangan rill.
Maks(Min) Maks(Min)
Maks(Min)
Maks(Min)
Tanda ⨁,⊝, ⊗, ≤ℜ, ≥ℜ, =ℜ merupakan operator yang digunakan dalam perhitungan fuzzy.Artinya oerator tesebut menandakan bahwa parameter yang
terlibat dalam perhitung merupakan bilangan fuzzy yang terefinisi dalam
himpunan bilangan rill.
Langkah-langkah dalam menerapkan metode Bound and Decomposition
pada permasalahan program linier fuzzy penuh untuk trapezoidal fuzzy adalah:
1. Uraikan permasalahan program linier fuzzy penuh ke dalam empat bentuk
Crisp Linear Programming(CLP) yaitu Middle Level Problem I (MLP
I),Middle Level Problem II (MLP II), Upper Level Problem (ULP),dan
Lower Level Problem (LLP).
Gunakan operasi aritmatika bilanangan trapezoidal fuzzy untuk
menguraikan model permasalahan program linier fuzzy penuh sebagai
Maks(Min)
dan semua variabel keputusan adalah non-negative.
Dari hasil penguraianmodel permasalahan program linier fuzzy penuh
tersebut, bentuklah permasalahan menjadi empat model Crisp Linier
Programming (CLP) yang terdiri dari Middle Level Problem I (MLP I),
Middle Level Problem II (MLP II), Upper Level Problem (ULP),dan
Lower Level Problem (LLP)sebagai berikut:
(MLP I)
�nilai tengah I dari �
�nilai tengah II dari �
�=1
����,���,���,ℎ���⨂���,��,��,��� ≤ℜ��
Maks(Min)
2. Gunakan teknik penyelesaian pada program linier untuk mendapatkan
penyelesaian optiml dari MLP I, MLP II, ULP, dan LLP
3. Penyelesaian optimal dari MLP I, MLP II, ULP, dan LLP merupakan
BAB 4 PEMBAHASAN
Diberikan sebuah permasalahan program linier fuzzy penuh tikutip dari tulisan A.
Kumuar et all (2010) sebagai berikut:
Maksimumkan �̃=�(0,1,2,3)⊗ ��1⊕(2,3,4,5)⊗ ��2�
Kendala (1,2,3,4)⊗ ��1⊕(−3,2,5,10)⊗ ��2 ≤ℜ(−15,10,32,72) (−2,3,5,6)⊗ ��1⊕(4,5,7,11)⊗ ��2 ≥ℜ(−8,21,48,76) (0,1,2,3)⊗ ��1⊕(2,4,6,8)⊗ ��2 = (2,14,32,58) ��1,��2adalah bilangan non-negativetrapezoidal fuzzy.
Langkah pertama, uraikan bentuk permasalahan program linier fuzzy
penuh dengan menerapkan aritmatika perhitungan bilangan trapezoidal fuzzy ke
dalam bentuk permasalahan program linier.
Maksimumkan �̃=�(0,1,2,3)⊗(�1,�1,�1,�1)⊕(2,3,4,5)⊗(�2,�2,�2,�2)�
=�min(0�1, 0�1, 3�1, 3�1), min��1,�1,2�1,2�1�, max��1,�1,2�1,2�1�, max(0�1, 0�1, 3�1, 3�1)
� ⨁
�min(2�2, 2�2, 5�2, 5�2), min�3�2, 3�2,4�2,4�2�, max�3�2, 3�2,4�2,4�2�, max(2�2, 2�2, 5�2, 5�2)
�
= (0�1,�1, 2�1, 3�1)⊕(2�2, 3�2, 4�2, 5�2)
=�(0�1+ 2�2), (�1 + 3�2), (2�1+ 4�2), (3�1 + 5�2)�
Perhitungan yang sama juga dilakukan pada fungsi kendala, sehingga diperoleh:
Kendala
Dari hasil penguraian permasalahan program linier fuzzy penuh tersebut,
selanjutnya kelompokkan permasalahan tersebut menjadi empat bentuk persoalan
CLP yaitu Middle Level Problem I (MLP I),Middle Level Problem II (MLP
II),Upper Level Problem (ULP), dan Lower Level Problem (LLP) dan
masing-masing diselesaikan dengan metodeBig M sebagai berikut:
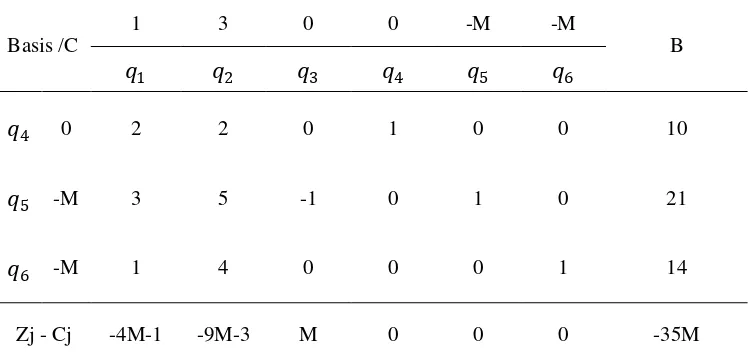
Middle Level Problem I (MLP I)
Maksimumkan �2 =�1 + 3�2
Tabel 3.1 Tabel Simpleks Awal
Basis /C
Dari tabel 3.1terlihat bahwa penyelesaian optimal belum dicapai, karena nilai
pada baris Zj - Cj< 0 (masih mengandung harga negatif). Harga Zj - Cj terkecildari
tabel diatas adalah -9M-3, sehingga variabel yang masuk dalam basis
���� �102 ,215 ,144�= 144 = 3,5
Maka variabel �6 keluar dari basis.
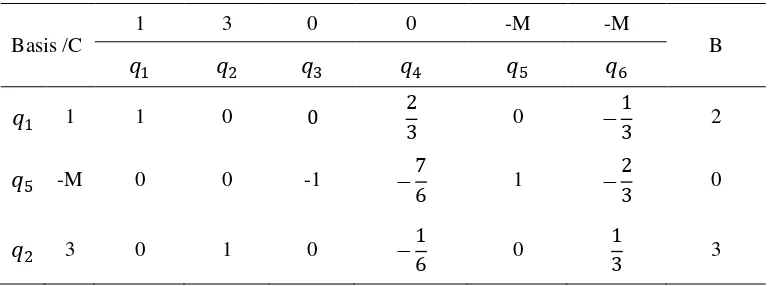
Tabel 3.2 Tabel Simpleks Iterasi 1
Basis /C
Dari tabel 3.2terlihat bahwa penyelesaian optimal masih belum dicapai, karena
masih adanilai pada baris Zj - Cj< 0.Harga Zj - Cj terkecildari tabel diatas adalah
−7
4M−
1
4, sehingga variabel yang masuk dalam basis adalahvariabel �1,kolom
variabel �1menjadi kolom kunci, harga positif terkecil pada kolom�1yang dapat
masuk ke dalam basis adalah :
���� �
Tabel 3.3 Tabel Simpleks Iterasi 2
Zj - Cj 0 0 M 7
Karena nilai pada baris �� − �� ≥0, maka penyelesaian optimal telah terpenuhi dengan nilai maksimum �2 = 11 untuk �1 = 2 dan �2 = 3.
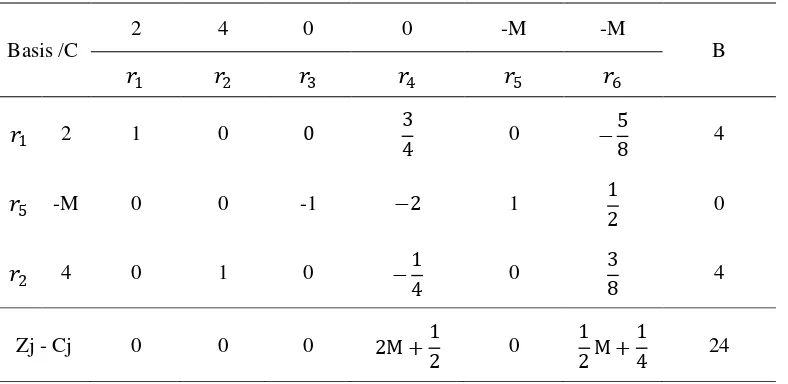
Middle Level Problem II (MLP II)
Maksimumkan �3 = 2�1 + 4�2
Dengan perhitungan metode Big M diperoleh tabel optimal simpleks sebagai
berikut:
Tabel 3.4 Tabel Optimal Simpleks MLP II
Basis /C
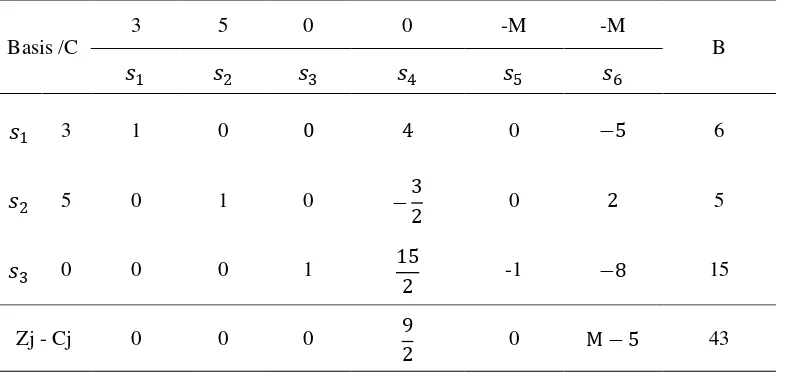
Upper Level Problem (ULP)
Dengan perhitunganmetode Big M diperoleh tabel optimal simpleks sebagai
berikut:
Tabel 3.5 Tabel Optimal Simpleks ULP
Basis /C
Penyelesaian optimal telah terpenuhi dengan nilai maksimum �4 = 32 untuk
�1 = 6dan �2 = 5.
Lower Level Problem (LLP)
Maksimumkan �1 = 0�1+ 2�2
Kendala �1−3�2 ≤ −15
Untuk permaslahan ini dapat diperoleh penyelesaian secara langsung tanpa
menggunkan metode Big M yaitu maksimum �1 = 2 untuk �1 = 0 dan �2 = 1.
Berdasarka teori metode Bound and Decomposition, penyelesaian optimal
dari MLP I, MLP II, ULP dan LLP merupakan penyelesaian dari permasalahan
program linier fuzzy penuh. Dari proses perhitungan yang telah dilakukan diperoh
penyelessaian untuk
LLP : maksimum �1 = 2 untuk �1 = 0 dan �2 = 1
MLP I : maksimum �2 = 11 untuk �1 = 2 dan �2 = 3
MLP II : maksimum �3 = 24 untuk �1 = 4 dan �2 = 4
ULP : maksimum �4 = 32 untuk �1 = 6 dan �2 = 5
Sehingga nilai maksimum �̃= (�1,�2,�3,�4) = (2, 11, 24, 32)untuk ��1 =
(�1,�1,�1,�1) = (0, 2, 4, 6)dan ��2 = (�2,�2,�2,�2) = (1, 3, 4, 5).
Jika diujikan kembali ke dalam fungsi tujian dengan mensubstitusikan
nilai ��1 = (0, 2, 4, 6)dan ��2 = (1, 3, 4, 5), maka akan diperoleh:
Maksimum�̃ =�(0,1,2,3)⊗ ��1⊕(2,3,4,5)⊗ ��2�
= �(0,1,2,3)⊗(�1,�1,�1,�1)⊕(2,3,4,5)⊗(�2,�2,�2,�2)�
= ((0,1,2,3)⊗(0,2,4,6)⊕(2,3,4,5)⊗(1,3,4,5))
= �min(0,0,0,18), min(2,4,4,8), max(2,4,4,8), max(0,0,0,18)� ⨁
�min(2,10,5,25), min(9,12,12,16),max(9,12,12,16), max(2,10,5,25)�
= (0,2,8,18)⊕(2,9,16,25)
= �(0 + 2), (2 + 9), (8 + 16), (18 + 25)�
= (2,11,24,43)
Dengan menggunakan fungsi rangking diperoleh penyelesaian optimal sebagai
berikut:
ℜ(�̃) =1
Sehingga maksimum �̃ = 20.
Jadi, dengan menguraikan bentuk permasalahan program linier fuzzy
penuh yang mana semua parameter dan variabelnya merupakan bilangan fuzzy
menjadi bentuk program linier, yang artinya semua variabel dan parameternya
berbentuk bilangan rill akan lebih mudah untuk menemukan penyelesaian
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Metode Bound and Decomposition memberikan prosedur yang mudah dalam
menentukan penyelesaian optimal dari permasalahan program linier fuzzy penuh.
Dengan menguraikan permasalahn program linier fuzzy penuh ke dalam bentuk
program linier, penyelesaian optimal akan mudah untuk diperoleh.
5.2 Saran
Penulis berharap ada penelitian lebih lanjut tentang cara menyelesaikan
permasalahan Program Linier Fuzzy Penuhyang lebih praktis dan mudah
DAFTAR PUSTAKA
Afriani, A.T., Kusumastuti, N., dan Prihandono, B. 2012. Metode Simpleks Fuzzy untuk Permasalahn Pemograman Linier Variabel Trapezoidal Fuzzy.Buletin Ilmiah Mat.Stat. Dan Terapannya (Bimaster), Vol. 2, No.1, hal 23 – 30.
Allahviranloo, T., Lotfi, F.H., Kiasary, M.Kh., Kiani, N.A., and Alzadeh, L. 2008. Solving Fully Fuzzy Linear Programming Problem by Ranking Function.Applied Mathematical Sciences, Vol. 2, No. 1, 19 – 32.
Jayalakshmi, M. and Pandian, P. 2012. A New Method for Finding an Optimal Fuzzy Solution for Fully Fuzzy Linear Programming Problems.International Journl of Enginnering Research and Applications (IJERA), Vol 2, Issue 4, pp. 247-254.
Kumar, A. and Kaur, J. 2011. A New Method for Solving Fuzzy Linear Programs with Trapezoidal Fuzzy Number.Journal of Fuzzy Set Value Analysis, Vol. 2011, Article ID jfsva-00102, 12 pages.
Kusumadewi, Sri. 2002. Analisis & Desain Sistem Fuzzy Menggunakan Toolbox Mathlab. Yogjakarta: Graha Ilmu.
Nasseri, S.H., Ebrahimnejad, A., Mizuno, S. 2010. Duality in Fuzzy Linear Programming with Symmetric Trapezoidal Number.Aplication and Applied Mathematics: An International Journal (AAM), Vol 05, Issue 10, pp, 1467 – 1482.
Siagian, P. 2006. Penelitian Operasional : Teori dan Praktek. Jakarta: UI-Press.
Siringoringo, Hotniar. 2005.Seri Teknik Riset Operasional. Pemrograman Linier. Yogyakarta: Graha Ilmu.
Susilo, Frans. 2006. Himpuan & Logika Kabur Serta Aplikasinya. Yogyakarta: Graha Ilmu.