2.1. Program Linier
Program linier disusun oleh George B. Dantzig tahun 1947 pada saat memimpin Air Force Statistical Control’s Combat Analysis Branch di Pentagon. Saat Dantzig menganalisis masalah perencanaan Air Force dia menyadari dapat merumuskan sistem ketidaksamaan linier. Hal di atas merupakan awal pemberian nama untuk teknik “program dan struktur linier”, yang belakangan ini disederhanakan menjadi program linier (Taylor, 2001).
Program linier merupakan model matematik untuk mendapatkan alternatif penggunaan terbaik atas sumber-sumber organisasi. Kata sifat linier digunakan untuk menunjukkan fungsi-fungsi matematik yang digunakan dalam bentuk linier dalam arti hubungan langsung dan persis proporsional. Program menyatakan penggunaan teknik matematika tertentu. Jadi program linier adalah suatu teknik perencanaan yang bersifat analitis menggunakan model matematis dengan tujuan menemukan beberapa kombinasi alternatif pemecahan optimum terhadap persoalan (Aminuddin, 2005).
Program linier adalah suatu teknik penyelesaian optimal atas suatu
2.1.1. Persyaratan Penyelesaian Program Linier
Syarat-syarat yang harus dipenuhi dalam merumuskan suatu problema keputusan ke dalam model matematik persamaan linier adalah sebagai berikut (Sitorus, 1997):
1. Tujuan
Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi tujuan.
2. Alternatif Perbandingan
Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan, misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu terlambat dan biaya terendah.
3. Sumber Daya
Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas. 4. Perumusan Kuantitatif
Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif sesuai dengan yang disebut dalam model matematika.
5. Keterkaitan Peubah
Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut harus memiliki hubungan fungsional atau hubungan keterkaitan.
2.1.2. Model Umum Matematik Program Linier
Model umum program linier dapat dirumuskan ke dalam bentuk matematik sebagai berikut (Sitorus, 1997):
Optimumkan:
= ∑ untuk = 1, 2, 3, … , Kendala:
≥ 0 untuk = 1, 2, 3, … , Keterangan:
= Fungsi tujuan
= Variabel keputusan
= Nilai kontribusi dari variabel keputusan
= Koefisien teknologi dari variabel keputusan dalam kendala ke-
= Sumber daya yang tersedia dalam kendala ke-
2.1.3. Karakteristik Program Linier
Karakteristik-karakteristik dalam program linier yang biasa digunakan untuk memodelkan suatu masalah dan memformulasikannya secara matematik, yaitu (Siswanto, 2006):
1. Variabel Keputusan
Variabel keputusan adalah variabel yang secara lengkap menguraikan keputusan-keputusan yang akan dibuat.
2. Fungsi Tujuan
Fungsi tujuan merupakan suatu hubungan linier dari variabel keputusan yang berupa fungsi maksimum atau minimum.
3. Fungsi Kendala
Fungsi kendala merupakan batasan-batasan dalam penyelesaian program linier yang harus diperhatikan. Kendala diekspresikan dalam persamaan dan pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumber daya dalam suatu masalah.
2.1.4. Metode Simpleks
besar permasalahan program linier mempunyai lebih dari dua variabel keputusan. Hal ini tentu sulit untuk menerapkan pendekatan grafikal untuk memperoleh penyelesaian dari permasalahan tersebut.
Oleh karena itu, pada tahun 1947 George Dantzig mengajukan suatu metode yang tepat untuk menyelesaikan permasalahan program linier yang disebut metode simpleks. Metode simpleks merupakan prosedur aljabar yang bersifat iteratif yang bergerak selangkah demi selangkah, dimulai dari titik ekstrim pada daerah feasible (ruang sousi) menuju titik ekstrim yang optimum.
Berikut langkah-langkah dalam menyelesaikan permasalahan program linier dengan metode simpleks (Handayani, 2014):
1. Konversikan formulasi persoalan ke dalam bentuk standar.
Agar persamaan garis batasan memenuhi persyaratan penyelesaian daerah kelayakan (feasible) maka semua pertidaksamaan diubah menjadi persamaan dengan cara menambahkan variabel slack, surplus dan variabel buatan (artifisial variabel) pada tiap batasan (constraint) serta memberi harga nol pada setiap koefisien tujuannya. Batasan dapat dimodifikasi sebagai berikut:
a. Untuk batasan bernotasi ≤ diubah ke dalam bentuk persamaan
dengan menambahkan variabel slack.
b. Untuk batsan bernotasi ≥ atau = diselesaikan dengan
menambahkan variabel surplus dan variabel buatan. Dengan penambahan variabel buatan ini akan merusak sistem batasan, hal ini dapat diatasi dengan membuat suatu bilangan penalty M (M bilangan positif yang sangan besar) sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Untuk kasus maksimasi maka dibuat –M sebagai harga dari variabel buatan dan untuk kasus minimasi dibuat +M sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M method).
Tabel 2.1. Bentuk Tabel Simpleks perbandingan nilai kanan dengan kolom kunci,
5. Tentukan nilai elemen cell, yaitu nilai perpotongan antara kolom kunci dan baris kunci.
6. Lakukan iterasi dengan menentukan baris kunci baru, baris Z baru, dan
baris variabel-variabel slack baru.
a. Baris kunci baru ditentukan dengan membagi baris kunci lama dengan
elemen cell.
b. Baris Z baru dan baris-baris lainnya ditentukan dengan cara:
Baris lama – (nilai kolom kunci baris yang sesuai × baris kunci baru) c. Letakkan nilai-nilai baris yang baru diperoleh ke dalam tabel.
7. Lakukan uji optimalisasi. Jika semua koefisien pada baris # − $ sudah
2.2. Program Bilangan Bulat
Program bilangan bulat ialah persoalan program linier di mana pemecahan optimalnya harus menghasilkan bilangan bulat. Dengan kata lain dari antara berbagai bilangan bulat diharuskan mencari nilai-nilai variabel yang fisibel dan membuat fungsi tujuan optimum. Ada beberapa persoalan program linier yang solusinya tidak masuk akal jika solusi yang dihasilkan berupa bilangan pecahan. Diadalam persoalan ekonomi sering kali djumpai variabel-variabel yang nilainya harus positif misalnya produksi mobil, produksi kapal terbang, jumlah jembatan, jumlah gedung, kebutuhan tenaga kerja, jumlah penganggur, jumlah ternak, dan lain sebagainya. Dalam persoalan ini bilangan-bilangan pecahan tidak mempunyai arti (Supranto, 1983).
Program bilangan bulat merupakan suatu model program linier yang khusus digunakan untuk menyesuaikan suatu problem program linier di mana nilai-nilai variabel-variabel keputusan dalam penyelesaian optimal harus merupakan bilangan bulat. Persyaratan bahwa nilai variabel keputusan harus bulat mengingat nilai tidak mungkin dalam bilangan pecahan, seperti rumah, pabrik, tugas, dan lain sebagainya (Sitorus, 1997). Pada saat menggunakan program linier biasa sering dijumpai solusi yang berupa bilangan pecahan kadang diasumsikan bahwa nilai tersebut dapat dibulatkan ke nilai bilangan bulat terdekat. Metode ini
tidak akan menyebabkan kesulitan, jika contohnya hasil yang didapat = 8,4 paku dibulatkan menjadi = 8 paku, mengingat harga paku hanya beberapa sen
saja perbuahnya. Akan tetapi, jika masalah yang dihadapi adalah mempertimbangkan produksi suatu jet pesawat dan solusi yang dihasilkan adalah
= 7,4 jet, maka pembulatan dapat mempengaruhi keuntungan bermiliar-miliar
dolar. Dalam hal ini maka program bilangan bulat hadir menyelesaikan permasalahan sedemikian rupa sehingga suatu solusi bilangan bulat optimal dijamin tercapai (Taylor, 2001).
maks/min: Z = 1
kendala: 1 1
!
≤, =, ≥
≥ 0 adalah bilangan bulat
di mana: = fungsi tujuan
= koefisien dari variabel keputusan dalam fungsi tujuan
= variabel keputusan
= koefisien dari variabel keputusan dalam fungsi kendala
= sumber daya yang tersedia dalam fungsi kendala
Berdasarkan jenis keputusan yang akan diperoleh persoalan integer programming dapat dibedakan atas tiga jenis, yaitu (Ritonga, 2015):
1. Pemrograman bilangan bulat murni (pure integer programming), yaitu
merupakan pemrograman bilangan bulat di mana semua nilai variabel keputusan haruslah bilangan bulat.
2. Pemrograman bilangan bulat campuran (mixed integer programming), yaitu merupakan pemrograman bilangan bulat di mana nilai variabel keputusannya bernilai bilangan bulat dan variabel yang lainya bernilai bilangan desimal atau pecahan.
3. Pemrograman bilangan bulat biner (binary integer programming), yaitu nilai variabel keputusannya adalah bilangan biner (0 atau 1). Dalam aplikasi sehari-hari, masalah binary integer programming menyangkut masalah pengambilan keputusan, di mana jika solusi yang didapat berupa angka 1
berarti menyatakan “ya” atau angka 0 berarti menyatakan “tidak”.
2.2.1. Metode Penyelesaian Program Bilangan Bulat
2.2.1.1. Metode Pembulatan (Rounding Method)
Metode ini sangat sederhana dan cepat dalam menyelesaikan program bilangan bulat. Sebelum metode ini diterapkan, maka terlebih dahulu dicari penyelesaian dari problema dengan menggunakan metode program linier biasa, yaitu metode grafik. Selanjutnya, metode ini diterapkan dengan cara melakukan pembulatan hasil nilai variabel keputusan (bilangan pecahan) yang diperoleh dari metode grafik tersebut (Sitorus, 1997).
Kelemahan utama metode ini ialah bahwa hasil pembulatan yang dilakukan dapat menyimpang jauh dari penyelesaian optimal bilangan bulat sesungguhnya dalam penyelesaiannya dianggap tidak layak apabila hasilnya lebih besar daripada penyelesaaian optimal bilangan bulat atau penyelesaian optimal pecahan (metode grafik). Hasil penyelesaian optimal metode pembulatan tidak akan pernah nilai optimalnya lebih besar daripada hasil yang diperoleh dari metode grafik biasa (pecahan). Hal ini disebabkan bahwa adanya persyaratan pembulatan yang tidak boleh keluar dari daerah kelayakan (metode pembulatan) dan tambahan kendala (metode pembulatan), yang kesemuanya mengakibatkan luas daerah kelayakan bertambah kecil (Sitorus, 1997).
2.2.1.2 Metode Branch and Bound
Metode ini sering digunakan untuk menyelesaikan masalah program bilangan bulat karena hasil yang diperoleh dalam penyelsaian optimal lebih teliti dan lebih baik dari kedua metode lainnya. Kelemahan pokok metode ini adalah prosedur untuk mencapai hasil yang optimal sangat panjang (Sitorus, 1997).
Prosedur penyelesaian problema megoptimalkan proram linier bilangan bulat dengan metode ini adalah sebagai berikut (Sitorus, 1997):
Masalah yang dihadapi diselesaikan lebih dahulu menggunkan metode simpleks atau menggunakan metode grafik sampai diperoleh hasil yang optimal.
Langkah 2: Pemeriksaan Penyelesaian Optimal
Hasil optimal pada langkah 1 diperiksa apakah variabel keputusan yang diperoleh bernilai integer atau pecahan. Apabila semua nilai variabel keputusan yang dihasilkan telah bernilai integer maka solusi optimal telah tercapai. Apabila tidak maka proses iterasi dilanjutkan.
Langkah 3: Penyusunan Subproblema (Branching)
Apabila penyelesaian optimal belum tercapai, maka problema tersebut dimodifikasi ke dalam dua subproblema dengan memasukkan kendala baru ke masing-masing subproblema tersebut.
Langkah 4: Penentuan Nilai Batas (Bounding)
Hasil optimal yang diperoleh dengan metode program linier biasa merupakan nilai batas atas bagi setiap subproblema. Sedangkan hasil optimal dengan penyelesaian integer merupakan nilai batas bawah bagi masing-masing subproblema. Selanjutnya apabila subproblema yang memiliki batas atas yang lebih rendah dari batas bawah yang berlaku, maka subproblema tersebut tidak perlu
dianalisis lagi. Apabila dalam penyelesaian integer menghasilkan hasil yang sama atau lebih baik daripada nilai batas atas dari setiap problema, maka penyelesaian optimal integer telah tercapai. Apabila tidak, maka subproblema yang memiliki nilai batas atas yang terbaik dipilih selanjutnya menjadi subproblema baru. Proses iterasi kembali pada langkah 2 sehingga demikian seterusnya.
perjalanan yang terdapat pada persoalan pedagang keliling atau Travelling Salesman Problem (TSP) (Simarmata, 2015).
2.3. Fuzzy
Istilah fuzzy lahir dari gagasan seorang guru besar pada University of California, Berkeley, Amerika Serikat, Prof. Lotfi Asker Zadeh. Sejak tahun 1960 Zadeh telah merasa bahwa sistem analisis matematika tradisional yang dikenal sampai saat itu bersifat terlalu eksak sehingga tidak dapat berfungsi dalam banyak masalah dunia nyata yang seringkali amat kompleks. Pada akhirnya di tahun 1965 Zadeh mempublikasikan karangan ilmiahnya berjudul “Fuzzy Set”. Terobosan baru yang deperkenalkan oleh Zadeh ini telah memperluas konsep himpunan klasik menjadi himpunan fuzzy yang dapat mempresentasikan nilai-nilai ketidakpastian yang ditemui dalam kehidupan nyata (Handayani, 2014).
Menurut Zadeh, himpunan fuzzy (fuzzy set) adalah sebuah kelas dari obyek dengan serangkaian kesatuan dari nilai keanggotaan. Sebuah set dikarakterisasikan oleh sebuah fungsi keanggotaan yang memberikan tiap obyek sebuah nilai keanggotaan yang rentang nilainya antara 0 dan 1. Pada teori himpunan fuzzy, peranan derajat keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangatlah penting. Nilai keanggotaan atau derajat keanggotaan atau membership function menjadi cirri utama dari penalaran dengan
logika fuzzy tersebut (Kusumadewi & Purnomo, 2010).
2.3.1. Alasan Digunakannya Logika Fuzzy
1. Konsep logika fuzzy mudah dimengert. Karena logika fuzzy menggunakan dasar teori himpunan, maka konsep matematis yang mendasari penalaran fuzzy tersebut cukup mudah dimengerti.
2. Logika fuzzy sangat fleksibel, artinya mampu beradaptasi dengan
perubahan-perubahan, dan ketidakpastian yang menyertai permasalahan.
3. Logika fuzzy memiliki toleransi terhadap data yang tidak tepat. Jika diberikan
sekelompok data yang cukup homogen, dan kemudian ada beberapa data yang “eksklusif”, maka logika fuzzy memiliki kemampuan untuk menangani data eksklusif tersebut.
4. Logika fuzzy mampu memodelkan fungsi-fungsi nonlinier yang sangat kompleks.
5. Logika fuzzy dapat membangun dan mengaplikasikan pengalaman-pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan. Dalam hal ini, sering dikenal dengan nama Fuzzy Expert Systems menjadi bagian terpenting.
6. Logika fuzzy dapat bekerjasama dengan teknik-teknik kendali secara konvensional. Hal ini umumnya terjadi pada aplikasi di bidang teknik mesin maupun teknik elektro.
7. Logika fuzzy didasarkan pada bahasa alami. Logika fuzzy menggunakan bahasa sehari-hari sehingga mudah dimengerti.
2.3.2. Himpunan Fuzzy
• Nol (0), yang berarti bahwa suatu item tidak menjadi anggota dalam suatu himpunan.
a. Linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau
kondisi tertentu dengan menggunakan bahasa alami, seperti: muda, parobaya, tua.
b. Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu
variabel seperti: 40, 25, 50, dsb.
Misalkan diketahui klasifikasi sabagai berikut:
MUDA < <= < 35 @ ℎ<
SETENGAH BAYA 35 ≤ < <= ≤ 55 @ ℎ<
TUA < <= > 55 @ ℎ<
Dengan menggunakan pendekatan crisp, amatlah tidak adil untuk menetapkan nilai SETENGAH BAYA. Pendekatan ini bisa saja dilakukan untuk hal-hal yang bersifat diskontinu. Misalkan umur klasifikasi 55 tahun dan 56 tahun sangat jauh berbeda, umur 55 tahun termasuk SETENGAH BAYA, sedangkan perlahan menurun menuju 0 untuk umur di bawah 35 tahun dan di atas 55 tahun (Sihotang, 2011).
Ada beberapa hal yang perlu diketahui dalam memahami sistem fuzzy, yaitu (Kusumadewi & Purnomo, 2010):
a. Variabel fuzzy
Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem fuzzy. Contoh: umur, temperature, permintaan, dsb.
b. Himpunan fuzzy
Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy.
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan himpunan bilangan ril yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif.
d. Domain
Domain himpunan fuzzy adalah keseluruhan nilai yang diizinkan dalam semesta pembicaraan dan boleh dioperasikan dalam sutu himpunan fuzzy. Sepertinya semesta pembicaraan, domain merupakan himpunan bilangan ril yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai domain dapat berupa bilangan positif maupun negatif.
2.3.3. Fungsi Keanggotaan
Fungsi keanggotaan adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya (sering juga disebut dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah dengan melalui
pendekatan fungsi. Ada beberapa fungsi yang bisa digunakan (Kusumadewi & Purnomo, 2010).
2.3.3.1 Representasi Linier
memiliki derajat keanggotaan nol (0) bergerak ke kanan menuju nilai domain yang memiliki derajat keanggotaan lebih tinggi (Kusumadewi & Purnomo, 2010).
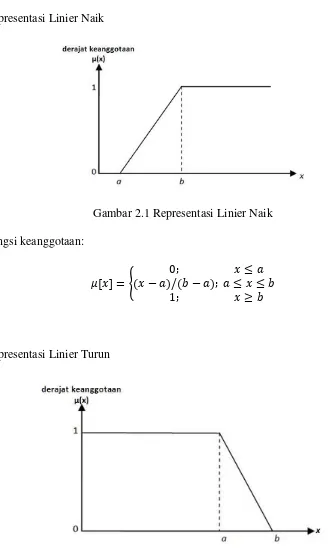
Representasi Linier Naik
Gambar 2.1 Representasi Linier Naik
Fungsi keanggotaan:
:C D = E − / −0;
1; ; G
≤ ≤ ≤
≥
Representasi Linier Turun
Fungsi Keanggotaan:
:C D = H − / − ;0; ≤ ≤≥ G
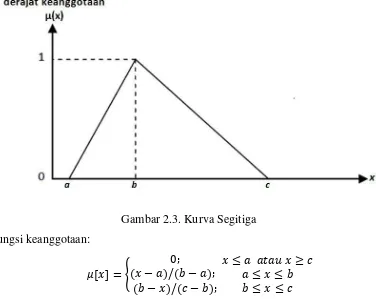
2.3.3.2 Representasi Kurva Segitiga
Kurva segitiga pada dasarnya merupakan gabungan antara 2 garis (linier).
Gambar 2.3. Kurva Segitiga Fungsi keanggotaan:
:C D = E − / − ; 0;
− / − ;G
≤ @ < ≥ ≤ ≤ ≤ ≤
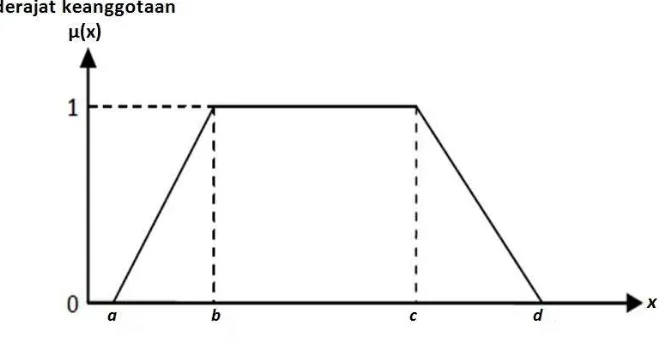
2.3.3.3. Representasi Kurva Trapesium
Gambar 2.4. Kurva Trapesium Fungsi keanggotaan:
:C D = I
0;
− / − ; 1;
J − / J − ;
≤ @ < ≥ J ≤ ≤ ≤ ≤ ≤ ≤ J