BAB 2
LANDASAN TEORI
2.1 Program Linier
Program linier merupakan suatu model matematika untuk mendapatkan alternatif penggunaan terbaik atas sumber-sumber yang tersedia. Kata linier digunakan untuk menunjukkan fungsi matematika yang digunakan dalam bentuk linier, sedangkan program merupakan penggunaan teknik matematika tertentu. Jadi pengertian program linier adalah suatu teknis perencanaan yang bersifat analitis yang analisisnya menggunakan model matematika, dengan tujuan menemukan beberapa alternatif pemecahaan optimum terhadap persoalan (Aminudin, 2005).
Program linier berkaitan dengan maksimalisasi atau minimalisasi dari fungsi tujuan linier dengan beberapa variabel yang memiliki kesamaan dan ketaksamaan fungsi kendala. Program linier menggunakan model matematika untuk menjelaskan persoalan yang dihadapi. Sifat “linier” memberi arti bahwa seluruh fungsi matematis dalam model merupakan fungsi yang linier, demikian kata “program” merupakan sinonim untuk perencanaan. Dengan demikian program linier adalah perencanaan aktivitas-aktivitas untuk memperoleh suatu hasil yang optimum, yaitu suatu hasil yang mencapai tujuan terbaik di antara alternatif yang layak (Dantzig & Thapa, 1997).
Dimyati dan A. Dimyati (1987) juga mendefinisikan program linier sebagai suatu cara untuk menyelesaikan persoalan pengalokasian sumber-sumber yang terbatas di antara beberapa aktivitas, dengan cara terbaik yang mungkin dapat dilakukan. Formulasi model matematika dari persoalan pengalokasian sumber-sumber pada permasalahan program linier adalah sebagai berikut (Sitorus, 1997).
∑
∑ ∑
di mana: fungsi tujuan
koefisien variabel keputusan dari fungsi tujuan variabel keputusan
koefisien variabel keputusan dari fungsi kendala sumber daya dalam fungsi kendala
Program linier bilangan bulat merupakan suatu model program linier yang khusus digunakan untuk menyesuaikan suatu problem di mana nilai variabel-variabel keputusan dalam penyelesaian optimal haruslah merupakan bilangan integer. Persyaratan bahwa nilai variabel keputusan harus bilangan bulat mengingat jumlahnya tidak mungkin dalam bentuk pecahan, seperti rumah, pabrik, tugas, dan lain sebagainya (Sitorus, 1997).
2.1.1 Syarat Utama Program Linier
Agar dapat menyusun dan merumuskan suatu persoalan atau permasalahan yang dihadapi ke dalam model program linier, maka ada lima syarat yang harus dipenuhi (Sitorus, 1997):
1. Tujuan
Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dipecahkan dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi tujuan.
2. Alternatif Perbandingan
Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan, misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu terlambat dan biaya terendah.
3. Sumber Daya
4. Perumusan Kuantitatif
Fungsi tujuan dan kendala harus dapat dirumuskan secara kuantitatif sesuai dengan yang disebut dalam model matematika.
5. Keterkaitan Variabel
Variabel-variabel yang membentuk fungsi tujuan dan kendala tersebut harus memiliki hubungan fungsional atau hubungan keterkaitan.
2.1.2 Jenis-jenis Fungsi Program Linier
Model program linier merupakan bentuk dan susunan dalam menyajikan masalah-masalah yang akan dipecahkan dengan teknik program linier. Dalam model program linier dikenal 2 (dua) jenis fungsi, yaitu:
1. Fungsi Tujuan (objective function) adalah fungsi yang menggambarkan tujuan/sasaran di dalam permasalahan program linier yang berkaitan dengan pengaturan secara optimal, untuk memperoleh keuntungan maksimum atau biaya minimum. Pada umumnya nilai yang akan dioptimalkan dinyatakan sebagai Z.
2. Fungsi Kendala (constraint function) adalah bentuk penyajian secara matematis batasan-batasan kapasitas yang tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.
2.1.3 Karakteristik Program Linier
Karakteristik-karakteristik dalam program linier yang biasa digunakan untuk memodelkan suatu masalah dan memformulasikannya secara matematika, yaitu (Siswanto, 2006):
1. Variabel Keputusan
Variabel keputusan adalah variabel yang menguraikan secara lengkap keputusan-keputusan yang akan dibuat. Variabel keputusan tidak negatif. 2. Fungsi Tujuan
ini dibatasi oleh kendala yang mencerminkan keterbatasan dari kapasitas waktu produksi kemampuan yang dimiliki.
3. Fungsi Kendala
Fungsi kendala merupakan batasan-batasan dalam penyelesaian program linier yang harus diperhatikan. Kendala diekspresikan dalam persamaan dan pertidaksamaan yang juga merupakan hubungan linier dari variabel keputusan yang mencerminkan keterbatasan sumber daya dalam suatu masalah.
2.1.4 Asumsi dalam Program Linier
Dalam menggunakan model program linier, diperlukan beberapa asumsi sebagai berikut:
1. Asumsi Linieritas (Linearity)
Fungsi tujuan (objective function) dan fungsi kendala (constraint) dibuat dalam fungsi linier. Sifat linieritas suatu kasus dapat ditentukan dengan menggunakan beberapa cara, misalnya dengan menggunakan grafik.
2. Asumsi Kesebandingan (Propotionality)
a. Kontribusi variabel keputusan terhadap fungsi tujuan adalah sebanding dengan nilai variabel keputusan.
b. Kontribusi variabel keputusan terhadap ruas kiri dari setiap pembatas juga sebanding dengan nilai variabel keputusan itu.
3. Asumsi Penambahan (Additivity)
Sifat penambahan mengasumsikan bahwa tidak terdapat bentuk perkalian silang pada model, baik fungsi tujuan maupun fungsi kendala.
4. Asumsi Pembagian (Divisibility)
Dalam persoalan program linier, variabel keputusan boleh diasumsikan berupa bilangan bulat (integer) atau bilangan pecahan.
5. Asumsi Kepastian (Certainty)
6. Asumsi Ketidaknegatifan (Nonnegativity)
Nilai variabel keputusan harus lebih besar atau sama dengan nol.
2.1.5 Istilah-istilah yang digunakan dalam Program Linier
Dalam program linier, dikenal dengan istilah-istilah sebagai berikut: 1. Solusi Fisibel dan Solusi Infisibel
Solusi fisibel adalah solusi yang memenuhi semua syarat pembatas, sedangkan solusi infisibel adalah solusi yang sekurang-kurangnya memuat tidak memenuhi salah satu syarat pembatas.
2. Solusi Optimal
Solusi optimal adalah solusi fisibel yang memiliki nilai fungsi tujuan paling menguntungkan. Nilai fungsi tujuan paling menguntungkan adalah nilai terbesar untuk fungsi tujuan maksimum, dan nilai terkecil untuk fungsi tujuan minimum. Kebanyakan masalah dalam program linier hanya memiliki sebuah nilai optimum, akan tetapi dimungkinkan adanya jawaban optimum yang tidak tunggal. Jika ditemukan jawaban optimum tidak tunggal umumnya jawaban optimum tersebut adalah banyak.
3. Solusi Fisibel Titik Ujung (ekstrim)
Solusi fisibel titik ujung (ekstrim) adalah solusi yang terletak pada titik- ujung (titik ekstrim).
2.2 Program Bilangan Bulat
Menurut Mulyono (2004), program bilangan bulat dibutuhkan ketika keputusan harus dalam bentuk bilangan integer. Model matematika dari program bilangan bulat sebenarnya sama dengan model program linier, dengan tambahan batasan bahwa variabel keputusannya harus bilangan integer. Program bilangan bulat adalah suatu program linier dengan tambahan persyaratan bahwa semua atau beberapa variabel bernilai bulat non negative.
solusi yang diperoleh adalah bilangan bulat bukan bilangan pecahan. Contoh persoalan yang sering ditemui misalnya menentukan banyaknya mobil yang harus diproduksi, banyaknya unit rumah yang akan dibangun pada suatu proyek perumahan, banyaknya orang yang diperlukan untuk mengerjakan suatu proyek dan sebagainya. Program bilangan bulat memiliki model matematika yang sama dengan model program linier pada umumnya hanya saja ditambah batasan bahwa variabelnya harus bilangan bulat sebagai berikut (Syahputra, 2012).
∑
∑ ∑
di mana: fungsi tujuan
koefisien variabel keputusan dalam fungsi tujuan variabel keputusan
koefisien variabel keputusan dalam fungsi kendala sumber daya dalam fungsi kendala
2.2.1 Beberapa Jenis Keputusan Persoalan Integer Programming
2.2.1.1 Pemrograman Bilangan Bulat Murni (Pure Integer Programming)
Pure Integer Programming (PIP) merupakan pemrograman bilangan bulat di
mana semua nilai variabel keputusan haruslah bilangan bulat. Bentuk umum pure
integer programming sama dengan bentuk umum program bilangan bulat yang
terdapat pada rumus 2.2.
2.2.1.2 Program Bilangan Bulat Campuran (Mixed Integer Programming)
Mixed Integer Programming (MIP) merupakan pemrograman bilangan bulat di
bernilai bilangan desimal atau pecahan. Bentuk umum mixed integer variabel keputusan tidak harus bilangan bulat
koefisien variabel keputusan dalam fungsi kendala
2.2.1.3 Program Bilangan Bulat Biner (Binary Integer Programming)
Bentuk lain dari masalah program bilangan bulat adalah Binary Integer
Programming (BIP). Dalam persoalan binary integer programming nilai variabel
keputusannya adalah bilangan biner (0 atau 1).
Dalam aplikasi sehari-hari, masalah binary integer programming menyangkut masalah pengambilan keputusan, di mana jika solusi yang didapat berupa angka 1 berarti menyatakan “ya” atau angka 0 berarti menyatakan “tidak”. Bentuk umum dari binary integer programming, yaitu (Syahputra, 2012).
∑
∑ ∑
di mana: fungsi tujuan
koefisien variabel keputusan dalam fungsi tujuan variabel keputusan
koefisien variabel keputusan dalam fungsi kendala sumber daya dalam fungsi kendala
2.2.2 Metode Penyelesaian Integer Programming
Beberapa metode penyelesaian masalah program bilangan bulat adalah metode pembulatan (rounding method) dan metode grafik (graphic method).
2.2.2.1 Metode Pembulatan (Rounding Method)
Metode pembulatan sangat sederhana dan cepat dalam menyelesaikan masalah yang dihadapi. Sebelum metode ini diterapkan, maka terlebih dahulu dicari penyelesaian optimal dari problema dengan menggunakan metode program linier biasa. Selanjutnya, metode pembulatan diterapkan dengan cara melakukan pembulatan hasil nilai variabel keputusan (bilangan pecahan) yang diperoleh dari metode program linier (Sitorus, 1997).
2.2.2.2 Metode Grafik (Graphic Method)
Metode grafik relatif lebih mudah untuk menyelesaikan masalah program bilangan bulat dengan dua variabel yaitu dengan menggambar grafik di atas kertas grafik kemudian menggambarkan sekumpulan titik-titik bilangan bulat dalam ruang solusi layak (Syahputra, 2012).
Metode grafik hanya dapat dilakukan apabila jumlah variabel keputusan adalah dua. Metode ini menggunakan pendekatan pencarian. Untuk mencari penyelesaian optimal, dilakukan dengan cara mencari titik penyelesaian optimal yang terdapat di dalam daerah kelayakan dengan koordinatnya harus bilangan integer yang mendekati titik optimal yang diperoleh dengan menggunakan metode grafik biasa.
Diberikan suatu permasalahan yang akan diselesaikan dengan pendekatan grafik sebagai berikut:
Contoh 2.1
Tentukan nilai bilangan bulat dari masalah berikut: Maksimumkan Z = 3 + 4
Kendala + 6
+ 9
adalah bilangan bulat
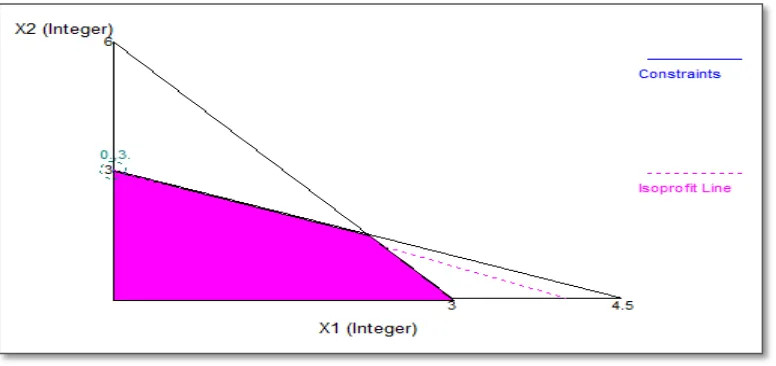
Model ini serupa dengan model program linier biasa. Perbedaannya terletak pada kendala terakhir yang menginginkan solusi bernilai bilangan bulat positif, solusi grafik untuk masalah ini ditunjukkan pada Gambar 2.1:
Solusi optimum pada contoh 2.1 dapat dilihat berdasarkan Gambar 2.1 yaitu , dan . Untuk mencari solusi optimum yang bernilai bilangan bulat pada contoh 2.1, garis Z digeser secara sejajar dari titik yang menunjukkan solusi optimum menuju titik asal. Solusi optimum yang benilai bilangan bulat adalah titik bilangan bulat pertama yang bersinggungan dengan garis Z yaitu , dan .
2.3 Metode Simpleks
Pada tahun 1947 George Dantzig mengajukan suatu metode yang tepat untuk menyelesaikan permasalahan program linier yang disebut metode simpleks. Metode simpleks merupakan prosedur aljabar yang bersifat iteratif yang bergerak selangkah demi selangkah, dimulai dari titik ekstrim pada daerah layak menuju titik ekstrim optimum (Siagian, 2006).
Ada beberapa istilah yang sering digunakan dalam metode simpleks, di antaranya:
1. Iterasi adalah tahapan perhitungan di mana nilai dalam perhitungan itu tergantung dari nilai tabel sebelumnya.
2. Variabel non basis adalah variabel yang nilainya diatur menjadi nol pada sembarang iterasi. Dalam terminologi umum, jumlah variabel non basis selalu sama dengan derajat bebas dalam sistim persamaan.
3. Variabel basis merupakan variabel yang nilainya bukan nol pada sembarang iterasi. Pada solusi awal, variabel basis merupakan variabel slack (jika fungsi kendala merupakan pertidaksamaan ≤) atau variabel buatan (jika fungsi kendala menggunakan pertidaksamaan ≥ atau =). Secara umum, jumlah variabel basis selalu sama dengan jumlah fungsi pembatas (tanpa fungsi non negatif).
4. Solusi atau nilai kanan merupakan nilai sumber daya pembatas yang masih tersedia. Pada solusi awal, nilai kanan atau solusi sama dengan jumlah sumber daya pembatas awal yang ada, karena aktivitas belum dilaksanakan. 5. Variabel slack adalah variabel yang ditambahkan ke model matematika
Penambahan variabel ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel slack akan berfungsi sebagai variabel basis.
6. Variabel surplus adalah variabel yang dikurangkan dari model matematika kendala untuk mengkonversikan pertidaksamaan ≥ menjadi persamaan (=). Penambahan ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel surplus tidak dapat berfungsi sebagai variabel basis.
7. Variabel buatan adalah variabel yang ditambahkan ke model matematika kendala dengan bentuk ≥ atau = untuk difungsikan sebagai variabel basis awal. Penambahan variabel ini terjadi pada tahap inisialisasi. Variabel ini harus bernilai 0 pada solusi optimal, karena kenyataannya variabel ini tidak ada. Variabel hanya ada di atas kertas.
8. Kolom pivot (kolom kerja) adalah kolom yang memuat variabel masuk. Koefisien pada kolom ini akan menjadi pembagi nilai kanan untuk menentukan baris pivot (baris kerja).
9. Baris pivot (baris kerja) adalah salah satu baris dari antara variabel basis yang memuat variabel keluar.
10. Elemen pivot (elemen kerja) adalah elemen yang terletak pada perpotongan kolom dan baris pivot. Elemen pivot akan menjadi dasar perhitungan untuk tabel simpleks berikutnya.
11. Variabel masuk adalah variabel yang terpilih untuk menjadi variabel basis pada iterasi berikutnya. Variabel masuk dipilih satu dari antara variabel non basis pada setiap iterasi. Variabel ini pada iterasi berikutnya akan bernilai positif.
12. Variabel keluar adalah variabel yang keluar dari variabel basis pada iterasi berikutnya dan digantikan oleh variabel masuk. Variabel keluar dipilih satu dari antara variabel basis pada setiap iterasi. Variabel ini pada iterasi berikutnya akan bernilai nol.
Berikut langkah-langkah dalam menyelesaikan permasalahan program linier dengan metode simpleks (Handayani, 2014):
1. Konversikan formulasi persoalan ke dalam bentuk standar.
dengan cara menambahkan variabel slack, surplus dan variabel buatan (artifisial variabel) pada tiap batasan (constraint) serta memberi harga nol pada setiap koefisien tujuannya. Batasan dapat dimodifikasi sebagai berikut: a. Untuk batasan bernotasi diubah ke dalam bentuk persamaan dengan
menambahkan variabel slack.
b. Untuk batasan bernotasi atau diselesaikan dengan menambahkan variabel surplus dan variabel buatan. Dengan penambahan variabel buatan ini akan merusak sistim batasan, hal ini dapat diatasi dengan membuat suatu bilangan penalty M (M bilangan positif yang sangat besar) sebagai harga dari variabel buatan tersebut dalam fungsi tujuan. Untuk kasus maksimasi maka dibuat –M sebagai harga dari variabel buatan dan untuk kasus minimasi dibuat +M sebagai harga dari variabel buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M method).
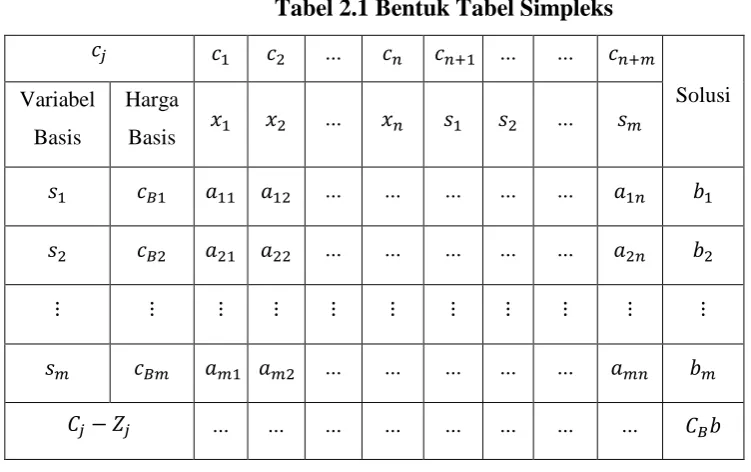
2. Susun persamaan-persamaan ke dalam tabel simpleks Tabel 2.1 Bentuk Tabel Simpleks
... ... ...
Solusi Variabel
Basis
Harga
Basis ... ...
... ... ... ... ...
... ... ... ... ...
... ... ... ... ...
... ... ... ... ... ... ... ...
3. Pilih kolom kunci, yaitu kolom yang memiliki nilai ( ) yang paling
positif untuk kasus maksimasi atau yang memiliki nilai ( ) yang paling negatif untuk kasus minimasi.
5. Tentukan nilai elemen cell, yaitu nilai perpotongan antara kolom kunci dan baris kunci.
6. Lakukan iterasi dengan menentukan baris kunci baru, baris Z baru, dan baris variabel-variabel slack baru.
a. Baris kunci baru ditentukan dengan membagi baris kunci lama dengan elemen cell.
b. Baris Z baru dan baris-baris lainnya ditentukan dengan cara:
Baris lama – (nilai kolom kunci baris yang sesuai × baris kunci baru) c. Letakkan nilai-nilai baris yang baru diperoleh ke dalam tabel.
7. Lakukan uji optimalisasi. Jika semua koefisien pada baris ( ) sudah tidak ada lagi yang bernilai positif (untuk kasus maksimasi) atau sudah tidak ada lagi yang bernilai negatif (untuk kasus minimasi) berarti sudah optimal. Jika kriteria belum terpenuhi, diulangi dari langkah 3.
Diberikan suatu permasalahan yang akan diselesaikan dengan metode simpleks sebagai berikut:
Contoh 2.2
Tentukan nilai bilangan bulat dan dari masalah berikut: maksimumkan Z = +
kendala + 60
+ 48
adalah bilangan bulat Penyelesaian:
a. Konversikan formulasi persoalan ke dalam bentuk standar sebagai berikut: maksimumkan Z = +
kendala + + + = 60 + + + = 48
b. Menyusun persamaan-persamaan ke dalam tabel simpleks sebagai berikut:
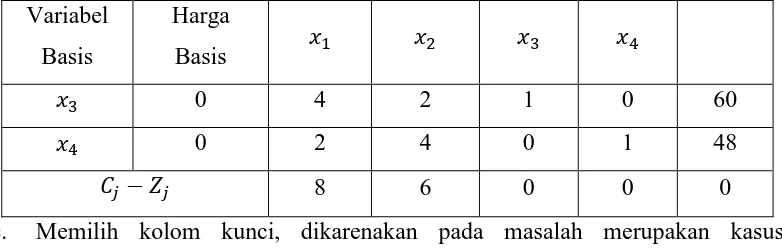
Tabel 2.2 Tabel Simpleks Iterasi 0 pada Contoh 2.2
Variabel
c. Memilih kolom kunci, dikarenakan pada masalah merupakan kasus maksimasi maka dipilih nilai yang paling positif sebagai berikut: Tabel 2.3 Proses 1 Tabel Simpleks Menuju Iterasi 1 pada Contoh 2.2
8 6 0 0 kunci yang telah dipilih, kemudian dipilih nilai yang paling terkecil sebagai berikut:
( )
maka keluar dari variabel basis dan masuk dalam variabel basis, sehingga diperoleh sebagai berikut:
Tabel 2.4 Proses 2 Tabel Simpleks Menuju Iterasi 1 pada Contoh 2.2
8 6 0 0
dan menentukan baris yang lainnya yaitu dengan cara sebagai berikut:
serta menentukan baris yang baru yaitu dengan cara sebagai berikut: mengalikan nilai variabel basis pada kolom harga basis dengan kolom
masing-masing variabel, kemudian baris dikurang dengan hasil , sehingga hasilnya diperoleh sebagai berikut:
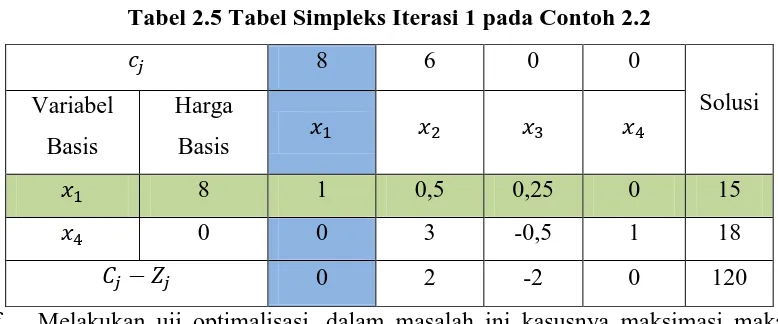
Tabel 2.5 Tabel Simpleks Iterasi 1 pada Contoh 2.2
8 6 0 0
f. Melakukan uji optimalisasi, dalam masalah ini kasusnya maksimasi maka nilai pada baris tidak ada lagi yang bernilai positif.
Dan terlihat bahwa pada Tabel 2.5 masih ada yang bernilai positif maka dilanjutkan ke iterasi 2, proses pengerjaan pada iterasi 2 sama dengan proses pengerjaan pada iterasi 1, sehingga diperoleh solusi optimumnya pada iterasi 2, setelah menguji optimalisasi pada iterasi 2 terlihat bahwa baris tidak ada lagi yang bernilai positif, dapat dilihat Tabel 2.6 sebagai berikut:
Tabel 2.6 Solusi Optimum Awal pada Iterasi 2 Contoh 2.2
2.4 Metode Branch and Bound
Menurut Fien Zulfikarijah (2004), branch and bound adalah metode umum untuk mencari solusi optimal dari berbagai masalah optimasi. Metode ini pertama kali diperkenalkan oleh A.H. Land dan A.G. Doig pada tahun 1960.
Metode branch and bound adalah salah satu metode untuk mendapatkan penyelesaian optimal pada program linier yang menghasilkan variabel-variabel keputusan bilangan bulat. Metode ini membatasi penyelesaian optimum yang akan menghasilkan bilangan pecahan dengan cara membuat cabang atas dan bawah bagi masing-masing variabel keputusan yang bernilai pecahan agar bernilai bulat sehingga setiap pembatasan akan menghasilkan cabang baru.
Prinsip dasar metode ini adalah memecah daerah fisibel layak suatu masalah program linier dengan membuat submasalah. Ada dua konsep dasar dalam metode branch and bound:
1. Branching adalah proses membagi-bagi permasalahan menjadi
subproblem-subproblem yang mungkin mengarah ke solusi.
2. Bounding adalah suatu proses untuk mencari/menghitung batas atas dan batas
bawah untuk solusi optimal pada subproblem yang mengarah ke solusi. Prosedur penyelesaian problema program linier integer dengan metode ini adalah sebagai berikut:
1. Penyelesaian Optimal Dengan Metode Program Linier Biasa
Problema yang dihadapi diselesaikan terlebih dahulu dengan menggunakan metode program linier biasa (metode grafik atau metode simpleks) sampai diperoleh hasil optimal.
2. Pemeriksaan Penyelesaian Optimal
Hasil optimal pada langkah 1 diperiksa apakah variabel keputusan yang diperoleh bernilai integer atau pecahan. Apabila ternyata nilai semua variabel keputusan tersebut merupakan bilangan bulat positif, maka penyelesaian optimal telah tercapai. Apabila tidak, maka proses iterasi dilanjutkan.
Apabila penyelesaian optimal belum tercapai, maka peroblema tersebut dimodifikasi ke dalam dua subproblema (branching) dengan memasukkan kendala baru ke masing-masing subproblema tersebut.
4. Penentuan Nilai Batas (Bounding)
Hasil optimal yang diperoleh dengan metode program linier biasa merupakan nilai batas atas bagi setiap subproblema. Sedangkan hasil optimal dengan penyelesaian integer merupakan nilai batas bawah bagi masing-masing subproblema. Selanjutnya apabila subproblema yang memiliki batas atas yang lebih rendah dari batas bawah yang berlaku, maka subproblema tersebut tidak perlu dianalisis lagi. Apabila dalam penyelesaian integer menghasilkan hasil yang sama atau lebih baik dari pada nilai batas atas dari setiap problema, maka penyelesaian optimal integer telah tercapai. Apabila tidak, maka subproblema yang memiliki nilai batas atas yang terbaik dipilih selanjutnya menjadi subproblema baru. Proses iterasi kembali pada langkah 2 sehingga demikian seterusnya.
Penggunaan metode branch and bound banyak sekali di antaranya knapsack problem, integer programming, travelling sales problem, cutting stock problem dan banyak lagi kegunaannya. Penggunaan metode ini tentulah untuk mencari nilai pembulatan terbaik pada masing-masing masalah.
2.5 Metode Cutting Plane
Metode cutting plane dikembangkan untuk menemukan solusi optimum bagi program bilangan bulat. Metode ini dilakukan dengan menambahkan suatu kendala yang dinamakan kendala gomory. Penambahan kendala gomory dilakukan pada tabel optimal sehingga dapat mempersingkat perhitungan (Siagian, 2006).
ruang penyelesaian yang tidak berisi titik bilangan bulat yang layak, tetapi tidak pernah menyingkirkan satupun titik bilangan bulat yang layak (Taha, 1996).
Metode cutting plane digunakan untuk permasalahan yang variabel keputusannya harus bernilai bilangan bulat. Program linier tidak efektif untuk menyelesaikan permasalahan tersebut sehingga dikembangkan metode cutting
plane yang lebih efektif dan memberikan hasil yang lebih baik. Langkah-langkah
penyelesaian program bilangan bulat dengan metode cutting plane sebagai berikut:
1. Selesaikan masalah program bilangan bulat dengan menggunakan metode simpleks. Jika masalah sederhana, kendala gomory dapat diselesaikan dengan pendekatan grafik, sehingga pendekatan kendala gomory kurang efisien. 2. Periksa solusi optimum. Jika semua variabel basis memiliki nilai bilangan
bulat, solusi optimum yang berupa bilangan bulat telah diperoleh dan proses solusi telah berakhir. Jika satu atau lebih variabel basis masih memiliki nilai pecah, teruskan ke tahap 3.
3. Buatlah suatu kendala gomory dan cari solusi optimum melalui prosedur dual simpleks. Kembali ke tahap 2 (Taha, 1996).
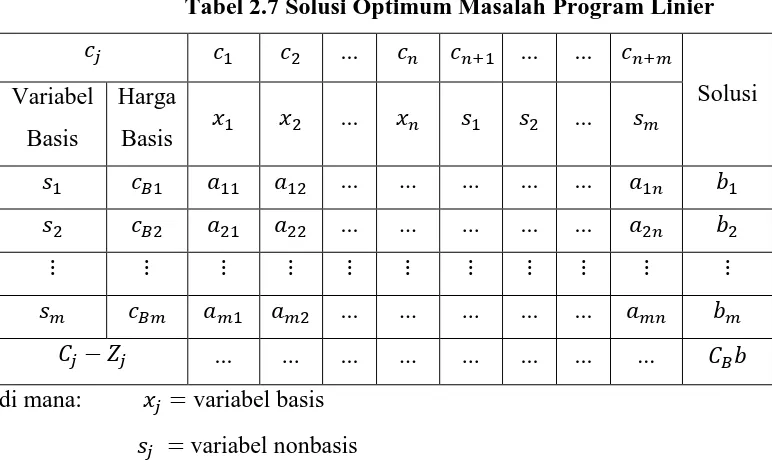
Tabel 2.7 Solusi Optimum Masalah Program Linier
... ... ...
Solusi Variabel
Basis
Harga
Basis ... ...
... ... ... ... ... ... ... ... ... ...
... ... ... ... ...
... ... ... ... ... ... ... ... di mana: variabel basis
variabel nonbasis
∑ ∑
di mana: = variabel basis variabel nonbasis
koefisien variabel keputusan dalam fungsi kendala berupa noninteger
sumber daya dalam fungsi kendala berupa noninteger
kemudian pisahkan dan menjadi bagian yang bulat dan bagian pecah non negatif seperti berikut:
̅
sehingga ̅, di mana
̅̅̅̅
sehingga ̅̅̅̅ , di mana dapat lihat contoh berikut:
̅ ̅̅̅̅
1
0 0
2
sehingga adapun kendala gomory yang diinginkan sebagai berikut:
∑ ∑
di mana: slack gomory variable
bagian pecahan dari bagian pecahan dari variabel nonbasis
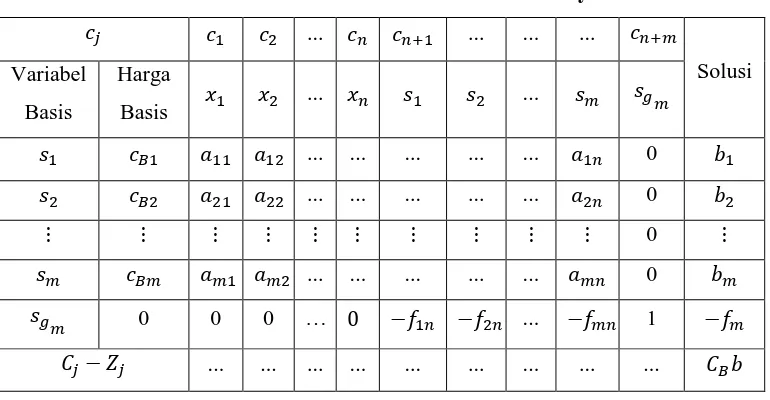
main biasanya dipilih persamaan yang memiliki maksimum. Adapun tabel baru setelah penambahan kendala gomory disajikan pada Tabel 2.8 sebagai berikut:
Tabel 2.8 Penambahan Kendala Gomory
Karena diperoleh solusi primal optimum tetapi tidak layak maka digunakan metode dual simpleks. Proses pembentukan kendala gomory berakhir jika solusi optimum diperoleh bilangan bulat. Jika tidak, suatu kendala gomory baru dibuat kembali dari tabel yang dihasilkan dan metode dual simpleks digunakan kembali untuk mengatasi ketidaklayakan. Jika pada setiap iterasi metode dual simpleks menunjukkan bahwa tidak ada solusi layak, berarti masalah itu tidak memiliki solusi integer yang layak. Metode cutting plane mempunyai dua kelemahan sebagai berikut:
1. Kesalahan pembulatan yang muncul dalam perhitungan otomatis akan mendistorsi data semula terutama dengan bertambahnya ukuran masalah. 2. Solusi masalah tetap tidak layak, artinya tidak ada solusi integer yang dapat
diperoleh sampai solusi integer optimum dicapai. Ini berarti bahwa tidak ada solusi integer yang baik jika perhitungan dihentikan sebelum mencapai solusi
integer yang optimum (Taha, 1996).
Kelemahan pertama dapat diatasi dengan penggunaan integer murni. Metode ini dimulai dengan tabel awal yang semuanya terdiri dari integer yang sesuai dengan metode dual simpleks. Kemudian dilakukan penambahan kendala
gomory sehingga penambahannya ke tabel akan mempertahankan sifat integer