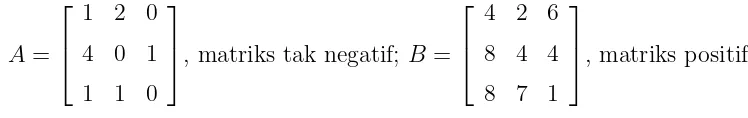SCRAMBLING INDEX DARI GRAF RING-STAR DAN
VARIASINYA
SKRIPSI
FITRIANA 100803027
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SCRAMBLING INDEX DARI GRAF RING STAR DAN
VARIASINYA
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat mencapai gelar Sarjana Sains
FITRIANA 100803027
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Scrambling Index dari Graf Ring Star dan Variasinya Kategori : Skripsi
Nama : Fitriana
Nomor Induk Mahasiswa : 100803027
Program Studi : Sarjana (S1) Matematika Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Medan, Oktober 2014
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc NIP.19630405 198811 2 001 NIP.19640109 198803 1 004
Diketahui oleh :
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
SCRAMBLING INDEX DARI GRAF RING STAR DAN VARIASINYA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan penting yang masing-masing disebutkan sumbernya.
Medan, Oktober 2014
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Allah Tuhan Yang Maha Esa yang telah melimpahkan rahmat dan ridho-Nya sehingga penulis dapat menye-lesaikan skripsi ini yang berjudul ”SCRAMBLING INDEX DARI GRAF RING STAR DAN VARIASINYA” . Shalawat dan salam dipersembahkan kepada Rasulullah Muhammad SAW, semoga keberkahan selalu tercurah kepada beliau, keluarga, sahabat dan para pengikutnya.
Dalam menyelesaikan skripsi ini penulis banyak mendapatkan bantuan, mo-tivasi, do’a dari berbagai pihak. Pada kesempatan ini penulis mengucapkan teri-ma kasih kepada:
1. Bapak Prof. Dr. Tulus, M.Si, dan Ibu Dr. Mardiningsih, M.Si, selaku Ketua dan Sekretaris Departemen Matematika FMIPA USU Medan.
2. Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Dosen Pembimbing I dan Ibu Dr. Mardiningsih, M.Si, selaku Dosen Pembimbing II, yang telah banyak membantu penulis dan memberikan dukungan baik berupa nasihat, moti-vasi maupun ilmu pengetahuan kepada penulis dalam menyelesaikan pene-litian ini.
3. Bapak Dr. Suwarno Ariswoyo, M.Si, selaku Dosen Pembanding I, dan Ba-pak Prof. Dr. Tulus, M.Si, selaku Dosen Pembanding II, yang telah mem-berikan nasehat, kritik dan saran yang membangun selama penelitian.
4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fa-kultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara, Medan.
Penulis juga menyampaikan terima kasih kepada teman-teman (Ayu, Ibah, Dewi, Husna, Lani, Rika dan Tria) yang senantiasa saling menyemangati dan saling memotivasi dalam menyelesaikan skripsi ini, semoga Allah meridhoi semua usaha yang dilakukan. Terima kasih kepada rekan-rekan Komutatif 2010, Murni 2010, Al FALAK, IM3, HMM, dan lainnya yang telah banyak memberikan in-spirasi dan pengalaman yang berharga dan berguna untuk bekal hidup di masa yang akan datang, hanya Tuhan yang dapat membalasnya.
Penulis menyadari masih banyak kekurangan dalam penulisan skripsi ini, untuk itu saran dan kritik yang membangun dari pembaca sangat diharapkan. Penulis menyampaikan terima kasih atas perhatiannya, semoga tulisan ini dapat bermanfaat.
Medan, Oktober 2014
SCRAMBLING INDEX DARI GRAF RING STAR DAN VARIASINYA
ABSTRAK
Sebuah graf terhubungGdikatakan primitif bila terdapat bilangan bulat positifk sehingga untuk setiap pasangan titik u dan v terdapat jalan yang menghubung-kan u dan v dengan panjang k. Scrambling index dari sebuah graf primitf G, k(G), adalah bilangan bulat positif terkecil k sehingga untuk setiap dua titik u dan v yang berbeda terdapat sebuah titik w dengan sifat bahwa ada jalan yang menghubungkanu danw dengan panjangk. Untuk sebuahs-ring starR dengan panjang lingkaran ganjil s diperlihatkan bahwa k(R) = (s+ 1)/2. Dua variasi graf ring star yang lainnya adalah grafs-wheel (W) yang dan grafs-steering ship (S) dengan nilai scrambling index masing-masing graf adalah k(W) = 1 untuk graf s-wheel dan k(S) = 2 untuk graf s-steering ship.
SCRAMBLING INDEX OF RING STAR GRAPH AND ITS VARIATION
ABSTRACT
A connected graph G is called primitive provided that there is a positive integer
k such that for each pair of vertices u dan v in G there is a walk of length k
connecting u and v. A scrambling index of a primitive graph G, k(G), is the smallest positive integer k such that for each pair of distinct vertices u and v
there is a vertex w with the property that there is a walk connecting u and v and a walk connecting v and w of length k. For a s-ring star R with cycle of odd length s we show that k(R) = (s+ 1)/2. Two others variation of ring star graph iss-wheel (W) graphands-steering ship (S), we show that k(W) = 1 fors-wheel graph and k(S) = 2 for s-steering ship graph.
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK v
ABSTRACT vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 4
1.3 Tujuan Penelitian 5
1.4 Manfaat Penelitian 5
BAB 2 TINJAUAN PUSTAKA 6
2.1 Graf 6
2.2 Matriks Ketetanggaan (Adjacency) 7
2.3 Graf Terhubung 9
2.4 Primitifitas suatu Graf 11
2.5 Matriks Tak Negatif dan Eksponen dari Graf 12
2.5.1 Matriks Tak Negatif 12
2.5.2 Eksponen dari Graf 14
2.6 Scrambling Index 15
2.6.3 Graf dengan Scrambling Index 1 18
BAB 3 METODE PENELITIAN 20
BAB 4 HASIL DAN PEMBAHASAN 21
4.1 Scrambling Index dari Graf Ring Star 21 4.2 Scrambling Index dari Graf Wheel 22 4.3 Scrambling Index dari Graf Steering Ship 24
BAB 5 KESIMPULAN DAN SARAN 25
5.1 Kesimpulan 25
5.2 Saran 26
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
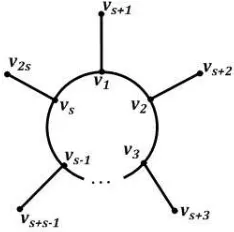
1.1 Bentuk umum graf primitif s-ring star (R) 3 1.2 Bentuk umum graf primitif s-wheel (W) 4 1.3 Bentuk umum graf primitif s-steering ship (S) 4
2.1 Sebuah graf 6
2.2 Graf 4-wheel (W) 8
2.3 Contoh graf terhubung dan graf tidak terhubung 10
2.4 Contoh graf primitif 12
4.1 Lintasan terpendek yang menghubungkan vs+1 dan v2s 21
SCRAMBLING INDEX DARI GRAF RING STAR DAN VARIASINYA
ABSTRAK
Sebuah graf terhubungGdikatakan primitif bila terdapat bilangan bulat positifk sehingga untuk setiap pasangan titik u dan v terdapat jalan yang menghubung-kan u dan v dengan panjang k. Scrambling index dari sebuah graf primitf G, k(G), adalah bilangan bulat positif terkecil k sehingga untuk setiap dua titik u dan v yang berbeda terdapat sebuah titik w dengan sifat bahwa ada jalan yang menghubungkanu danw dengan panjangk. Untuk sebuahs-ring starR dengan panjang lingkaran ganjil s diperlihatkan bahwa k(R) = (s+ 1)/2. Dua variasi graf ring star yang lainnya adalah grafs-wheel (W) yang dan grafs-steering ship (S) dengan nilai scrambling index masing-masing graf adalah k(W) = 1 untuk graf s-wheel dan k(S) = 2 untuk graf s-steering ship.
SCRAMBLING INDEX OF RING STAR GRAPH AND ITS VARIATION
ABSTRACT
A connected graph G is called primitive provided that there is a positive integer
k such that for each pair of vertices u dan v in G there is a walk of length k
connecting u and v. A scrambling index of a primitive graph G, k(G), is the smallest positive integer k such that for each pair of distinct vertices u and v
there is a vertex w with the property that there is a walk connecting u and v and a walk connecting v and w of length k. For a s-ring star R with cycle of odd length s we show that k(R) = (s+ 1)/2. Two others variation of ring star graph iss-wheel (W) graphands-steering ship (S), we show that k(W) = 1 fors-wheel graph and k(S) = 2 for s-steering ship graph.
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Teori graf adalah cabang kajian matematika yang mempelajari sifat-sifat graf. Secara sederhana, suatu graf adalah himpunan benda-benda yang disebut titik yang terhubung oleh sisi. Biasanya graf digambarkan sebagai kumpulan titik-titik yang dihubungkan oleh garis-garis (melambangkan sisi). Suatu sisi dapat menghubungkan suatu titik dengan titik yang sama. Sisi yang demikian disebut loop.
AndaikanGadalah sebuah graf. Sebuah jalan dengan panjangtyang meng-hubungkan titikudanvdi G merupakan sebuah barisantbuah sisi dalam bentuk
{u=u0, u1},{u1, u2},{u2, u3}, ...,{ut−1, ut=v}
yang dapat dinotasikan denganu=v0 ↔v1 ↔v2 ↔ · · · ↔vt−1 ↔vt=v. Lebih
sederhananya, sebuah jalan dengan panjangtyang menghubungkan titikudanv dinotasikan dengan u←→t v. Sebuah jalan dengan u6=v dikatakan terbuka dan sebuah jalan denganu=v dikatakan tertutup. Sebuah jalan adakalanya memuat sisi yang berulang. Sebuah jalan tanpa perulangan sisi disebut sebagai lintasan. Panjang lintasan adalah jumlah sisi pada lintasan tersebut. Jarak dari u dan v, yaitu d(u, v) merupakan panjang dari lintasan terpendek yang menghubungkan u dan v. Sebuah lintasan dikatakan tertutup apabila u = v. Sebuah lingkaran adalah suatu lintasan tertutup.
2
Penelitian mengenai eksponen telah banyak dilakukan diantaranya Fuyi et al. (1999) yang membuktikan bahwa setiap graf primitif ganjil harus memuat 2 titik yang saling lepas dengan lingkaran ganjil, serta menggolongkan keluarga dari graf primitif ganjil yang eksponennya mencapai batas atas.
Akelbek dan Kirkland (2009) pertama kali memperkenalkan scrambling in-dex dengan mendefinisikan scrambling inin-dex dari graf primitif G, dinotasikan dengan k(G) adalah bilangan bulat positif terkecil k sehingga untuk setiap dua titik u dan v yang berbeda di G, terdapat sebuah titik w dengan sifat terdapat u ↔k w dan v ↔k w. Untuk setiap dua titik u dan v yang berbeda, scrambling index lokal dari u dan v adalah bilangan bulat positif ku,v(G) yang didefinisikan
sebagai
ku,v(G) = min w∈V{k :u
k
↔w dan v ↔k w}
Dari definisi scrambling index k(G) dan scrambling index lokal ku,v(G)
diperoleh hubungan k(G) ≥ ku,v(G). Karena G adalah graf terhubung, maka
untuk setiap bilangan bulatl ≥ku,v(G) dapat ditemukan sebuah titikw
′
sehing-ga terdapat u ↔l w′
dan v ↔l w′
. Hal ini mengakibatkan nilai dari k(G) yang juga disebut dengan scrambling index global adalah maksimum dari nilai-nilai scrambling index lokal ku,v(G) yang didefinisikan sebagai
k(G) = max
u6=v{ku,v(G)}
Scrambling index dari sebuah graf primitif G dapat diselesaikan meng-gunakan matriks ketetanggaan dari G yaitu matriks A(G)n×n = (aij), dimana
aij = 1 jika vi adjacent terhadap vj dan aij = 0 untuk lainnya. Karena aij =aji
maka A adalah matriks simetris. Scrambling index dariA adalah bilangan bulat positif terkecil k sedemikian sehingga untuk setiap dua baris dari Ak memiliki
paling sedikit satu entri positif pada kolom yang sama, dinotasikan dengank(A).
3
Chen dan Liu (2010) memperlihatkan hubungan antara scrambling index dan eksponen dari graf primitif, jika G adalah graf primitif dengan order n ≥ 2 dan u, v adalah pasangan titik dariG adalah
ku,v(G)≤
expG(u,v) 2
dan k(G) = lexp(G)2 m dengan ⌈a⌉ adalah integer terkecil ≥a.
Chen dan Liu juga mendiskusikan tentang karakteristik graf primitif yang scrambling index sama dengan nilai maksimum dari scrambling index graf primitif G. Selanjutnya, Liu dan Huang (2010) memberikan batas atas untuk scrambling index dari graf primitif dengan lingkaran sepanjangs yaitu
k(G)≤(s−1)/2 + (n−s)
Batas ini dicapai untuk graf primitif G dengan lingkaran ganjil Cs sepanjang s
dengan maxv∈V{d(v,Cs)}= n−s.
Gao dan Shao (2013) melakukan penelitian tentang scrambling index dari graf primitif berbentuk lingkaran atas n titik ganjil Cs :v1 ↔ v2 ↔v3 ↔ · · · ↔ vs ↔v1, yaitu k(Cn) = (n−1)/2. Penelitian ini akan secara khusus membahas
mengenai scrambling index dari kelas graf primitif ring star dan 2 buah variasinya yaitu graf wheel dan steering ship, dengan definisi sebagai berikut:
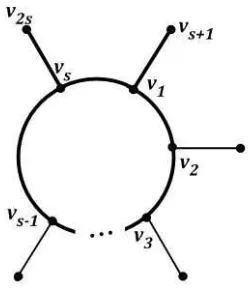
1. Graf s-Ring star (R) terdiri dari sebuah lingkaran dengan panjang s ≥ 3 dimanas adalah ganjil bersama s buah sisi yang menghubungkan masing-masing titik pada lingkaran dengan sebuah titik lain di luar lingkaran.
4
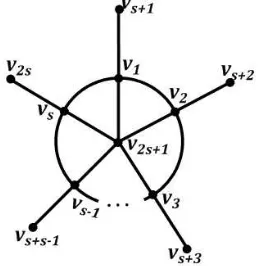
2. Graf s-Wheel (W) terdiri dari satu buah lingkaran dengan panjang s ≥ 2 dan s buah sisi yang menghubungkan masing-masing titik pada lingkaran dengan satu buah titik di dalam lingkaran.
Gambar 1.2 : Bentuk umum graf primitif s-wheel (W)
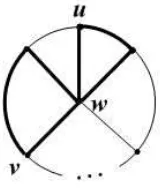
3. Graf s-Steering Ship (S) terdiri dari satu buah lingkaran dengan panjang s ≥ 2 dan 1 buah titik di dalam lingkaran yang menghubungkan dirinya dengan semua titik pada lingkaran serta s buah sisi yang menghubungkan masing-masing titik pada lingkaran dengan 1 buah titik lain di luar lingka-ran.
Gambar 1.3 : Bentuk umum graf primitif s-steering ship (S)
1.2 Perumusan Masalah
5
1.3 Tujuan Penelitian
Tujuan dari penelitian ini adalah mendapatkan pola atau bentuk umum nilai scrambling index dari kelas graf primitif s-ring star (R), s-wheel (W) dan s-steering ship (S).
1.4 Manfaat Penelitian
BAB 2
TINJAUAN PUSTAKA
Pada bagian ini akan dijelaskan beberapa konsep dasar yang berkaitan dengan permasalahan, seperti definisi dan teorema yang dijadikan landasan dalam pene-litian ini.
2.1 Graf
Graf G adalah pasangan (V(G), E(G)) dengan V(G) adalah himpunan tidak kosong dan berhingga dari objek-objek yang disebut titik, danE(G) adalah him-punan (mungkin kosong) pasangan tak berurut dari titik-titik yang berbeda di V(G) yang disebut sisi (Abdusakir et al.,2009). Titik disajikan dalam bentuk noktah atau lingkaran kecil dan sisi disajikan dalam bentuk garis atau kurva yang memasangkan dua titik. Titik pada graf dapat dinomori dengan huruf, seperti a, b, c,· · · , u, v,· · ·, dengan bilangan asli, 1,2,3,· · · atau gabungan ked-uanya. Sedangkan sisi yang menghubungkan titik u dengan titik v dinyatakan dengan pasangan (u, v) atau dinyatakan dengan lambang e1, e2,· · ·. Jadi, jika e adalah sisi yang menghubungkan titikudan titikv, makaedapat ditulis sebagai e= (u, v),u dan v disebut sebagai titik ujung dari sisi e. Sisi-sisi yang memiliki titik ujung sama disebut sisi ganda dan suatu sisi yang menghubungkan sebuah titik ke dirinya sendiri disebut loop. Cara yang paling mudah dalam menya-jikan graf adalah dengan menggunakan gambar atau grafis, dengan bentuk inilah sifat-sifat graf dapat dikenali secara detail.
Contoh 2.1 Berikut merupakan contoh representasi grafis dari sebuah graf
7
AndaikanGadalah sebuah graf. Misalkanudanvadalah titik diG. Sebuah jalan dengan panjangm yang menghubungkan titik udan v diG merupakan se-buah barisan m sisi dalam bentuk{u =vv, u1},{v1, v2}, ...,{vm−1, vm =v}, juga
dapat dinotasikan dengan u = v0 ↔ v1 ↔ v2 ↔ · · · ↔ vm−1 ↔ vm = v. Untuk
lebih sederhananya, sebuah jalan dengan panjang m yang menghubungkan titik u dan v dinotasikan dengan u ←→t v. Sebuah jalan dengan u 6= v dikatakan terbuka dan sebuah jalan denganu=v dikatakan tertutup. Sebuah jalan memu-ngkinkan terdapat sisi yang berulang. Sebuah jalan tanpa perulangan sisi disebut sebagai lintasan. Lebih lanjut dalam sebuah lintasan sangat memungkinkan juga terdapat penggunaan titik secara berulang. Sebuah lintasan tanpa pengulan-gan titik, kecuali mungkin titik-titik ujungnya, disebut sebagai sebuah lintasan sederhana. Panjang lintasan adalah jumlah sisi pada lintasan tersebut. Sebuah lintasan dikatakan terbuka apabila u6=v dan dikatakan tertutup (cycle) apabila u = v. Sebuah lingkaran adalah suatu lintasan tertutup. Jarak dari u dan v, yaitu d(u, v) merupakan panjang dari lintasan terpendek yang menghubungkan u dan v.
Teorema 2.1AndaikanGadalah sebuah graf. Setiap jalan yang menghubungkan titik u dan titik v di G memuat lintasan yang menghubungkan titik u dan titik v.
Bukti. Andaikan W : u = v0 ↔ v1 ↔ v2 ↔ · · · ↔ vm = v adalah sebuah
jalan yang menghubungkan titik u dan titik v. Jika semua titik v1, v2,· · ·vt−1 adalah berbeda, maka W adalah sebuah lintasan yang menghubungkan u dan v. Jika tidak, maka terdapat bilangan i dan j dengan i ≤ j sehingga vi = vj.
Buang jalan vi ↔ vi+1 ↔ · · · ↔ vj−1 sehingga dihasilkan sebuah jalan W′ yang menghubungkan u dengan v dan lebih pendek dari jalan W. Jika W′ memuat titik tengah yang berulang, maka ulangi proses di atas sehingga pada akhirnya ditemukan sebuah jalanW′′ yang tidak memuat titik tengah berulang. jalan W′′ adalah sebuah lintasan yang menghubungkan titiku dengan titik v.
2.2 Matriks Ketetanggaan (Adjacency)
ap-8
kemudahan untuk menyelesaikan permasalahan yang melibatkan graf dengan bantuan komputer.
Matriks ketetanggaan dari grafG, dinotasikan denganA(G), adalah matriks (n × n) dengan unsur pada baris ke-i dan kolom ke-j bernilai 1 jika titik vi
terhubung langsung dengan titik vj serta bernilai 0 jika titik vi tidak terhubung
langsung dengan titik vj.
aij =
Oleh definisi matriks ketetanggaan, diperolehaij =aji untuk semua 1≤i, j ≤n.
Akibatnya, matriks ketetanggaanA(G) dari G adalah matriks simetris.
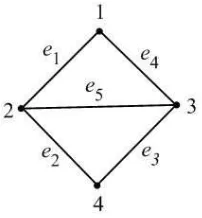
Contoh 2.2 Berikut adalah sebuah graf
Gambar 2.2 : Graf 4-wheel (W)
Matriks ketetanggaan dari graf pada gambar 2.2 adalah
9
2.3 Graf Terhubung
Titik u dan v di G dikatakan terhubung jika terdapat sebuah jalan di G yang menghubungkan titikudengan titikv. Sebuah titik dalam sebuah graf adalah ter-hubung dengan dirinya sendiri. Sehingga relasi 2 titik terter-hubung adalah refleksif. Jika u dan v adalah 2 titik yang terhubung maka terdapat jalan yang menghu-bungkanudenganv, tetapi dengan bergerak mundur diperoleh sebuah jalan yang menghubungkanv dengan u. Sehingga v terhubung denganu. Jadi relasi 2 titik terhubung adalah relasi simetrik. Selanjutnya jikaudanv adalah terhubung dan titik v dan w adalah terhubung, maka terdapat jalan yang menghubungkan u dengan v dan jalan yang menghubungkan v dengan u. Hal ini berakibat bahwa jalan yang menghubungkanu denganv, kemudian dilanjutkan dengan jalan yang menghubungkan v dengan w adalah sebuah jalan yang menghubungkan u de-nganw. Sehingga titik uterhubung dengan titikw. Jadi relasi 2 titik terhubung adalah transitif. Dapat disimpulkan bahwa relasi 2 titik terhubung adalah relasi ekivalensi.
Kelas ekivalensi dari relasi 2 titik terhubung disebut sebagai komponen ter-hubung dari grafG. Sebuah grafGdikatakan terhubung jikaGmempunyai tepat satu komponen terhubung, artinya sebuah graf dikatakan terhubung jika untuk setiap pasangan titikudanv terdapat sebuah jalan yang menghubungkan titiku dengan titik v. Berikut diberikan sebuah cara untuk mendeteksi keterhubungan dari sebuah graf.
Teorema 2.2 Andaikan G adalah sebuah graf atas n titik dengan matriks kete-tanggaanA. GrafG adalah terhubung jika dan hanya jika matriksA+A2+· · ·+ An−1 mempunyai entri yang semuanya positif.
10
lingkaran dengan panjang 2 yang memuat titik i, sehingga entri a(2)ii ≥ 0 untuk semua i = 1,2,· · · , n. Jadi entri diagonal dari matriks B adalah positif. Dapat disimpulkan bahwa semua entri dari matriks B = A+A2 +· · ·+An−1 adalah
positif.
Selanjutnya, misalkan setiap entri dari matriksA+A2+· · ·+An−1 adalah positif. Akibatnya untuk setiap pasangan titiki dan j terdapat sebuah bilangan positif k dengan 1 ≤ k ≤ n− 1 sehingga a(ijk) ≥ 0. Hal ini berarti untuk se-tiap pasangan titik i dan j di G terdapat sebuah jalan dengan panjang k yang menghubungkanidan j. Sehingga oleh definisi Gadalah sebuah graf terhubung.
Contoh 2.3 Berikut contoh graf terhubung dan tidak terhubung
Gambar 2.3 : Contoh graf terhubung dan graf tidak terhubung
Gambar 2.3(a) menunjukkan graf terhubung karena terdapat jalan dari seti-ap pasangan titik di G dan gambar 2.3(b) menunjukkan graf yang tidak terhubung karena tidak terdapat jalan yang menghubungkan titikv5 dengan titik lainnya.
Proposisi-proposisi berikut menjelaskan beberapa sifat-sifat jalan pada se-buah graf terhubung.
Proposisi 2.3 Misalkan G merupakan sebuah graf terhubung dengan u, v ∈ G. Maka, setiap jalan u ←→m v dapat diperpanjang menjadi jalan u m←→+2t v untuk suatu bilangan bulat positif t.
Bukti. Ambil u dan v merupakan titik di G dan misalkan W : u = v0 ↔ v1 ↔ v2 ↔ · · · ↔vm−1 ↔vm =v merupakan jalan u
m
←→v diG. Maka jalan W′ yang dimulai dari u berjalan ke v sepanjang jalan W dan kemudian berpindah t kali mengelilingi lingkaran v ↔vt−1 ↔v merupakan sebuah jalan u
m+2t
11
Proposisi 2.4 Misalkan G merupakan sebuah graf terhubung dengan u, v, w
adalah titik yang berbeda di G dan m adalah sebuah bilangan positif. Terdapat
u←→m w dan v ←→m w jika dan hanya jika terdapat u←→2m v di G.
Bukti. Andaikanudan v adalah dua titik berbeda diGsehingga terdapat u←→m w dan v ←→m w untuk suatu titik w di G. Maka u ←→m w yang dilanjutkan dengan jalan w←→m v adalah sebuah u←→2m v. Sebaliknya, asumsikan bahwa
W :u=v0 ↔v1 ↔v2 ↔ · · · ↔v2m−1 ↔v2m =v
merupakan u←→2m v di G. Jikaw=vm, maka terdapat u m
←→w dan v ←→m w di
G.
2.4 Primitifitas suatu Graf
Sebuah graf terhubungG dikatakan primitif, jika terdapat bilangan bulat positif k sedemikian hingga untuk setiap pasangan titik u dan v di G terdapat jalan u←→k v.
Teorema 2.5AndaikanGadalah suatu graf,Gdikatakan primitif jika dan hanya jika terhubung dan mengandung lingkaran dengan panjang ganjil.
Bukti. Andaikan G adalah suatu graf dan G adalah primitif, maka terdapat bilangan bulat positif k sehingga untuk setiap pasangan titik u dan titik v di G terdapat u ←→k v. Akibatnya, G adalah terhubung. Untuk setiap pasangan titik u dan titik v di G terdapat jalan dengan panjang m untuk semua m ≥ k. Misalkan m adalah ganjil. Untuk setiap titik u dan titik v di G dapat dibentuk
jalan dengan panjang ganjil.
Andaikan u ←→ u adalah jalan yang menghubungkan titik u ke dirinya sendiri. Misalkan puv adalah lintasan yang menghubungkan titik u ke titik v.
Jalan u ←→ v dapat dibentuk dari titik u ke titik v melalui lintasan puv dan
kembali ke titikumelalui lintasanpuvyang sama. Misalkanl(wuu) adalah panjang
jalan dari titik u ke titik u. l(wuu) adalah genap, agar wuu mempunyai panjang
ganjil makawuu harus melewati 1 lingkaran ganjil disebarang titik, misalkan titik
x. Jalanwuu yang terdiri dari lintasan pux, lintasanpxx, dan lintasan pxu adalah
12
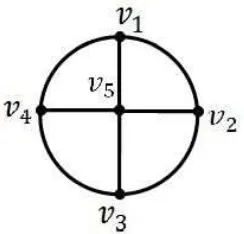
Contoh 2.4 Berikut contoh graf primitif
Gambar 2.4 : Contoh graf primitif
Pada Gambar 2.4, graf tersebut merupakan graf primitif karena memuat lingkaran dengan panjang ganjil 3 yaituv1 ↔v5 ↔v2 ↔v1.
2.5 Matriks Tak Negatif dan Eksponen dari Graf 2.5.1 Matriks Tak Negatif
Matriks tak negatif A merupakan sebuah matriks yang setiap entri aij dari A
adalah bilangan bulat tak negatif. Jika setiap entri aij dari matriks A adalah
bilangan bulat positif, maka matriks tersebut disebut matriks positif. Contoh matriks tak negatif dan matriks positif dapat dilihat pada 2 buah matriks berikut.
A=
Secara umum, sebuah matriks ketetanggaan A dikatakan primitif jika terdapat sebuah bilangan bulat positif k sedemikian sehingga Ak adalah sebuah matriks
positif. Matrik ketetanggaan dari graf pada gambar 2.4 adalah sebagai berikut
13
Matriks ketetanggaan dikatakan primitif jika semua entri ak
ij dari matriks
Ak bernilai positif. Perhatikan matriks berikut
a. Untuk k = 1; diperolehA1 =
Bukan merupakan matriks positif karena terdapat 11 entri bernilai 0 yang bukan merupakan bilangan bulat positif.
b. Untuk k = 2; diperolehA2 =
Bukan merupakan matriks positif karena terdapat 4 entri bernilai 0 yang bukan merupakan bilangan bulat positif.
c. Untuk k = 3; diperolehA3 =
Bukan merupakan matriks positif karena terdapat 1 entri bernilai 0 yang bukan merupakan bilangan bulat positif.
d. Untuk k = 4; diperolehA4 =
Karena seluruh entriaij ≥0, maka A4 merupakan matriks positif, sehingga
14
2.5.2 Eksponen dari Graf
Eksponen dari sebuah grafGmerupakan bilangan bulat positif terkecilksehingga untuk setiap pasang titikudanvdiGterdapat jalan dariukev dengan panjangk dan dinotasikan dengan exp(G). Eksponen lokaludanv, dinotasikan expG(u, v), merupakan bilangan bulat terkecil k sehingga u ←→m v untuk semua m ≥ k, sehingga
exp(G) = maxu,v∈V(G){expG(u, v)}
Teorema 2.6 Andaikan G adalah sebuah graf dan A = (aij) adalah sebuah ma-triks ketetanggaan dari G. Misalkan ak
ij adalah elemen (i, j) dari matriks Ak, maka ak
ij menyatakan banyaknya jalan berbeda dengan panjang k yang menghu-bungkan titik i dengan titik j di G.
Bukti. Pembuktian dilakukan dengan induksi matematika. Untuk k = 1, entri a1
ij = aij dari A menyatakan banyaknya jalan dengan panjang 1 yang
menghu-bungkan titik i dengan titik j. Asumsikan bahwa entri akij dari Ak menyatakan
banyaknya jalan dengan panjang k yang menghubungkan titik i dengan titik j. Selanjutnya akan diperlihatkan bahwa a(ijk+1) adalah banyaknya jalan dari i ke j dengan panjang k+ 1 di Gdengan k≥1.
Setiap jalan dari titik i ke j di G dengan panjang k + 1 yang terdiri dari jalan i kel dengan panjang k untuk l = 1,2,· · · , n, dan dilanjutkan dengan sisi dari titik l ke titik j, sehingga ak
ilalj menyatakan jalan dengan panjang k + 1
dari titik i ke titik j di G untuk k = 1,2,· · · , n. Jika tidak terdapat jalan yang panjangnya k dari titik i ke titik j di G, maka aij(k) = 0 sehingga a(ijk)aij = 0.
15
Sehingga a(ijk+1)adalah menyatakan banyaknya jalan dari titik i ke titik j yang
panjangnyak+ 1 di G.
Contoh matriks untuk graf pada Gambar 2.4, nilai k = 6 yang diperoleh adalah jalan dengan panjang terkecil dari setiap pasang titik yang ada diG, maka eksponen dari graf pada Gambar 2.4 adalah exp(A)=exp (G(A))=4.
2.6 Scrambling Index
2.6.1 Scrambling Index Graf Primitif
Sebuah graf dikatakan primitif jika dan hanya jika terhubung dan mengandung lingkaran dengan panjang ganjil. Menurut Alkelbek dan Kirkland (2009a), untuk titik u, v dan w dari graf G, jika {u, w},{v, w} ∈ E(G), maka titik w dikatakan sebagai tetangga persekutuan luar bersama (common out-neighbour) dari titik u dan v. Scrambling index dari graf primitif G adalah bilangan bulat positif terkecil k sehingga untuk setiap pasang dua titik u dan v yang berbeda di G, terdapat sebuah titik w dengan sifat terdapat u ↔k w dan v ↔k w, yang dapat juga dikatakan sebagai bilangan bulat terkecilksehingga setiap pasang titik dari G mempunyai tetangga persekutuan luar bersama di Gk. Scrambling index dari
G akan dinotasikan sebagai k(G). Untuk setiap dua titik u dan v yang berbeda, scrambling index lokal dari u dan v adalah bilangan bulat positif ku,v(G) yang
didefinisikan sebagai
ku,v(G) = min w∈V{k :u
k
↔w dan v ↔k w}
Dari definisi scrambling index k(G) dan scrambling index lokal ku,v(G)
diperoleh hubungan k(G) ≥ ku,v(G). Karena G adalah graf terhubung, maka
untuk setiap bilangan bulatl ≥ku,v(G) dapat ditemukan sebuah titikw
′
sehing-ga terdapat u ↔l w′
dan v ↔l w′
. Hal ini mengakibatkan nilai dari k(G) yang juga disebut dengan scrambling index global adalah maksimum dari nilai-nilai scrambling index lokal ku,v(G) yang didefinisikan sebagai berikut:
k(G) = max
16
Berdasarkan definisi, scrambling index lokal dari graf pada Gambar 2.4 sebagai berikut,
Sehingga scrambling index dari graf diatask(G) = 2.
Scrambling index dari suatu graf dapat diperoleh dari matriks ketetang-gaannya. Scrambling index dari matriks primitif Aadalah bilangan bulat positif terkecilksedemikian sehingga untuk setiap dua baris dari Ak memiliki paling
se-dikit satu entri positif pada kolom yang sama, dan dinotasikan olehk(A). Scram-bling index dari matriks primitifAjuga dapat didefinisikan sebagai bilangan bulat positif terkecil k sedemikian sehingga Ak(AT)k seluruh entrinya bernilai positif.
Perhatikan contoh matriks dari graf primitif pada Gambar 2.4.
17
Atidak memiliki scrambling index 1, karena pada baris ketiga dan keempat tidak memiliki entri positif di kolom yang sama.
2. Untuk k = 2, diperoleh
karena setiap dua baris dariAk dengan k = 2 memiliki paling sedikit satu
entri positif pada kolom yang sama, maka k(A)=2.
Chen dan Liu (2010) memperlihatkan hubungan antara scrambling index dan eksponen dari graf primitif, jika G adalah graf primitif dengan order n ≥ 2 dan u, v adalah pasangan titik dariG
ku,v(G)≤
dimana⌈a⌉ adalah integer terkecil ≥a.
Graf pada Gambar 2.4 memiliki exp(G) = 4, maka nilai scrambling indexnya adalah
2.6.2 Scrambling Index dari Lingkaran Ganjil
18
sering disebut sebagai graf lingkaran karena gambarnya dapat dibentuk menjadi lingkaran. Gao dan Shao (2013) memberikan teori mengenai scrambling index pada lingkaran dengan panjang s adalah ganjil,
Cs:v1 ↔v2 ↔ · · · ↔vs−1↔vs ↔v1
Proposisi 2.7AndaikanCs adalah sebuah lingkaran dengan panjang ganjils≥3, maka k(Cs) = (s−1)/2.
Bukti. Jalan yang menghubungkan titik v1 dengan vs dengan panjang genap
terpendek adalah
v1 ↔v2 ↔ · · · ↔vs−1 ↔vs
dengan panjang s−1. Oleh proposisi 2.4 terdapat titik w ∈ Cs sehingga ada
jalan v1
Selanjutnya diperlihatkan bahwak(Cs)≤(s−1)/2. Pertama, diperlihatkan
bahwa untuk setiap dua titik berbedavidanvj diCsterdapat jalan yang
menghu-bungkanvidanvj dengan panjang genapm≤(s−1). Jikad(vi, vj) adalah genap,
maka terdapat jalan dari vi ke vj dengan panjang genap m = d(vi, vj) ≤ s−1.
Jika d(vi, vj) adalah ganjil, maka terdapat jalan yang menghubungkan u dan v
dengan panjang genap m=s−d(vi, vj)≤s−1. Proposisi 2.3 menjamin bahwa
untuk setiap dua titikvi dan vj yang berbeda terdapat vi
(s−1)
←→vj. Oleh proposisi
2.4, untuk setiap dua titik udan v yang berbeda terdapat titikw diCs sehingga
ada jalan vi
2.6.3 Graf dengan Scrambling Index 1
Walni (inpress) memberikan syarat perlu dan cukup untuk graf dengan scram-bling index 1.
19
berikut.
1. Setiap titik dari graf G berada pada sebuah segitiga.
2. Untuk titik u dan v yang terletak pada dua segitiga berbeda, terdapat jalan dengan panjang 2 yang menghubungkan u dan v.
Bukti. Andaikan k(G) = 1, dan misalkan u adalah sebarang titik di G. Karena G terhubung, maka terdapat sebuah titik v di G sehingga {u, v} adalah sebuah sisi di G. Karena k(G) = 1, terdapat sebuah titik w sehingga {u, w} dan {v, w} masing-masing adalah sebuah sisi dari grafG. Akibatnya, sisi{u, v}, {u, w}dan {v, w}membentuk sebuah segitiga yang memuatu. Jadi setiap titik diGterletak pada sebuah segitiga. Andaikanx dan yadalah dua titik di grafG yang terletak pada sebuah segitiga berbeda. Karena k(G) = 1, maka terdapat sebuah titik z di G sehingga {x, z} dan {y, z} masing-masing adalah sebuah sisi pada graf G. Akibatnya jalan x ↔ z ↔y adalah sebuah jalan yang menghubungkan x dan y dengan panjang 2.
Sekarang misalkanGadalah primitif dan memenuhi kondisi (1) dan kondisi (2) pada proposisi 2.8. Untuk setiap dua titikudanvyang berbeda diperlihatkan bahwa ku,v(G) = 1. Jika u dan v terletak pada sebuah segitiga, maka terdapat
titikwpada segitiga sehingga ada jalanu←→1 wdanv ←→1 w. Jadiku,v(G) = 1.
Jikaudan v berada pada dua segitiga yang berbeda, maka kondisi (2) menjamin bahwa terdapat jalan dengan panjang 2 yang menghubungkan u dan v. Hal ini berakibat terdapat titik w di graf G sehingga ada u ↔1 w dan v ↔1 w. Jadi ku,v(G) = 1. Oleh definisik(G) = max
BAB 3
METODE PENELITIAN
Permasalahan pada penelitian ini diselesaikan dengan mengikuti langkah-langkah sebagai berikut: langkah awal adalah melakukan simulasi untuk mendapatkan po-la dan sifat-sifat scrambling index dari graf primitif ring star, wheel, dan steering-ship. Kemudian berdasarkan pola atau bentuk umum scrambling index yang diperoleh dari simulasi dibentuk teori.
1. Algoritma untuk scrambling index
Andaikan A adalah matrik adjacency dari graf primitif, scrambling index dari graf primitif dapat dihitung dengan algoritma berikut ini.
Algoritma 3.1 Scrambling Index Graf Primitif
Input : Matrik adjacency A
Output : Scrambling Index k
k=1; B=A;
while (B not scrambling)
k=k+1
B=B^k
end
BAB 4
HASIL DAN PEMBAHASAN
4.1 Scrambling Index dari Graf Ring Star
Bagian ini membahas mengenai scrambling index dari sebuahs-ring star primitif (R), yakni sebuah graf terhubung yang terdiri dari sebuah lingkaran
Cs:v1 ↔v2 ↔v3 ↔ · · · ↔vs ↔v1
dengan panjang s ≥ 3 dan s buah sisi dalam bentuk {vs+i, v2s} dengan i =
1,2,· · · , s. karena ring star adalah graf primitif maka s haruslah ganjil.
Teorema 4.1 Untuk s-ring star (R) dengan s ≥ 3 adalah ganjil, maka k(R) = (s+ 1)/2.
Bukti Untuk s adalah ganjil akan diperlihatkan k(R) ≥ (s + 1)/2. Karena d(vs+1, v2s) = 3, maka lintasan terpendek dengan panjang genap yang
meng-hubungkan vs+1 dan v2s adalah lintasanvs+1 ↔v1 ↔v2 ↔ v3 ↔ · · · ↔ vs ↔v2s
dengan panjang s+ 1.
Gambar 4.1 : Lintasan terpendek yang menghubungkan vs+1 dan v2s
Proposisi 2.4 mengakibatkan kvs+1, v2s(R) = (s + 1)/2. Akibatnya k(R) ≥
(s+ 1)/2.
22
Untuk setiap pasang titikudanvyang berbedad(u, v)≤(s−1)/2+2. Jika d(u, v) adalah genap, maka terdapat jalan u↔m v dengan panjang m=d(u, v)≤ (s+ 1). Untuk d(u, v) adalah ganjil, maka bukti dibagi menjadi tiga kasus:
1. Bila u=vi danv =vj keduanya berada pada lingkaranCs, maka proposisi
2.7 menjamin ada jalanu←→s−1 v.
2. Bilau∈Csdanv /∈Cs, makau=vidanv =vj+suntuk suatu 1≤i, j ≤s.
Karena d(u, v) = 1 +d(vi, vj), akibatnya terdapat u m
↔ v dengan panjang genapm = 1 +s−d(vi, vj)≤s+ 1.
3. Bilau, v /∈Cs, makau=vi+sdanv =vj+suntuk suatu 1≤i, j ≤s. Karena
d(u, v) = d(vi, vj) + 2, akibatnya terdapat u ↔m v dengan panjang genap
m = 2 +s−d(vi, vj)< s+ 1, karena d(vi, vj) ≥ 1. Sehingga untuk setiap
titik u dan v di M, terdapat jalan yang menghubungkan u dan v dengan panjang genapm ≤(s+ 1). Proposisi 2.3 menjamin terdapat jalanu←→m v dengan panjangm =s+ 1. Proposisi 2.4 menjamin terdapat titik w diM sehingga ada jalanu(s←→+1)/2 wdanv (s←→+1)/2w. Jadik(R)≤(s+1)/2. Karena k(R)≥(s+ 1)/2 dank(R)≤(s+ 1)/2 terpenuhi, makak(R) = (s+ 1)/2.
4.2 Scrambling Index dari Graf Wheel
Bagian ini membahas mengenai scrambling index dari sebuah graf primitif Wheel W yang terdiri dari satu buah lingkaran
Cs:v1 ↔v2 ↔v3 ↔ · · · ↔vs ↔v1
dengan panjang s ≥ 2 dan 1 buah titik dalam lingkaran vs+1 yang terhubung dengan seluruh titik padaCs.
Teorema 4.2 Untuk s-wheel W dengan s≥2, maka k(W) = 1.
23
Graf (W) harus memenuhi 2 kondisi dari proposisi 2.8 yaitu
1. Setiap titik dari Graf W berada pada sebuah segitiga.
Andaikan u = vi dan v = vj untuk suatu 1 ≤ i, j ≤ s + 1 dan {u, v}
adalah sebarang sisi diG, maka terdapat sebarang titik w sehingga {u, w} dan {v, w} masing-masing adalah sebuah sisi dari graf W. Akibatnya, sisi {u, v},{u, w}dan{v, w}membentuk sebuah segitiga yang memuatu. kare-na sisi{u, v}dan titik wadalah sebarang di Gmaka setiap titik di grafW terletak pada sebuah segitiga.
Gambar 4.2 : Setiap titik di W berada pada sebuah segitiga
2. Untuk setiap 2 titikudanv yang terletak pada 2 segitiga berbeda, terdapat jalan dengan panjang 2 yang menghubungkan u dan v.
Andaikan u = vi dan v = vj untuk suatu 1 ≤ i, j ≤ s, terdapat titik w
yaitu titikvs+1yang terhubung dengan semua titik yang ada pada lingkaran, sehingga untukudanv yang terletak pada 2 segitiga yang berbeda terdapat sebuah titik yang menghubungkan u dan v yaitu titik vs+1 sehingga u ↔ w↔v adalah jalan dengan panjang 2.
Gambar 4.3 : u, v pada 2 segitiga berbeda terhubung dengan panjang jalan = 2
Maka terbukti bahwa scrambling index dari graf Wheel (W) dengans≥2 adalah
24
4.3 Scrambling Index dari Graf Steering Ship
Bagian ini membahas mengenai scrambling index dari sebuah graf primitif Steer-ing Ship S yang terdiri dari 1 buah lingkaran
Cs:v1 ↔v2 ↔v3 ↔ · · · ↔vs ↔v1
dengan panjang s ≥ 2 dan s buah sisi dalam bentuk {vs+i, v2s} dimana i =
1,2,· · · , s serta 1 buah titik v2s+1 yang terhubung dengan seluruh titik padaCs.
Teorema 4.3 Untuk s-Steering Ship S dengan s ≥2, maka k(S) = 2.
Bukti. Untuk s ≥ 2 akan diperlihatkan k(S) ≥ 2. Andaikan u, v /∈ Cs, di mana
u =vi+s dan v = vj+s untuk suatu 1 ≤ i, j ≤ s. Karena d(u, v) = d(vi, vj) + 2,
akibatnya terdapat jalan dengan panjang m = 2 +s−d(vi, vj) ≥ 4. Sehingga
untuk setiap titik u dan v di S, terdapat jalan yang menghubungkan u dan v dengan panjang m ≥ 4. Proposisi 2.3 menjamin terdapat u ←→m v dengan panjang m = 4. Proposisi 2.4 menjamin terdapat titik w di Cs sehingga ada
u←→2 w dan v ←→2 w. Jadi k(S)≥2.
Selanjutnya, akan diperlihatkank(S)≤2. Hal ini dibagi menjadi tiga kasus:
1. Pertama, untuk u, v ∈ Cs, setiap titik dari u, v ∈ Cs terletak pada
se-buah segitiga dan terdapat titikw=v2s+1 yang menghubungkan u, v ∈Cs
dengan panjang m= 2, maka proposisi 2.8 menjamin terdapat u←→2 v.
2. Kedua, untuku=v2s+1 danv ∈Cs, Karenad(u, v) = 1, akibatnya terdapat
u↔m v dengan panjang m=d(u, v)≤4.
3. Ketiga, untuku=v2s+1danv /∈Cs, Karenad(u, v) = 2, akibatnya terdapat
u↔m v dengan panjang m = d(u, v) ≤ 4. Proposisi 2.3 menjamin terdapat u←→m v dengan panjang m=4. Proposisi 2.4 menjamin terdapat titik w di S sehingga ada jalan u←→2 wdan v ←→2 w. Akibatnya,k(S)≤2. Karena k(S)≥2 dan k(S)≤2 terpenuhi, maka k(S) = 2.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Pada penelitian ini memperlihatkan scrambling index dari graf ring star dan variasinya. Hasil-hasil yang diperoleh adalah sebagai berikut:
1. Andaikan terdapat graf primitif Ring Star (R) yang terdiri atas 1 buah lingkaran
Cs:v1 ↔v2 ↔v3 ↔ · · · ↔vs↔v1
dengan panjang s ≥ 3 dan s buah sisi dalam bentuk {vs+i, v2s} dengan
i= 1,2,· · · , s, maka scrambling index dari graf Ring Star (R) adalah
k(R) = (s+ 1)/2 dengan s≥3 dan s adalah ganjil.
2. Andaikan terdapat graf primitif Wheel (W) yang terdiri dari 1 buah ling-karan
Cs:v1 ↔v2 ↔v3 ↔ · · · ↔vs↔v1
dengan panjangs ≥2 dan 1 buah titik dalam lingkaranvs+1yang terhubung dengan seluruh titik pada Cs, maka scrambling index dari graf Wheel (W)
adalah
k(W) = 1 dengan s≥2.
3. Andaikan terdapat graf primitif Steering Ship (S) yang terdiri dari satu buah lingkaran
Cs:v1 ↔v2 ↔v3 ↔ · · · ↔vs↔v1
dengan panjang s ≥ 2 dan s buah sisi dalam bentuk {vs+i, v2s} dengan
i= 1,2,· · · , sserta 1 buah titik v2s+1 yang terhubung dengan seluruh titik pada Cs, maka scrambling index dari graf steering ship (S) adalah
26
5.2 Saran
DAFTAR PUSTAKA
Akelbek, M. dan Kirkland, S. 2009a. Coefficients of ergodicity and the scrambling index. Linear Algebra and its Applications, Volume 430, Issue 4, 1111-1130. Akelbek, M. dan Kirkland, S. 2009b. Primitive digraphs with the largest scram-bling index.Linear Algebra and its Applications, Volume 430, Issue 4, 1099-1110.
Azizah, N.N., Nofandika, F.F., Abdusakir. 2009. Teori Graf. UIN-Malang Press. Malang.
Chen, S. dan Liu, B. 2010. The scrambling index of symmetric primitive matrices.
Linear Algebra Appl, 433, 1110-1126.
Fuyi, W. Maoquan, C. dan Jianzhong, W. 1999. On Odd primitive graphs. Aus-tralasian Journal of Combinatorics , 19, 11-15.
Kim B.M. Song B.C. dan Huang, W. (2006). Nonnegative primitive matrices with exponents 2. Linear Algebra Appl, 407, 162-168.
Kim B.M. Song B.C. dan Huang, W. (2007). Primitive graphs with given expo-nentsand minimum number of edges. Linear Algebra Appl, 420, 648-662. Walni, N.V. 2014. Graf Jarang dengan Scrambling Index 1. [Skripsi]. Medan: