Persamaan Black-Scholes-Barenblatt untuk opsi dengan volatilitas dan suku bunga tak pasti

PERSAMAAN

BLACK-SCHOLES-BARENBLATT

UNTUK OPSI DENGAN

VOLATILITAS DAN SUKU BUNGA TAK PASTI

Oleh:

MERDINA YESI NUSA ASMARA

G54102016

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

MERDINA YESI NUSA ASMARA. Persamaan Black-Scholes-Barenblatt untuk Opsi dengan Volatilitas dan Suku Bunga Tak Pasti. Dibimbing oleh EFFENDI SYAHRIL dan ANNIS DINIATI RAKSANAGARA.

Opsi merupakan salah satu jenis dari instrumen keuangan yang nilainya bergantung pada nilai aset lain yang mendasari. Opsi memberikan hak untuk membeli (opsi call ) atau menjual (opsi put) aset yang mendasarinya pada waktu tertentu (waktu jatuh tempo) dan harga tertentu (harga eksekusi). Sejak awal tahun sembilan puluhan sudah banyak peneliti yang bekerja keras mencari formula untuk penilaian opsi. Dengan bantuan Robert Merton, pada tahun 1973 Fisher Black dan Myron Scholes menghadirkan formula penilaian opsi dalam bentuk persamaan diferensial yang dapat membantu para pialang saham menentukan apakah sebuah opsi terlalu mahal atau sebaliknya terlalu murah relatif terhadap harga saham pada saat itu, persamaan diferensial tersebut dikenal dengan persamaan Black-Scholes.

Salah satu parameter dari formula Black-Scholes (B-S) yang tidak bisa dilihat nilainya secara langsung adalah volatilitas dari aset yang mendasari. Volatilitas menunjukkan peluang suatu saham untuk berfluktuasi yang dapat dihubungkan dengan jumlah informasi masuk setiap saat. Volatilitas dan suku bunga dalam persamaan B-S diasumsikan konstan, dan ini tidaklah sesuai dengan kenyataan yang ada.

PERSAMAAN

BLACK-SCHOLES-BARENBLATT

UNTUK OPSI DENGAN

VOLATILITAS DAN SUKU BUNGA TAK PASTI

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

Oleh:

MERDINA YESI NUSA ASMARA

G541020165

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul :

Persamaan

Black-Scholes-Barenblatt

untuk Opsi dengan Volatilitas

dan Suku Bunga Tak Pasti

Nama : Merdina Yesi Nusa Asmara

NRP

: G54102016

Menyetujui :

Pembimbing I,

Pembimbing II,

Drs. Effendi Syahril, Grad. Dipl

NIP. 131804163

Dra. Annis Diniati R, M.Si

NIP. 132133396

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, MS

NIP. 131473999

KATA PENGANTAR

Puji syukur penulis panjatkan kehadirat Allah SWT, karena dengan rahmat, hidayah, serta izin-Nya lah penulis dapat menyelesaikan penulisan skripsi ini. Shalawat serta salam marilah kita tujukan pada junjungan besar kita Nabi Muhammad Saw, seorang pemimpin besar yang menjadi panutan dunia dan akhirat.

Skripsi yang berjudul, Persamaan Black-Scholes-Barenblatt untuk Opsi dengan Volatilitas dan Suku Bunga Tak Pasti, ini merupakan syarat untuk mendapatkan gelar Sarjana Sains (S.Si).

Tanpa bantuan, doa, serta dorongan yang diberikan oleh berbagai pihak, penulis tidak akan mampu menyelesaiakan penyusunan skripsi ini. Untuk itu, penulis ingin mengucapkan terima kasih kepada:

1. Mami dan Papi, karena berkat mereka berdualah penulis sekarang ini ada dan akhirnya lulus juga dari IPB.

2. Bpk. Drs. Effendi Syahril, Grad. Dipl dan Ibu Dra. Annis D. Raksanagara, M.Si selaku pembimbing I dan II, serta Ibu Ir. Retno Budiarti, MS selaku penguji. 3. Kakak-kakakku “Mbak Deki, Mbak Rita, Mas Juni, dan Mas Hendri”, terima kasih

doa dan semangatnya. “Manda dan Icha”, tante sudah lulus sekarang.

4. Aditya Kresna Priambudi ” atas kesabaran, semangat, bantuan, cinta dan sayangnyalah penulis dapat menyelesaikan skripsi ini, juga untuk Mama terima kasih atas perhatiannya selama ini.

5. Nely, Nita, dan Ike yang sudah bersedia menjadi pembahas dalam seminar penulis. 6. Teman-teman di Math_39: (Tika, Eryt, Dina, Rani, Ade, Tami, dan Desi), terima

kasih atas kebersamaannya selama ini. Aden, Yana, Irwan, Fitrah, Febi, Arif, Kabul, dkk (yang tidak bisa penulis sebutkan satu-persatu) terima kasih untuk keceriaannya selama kurang lebih 4 tahun kita bersama.

7. Teman-teman di “bkl_bkp@D2”(Iwan, Angga, Feri, dan Mas Yan terima kasih untuk tumpangannya selami ini...buat mpus dan anak-anaknya) dan di “Radar 59” (Mbak Niken, Mbak Lala, Ayu dan Muli, terima kasih atas semangat dan bantuan-bantuannya).

8. Bu Susi, Bu Ade, Bu Marisi, Mas Bono, Mas Deni, dan Mas Yono terima kasih atas bantuannya.

9. Kakak-kakak kelas Math_35, 36, 37, dan 38. Adik-adikku Math_40 dan 41 terima kasih semangatnya.

Penulis tidak akan melupakan semua kebaikan yang telah diberikan. Terima kasih.

Bogor, Agustus 2006

RIWAYAT HIDUP

Penulis lahir pada tanggal 12 Desember 1983 di Blitar Jawa Timur, sebagai putri bungsu dari tiga bersaudara, dari pasangan Untung Sardjono Atmojo, Bsc dan Nanik Suwiyani.

Tahun 2002 penulis lulus dari SMU I Talun, Blitar. Pada tahun yang sama, penulis masuk IPB melalui jalur USMI (Undangan Seleksi Masuk IPB) dan memilih Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam.

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... iv

PENDAHULUAN... 1

1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

1.3 Metode dan Sistematika Penulisan ... 1

LANDASAN TEORI ... 1

2.1 Gerak Brown Dimensi Satu ... 2

2.2 Kalkulus Stokastik... 2

2.3 Model untuk Harga Saham ... 3

2.4 PDS Fungsional dari Harga Saham ... 3

2.5 Penilaian Opsi... 3

2.6 Formula Black-Scholes untuk Opsi Call... 4

2.7 Put-Call Parity... 4

2.8 Formula Black-Scholes untuk Opsi Put... 4

2.9 Opsi Barrier... 5

2.10 Model Difusi... 5

2.11 Persamaan Barenblatt... 5

2.12 Uji Turunan Kedua... 5

2.13 Persamaan Parabola... 6

PENENTUAN BATAS-BATAS OPSI DAN PERSAMAAN BLACK- SCHOLES-BARENBLATT... 6

3.1 Penentuan Batas-Batas Opsi Tipe Eropa ... 6

3.1.1 Penentuan Batas Bawah Opsi Tipe Eropa ... 7

3.1.2 Penentuan Batas Atas Opsi Tipe Eropa... 7

3.2 Pengertian Persamaan Black-Scholes-Barenblatt (BSB) ... 8

3.3 Persamaan BSB untuk Batas-Batas Opsi Tipe Eropa ... 8

3.4 Penentuan Batas-Batas Opsi Tipe Amerika... 9

3.4.1 Penentuan Batas Bawah Opsi Tipe Amerika ... 9

3.4.2 Penentuan Batas Atas Opsi Tipe Amerika ... 9

3.5 Persamaan BSB untuk Batas-Batas Opsi Tipe Amerika ... 10

3.6 Penentuan Batas-Batas Eksekusi Awal Opsi Tipe Amerika ... 10

3.6.1 Penentuan Batas Atas Eksekusi Awal Opsi Tipe Amerika... 11

3.6.2 Penentuan Batas Bawah Eksekusi Awal Opsi Tipe Amerika ... 11

PENENTUAN BATAS-BATAS DELTA... 12

4.1 Pengertian Delta ... 12

4.2 Penentuan Batas Delta... 13

4.2.1 Penentuan Batas Bawah Delta ... 13

4.2.2 Penentuan Batas Atas Delta ... 14

4.3 Persamaan BSB untuk Batas-Batas Delta... 14

SIMPULAN DAN SARAN ... 15

DAFTAR GAMBAR

I PENDAHULUAN

1.1 Latar Belakang

Produk turunan adalah suatu instrumen keuangan yang nilainya bergantung pada aset lain yang mendasari (underlying asset). Produk turunan sekarang ini sudah banyak diperdagangkan dalam berbagai bursa di dunia, misalkan saja di CBOE (Chicago Board Options Exchange) pada tahun 1973 mulai menjual opsi dari 16 saham, dan sekarang ini CBOE telah menjual opsi lebih dari 1200 saham (Hull 2003).

Opsi merupakan salah satu jenis dari produk turunan. Opsi memberikan hak untuk membeli (opsi call ) atau menjual (opsi put) aset yang mendasarinya pada waktu tertentu (waktu jatuh tempo) dan harga tertentu (harga eksekusi).

Salah satu cara yang digunakan untuk menentukan nilai opsi adalah formula Black- Scholes. Pada aplikasinya di pasar, para praktisi pasar modal tidaklah sepenuhnya menerapkan asumsi yang digunakan dalam formula Black-Scholes. Hal ini karena, parameter-parameter yang digunakan dalam formula Black-Scholes adalah konstan termasuk nilai volatilitas dan suku bunganya. Pada kenyataannya, volatilitas dan suku bunga bukanlah parameter yang konstan.

Volatilitas yang dinotasikan dengan σ, merupakan simpangan baku dari harga aset yang mendasari kontrak opsi. Harga aset sendiri selalu berubah-ubah setiap waktu, hal ini mengakibatkan volatilitas juga berubah-ubah setiap waktu. Suku bunga yang dinotasikan dengan r dipengaruhi oleh banyak hal, salah satunya adalah nilai tukar mata uang asing, dan ini menyebabkan suku bunga tidak bernilai konstan. Dalam karya ilmiah ini akan dibahas tentang nilai batas suatu opsi apabila diketahui volatilitas dan suku bunga yang digunakan tidak konstan (tak pasti), namun terletak dalam suatu batas tertentu. Bentuk persamaan dari batas-batas opsi tersebut akan dibahas juga dalam karya ilmiah ini, yang selanjutnya disebut dengan

persamaan Black-Scholes-Barenblatt (BSB). Persamaan BSB ini merupakan perluasan dari persamaan Black-Scholes dengan volatilitas dan suku bunga tak konstan. Dalam karya ilmiah ini akan dibahas juga mengenai penurunan batas dari delta, yaitu tingkat perubahan rata-rata nilai opsi terhadap harga aset yang mendasari. Delta merupakan salah satu alat untuk mengendalikan resiko yang ditimbulkan oleh adanya transaksi dari opsi.

1.2 Tujuan Penulisan

Tujuan dari karya ilmiah ini adalah untuk mempelajari :

1. Penentuan batas atas dan batas bawah opsi untuk underlying asset yang mempunyai volatilitas tidak konstan dan suku bunga tidak konstan (tak pasti).

2. Perumusan persamaan Black- Scholes- Barenblatt .

3. Penentuan batas-batas delta.

1.3 Metode dan Sistematika Penulisan Metode penulisan karya ilmiah ini adalah studi literatur dan materi utamanya mengacu pada jurnal “ The Black Scholes Barenblatt Equation for Options with Uncertain Volatility and its Application to Static Hedging “ oleh Gunter H. Meyer tahun 2004.

Pada bab pertama dijelaskan latar belakang dan tujuan dari penulisan karya ilmiah ini. Dalam bab kedua berisi landasan teori yang menjadi konsep dasar dalam penyusunan pembahasan. Pada bab ketiga akan dijelaskan tentang penentuan batas-batas opsi dan persamaan Black-Scholes-Barenblatt (BSB). Kemudian di bab keempat berisikan tentang penentuan batas-batas dari suatu delta. Di bab kelima diberikan saran dan kesimpulan dari karya ilmiah ini, dan yang terakhir yaitu bab keenam berisi daftar pustaka yang menjadi acuan dalam penulisan karya ilmiah ini.

II LANDASAN TEORI

Bab ini berisikan teori yang menjadi konsep dasar dalam pengerjaan karya ilmiah.

Bahasan dari karya ilmiah ini merupakan perluasan dari persamaan Black-Scholes, maka landasan teori yang dipergunakan dalam karya ilmiah ini sebagian besar mengacu pada

Hal-hal yang perlu dikaji lebih lanjut dan berhubungan dengan pembahasan karya ilmiah ini akan dijelaskan sebagai berikut:

2.1 Gerak Brown Dimensi Satu

Sebelum membahas mengenai gerak Brown, terlebih dahulu perlu diketahui tentang proses stokastik.

Definisi 1 [Proses Stokastik]

Proses stokastik adalah sekumpulan parameter dari peubah acak

{

X(t)

}

t∈T (2.1) yang didefinisikan pada ruang probabilitas

(

Ω,F,P

)

dan nilainya berada pada Rn. t adalah waktu. Parameter T terdefinisi pada selang [0,∞), selang [a,b] dengan a,b ∈R+, atau bilangan bulat tak negatif.

(Øksendal 1995) Proses stokastik gerak Brown dimensi satu adalah proses stokastik yang digunakan dalam karya ilmiah ini. Proses stokastik gerak Brown dimensi satu didefinisikan sebagai berikut.

Definisi 2 [Gerak Brown Dimensi Satu] Proses stokastik

{

B(t)|t≥0

}

dikatakan sebagai gerak Brown dimensi satu, apabila

) (t

B memiliki sifat-sifat berikut: 1. 0B(0)= .

2. Untuk 0≤t₁≤t₂≤...≤t_n, peubah acak B(t_i)−B(t_i−1) adalah saling bebas untuk i=1,2,3....

3. Untuk 0≤s≤t, maka B(t)−B(s)~N(0,t−s).

(Karatzas dan Shreve 1987)

2.2 Kalkulus Stokastik

Model persamaan diferensial yang melibatkan peubah acak menurut waktu, dapat dijelaskan dengan menggunakan kalkulus stokastik. Peubah yang bernilai acak ini dinyatakan sebagai proses stokastik. Pada umumnya, suatu sistem dimodelkan oleh suatu persamaan diferensial deterministik:

f(x,t), dt

dx₌

(2.2)

x(0)=x0 (2.3) dengan

x

dan

f

masing-masing adalah variabel dan fungsi deterministik. Jika perubahan dari sistem menjadi tidak deterministik, tetapi ada noise, maka perubahan sistem yang merupakan suatu

peubah acak X(t) dapat dituliskan dalam persamaan diferensial berikut:

+ = ( (), ) )

(t a X t t

dX ’noise’ (2.4)

0 ) 0

( X

X = . (2.5)

Terdapatnya noise atau gangguan menjadikan solusi persamaan diferensial di atas tidak lagi deterministik, karena noise ini juga akan mempengaruhi solusi yang diperoleh. Oleh karena itu diperlukan suatu model untuk menggambarkan noise tersebut. Model yang akan digunakan adalah proses stokastik yang didasari oleh gerak Brown dimensi satu.

Definisi 3 [Proses Itô atau Integral Stokastik]

Misal B(t)adalah gerak Brown dimensi satu pada

(

Ω,F,P

)

. Proses Itô (integral stokastik) adalah proses stokastik X(t) pada

(

Ω,F,P

)

dari bentuk

. ) ( ) ), ( ( ) ), ( ( ) 0 ( ) (

0

0

∫

∫

+

+ =

t t

s dB s s X b ds s s X a X t X

(2.6) Proses Itô

X

(

t

)

dapat juga dituliskan dalam

bentuk persamaan diferensial stokastik (PDS) berikut:

. ) ( ) ), ( ( ) ), ( ( )

(t a X t t dt b X t t dBt

dX = + (2.7)

(Øksendal 1995)

Teorema 1

Misalkan proses stokastik

{

X(t)|t≥0

}

mempunyai diferensial stokastik

) ( ) ), ( ( ) ), ( ( )

(t a X t t dt b X t t dBt

dX = + .

Misalkan fungsi g:

[ )

0,∞ ×R→R merupakan fungsi kontinu yang mempunyai turunan parsial kontinu. Maka proses

( )

(

X t t

)

g

(

X

( )

t t

)

Y , = , adalah proses Itô , sehingga didefinisikan

( )

(

( )

)

(

( )

) ( )

( )

(

,

) ( )

(

)

, 2

1

, ,

2 t dX t t X g

t dX t t X g dt t t X g t dY

xx

x t

+

+ =

(2.8)

dimana t g gt _∂

∂

= ,

X g gx _∂

∂

= , ₂

2

X g gxx

∂ ∂

= .

Dengan dt2 =dB(t)dt=dtdB(t)=0

dan (dB(t))2=dt.

Teorema 2

Perhatikan PDS berikut :

( )

t a

(

X

( )

t,t

)

dt b

(

X

( )

t,t

) ( )

dBt .

dX = +

Misalkan fungsi a

(

X

( )

t,t

)

dan b

(

X

( )

t,t

)

mempunyai turunan pertama dan kedua yang kontinu dan terbatas.

Misalkan u

( )

x,t =E

[

g

(

X

( )

s

) ( )

X t =x

]

, s

tetap , t≤s dan g∈C2

( )

Rn . Atau dapat juga dituliskan

( )

x t E

[

g

(

X

( )

s

)

]

u , = x,t . (2.9) Maka u

( )

x,t memenuhi persamaan Kolmogorov mundur,

, ,

0 t s x L

t u

u= ≤ ∀

+ ∂ ∂

(2.10)

( ) ( )

_{= →} − s t x g t x

u , , (2.11) dengan

( ) ( )

( )

,

( )

, . 2

1 ,

, ₂

2 2

t x x

u t x b t x x u t x a Lu

∂ ∂ +

∂ ∂

= (2.12)

(Øksendal 1995) Bukti dapat dilihat pada Øksendal (1995) dan Amellia (2005).

2.3 Model untuk Harga Saham

Harga saham yang berubah secara acak menurut waktu diasumsikan sebagai suatu proses stokastik, diasumsikan juga tidak ada pembayaran dividen atas saham.

Misalkan harga saham S(t) pada waktu t. Pada selang waktu yang kecil dt, harga saham S(t)akan berubah menjadi

) ( ) (t dS t

S + . Tingkat pengembalian untuk

saham, ) (

) ( t S

t dS

, dapat dimodelkan dalam dua

bentuk yaitu yang pertama adalah bentuk pengembalian dari harga saham yang dapat bersifat deterministik yaitu μdt dengan μ adalah tingkat rata-rata pertumbuhan harga saham (drift), dan bentuk yang kedua adalah pengembalian dari harga saham yang bersifat stokastik yaitu σdB(t) dengan σ adalah volatilitas harga saham dan dB(t) adalah bentuk keacakan yang mempengaruhi harga saham.

Dengan adanya bentuk pengembalian saham seperti di atas, harga saham dapat dituliskan sebagai persamaan diferensial stokastik:

) ( ) ( ) ( )

(t S t dt S t dBt

dS =μ +σ (2.13)

dengan t∈

[ )

0,∞ ,S(t)∈

[ )

0,∞ , dan B(t) adalah gerak Brown dimensi satu.

2.4 PDS Fungsional dari Harga Saham Pada bagian ini diberikan bentuk PDS untuk suatu peubah yang nilainya bergantung pada harga saham S(t) dan waktu t. Perubahan dari S(t) dapat dimodelkan dengan memanfaatkan formula Itô. Misalkan diberikan peubah Y(t) yang bergantung pada

) (t

S dan t. Berdasar Hull (1997), apabila harga saham S(t) mengikuti model saham (2.13), maka bentuk PDS untuk Y(t) ditentukan oleh teorema berikut.

Teorema 3

Misalkan diberikan Y(t)=g(S(t),t) dengan

[ )

∞ ∈0,

t dan S

( )

t memiliki persamaan diferensial stokastik (2.13), maka persamaan diferensial stokastik bagi fungsi Y(t) dapat dinyatakan dalam bentuk:

( )

( )

( )

( )

. 2 1 )

(

2 2 2 2

t dB S g t S

dt S

g t S t

g S g t S t dY

∂ ∂ +

⎟ ⎟ ⎠ ⎞ ⎜

⎜ ⎝ ⎛

∂ ∂ +

∂ ∂ + ∂ ∂ =

σ

σ μ

(2.14) (Hull 1997) Bukti dapat dilihat pada Hull (1997) dan Amellia (2005).

2.5 Penilaian Opsi

Nilai opsi adalah besarnya biaya (premi) yang dikeluarkan oleh seorang investor untuk mendapatkan kontrak opsi dan pembayarannya dilakukan pada saat kontrak dibuat. Nilai opsi yang dibahas oleh Fisher Black dan Myron Scholes hanya yang bergantung pada harga saham, waktu, dan parameter lain yang bernilai konstan.

Penilaian opsi merupakan suatu masalah yang berkembang cukup lama dalam finansial. Secara khusus, terdapat suatu riset yang memfokuskan mengenai ada atau tidaknya hubungan antara harga saham dan kontrak opsi yang tertulis pada saham tersebut.

Masalah ini telah dipecahkan pada tahun 1973 oleh Fisher Black dan Myron Scholes, yang kemudian formulanya dikenal dengan formula Black-Scholes. Sehingga diperoleh teorema berikut.

Teorema 4

0 2

1

2 2 2

2 _{− =}

∂ ∂ + ∂ ∂ +

∂ ∂

rV S V rS S

V S t

V _σ

. (2.15)

(Hull 1997) Bukti dapat di lihat pada Hull (1997) dan Amellia (2005).

2.6 Formula Black-Scholes untuk Opsi Call

Misalkan S_T adalah harga saham dan K adalah harga eksekusi yang disepakati. Apabila K<S_T pada saat jatuh tempo, maka pemegang kontrak opsi akan mengeksekusi kontraknya karena investor mendapatkan untung sebesar ST −K, sebaliknya jika

K

ST < pada saat jatuh tempo, maka pemegang kontrak opsi tidak akan mengeksekusi kontraknya, karena investor akan rugi sebesarK−S_T, untuk kondisi ini opsi tidak mempunyai nilai pada saat jatuh tempo. Jadi nilai intrinsik opsi call pada saat jatuh tempo dapat dituliskan sebagai suatu payoff (penerimaan) bagi pemegang kontrak sebagai berikut:

) 0 , max( ) ,

(S T S K

C = T− .

Menurut persamaan (2.13), jika S bernilai 0, maka dS juga akan bernilai 0, akibatnya S tidak akan pernah berubah. Ini merupakan masalah deterministik dari PDS (2.13). Jadi jika S=0 pada saat jatuh tempo, maka payoff bernilai nol. Akibatnya opsi call tidak mempunyai nilai pada saat S=0, walaupun belum jatuh tempo. Jadi pada saatS=0, dipunyai

( )

0,t =0

C .

Sehingga didapat teorema berikut.

Teorema 5

Solusi dari persamaan diferensial parsial Black-Scholes

0 2

1

2 2 2

2 _{− =}

∂ ∂ + ∂ ∂ +

∂ ∂

rC S C rS S

C S t

C _σ

(2.16) dengan syarat batas

) 0 , max( ) ,

(S T S K

C = T − ,

C

( )

0,t =0. (2.17) adalah nilai opsi call yang diberikan oleh:

(

)

( )

( )

( )

[

T

]

t

d N Ke

d SN t S

C rT t

, 0

, 1 2

∈

−

= − −

(2.18)

dengan

(

)

(

)

(

)

, 2 / /

ln 2

1

t T

t T r

K S d

−

− +

+ =

σ σ

(2.19)

, 1

2 d T t

d = −σ − (2.20) dan N

( )

d_i adalah fungsi sebaran normal kumulatif dan berbentuk :

( )

.

2

1 2

2 1

dy e d

N

i d

y

i

∫

∞ −

−

=

π (2.21)

(Hull 1997) Bukti dapat dilihat pada Hull (1997) dan Amellia (2005).

2.7 Put-Call Parity

Berdasarkan definisi terlihat bahwa opsi put dan opsi call mempunyai perilaku yang bertolak belakang. Dalam praktiknya, put dan call dapat dikombinasikan dalam suatu bentuk dimana kolerasinya sangat dekat. Hal ini diperlihatkan dalam teorema berikut.

Teorema 6

Nilai dari opsi call dan put dapat dinyatakan sebagai put-call parity dan memenuhi persamaan

. )

, ( ) ,

(S t C S t Ke r(T t) P

S+ − = − − (2.22)

(Hull 1997) Bukti dapat dilihat pada Hull (1997) dan Amellia (2005).

2.8 Formula Black-Scholes untuk Opsi Put

Dengan menggunakan konsep put-call parity, jika nilai opsi call sudah diketahui, maka nilai opsi put juga dapat ditentukan. Dari segi holder (pemegang kontrak opsi) payoff yang didapat dari adanya kontrak opsi adalah

) 0 , max( ) ,

(S T S K

C = T− .

Sedangkan dari segi written (pembuat kontrak opsi), payoff yang diterima adalah sebesar

) 0 , max( ) ,

(S T K ST

P = − .

Teorema 7

Nilai opsi put diberikan oleh

) ( ) ( )

,

(St Ke ( )N d₂ SN d₁

P = −rT−t − − − (2.23) dengan syarat batas

( )

0 ) , 0 (

, ) 0 , max( ,

=

− =

t P

S K T

S

P T

dan d1 dan d2seperti pada persamaan (2.19) dan (2.20).

(Hull 1997)

2.9 Opsi Barrier

Opsi barrier adalah opsi yang payoff (penerimaan) nya bergantung pada harga aset yang mendasari yang mencapai suatu tingkat tertentu selama periode waktu tertentu. Opsi barrier ini mempunyai beberapa tipe yaitu:

1. Up and out call adalah jenis opsi call yang segera dieksekusi jika nilai asetnya mencapai tingkat barrier tertentu yaitu X, yang nilainya lebih besar dari nilai aset pada waktu awal kontrak

2. Up and out put adalah jenis opsi put yang segera dieksekusi jika nilai asetnya mencapai tingkat barrier tertentu yaitu X, yang nilainya lebih besar dari nilai aset pada waktu awal kontrak .

Untuk up and out call, jika nilai X≤K maka nilai dari up and out call adalah 0, dengan X adalah tingkat barrier dan K adalah harga eksekusi. Jika X >K maka nilai up and out call

( )

c_uo dirumuskan sebagai berikut:

( )

(

)

(

)

( )

(

)

(

)

(

)

(

)

]] , [ / ] [ / [ 1 2 2 1 2 1 1 T y N T y N S H Ke y N y N S H Se T x N Ke e x SN c c rT qT rT qT uo σ σ σ λ λ + − − + − + − − − − − − − = − − − − − dengan

q= tingkat yield (penerimaan yang dinyatakan dengan persen yang diperoleh dari hasil investasi).

( )

d1 Ke N

( )

d2

N Se

c = −qT − −rT ,

(

)

(

)

, 2 / / ln 2 1 T T q r K S d σ σ + − + = , 1 2 d T d = −σ

, 2 / 2 2 σ σ λ=r−q+

[

/

]

_, ln 2 T T SK H y λσ σ + =

(

)

, / ln 1 T T H S x λσ σ + =

(

)

. / ln 1 T T S H y λσ σ + =

Untuk up and out put, jika X≥K maka nilai up and out put

( )

puo adalah

(

)

( )

(

/

)

(

)

. / [ 2 2 2 T y N S H Ke y N S H Se p

p_uo qT rT

σ λ λ + − + − − − = − − −

Jika X<K, maka nilai

( )

puo adalah

( )

(

)

(

)

( ) ( )

(

)

(

)

(

)

], [ / ] [ / 1 2 2 1 2 1 1 T y N T y N S H Ke y N y N S H Se T x N Ke e x SN p rT qT rT qT uo σ σ σ λ λ − − − − − + + − + − − = − − − − − dengan

(

d2

)

Se N

(

d1

)

. N

Ke

p = −rT − − −qT −

(Hull 2003)

2.10 Model Difusi

Model difusi dalam fisika digunakan untuk memodelkan penyebaran kepadatan suatu kuantitas. Pada pasar keuangan hal ini bisa digunakan untuk memodelkan penyebaran nilai fluktuasi suatu data keuangan.

Model difusi biasanya memiliki bentuk dasar

P t P_=∇2

∂ ∂

atau dapat dituliskan sebagai

( )

( )

2 2 2 _, 2 , x t x P t t x P ∂ ∂ = ∂ ∂ δ .

(Hariadi Y dan Surya Y 2006)

2.11 Persamaan Barenblatt

Persamaan Barenblatt adalah nama lain dari persamaan difusi yang tak linier. Persamaan ini memiliki koefisien difusi yang tidak kontinu.

Bentuk persamaan Barenblatt adalah sebagai berikut:

( ) ( ) ( )

, − ∂2 , =0,

∂_tux t Du _xu x t dengan,

( )

u k

[

g

(

u

)

]

D ≡ 1+ θ −α∂_t ,

adalah koefisien difusi tak linier dengan konstanta α>0. Dan θ

( )

x di definisikan sebagai berikut:

( )

⎩ ⎨ ⎧ < > = , 0 , 1 0 , 0 x x x θ

g adalah konstanta pengontrol ketidaklinieran koefisien difusi.

(Fukui T dan Yoshida S 2006)

2.12 Uji Turunan Kedua Andaikan "f kontinu dekat c

1. Jika f'

( )

c =0dan f"

( )

c >0, maka f mempunyai minimum lokal pada c.

2. Jika f'

( )

c =0dan f"

( )

c <0, maka f mempunyai maksimum lokal pada c.

2.13 Persamaan Parabola

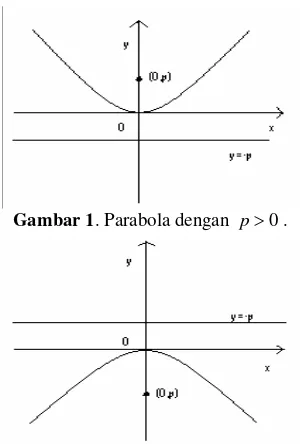
Persamaan Black-Scholes merupakan persamaan diferensial yang berbentuk parabola. Sebuah parabola adalah himpunan titik-titik di suatu bidang yang berjarak sama pada suatu titik tetap (fokus) dan suatu garis tetap (direktriks). Persamaan parabola dengan fokus

( )

0,p dan direktriks y=−p adalah

py x2=4 .

Persamaan di atas dapat dituliskan menjadi: 0

4 2_{− =}

py

x .

Jika x2−4py<0 , maka p>0. Jika

0 4 2_{− >}

py

x , maka p<0.

[image:14.612.343.493.77.299.2]

Parabola ini akan terbuka ke atas jika p>0, dan ke bawah jika p<0.

Gambar 1. Parabola dengan p>0.

Gambar 2. Parabola dengan p<0. (Stewart 2003)

III PENENTUAN BATAS-BATAS OPSI DAN PERSAMAAN

BLACK-SCHOLES-BARENBLATT

Sejak awal tahun sembilan puluhan sudah banyak peneliti yang bekerja keras mencari formula untuk penilaian opsi. Mereka mencoba membuat formula dengan menggunakan berbagai asumsi untuk mendukung hasil kerjanya. Asumsi-asumsi yang digunakan dari tahun ke tahun mengalami banyak perubahan sebagai penyempurnaan dari asumsi-asumsi sebelumnya. Dengan bantuan Robert Merton, pada tahun 1973 Fisher Black dan Myron Scholes menghadirkan formula penilaian opsi dalam bentuk persamaan diferensial yang dapat membantu para pialang saham menentukan apakah sebuah opsi terlalu mahal atau sebaliknya terlalu murah relatif terhadap harga saham pada saat itu.

Salah satu parameter dari formula Black-Scholes yang tidak bisa dilihat nilainya secara langsung adalah volatilitas dari aset yang mendasari. Dengan kenyataan tersebut, maka para pelaku perdagangan opsi mulai menggunakan implied volatilities untuk mengetahui nilai volatilitas yang berlaku di pasar. Implied volatilities adalah suatu volatilitas yang berimplikasi dengan harga opsi yang terbentuk di pasar.

Selain menggunakan implied volatilities untuk mengatasi ketidaksempurnaan formula

Black-Scholes (B-S), maka dalam bab ini akan dibahas mengenai batas-batas dari nilai opsi yang bersesuaian dengan volatilitas dan suku bunga yang terletak dalam suatu batas tertentu.

Penentuan suatu persamaan yang merupakan perluasan dari persamaan Black-Scholes untuk menentukan nilai batas opsi juga akan dibahas dalam bab ini. Persamaan tersebut selanjutnya dikenal sebagai persamaan Black-Scholes-Barenblatt (BSB).

3.1 Penentuan Batas-Batas Opsi Tipe Eropa

Asumsikan opsi yang digunakan adalah up and out call tipe Eropa V

( )

S,t dengan waktu jatuh tempo T, harga eksekusi K, harga saham S dan tingkat up and out barrier adalah X, dengan X >K. Selain itu diasumsikan juga bahwa S∈

(

0,X

)

dan

(

T

]

t∈ 0, , maka menurut Teorema 4, bentuk persamaan Black Scholesnya adalah sebagai berikut :

( )

( )

( )

( )

, 0

, ,

2 1

, 2 2

= + −

+ ≡

Η

t

S SS

V V t S r

SV t S r V S t S V

r σ

σ

dengan nilai σ dan r sudah ditentukan, dan dengan syarat batas :

( ) ( )

0,t =V X,t =0. V

Syarat awal dari persamaan (3.1) adalah

( )

S,0

V , yang dipartisi menjadi:

( )

(

)

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ < < − − − − − ≤ ≤ − < = X S X S X K X X S K K S K S S V ε ε ε ε , , , 0 0 ,

untuk suatu ε yang sangat kecil dan positif. Persamaan (3.1) hanya berlaku untuk nilai

σ dan r yang konstan. Padahal kedua nilai tersebut tidaklah mungkin konstan dalam dunia nyata. Agar memudahkan perhitungan dengan melihat kenyataan yang ada, diasumsikan bahwa σ dan r terletak dalam suatu batas tertentu, namun tetap memiliki nilai yang tidak pasti, yaitu sebagai berikut:

( ) ( ) ( )

, , ₁ , ,

0St

σ

St

σ

St

σ

≤ ≤ (3.2) dan

( ) ( ) ( )

,

,

₁

,

,

0

S

t

r

S

t

r

S

t

r

≤

≤

(3.3) dengan σ₀

( )

S,t >0 merupakan nilai terendah dari volatilitas aset yang mendasari, dan

( )

S,t 1

σ adalah nilai tertinggi dari volatilitas aset yang mendasari. Notasi r0

( )

S,t ≥0dan

( )

S t

r1 , masing-masing adalah batas nilai terendah dan batas tertinggi dari suku bunga .

Nilai dari volatilitas dan suku bunga yang digunakan untuk memodelkan harga opsi masing-masing terletak dalam suatu batas tertentu, maka secara otomatis harga dari opsi akan terletak dalam suatu batas tertentu juga. Akan ditunjukkan bahwa:

( ) ( )

, , ₁

( )

, . 0 S t V S t V S t

V ≤ ≤ (3.4)

3.1.1 Penentuan Batas Bawah Opsi Tipe Eropa

Pembuktian dari pertidaksamaan (3.4) dimulai dengan menunjukkan

( )

S t V

( )

S t V0 , ≤ , .

Perhatikan persamaan di bawah ini:

( )

− + − + − + − + − + − − + − − + − + − = Η t t S S SS SS V V V SV r r V SV r r V V S V r 0 0 0 0 1 0 0 0 0 2 1 2 0 2 0 2 2 0 ) 1 1 ( ) 1 1 ( ] ) ( ) ( ) ( ) [( ] ) ( ) [( 2 1 , σ σ σ σ σ . 0 ] ) ( ) ( ) ( ) [( ] ) ( ) [( 2 1 0 0 1 0 0 0 0 2 1 2 0 2 0 2 2 ≥ − − + − − + − + − = − + − + V SV r r V SV r r V V S S S SS SS σ σ

σ σ

(3.5)

Persamaan di atas memiliki syarat batas yang sama seperti syarat batas pada persamaan (3.1). Η

( )

σ,r adalah suatu operator B-S

pada persamaan (3.1), V0SS+ = V0SS≥0, −

SS

V0 =V0SS<0,

(

)

+

− ₀

0 V

SV S adalah

{

,0

}

maxSV0S−V0 , dan

(

)

−

− 0 0 V

SV _S adalah

{

,0

}

minSV0S −V0 .

Persamaan (3.5) dapat dituliskan dalam bentuk

Η

( )

σ,rV0=F0

(

S,V0,V0S,V0SS

)

, (3.6) untuk penyederhanaan tulisan.F0 adalah sisi kanan dari persamaan (3.5), dan nilainya adalah:

(

, ₀, ₀ , ₀

)

0 0 SV VS VSS ≥

F .

Asumsikan bahwa V0 merupakan solusi dari persamaan (3.5) pada daerah asal D

(

0,T

] ( )

× 0,X yang kontinu pada

[ ] [ ]

0,T ×0,X dengan syarat batas seperti pada persamaan (3.1). Jika didefinisikan :

( )

S t V

( ) ( )

S t V S t e , = ₀ , − , maka

( )

, ≥0

Ησ re ,

pada D=

(

0,X

) (

× 0,T

]

. Berdasarkan prinsip standar maksimum parabola, fungsi e

( )

S,t tidak mempunyai nilai maksimum yang positif pada D. Jadi e

( )

S,t ≤0 pada D. Ini berarti bahwa:

( ) ( )

, , , 0 S t V S t

V ≤

sehingga terbukti V₀

( )

S,t merupakan batas bawah dari harga opsi untuk nilai σ dan r yang berada dalam pertidaksamaan (3.2) dan (3.3).

3.1.2 Penentuan Batas Atas Opsi Tipe Eropa

Jika pada persamaan (3.5) fungsi maksimum dan minimum pada F ditukar yaitu: V0SS+→V1SS−,

(

SV0S−V0

) (

+→SV1S−V1

)

− dan notasi V₀ →V₁, maka dengan melakukan proses yang sama dengan persamaan (3.5), didapat persamaan baru sebagai berikut:

( )

, 0 ] ) ( ) ( ) ( ) [( ] ) ( ) [( 2 1 , 1 1 1 1 1 0 1 2 1 2 1 2 0 2 2 1 ≤ − − + − − + − + − = Η + − + − V SV r r V SV r r V V S V r S S SS SS σ σ

σ σ σ

(3.7)

dengan V1_SS+ = V1SS ≥0, − SS

V1 = V1SS <0,

(

₋

)

+

1 1 V

SV_S adalah max

{

SV1S −V1,0

}

, dan

(

₋

)

−

1 1 V

Persamaan (3.7) disederhanakan menjadi:

(

SV VS VSS

)

F

V1= 1 , 1, 1 , 1

Η (3.8)

dimana nilai F₁ adalah :

(

, ₁, ₁ , ₁

)

0. 1 S V VS VSS ≤ F

Asumsikan bahwa V1 merupakan solusi dari persamaan (3.7) pada daerah asal D

(

0,T

] ( )

× 0,X , yang kontinu pada

[ ] [ ]

0,T ×0,X dengan syarat batas seperti pada persamaan (3.1).

Didefinisikan

( )

S t V

( ) ( )

S t V S t d , = ₁ , − , , maka

( )

, ≤0

Ησ r d

pada D=

(

0,X

) (

× 0,T

]

. Dengan menggunakan prinsip standar maksimum parabola, maka d

( )

S,t tidak mempunyai nilai minimum yang negatif pada D, sehingga

( )

S,t ≥0

d . Jadi V

( ) ( )

S,t ≤V1S,t . Terbukti bahwa V₁

( )

S,t merupakan batas atas dari harga opsi untuk nilai σ dan r yang berada dalam persamaan (3.2) dan (3.3). Dengan demikian pertidaksamaan pada (3.4) terbukti. Catatan:

1. Jika ternyata harga opsi call yang ada di pasar lebih tinggi dari batas atas harga opsi call teoritis, maka investor lebih baik tidak mengeksekusi call tersebut, karena akan mengalami kerugian.

2. Jika ternyata harga opsi call pasar lebih rendah dari batas bawah harga opsi teoritis, maka lebih baik investor membeli call tersebut dan menjual saham untuk mendapatkan keuntungan. Batas-batas dari nilai opsi sudah ada dan sudah dibuktikan kebenarannya, selanjutnya diperlihatkan bentuk persamaan yang bersesuaian dengan kedua batas nilai opsi di atas.

3.2 Pengertian Persamaan Black-Scholes- Barenblatt (BSB)

Persamaan Black-Scholes-Barenblatt (BSB) adalah suatu persamaan yang digunakan untuk menyelesaiakan harga dari produk turunan (misalkan opsi) berdasarkan harga aset yang mendasari (misalkan saham), yang mempunyai dua nilai volatilitas yang berbeda. Kedua nilai volatilitas tersebut bergantung pada tanda dari gamma (V_SS). Gamma adalah tingkat perubahan rata-rata delta terhadap harga aset yang mendasari. Delta (V_S) adalah tingkat perubahan rata-rata

nilai produk turunan terhadap harga aset yang mendasari .

(www.wilmottmagazine.com/messageview)

3.3 Persamaan BSB untuk Batas-Batas Opsi Tipe Eropa.

Dari bahasan sebelumnya, telah dijelaskan bagaimana menentukan batas-batas opsi V₀ dan V1. Dalam bahasan ini diperkenalkan suatu persamaan yang bersesuaian dengan batas-batas V₀ dan V₁.

Perhatikan persamaan di bawah ini

( )

( )(

)

0

2 1 0 0 0 0 0 2 2 0 0 0 = + − + ≡ Η t S SS BSB V V SV r g V S f V σ (3.9) dengan

( )

(

(

)

)

⎩ ⎨ ⎧ < ≥ = 0 jika , , 0 jika , , 0 1 0 0 0 SS SS V t S V t S f σ σ σ dan

( )

( )

( )

(

(

)

)

⎩ ⎨ ⎧ < − ≥ − = . 0 jika , , 0 jika , , 0 0 1 0 0 0 0 V SV t S r V SV t S r r g S S

Persamaan (3.9) merupakan persamaan yang bersesuaian dengan batas bawah opsi V0.

Persamaan yang bersesuaian dengan batas atas opsi adalah sebagai berikut

( )

( )(

)

0

2 1 1 1 1 1 1 2 2 1 1 1 = + − + ≡ Η t S SS BSB V V SV r g V S f V σ (3.10) dengan

( )

(

(

)

)

⎩ ⎨ ⎧ > ≤ = 0 jika , , 0 jika , , 1 1 1 0 1 SS SS V t S V t S f σ σ σ dan

( )

( )

( )

(

(

)

)

⎩ ⎨ ⎧ > − ≤ − = . 0 jika , , 0 jika , , 1 1 1 1 1 0 1 V SV t S r V SV t S r r g S S

Dalam karya ilmiah ini, persamaan (3.9) dan(3.10) disebut sebagai persamaan Black-Scholes-Barenblatt (BSB), karena persamaan ini merupakan gabungan dari persamaan Black-Scholes dan persamaan Barenblatt.

3.4 Penentuan Batas-Batas Opsi Tipe Amerika.

Asumsikan opsi Amerika yang digunakan adalah jenis opsi up and out put V

( )

S,t . Persamaan Black Scholes yang digunakan dalam opsi up and out put Amerika ini adalah sebagai berikut:

( )

( )

( )

( )

, 0,

, ,

2 1

, 2 2

dengan syarat batas

( )

(

)

( )

( )

(

)

( )

, 0, , 1 , , , = − = − = t X V t t s V t s K t t s V S

dan syarat awal yang digunakan adalah sebagai berikut:

( )

0 K, s =

( )

S t K S S

[

s

( )

t

]

V , = − , ∈ 0, , dengan s

( )

t adalah batas eksekusi awal, K adalah harga eksekusi, S adalah harga aset yang mendasari, dan X adalah tingkat opsi barrier.

Persamaan (3.11) hanya berlaku untuk nilai σ dan r yang konstan. Namun kenyataannya nilai-nilai tersebut tidaklah konstan, sehingga untuk menyempurnakannya diasumsikan bahwa nilai σ dan r terletak dalam suatu batas tertentu, seperti pada pertidaksamaan (3.2) dan (3.3). Karena σ dan r terletak dalam batas, maka harga opsinya juga akan terletak dalam batas tertentu. Akan ditunjukkan

( )

S t V

( )

S t V

( )

S t V₀ , ≤ , ≤ ₁ , .

3.4.1 Penentuan Batas Bawah Opsi Tipe Amerika

Pembuktian V₀

( )

S,t ≤V

( )

S,t ≤V₁

( )

S,t dimulai dengan menunjukkan

( )

S t V

( )

S t V₀ , ≤ , .

Dengan batas nilai σ dan r seperti pada (3.2) dan (3.3), perhatikan persamaan di bawah ini.

( )

− + − + − + − + − + − − + − − + − + − = Α t t S S SS SS V V V SV r r V SV r r V V S V r 0 0 0 0 1 0 0 0 0 2 1 2 0 2 0 2 2 0 ) 1 1 ( ) 1 1 ( ] ) ( ) ( ) ( ) [( ] ) ( ) [( 2 1 , σ σ σ σ σ , 0 ] ) ( ) ( ) ( ) [( ] ) ( ) [( 2 1 0 0 1 0 0 0 0 2 1 2 0 2 0 2 2 ≥ − − + − − + − + − = − + − + V SV r r V SV r r V V S S S SS SS σ σ

σ σ

(3.12) dengan: V0_SS+=V0SS≥0,

− SS

V0 =V0SS<0,

(

₋

)

+

0 0 V

SVS =max

{

SV0S−V0,0

}

,

(

₋

)

−

0 0 V

SV_S = min

{

SV0S−V0,0

}

. Dalam persamaan (3.5) diketahui bahwa

0

V merupakan solusi dari

( )

, ₀ = ₀

(

, ₀, ₀ , ₀

)

≥0

Ησ rV F SV V _S V_SS .

Maka dalam bahasan ini diasumsikan juga bahwa V₀ adalah solusi dari persamaan (3.12), yang disederhanakan penulisannya dengan:

( )

, 0= 0

(

, 0, 0, 0

)

≥0.

ΑσrV F SV V_SV_SS (3.13) Syarat batas dan syarat awal yang digunakan dalam opsi put Amerika dan opsi call Eropa sedikit berbeda. Syarat batas dan awal opsi put Amerika secara umum dapat dilihat pada sub bab 3.4. Sedangkan syarat-syarat yang bersesuaian dengan opsi put Amerika pada persamaan (3.12) adalah sebagai berikut:

( )

(

)

( )

( )

(

,

)

1,

, , 0 0 0 0 0 − = − = t t s V t s K t t s V S

( ) (

,0

)

max

{

,0

}

0 S K S K S

V = − + = − ,

( )

. ) , ( , 0 , 0 0 S K t S V t X V − = =

dengan s0

( )

t adalah batas eksekusi untuk V0,

K adalah harga eksekusi, S adalah harga aset yang mendasari, dan X adalah tingkat opsi barrier.

Akan dibuktikan V0

( ) ( )

S,t ≤VS,t. Terlebih dahulu asumsikan solusi untuk

{

V0

( ) ( )

S,t,s0 t

}

ada dan tunggal, dan

( )

(

( )

)

(

]

{

S,t :S s₀ t,X ,t 0,T

}

.

D= ∈ ∈

Asumsikan

( )

S t V

( ) ( )

S t V S t e , = ₀ , − , , maka

( )

, ≥0

Ασ r e ,

D S⊂

∀ dan t>0. Berdasar prinsip standar maksimum parabola, e

( )

S, tidak mempunyai t nilai maksimum yang positif. Jadi

( )

S,t ≤0

e pada D.

Sehingga V₀

( )

S,t ≤V

( )

S,t pada D dan kontinu pada

( ) (

0,X ×0,T

]

.

3.4.2 Penentuan Batas Atas Opsi Tipe Amerika

Pada bagian ini akan dibuktikan bahwa:

( ) ( )

St V St

dengan V1SS+ =V1SS≥0, − SS

V1 =V1SS<0,

(

₋

)

+

1 1 V

SV_S adalah max

{

SV1S −V1,0

}

, dan

(

₋

)

−

1 1 V

SV_S adalah min

{

SV_1S −V₁,0

}

. Persamaan 3.14 disederhanakan menjadi

(

, ₁, ₁ , ₁

)

, 1

1 F S V VS VSS V =

Α (3.15)

dimana nilai F1 adalah

(

, 1, 1 , 1

)

0 1 SV VS VSS ≤ F

Syarat-syarat yang bersesuaian dengan opsi put Amerika pada persamaan (3.14) adalah sebagai berikut:

( )

(

)

( )

( )

(

,

)

1,

, , 1 1 1 1 1 − = − = t t s V t s K t t s V S

( ) (

,0

)

max

{

,0

}

1 S K S K S

V = − + = − ,

( )

. ) , ( , 0 , 1 1 S K t S V t X V − = =

dengan s1

( )

t adalah batas eksekusi untuk V1, K adalah harga eksekusi, S adalah harga aset yang mendasari, dan X adalah tingkat opsi barrier.

Pembuktian pertidaksamaan

( )

St V

( )

S t

V , ≤ 1 , , dimulai dengan

mengasumsikan solusi untuk

{

V1

( ) ( )

S,t,s1t

}

ada dan tunggal., dan

( )

(

( )

)

(

]

{

S,t :S s1t,X ,t 0,T

}

.

D= ∈ ∈

Asumsikan

( )

S t V

( ) ( )

S t V S t e , = ₁ , − , , maka

( )

, ≤0

Ασ re ,

D S⊂

∀ dan t>0. Berdasar prinsip standar maksimum parabola, e

( )

S,t tidak mempunyai nilai minimum yang negatif. Jadi

( )

S,t ≥0

e pada D.

Sehingga V

( )

S,t ≤V₁

( )

S,t pada D dan kontinu pada

( ) (

0,X ×0,T

]

. Jadi terbukti bahwa nilai opsi up and out put Amerika terletak pada

( )

S t V

( )

S t V

( )

S t V₀ , ≤ , ≤ ₁ , . Catatan:

1. Jika ternyata harga opsi put yang ada di pasar lebih tinggi dari batas atas harga opsi put teoritis, maka investor lebih baik mengeksekusi opsi put dan menjual sahamnya, karena akan mendapatkan keuntungan.

2. Jika ternyata harga opsi put pasar lebih rendah dari batas bawah harga opsi put teoritis, maka lebih baik investor tidak mengeksekusi opsi put, karena akan menderita kerugian.

Batas-batas dari nilai opsi sudah dibuktikan kebenarannya, selanjutnya akan diperlihatkan bentuk persamaan yang bersesuaian dengan batas-batas opsi opsi up and out put Amerika di atas.

3.5 Persamaan BSB untuk Batas-Batas Opsi Tipe Amerika

Persamaan BSB pada opsi up and out call Eropa di atas dapat juga diterapkan untuk opsi tipe Amerika. Perbedaan opsi tipe Eropa dan opsi tipe Amerika hanyalah terletak pada waktu eksekusinya. Opsi tipe Eropa hanya dapat dieksekusi pada saat jatuh tempo, sedangkan opsi tipe Amerika dapat dieksekusi kapan saja sampai waktu jatuh tempo. Persamaan BSB yang bersesuaian dengan nilai batas bawah opsi Amerika adalah sebagai berikut:

( )

( )(

)

0

2 1 0 0 0 0 0 2 2 0 0 0 = + − + ≡ Α t S SS BSB V V SV r g V S f V σ (3.16) dengan

( )

(

(

)

)

⎩ ⎨ ⎧ < ≥ = 0 jika , , 0 jika , , 0 1 0 0 0 SS SS V t S V t S f σ σ_σ

dan

( )

( )

( )

(

(

)

)

⎩ ⎨ ⎧ < − ≥ − = . 0 jika , , 0 jika , , 0 0 1 0 0 0 0 V SV t S r V SV t S r r g S S

Sedangkan persamaan BSB yang bersesuaian dengan nilai batas atas opsi Amerika adalah sebagai berikut:

( )

( )(

)

0,

2 1 1 1 1 1 1 2 2 1 1 1 = + − + ≡ Α t S SS BSB V V SV r g V S f V σ (3.17) dengan

( )

(

(

)

)

⎩ ⎨ ⎧ > ≤ = 0 jika , , 0 jika , , 1 1 1 0 1 SS SS V t S V t S f σ _σσ

dan

( )

( )

( )

(

(

)

)

⎩ ⎨ ⎧ > − ≤ − = . 0 jika , , 0 jika , , 1 1 1 1 1 0 1 V SV t S r V SV t S r r g S S

3.6 Penentuan Batas-Batas Eksekusi Awal Opsi Tipe Amerika

3.6.1 Penentuan Batas Atas Eksekusi Awal Opsi Tipe Amerika

Dalam bahasan penentuan batas bawah opsi Amerika (3.4.1) di atas, sebelumnya diasumsikan

( )

(

( )

)

(

]

{

S t S s t X t T

}

D= , : ∈ ₀ , , ∈ 0, , dan diasumsikan juga

( )

S t V

( ) ( )

S t V S t e , = ₀ , − , . Maka

( )

, ≥0

Ασ re ,

D S⊂

∀ dan t>0, e

( )

S,t tidak akan mempunyai nilai maksimum yang positif. Jika s0

( ) ( )

t ≥st maka

( )

(

)

( )

(

( )

)

. 0 , 0 0 0 ≤ − − − = − = t s K t s K V V t t s e .

Untuk membuktikan hal ini benar, pertama asumsikan ada t* yang mengakibatkan

( ) ( )

* * 0 t st

s ≤ dan juga mengakibatkan

( )

(

)

(

( )

)

(

( )

)

( )

1 0. 1 * , * * , * * ,

* 0 0

0 = − − − = −

=V s t t V st t

t t s

eS S S

Dengan adanya syarat batas

( )

(

0 *, *

)

0

( )

* 0 s t t K s t

V = − ,

maka

( )

(

0 *, *

)

0 0 s t t =

V _t .

Persamaan (3.18) menjadi

( )

( )(

)

0.

2 1 0 0 0 0 2 2 0 0 0 = − + ≡ Α V SV r g V S f V S SS BSB _σ Ini berarti

( )

( )(

)

, 2 1 0 0 0 0 2 2

0 S V g r SV V

f σ _SS =− _S −

sehingga ( )

( )

( ) ( )

(

)

( ) ( )( )

(

(

( )

)

)

( )

. 1 2 1 lim 0 0 0 0 0 0 0 0 0 2 2 0 0 K r g t s K t s r g V V t s r g V S

f _{SS S}

t s S = − − − − = − − = → σ

Dari persamaan (3.15) didapat

( )

, ₀= ₀

(

, ₀, ₀ , ₀

)

≥0

Ασ rV F SV V_SV_SS .

Ini mengakibatkan

( )

(

)

( )

( )

(

( )

*

)

0

2 * , * ₂ 0 2 0 0 0

0 ≥ >

t s f K r g t t s V _SS σ ,

sehingga V₀SS

(

s₀

( )

t*,t*

)

>0.

Nilai V₀SS

(

s₀

( )

t*,t*

)

>0 , maka

( )

(

)

(

( )

)

(

( )

)

. 0 * , * * , * * ,

* 0 0

0

>

−

=V s t t V st t

t t s

eSS SS SS

Menurut uji turunan kedua, karena

( )

(

s0 t*,t*

)

=0

eS dan eSS

(

s0

( )

t*,t*

)

>0 maka

e

(

s0

( )

t*,t*

)

mempunyai nilai

minimum lokal pada

(

s₀

( )

t*,t*

)

. Artinya fungsi e akan terus naik pada suatu harga tertentu, yaitu S yang nilainya lebih besar dari s0

( )

t* , dan karena waktu yang berlaku dalam D adalah t∈

(

0,T

]

, maka e akan mempunyai nilai maksimum yang positif. Hal ini kontradiksi dengan pernyataan dari definisi

( )

S t

e , tidak akan punya nilai maksimum yang positif pada

D

. Jadi haruslah s

( )

t ≤s0

( )

t untuk t∈

(

0,T

]

. Batas atas dari eksekusi awal opsi ini berhubungan dengan batas bawah harga opsinya V0.

3.6.2 Penentuan Batas Bawah Eksekusi Awal Opsi Tipe Amerika

Dalam bahasan penentuan batas atas opsi Amerika (3.4.2), diasumsikan

( )

(

( )

)

(

]

{

S t S s t X t T

}

D= , : ∈ ₁ , , ∈ 0, , dan diasumsikan juga

( )

S t V

( ) ( )

S t V S t e , = 1 , − , . Maka

( )

, ≤0

Ασ re , ∀S⊂D dan t>0, e

( )

S, t tidak mempunyai nilai minimum yang negatif. Jikas1

( ) ( )

t ≤st maka e

(

s1

( )

t,t

)

≥0. Untuk

membuktikannya, pertama asumsikan ada t* yang mengakibatkan s1

( ) ( )

t* >st* dan juga mengakibatkan

( )

(

)

(

( )

)

(

( )

)

( )

1 0. 1 * , * * , * * ,

* 1 1

1 = − − − = −

=V s t t V st t

t t s

e_{S S S}

Dengan adanya syarat batas

( )

(

₁ *, *

)

₁

( )

* 1 s t t K s t

V = − ,

maka

( )

(

₁ *, *

)

0 1 s t t =

Vt .

Jadi bentuk persamaan (3.21) menjadi

( )

( )(

)

0.

2 1 1 1 1 0 2 2 1 1 1 = − + ≡ Α V SV r g V S f V S SS BSB _σ Ini berarti:

( )

1 1

( )(

1 1

)

2 2 1 2 1 V SV r g V S

f σ _SS =− _S − . Sehingga ( )

( )

( ) (

)

( ) ( )

( ) ( )

(

( )

)

( )

. 1 2 1 lim 1 1 1 1 1 1 1 1 2 2 1 1 K r g t s K t s r g V V S r g V S

f SS S

t s S = − − − − = − − = → σ

Dari persamaan (3.17) di atas terlihat bahwa

(

, ₁, ₁ , ₁

)

0 1

1 = ≤

Jadi

( )

(

)

( )

( )

(

( )

*, *

)

0

2 *

,

* ₂

1 2 1

1 1

1 ≤ >

t t s f

K r g t

t s V_SS

σ ,

sehingga V1SS

(

s1

( )

t*,t*

)

<0.

Nilai V1SS

(

s1

( )

t*,t*

)

<0, maka:

( )

(

)

(

( )

)

(

( )

)

. 0

* , * *

, * *

,

* 1 1

1

<

−

=V s t t V st t

t t s

eSS SS SS

Menurut uji turunan kedua, karena

( )

(

s1t*,t*

)

=0

e_S dan eSS

(

s1

( )

t*,t*

)

<0 maka

e

(

s₁

( )

t*,t*

)

mempunyai nilai maksimum lokal pada

(

s₁

( )

t*,t*

)

. Artinya fungsi e akan turun pada suatu harga tertentu, yaitu semua S yang nilainya lebih

kecil dari s₁

( )

t* , dan karena waktu yang berlaku dalam D adalah tertutup, maka e akan mempunyai nilai minimum yang negatif. Hal ini kontradiksi dengan pernyataan dari definisi e

( )

S,t tidak akan punya nilai minimum yang negatif pada D. Jadi haruslah

( ) ( )

t st

s1 ≤ . Batas bawah dari eksekusi awal opsi ini berhubungan dengan batas atas harga opsinya V1. Sehingga batas eksekusi awal dari opsi up and out put Amerika terletak pada:

( )

t s

( )

t s

( )

t s1 ≤ ≤ 0 .

IV PENENTUAN BATAS-BATAS DELTA

Pada Bab ini, akan dibahas mengenai penentuan batas dari delta. Manfaat menggunakan suatu opsi dalam dunia finansial adalah untuk:

1. Spekulasi menentukan keuntungan atau kerugian.

2. Pengendalian resiko (hedging) yang ditimbulkan oleh adanya transaksi dari opsi.

Delta adalah salah satu parameter penting dalam penilaian opsi dan hedging.

4.1 Pengertian Delta

Delta

( )

VS adalah tingkat perubahan rata-rata nilai opsi

( )

V terhadap harga aset yang mendasari

( )

S , yang dirumuskan sebagai

S V V_S

∂ ∂

= . (4.1)

Delta merupakan kemiringan dari kurva hubungan antara nilai opsi dengan harga underlying asset (misalkan saham).

Untuk mengetahui peranan delta untuk mengendalikan resiko (hedging), perhatikan ilustrasi berikut yang dikutip dari Hull (2003).

Ilustrasi

Asumsikan delta untuk opsi call adalah 0.6. Ini berarti ketika harga saham berubah dengan perubahan jumlah yang kecil, maka nilai opsi berubah 60% dari jumlah tersebut. Misalkan harga saham

( )

S adalah =$100 dan nilai opsi

( )

V adalah =$10.

Misalkan saja investor menjual 20 kontrak opsi (1 kontrak opsi adalah 100 saham), dan membeli 2000 saham.

Posisi investor setelah di hedging untuk membeli saham adalah 0.6×2000=1200, artinya sebelum membeli 2000 saham sebaiknya membeli 1200 saham dahulu. Resiko (untung dan rugi) dari posisi opsi dapat diimbangi dengan untung rugi dari posisi saham.

Untuk lebih jelasnya perhatikan ilustrasi berikut.

Jika harga saham naik sebesar $1, maka akan mendapat keuntungan $1200 dalam pembelian saham, nilai opsi akan meningkat menjadi

6 . 0 $ 1 $ 6 .

0 × = pada kontrak opsi, maka investor akan rugi sebesar $0.6×2000=$1200. Jika harga saham turun sebesar $1, maka investor akan rugi sebesar $1200 dalam pembelian saham. Dan nilai opsi turun sebesar

6 . 0 $ 1 $ 6 .

0 × = pada kontrak opsi, maka investor akan mendapat keuntungan sebesar

1200 $ 2000 6 . 0

$ × = .

Dari ilustrasi di atas dapat dilihat bahwa investor tidak mengalami kerugian ataupun keuntungan walaupun harga saham naik dan turun.

Untuk opsi call Eropa, delta call didapat dengan menggunakan nilai opsi call dalam Teorema 5, sehingga diperoleh teorema berikut.

Teorema 8

Nilai delta untuk opsi call diberikan oleh

( )

d1 N

dengan N

( )

d1 adalah fungsi sebaran normal kumulatif seperti persamaan (2.21) dan

dengan ln

(

/

)

(

/2

)

(

)

. 2 1 t T t T r K S d − − + + = σ σ (Hull 1997) Bukti dapat dilihat pada Hull (1997) dan Bahri (2005).

Delta untuk opsi call nilainya selalu positif, yaitu 0≤V_SC ≤1. Ini dikarenakan peningkatan harga underlying asset akan mempengaruhi peningkatan opsi call, sehingga dapat dimengerti bahwa meningkatnya underlying asset akan meningkatkan peluang nilai payoff positif.

Sedangkan opsi put tipe Eropa, delta put didapat dengan menggunakan Teorema 6, sehingga didapatkan teorema berikut.

Teorema 9

Nilai delta untuk opsi put diberikan oleh

( )

₁ −1

=N d

V_SP (4.3) dengan N

( )

d1 adalah fungsi sebaran normal kumulatif seperti persamaan (2.21) dan dengan

(

)

(

)

(

)

, 2 / / ln 2 1 t T t T r K S d − − + + = σ σ (Hull 1997) Bukti dapat dilihat pada Hull (1997) dan Bahri (2005) .

Delta untuk opsi put nilainya selalu negatif, yaitu −1≤V_SP≤0.

4.2 Penentuan Batas Delta

Delta berhubungan positif dengan nilai opsi dan merupakan suatu teknik untuk melakukan hedging, untuk itu batas-batas dari nilai delta perlu diketahui.

Sebelum menentukan batas-batas dari delta, terlebih dahulu asumsikan bahwa opsi yang digunakan adalah opsi call tipe Eropa. Selanjutnya asumsikan juga bahwa σ dan r masing-masing adalah konstan atau hanya tergantung dari t saja.

Diketahui persamaan Black-Scholes untuk nilai opsi adalah sebagai berikut:

(

)

( )

( )

( )

, 0.

, ,

2 1

, 2 2

= + − + ≡ Η t S SS V V t S r SV t S r V S t S V r σ σ

Dengan menurunkan persamaan di atas terhadap S, maka didapat persamaan Black Scholes yang memenuhi delta, yaitu sebagai berikut:

( )

0 2

1

, 2 2 2

= + − + + + ≡ Η tS S SS S SSS SS S V rV rSV rV V S SV V

r σ σ

σ

Notasikan VS =δ

( )

S,t dan

( )

σ,r =Μ

( )

σ,r

Η . Sehingga persamaan di

atas menjadi

( )

( )

0.

2 1 0 2 1 , 2 2 2 2 2 2 = − + + = = + − + + + ≡ t S SS t S SS S S r S r rS r S S r M δ δ σ δ σ δ δ δ δ δ σ δ σ δ σ (4.4)

Syarat awal dari persamaan di atas adalah

( )

⎩ ⎨ ⎧ > < = . , 1 , 0 0 , K S K S S

δ (4.5)

Selama solusi dari persamaan Black Scholes untuk σ dan r yang berada dalam pertidaksamaan (3.2) dan (3.3), dan selama nilai opsi berada dalam batas seperti pada pertidaksamaan (3.4), serta nilai

( )

t V

( )

t

V0 0, = 10, dan V0

( )

X,t =V1

( )

X,t , maka

( )

( )

( )

(

,

)

(

,

)

(

,

)

. , , 0 , 0 , 0 0 1 1 0 t X V t X t X V t V t t V S S S S ≤ ≤ ≤ ≤ δ δ

Jika nilai dari V0 dan V1 dapat dihitung, maka nilai turunannya juga dapat diketahui nilainya. Setelah mengetahui model persamaan untuk delta yaitu seperti pada persamaan (4.4), selanjutnya akan ditunjukkan batas-batas dari nilai delta,