BAB VI INTEGRAL LIPAT DUA DAN TIGA

1 BAB VI

INTEGRAL LIPAT DUA DAN TIGA

y

yi + yi D i y1

[image:1.595.124.321.134.262.2]

X x1 x1 + xi

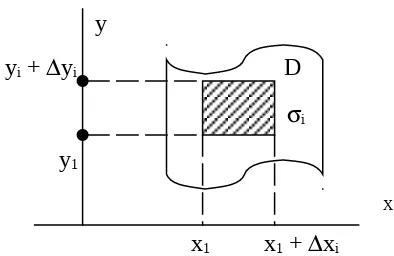
Gambar di atas adalah daerah D pada bidang xy dan i adalah elemen kecilnya.

i i i x y

 _{, jika diambil jumlah elemen buah, maka daerah D seluruhnya}

dinyatakan dengan : ~



;





0 ; 0



~ lim

1

  

   





 i i

i

i i i i

n f x y x y x y

Limit ini bila ada dilambangkan :







D

dy dx y x

f , _{(Integral lipat dua = double integral)}

Dalam penyelesaiannya :











 

   

    

D

y

y

x

x

dx dy y x f dx

dy y x f

2 1

2 1

, ,

Dalam hal ini pertama diintegralkan terhadap y sementara x dianggap konstan, selanjutnya di integrasikan terhadap x.

x1 = batas kiri dan, x2 = batas kanan y1 = batas bawah, y2 = batas atas

Contoh : Hitunglah integral :

 



 





1

0 0

2

x

x x y

y

dx dy xy I

Solusi : 













1

0

1

0 5 2 1 0

2 2 1

12 1

2

dx x dx

xy I

x y

y

I

y

= x2

y

x y = x2

1

1 2

0

Jika terhadap x lebih dulu diintegral, maka :

Untuk : y = x2 _{diperoleh : x = y batas kiri dan batas kanan : x = 1.} Untuk y dimana batas bawah y = 0 dan batas atas y = x2 _{= 1.}

Sehingga bentuk integral yang baru dengan batas baru dituliskan :























 











1

0

1

0

1

0

2 2

1 1

2 1 1

12

1

I

y

y

y

y

x

y x x

y x

dy

y

y

dy

x

y

dy

dx

xy

Contoh : Buat sketsa dari daerah Dxy oleh f(x,y) = xy dalam bidang xy yang dibatasi oleh : y = x2 _{; x = 2 dan y = 1. Hitung integralnya.}

Solusi :

Dari sketsa dapat dilihat x1 = 1 dan x2 = 2

y1 = 1 dan y2 = x2 jadi bentuk integralnya :











 









2

1 1

2

1

2

1

2 1 5

2 1 x

1 2 2 1

2 ₂

4

I

x x y

dx

x

x

dx

xy

dx

dy

xy

Transformasi dari integral lipat dua.

Dalam menghitung integral lipat atas suatu daerah D sering lebih mudah jika dipakai koordinat lain dari pada koordinat kartesian.

Misalnya : Titik (x,y) pada bidang xy ke titik (u,v) pada bidang uv dan daerahnya dari D menjadi D1, maka persamaan transforamsi : x = f(u,v) dan y = f(u,v).

Maka :



 



 















D D

dv

du

v

u

y

x

v

u

G

dy

dx

y

x

F

J

1

,

,

,

,

Dimana :



u,v



F



f



u,v

 

,g u,v





dan Jacobian dari xdan y terhadapu danvadalah:



























































y

x

v

u

v

u

y

x

juga

berlaku

atau

v

y

u

y

v

x

u

x

v

u

y

x

J

J

J

,

,

,

,

:

det

,

,

Contoh : Transformasi koordinat kartesian (x,y) ke dalam koordinat polar (r, ). Solusi : Persamaan transformasi koordinat

x = r cos  y = r sin 

x y tg x y arctg y

x

r_ 2_ 2_{;  } 1

Jadi : cos sin

  

 

r y r

x

 



 sin rcos

y r

x

   

 



Sehingga :

r

r

r

y

r

y

x

r

x

r

y

x

J



















































sin

cos

sin

cos

det

det

,

,

maka :















     

D D

d dr r

y x r

G dy

dx y x

f

J

1 ,

, ,

, 

 

















D D

d dr r r G dy

dx y x f

1

,

,  

Contoh : Hitung x y dxdy

D

y D

0 r₁

r₂ x



2 

0 1 2 3 r

D

1

Solusi :

x2 _{+ y}2 _{= r}2 _{, maka r1}2 _{= 4 ;  r1 = 2} r22 _{= 9 ;  r2 = 3}

x2 _{+ y}2 _{= r}2 _{persamaan lingkaran dengan pusatnya pada (0,0)} r1 = 2 dan r2 = 3

1 = 0 dan 2 = 2 

Jadi :





 



 





1

2

0 3

2 2 2

2

3 38

D D

d dr r d

dr r r dy dx y x



 



Besaran Fisika Sebagai Integral Lipat Dua. Titik pusat dan momentum Inersia Luasan. Jika : f(x,y) = 1 ; 









_{ } 



  



 

2 1

d dr r dy

dx A

D

Maka titik pusat suatu daerah datar dengan luas :









D D

hubungan memenuhi

dy dx dA

A :

Mx y A dan My x

A    _{atau :}











 

D D D

x

y x dA x dA dan Y ydA M

M

Momen inersia daerah D terhadap sumbu-sumbu koordinat :









D D

y

x y dA dan I x dA

I 2 2

Momen inersia polar (momen inersia terhadap garis yang lewat titik dan tegak lurus bidang luasan) suatu daerah datar D :











 



 

 

D D

y

x I x y dA x y dydx

I

I 2 2 2 2

0

Contoh :

y

0

y = x

y = 6x – x2 (5, 5)

5 D

x

z

0

x

y z v

y x

x Solusi :

Titik potong : y = 6x – x2 _{dan y = x adalah} 6x – x2 _{= x  x = 0 dan x = 5} Maka :

 



 

5

0 6 2

6 125

x x

x

dx dy A



 



 



5

0 6 2

12 625

x x

x

y xdA xdydx

M





 



 



5

0 6 2

6 625

x x

x

x ydA ydydx

M

Jadi :

2 5 125

6 12 625

   

A M

x y

5 125

6 6 625

   

A M y x

maka koordinat titik pusat : (5/2, 5). Integral Lipat Tiga

Perhatikan gambar v = x y z = lemen volume Untuk v dalam jumlah n buah dinyatakan V yaitu :









   

lim_~ ~ , ,

1

i

i i i i i i

n f x y z x y z

v







v

dz dy dx z y x f , ,

Contoh : Hitunglah :



1

0 3

2 2

0

dz dy dx xyz

Solusi :

dz dy yz x dz

dy dx

xyz







1

0 3

2 2

0 2 2 1 1

0 3

2 2

0

I





yz dy dz 



y z dx 1

0 3

2

1

0

3

2 2 2

1

I

2 2





  

1

0

2 1 1

0 2 2

1 ₂

5

5 z dz z

I

Hitunglah :



2

0 1

0 2

0

2_sin











dz d d

z

Solusi :

















 

d d z

d d dz

z sin 2 2sin

0 1

0 2

0 2 2 1 2

0 1

0 2

0

2

I











3

2

cos

3

2

sin

2

2

0 2

0

1

0 3 1

I

I













 









d

Transformasi dari Integral Lipat Tiga

P(x,y,z)  (r,,z) z

x r

y 

P(x,y,z)  (r,,) z

x

y r





w

z

v

z

u

z

w

y

v

y

u

y

w

x

v

x

u

x

w

v

u

z

y

x

J



















































det

,

,

,

,

dan















  

  

v v

dw dv du w v u

z y x w

v u G dz

dy dx z y x

f

J

1 , ,

, , ,

, ,

,

Transformasi pada Koordinat Silinder

Dalam hal ini :

x = r cos ; y = r sin  z = z

maka :

dz

d

dr

r

dz

dy

dx

dv

maka

r

r

r

z

r

z

y

x

J



































1

0

0

0

cos

sin

0

sin

cos

det

,

,

,

,

Jadi :















v v

dz d dr r z r G dz

dy dx z y x f

1

, , ,

,  

Transformasi pada Koordinat Bola

M r(x_k,y_k,z_k)

y x

z

maka : 

 

  

 



  

 





 sin

0 sin

cos

cos sin sin

cos sin

sin

sin sin cos

cos cos

sin det ,

, ,

, _r2

r

r r

r r

r z y x

J





 

   

 

Maka : dv = dx dy dz = r2 _{sin  dr d d}

Jadi :















v v

d d dr r

r G dz

dy dx z y x f

1

sin ,

, ,

, _{ } 2 _{  }

Besaran Fisika Sebagai Integral Lipat Tiga

Titik pusat dan momen inersia suatu volume. Tinjau f(x,y,z) = (x,y,z) adalah massa benda menempati volume v. Maka massa M =  dv.

Perhatikan gambar : L = sumbu ; r = jarak

Maka momen inersia terhadap L.



  

v

dv r

M r

I 2 2 

Hal-hal khusus : Jika :







 

  



v

z x y dv

I maka y

x r z

sb

L 2 2 2_{, :} 2 2 







 

  



v

x y z dv

I maka z

y r x

sb

L 2 2 2_{, :} 2 2 







 

  



v

y x z dv

I maka z

x r y

sb

L 2 2 2_{, :} 2 2 

Momen massa M terhadap bidang :







 



v v

xz v

xy

yz x dv M z dv M y dv

M  ;  ; 

maka koordinat pusat massa (x,y,z) adalah :

M M z M M y M

M

x yz xz yz

 

z

z = 2

x

y Contoh :

Cari koordinat titik pusat volume di dalam silinder :  = 2 cos , yang dibatasi di atas oleh parabolaid : z = 2 _{dan di bawah oleh bidang z = 0.} Solusi :

Dalam hal ini r =  = jari-jari, maka dari gambar maka :

Volume :

  



2

0 cos 2

0 0

2

2



 

   dz d d v

 



2

0 cos 2

0 3 2

 _







d d v







2

0

2 3 4

cos 8









d v













 v

yz x dv dz d d

M

2

0 cos 2

0 2

0

2 cos

2

  











Maka :

3 4 2

2

3 

 

 

M M x yz

Karena sumbu simetri : y 0











  

3 5

2 2

0 cos 2

0 2

0

2

 









zdv







dzd d M

v xy

9

10

2 3

3 5









z

Jadi koordinat pusat massa :    

 

9 10 , 0 , 3 4

Contoh :

Tentukan massa dan pusat massa suatu tabung pejal S, dengan menganggap kerapatan sebanding terhadap jarak dari alas ( = k z) dengan k = konstanta dan f(x,y,z) = kz.

S z

x

y z = h

x2 _{+ y}2 _{= a}2 Perhatikan gambar : x2 _{+ y}2 _{= a}2

Dari gambar dapat dilihat bahwa massa benda tersebut dapat dinyatakan :











v

dv z y x f

m , ,





d dr dz r z k

m

h a









0 0 2

0

2 2 2

1_{k h a}

m 

Sumbunya sb z, maka :











 

2

0 0 0 2 a h

v

xy z dv k z rdz dr d

M

2 3

3 1

a h k M_xy  

maka :

h a

h k

a h k m

M

z xy

3 2 2 2 2 1

2 3 3 1

 







Jadi : massanya : m21k h2 a2 pusat massanya :

2

3

h

Soal – soal :

1. Hitunglah





x y



dydx



 4

1 2

1

2

2. Hitunglah fungsi _f



_x,y



_x2_y2

 terhadap daerah yang dibatasi oleh garis-garis : y = 1 ; y = 2 dan x = y , x = 0

3. Dengan memakai transformasi : x + y = u dan y = uv, tunjukkan bahwa :

 



₁



2 1

1

0 1

0

  





 _{dydx e}

e

4. hitunglah

 



 5

2 3

0 2

4

x x

y

dx dy dz

5. Hitunglah volume dari D yang dibatasi oleh silinder z = 4 – x2 _{dan bidang-bidang} x = 0, y = 0 dan z = 0, y = 6

6. Dengan menggunakan koordinat silinder, hitunglah volume daerah D yang terletak di dalam _r2 _16_{, di atas z = 0, di bawah 2z = y}

7. Hitunglah integral lipat tiga





r r

F ,, 1 pada daerah D dalam oktav pertama

yang dibatasi oleh kerucut :

4



 _dan arctg2 _{dan bola} r 6

8. Carilah titik pusat luasan yang dibatasi parabola-parabola : _{y2x x}2 _dan x

x y _3 2 _ 6