Penjadwalan Pengawas Ujian Menggunakan Goal programming: Studi Kasus di Departemen Matematika FMIPA IPB

(1)

PENJADWALAN PENGAWAS UJIAN MENGGUNAKAN

GOAL PROGRAMMING: STUDI KASUS DI

DEPARTEMEN MATEMATIKA

FMIPA IPB

MIRA AISYAH ROMLIYAH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Penjadwalan Pengawas Ujian Menggunakan Goal Programming: Studi Kasus di Departemen Matematika FMIPA IPB adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Oktober 2014

Mira Aisyah Romliyah

(4)

ABSTRAK

MIRA AISYAH ROMLIYAH. Penjadwalan Pengawas Ujian Menggunakan Goal Programming: Studi Kasus di Departemen Matematika FMIPA IPB. Dibimb ing oleh FARIDA HANUM dan TONI BAKHTIAR.

Penjadwalan pengawas ujian telah umum dilakukan dengan cara konvensional. Pada karya ilmiah ini, waktu ujian, banyaknya mata kuliah, ketersediaan ruangan, banyaknya peserta ujian, dan ketersediaan pengawas ujian merupakan komponen yang berkaitan dengan pelaksanaan ujian. Untuk mengatasi kelemahan metode penjadwalan secara konvensional diadopsi metode penjadwalan pengawas menggunakan pendekatan operation research/management science

(OR/MS). Goal programming adalah salah satu metode yang bisa diterapkan. Pada karya ilmiah ini digunakan metode nonpreemptive goal programming untuk memformulasikan masalah, di mana dua macam kendala ditinjau, yakni hard dan

soft constraint. Hard constraint harus terpenuhi dan soft constraint adalah kendala tambahan yang harus dipenuhi semaksimal mungkin. Dalam kerangka masalah ini, penyimpangan soft constraint dari tingkat idealnya diminimumkan. Model kemudian diaplikasikan pada masalah penjadwalan pengawas ujian di Departemen Matematika FMIPA Institut Pertanian Bogor.

Kata kunci: goal programming, nonpreemptive goal programming, penjadwalan

ABSTRACT

MIRA AISYAH ROMLIYAH. Scheduling of Exam Invigilators Using Goal Programming: Case Studies at Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University. Supervised by FARIDA HANUM dan TONI BAKHTIAR.

Scheduling of exam invigilators has been commonly done in conventio na l manner. In this activity, exam period, the number of courses, availability of rooms, the number of examinees, and availability of invigilators are components which relate to exam execution. To overcome the limitation of the conventio na l scheduling method, we adopt the scheduling method by using operation research/management science (OR/MS) approaches. Goal programming is one of methods that can be applied. In this work, we used nonpreemptive goal programming method to formulate the problem, where we consider two types of constraint, namely hard and soft constraints. The former must be fulfilled and the later are additional constraints which should be satisfied as closely as possible. In this framework, we aim to minimize deviations of soft constraints from their ideal level. The model has been applied to the problem of scheduling the invigilator at Department Mathematics Faculty of Mathematics and Natural Sciences Bogor Agricultural University.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PENJADWALAN PENGAWAS UJIAN MENGGUNAKAN

GOAL PROGRAMMING: STUDI KASUS DI

DEPARTEMEN MATEMATIKA

FMIPA IPB

MIRA AISYAH ROMLIYAH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

Judul Skripsi : Penjadwalan Pengawas Ujian Menggunakan Goal Programming: Studi Kasus di Departemen Matematika FMIPA IPB

Nama : Mira Aisyah Romliyah NIM : G54100029

Disetujui oleh

Dra Farida Hanum, MSi Pembimbing I

Dr Toni Bakhtiar, MSc Pembimbing II

Diketahui oleh

Dr Toni Bakhtiar, MSc Pembimbing II

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala nikmat, rahmat, karunia, dan pertolongan yang telah diberikan sehingga karya ilmiah ini berhasil diselesaikan. Judul karya ilmiah ini adalah Penjadwalan Pengawas Ujian Menggunakan Goal Programming: Studi Kasus di Departemen Matematika FMIPA IPB. Penyusunan karya ilmiah ini tidak lepas dari bantuan beberapa pihak. Oleh karena itu, penulis mengucapkan terimakasih kepada:

1 Allah SWT atas segala rahmat dan karunia-Nya,

2 Nabi besar Muhammad SAW sebagai nabi akhir zaman,

3 keluarga tercinta: Ibunda Ai Maryam dan Ayahanda Naiman, serta kedua adik saya Fakhri dan Malki yang selalu memberikan doa, motivasi dan kasih sayang tiada henti,

4 beasiswa dikti BIDIK MISI yang telah memberikan bantuan materiil dan sarana untuk mengembangkan softskill selama perkuliahan,

5 Ibu Dra Farida Hanum, MSi, dan Bapak Dr Toni Bakhtiar, MSc selaku dosen pembimbing, terima kasih atas segala kesabaran, ilmu, saran dan motivas inya selama membimbing menulis, serta Bapak Ruhiyat, SSi MSi selaku dosen penguji,

6 staf tata usaha Departemen Matematika IPB,

7 keluarga Hadeers tercinta Mezi, Lola, Amel, Wilda, Deni, Ayu, Indah, Yani, Mutia dan keluarga Arundina yang telah memberikan motivasi, bantuan, keceriaan, dan arti sahabat juga keluarga bagi penulis,

8 sahabat-sahabat penulis Leny, Novia, Yuli, Vina, Kiki Septiani, Nindya, Atika, Lusi, Ikhsan, Jepri, Fahmi, Agung, Rahma, terima kasih atas semangat, motivasi, dan doanya, Irfan Chahyadi yang telah membantu dalam mempelajari software LINGO 11.0, serta Miftakhul Huda atas kasih sayang, doa, semangat, dan kebersamaannya selama ini,

9 teman-teman satu bimbingan: Ale, Putri, Vivi, Fikri yang senantiasa saling mengingatkan dan memberikan motivasi dalam penyusunan karya ilmiah ini, 10 teman-teman mahasiswa Matematika 47, PSDM Gumatika 2011/2012 dan

BUMI Gumatika 2012/2013 terimakasih atas doa, semangat, serta kebersamaannya selama ini,

11 semua pihak yang telah membantu dalam penyusunan karya ilmiah ini, terima kasih.

Bogor, Oktober 2014

(9)

DAFTAR ISI

DAFTAR LAMPIRAN viii

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 1

TINJAUAN PUSTAKA 1

Nonpreemptive Goal Programming 1 MODEL PENJADWALAN PENGAWAS UJIAN DI DEPARTEMEN

MATEMATIKA FMIPA IPB 3

Deskripsi Masalah 3

Model Matematika 4

IMPLEMENTASI MODEL 7

Skenario 1 7

Skenario 2 14

HASIL DAN PEMBAHASAN 15

Skenario 1 15

Skenario 2 19

SIMPULAN 24

DAFTAR PUSTAKA 25

LAMPIRAN 26

(10)

DAFTAR LAMPIRAN

1 Sintaks Komputasi LINGO 11.0 untuk menyelesaikan Skenario 1 26

2 Hasil Komputasi LINGO 11.0 untuk Skenario 1 29

3 Sintaks komputasi LINGO 11.0 untuk menyelesaikan Skenario 2 33

(11)

PENDAHULUAN

Latar Belakang

Dalam perkembangannya masalah penjadwalan staf atau pekerja telah banyak dibahas dalam berbagai masalah kehidupan sehari-hari, seperti penjadwalan pekerja pada pelayanan publik, dan tak terkecuali dalam bidang pendidikan. Sistem pendidikan tidak terlepas dari ujian tertulis sebagai evaluasi belajar dalam kurun waktu tertentu. Setiap ujian tersebut perlu adanya pengawas untuk menjaga kejujuran peserta ujian.

Beberapa komponen yang berkaitan dengan ujian tertulis selain pengawas di antaranya ialah: waktu ujian, mata kuliah, ruangan, dan banyaknya peserta ujian. Dalam hal peserta ujian, semakin banyak peserta ujian maka semakin banyak pula pengawas ujian dan ruangan yang dibutuhkan. Selain itu, akan terdapat juga kendala-kendala atau batasan-batasan lain mengenai pengawas ujian tersebut, sehingga perlu strategi dalam penjadwalan pengawas ujian.

Penjadwalan ujian sering kali dibuat secara konvensional dengan mencoba beberapa kemungkinan yang ada. Dengan cara seperti itu biasanya aturan-atura n yang ada tidak semua terpenuhi dan terkadang tidak sesuai dengan keinginan dari pengawas itu sendiri. Kelemahan lain yang mungkin terjadi dengan jadwal konvensional ialah tidak meratanya jumlah tugas mengawas ujian untuk para pengawas. Atas dasar itulah dibuat penjadwalan pengawas ujian dengan suatu metode berlandaskan pemrograman linear untuk memperbaiki berbagai aspek kekurangan jika penjadwalan dilakukan secara konvensional.

Permasalahan penjadwalan pengawas ujian ini dengan studi kasus di Departemen Matematika FMIPA IPB pada ujian akhir semester ganjil tahun 2013/2014 akan dimodelkan sebagai masalah goal programming.

Tujuan Penelitian

Karya ilmiah ini disusun dengan tujuan memodelkan masalah penjadwalan pengawas ujian menggunakan metode nonpreemptive goal programming serta mengaplikasikannya pada masalah penjadwalan pengawas ujian di Departemen Matematika FMIPA IPB.

TINJAUAN PUSTAKA

Nonpreemptive Goal Programming

(12)

Seperti yang telah disebutkan, goal programming merupakan perluasan pemrograman linear, sehingga seluruh asumsi, notasi, formulasi model matematis, prosedur perumusan model dan penyelesaiannya tidak berbeda. Letak perbedaannya yaitu pada goal programming terdapat sepasang variabel deviasi yang akan muncul di fungsi tujuan/goal dan di fungsi- fungsi kendala. Sepasang variabel tersebut ialah �− dan �+ yang taknegatif.

Ada beberapa komponen dalam model goal programming di antaranya ialah: 1 variabel keputusan (decision varible): sama seperti pada pemrograman linear yang merupakan nilai-nilai yang tidak diketahui yang berada di bawah kontrol pengambilan keputusan, yang berpengaruh terhadap solusi permasalahan dan keputusan yang diambil.

2 variabel deviasi,

3 kendala sistem: kendala yang identik dengan kendala pada pemrograman linear tanpa disertai deviasinya,

4 kendala goal: terdapat nilai- nilai target yang harus terpenuhi dan disertai dengan deviasinya,

5 fungsi objektif (objective function): minimisasi penyimpangan atau minimisas i variabel deviasi (Sarker dan Newton 2008).

Variabel deviasi berfungsi untuk menampung penyimpangan atau deviasi yang akan terjadi pada nilai ruas kiri suatu persamaan kendala terhadap nilai ruas kanannya. Agar deviasi itu minimum, artinya nilai ruas kiri suatu persamaan kendala sebisa mungkin mendekati nilai ruas kanannya, maka variabel deviasi itu harus diminimumkan dalam fungsi tujuan/goal. Variabel tersebut dibedakan menjadi dua, yaitu variabel deviasi untuk menampung deviasi yang berada di bawah sasaran yang dikehendaki, dengan kata lain untuk menampung deviasi negatif yang dinotasikan dengan �−, dan variabel deviasi untuk menampung deviasi yang berada di atas sasaran, dengan kata lain untuk menampung deviasi positif, yang dinotasika n dengan �+.

Secara umum terdapat dua macam metode untuk menyelesaikan goal programming yaitu nonpreemptive goal programming dan preemptive goal programming. Metode preemptive goal programming yaitu metode goal programming dengan mengurutkan prioritas goal dari yang paling penting hingga tujuan/goal yang tidak terlalu penting, sedangkan metode nonpreemptive goal programming yaitu metode goal programming dengan pembobotan. Kedua metode tersebut sama-sama menggabungkan tujuan banyak menjadi tujuan tunggal. Secara umum keduanya tidak menghasilkan solusi yang sama (Taha 1975).

Dalam metode nonpreemptive goal programming atau pembobotan, fungs i objektifnya merupakan penjumlahan dari nilai deviasi yang masing- masing telah diberikan bobot. Pemberian bobot disesuaikan dengan prioritas goal yang ingin dicapai. Jika goal semakin penting maka diberikan bobot yang lebih besar, dan berlaku untuk sebaliknya. Namun, penentuan nilai dari setiap bobot bersifat subjektif (Winston 2004).

(13)

Fungsi objektif:

min ∑ � ,

dengan � merupakan variabel deviasi dari goal ke-� yang ingin dicapai yang dapat berupa variabel deviasi negatif �− dan variabel deviasi positif �+, sedangkan parameter merupakan bobot yang akan diberikan untuk setiap variabel deviasi.

Secara umum terdapat tiga kemungkinan tujuan/goal yang ingin dicapai yaitu:

1 ,

2 ,

3 = ,

dengan variabel ialah variabel keputusan untuk model nonpreemptive goal programming ini.

Setelah diberi variabel deviasi, maka tiga kemungkinan goal tersebut secara berturut-turut diubah menjadi kendala tambahan (soft constraint) ialah sebagai berikut:

1 + �−− �+ = , dan nilai dari �− diminimumkan, 2 + �−− �+ = , dan nilai dari �+ diminimumkan, 3 + �−− �+ = , dan nilai dari �+ + �−diminimumkan.

Sedangkan bentuk umum kendala utama (hard constraint) goal programming ini ialah sebagai berikut:

, ∀ dan ∀ , , ∀ dan ∀ ,

= , ∀ dan ∀ (Sarker dan Newton 2008).

MODEL PENJADWALAN PENGAWAS UJIAN DI

DEPARTEMEN MATEMATIKA FMIPA IPB

Deskripsi Masalah

Masalah yang dibahas dalam karya ilmiah ini ialah masalah penjadwalan pengawas ujian di Departemen Matematika FMIPA IPB. Departemen Matematika FMIPA IPB mengampu dua program studi, yaitu program S1 dan S2. Masa ujian kedua program studi tersebut biasanya di pekan yang sama. Karena keterbatasan kapasitas ruangan, maka ujian untuk satu mata kuliah dapat saja diselenggarakan di beberapa ruangan sekaligus (kelas paralel).

(14)

Asumsi yang digunakan dalam memodelkan masalah penjadwalan pengawas ini ialah:

1 waktu pelaksanaan ujian sudah ditentukan sebelum memodelkan permasalaha n penjadwalan,

2 ruangan sudah ditentukan sebelumnya sesuai dengan jumlah peserta,

3 mahasiswa asisten selalu bisa mengawas ujian pada mata kuliah yang bersangkutan.

Penjadwalan pengawas ujian umumnya memiliki aturan-aturan tertentu yang mungkin berbeda untuk satu institusi dengan institusi lainnya. Aturan dari penyelenggara ujian itu sendiri dapat dinyatakan sebagai kendala utama (hard constraint), sedangkan tambahan kendala yang tidak harus selalu terpenuhi dirumuskan ke dalam kendala tambahan (soft constraint/goal).

Berikut ini diberikan aturan-aturan dalam memodelkan masalah penjadwalan pengawas ujian di Departemen Matematika FMIPA IPB. Aturan umum penjadwalan pengawas ujian di Departemen Matematika FMIPA IPB yang harus dipenuhi (hard constraint) ialah:

1 setiap pegawai hanya mengawas satu ujian dalam satu waktu,

2 satu pengawas ujian mengawasi maksimal 25 mahasiswa peserta ujian,

3 setiap ujian mata kuliah program studi S1 diawasi oleh 1 orang pegawai dan pengawas mahasiswa yaitu asisten mata kuliah (untuk mata kuliah yang memiliki asisten) atau mahasiswa bukan asisten,

4 mahasiswa tidak boleh mengawas mata ujian S2 (hanya pegawai saja),

5 agar tetap dapat melayani administrasi bagi mahasiswa, maka pegawai A dan pegawai B tidak boleh mengawas pada waktu yang sama (baik S1 atau S2) atau pada kelas ujian yang beririsan waktunya,

6 setiap pegawai hanya boleh mengawas maksimum d ujian per harinya,

7 karena keterbatasan waktu, pegawai-pegawai tertentu tidak dapat mengawas di hari Sabtu atau tidak dapat mengawas ujian yang dimulai pada pukul 08.00. Sementara aturan tambahan (soft constraint/goal) dalam penjadwalan pengawas ujian di Departemen Matematika FMIPA IPB ialah sebagai berikut:

1 rata-rata banyaknya mengawas ujian per pegawai ialah sama,

2 rata-rata banyaknya mengawas ujian pada pukul 08.00 per pegawai ialah sama. Berdasarkan aturan-aturan yang ada, baik itu aturan umum maupun aturan tambahan, maka dibuat model matematika dari masalah penjadwalan pengawas ujian.

Model Matematika

Indeks

� = tujuan/goal ke-t yang ingin dicapai

= kelas ujian (terdiri atas hari, tanggal, waktu, dan mata kuliah), yaitu i = 1,2, …, n

= pegawai, yaitu j= 1,2, …, m.

Himpunan

� = himpunan kelas ujian, yaitu I={1, 2, …, n}

(15)

� = himpunan kelas ujian mata kuliah S2, dengan � ⊆ �

� = himpunan kelas ujian pada pukul 08.00, dengan � ⊆ �

� = himpunan kelas ujian pada jam dan hari yang sama serta waktu yang

overlapping

� = himpunan kelas ujian pada hari Sabtu, dengan � ⊆ �

�_ℎ = himpunan kelas ujian pada suatu hari Parameter

= banyaknya peserta ujian pada kelas ujian i

� = banyaknya pengawas yang diperlukan pada kelas ujian i � = banyaknya asisten yang mengawas pada kelas ujian i

= banyaknya mahasiswa nonasisten yang mengawas pada kelas ujian i

= banyaknya pegawai yang akan dijadwalkan

n = banyaknya kelas ujian dalam model penjadwalan pengawas ujian

= banyaknya pegawai yang akan dijadwalkan pada kelas ujian yang dimula i pukul 08.00

� = jumlah maksimal mengawas bagi pegawai setiap harinya Parameter Bobot

, = bobot untuk goal ke-t untuk setiap pegawai j Variabel Keputusan

, = { ,_, jika pegawai _jika _pegawai_{tidak mengawas}mengawas pada kelas ujian _{pada kelas ujian} _(selainnya)

� = { ,_, jika_selainnya mod , =

Kendala Utama (harus dipenuhi)

1 Total banyaknya pengawas yang diperlukan untuk setiap kelas ujian disesuaikan dengan banyaknya peserta, yaitu satu pengawas ujian mengawas i maksimal 25 mahasiswa peserta ujian,

� = / + � , ∀ .

2 Hanya satu orang pegawai yang mengawasi ujian mata kuliah S1,

∑ , =

= , ∀ ∈ � .

3 Terdapat pengawas tambahan, yaitu mahasiswa nonasisten, pada ujian mata kuliah S1,

= � − − � , ∀ ∈ � .

4 Mahasiswa tidak ikut mengawas ujian mata kuliah S2,

∑ _,

=

= � , ∀ ∈ � .

5 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di jam dan hari yang sama serta pada waktu yang overlapping,

∑ _,

∈

(16)

6 Dua orang pegawai tertentu, misalkan dan , tidak boleh mengawas bersamaan pada kelas ujian tertentu, yaitu

a pada ujian mata kuliah S2,

∑ _,

=

, ∈ { , }, ∀ ∈ � ,

b pada kelas ujian pada jam dan hari yang sama serta pada waktu yang

overlapping,

∑ ∑ _, , ∈ { , }, ∈ � .

7 Pegawai tertentu, misalkan , tidak bisa mengawas ujian yang dimulai pada pukul 08.00,

,� = , ∀ ∈ � .

8 Pegawai tertentu, misalkan , tidak bisa mengawas ujian pada hari Sabtu, ,� = , ∀ ∈ � .

9 Setiap pegawai mengawas maksimal sebanyak d kali setiap hari nya,

∑ _,

=

�, ∈ �_ℎ , ∀ , ∀ℎ� .

10 Semua variabel keputusan ialah integer nol atau satu, , ∈ { , }, ∀ , ,

� ∈ { , }, ∀ , .

Variabel Deviasi

Variabel deviasi yang terdapat pada masalah penjadwalan pengawas ujian ialah:

�+_{= nilai yang menampung deviasi yang berada di atas}_goal_ke-_t_{untuk pegawai}

j

�−_{= nilai yang menampung deviasi yang berada di bawah} _goal_ke-_t_untuk pegawai j

Kendala Tambahan (Goal)

1 Jumlah mengawas untuk semua pegawai sama rata pada satu periode waktu penjadwalan,

∑ _,

=

=∑= � − ∑= � − ∑= , ∀ .

2 Jumlah mengawas pukul 08.00 untuk semua pegawai ialah sama rata,

∑ _,

∈

=∑∈ � − ∑∈ � − ∑∈ , ∀ .

Kendala tambahan tidak harus terpenuhi, namun untuk mengetahui seberapa besar menyimpangnya kendala ini diberikan variabel deviasi. Setelah diberikan variabel deviasi, kendalanya menjadi:

(17)

∑ _,

=

+ �− _{− �}+ ₌∑= � − ∑= � − ∑ = _{, ∀ .}

2 Jumlah mengawas pukul 08.00 untuk semua pegawai ialah sama rata,

∑ _,

∈

+ �− _{− �}+ ₌∑∈ � − ∑∈ � − ∑∈ _{, ∀ .}

Fungsi Objektif

Fungsi objektif pada penjadwalan pengawas ujian ialah meminimumkan deviasi (kekurangan atau kelebihan) terhadap sasaran yang ingin dicapai yaitu:

min ∑ ∑ , (�+ + �−), ∀ �, .

IMPLEMENTASI MODEL

Pembahasan masalah penjadwalan pengawas ujian di Departemen Matematika FMIPA IPB dituangkan ke dalam dua skenario. Skenario 1 merupakan model penjadwalan dengan menggunakan aturan umum serta aturan tambahan yang terdapat di Departemen Matematika IPB, sedangkan Skenario 2 merupakan model penjadwalan yang merupakan modifikasi dari Skenario 1.

Pada semester ganjil tahun akademik 2013/2014 Departemen Matematika FMIPA IPB harus mengalokasikan pengawas untuk 44 kelas ujian. Satu ujian dijadwalkan selama 2 jam di hari Senin s.d Sabtu. Waktu-waktu diselenggarakannya ujian mata kuliah S1 ialah pukul 08.00-10.00, 10.30-12.30, atau 13.30-15.30, sedangkan waktu ujian mata kuliah S2 ialah 09.00-11.00 atau 13.00-15.00.

Skenario 1

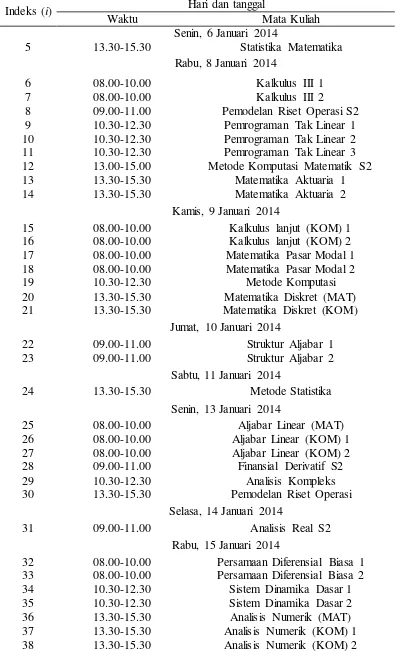
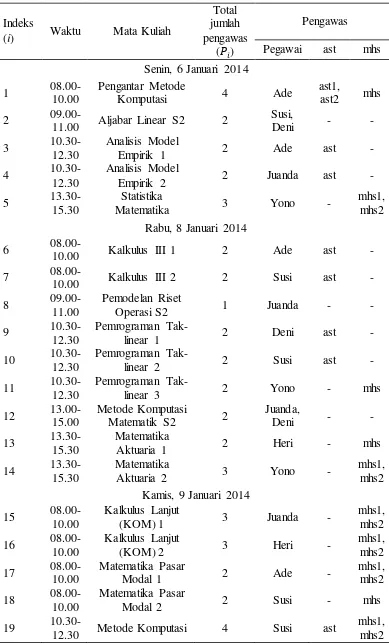
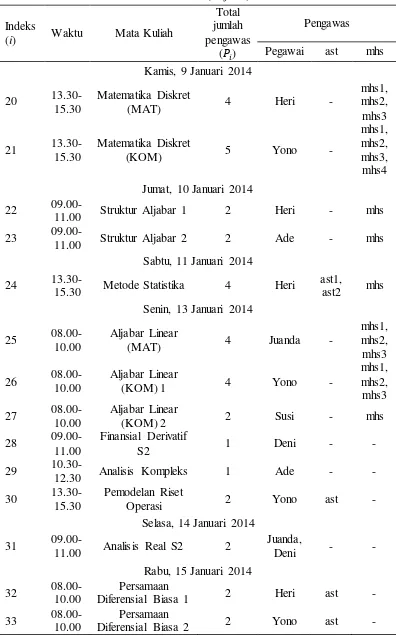
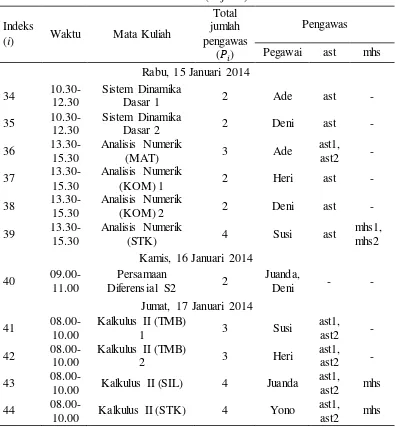
Pada skenario pertama ini dimodelkan masalah penjadwalan pengawas ujian seperti yang telah dijelaskan pada bab sebelumnya dengan data waktu pelaksanaan ujian dan mata kuliah pada semester ganjil 2013/2014 di Departemen Matematika IPB yang ditampilkan pada Tabel 1 dan data pegawai pada Tabel 2 berikut:

Tabel 1 Waktu pelaksanaan ujian dan mata kuliahnya

Indeks (i) Hari dan tanggal

Waktu Mata Kuliah

Senin, 6 Januari 2014

1 08.00-10.00 Pengantar Metode Komputasi

2 09.00-11.00 Aljabar Linear S2

3 10.30-12.30 Analisis Model Empirik 1

(18)

Tabel 1 Waktu pelaksanaan ujian dan mata kuliahnya (lanjutan)

Waktu Mata Kuliah

5 13.30-15.30 Statistika Matematika

Rabu, 8 Januari 2014

6 08.00-10.00 Kalkulus III 1

7 08.00-10.00 Kalkulus III 2

8 09.00-11.00 Pemodelan Riset Operasi S2

9 10.30-12.30 Pemrograman Tak Linear 1

12 13.00-15.00 Metode Komputasi Matematik S2

13 13.30-15.30 Matematika Aktuaria 1

14 13.30-15.30 Matematika Aktuaria 2

Kamis, 9 Januari 2014

15 08.00-10.00 Kalkulus lanjut (KOM) 1

16 08.00-10.00 Kalkulus lanjut (KOM) 2

17 08.00-10.00 Matematika Pasar Modal 1

18 08.00-10.00 Matematika Pasar Modal 2

19 10.30-12.30 Metode Komputasi

20 13.30-15.30 Matematika Diskret (MAT)

21 13.30-15.30 Matematika Diskret (KOM)

Jumat, 10 Januari 2014

22 09.00-11.00 Struktur Aljabar 1

23 09.00-11.00 Struktur Aljabar 2

Sabtu, 11 Januari 2014

24 13.30-15.30 Metode Statistika

25 08.00-10.00 Aljabar Linear (MAT)

26 08.00-10.00 Aljabar Linear (KOM) 1

27 08.00-10.00 Aljabar Linear (KOM) 2

28 09.00-11.00 Finansial Derivatif S2

29 10.30-12.30 Analisis Kompleks

30 13.30-15.30 Pemodelan Riset Operasi

Selasa, 14 Januari 2014

31 09.00-11.00 Analisis Real S2

32 08.00-10.00 Persamaan Diferensial Biasa 1 33 08.00-10.00 Persamaan Diferensial Biasa 2

34 10.30-12.30 Sistem Dinamika Dasar 1

35 10.30-12.30 Sistem Dinamika Dasar 2

36 13.30-15.30 Analisis Numerik (MAT)

37 13.30-15.30 Analisis Numerik (KOM) 1

(19)

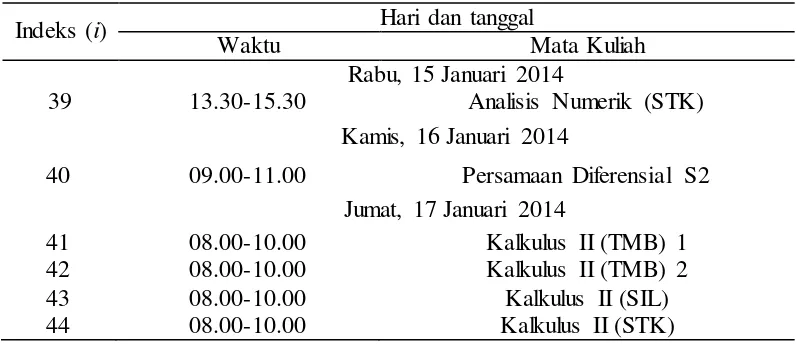
Tabel 1 Waktu pelaksanaan ujian dan mata kuliahnya (lanjutan)

Waktu Mata Kuliah

39 13.30-15.30 Analisis Numerik (STK)

Kamis, 16 Januari 2014

40 09.00-11.00 Persamaan Diferensial S2

Jumat, 17 Januari 2014

41 08.00-10.00 Kalkulus II (TMB) 1

42 08.00-10.00 Kalkulus II (TMB) 2

43 08.00-10.00 Kalkulus II (SIL)

44 08.00-10.00 Kalkulus II (STK)

Tabel 2 Daftar pegawai Indeks (j) Pegawai

1 Yono

2 Ade

3 Susi

4 Juanda

5 Deni

6 Heri

Himpunan

� = himpunan kelas ujian, yaitu I={1, 2, …, 44}

� = himpunan kelas ujian mata kuliah S2 = {2, 8, 12, 28, 31, 40}

� = himpunan kelas ujian mata kuliah S1, � = � − �

� = himpunan kelas ujian pada pukul 08.00 = {1, 6, 7, 15, 16, 17, 18, 25, 26, 27, 32, 33, 41, 42, 43, 44}

� = himpunan kelas ujian pada jam dan hari yang sama serta waktu yang

overlapping= {{3, 4}, {6, 7}, {9, 10, 11}, {13, 14}, {15, …, 18}, {20, 21},

{22, 23}, {25, 26, 27}, {32, 33}, {34, 35}, {36, …, 39}, {41, …, 44}, {1, 2}, {2, 3, 4}, {6, 7, 8}, {9, …, 12}, {12, 13, 14}, {25, …, 28}, {28, 29, 30}}

� = himpunan kelas ujian pada hari Sabtu = {24}

�_ℎ = himpunan kelas ujian pada suatu hari : �_� ={1, …, 5}; � ={6, …, 14}; � ={15, …, 21}; � ={22, 23}; � ={24}; �_� ={25,

…, 30}; �_� ={31}; � {32, …, 39}; � ={40}; � ={41,

…, 44}.

Parameter

= banyaknya peserta ujian pada kelas ujian i (dapat dilihat di Tabel 3)

� = banyaknya pengawas yang diperlukan pada kelas ujian i

� = banyaknya asisten yang mengawas pada kelas ujian i (dapat dilihat di Tabel 3)

= banyaknya mahasiswa nonasisten yang mengawas pada kelas ujian i

(20)

= 5

� = 2

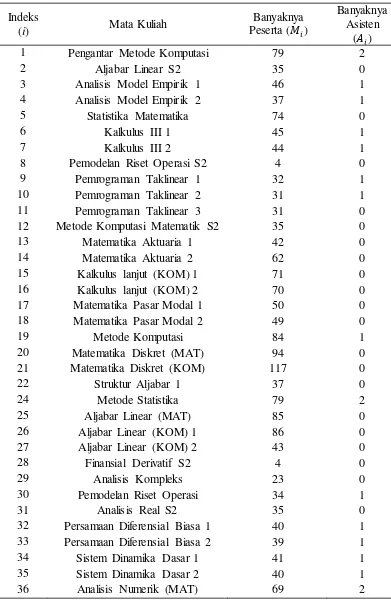
Tabel 3 Banyaknya peserta ujian dan banyaknya asisten mata kuliah di Departemen Matematika IPB

Indeks

(i) Mata Kuliah

Banyaknya Peserta ( )

Banyaknya Asisten

(�)

1 Pengantar Metode Komputasi 79 2

2 Aljabar Linear S2 35 0

3 Analisis Model Empirik 1 46 1

4 Analisis Model Empirik 2 37 1

5 Statistika Matematika 74 0

6 Kalkulus III 1 45 1

7 Kalkulus III 2 44 1

8 Pemodelan Riset Operasi S2 4 0

9 Pemrograman Taklinear 1 32 1

12 Metode Komputasi Matematik S2 35 0

13 Matematika Aktuaria 1 42 0

14 Matematika Aktuaria 2 62 0

15 Kalkulus lanjut (KOM) 1 71 0

16 Kalkulus lanjut (KOM) 2 70 0

17 Matematika Pasar Modal 1 50 0

18 Matematika Pasar Modal 2 49 0

19 Metode Komputasi 84 1

20 Matematika Diskret (MAT) 94 0

21 Matematika Diskret (KOM) 117 0

22 Struktur Aljabar 1 37 0

24 Metode Statistika 79 2

25 Aljabar Linear (MAT) 85 0

26 Aljabar Linear (KOM) 1 86 0

27 Aljabar Linear (KOM) 2 43 0

28 Finansial Derivatif S2 4 0

29 Analisis Kompleks 23 0

30 Pemodelan Riset Operasi 34 1

31 Analisis Real S2 35 0

32 Persamaan Diferensial Biasa 1 40 1

33 Persamaan Diferensial Biasa 2 39 1

34 Sistem Dinamika Dasar 1 41 1

35 Sistem Dinamika Dasar 2 40 1

(21)

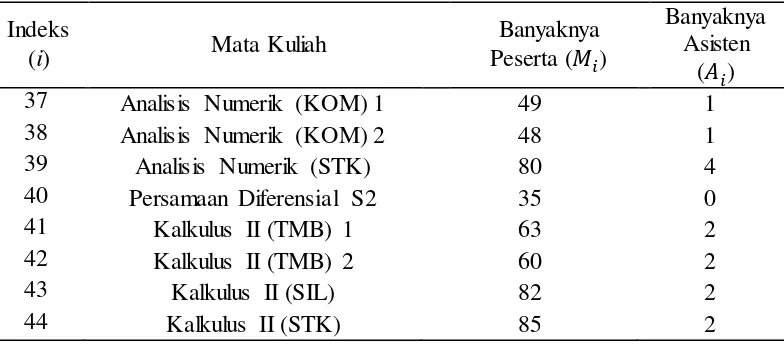
Tabel 3 Banyaknya peserta ujian dan banyaknya asisten mata kuliah di Departemen Matematika IPB (lanjutan)

Indeks

(i) Mata Kuliah

Banyaknya Peserta ( )

Banyaknya Asisten

(� )

37 Analisis Numerik (KOM) 1 49 1

38 Analisis Numerik (KOM) 2 48 1

39 Analisis Numerik (STK) 80 4

40 Persamaan Diferensial S2 35 0

41 Kalkulus II (TMB) 1 63 2

42 Kalkulus II (TMB) 2 60 2

43 Kalkulus II (SIL) 82 2

44 _{Kalkulus II (STK)} ₈₅ ₂

Kendala-kendala pada model penjadwalan pengawas ujian di Departemen Matematika IPB ialah sebagai berikut.

Kendala Utama

1 Total banyaknya pengawas yang diperlukan untuk setiap kelas ujian disesuaikan dengan banyaknya peserta, yaitu satu pengawas ujian mengawas i maksimal 25 mahasiswa peserta ujian,

� = / + � , ∀ = , , … , .

2 Hanya satu orang pegawai yang mengawasi ujian mata kuliah S1,

∑ _,

=

= , ∀ ∈ � .

3 Terdapat pengawas tambahan, yaitu mahasiswa nonasisten, pada ujian mata kuliah S1,

= � − − � , ∀ ∈ � .

4 Mahasiswa tidak ikut mengawas ujian mata kuliah S2,

∑ _,

=

= � , ∀ ∈ � .

5 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di jam dan hari yang sama,

∑₌ _, , ∀ ,

(22)

∑₌ _, , ∀ ,

6 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di waktu yang

overlapping,

∑₌ _, , ∀ ,

∑₌ _, , ∀ .

7 Dua orang pegawai, yaitu Yono dan Ade, tidak boleh mengawas bersamaan pada kelas ujian tertentu, yaitu

∑ _,

=

, ∀ ∈ � ,

b pad kelas ujian di jam dan hari yang sama,

∑₌ ∑ ₌ _, ,

(23)

c pada waktu yang overlapping, ∑₌ ∑ ₌ _, ,

∑₌ ∑ ₌ _, ,

∑₌ ∑ ₌ _, .

8 Salah satu pegawai, yaitu Deni, tidak bisa mengawas ujian yang dimulai pada pukul 08.00,

, = , ∀ ∈ � .

9 Salah satu pegawai, yaitu Deni, tidak bisa mengawas ujian pada hari Sabtu, , = , ∀ ∈ � .

10 Setiap pegawai mengawas maksimal sebanyak d = 2 kali setiap harinya,

∑ _,

=

, ∈ �_ℎ , ∀ , ∀ℎ� .

11 Semua variabel keputusan ialah integer nol atau satu, , ∈ { , }, ∀ , ,

� ∈ { , }, ∀ , .

Kendala Tambahan (Goal)

∑ _,

=

+ �− _{− �}+ ₌∑= � − ∑= � − ∑= _{, ∀ .}

2 Jumlah mengawas ujian pukul 08.00 untuk semua pegawai ialah sama rata,

∑ _,

∈

+ �− _{− �}+ ₌ ∑∈ � − ∑∈ � − ∑∈ _{, ∀ .}

Fungsi Objektif

Goal ke-2 dianggap lebih penting dibandingkan dengan goal ke-1, maka diberikan bobot untuk setiap goal sebagai berikut: _, = dan _, = , sehingga fungs i objektifnya menjadi:

min ∑ �+ _{+ �}− =

+ ∑ �+ _{+ �}− =

(24)

Skenario 2

Skenario kedua merupakan modifikasi dari skenario pertama. Model matematika secara umum sama untuk keduanya, perbedaannya ialah adanya pegawai yang mengundurkan diri (resign) dari Departemen Matematika. Ini menyebabkan banyaknya pegawai yang dapat mengawas menjadi berkurang sehingga aturan ke-5 pada hard constraint atau kendala utama ke-7 yang terdapat pada kendala utama di Skenario 1 tidak akan dapat dipenuhi. Oleh karena itu perlu dilakukan modifikasi model tersebut dengan mengubah aturan/kendala tersebut menjadi soft constraint/goal.

Pada Skenario 2, banyaknya pegawai (m) ialah 5 orang dengan rincian pada Tabel 4 sebagai berikut:

Tabel 4 Daftar pegawai Indeks (j) Pegawai

1 Yono

2 Ade

3 Susi

4 Juanda

5 Deni

Akan dibuat penjadwalan pengawas ujian dengan kendala utama sama seperti Skenario pertama kecuali kendala ke-7 pada Skenario pertama yang menjadi kendala tambahan pada model kedua ini.

Kendala Tambahan

∑ _,

=

+ �− _{− �}+ ₌∑= � − ∑= � − ∑= _, _∀ _.

2 Jumlah mengawas untuk semua pegawai yang mengawas pukul 08.00 sama rata,

∑ _,

=

+ �− _{− �}+ ₌ ∑ � − ∑ � − ∑ _{, ∀ ∈ �} , .

3 Dua orang pegawai, yaitu Yono dan Ade, tidak boleh mengawas bersamaan pada kelas ujian tertentu, yaitu

∑ _, + �− _{− �}+ _{= ,}_{∈ { , },} _∀ _{∈ � ,}

dengan �− = nilai yang menampung deviasi yang berada di bawah goal ke-3 untuk kelas ujian i,

(25)

b pada kelas ujian di jam dan hari yang sama serta pada waktu yang overlapping,

∑ ∑ _, + �− _{− �}+ _{= ,}_{∈ { , },} _{∈ � ,}

dengan �− = nilai yang menampung deviasi yang berada di bawah goal ke-4 untuk pegawai j dan kelas ujian i,

�+ _{= nilai yang menampung deviasi yang berada di atas}_goal_ke-4 untuk pegawai j dan kelas ujian i.

Fungsi Objektif

Fungsi objektif dari nonpreemptive goal programming ini ialah meminimumk a n jumlah variabel deviasi dari �+, �−, dan jumlah variabel deviasi dari �+, �−, serta variabel deviasi �+ dan �+ . Misalkan bobot untuk variabel deviasi yang akan diminimumkan ialah _, = , _, = , _, = , _{, ,} = , maka fungs i objektifnya menjadi

min ∑ �+ _{+ �}− =

+ ∑ �+ _{+ �}− =

+ ∑

=

�+ _{+ ∑∑} =

�+ =

,

dengan _, = bobot untuk goal ke-1 untuk setiap pegawai j, , = bobot untuk goal ke-2 untuk setiap pegawai j, , = bobot untuk goal ke-3 untuk setiap kelas ujian i,

, , = bobot untuk goal ke-4 untuk setiap pegawai j dan kelas ujiani.

HASIL DAN PEMBAHASAN

Masalah penjadwalan pengawas ujian yang telah dimodelkan dan dipaparkan sebelumnya pada Skenario 1 dan 2 kemudian dimasukkan ke dalam proses komputasi menggunakan bantuan software LINGO 11.0.

Skenario 1

(26)

Tabel 5 Jadwal pengawas ujian Departemen Matematika semester ganjil 2013-2014 untuk Skenario 1

(27)

Tabel 5 Jadwal pengawas ujian Departemen Matematika semester ganjil 2013-2014 untuk Skenario 1 (lanjutan)

(28)

(29)

Tabel 6 Nilai variabel deviasi Skenario 1

Variabel Keterangan Nilai

∑ �+ Total penyimpangan yang

menampung goal ke-1 yang berada di atas sasaran.

0

∑ �− Total penyimpangan yang

menampung goal ke-1 yang berada di bawah sasaran.

0

∑ �+ Total penyimpangan yang

menampung goal ke-2 yang berada di atas sasaran.

0.8

∑ �− Total penyimpangan yang

menampung goal ke-2 yang berada di bawah sasaran.

0.8

Sementara itu, total jumlah mengawas pada ujian periode semester ganjil tahun 2013-2014, serta banyaknya mengawas pada pukul 08.00 pagi untuk setiap pegawai berdasarkan hasil nonpreemptive goal programming dapat dilihat pada tabel berikut:

Tabel 7 Jumlah mengawas bagi setiap pegawai pada Skenario 1

Pegawai Total Jumlah Mengawas Banyaknya Mengawas pada Pukul 08.00

Yono 8 3

Ade 8 3

Susi 8 4

Juanda 8 3

Deni 8 -

Heri 8 3

Pada Tabel 7 terlihat bahwa total jumlah mengawas (goal ke-1) untuk setiap pegawai sama rata yakni 8 kali dalam satu periode ujian semester ganjil tahun akademik 2013-2014, namun pada jumlah banyaknya mengawas pada pukul 08.00 (goal ke-2) terdapat perbedaan, tidak keseluruhan sama rata mengawas pukul 08.00 untuk setiap pegawai. Hal ini ditandai juga dengan nilai dari variabel deviasi untuk

goal ke-2 tersebut tidak bernilai 0 (dapat dilihat di Tabel 6).

Skenario 2

(30)

(31)

(32)

Indeks

ast: asisten, mhs: mahasiswa nonasisten

(33)

Tabel 9 Nilai variabel deviasi Skenario 2

Variabel Keterangan Nilai

∑ �+ Total penyimpangan yang menampung goal ke-1 yang berada di atas sasaran.

1.2

∑ �− Total penyimpangan yang menampung goal ke-1 yang berada di bawah sasaran.

1.2

0

5

∑ ∑ �+ Total penyimpangan yang menampung goal ke-4 yang berada di atas sasaran.

3

∑ ∑ �− Total penyimpangan yang menampung goal ke-4 yang berada di bawah sasaran.

0

Semetara itu, untuk goal ke-1 dan ke-2 yang terdapat pada kendala tambahan direpresentasikan pada tabel berikut:

Tabel 10 Jumlah mengawas bagi setiap pegawai pada Skenario 2

Pegawai Total Jumlah

Mengawas

Banyaknya Mengawas pada Pukul 08.00

Yono 10 4

Ade 9 4

Susi 9 4

Juanda 10 4

(34)

Pada tabel tersebut terlihat untuk goal ke-1, yaitu total jumlah mengawas untuk setiap pegawai hampir sama rata hanya terdapat sedikit perbedaan. Hal ini ditandai dengan terdapat nilai positif pada variabel deviasi �+ dan �− pada goal

ke-1 tersebut dan untuk banyaknya mengawas pada pukul 08.00 untuk setiap pegawai sama rata artinya untuk goal ke-2 ini terpenuhi. Sementara persentase pemenuhan kendala untuk goal ke-3 dan ke-4 pada kendala tambahan direpresentasikan pada Tabel 11 berikut:

Tabel 11 Pemenuhan kendala tambahan/goal ke-3 dan ke-4

Kendala Tambahan Persentase Pemenuhan Kendala

Pada ujian mata kuliah S2 100%

Kelas ujian di jam dan hari yang sama

serta pada waktu yang overlapping 84.21%

Karena goal ke-3 berupa pertaksamaan , maka variabel deviasi yang diminimumkan ialah �+. Dari hasil LINGO 11.0 nilai ∑ �+ = , maka goal ke-3 ini dipenuhi. Goal ke-4 tidak dipenuhi karena ∑ ∑ �+ > , artinya terdapat kelas ujian sehingga pegawai Yono dan Ade mengawas ujian bersamaan yaitu pada (i) Rabu, 8 Januari 2014 di waktu yang overlapping (13.00-15.00 dan 13.30-15.30), (ii) Kamis, 9 Januari 2014 di jam yang sama (08.00-10.00), (iii) Jumat, 17 Januari 2014 di jam yang sama (08.00-10.00).

SIMPULAN

Dalam karya ilmiah ini telah diperlihatkan bahwa masalah penjadwalan pengawas ujian di Departemen Matematika IPB dapat dimodelkan menggunak a n metode nonpreemptive goal programming dan dapat diselesaikan menggunak a n

(35)

DAFTAR PUSTAKA

Sarker RA, Newton CS. 2008. Optimization Modelling-A Practical Approach. Boca Raton (US): CRC Press Taylor & Francis Group.

Taha HA. 2007. Operations Research: An Introduction. Ed ke-8. New Jersey (US): Pearson Education, Inc.

(36)

Lampiran 1 Sintaks Komputasi LINGO 11.0 untuk menyelesaikan Skenario 1

MODEL:

TITLE: Skenario 1;

SETS:

WNM/1..44/:U,M,P,A,N; WS2(WNM)/2,8,12,28,31,40/;

WS1(WNM)|#NOT#@IN(WS2,&1);

WD(WNM)/1,6,7,15,16,17,18,25,26,27,32,33,41,42,43,44/; Pegawai/1..6/:d1m,d2m,d1p,d2p;

Kombinasi(WNM,Pegawai):X;

ENDSETS

DATA:

A=@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','A');

@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','P')=P;

M=@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','M');

@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','N')=N;

ENDDATA

!Kendala;

!1 Total banyaknya pengawas yang diperlukan untuk setiap kelas ujian disesuaikan dengan banyaknya peserta;

@FOR(WNM(I):P(I)=@FLOOR(M(I)/25)+U(I));

@FOR(WNM(I):U(I)=@IF(@MOD(M(I),25)#EQ#0,0,1));

!2 Hanya satu orang pegawai yang mengawasi ujian mata kuiah S1;

@FOR(WS1(I):@SUM(Pegawai(J):X(I,J))=1);

!3 Terdapat pengawas tambahan, yaitu mahasiswa nonasisten, pada ujian mata kuliah S1;

@FOR(WS1(I):N(I)=P(I)-1-A(I));

@FOR(WS2(I):N(I)=0);

!4 Mahasiswa tidak ikut mengawas ujian mata kuliah S2;

@FOR(WS2(I):@SUM(Pegawai(J):X(I,J))=P(I));

!5 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di jam dan hari yang sama;

@FOR(Pegawai(J):@SUM(WNM(I)|I#GE#3 #AND# I#LE#4:X(I,J))<=1);

!6 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di waktu yang overlapping;

(37)

!7 Dua orang pegawai,yaitu Yono dan Ade, tidak boleh mengawas bersamaan pada waktu penyelenggaran ujian tertentu, yaitu; !a pada ujian mata kuliah S2;

@FOR(WS2(I):@SUM(Pegawai(J)|J#GE#1 #AND# J#LE#2:X(I,J))<=1);

!b pada kelas ujian di jam dan hari yang sama;

@SUM(WNM(I)|I#GE#3 #AND# I#LE#4:@SUM(Pegawai(J)|J#GE#1 #AND#

J#LE#2:X(I,J)))<=1;

x(13,1)+x(13,2)+x(14,1)+x(14,2)<=1;

J#LE#2:X(I,J)))<=1;

!c pada waktu yang overlapping;

J#LE#2:X(I,J)))<=1;

!8 Salah satu pegawai, yaitu Deni, tidak bisa mengawas ujian yang dimulai pada pukul 08.00;

@FOR(WD(I):X(I,5)=0);

!9 Salah satu pegawai, yaitu Deni, tidak bisa mengawas ujian pada hari Sabtu;

X(24,5)=0;

(38)

@FOR(Pegawai(J):@SUM(WNM(I)|I#EQ#24:X(I,J))<=2);

!Kendala Tambahan;

@FOR(Pegawai(J):@SUM

(WNM(I):X(I,J))+d1m(J)-d1p(J)=(@SUM(WNM(I):P(I))-@SUM(WNM(I):A(I))-@SUM(WNM(I):N(I)))/6);

@FOR(Pegawai(J)|J#NE#5:@SUM

(WD(I):X(I,J))+d2m(J)-d2p(J)=(@SUM(WD(I):P(I)-@SUM(WD(I):A(I)-@SUM(WD(I):N(I))/5);

!Fungsi Objektif;

MIN=@SUM(Pegawai(J):d1m(J)+d1p(J))+2*@SUM(Pegawai(J):d2m(J)+d2p(J)

);

@FOR(KOMBINASI(I,J):@BIN(X));

@FOR(WNM(I):@BIN(U(I)));

(39)

Lampiran 2 Hasil Komputasi LINGO 11.0 untuk Skenario 1

Global optimal solution found.

Objective value: 3.200000 Objective bound: 3.200000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 516

Export Summary Report ---

Transfer Method: OLE BASED

Workbook: D:\SKRIPSI\!DRAFT TA\coba excel 3.xlsx Ranges Specified: 1

P

Ranges Found: 1 Range Size Mismatches: 0 Values Transferred: 44

M

(40)

(41)

(42)

(43)

Lampiran 3 Sintaks komputasi LINGO 11.0 untuk menyelesaikan Skenario 2

MODEL:

TITLE: Skenario 2;

SETS:

WNM/1..44/:U,M,P,A,N;

WS2(WNM)/2,8,12,28,31,40/:d3m,d3p;

WS1(WNM)|#NOT#@IN(WS2,&1);

WD(WNM)/1,6,7,15,16,17,18,25,26,27,32,33,41,42,43,44/; Pegawai/1..5/:d1m,d2m,d1p,d2p;

Kombinasi(WNM,Pegawai):X,d41m,d42m,d43m,d44m,d45m,d46m,d47m,d48m,d 49m,d410m,d411m,d412m,d41p,d42p,d43p,d44p,d45p,d46p,d47p,d48p,d49p ,d410p,d411p,d412p,

d51m,d52m,d53m,d54m,d55m,d56m,d57m,d51p,d52p,d53p,d54p,d55p,d56p,d 57p;

ENDSETS

DATA:

A=@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','A');

@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','P')=P;

M=@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','M');

@OLE('D:\SKRIPSI\!DRAFT TA\excel mira.xlsx','N')=N;

ENDDATA

!Kendala;

!1 Total banyaknya pengawas yang diperlukan untuk setiap kelas ujian disesuaikan dengan banyaknya peserta;

@FOR(WNM(I):P(I)=@FLOOR(M(I)/25)+U(I));

@FOR(WNM(I):U(I)=@IF(@MOD(M(I),25)#EQ#0,0,1));

!2 Hanya satu orang pegawai yang mengawasi ujian mata kuiah S1;

@FOR(WS1(I):@SUM(Pegawai(J):X(I,J))=1);

!3 Terdapat pengawas tambahan, yaitu mahasiswa nonasisten, pada ujian mata kuliah S1;

@FOR(WS1(I):N(I)=P(I)-1-A(I));

@FOR(WS2(I):N(I)=0);

!4 Mahasiwa tidak ikut mengawas ujian mata kuliah S2;

@FOR(WS2(I):@SUM(Pegawai(J):X(I,J))=P(I));

!5 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di jam dan hari yang sama;

!6 Setiap pegawai hanya mengawasi satu ujian pada ujian-ujian di waktu yang overlapping;

(44)

!7 Salah satu pegawai, yaitu Deni, tidak bisa mengawas ujian yang dimulai pada pukul 08.00;

@FOR(WD(I):X(I,5)=0);

!8 Salah satu pegawai, yaitu Deni, tidak bisa mengawas ujian pada hari Sabtu;

X(24,5)=0;

!9 Setiap pegawai mengawa maksimal sebanyak d=2 kali setiap harinya;

!Kendala Tambahan;

@@FOR(Pegawai(J):@SUM

(WNM(I):X(I,J))+d1m(J)-d1p(J)=(@SUM(WNM(I):P(I))-@SUM(WNM(I):A(I))-@SUM(WNM(I):N(I)))/6);

@FOR(Pegawai(J)|J#NE#5:@SUM

(WD(I):X(I,J))+d2m(J)-d2p(J)=(@SUM(WD(I):P(I)-@SUM(WD(I):A(I)-@SUM(WD(I):N(I))/5);

@FOR(WS2(I):@SUM(Pegawai(J)|J#GE#1 #AND#

J#LE#2:X(I,J))+d3m(I)-d3p(I)=1);

J#LE#2:X(I,J)+d41m(I,J)-d41p(I,J)))=1;

J#LE#2:X(I,J)+d42m(I,J)-d42p(I,J)))=1;

J#LE#2:X(I,J)+d43m(I,J)-d43p(I,J)))=1;

J#LE#2:X(I,J)+d44m(I,J)-d44p(I,J)))=1;

J#LE#2:X(I,J)+d45m(I,J)-d45p(I,J)))=1;

J#LE#2:X(I,J)+d46m(I,J)-d46p(I,J)))=1;

J#LE#2:X(I,J)+d47m(I,J)-d47p(I,J)))=1;

J#LE#2:X(I,J)+d48m(I,J)-d48p(I,J)))=1;

J#LE#2:X(I,J)+d49m(I,J)-d49p(I,J)))=1;

J#LE#2:X(I,J)+d410m(I,J)-d410p(I,J)))=1;

J#LE#2:X(I,J)+d411m(I,J)-d411p(I,J)))=1;

(45)

@SUM(WNM(I)|I#GE#1 #AND# I#LE#2:@SUM(Pegawai(J)|J#GE#1 #AND# J#LE#2:X(I,J)+d51m(I,j)-d51p(I,J)))=1;

J#LE#2:X(I,J)+d52m(I,j)-d52p(I,J)))=1;

J#LE#2:X(I,J)+d53m(I,j)-d53p(I,J)))=1;

J#LE#2:X(I,J)+d54m(I,j)-d54p(I,J)))=1;

J#LE#2:X(I,J)+d55m(I,j)-d55p(I,J)))=1;

J#LE#2:X(I,J)+d56m(I,j)-d56p(I,J)))=1;

J#LE#2:X(I,J)+d57m(I,j)-d57p(I,J)))=1;

!Fungsi Objektif;

MIN=@SUM(Pegawai(J):d1m(J)+d1p(J))+2*@SUM(Pegawai(J):d2m(J)+d2p(J)

)+2*@SUM(WS2(I):d3p(I))

+2*@SUM(WNM(I)|I#GE#3 #AND# I#LE#4:@SUM(Pegawai(J)|J#GE#1 #AND#

J#LE#2:d41p(I,J)))

J#LE#2:d42p(I,J)))

J#LE#2:d43p(I,J)))

J#LE#2:d44p(I,J)))

J#LE#2:d45p(I,J)))

J#LE#2:d46p(I,J)))

J#LE#2:d47p(I,J)))

J#LE#2:d48p(I,J)))

J#LE#2:d49p(I,J)))

J#LE#2:d410p(I,J)))

J#LE#2:d411p(I,J)))

J#LE#2:d412p(I,J)))

J#LE#2:d51p(I,J)))

J#LE#2:d52p(I,J)))

J#LE#2:d53p(I,J)))

J#LE#2:d54p(I,J)))

J#LE#2:d55p(I,J)))

J#LE#2:d56p(I,J)))

J#LE#2:d56p(I,J)));

@FOR(KOMBINASI(I,J):@BIN(X));

(46)

Lampiran 4 Hasil komputasi LINGO 11.0 untuk Skenario 2

Global optimal solution found.

Objective value: 8.400000 Objective bound: 8.400000 Infeasibilities: 0.6661338E-15 Extended solver steps: 0 Total solver iterations: 334

P

Ranges Found: 1 Range Size Mismatches: 0 Values Transferred: 44

N

(47)

(48)

(49)

(50)

RIWAYAT HIDUP

Penulis dilahirkan pada tanggal 19 Maret 1992 di Sukabumi, Jawa Barat. Penulis merupakan anak pertama dari tiga bersaudara dari pasangan Bapak Naiman dan Ibu Ai Maryam. Tahun 2010 penulis lulus dari SMA Negeri 1 Cibadak dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui Undangan Seleksi Masuk IPB dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam dengan memperoleh beasiswa Bidikmisi.