UJI KOMPUTASI ALGORITME VARIAN METODE
NEWTON PADA PERMASALAHAN OPTIMASI
NONLINEAR
TANPA KENDALA
NURUL HAQUEQY
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa tesis berjudul Uji Komputasi Algoritme Varian Metode Newton Pada Permasalahan Optimasi Nonlinear Tanpa Kendala adalah benar karya saya denganarahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Agustus 2016
Nurul Haqueqy
RINGKASAN
NURUL HAQUEQY. Uji Komputasi Algoritme Varian Metode Newton pada Permasalahan Optimasi Nonlinear Tanpa Kendala. Dibimbing oleh BIB PARUHUM SILALAHI dan IMAS SUKAESIH SITANGGANG.
Optimasi merupakan suatu cara yang dapat dilakukan ketika bekerja dalam bidang ilmu eksperimental dan keteknikan, yang meliputi fungsi matematika dan proses industri. Prinsip utama dalam optimasi adalah untuk menentukan solusi terbaik yang optimal (maksimum/minimum) dari suatu tujuan yang dimodelkan melalui fungsi objektif. Secara garis besar, optimasi memiliki masalah-masalah yang harus diselesaikan. Untuk menyelesaikan permasalahan dalam optimasi dapat dilakukan dengan menggunakan metode numerik. Metode numerik merupakan teknik yang digunakan untuk memformulasikan persoalan matematika. Sehingga dapat dipecahkan dengan menggunakan operasi perhitungan dan dapat dibuat ke dalam bentuk algoritme yang dapat dihitung secara cepat dan mudah. Salah satu medote numerik yang dapat digunakan adalah metode Newton dan metode Halley. Metode Newton merupakan salah satu metode terbaik untuk menentukan solusi akar dari persamaan nonlinear. Metode Newton sering konvergen dengan cepat, terutama bila iterasi dimulai cukup dekat dengan akar yang diinginkan. Metode Halley merupakan metode dengan kovergen orde ketiga yang mana metode ini memiliki orde kekonvergenan yang lebih tinggi jika dibandingkan dengan metode Newton. Oleh karena itu, tujuan dari penelitian ini adalah mengkombinasikan metode Newton, Aturan Trapesium dengan metode Halley serta membandingkan hasil uji komputasi antara algoritme baru dengan algoritme metode Newton untuk permasalahan optimasi nonlinear tanpa kendala.
Hasil dari penelitian ini menunjukkan bahwa perbandingan antara metode NTH dengan beberapa metode yang diujikan memperlihatkan bahwa hasil yang diperoleh dari segi jumlah iterasi pada kombinasi metode NTH lebih baik. Sedangkan dari aspek running time metode NTH membutuhkan waktu yang cukup lama dibandingkan dengan metode lain yang proses pencarian akarnya hanya melakukan satu kali evaluasi fungsi. Jika dibandingkan dengan metode kombinasi lain yang melakukan dua kali evaluasi fungsi dalam satu kali iterasi, waktu yang digunakan oleh metode NTH dalam mencari nilai akar lebih cepat. Hasil yang diperoleh dengan menggunakan metode NTH memperlihatkan bahwa nilai akar yang diperoleh menggunakan sembilan fungsi yang diujikan hampir secara keseluruhan mendekati true value. Tetapi pada persamaan =
sin ( ) + exp[ cos( ) sin( )] − 28 , hasil nilai akar yang diperoleh menggunakan masing-masing metode yang diujikan dengan true value memperlihatkan perbedaan yang cukup jelas. Jika dilihat perbedaan nilai akar antara true value dengan metode NTH maka hasil yang diperoleh tidak terlalu berbeda signifikan. Oleh sebab itu, hasil yang diperoleh dengan melakukan uji komputasi dalam penelitian ini menunjukkan bahwa kombinasi algoritme metode Newton, Aturan Trapesium dan metode Halley (NTH) baik digunakan untuk pencarian nilai akar dari fungsi nonlinear.
SUMMARY
NURUL HAQUEQY. Computational Test Varian Newton’s Method Algorithm on Non-Linear Optimization Problems Without Constraint. Supervised by BIB PARUHUM SILALAHI and IMAS SUKAESIH SITANGGANG.
Optimization is a way that can be done when working in the field of experimental science and engineering, which includes mathematical functions, and process industries. The mains principle in the optimization is to determine the best solution is optimal (maximum/minimum) of a goal objective function that modeled. In generally, optimization problems have to be solved. To resolve the optimization problem can be done by using numerical methods. The numerical method is a technique used for formulating a mathematical problem. So That can be solved using arithmetic operations and made into the form of algorithms that calculated quickly and easily. One of the numerical methods can be used Newton's method and Halley's method. Newton's method is one of the best methods to determine the root of the solution of nonlinear equations. Newton's method often converges quickly, especially if iteration begins quite close to the root. Halley’s method is a third-order convergent method which the convergence of this method has an order higher than the Newton’s method. The purpose of this research to combine the Newton's method, Halley's method, Rules Trapezoid and computational comparing test results between the new algorithm with Newton’s method for nonlinear optimization problem without constraints.
The results of this study indicate that the comparison between the NTH’s method with some methods that were tested showed that NTH method is superior terms of the number of iterations. But, NTH's method has required a long time of running time compared with the process of finding the root another method which made only one evaluation function. When compared to other combination methods that perform two times of the evaluation function in one iteration, the running time taken by NTH's method for finding the root of value is more quickly. Results obtained by using the NTH’s method shows that the root value obtained using the tested nine functions almost as a whole closer to the true value. But the equation = sin ( ) + exp[ cos( ) sin( )] − 28, results of root value obtained using each method tested with true value show the difference quite clearly. If the views, the difference in value between the true root NTH's method, the results are not too different significantly. Therefore, the results obtained by a computational test in this study indicate that the combination of algorithmic Newton’s method, Trapezoid Rule and Halley’s method (NTH) both used to search root value of a nonlinear function.
© Hak Cipta Milik IPB, Tahun 2016
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Ilmu Komputer
UJI KOMPUTASI ALGORITME VARIAN METODE
NEWTON PADA PERMASALAHAN OPTIMASI
NONLINEAR
TANPA KENDALA
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2016
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala rahmat dan karunia-Nya sehingga penulis berhasil menyelesaikan tugas akhir ini. Tugas akhir ini disusun sebagai laporan penelitian yang telah dilakukan penulis sejak bulan januari 2016 dengan judul Uji Komputasi Algoritme Varian Metode Newton pada Permasalahan Optimasi Nonlinear Tanpa Kendala
Alhamdulillah atas bimbingan dan petunjuk dari Allah Subhana wa ta'ala serta bimbingan dari semua pihak, penyusunan tugas akhir ini dapat diselesaikan. Tugas akhir ini tidak mungkin dapat diselesaikan tanpa adanya bantuan dari berbagai pihak. Oleh karena itu, penulis ingin mengucapkan terimakasih dan penghargaan yang setinggi-tingginya kepada:
1. Ayah, Ibu serta kakak-kakak yang selalu mendoakan, memberi nasihat, kasih sayang, semangat, dan dukungan sehingga penelitian ini bisa diselesaikan dengan baik.
2. Bapak Dr Ir Bib Paruhum Silalahi, MKom dan Ibu Dr Imas Sukaesih Sitanggang, SSi MKom selaku dosen pembimbing I dan II yang selalu bersedia membantu, memberi saran, masukan dan ide-ide dalam penelitian ini.
3. Bapak Dr Eng Wisnu Ananta Kusuma, ST MT selaku dosen penguji atas kesediannya sebagai penguji pada tugas akhir.
4. Teman-teman mahasiswa Magister Ilmu Komputer angkatan 2014 yang selama dua tahun ini telah bersedia berbagi ilmunya selama masa perkuliahan dan pelaksanaan penelitian.
5. Departemen Ilmu Komputer IPB, staf dan dosen yang telah banyak membantu selama masa perkuliahan hingga penelitian.
Semoga tesis ini dapat bermanfaat.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang 1
Perumusan Masalah 2
Tujuan Penelitian 2
Manfaat Penelitian 3
2 TINJAUAN PUSTAKA 3
Optimasi Matematik 3
Definisi Orde Konvergesi 3
Metode Newton Raphson 3
Metode Newton Halley 4
Metode Newton Trapesium Secant 5
Metode Newton Trapesium 5
Metode Trapesium Halley 6
Metode Halley 6
3 METODE 7
Tempat dan Waktu Penelitian 7
Perangkat Penelitian 7
Tahapan Penelitian 7
4 HASIL DAN PEMBAHASAN 9
Studi Literatur 9
Kombinasi dan Formulasi Metode Newton, Aturan Trapesium dan Metode
Halley 9
Pembuatan Algoritme 10
Implementasi Algoritme 11
Pengujian Komputasi 11
5 SIMPULAN DAN SARAN 17
Simpulan 17
Saran 17
DAFTAR PUSTAKA 17
LAMPIRAN 19
DAFTAR TABEL
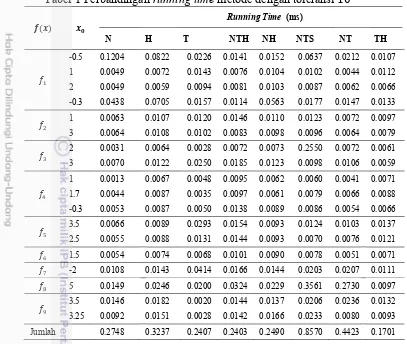
1 Perbandingan running time masing-masing metode untuk toleransi 10 12 2 Perbandingan jumlah iterasi masing-masing metode untuk toleransi 10 13 3 Perbandingan nilai akar masing-masing metode dengan tolerans10 14
DAFTAR GAMBAR
1 Tahapan penelitian 8
2 Perbandingan jumlah iterasi dan running time(a) dengan = 1 toleransi 10 dan (b) dengan = 3 toleransi 10 15 3 Perbandingan jumlah iterasi dan running time (a) dengan =
2toleransi 10 dan (b) dengan = 1 toleransi 10 16 4 Perbandingan jumlah iterasi dan running time (a) dengan = 2.5
toleransi 10 dan (b) dengan = 1.5 toleransi 10 16 5 Perbandingan jumlah iterasi dan running time(a) dengan = −2
toleransi 10 dan (b) dengan = 5 toleransi 10 16 6 Perbandingan jumlah iterasi dan running time dengan = 3.25
toleransi 10 17
DAFTAR LAMPIRAN
1 Implementasi setiap metode menggunakan Matlab 20
2 Tabel perbandingan running time masing-masing metode untuk toleransi
10 28
3 Tabel perbandingan jumlah iterasi untuk masing-masing metode dengan
toleransi 10 29
4 Tabel perbandingan nilai akar masing-masing metode untuk toleransi
10 30
5 Grafik perbandingan jumlah iterasi dan running time masing-masing
1
1
PENDAHULUAN
Latar Belakang
Optimasi merupakan suatu cara yang dapat dilakukan ketika bekerja dalam bidang ilmu eksperimental dan keteknikan, yang meliputi fungsi matematika dan proses industri untuk mendapatkan metode analisis baru (Cerdà et al. 2015). Prinsip utama dalam pemodelan optimasi adalah menentukan solusi terbaik yang optimal (minimum/maksimum) dari suatu tujuan yang dimodelkan melalui fungsi objektif. Secara garis besar, masalah dalam optimasi dikategorikan menjadi dua bagian, yaitu masalah optimasi dengan kendala dan masalah optimasi tanpa kendala. Masalah optimasi tanpa kendala merupakan masalah optimasi yang tidak memiliki batasan. Sedangkan masalah optimasi dengan kendala merupakan masalah pengoptimuman fungsi objektif yang memiliki batasan atau kendala. Penyelesaian dalam fungsi optimasi dibagi menjadi dua yaitu penyelesaian fungsi optimasi dengan analitik dan penyelesaian fungsi optimasi dengan pendekatan numerik. Metode numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan atau aritmatika biasa. Penyelesaian menggunakan metode numerik biasanya melibatkan proses iterasi. Apabila proses iterasi dilakukan menggunakan perhitungan matematis, maka akan membutuhkan waktu yang lama dan memungkinkan terjadinya human error.
2
konvergen dengan cepat menurut Kumar et al. (2012), terutama bila iterasi dimulai cukup dekat dengan akar yang diinginkan. Metode Halley sendiri merupakan metode dengan konvergen orde ketiga (Narang et al. 2015) dimana metode ini berarti memiliki orde kekonvergenan yang lebih tinggi dibandingkan dengan metode Newton.
Para peneliti umumnya berusaha untuk menemukan metode dengan algoritme yang paling efektif dan efisien untuk dapat menyelesaikan masalah optimasi linear maupun nonlinear. Seperti yang telah dilakukan oleh Weerakoon dan Fernando (2000) yang mengembangkan metode Newton dengan cara memodifikasi metode Newton dan Aturan Trapesium. Modifikasi metode Newton dengan Aturan Trapesium menghasilkan konvergen orde ketiga. Adapun metode Newton sendiri masih menghasilkan konvergen orde kedua. Sehingga modifikasi metode ini menghasilkan iterasi yang lebih sedikit apabila dibandingkan dengan metode Newton. Homeier (2005) melakukan penelitian mengenai metode Newton dengan menggunakan fungsi invers. Ini juga merupakan modifikasi dari metode Newton. Penelitian ini menghasilkan metode dengan konvergen orde ketiga. Jain (2013) melakukan modifikasi pada metode Newton yang sebelumnya telah dilakukan oleh Homeir dan Weerakoon dengan menambahkan metode Secant ke dalam metode Newton dengan Aturan Trapesium dan metode Newton dengan menggunakan fungsi invers. Penelitian ini menghasilkan metode Secant Trapesium Newton dan metode Secant Invers Newton dengan konvergen orde keempat. Selanjutnya Noor (2007) melakukan modifikasi metode Halley dan menghasilkan pengembangan baru dari metode Halley sehingga menghasilkan metode yang lebih baik dengan konvergen orde kelima.
Oleh karena itu, dengan kelebihan dan kekurangan yang dimiliki oleh masing-masing metode Newton dan metode Halley dalam menyelesaikan permasalahan persamaan linear maupun nonlinear, maka pada penelitian ini akan diusulkan metode kombinasi antara varian metode Newton dengan Aturan Trapesium yang telah dilakukan oleh Weerakoon dan Fernando (2000) dan metode Halley.
Perumusan Masalah
Berdasarkan latar belakang masalah, penelitian ini dapat dirumuskan sebagai berikut:
1. Bagaimana mengkombinasikan metode Newton, Aturan Trapesium dan metode Halley?
2. Bagaimana perbandingan hasil uji komputasi antara algoritme kombinasi metode Newton, Aturan Trapesium dan metode Halley dengan algoritme metode Newton menggunakan beberapa fungsi nonlinear?
Tujuan Penelitian
Tujuan dari penelitian ini adalah:
1. Mengkombinasikan metode Newton, Aturan Trapesium dan metode Halley, 2. Membandingkan hasil uji komputasi antara algoritme kombinasi metode
3
Manfaat Penelitian
Manfaat penelitian ini adalah agar dapat menghasilkan suatu metode baru dengan algoritme yang dapat digunakan untuk menyelesaikan permasalahan nonlinear tanpa kendala sehingga mendapatkan hasil yang akurat dan iterasi yang lebih sedikit.
2
TINJAUAN PUSTAKA
Optimasi Matematik
Optimasi matematik sering disebut dengan nonlinear programing, pemrograman matematika atau optimasi numerik. Istilah optimasi matematik dapat dijelaskan sebagai suatu ilmu untuk menentukan solusi terbaik secara matematik pada suatu permasalahan. Pada umumnya optimasi matematik menurut Snyman (2005) adalah proses dari :
(i) Formulasi
(ii) Solusi dari masalah optimasi dibatasi dari bentuk umum matematik : Meminimumkan ( ), = [ , , … , ] ∈ ℝ harus memenuhi kendala :
≤ 0, = 1,2, … , (1) ℎ = 0, = 1,2, … ,
dimana ( ), dan ℎ adalah fungsi skalar, pada komponen disebut dengan desain variabel, ( ) adalah fungsi tujuan, disebut fungsi kendala dan ℎ disebut dengan fungsi kendala kesetaraan.
Defenisi Orde Konvergensi
Misalkan adalah akar dari persamaan nonlinear dan adalah barisan yang konvergen ke , definisikan nilai error sebagai berikut (Chavnov 2012):
= − (2)
Untuk besar memiliki hubungan penaksiran :
| + 1| = | | (3)
Nilai disebut orde konvergensi, dengan adalah konstanta positif.
Metode Newton Raphson (N)
Nilai minimum terjadi apabila ′( ) = 0, berarti solusi yang dapat diberikan adalah sebagai berikut (Snyman 2005):
4
Jika f (x) memiliki bentuk yang lebih umum, maka solusi yang diberikan tidak memungkinkan secara umum. Dalam hal ini, solusi dapat diperoleh secara numerik melalui algoritme Newton Raphson.
Diberikan sebuah pendekatan , maka menghitung nilai iterasinya adalah : = − ( )( ); = 0, 1, 2, … (5) Diharapkan lim→ = ∗ , adalah iterasi konvergen, dalam hal ini merupakan solusi numerik yang cukup akurat untuk diperoleh dengan jumlah iterasi yang terbatas.
Metode Newton Halley (NH)
Metode iterasi merupkan metode untuk menemukan akar sederhana dari persamaan nonlinear (Noor et al. 2007) : Dimana γ adalah tebakan awal.
Dari persamaan (7), diperoleh (Noor et al. 2007):
= γ − ( )( ) (8)
Dari persamaan (7) juga diperoleh
= γ − ( ) ( )( ) ( )"( ) (10) Persamaan (10) memperlihatkan metode iterasi yang dapat digunakan untuk memecahkan persamaan nonlinear.
Langkah 2. Untuk nilai yang diberikan, hitung solusi akar dengan skema iterasi
= − ( ) ( )( ) ( )"( ) (11)
5
= − ( )( ), (12)
= − ( ) ( )( ) ( )"( ) (13)
Metode Newton Trapesium Secant (NTS)
Jain (2013) pada penelitiannya menggunakan kombinasi metode secant dengan modifikasi metode Newton yang telah dikembangkan oleh Weerakoon dan Fernando (2000) yaitu Aturan Trapesium dan Homeier (2005) yaitu fungsi invers. Jain (2013) mendapatkan formula yang disebut dengan metode secant trapesium Newton dan metode secant invers Newton. Adapun bentuk modifikasi dari metode Secant Trapesium Newton (Jain 2013):
= ̅ − ( ̅ ) ( )̅ ( ̅ ) (14) dimana
̅ = − ( )
( ∗) ( ) (15)
dengan
∗ = − ( )
( ) (16)
Pada modifikasi metode Jain, tahapan yang dilakukan adalah menghitung metode Newton terlebih dahulu, hasil dari metode Newton berupa titik ∗. Tahapan selanjutnya, titik ∗ disubstitusikan ke metode Aturan Trapesium. Hasil dari Aturan Trapesium berupa titik ̅ . Tahap akhir adalah titik ̅ yang merupakan hasil dari Aturan Trapesium akan disubstitusikan kembali ke metode Secant seperti terlihat pada persamaan 14.
Metode Newton Trapesium (NT)
Metode Newton dengan Aturan Trapesium diperkenalkan oleh Weerakoon et al (2000). Metode ini merupakan varian metode Newton dengan hasil berupa orde konvergen yang lebih tinggi daripada metode Newton sendiri. Sehingga dalam melakukan pemecahan masalah untuk optimasi akan menggunakan iterasi yang lebih sedikit (Weerakoon 2000).
Langkah pertama dengan teorema Newton,
( ) = ( ) + ∫ ( ) (17)
pada skema diusulkan dengan menggunakan Aturan Trapesium ABCD,
∫ ( ) ≈ ( − )[ ( ) + ( )] (18)
sehingga persamaan yang ekivalen dengan persamaan :
( ) = ( ∗ ) + ( ∗ )( − ∗ ) (19)
adalah
( ) = ( ) + ( − )[ ( ) + ( )] (20)
6
metode Newton sesuai dengan nilai dari kemiringan ( ) sebuah fungsi, ini bukan berarti juga sesuai dengan kurva dari fungsi "( ).
Lakukan iterasi selanjutnya sebagai dasar dari model persamaan (21) ( ) − 0,
⇒ ( ) + 12 ( )[ ( ) + ( )] = 0
⇒ = − [ ( )( )( )] (22)
jelas terlihat bahwa hal ini merupakan skema implisit, yang harus memiliki turunan dari fungsi pada ( + 1) tahapan iterasi untuk menjumlahkan ( + 1) iterasi itu sendiri. Ini dapat diatasi dengan memanfaatkan tahapan iterasi Newton untuk menghitung ( + 1) pada sisi kanan.
Maka hasil dari skema baru adalah :
= − [ ( ) ( )( ∗ )], n = 0, 1, 2,..., dimana ∗ = − ( )
( ). (23)
Metode Trapesium Halley (TH)
Metode Halley merupakan metode dengan konvergen orde ketiga untuk akar sederhana dan memerlukan turunan kedua fungsi yang terkadang memerlukan cost yang besar untuk memperolehnya (Putra et al. 2012). Untuk kombinasi metode TH dilakukan dengan menghitung metode Aturan Trapesium pada persamaan 24 (Weerakoon 2000) :
∗ = − [ ( ) ( )( )] (24) dan disubstitusikan dengan menggunakan metode Halley seperti yang terlihat pada persamaan 25 (Noor et al. 2007):
= ∗− ( ∗() (∗) (∗)∗)"( ∗) (25)
Metode Halley
Metode Halley merupakan metode dengan algoritme orde ketiga. Algoritme tersebut memiliki konvergen orde ketiga yang mana jumlah signifikan digit akhirnya sebanyak tiga untuk setiap kali iterasi. Metode Halley tidak hanya melakukan turunan pertama dari orde ketiga iterasi fungsi, tetapi berlanjut pada turunan kedua (Scavo dan Thoo 1994).
S eperti yang diketahui bahwa metode Newton merupakan metode iteratif untuk menghitung pendekatan dari akar dengan menggunakan persamaan 26 (Scavo dan Thoo 1994):
= − ( )( ), = 0,1, … (26) Berdasarkan persamaan 26 yang diturunkan menggunakan deret taylor polynomial tingkat pertama, maka diperoleh rumus metode Halley dengan menggunakan turunan dari deret taylor polinomial tingkat dua seperti pada persamaan 27 (Scavo dan Thoo 1994) :
7
3
METODE
Tempat dan Waktu Penelitian
Penelitian ini dilaksanakan pada bulan Januari 2016 sampai dengan bulan Juni 2016. Lokasi penelitian bertempat di Institut Pertanian Bogor (IPB), Fakultas Matematika dan Ilmu Pengetahuan Alam, Departemen Ilmu Komputer, Laboratorium Computer Intelligent (CI).
Perangkat Penelitian
Penelitian ini dilakukan dengan menggunakan perangkat keras dan perangkat lunak sebagai berikut :
Perangkat keras berupa komputer personal dengan spesifikasi : ProcessorIntel (R) Pentium (R) CPU [email protected] RAM 2 GB
Mouse dan keyboard
Perangkat lunak yang digunakan adalah : Sistem operasi windows 7 Ultimate 32-bit Microsoft Excel 2013 untuk pegolahan data
Matlab R2010b ver. 7.11.0 untuk implementasi algoritme dan pengujian komputasi
Tahapan Penelitian
Dalam penelitian ini akan dilakukan beberapa tahapan, seperti yang akan dijelaskan pada Gambar 1.
Gambar 1 Diagram alur penelitian
Studi Literatur
8
digunakan yaitu metode Newton dan metode Halley beserta kelebihan dan kekurangan masing-masing yang dimiliki oleh metode tersebut.
Kombinasi Metode Newton, Aturan Trapesium dan Metode Halley
Tahap ini akan dilakukan kombinasi varian metode Newton dan Aturan Trapesium yang sebelumnya telah dilakukan oleh Weerakoon dan Fernando (2000) :
= − [ ( ) ( )( ∗ )], n = 0, 1, 2,..., dimana ∗ = − ( )
( ). (28) dengan metode optimasi lainnya yaitu metode Halley.
= ∗ ( ( ∗))( ∗) (( ∗) (∗) ∗) (29) Kombinasi dilakukan dengan cara mensubstitusikan hasil yang diperoleh dari satu metode ke metode lainnya.
Pembuatan Algoritme Metode Kombinasi
Pada tahap ini, kombinasi metode Newton, Aturan Trapesium dan metode Halley akan dibentuk kesebuah algoritme baru untuk penyelesaian masalah optimasi nonlinear tanpa kendala.
Implementasi Algoritme Metode Kombinasi
Implementasi algoritme dilakukan dengan cara menginputkan algoritme baru dan mengimplementasikannya menggunakan software yang dapat digunakan untuk menjalankan algoritme ini.
Pengujian Komputasi
Pada tahap ini akan dilakukan uji komputasi dengan menggunakan algoritme metode Newton dan algoritme baru yang dilakukan dari hasil kombinasi metode dengan menggunakan beberapa fungsi nonlinear (Weerakoon dan Fernando 2000) :
+ 4 − 10
sin ( ) − + 1
− − 3 + 2
cos( ) − ( − 1) − 1
− 10
exp( ) − sin ( ) + 3 cos( ) + 5 sin ( ) + exp[ cos( ) sin( )] − 28 exp( + 7 − 30) − 1
9
4
HASIL DAN PEMBAHASAN
Studi Literatur
Pada penelitian ini dilakukan studi literatur mengenai metode Newton dan metode Halley. Dalam beberapa studi literatur yang ditemukan, terdapat beberapa kombinasi metode menggunakan metode Newton dan metode Halley. Weerakoon dan Fernando (2000) melakukan modifikasi metode Newton dan Aturan Trapesium (NT) sehingga menghasilkan metode baru dengan penggunaan jumlah iterasi yang lebih sedikit dibandingkan dengan metode Newton, serta menghasilkan konvergen orde ketiga. Jain (2013) melakukan modifikasi metode Newton yang sebelumnya telah dilakukan oleh Weerakoon dan Fernando (2000) dengan menambahkan metode Secant ke dalam metode Newton dengan Aturan Trapesium. Penelitian ini menghasilkan metode Newton Trapesium Secant (NTS) dengan konvergen orde keempat. Selanjutnya Noor (2007) melakukan modifikasi metode Halley dan menghasilkan pengembangan baru dari metode Halley sehingga menghasilkan metode yang lebih baik dengan konvergen orde kelima. Narang et al. (2000) menyatakan bahwa metode Halley merupakan metode numerik dengan konvergen orde ketiga. Sehingga dapat disimpulkan bahwa metode Halley memiliki orde kekonvergenan yang lebih tinggi dibandingkan metode Newton yang memiliki konvergen orde kedua.
Kombinasi Metode Newton, Aturan Trapesium dan Metode Halley
Pada penelitian ini dilakukan kombinasi metode dengan menggunakan beberapa metode iterasi, yaitu metode Newton, Aturan Trapesium dan Metode Halley yang bertujuan untuk mencari akar dari suatu fungsi nonlinear. Kombinasi metode ini, setiap iterasinya dilakukan tiga kali evaluasi fungsi dengan cara menggabungkan ketiga metode tersebut.
Langkah pertama untuk setiap satu kali iterasi dimulai dengan menggunakan metode Newton seperti persamaan (Luenberger dan Ye 2008) :
∗ = − ( )
( ) (30)
dengan = adalah titik tebakan awal dan ( ) merupakan turunan pertama fungsi dengan mensubstitusikan titik tebakan awal. Pemilihan metode Newton sebagai fungsi pertama pada kombinasi ini dikarenakan metode Newton tidak memerlukan cost yang besar dalam pencarian akar.
Tahap selanjutnya, akar yang diperoleh dari langkah pertama akan disubstitusikan ke dalam formula Aturan Trapesium seperti berikut (Weerakoon dan Fernando 2000):
∗ = − [ ( )( )( ∗ )] (31)
10
sebelumnya oleh (Weerakoon dan Fernando 2000), dengan mengkombinasikan metode Newton dan Aturan Trapesium. Metode yang dikembangkan oleh Weerakoon dan Fernando ini menghasilkan jumlah iterasi yang lebih sedikit dibandingkan dengan menggunakan metode Newton tanpa kombinasi dan menghasilkan konvergen orde ketiga.
Dan pada tahap terakhir untuk setiap satu kali iterasi akan ditambahkan dengan menggunakan formula metode Halley. Metode Halley merupakan salah satu metode iterasi dengan konvergen orde ketiga. Formula metode Halley akan disubtitusikan pada persamaan (32)
= ∗ − ( ( ∗))( ∗) (( ∗) (∗) ∗) (32) dengan ∗ merupakan hasil yang diperoleh dari kombinasi metode Newton dan Aturan Trapesium.
Pembuatan Algoritme
Dalam pembuatan algoritme metode Newton, Aturan Trapesium dan metode Halley, diperlukan beberapa tahapan, yaitu :
Langkah 1. Definisikan fungsi ( )
Langkah 2. Inputkan titik tebakan awal ℝ Langkah 3. Inputkan batas toleransi 0 < < 1 Langkah 4. Inputkan batas maksimum iterasi Langkah 5. Hitung = − (( ))
Hitung ∗ = − [ ( () )( )]
Hitung = ∗ ( ( ∗))( ∗) (( ∗) (∗) ∗)
Langkah 6. Hitung | − | < atau jika jumlah iterasi mencapai batas maksimum maka berhenti, jika tidak kembali ke langkah 5. Langkah yang dilakukan dalam algoritme metode NTH adalah mendefiniskan ( ), yang selanjutnya dilakukan peng-input-an titik tebakan awal . Dilanjutkan dengan meng-input-kan batas toleransi dan batas maksimum iterasi. Setelah itu dilakukan perhitungan masing-masing metode yang dimulai dengan metode Newton. Hasil yang diperoleh dari metode Newton disubtitusikan ke persamaan selanjutnya, yaitu persamaan Aturan Trapesium. Hasil yang diperoleh dari perhitungan Aturan Trapesium, akan disubtitusikan kembali ke metode Halley. Proses perhitungan ini akan terus berlanjut sampai kriteria pemberhentian terpenuhi. Pada dasarnya untuk menentukan solusi numerik mempunyai kriteria pemberhentian adalah sama untuk semua metode. Salah satu kriteria untuk pembatasan proses iterasi program komputasi atau uji konvergesi adalah selisih dua nilai atau titik terakhir yang disimbolkan dengan | −
11
2011). Ketika salah satu kriteria terpenuhi maka proses iterasi komputasi akan berhenti.
Algoritme metode Newton Trapesium Halley (NTH) membutuhkan titik tebakan awal yaitu untuk menyelesaikan suatu fungsi persamaan. Semakin dekat titik tebakan awal yang digunakan, maka akan semakin sedikit jumlah iterasi dan semakin kecil running time yang diperlukan. Selanjutnya menginputkan batas toleransi untuk menentukan tingkat ketelitian dari hasil yang diperoleh. Semakin kecil nilai toleransi yang digunakan, maka hasil yang diperoleh akan semakin mendekati nilai eksak.
Implementasi Algoritme
Implementasi algoritme varian metode Newton Trapesium Halley (NTH) dilakukan dengan cara menginputkan algoritme metode ke sebuah software. Hal ini dilakukan untuk mempermudah pengujian komputasi terhadap metode-metode yang akan diujikan. Hasil yang diperoleh dari tahap pembuatan algoritme metode NTH diimpelementasikan ke dalam sebuah program. Untuk lebih lengkapnya, implementasi algoritme NTH dapat dilihat pada Lampiran 1.
Pengujian Komputasi
Pengujian komputasi dilakukan dengan menggunakan beberapa fungsi nonlinear standar yang telah digunakan oleh peneliti sebelumnya dengan meng-input-kan dua buah nilai toleransi yang berbeda, yaitu 10 dan 10 . Hal ini dilakukan untuk membandingkan seberapa jauh perbedaan antara jumlah iterasi dan running time yang dihasilkan. Metode yang digunakan pada pengujian komputasi menggunakan delapan metode, yaitu metode Newton (N), metode Halley (H), Aturan Trapesium (T), metode kombinasi Newton Trapesium Halley (NTH), Newton Halley (NH), Newton Trapesium Secant (NTS), Newton Trapesium (NT) dan Trapesium Halley (TH).
12
dibandingkan dengan metode Newton dan metode Trapesium pada penggunaan toleransi 10 . Tetapi jika dibandingkan dengan metode lainn
merupakan metode kombinasi,
secara umum terlihat jauh lebih kecil. NTS menghasilkan running time
lainnya. Jika dijumlahkan untuk semua fungsi yang digunakan, diperoleh oleh metode NTS adalah 0.8570 ms.
memperoleh jumlah running time
Running time yang dihasilkan terlihat lebih sedikit dari beberapa metode lainnya yaitu metode N dengan 0.2748
dengan 0.2407 ms, metode NH dengan 0.2490 ms. Untuk metode TH sendiri menghasilkan dibandingkan dengan metode lainnya.
oleh banyaknya evaluasi fungsi yang dilakukan dalam satu kali iterasi dan besar cost yang dihasilkan pada
dengan menggunakan toleransi
toleransi 10 yang dapat dilihat pada Lampiran 2
yang diperoleh dengan menggunakan metode usulan NTH lebih baik daripada metode lainnya dengan hasil 0.2323 ms. Metode NTS menghasilkan
yang lebih besar dibandingkan metode lainnya, yaitu 2.4954 ms. Sedangkan Perbandingan running time metode dengan toleransi 10
Running Time (ms)
terlihat bahwa metode yang diusulkan dalam penelitian ini, yaitu metode NTH menghasilkan running time yang cukup besar dibandingkan dengan metode Newton dan metode Trapesium pada penggunaan
. Tetapi jika dibandingkan dengan metode lainnya yang juga merupakan metode kombinasi, running time yang dihasilkan oleh metode NTH secara umum terlihat jauh lebih kecil. Secara garis besar, dapat terlihat metode running time yang lebih besar dibandingkan dengan metode dijumlahkan untuk semua fungsi yang digunakan, running time diperoleh oleh metode NTS adalah 0.8570 ms. Metode usulan yaitu metode NTH,
running time untuk keseluruhan fungsi adalah 0.2403 ms. yang dihasilkan terlihat lebih sedikit dari beberapa metode lainnya yaitu metode N dengan 0.2748 ms, metode H dengan 0.3237 ms, metode T , metode NH dengan 0.2490 ms dan metode NT dengan 0.4423 Untuk metode TH sendiri menghasilkan running time yang lebih sedikit dibandingkan dengan metode lainnya. Running time yang dihasilkan dipengaruhi oleh banyaknya evaluasi fungsi yang dilakukan dalam satu kali iterasi dan besar
dihasilkan pada setiap metode kombinasi. Untuk hasil yang dip dengan menggunakan toleransi 10 tidak jauh berbeda dengan penggunaan
ng dapat dilihat pada Lampiran 2. Tetapi jumlah running time yang diperoleh dengan menggunakan metode usulan NTH lebih baik daripada metode lainnya dengan hasil 0.2323 ms. Metode NTS menghasilkan running time yang lebih besar dibandingkan metode lainnya, yaitu 2.4954 ms. Sedangkan
TH
terlihat bahwa metode yang diusulkan dalam penelitian yang cukup besar jika dibandingkan dengan metode Newton dan metode Trapesium pada penggunaan ya yang juga yang dihasilkan oleh metode NTH Secara garis besar, dapat terlihat metode yang lebih besar dibandingkan dengan metode running time yang Metode usulan yaitu metode NTH, untuk keseluruhan fungsi adalah 0.2403 ms. yang dihasilkan terlihat lebih sedikit dari beberapa metode lainnya , metode T dan metode NT dengan 0.4423 yang lebih sedikit dipengaruhi oleh banyaknya evaluasi fungsi yang dilakukan dalam satu kali iterasi dan besar asil yang diperoleh tidak jauh berbeda dengan penggunaan running time yang diperoleh dengan menggunakan metode usulan NTH lebih baik daripada
13
metode N dengan 0.2746 ms, metode T dengan 0.3370 ms, metode NH dengan 0.2808 ms, metode NT dengan 0.4696 ms dan metode TH dengan 0.2451 ms. Tabel 2 menujukkan perbandingan jumlah iterasi dengan menggunakan toleransi 10 .
Tabel 2 Perbandingan jumlah iterasi menggunakan toleransi 10
( ) N T H NTH TH NH NTS NT Jumlah Iterasi
Berdasarkan Tabel 2 jumlah iterasi yang diperoleh oleh masing-masing metode manggunakan toleransi10 , dapat dilihat secara keseluruhan bahwa metode yang diusulkan yaitu metode NTH menghasilkan jumlah iterasi yang lebih sedikit dibandingkan dengan metode lainnya dengan 49 iterasi. Sedangkan metode Newton sendiri menghasilkan jumlah iterasi yang paling banyak diantara semua metode dengan jumlah 264 iterasi. Penggunaan titik tebakan awal dan batas toleransi sangat berpengaruh. Jika titik tebakan awal yang digunakan mendekati nilai sebenarnya, maka jumlah iterasi yang diperoleh akan semakin sedikit. Batas toleransi juga mempengaruhi proses pencarian akar, jika kriteria pemberhentian proses iterasi belum terpenuhi yaitu | − | <
14
90 iterasi, metode NTS dengan 62 iterasi dan metode NT dengan 206 iterasi. Pada Tabel 3 menunjukkan perbandingan nilai akar menggunakan toleransi 10 .
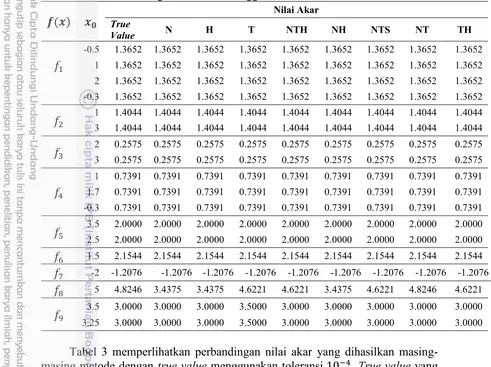
Tabel 3 Perbandingan nilai akar menggunakan toleransi 10
( ) True Nilai Akar
15
menggunakan toleransi 10 tidak jauh berbeda dengan menggunakan toleransi 10 .
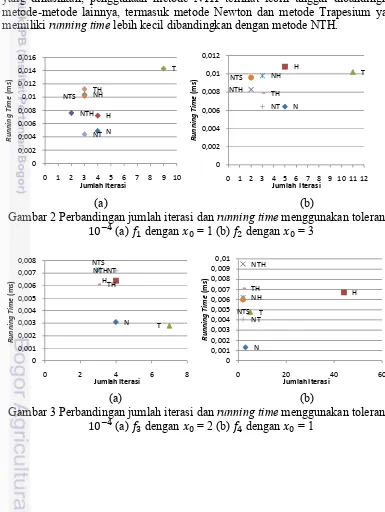
Gambar 2 sampai dengan Gambar 6 menunjukkan grafik perbandingan antara jumlah iterasi dan running time yang dihasilkan dengan melakukan percobaan uji komputasi menggunakan batas toleransi 10 . Untuk grafik perbandingan jumlah iterasi dan running time dengan menggunakan toleransi 10 dapat dilihat pada Lampiran 5. Perbandingan tersebut memperlihatkan bahwa running time tidak bergantung kepada jumlah iterasi yang dihasilkan. Hal ini terjadi karena masing-masing metode yang digunakan melakukan jumlah evaluasi fungsi kerja yang berbeda-beda untuk setiap masing-masing iterasi, sehingga mempengaruhi waktu yang digunakan untuk melakukan pencarian solusi. Untuk metode yang diusulkan yaitu metode NTH, running time yang dimiliki cukup besar dibandingkan beberapa metode lainnya seperti metode Newton dan metode Trapesium. Hal ini dikarenakan metode NTH melakukan tiga kali evaluasi fungsi sedangkan metode Newton dan metode Trapesium hanya melakukan satu kali evaluasi fungsi untuk setiap iterasinya. Tetapi jika dilihat dari jumlah iterasi yang dihasilkan, penggunaan metode NTH terlihat lebih unggul dibandingkan metode-metode lainnya, termasuk metode Newton dan metode Trapesium yang memiliki running time lebih kecil dibandingkan dengan metode NTH.
(a) (b)
Gambar 2 Perbandingan jumlah iterasi dan running time menggunakan toleransi 10 (a) dengan = 1 (b) dengan = 3
(a) (b)
16
(a) (b)
Gambar 4 Perbandingan jumlah iterasi dan running time menggunakan toleransi 10 (a) dengan = 2.5 (b) dengan = 1.5
(a) (b)
Gambar 5 Perbandingan jumlah iterasi dan running time menggunakan toleransi 10 (a) dengan = -2 (b) dengan = 5
17
5
SIMPULAN DAN SARAN
Simpulan
Metode Newton merupakan salah satu metode numerik terbaik yang digunakan untuk mencari nilai akar dari suatu fungsi. Akan tetapi pencarian solusi dengan menggunakan metode Newton masih menghasilkan jumlah iterasi yang cukup banyak. Oleh karena itu, pada penelitian ini diusulkan metode kombinasi Newton Trapesium Halley (NTH) untuk mencari nilai akar dari fungsi nonlinear. Perbandingan antara metode NTH dengan beberapa metode yaitu, metode Newton (N), metode Halley (H), metode Aturan Trapesium (T), metode Newton Halley (NH), metode Newton Trapesium Secant (NTS), metode Newton Trapesium (NT) dam metode Trapesium Halley (TH) memperlihatkan bahwa hasil pencarian solusi yang diperoleh dari segi jumlah iterasi pada kombinasi metode NTH lebih bagus. Jika dilihat dari running time yang digunakan metode NTH membutuhkan waktu yang cukup lama dibandingkan dengan metode yang proses pencarian akarnya hanya melakukan satu kali evaluasi fungsi dalam satu kali iterasi. Tetapi apabila dibandingkan dengan metode kombinasi lain yang melakukan beberapa kali evaluasi fungsi dalam satu kali iterasi, waktu yang digunakan oleh metode NTH dalam mencari nilai akar lebih cepat. Hasil yang diperoleh dengan menggunakan metode NTH memperlihatkan bahwa nilai akar yang diperoleh menggunakan sembilan fungsi yang diujikan hampir secara keseluruhan mendekati true value. Tetapi pada persamaan = sin ( ) + exp[ cos( ) sin( )] − 28, hasil nilai akar yang diperoleh menggunakan masing-masing metode yang diujikan dengan true value memperlihatkan perbedaan yang cukup jelas. Jika dilihat pada perbedaan nilai akar antara true value dengan metode NTH tidak terlalu jauh. Oleh sebab itu, hasil yang diperoleh dengan melakukan uji komputasi dalam penelitian ini menunjukkan bahwa kombinasi algoritme metode Newton, Aturan Trapesium dan metode Halley (NTH) baik digunakan untuk pencarian nilai akar dari fungsi nonlinear.
Saran
Untuk penelitian selanjutnya, perlu dilakukan uji komputasi dengan fungsi-fungsi nonlinear lain dan kasus-kasus real yang dapat dipecahkan menggunakan metode numerik khususnya metode usulan yaitu metode NTH.
DAFTAR PUSTAKA
Chavnov JR. 2012. Introduction to Numerical Method. The Hongkong University of Science and Technology, Hogkong :Creative Commons Attribution 3.0 Hong Kong
Cerdà V, Cerdà JL, Idris AM. 2015. Optimization using the gradient and simplex methods. Talanta. Doi : 10.1016/j.talanta.2015.05.061.
18
Homeier HHH. 2005. On Newton-type Methods with Cubic Convergence. Journal of Computational and Applied Mathematic 176: 425-432.
Jain D. 2013. Families of Newton-Like Methods with Fourth-Order Convergence. International Journal of Computer Mathematic 90(5): 1072-1082.
Kumar M, Singh AK, Srivastava A. 2012. Various Newton-type Iterative Methods for Solving Nonlinear Equations. Journal of the Egyptian Mathematic Society 21,334-339.
Luenberger DG, Ye Y. 2008. Linear and Nonlinear Programing Third Edition. Stanford, California: Springer.
Narang M, Bathia S, Kanwar GV. 2015. Newton two-parameter Chebyshev-Halley-like family of fourth and sixth-order methods for systems of nonlinear equation. Applied Mathematics and Computation 275 (2016) 394-403.
Noor MA, Khan WA, Hussain A. 2007. A new modified Halley method without second derivatives for nonlinear equation. 189: 1268–1273.
Putra S, Agusni, Restu YP. 2012. Kombinasi Metode Newton dengan Metode Iterasi yang Diturunkan Berdasarkan Kombinasi Linear Beberapa Kuadratur untuk Menyelesaikan Persamaan Nonlinear. Jurnal Sains, teknologi Industri. 10 (1): 85-89
Sánchez MG. 2009. Improving Order and Efficiency: Composition with a Modified Newton’s Method. Journal of Computational and Applied Mathematics 231, 592-597.
Scavo TR, Thoo JB. 1994. American Mathematical Monthly.
Snyman JA. 2005. Practical Mathematical Optimization. An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. University of Pretoria, Pretoria, South Africa : Springer.
Utami NNR, Widan IN, Asih ND. 2013. Perbandingan Solusi Sistem Persamaan Nonlinear Menggunakan Metode Newton-Raphson dan Metode Jacobian. E-jurnal Matematika 2(2): 11-17.
20
Lampiran 1 Implementasi setiap metode menggunakan Matlab
Sintaks untuk metode Newton
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_new= y - [f(y)/f1(y)];
n(i)= x_new y = n(i);
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi) break;
end end end
21
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk Aturan Trapesium
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_trap= y - (2*f(y))/[f1(y)+f1(y+1)];
n(i)= x_trap y = n(i);
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi)
break;
end end end
22
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk metode Halley
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_halley = y - [(2*f(y)*f1(y))/(2*(f1(y))^2-f2(y)*f(y))];
n(i)= x_halley y = n(i);
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi) break;
end end end
23
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk Aturan Trapesium Halley (TH)
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_trap= y - (2*f(y))/[f1(y)+f1(y+1)];
x_halley = x_trap-[(2*f(x_trap)*f1(x_trap))/(2*(f1(x_trap))^2-f2(x_trap)*f(x_trap))];
n(i)= x_halley y = n(i);
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi)
break;
end end end
24
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk Newton Trapesium Secant (NTS)
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_new= y - [f(y)/f1(y)];
x_trap= y - (2*f(y))/[f1(y)+f1(x_new)];
x_sec= x_trap - [2*(x_trap-y)/(f(x_trap)-f(y))]*[f(x_trap)];
n(i)= x_sec y = n(i); check_fx = [f(y)];
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi) || (check_fx == 0)
break; end end end
25
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk Newton Trapesium (NT)
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_new= y - [f(y)/f1(y)];
x_trap= y - (2*f(y))/[f1(y)+f1(x_new)];
n(i)= x_trap y = n(i);
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi)
break;
end end end
26
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk Newton Trapesium Halley (NTH)
syms x; %
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_new= y - [f(y)/f1(y)];
x_trap= y - (2*f(y))/[f1(y)+f1(x_new)];
x_halley = x_trap-[(2*f(x_trap)*f1(x_trap))/(2*(f1(x_trap))^2-f2(x_trap)*f(x_trap))];
n(i)= x_halley y = n(i);
if i==1
else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi)
break;
end end end
27
Lampiran 1 Lanjutan Implementasi setiap metode menggunakan Matlab
Sintaks untuk Newton Halley (NH)
syms x;
fun = input ('input f(x): '); f=inline(fun);
z=diff(f(x)); s=diff(z); f1=inline(z); f2=inline(s);
x0=input('input nilai X:');
toleransi = input ('input nilai toleransi:'); max_iterasi = input ('input max iterasi:');
tic;
y=x0;
for i=1:max_iterasi
x_new= y - [f(y)/f1(y)];
x_halley = x_new - [(2*f(x_new)*f1(x_new))/(2*(f1(x_new))^2-f2(x_new)*f(x_new))];
n(i)= x_halley y = n(i);
if i==1 else
b = n(i)-n(i-1); c = abs(b);
if (c <= toleransi) break;
end end end
28
Lampiran 2 Perbandingan 10
Perbandingan running time masing-masing metode untuk toleransi
Running Time (ms)
H T NTH NH NTS
0.0743 0.0598 0.0117 0.0291 0.0720 0 0.0097 0.0312 0.0122 0.0101 0.0176 0 0.0097 0.0351 0.0080 0.0102 0.2269 0 0.0524 0.0671 0.0117 0.0510 0.2332 0 0.0132 0.0302 0.0126 0.0113 0.0198 0 0.0134 0.0476 0.0141 0.0146 0.0137 0 0.0060 0.0022 0.0056 0.0082 0.2335 0 0.0146 0.0640 0.0137 0.0098 0.2484 0 0.0070 0.0123 0.0060 0.0091 0.0085 0 0.0087 0.0092 0.0096 0.0092 0.1806 0 0.0111 0.0152 0.0097 0.0118 0.2016 0 0.0111 0.0468 0.0131 0.0121 0.2021 0 0.0112 0.0562 0.0104 0.0122 0.2121 0 0.0085 0.0312 0.0093 0.0089 0.0220 0 0.0179 0.1701 0.0233 0.0197 0.0223 0 0.0296 0.0964 0.0270 0.0270 0.3126 0 0.0207 0.1133 0.0220 0.0202 0.2446 0 0.0179 0.1052 0.0123 0.0063 0.0239 0 0.3370 0.9931 0.2323 0.2808 2.4954 0.4696
masing metode untuk toleransi
29
Lampiran 3 Perbandingan jumlah iterasi masing-masing metode untuk toleransi 10
( ) N T H NTH TH Jumlah Iterasi NH NTS NT
-0,5 132 39 73 4 5 8 31 7
1 6 32 3 3 3 3 4 4
2 6 33 3 3 3 3 3 4
-0,3 54 36 52 4 4 25 7 7
1 7 35 4 3 3 3 5 5
3 7 36 2 3 3 4 4 4
2 2 2 3 2 2 2 4 2
3 7 47 2 3 3 4 4 5
1 5 14 2 2 2 3 3 3
1,7 5 15 3 3 3 3 3 4
-0,3 6 14 3 3 2 4 3 4
3,5 8 64 3 4 4 4 4 6
2,5 7 62 3 3 3 4 3 5
1,5 7 32 3 3 3 3 5 5
-2 9 133 4 4 3 4 5 6
5 10 68 4 4 3 5 3 119
3,5 13 2 4 5 6 4 6 9
3,25 9 2 4 4 4 4 5 7
( ) Nilai Akar
N T H NTH TH NH NTS NT
-0.5 1.365230013414090 1.365230013414090 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341448 1 1.365230013414090 1.365230013414090 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341448 2 1.365230013414090 1.365230013414090 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341448 -0.3 1.365230013414090 1.365230013414090 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341409 1.36523001341448 1 1.404491648215340 1.404491648215340 1.40449164821534 1.40449164821534 1.40449164821534 1.40449164821534 1.40449164821534 1.40449164821621 3 1.404491648215340 1.404491648215340 1.40449164821534 1.40449164821534 1.40449164821534 1.40449164821534 1.40449164821534 1.40449164821621 2 0.257530285439771 0.257530285439771 0.257530285439771 0.25753028543977 0.25753028543977 0.25753028543977 0.25753028543977 0.25753028543977 3 0.257530285439771 0.257530285439771 0.257530285439771 0.25753028543977 0.25753028543977 0.25753028543977 0.25753028543977 0.25753028543977 1 0.739085133215161 0.739085133215161 0.739085133215161 0.73908513321516 0.73908513321516 0.73908513321516 0.73908513321516 0.73908513321476 1.7 0.739085133215161 0.739085133215161 0.739085133215161 0.73908513321516 0.73908513321516 0.73908513321516 0.73908513321516 0.73908513321476 -0.3 0.739085133215161 0.739085133215161 0.739085133215161 0.73908513321516 0.73908513321516 0.73908513321516 0.73908513321516 0.73908513321476 3.5 2.000000000000000 2.000000000000000 2.000000000000000 2.00000000000000 2.00000000000000 2.00000000000000 2.00000000000000 2.00000000000000 2.5 2.000000000000000 2.000000000000000 2.000000000000000 2.00000000000000 2.00000000000000 2.00000000000000 2.00000000000000 2.00000000000000 1.5 2.154434690031880 2.154434690031880 2.15443469003188 2.15443469003188 2.15443469003188 2.15443469003188 2.15443469003188 2.15443469003367 -2 -1.20764782713013 -1.20764782713013 -1.20764782713013 -1.20764782713013 -1.20764782713013 -1.20764782713013 -1.20764782713013 -1.20764782713013 5 3.437471743421760 4.622104163552840 3.43747174342176 4.62210416355283 4.62210416355283 3.43747174342176 4.62210416355283 4.82458931731526 3.5 3.000000000000000 3.500000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.25 3.000000000000000 3.500000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.00000000000000 3.00000000000000
Lampiran 4 Perbandingan nilai akar untuk masing-masing metode dengan toleransi10
31
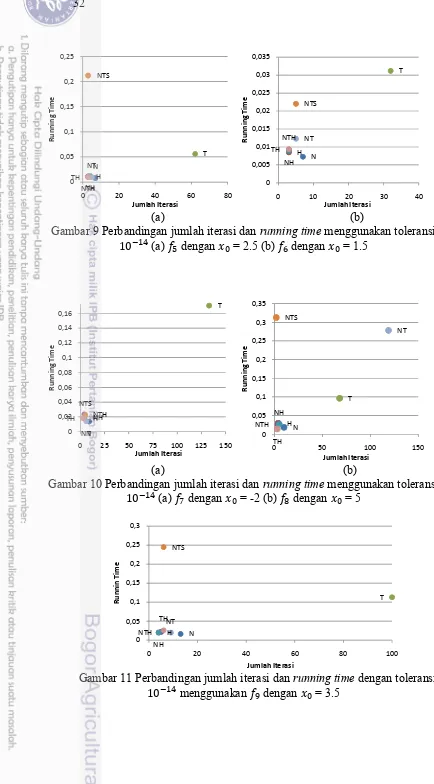
Lampiran 5 Perbandingan jumlah iterasi dan running time dan masing-masing metode untuk toleransi 10
(a) (b)
Gambar 7 Perbandingan jumlah iterasi dan running time menggunakan toleransi 10 (a) dengan = 2 (b) dengan = 1
(a) (b)
32
(a) (b)
Gambar 9 Perbandingan jumlah iterasi dan running time menggunakan toleransi 10 (a) dengan = 2.5 (b) dengan = 1.5
(a) (b)
Gambar 10 Perbandingan jumlah iterasi dan running time menggunakan toleransi 10 (a) dengan = -2 (b) dengan = 5
33