Aplikasi Metode Maksimum Likelihood Dalam Regresi Linier Berganda

APLIKASI METODE MAKSIMUM LIKELIHOOD DALAM REGRESI LINIER BERGANDA

SKRIPSI

CITRA JULIANA HASIBUAN 090823023

KEMENTRIAN PENDIDIKAN NASIONAL

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

APLIKASI METODE MAKSIMUM LIKELIHOOD DALAM REGRESI LINIER BERGANDA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

CITRA JULIANA HASIBUAN 090823023

KEMENTRIAN PENDIDIKAN NASIONAL

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : APLIKASI METODE MAKSIMUM LIKELIHOOD DALAM REGRESI LINIER BERGANDA

Kategori : SKRIPSI

Nama : CITRA JULIANA HASIBUAN

Nomor Induk Mahasiswa : 090823023

Program Studi : S1 STATISTIKA EKSTENSI Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (MIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juli 2011

Komisi Pembimbing :

Pembimbing 2, Pembimbing 1,

Drs. Rachmad Sitepu, M. Si Drs. Ujian Sinulingga, M. Si

NIP. 19530418 198703 1 001 NIP. 19560303 198403 1 004

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si

PERNYATAAN

APLIKASI METODE MAKSIMUM LIKELIHOOD DALAM REGRESI LINIER BERGANDA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2011

PENGHARGAAN

Diawali dengan mengucapkan Puji Syukur Kehadirat Allah SWT, yang selama ini telah memberikan Penulis kekuatan dan semangat sehingga penyusunan Skripsi ini dapat diselesaikan dengan baik dan tepat waktu.

Adapun tujuan dari penulisan Skripsi ini adalah merupakan salah satu syarat untuk menyelesaikan Program S1 Statistika Ekstensi pada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

Sebagai salah satu perwujudan dari proses pendidikan kemahasiswaan, penyusunan Skripsi ini disajikan berdasarkan pembahasan oleh penulis dari Model Eksponen Berganda.

Selama dalam penyusunan Skripsi ini penulis telah banyak memperoleh bantuan dan bimbingan, untuk itu pada kesempatan ini Penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Kepada Ayahanda Bahrain Hasibuan dan Ibunda Rikhwaniah yang telah memberikan bantuan materil, ridho dan do’a yang tiada hentinya untuk penulis dari awal perkuliahan sampai selesainya penyusunan Skripsi ini, kepada Abangda M. Darma Wijaya Hasibuan dan Adikku M. Arief Kurniawan Hasibuan yang selalu memberi semangat dan motivasi kepada penulis

2. Bapak Drs. Sutarman, M.Sc selaku Dekan FMIPA USU

3. Bapak Prof Dr. Tulus, M.Si selaku Ketua Departemen Matematika FMIPA USU

4. Bapak Drs. Pengarapen Bangun, M.Si selaku Ketua Pelaksana Jurusan Program S1 Statistika Ekstensi

5. Bapak Drs. Ujian Sinulingga, M.Si selaku dosen pembimbing 1 pada penulisan Skripsi ini yang telah bersedia memberikan arahan, bimbingan dan petunjuk kepada penulis dalam menyelesaikan Skripsi ini

6. Bapak Drs. Rachmad Sitepu, M.Si selaku dosen pembimbing 2 pada penulisan Skripsi ini yang telah bersedia memberikan arahan, bimbingan dan petunjuk kepada penulis dalam menyelesaikan Skripsi ini

7. Bapak Drs. Pasukat Sembiring, M.Si dan Bapak Drs. H. Haluddin Panjaitan selaku dosen penguji yang telah memberikan masukan positif dalam penyelesaian skripsi ini.

8. Seluruh Staff Pengajar di Fakultas Matematika dan lmu Pengetahuan Alam Universitas Sumatera Utara khususnya Jurusan Matematika

9. Teman-teman Matematika Statistik stambuk 2009 atas kerja samanya dan yang selalu memberi motivasi, dukungan dan kepercayaannya.

Sepenuhnya Penulis menyadari bahwa dalam penyusunan Skripsi ini masih banyak terdapat kekurangan. Untuk itu penulis mengharapkan saran dan kritik yang bersifat membangun, dimana saran dan kritik tersebut dapat dimanfaatkan untuk kemajuan ilmu pengetahuan pada saat ini dan yang akan datang.

Semoga Penulisan Skripsi ini dapat memberikan manfaat dan berguna bagi pembaca dan penulis pada khususnya. Akhir kata penulis mengucapkan banyak terima kasih.

Medan, Juli 2011

ABSTRAK

Regresi linier berganda merupakan regresi linier yang melibatkan hubungan fungsional antara variabel terikat dengan dua atau lebih variabel bebas. Untuk mengestimasi model regresi linier berganda digunakan metode maksimum likelihood. Estimasi maksimum likelihood berguna untuk menentukan parameter yang memaksimalkan kemungkinan dari data sampel. Dari sudut pandang statistik, metode maksimum likelihood dianggap lebih kuat pada hasil estimator dengan sifat statistik. Bentuk umum persamaan model regresi linier berganda yaitu:

ε β

β

β + + +

= Xi kXk

Y _{0 1} ....

ABSTRACT

Multiple linear regression is a linear regression involving a functional relationship between the dependent variable with two or more independent variables. To estimate the linear regression model used the maximum likelihood method. Maximum likelihood estimation is useful for determining the parameters that maximize the likelihood of the data sample. From the statistical point of view, the method is considered more robust maximum likelihood estimator on the results of the statistical properties. A common form of multiple linear regression model equation is:

Y =β₀ +β₁X_i....+β_kX_k +ε

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel viii

BAB 1 PENDAHULUAN 1

1.1 Pendahuluan 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Kontribusi Penelitian 3

1.5 Tinjauan Pustaka 3

1.6 Metode Penelitian 5

BAB 2 LANDASAN TEORI 6

2.1 Analisis Regresi 6

2.1.1 Regresi Linier Sederhana 7

2.1.2 Regresi Linier Berganda 9

2.2 Estimasi 11

2.2.1 Estimasi Maksimum Likelihood 12 2.2.2 Maksimum Likelihood dalam Regresi Linier Berganda 13

BAB 3 PEMBAHASAN 17

3.1 Estimasi Parameter Menggunakan Maksimum Likelihood 17 3.2 Estimasi Interval Untuk Parameter Regresi Linier Berganda 20

3.3 Pengujian Hipotesis 25

BAB 4 KESIMPULAN DAN SARAN 28

4.1 Kesimpulan 28

4.2 Saran 28

DAFTAR TABEL

Tabel 3.1 Pengeluaran Pendapatan dan Jumlah Orang dalam Keluarga 17

Tabel 3.2 Penentuan nilai e 2 21

Tabel 3.3 Interval Korelasi 22

ABSTRAK

Regresi linier berganda merupakan regresi linier yang melibatkan hubungan fungsional antara variabel terikat dengan dua atau lebih variabel bebas. Untuk mengestimasi model regresi linier berganda digunakan metode maksimum likelihood. Estimasi maksimum likelihood berguna untuk menentukan parameter yang memaksimalkan kemungkinan dari data sampel. Dari sudut pandang statistik, metode maksimum likelihood dianggap lebih kuat pada hasil estimator dengan sifat statistik. Bentuk umum persamaan model regresi linier berganda yaitu:

ε β

β

β + + +

= Xi kXk

Y _{0 1} ....

ABSTRACT

Multiple linear regression is a linear regression involving a functional relationship between the dependent variable with two or more independent variables. To estimate the linear regression model used the maximum likelihood method. Maximum likelihood estimation is useful for determining the parameters that maximize the likelihood of the data sample. From the statistical point of view, the method is considered more robust maximum likelihood estimator on the results of the statistical properties. A common form of multiple linear regression model equation is:

Y =β₀ +β₁X_i....+β_kX_k +ε

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Metode analisis yang telah dibicarakan hingga sekarang adalah analisis terhadap data mengenai sebuah karakteristik atau atribut (jika data itu kualitatig) dan mengenai sebuah karakteristik (jika data itu kuantitatif). Tetepi, sebagaimana disadari banyak persoalan atau fenomena yang meliputi lebih dari sebuah variabel. Misalnya, berta orang dewasa laki-laki sampai taraf tertentu bergantung pada tingginya, tekanan semacam gas bergantung pada temperatur, hasil produksi padi tergantung pada jumlah pupuk yang digunakan, banyak curah hujan, cuaca dan sebagainya.

Maka dalam hal ini dirasa perlu untuk mempelajari analisis data yang terdiri atas banyak variabel. Jika kita mempunyai data yang terdiri atas dua variabel atau lebih variabel, adalah sewajarnya untuk mempelajari cara bagaimana variabel-variabel itu berhubungan. Hubungan yang didapat pada umumnya dinyatakan dalam bentuk persamaan matematik yang menyatakan hubungan fungsional antara variabel-variabel. Analisa yang menyangkut masalah ini dikenal dengan analisis regresi.

terikat. Untuk keperluan analisis, variabel bebas akan dinyatakan dengan )

1 ( , , ₂

1 X X k ≥

X  _k , sedangkan variabel terikat akan dinyatakan dengan Y.

Statistika bermaksud menyimpulkan populasi yang pada umumnya dengan menggunakan hasil analisis data sampel. Khusus mengenai regresi dalam menentukan hubungan fungsional yang diharapkan berlaku untuk populasi berdasarkan data sampel yang diambil dari populasi yang bersangkutan. Seperti dikatakan di atas, hubungan fungsional ini akan dituliskan dalam bentuk persamaan matematik yang disebut dengan persamaan regresi dan bergantung pada parameter-parameter.

Regresi linier merupakan suatu metode analisis statistik yang mempelajari pola hubungan anatara dua atau lebih variabel. Pada kenyataan sahari-hari sering dijumpai sebuah kejadian dipengaruhi oleh lebih dari satu variabel, oleh karenanya dikembangkan analisis regresi linier berganda. Regresi linier berganda adalah perluasan dari regresi sederhana yang mempunyai lebih dari satu variabel bebas X. Regresi linier berganda digunakan untuk memodelkan hubungan antara variabel terikat dan variabel bebas. Untuk mendapatkan estimasi β₀,β₁,,β_k digunakan metode maksimum likelihood, dimana metode ini secara prinsip dapat meminimumkan jumlah kuadrat kesalahan.

ketelitian dari estimator. Jika ukuran sampel sama dengan populasi, maka estimator memiliki sifat tidak bias, konsisten, dan efisien.

1.2 Perumusan Masalah

Masalah dalam penelitian ini adalah bagaimana menetukan model koefisien regresi linier berganda dengan menggunakan maksimum likelihood.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk menguraikan cara mengestimasi parameter regresi linier berganda dengan meminimumkan error menggunakan maksimum likelihood.

1.4 Kontribusi Penelitian

Kontribusi penelitian ini adalah:

1. Menambah wawasan dan memperkaya literature dalam bidang statistika yang berhubungan dengan regresi linier berganda dan maksimum likelihood.

2. Dengan diketahuinya bagaimana cara mengestimasi parameter regresi linier berganda menggunakan maksimum likehood diharapkan dapat meminimumkan jarak antara titik data dan garis regresi.

3. Untuk mengetahui besarnya pengaruh dari setiap variabel bebas ( yang tercakup) dalam persamaan) terhadap varabel tak bebas.

Dalam penelitian ini penulis menggunakan buku - buku berikut sebagai sumber utama, diantaranya adalah:

1 Supranto J : apabila variabel mempunyai hubungan linier dengan n buah variabel X, maka model matematik regresi bergandanya adalah:

ε β

β

β + + + +

= X kXk

Y _{0 1 1} 

Keterngan:

Y = variabel terikat

k

X X

X1, 2, = variabel bebas

k

β β

β₀, ₁,, = parameter regresi

ε = nilai kesalahan (error)

2. Wonnacott, T. H dan Wonnacott, R. J : jika X dikurangi dengan rata-ratanya, maka akan diperoleh variabel baru x

(

xi = Xi −X

)

. Dan persamaan regresi

linier bergandanya menjadi:

ε β

β

β + + + +

= i k ki

i x x

Y _{0 1 1} 

Keterangan:

i

Y = variabel terikat ke-i

ki i x

x₁,, = selisih antara variabel bebas X dengan nilai rata-ratanya pada pengamatan ke-i

k

β β

β0, 1,, = parameter regresi

ε = nilai kesalahan (error)

) , , , / , , ,

(Y₁ Y₂ Y_{k 0 1 k}

p  β β  β

( ) ( )                    = −  − + + +  −  − + + +  2 1 1 0 2 2 1 1 0 2 1 2 1 2 1 2

1 β β _σ β β β _σ β

π σ π σ ki k i ki k i

i x x Y x x

Y e e ( )

∏

₌ −  − + + +          = n i x x

Y_{i i k ki}

e 1 2 1 2 1 1 0 2

1 β β _σ β

π σ



Dengan

∏

=

n

i 1

menyatakan hasil kali kemungkinan bersama untuk nilai Y yang _i

penggunaannya dikenal dengan penjumlahan eksponen:

) , , , / , , ,

(Y₁ Y₂ Y_{k 0 1 k}

p  β β  β = ( )

( ) ∑     =     − + + + − n i ki k i i x x Y n e 1 2 1 1 0 2 1 2

1 β β σ β

π σ



Mengingat Y amatan yang diberikan dipertimbangkan untuk berbagai nilai _i

k

β β

β0, 1,, . Sehingga persamaan diatas dinamakan fungsi likelihood:

(

k

)

L β₀,β₁,β =

( )

∑=      − − − − − n i ki k i i x x Y n e 1 2 1 1 0 2 1 2

1 β β σ β

π σ



Keterangan:

(

k

)

L β0,β1,β = fungsi maksimum likelihood pada parameter β0,β1,,βk

σ = parameter yang merupakan simpangan baku untuk distribusi

π = nilai konstan (π= 3,14) n = banyak data sampel

e = bilangan konstan (e= 2,718)

i

Y = variabel terikat ke-i

i

1.6 Metode Penelitian

Uraian metode yang digunakan dalam penelitian secara rinci meliputi: a. Membentuk persamaan dari data dengan cara subsitusi.

BAB 2

LANDASAN TEORI

2.1 Analisis Regresi

Perubahan nilai suatu variabel tidak selalu tejadi dengan sendirinya, namun perubahan nilai variabel itu dapat pula disebabkan oleh berubahnya variabel lain yang berhubungan dengan variabel tersebut. Untuk mengetahui pola nilai suatu variabel yang disebabkan oleh variabel lain diperlukan alat analisis yang memungkinkan untuk membuat perkiraan nilai variabel tersebut pada nilai tertentu variabel yang mempengaruhinya.

Teknik yang umum digunakan untuk menganalisis hubungan antara dua atau lebih variabel dalam ilmu statistik adalah analisis regresi. Analisis regresi adalah teknik statistik yang berguna untuk memeriksa dan memodelkan hubungan diantara variabel-variabel. Analisis regresi berguna dalam menelaah hubungan dua variabel atau lebih dan terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan sempurna, sehingga dalam penerapannya lebih bersifat eksploratif.

Persamaan regresi yang digunakan untuk membuat taksiran mengenai nilai variabel terikat disebut persamaan regresi estimasi, yaitu suatu formula matematis yang menunjukkan hubungan keterkaitan antara satu atau beberapa variabel yang nilainya sudah diketahui dengan satu variabel yang nilainya belum diketahui. Sifat hubungan antar variabel dalam persamaan regresi merupakan hubungan sebab akibat.

dengan penelitiannya terhadap manusia. Penelitian tersebut membandingkan antara tinggi anak laki-laki dan tinggi badan orang tuanya. Istilah regresi pada mulanya bertujuan untuk membuat perkiraan nilai suatu variabel (tinggi badan anak) terhadap suatu variabel yang lain (tinggi badan orang tua). Pada perkembangan selanjutnya, analisis regresi dapat digunakan sebagai alat untuk membuat perkiraan nilai suatu variabel dengan menggunakan beberapa variabel lain yang berhubungan dengan variabel tersebut.

2.1.1 Regresi Linier Sederhana

Regresi linier sederhana adalah analisis regresi yang melibatkan hubungan fungsional antara satu variabel terikat dengan satu variabel bebas. Variabel terikat merupakan variabel yang nilainya selalu bergantung dengan nilai variabel lain. Dalam hal ini variabel terikat yang nilainya selalu dipengaruhi oleh variabel bebas, sedangkan variabel bebas adalah variabel yang nilainya tidak bergantung pada nilai variabel lain. Dan biasanya variabel terikat dinotasikan dengan X. Hubungan-hubungan tersebut dinyatakan dalam model matematis yang memberikan persamaan-persamaan tertentu.

Bentuk umum persamaan regresi linier sederhana yang menunjukkan hubungan antara dua variabel, yaitu variabel X sebagai variabel bebas dan variabel Y sebagai variabel terikat adalah

i i a bX

Y = + (2.1)

Keterangan:

i

Y = variabel terikat ke-i

i

X = variabel bebas ke-i

Metode kuadrat terkecil adalah suatu metode untuk menghitung a dan b sebagai perkiraan A dan B, sedemikian rupa sehungga jumlah deviasi kuadrat (SSD=

∑

ei2) memiliki niali terkecil.

Model sebenarnya : Y = A + BX + ε Model perkiraan : Y = a + bX +e

a, b merupakan perkiraan / taksiran atas A, B.

Jika X dikurangi rata-ratanya (x_i = X_i −X ) akan diperoleh variabel baru x

dengan

∑

x_i =0. Maka persamaannya menjadi:

i i i a bx e

Y = + +

(

i

)

i

i Y a bx

e = − +

(

)

[

]

2 2

∑

∑

= − +

= ei Yi a bxi

SSD (2.2)

Metode meminimumkan jumlah deviasi kuadrat (regresi kuadrat terkecil) yang didasarkan pada pemilihan a dan b, sehungga meminimalkan jumlah kuadrat deviasi titik-titik data dari garis yang dicocokkan.

Kemudian akan ditaksir a dan b sehingga jika taksiran ini disubstitusikan ke dalam persamaan (2.2), maka jumlah deviasi kuadrat menjadi minimum. Dengan mendifferensialkan persamaan (2.2) terhadap a dan b dengan menetapkan derivatif parsial yang dihasilkan sama dengan nol, diperoleh:

∑

∑

∑

∑

∑

_{− − = − − = → =}

∂∂ = ∂ ∂

0 0

)

( 2

2

i i

i i

i i

x x

b na Y bx

a Y a a

e

Y n

Y a = i =

∑

∑

∑

∑

∑

∑

_{− − = − − = → =}

∂∂ = ∂ ∂

0 0

)

( 2 2

2

i i

i i

i i

i i

x x

b x a Y x bx

a Y b b

e

∑

∑

= ⇒

i i i

x Y x

bˆ ₂ (2.4)

Nilai aˆdan bˆ yang diperoleh dan cara ini disebut taksiran kuadrat terkecil masing-masing dari a dan b. Dengan demikian, taksiran persamaan regresi dapat ditulis sebagai, Yˆ =aˆ+bˆX yang disebut persamaan prediksi.

Garis regresi berguna untuk menentukan hubungan pengaruh perubahan variabel yang satu dengan yang lainnya. Selanjutnya dari hubungan dua variabel ini dapat dikembangkan untuk analisa tiga variabel atau lebih.

2.1.2 Regresi Linier Berganda

Regresi Linier Berganda merupakan regresi linier yang melibakan hubungan fungsional antara sebuah variabel terikat dengan dua atau lebih vaiabel bebas. Semakin banyak variabel bebas yang terlibat dalam suatu persamaan regresi semakin rumit menentukan nilai statistik yang diperlukan hingga diperoleh persamaan regresi estimasi. Regresi linier berganda berguna untuk mendapatkan pegaruh dua variabel kiteriumnya atau untuk mencari hubungan fungsional dua variabel bebas atau lebih dengan variabel kriteriumnya, atau untuk meramalkan dua variabel bebas atau lebih terhadap variabel kriteriumnya.

Hubungan linier lebih dari dua variabel yang bila dinyatakan dalam bentuk persamaan matematis adalah:

ε β

β

β + + + +

= X kXk

Y _{0 1 1}  (2.5)

Keterangan:

k

X

X ,...,₁ = variabel bebas pada variabel ke-1 sampai variabel ke-k

k

β β

β_{0, 1,}..., = parameter regresi

ε = nilai kesalahan (error)

Langkah-langkah dalam analisis regresi berganda:

1. Membuat hpotesis Ha dan H0 dalam bentuk kalimat:

H0 : Terdapat hubungan fungsional yang signifikan antara variabel

k

X X

X₁, ₂,, dengan variabel Y.

Ha : Tidak terdapat hubungan fungsional yang signifikan antara variabel

k

X X

X1, 2,, dengan variabel Y.

2. Kemudian mencari Rhitung dengan rumus:

∑

∑

+

∑

+ + ∑

= 2

2 2 1 1 2

) ,..., 2 , 1 (

y

y x y

x y

x

Ry k k k

β β

β 

(2.6)

3. Kemudian menghitung Fsign hitung dengan menggunakan rumus:

₂

) ,..., 2 , 1 ( 2

) ,..., 2 , 1 (

1 (

) 1 (

k y k y reg

R k

k n R

F

−

− −

= (2.7)

4. Dengan menggunakan taraf α = 0,05

5. Menghitung nilai Ftabel dengan mengunakan rumus:

F_tabel =F_{α(k.n−k−1)} (2.8)

Fhit > Ftabel : maka H0 ditolak signifikan

Fhit ≤ Ftabel : maka H0 diterima.

7. Membuat Kesimpulan

2.2 Estimasi

Estimasi adalah menaksir ciri-ciri tertentu dari populasi tertentu dari populasi atau memperkirakan nilai populasi (parameter) dengan memakai nilai sampel (statistik). Dengan statistika kita berusaha meyimpulkan populasi. Dalam kenyataannya, mengingat berbagai faktor untuk keperluan tersebut diambil sebuah sampel yang represntatif dan berdasarkan hasil analisis terhadap data sampel kesimpulan mengenai populasi dibuat. Cara pengambilan kesimpulan tentang parameter berhubugan dengan cara-cara menaksir harga parameter. Jadi, harga parameter sebenarnya yang tidak diketahui akan diestimasi berdasarkan statistik sampel yang diambil dari populasi yang bersangkutan.

Sifat atau ciri estimator yang baik yaitu tidak bias, efisien dan konsisten: 1. Estimator yang tidak bias

Estimator dikatakan tidak bias apabila dapat menghasilkan estimasi yang mengandung nilai parameter yang diestimasikan. Misalkan, estimtor ϑˆ dikatakan estimator yang tidak bias jika rata-rata semua harga ϑˆ yang mungkin akan sama dengan ϑ. Dalam ekspektasinya dapat ditulis dengan

θ θˆ)=

(

E .

2. Estimator yang efisien

varians untuk ϑˆ₁ lebih kecil dari varians untuk ϑˆ₂, maka ϑˆ₁ merupakan estimator bervarians minimum.

3. Estimator yang konsisten

Estimator dikatakan konsisten apabila sampel yang diambil berapa pun besarnya, pada rentangnya tetap mengandung nilai parameter yang sedang diestimasi. Misalkan, ϑˆ estimator untuk θ yang dihitung berdasrakan sebuah sampek acak berukuran n. Jika ukuran sampel n makin besar mendeteksi ukuran populasi menyebabkan ϑˆ mendekati θ, maka ϑˆ disebut estimator konsisten.

Estimasi nilai parameter memiliki dua cara, yaitu estimasi titik (point estimation) dan estimasi selang (Interval estimation).

a. Estimasi titik (point estimation)

Estimasi titik adalah estimasi dengan menyebut satu nilai atau untuk mengestimasi nilai parameter.

b. estimasi interval (Interval estimation)

Estimasi Interval dengan menyebut daerah pembatasan dimana kita menentukan batas minimum dan maksimum suatu estimator. Metode ini memuat nilai-nilai estimator yang masih dianggap benar dalam tingkat kepercayaan tertentu (confidence interval)

2.2.1 Estimasi Maksimum Likelihood

Untuk data sampel x ,...,₁ x_ndari distribusi yang kontinu dengan fungsi padat f(x;α ) ditentukan fungsi likelihood sebagai L(x₁,...,x_n;α)= f(x₁;α)...f(x_n;α).

Unuk data sampel distribusi yang diskrit dengan nilai kemungkinan

(

X x

)

p i r

p = _i = _i(α), =1,..., dan frekuensi f ,....,₁ f_k ditentukan dengan fungsi Likelihood sebagai berikut:

(

)

(

( )

)

(

( )

)

fr r f i

n p p

x x

L  α α 1 α

; , ,

1 = ,

∑

= =

n

i

i n

f 1

Karena ln L merupakan transformasi yang monoton naik daripada L, maka ln L mencapai maksimumnya pada nilai α yang sama. Menurut hitung differensial

persamaan menjadi ln =0

∂ ∂

α L

. Suatu akar persamaan ini αˆ =a

(

x1,...,xn

)

yang

memaksimumkan L, disebut estimasi maksimum likelihood untuk α .

2.2.2 Maksimum Likelihood dalam Regresi Linier Berganda

Maksimum Likelihood adalah metode yang dapat digunakan umtuk mengestimasi suatu parameter dalam regresi.

Jika X dikurangi dengan rata-atanya, maka maka akan diperoleh variabel baru x

(

x X X

)

i

i = − dan selisih antara X dan X merupakan perhitungan yang sederhana i

karena jumlah dari nilai x tersebut adalah sama dengan nol _i 

  





∑

₌

=

n

i i

x 1

0 . Dan

persamaan regresi linier berganda menjadi:

ε β

β

β + + + +

= k k

i X X

i

Y = variabel terikat ke-i

ki i x

x ,...,₁ = selisih antara variabel bebas X dengan nilai rata-ratanya pada pengamatan ke-i

k

β β

β0, 1,..., = parameter regresi

ε = nilai kesalahan(error)

Teknik estimasi maksimum likelihood mempertimbangkan berbagai populasi yang mungkin dengan perpindahan garis regresi dan regresi tersebut mengelilingi distribusi untuk semua posisi yang mungkin. Perbedaan posisi yang berhubungan dengan perbedaan nilai percobaan untuk β0,β1,...,β_k. Dalam hal ini, pengamatan likelihood dipilih hipotesis populasi yang maksimum dalam likelihood. Secara umum,

andaikan kita mempunyai sampel berukuran n dan kita ingin mengetahui kemungkinan sampel yang diamati. Diperlihatkan fungsi nilai kemungkinan sampel untuk β0,β1,...,βk:

(

Yi Y Yn k

)

p , 2,..., /β0,β1,...,β (2.8)

Mengingat kemungkinan nilai pertama Y adalah:

( )

( )

2 1

1 0

1 ...

2 1 2

1 − _ − + + + _

= β βσ β

π σ

ki k i x x Y

i e

Y

p (2.9)

Hal di atas adalah distribusi normal sederhana dengan rata-rata

ki k

i x

x β

β

β0+ 1 1 +...+ dan varians

( )

2

σ yang disubstitusi ke dalam:

( )



     −       −

= σµ

π σ

x

i e

Y

p 2

1

2 1

. Kemungkinan nilai kedua Y sama dengan (2.9), kecuali

angka satu diganti dengan dua dan deterusnya untuk semua nilai Y amatan lainnya.

(

Yi Y Yn k

)

p , ₂,..., /β₀,β₁,...,β

= ( ) ( ) ... 2 1 2 1 2 1 1 0 2 2 1 1 0 1 ... 2 1 ... 2 1                 _   − + + + −     − + + + − σ β β β σ β β β π σ π σ ki k i ki k

i x Y x x

x Y e e ( )

∏

₌ −  − + + +          = n i x x Y_{i i k ki}

e 1 ... 2 1 2 1 1 0 2

1 β β _σ β

π

σ (2.10)

Dengan

∏

=

n

i 1

menyatakan hasil kali n kemungkinan bersama untuk nilai Y _i

yang penggunaannya dik enal untuk eksponensial. Hasil (2.10) dapat diperlihatkan dengan penjumlahan ekspnen:

(

)

( ) ( ) 2 ... 2 1 1 0 2 1 1 1 1 0 2 1 ,..., , / ,..., , ∑     = =     − + + + − n i ki k i i x x Y n k n e Y Y Y p σ β β β π σ β β

β (2.11)

Mengingat Y amatan yang diberikan dipertimbangkan untuk berbagai nilai _i .

,..., , ₁ 0 β βk

β Sehingga persamaan (2.11) dinamakan fungsi likelihood:

(

)

=

( )

∑=      − − − − − n i ki k i i x x Y n k e L 1 2 1 1 0 ... 2 1 1 0 2 1 ,..., , σ β β β π σ β β

β (2.12)

Keterangan:

(

k

)

L β0,β1,...,β = fungsi maksimum likelihood pada parameter β0,β1,...,βk

σ = parameter yang merupakan simpangan baku untuk distribusi

π = nilai konstan (π= 3,1416) n = banyak data sampel

i

β = parameter regresi ke-i

Dari persamaan (2.12) diperoleh lnL

(

β₀,β₁,...,β_k

)

, yaitu:

Λ=

(

)

∑

=      − − − − − − − = n i ki k i i k x x Y n n L 1 2 1 1 0 1 0 ... 2 1 ln ) 2 ln( 2 ,..., , ln σ β β β σ π β β β (2.13)

Dengan mendiffrensialkan Λ terhadap setiap parameter β₀,β₁,...,β_k dan menetapkan derivatif parsial yang dihasilkan sama dengan nol, diperoeh:

∑

(

)

= − − − − = = ∂∂Λ n i ki k i

i x x

Y 1 1 1 0 2 0 0 ... 1 β β β σ β

∑

∑

∑

∑

∑

= − − = − − = = → = = = = = n i n i n i n i n i ki i ki k i

i n x x x x

Y

1 1 1 1 1

1 1

1

0 β ... β 0 0

β Y n Y n i = =

⇒

∑

=1

0 ˆ β (2.14)

∑

(

)

= − − − − = − = ∂∂Λ n i ki k i i

i Y x x

x 1 1 1 0 1 2 1 0 ... 1 β β β σ β

∑

₌ +

∑

₌ +

∑

₌ − −

∑

₌ = →

∑

₌ = − = n i n i n i n i i ki i k i n i i i

iY x x x x x

x

1 1 1 1

1 1 2 1 1 1 1 0

1 β β ... β 0 0

∑

₌ +

∑

₌ − −

∑

₌ = − ⇒ n i n i n i ki i k i i

iY x x x

x

1 1 1

1 2

1 1

1 β ... β 0

(2.15) 

∑

(

)

= − − − − − = = ∂∂Λ n i ki k i i

ki Y x x

x 1 1 1 0 2 2 0 ... 1 β β β σ β

∑

∑

∑

∑

∑

= − = + = − − = = → = = − = n i n i n i n i ki ki k ki i n i ki i

kiY x x x x x

x

1 1 1 1

2 1

1 1

0 β ... β 0 0

β

∑

₌ +

∑

₌ − −

∑

₌ = − ⇒ n i n i n i ki k ki i i

kiY x x x

x

1 1 1

2 1

1 ... β 0

BAB 3

PEMBAHASAN

3.1 Estimasi Parameter Menggunakan Maksimum Likelihood

Misalkan suatu persoalan yang dilakukan terhadap 8 keluarga, untuk menaksir pengeluaran membeli barang D dalam satu minggu.

Keterangan: X = Pendapatan / minggu (dalam ribuan rupiah) ₁

2

X = Jumlah Orang (dalam satuan jiwa)

[image:31.595.126.460.481.682.2]

Y = Pengeluaran untuk membeli barang D / minggu (dalam ratusan rupiah)

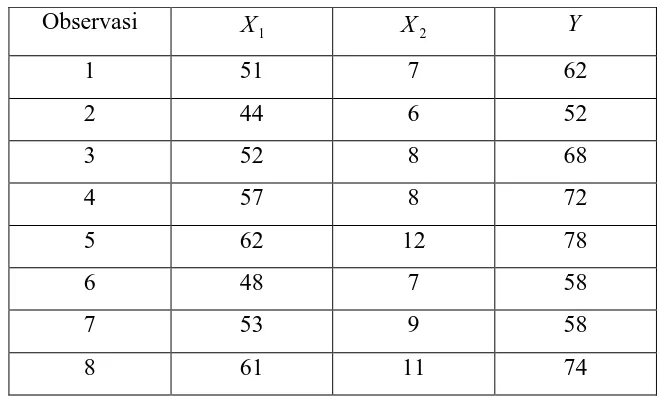
Tabel 3.1 Pengeluaran Pendapatan dan Jumlah Orang dalam Keluarga

Observasi X ₁ X ₂ Y

1 51 7 62

2 44 6 52

3 52 8 68

4 57 8 72

5 62 12 78

6 48 7 58

7 53 9 58

Dengan menggunakan regresi yang terdiri dari Yˆ =βˆ₀ +βˆ₁X₁ +βˆ₂X₂. Fungsi nilai kemungkinan untuk β₀,β₁,β₂ : p(Y₁,Y₂,,Y_k/β₀,β₁,β₂). Untuk nilai Y bebas dengan mengalikan semua kemungkinan bersama, dimana:

k

Y Y Y

p( 1, 2,, /β0,β1,β2)

( ) ( )                    = −  − + + +  −  − + + +  2 1 1 0 2 2 1 1 0 2 1 2 1 2 1 2

1 β β _σ β β β _σ β

π σ π σ ki k i ki k i

i x x Y x x

Y e e ( )

∏

₌ −  − + + +          = n i x x

Y_{i i k ki}

e 1 2 1 2 1 1 0 2

1 β β _σ β

π σ



Dengan

∏

=

n

i 1

menyatakan hasil kali kemungkinan bersama untuk nilai Y yang _i

penggunaannya dikenal dengan penjumlahan eksponen:

) , , , / , , ,

(Y1 Y2 Yk 0 1 k

p  β β  β = ( )

( ) ∑     =     − + + + − n i ki k i i x x Y n e 1 2 1 1 0 2 1 2

1 β β σ β

π σ



(3.1)

Mengingat Y amatan yang diberikan dipertimbangkan untuk berbagai nilai _i

k

β β

β₀, ₁,, . Sehingga persamaan diatas dinamakan fungsi likelihood:

(

k

)

L β₀,β₁,β =

( )

∑=      − − − − − n i ki k i i x x Y n e 1 2 1 1 0 2 1 2

1 β β σ β

π σ



(3.2)

Keterangan:

(

k

)

L β₀,β₁,β = fungsi maksimum likelihood pada parameter β₀,β₁,,β_k

σ = parameter yang merupakan simpangan baku untuk distribusi

π = nilai konstan (π= 3,14) n = banyak data sampel

e = bilangan konstan (e= 2,718)

i

Y = variabel terikat ke-i

i

Maka ln L

(

β₀,β₁,β_k

)

adalah:

Λ= ln L

(

β₀,β₁,β_k

)

=

2 1 1 1 0 2 1 ln ) 2 ln(

2

∑

₌ 

    − − − − − − − n i ki k i

i x x

Y n x n σ β β β

σ  (3.3)

Setelah diperoleh nilai Λmaka perhitungan differensialnya untuk β0,β1,,βk dan menetapkan derivatif parsial yang dihasilkan sama dengan nol, yaitu:

(

)

0

1 1 2 2 1 1 0 2 0 = − − − = ∂∂Λ

∑

= n i i i

i x x

Y β β β

σ β 0 0 1 2 1 1 1 1 2 2 1 1 1

0 − − = → = =

− =

∑

∑

∑

∑

∑

= = = = = n i i n i n i i n i i n i i

i n x x x x

Y β β β

Y n Y n i = =

⇒

∑

=1

0 ˆ

β (3.4)

(

)

0

1 1 2 2 1 1 0 1 2 1 = − − − − = ∂∂Λ

∑

= n i i i i

i Y x x

x β β β

σ β 0 0 1 1 1 1 2 1 2 1 2 1 1 1 1 0

1 + + + = → =

− =

∑

∑

∑

∑

∑

= = = = = n i n i i n i i i n i i n i i i

iY x x x x x

x β β β

∑

∑

∑

= + = + = = − ⇒ n i n i i i n i i i

iY x x x

x 1 1 2 1 2 1 2 1 1

1 β β 0 (3.5)

(

)

0

1 1 2 2 1 1 0 2 2 2 = − − − − = ∂∂Λ

∑

= n i i i i

i Y x x

x β β β

σ β 0 0 1 1 2 1 2 2 2 1 2 1 1 1 2 0

2 + + + = → =

− =

∑

∑

∑

∑

∑

= = = = = n i n i i n i i n i i i n i i i

iY x x x x x

x β β β

∑

∑

∑

= + = + = = − ⇒ n i n i i n i i i i

iY x x x

x 1 1 2 2 2 1 2 1 1

2 β β 0 (3.6)

Dari persamaan diperoleh,

Subsitusi nilai-nilai tabel di atas ke dalam persamaan (3.4),(3.5) dan (3.6) :

β

∂∂Λ Y

Y

n

i =

=

⇒

∑

=1

0 ˆ

1

β

∂∂Λ =−

∑

= +

∑

= +

∑

=

n

i

n

i

i i n

i i i

iY x x x

x

1 1

2 1 2 1

2 1 1

1 β β

= -371+β₁(270)+β₂(83)

⇒ 270β₁+ 83β₂= 371 (3.7)

2

β

∂∂Λ =−

∑

= +

∑

= +

∑

=

n

i

n

i i n

i

i i i

iY x x x

x

1 1

2 2 2 1

2 1 1

2 β β

= -107+β₁(83)+β₂(30)

⇒ 83β₁+ 30β₂=107 (3.8)

Dengan menggunakan persamaan (3.7) dan (3.8) diperoleh nilai β₁= 1,857 dan

2

β =-1,571.

Maka persamaan regresi linier bergandanya menjadi:

Yˆ = 65,25 + 1,857x + ₁ (−1,571)x₂

= 65,25+ 1,857(X₁ −53,5) −1,571(X₂ −8,5) =−20,74+ 1,857 X₁−1,571X 2

Ini berarti bahwa besarnya nilai Yˆ akan dipengaruhi oleh nilai parameter

74 , 20 ˆ

0 =−

β , βˆ₁= 1,875 dan βˆ₂= -1,571 . Dari regresi ini, dapat menaksir pengeluaran untuk membeli barang D jika keluarga yang terdiri atas lima orang berpenghasilan Rp. 30.000. ini berarti X = 30 dan ₁ X = 8, setelah disubsitusikan ke ₂ dalam persamaan maka hasilnya adalah:

Yˆ = −20,74+ 1,875(30)−1,571(8)= 22,94.

Maka, diperkirakan pengeluaran membeli barang D sebesar Rp. 2.294 untuk 8 orang dalam satu keluarga dengan penghasilan Rp. 30.000 .

Pada dasarnya, nilai-nilai dari koefisien regresi β₁bervariasi. Karena umumnya 2

σ tidak diketahui, maka σ2 _{diduga dengan} 2

e

s , sehingga perkiraan varians (β) adalah:

Var (β) = s_β2 ⇒s_e2=

1 2

− −

∑

k n

e_i

(3.9)

Keterangan: 2

e

s = varians dari kesalahan pengganggu n = banyak observasi

k = banyak variabel bebas

∑

2

i

e =

∑

( )

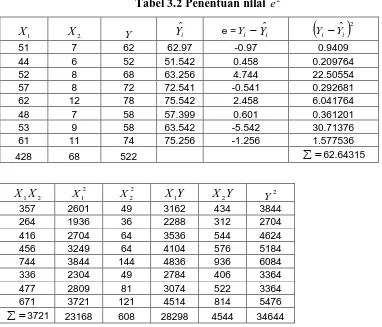
Y_i −Yˆ 2 dapat dihitung langsung dari Y_i −Yˆ_i yaitu selisih antara nilai [image:35.595.107.489.411.738.2]

observasi Y dengan nilai regresi _i Yˆ =βˆ0 +βˆ1X1i +βˆ2X2i.

Tabel 3.2 Penentuan nilai e 2 1

X X_{2 Y} Yˆi e =Yi −Yˆi

( )

2 ˆ

i i Y

Y −

51 7 62 62.97 -0.97 0.9409

44 6 52 51.542 0.458 0.209764

52 8 68 63.256 4.744 22.50554

57 8 72 72.541 -0.541 0.292681

62 12 78 75.542 2.458 6.041764

48 7 58 57.399 0.601 0.361201

53 9 58 63.542 -5.542 30.71376

61 11 74 75.256 -1.256 1.577536

428 68 522 ∑=62.64315

2 1X

X X12

2 2

X X1Y X2Y Y2

357 2601 49 3162 434 3844

264 1936 36 2288 312 2704

416 2704 64 3536 544 4624

456 3249 64 4104 576 5184

744 3844 144 4836 936 6084

336 2304 49 2784 406 3364

477 2809 81 3074 522 3364

671 3721 121 4514 814 5476

=

Dari hasil perhitungan tabel diatas diperoleh: 2 e s = 1 2 − −

∑

k n ei = 1 2 9 64315 , 62 − − = 12,528

Untuk hubungan 3 variabel tersebut dapat dihitung dengan menggunakan rumus

sebagai berikut:

1. Koefisien korelasi antara X dan ₁ Y

{

∑

∑

−

∑

∑

}{

∑

∑

−

∑

}

− = 2 2 2 1 2 1 1 1 1 ) ( ) ( ) )( ( i i i i i i i i yx Y Y n X X n Y X Y X n

r (3.10)

= 36 , 3175 2968 = 0,93

2. Koefisien korelasi antara X dan 2 Y

{

∑

∑

−

∑

∑

}{

∑

∑

−

∑

}

− = 2 2 2 2 2 2 2 2 2 ) ( ) ( ) )( ( i i i i i i i i yx Y Y n X X n Y X Y X n

r (3.11)

= 45 , 1058 856 = 0,81

3. Koefisien korelasi antara X dan ₁ X ₂

{

∑

∑

−

∑

∑

}{

∑

∑

−

∑

}

− = 2 2 2 2 2 1 2 1 2 1 2 1 2 1 ) ( ) ( ) )( ( i i i i i i i i x x X X n X X n X X X X n

r (3.12)

=

720 664

[image:37.595.106.524.93.224.2]

Tabel 3.3 Interval Korelasi

Interval nilai r Arti hubungan - 1,000 ≤r≥-0,800

- 0,790 ≤r≥-0,500 - 0,490 ≤r ≥ 0,490 0,500 ≤r≥ 0,790 0,800 ≤r ≥ 1,000

Korelasi kuat Korelasi sedang

Korelasi lemah Korelasi sedang

Korelasi kuat

Dari ketiga nilai r diatas dapat disimpulkan bahwa :

a. Pendapatan berkorelasi kuat terhadap pengeluaran membeli barang D.

b. Jumlah orang dalam keluarga berkorelasi kuat terhadap pengeluaran membeli barang D.

c. Pendapatan yang paling berpengaruh terhadap pengeluaran membeli barang D (per minggu) dalam satu keluarga (dalam pengamatan ini).

Tabel 3.4 Menentukan Persamaan dengan Matriks 1

X X_{2 Y} X₁X₂ X₁2 X₂2 X₁Y X₂Y

51 7 62 357 2601 49 3162 434

44 6 52 264 1936 36 2288 312

52 8 68 416 2704 64 3536 544

57 8 72 456 3249 64 4104 576

62 12 78 744 3844 144 4836 936

48 7 58 336 2304 49 2784 406

53 9 58 477 2809 81 3074 522

61 11 74 671 3721 121 4514 814

=

∑ 428 ∑=68 ∑=522 ∑=3721 ∑=23168 ∑=608 ∑=28298 ∑=4544

     =

68 428 8

X XT

3721 23168 428

    

[image:37.595.105.554.425.622.2]

Adj (XTX)=      − − 17164 664 2160 7196 240 664 − −      − − 240303 7196 17164 1 )

(XTX − = = X X X X Adj T T ) (      − − 7717 , 1 0685 , 0 2267 , 0 7428 , 0 0248 , 0 068 , 0 − −      − − 8004 , 24 7428 , 0 7717 , 1 Y XT =

          4544 28298 522 =

βˆ 1

)

(XTX − XTY=

          − − 57 , 1 866 , 1 74 , 20

Perkiraan 2 2

)

var(β =sβ =se

1 )

(XTX − dan apabila D= 1 )

(XTX − dan s s_ed_ii

i 2 2 =

β ,

dimana d adalah matriks dari baris ke i dan kolom i terletak pada diagonal pokok, _ii maka:

D=(XTX)−1=

     − − 7717 , 1 0685 , 0 2267 , 0 7428 , 0 0248 , 0 068 , 0 − −      − − 8004 , 24 7428 , 0 7717 , 1 Sehingga, 11 2 2

0 s d

sβ = e =12,528(0,2267)=2,84

685 , 1 84 , 2 2

0 = =

⇒sβ

22 2 2

1 s d

557 , 0 31 , 0 2

1 = =

⇒sβ

33 2 2

2 s d

sβ = e =12,528(24,8004)=310,699

626 , 17 699 , 310 2

2 = =

⇒sβ

Untuk menghitung estiasi interval untuk β₀, β₁, β₂ digunakan taraf signifikan α =0,05.

( 1) 0,05/2(8 2 1) 2,571

2

/ − − =t − − =

t_{α n k}

1. β₀ = −20,74 ,

0

β

s = 106,51

0 0 0 0 0,025

025 , 0

0 β β β β

β −t s ≤ ≤ +t s

) 685 , 1 ( 571 , 2 74 , 20 ) 685 , 1 ( 571 , 2 74 ,

20 − ≤ ₀ ≤− +

− β 407 , 16 07 ,

25 ≤ ₀ ≤−

− β

Ini berarti bahwa interval antara -25,07 dan -16,407 akan memuat β₀.

2. β₁ = 1,866 ,

1

β

s = 0,557

1 1 1 1 0,025

025 , 0

1 β β β β

β −t s ≤ ≤ +t s

) 557 , 0 ( 571 , 2 866 , 1 ) 557 , 0 ( 571 , 2 866 ,

1 − ≤β1 ≤ +

298 , 3 433

,

0 ≤β1 ≤

Ini berarti bahwa Interval antara 0,433 dan 3,298 akan memuat β₁.

3. β₂ = -1,57 ,

2

β

s = 17,626

2 2 2 2 0,025

025 , 0

2 β β β β

β −t s ≤ ≤ +t s

) 626 , 17 ( 571 , 2 57 , 1 ) 626 , 17 ( 571 , 2 57 ,

1 − ≤ ₂ ≤− +

− β 746 , 43 886 ,

46 ≤ 2 ≤

− β

3.3 Pengujian Hipotesis

Hipotesis berasal dari kata hipo dan tesis yang berasal dari bahasa Yunani. Hipo berarti dibawah, kurang atau lemah dan tesis proporsi. Jadi, secara umum hipotesis dapat didefinisikan sebagai asumsi atau dugaan / pernyataan sementara yang masih lemah kebenarannya. Pengujian Hipotesis dilakukan berdasarkan hasil penelitian pada sampel yang diambil dari populasi tersebut. Berikut ini adalah hipotesis yang diperoleh pada persoalan diatas:

1) Hipotesis

Ha : terdapat hubungan fungsional yang signifikan antara pendapatan dan

jumlah orang dalam satu keluarga dengan pengeluaran membeli barang D.

H0 : tidak terdapat hubungan fungsional yang signifikan antara pendapatan

dan jumlah orang dalam satu keluarga dengan pengeluaran membeli barang D.

2) R dapat diperoleh dengan: _hit

∑

∑

+

∑

= 2

2 2 1 1 2

) 2 , 1 (

y

y x y

x

R_y β β

= 5 , 583

85 , 520

= 0,893

3) Kemudian menghitung Fsign hitung dengan menggunakan rumus:

2 ) 2 , 1 ( 2

) 2 , 1 (

1 (

) 1 (

y y

reg

R k

k n R F

− − − =

= 215 , 0

463 , 4

5) Nilai Ftabel dengan menggunakan rumus:

) 1 . ( − −

= kn k

tabel F

F _α

79 , 5 ) 5 , 2 ( 05 , 0 ) 1 2 8 , 2 ( 05 ,

0 − − =F =

F

6) Membuat criteria pengujian, yaitu: Fhit > Ftabel : maka H0 ditolak signifikan

Fhit ≤ Ftabel : maka H0 diterima.

Karena Fhit > Ftabel , yaitu 20,77 > 5,79

Maka, H0 ditolak atau signifikan.

7) Kesimpulan

Karena H0 ditolak maka Ha diterima yang berarti bahwa terdapat hubungan

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Kesimpulan dari penelitian ini adalah :

1. Maksimum likelihood merupakan salah satu metode estimasi yang tepat dalam menentukan model koefisien regresi linier berganda.

2. Dalam perhitungan regresi linier berganda maksimum likelihood juga dapat berperan didalamnya, dan model matematis ini juga dapat berperan didalamnya, dan model matematis ini juga bisa diandalkan dalam melakukan estimasi.

3. Pemodelan matematis sangat diperlukan dalam menyelesaikan suatu permasalahan yang variabel-variabel belum diketahui apakah saling berhubungan atau tidak, maka penggunaan regresi linier berganda adalah penyelesaian yang tepat.

4.2 Saran

DAFTAR PUSTAKA

1. Hines, William W dan Montgomery D C. 1990 Probabilita dan Statistik dalam Ilmu Rekayasa dan Manejemen. Jakarta: Universitas Indonesia..

2. Hakim, Abdul. 2000. Statistika Induktif untuk ekonomi dan bisnis. Yogyakarta: Ekonisia.

3. Spiegel, Murray R. 1994. Statistika. Jakarta: Erlangga.

4. P A Surjadi.1983. Pendahuluan teori kemungkinan dan statistika. Bandung: ITB Bandung.

5. Sudjana.2002. Metoda Statistika. Bandung: Tarsito

6. Sudjana.1996. Teknik Analisis Regresi Dan Korelasi. Bandung: Tarsito

7. Sarwoko.2007. Statistik Inferensi untuk Ekonomi dan Bisnis. Yogyakarta: Andi Offset

8. Supranto, J. 1992. Statistika dan Sistem Informasi. Erlangga. Jakarta.

9. Usman, Husaini dan Purnomo Setiady Akbar.1995. Pengantar Statistika. Bumi Aksara. Yogyakarta.

10.Walpole dan Myers. 1995. Ilmu Peluang dan Statistika Untuk Insinyur dan Ilmuan. Bandung: ITB Bandung..