Penjadwalan mata kuliah menggunakan integer nonlinear programming: studi kasus di Bina Sarana Informatika Bogor

  ABSTRACT

ERLIYANA. Courses Scheduling Using Integer Nonlinear Programming. A Case Study of Bina

Sarana Informatika Bogor. Supervised by PRAPTO TRI SUPRIYO and FARIDA HANUM.

This research aims to formulate courses scheduling based on lecturers’ and students’ preferences and other constraints. The model used is Integer Nonlinear Programming (INLP), with lecturers’ and students’ preferences are represented by course weights. The smaller weights of subjects indicate that their preferences are more prefered. This model is implemented to schedule courses of 5th semester classes at the Academy of Bina Sarana Informatika Bogor. The solution of this model is carried out using Lingo 8.0. The result shows that the schedule fulfill 98,57% preferences of regular students, 100% of extension students, and 100% of lecturers.

   

  ABSTRAK

ERLIYANA. Penjadwalan Mata Kuliah Menggunakan Integer Nonlinear Programming. Studi

Kasus di Bina Sarana Informatika Bogor. Dibimbing Oleh PRAPTO TRI SUPRIYO dan

FARIDA HANUM.

Tujuan penelitian ini adalah membuat model penjadwalan mata kuliah berdasarkan preferensi dosen dan mahasiswa dan memenuhi berbagai kendala lain. Model yang digunakan adalah Integer Nonlinear Programming (INLP), sedangkan preferensi dosen dan mahasiswa direpresentasikan dengan suatu bobot. Bobot mata kuliah yang lebih kecil menandakan bahwa preferensinya lebih diutamakan. Model penjadwalan yang telah disusun diimplementasikan untuk menyusun jadwal mata kuliah semester 5 di Akademi Bina Sarana Informatika. Solusi yang diperoleh dari penyelesaian model dengan menggunakan Lingo 8.0 untuk studi kasus yang dilakukan adalah jadwal mata kuliah yang memenuhi 98,57% keinginan mahasiswa reguler, 100% keinginan mahasiswa ekstensi, dan 100% keinginan dosen.

 

I

PENDAHULUAN

1.1 Latar Belakang

Salah satu bagian penting yang tidak dapat dipisahkan dalam sekolah tinggi dan universitas adalah masalah penjadwalan mata kuliah dengan kendala waktu yang diinginkan (preferensi) dosen, mahasiswa, dan banyaknya ruangan yang terbatas. Oleh sebab itu perlu dibuat sebuah penjadwalan mata kuliah yang memenuhi semua kendala dan memuaskan semua pihak.

Bina Sarana Informatika (BSI) merupakan salah satu perguruan tinggi yang menyelenggarakan program regular dan ekstensi. Program regular diselenggarakan pada waktu pagi atau siang hari, sedangkan program ekstensi diselenggarakan pada waktu sore atau malam hari.

Setiap mahasiswa dan dosen mempunyai preferensi hari dan periode waktu dalam pelaksanaan kuliah. Atas dasar ini, masalah penjadwalan mata kuliah akan dibuat.

Permasalahan penjadwalan mata kuliah ini dapat dimodelkan sebagai masalah Integer Nonlinear Programming (INLP). INLP adalah suatu model pemrograman matematika dimana variabel keputusan berupa bilangan integer dengan fungsi objektif atau kendalanya nonlinear. Tulisan ini merupakan rekontruksi dari artikel A 0-1 integer programming approach to a university timetabling problem yang ditulis oleh M Akif Bakir dan Cihan Askop.

1.2 Tujuan

Tujuan dari karya ilmiah ini adalah memodelkan masalah penjadwalan mata kuliah yang meminimumkan ketidakpuasan mahasiswa dan dosen di Bina Sarana Informatika (BSI) Bogor ke dalam bentuk INLP. Selanjutnya model diselesaikan dengan bantuan software LINGO 8.0.

II

LANDASAN TEORI

Berikut ini akan dijelaskan definisi dan teori yang terkait dengan Integer Nonlinear Programming (INLP).

2.1 Pemrograman Linear

Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear.

Definisi 1 (Fungsi Linear)

Suatu fungsi f(x1,x2,...,xn) dalam

variabel-variabel x x₁, ₂,...,x_n adalah suatu fungsi linear jika dan hanya jika untuk suatu himpunan konstanta c c₁, ₂,...,c_n,

. ... )

,..., ,

(x1 x2 xn c1x1 c2x2 cnxn

f = + + +

(Winston 2004)

Sebagai contoh, f x x( ,_{1 2})=3x₁+4x₂

merupakan fungsi linear, sementara

2 2

1 2 1 2

( , )

f x x =x x bukan fungsi linear.

Definisi 2 (Pertidaksamaan dan Persamaan Linear)

Untuk sembarang fungsi linear

) ,..., , (x1 x2 xn

f dan sembarang bilangan b,

pertidaksamaan f(x1,x2,...,xn)≤b atau

b x x x

f( 1, 2,..., n)≥ adalah pertidaksamaan

linear.

Misalkan b sembarang bilangan, suatu persamaan f(x1,x2,...,xn)=b merupakan

persamaan linear.

(Winston 2004)

Pemrograman linear (PL) atau linear

programming (LP) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut:

a) Tujuan masalah tersebut adalah

memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap

variabel dalam masalah ini. Untuk sembarang variabel xi, pembatasan tanda menentukan xi harus taknegatif (xi ≥0) atau tidak dibatasi tandanya (unrestricted in sign).

1

I

PENDAHULUAN

1.1 Latar Belakang

Salah satu bagian penting yang tidak dapat dipisahkan dalam sekolah tinggi dan universitas adalah masalah penjadwalan mata kuliah dengan kendala waktu yang diinginkan (preferensi) dosen, mahasiswa, dan banyaknya ruangan yang terbatas. Oleh sebab itu perlu dibuat sebuah penjadwalan mata kuliah yang memenuhi semua kendala dan memuaskan semua pihak.

Bina Sarana Informatika (BSI) merupakan salah satu perguruan tinggi yang menyelenggarakan program regular dan ekstensi. Program regular diselenggarakan pada waktu pagi atau siang hari, sedangkan program ekstensi diselenggarakan pada waktu sore atau malam hari.

Setiap mahasiswa dan dosen mempunyai preferensi hari dan periode waktu dalam pelaksanaan kuliah. Atas dasar ini, masalah penjadwalan mata kuliah akan dibuat.

Permasalahan penjadwalan mata kuliah ini dapat dimodelkan sebagai masalah Integer Nonlinear Programming (INLP). INLP adalah suatu model pemrograman matematika dimana variabel keputusan berupa bilangan integer dengan fungsi objektif atau kendalanya nonlinear. Tulisan ini merupakan rekontruksi dari artikel A 0-1 integer programming approach to a university timetabling problem yang ditulis oleh M Akif Bakir dan Cihan Askop.

1.2 Tujuan

Tujuan dari karya ilmiah ini adalah memodelkan masalah penjadwalan mata kuliah yang meminimumkan ketidakpuasan mahasiswa dan dosen di Bina Sarana Informatika (BSI) Bogor ke dalam bentuk INLP. Selanjutnya model diselesaikan dengan bantuan software LINGO 8.0.

II

LANDASAN TEORI

Berikut ini akan dijelaskan definisi dan teori yang terkait dengan Integer Nonlinear Programming (INLP).

2.1 Pemrograman Linear

Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear.

Definisi 1 (Fungsi Linear)

Suatu fungsi f(x1,x2,...,xn) dalam

variabel-variabel x x₁, ₂,...,x_n adalah suatu fungsi linear jika dan hanya jika untuk suatu himpunan konstanta c c₁, ₂,...,c_n,

. ... )

,..., ,

(x1 x2 xn c1x1 c2x2 cnxn

f = + + +

(Winston 2004)

Sebagai contoh, f x x( ,_{1 2})=3x₁+4x₂

merupakan fungsi linear, sementara

2 2

1 2 1 2

( , )

f x x =x x bukan fungsi linear.

Definisi 2 (Pertidaksamaan dan Persamaan Linear)

Untuk sembarang fungsi linear

) ,..., , (x1 x2 xn

f dan sembarang bilangan b,

pertidaksamaan f(x1,x2,...,xn)≤b atau

b x x x

f( 1, 2,..., n)≥ adalah pertidaksamaan

linear.

Misalkan b sembarang bilangan, suatu persamaan f(x1,x2,...,xn)=b merupakan

persamaan linear.

(Winston 2004)

Pemrograman linear (PL) atau linear

programming (LP) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut:

a) Tujuan masalah tersebut adalah

memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap

variabel dalam masalah ini. Untuk sembarang variabel xi, pembatasan tanda menentukan xi harus taknegatif (xi ≥0) atau tidak dibatasi tandanya (unrestricted in sign).

Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar PL)

Suatu PL dikatakan berbentuk standar jika berbentuk:

min _z=_{c x}T

terhadap Ax=b (1) x≥0

dengan x dan c berupa vektor berukuran n, vektor b berukuran m, sedangkan A berupa matriks berukuran m × n yang disebut juga matriks kendala.

(Nash & Sofer 1996)

Sebagai catatan, yang dimaksud dengan

vektor berukuran n adalah vektor yang

memiliki dimensi (ukuran) n × 1.

Solusi Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimum bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947, dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan masalah PL. Metode ini berupa metode iteratif untuk menyelesaikan masalah PL berbentuk standar.

Pada masalah PL (1), vektor x yang

memenuhi kendala Ax=b disebut solusi PL (1). Misalkan matriks A dinyatakan sebagai

(

)

=

A B N , dengan B adalah matriks

taksingular berukuran m ×m yang elemennya

berupa koefisien variabel basis dan N

merupakan matriks berukuran m× −(n m) yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks B disebut matriks basis untuk PL (1).

Misalkan x dinyatakan sebagai vektor ⎛ ⎞

= ⎜ ⎟ ⎝ ⎠ B N

x x

x , dengan xB adalah vektor variabel

basis dan x_N adalah vektor variabel

nonbasis, maka Ax=b dapat dinyatakan

sebagai =

(

)

⎛_⎜ ⎞_⎟

⎝ ⎠ B N

x Ax B N

x

=Bx + NxB N=b. (2)

Karena matriks B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2)

B

x dapat dinyatakan sebagai:

.

= -1 − -1

B N

x B b B Nx (3)

Kemudian, fungsi objektifnya berubah menjadi:

min z

=

T T

.

B B N N

c x

+

c x

Definisi 4 (Daerah Fisibel)

Daerah fisibel suatu masalah PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada masalah PL tersebut.

(Winston 2004)

Definisi 5 (Solusi Basis)

Solusi dari suatu masalah PL disebut solusi basis jika memenuhi syarat berikut: i. solusi tersebut memenuhi kendala pada

masalah PL;

ii. kolom-kolom dari matriks kendala yang berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.

(Nash & Sofer 1996)

Definisi 6 (Solusi Basis Fisibel)

Vektor x disebut solusi basis fisibel jika x merupakan solusi basis dan x≥0.

(Nash & Sofer 1996)

Ilustrasi solusi basis dan solusi basis fisibel diberikan dalam Contoh 1.

Contoh 1

Misalkan diberikan masalah PL berikut:

1 2

min 3z= − x −2x ,

1 2 3

1 2 4

1 5

1 2 3 4 5

terhadap 2 3,

2 8,

5,

, , , , 0.

x x x

x x x

x x

x x x x x

− + + =

− + + =

+ = ≥

(4)

Dari PL tersebut diperoleh:

2 1 1 0 0 3

1 2 0 1 0 , 8

1 0 0 0 1 5

−

= − =

⎛

⎞

⎛ ⎞

⎜

⎟

⎜ ⎟

⎜

⎟

⎜ ⎟

⎝

⎠

⎝ ⎠

A b

.

Misalkan dipilih

(

3 4 5

)

dan

(

1 2

)

,

T T

x x x x x

= =

B N

x x

3

1 0 0 1 0 0

-1

= 0 1 0 , = 0 1 0 ,

0 0 1 0 0 1

⎛

⎞

⎛

⎞

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

B B

-2 1

-1 2

1 0

=

⎛

⎞

⎜

⎟

⎜

⎟

⎝

⎠

N

(

3 8 5

)

,

(

0 0

)

= =

T T

B N

c c

.

Dengan menggunakan matriks basis tersebut, diperoleh

(

)

(

)

,

0 0

= 3 8 5

z = 25

T

T =

= = − T -1 B N B

-1

x

x B b

c B b

(5)

Solusi (5) merupakan solusi basis, karena memenuhi kendala pada masalah PL (4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (5), yaitu B bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (5) juga merupakan solusi basis fisibel, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

Hal yang juga penting dalam konsep pemrograman linear untuk model ini adalah daerah fisibel dan solusi optimum yang didefinisikan sebagai berikut.

Definisi 7 (Solusi Optimum)

Untuk masalah maksimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimum suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston 2004)

2.2 Integer Programming

Integer programming (IP) atau

pemrograman integer adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer,

maka masalah tersebut dinamakan pure

integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming (MIP). IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

(Garfinkel & Nemhauser 1972)

Definisi 8 (Pemrograman Linear Relaksasi) Pemrograman linear relaksasi atau sering disebut PL-relaksasi merupakan suatu pemrograman linear yang diperoleh dari suatu IP dengan menghilangkan kendala integer atau kendala 0-1 pada setiap variabelnya.

Untuk masalah maksimisasi, nilai optimum fungsi objektif PL-relaksasi lebih besar atau sama dengan nilai optimum fungsi objektif IP, sedangkan untuk masalah minimisasi, nilai optimum fungsi objektif PL-relaksasi lebih kecil atau sama dengan nilai optimum fungsi objektif IP.

(Winston 2004)

2.3 Nonlinear Programming

Model nonlinear programming (NLP) meliputi pengoptimuman suatu kondisi berikut :

a) fungsi objektif nonlinear terhadap kendala linear,

b) fungsi objektif nonlinear terhadap kendala nonlinear,

c) fungsi objektif nonlinear dan

takberkendala.

(Sharma 2006)

Definisi 9 (bentuk umum suatu NLP)

Bentuk umum suatu nonlinear

programming adalah :

max (atau min) z = f(x1, x2, ..., xn)

terhadap kendala:

g1(x1, x2, ..., xn) ( , , )≤ = ≥ b1 g2(x1, x2, ..., xn) ( , , )≤ = ≥ b2

M

gm(x1, x2, ..., xn) ( , , )≤ = ≥ bm (6)

Komponen x1, x2, ..., xn merupakan variabel

keputusan dan b1,b2, ..., bm adalah konstanta.

f(x1, x2, ..., xn) adalah fungsi objektif dan

gj(x1, x2, ..., xn) menyatakan fungsi-fungsi

kendala persamaan atau pertaksamaan, dengan j = 1, 2, …, m. Jika bentuk umum memiliki kendala, maka masalah (6) dinamakan masalah nonlinear programming berkendala. Jika bentuk umum tidak memiliki kendala, maka masalah (6) dinamakan masalah nonlinear programming takberkendala.

(Winston 2004)

2.3.1 Konsep Dasar NLP

dasar, yaitu gradien dan matriks Hesse fungsi banyak variabel.

Vektor Gradien dan Matriks Hesse

Misalkan f adalah fungsi dari n variabel

1, 2,..., n

x x x (biasa dituliskan dengan

( )

f x = f x x( ,_{1 2},...,xn) dan terdiferensialkan

dua kali secara kontinu, dan dinyatakan dengan f∈C2. Untuk f∈C2 didefinisikan vektor gradien fungsi f di titik x adalah

1 2 ( ) ( ) ( ) ( ) n f x f x f f x ∂ ⎛ ⎞ ⎜_∂ ⎟ ⎜ ⎟ ⎜ ∂ ⎟ ⎜_∂ ⎟ ∇ _{= ⎜ ⎟} ⎜ ⎟ ⎜ ⎟ ∂ ⎜ ⎟ ⎜_∂ ⎟ ⎝ ⎠ x x x x M

Jika fungsi terdiferensialkan secara kontinu dua kali maka di titik x terdapat matriks turunan parsial yang disebut matriks Hesse (Hessian matrix)

2 2 ( ) ( ) ( ) i j f H f x x ⎧_∂ ⎫ ⎪ ⎪ =⎨_{∂ ∂} ⎬= ∇ ⎪ ⎪ ⎩ ⎭ x x x

2 2 2

2

1 2 1

1

2 2 2

2

2 1 2 2

2 2 2

2 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n

n n n

f f f

x x x x

x

f f f

x x x x x

f f f

x x x x x

⎛∂ ∂ ∂ ⎞ ⎜ ⎟ ∂ ∂ ∂ ∂ ∂ ⎜ ⎟ ⎜_{∂ ∂ ∂} ⎟ ⎜ ⎟ ⎜ ⎟ = ∂ ∂ ∂ ∂ ∂ ⎜ ⎟ ⎜ ⎟ ⎜_{∂ ∂ ∂} ⎟ ⎜ ⎟ ⎜_{∂ ∂ ∂ ∂ ∂} ⎟ ⎝ ⎠

x x x

x x x

x x x

L

K

M M O M

L

2.3.2 Fungsi Konveks dan Fungsi Konkaf Definisi 10 (Fungsi Konveks dan Konkaf) Fungsi f dikatakan fungsi konveks pada selang I jika hanya jika

1 2 1 2

( (1 ) ) ( ) (1 ) ( ),

f λx + −λ x ≤λf x + −λ f x

untuk setiap x x1, 2∈I dan untuk

setiap 0≤ ≤λ 1

.

Fungsi f dikatakan fungsi konkaf pada selang I jika hanya jika

1 2 1 2

( (1 ) ) ( ) (1 ) ( ),

f λx + −λ x ≥λf x + −λ f x

untuk setiap x x1, 2∈I dan untuk

setiap 0≤ ≤λ 1

.

(Ecker & Kupferschmid 1998)

2.3.3 Pengoptimuman Berkendala

Metode yang dapat digunakan dalam menyelesaikan pengoptimuman berkendala di antaranya adalah metode iteratif (metode

penalti) dan metode analitik (pengali Lagrange dan kondisi Karush-Kuhn-Tucker). Di bawah ini akan dibahas salah satu metode penyelesaian untuk pengoptimuman berkendala.

Kondisi Karush-Kuhn-Tucker (KKT)

Misalkan diberikan pengoptimuman kendala pertidaksamaan, maka salah satu alternatif penyelesaian adalah dengan mengubah semua pertaksamaan menjadi persamaan dengan menambah variabel tambahan, seperti:

( ) 0 ( ) 0

g x ≤ →g x + =y

Namun dengan cara ini tidak efektif jika terlalu banyak kendala yang harus diubah karena mengakibatkan bertambah banyak variabel keputusan yang harus dilibatkan. Teknik lain untuk menyelesaikan masalah tersebut adalah dengan menggunakan kondisi Karush-Kuhn-Tucker.

Misalkan diberikan masalah pengoptimuman:

min ( )f x … (8)

terhadap ( ) 0, 1, 2, ..., 1

( ) 0, , ..., dan

j

n j

g j m

g j m p R

= = −

≤ = ∈

x

x x

dengan f dan gjmerupakan fungsi-fungsi yang

mempunyai turunan pertama yang kontinu. Didefinisikan fungsi Lagrange

L(x,λ) = f(x) +

1 ( ) m j j j g λ =

∑

x

Karush (1939) dan Kuhn dan Tucker (1951) secara terpisah menurunkan syarat perlu yang harus dipenuhi oleh solusi (minimizer) x* dari masalah (8), yang disebut kondisi KKT, yaitu terdapat λ*∈Rn sehingga:

1. i

f x

∂ ∂ (x*)

* 1 m j j j i g x λ = ∂ + ∂

∑

(x*)=0,i=1, 2,...,l 2. g_j(x*)≤0, ,...,j=m p

3. *

jgj

λ (x*)=0, j=m,...,p 4. λ*j ≥0, ,...,j=m p

dengan λ*pengali Lagrange. Kondisi di atas dapat menjadi syarat cukup untuk strong globalminimizer x* jika f dan gj merupakan

fungsi konveks.

(Snyman 2005)

2.4 Integer Nonlinear Programming

Model integer nonlinear programming

5

berupa bilangan integer dengan fungsi

objektif atau kendalanya nonlinear.

(Ecker & Kupferschmid 1998)

Bentuk umum dari masalah integer nonlinear programming (INLP) adalah sebagai berikut:

min ( )f x

terhadap g_i( )x ≤b i_i, 1, 2,...,= m      

(9)       h_k( )x =c_k, 1, 2,...,k= l  

     x∈X ⊆Zn       dengan  f( )x ,g_i( )x ,h_k( )x merupakan fungsi bilangan real pada Rndan Znmerupakan himpunan nilai-nilai integer diRn.

° _X

xÎ adalah solusi fisibel pada masalah (9) jika ₍°₎

i i

g x £ b

,

untuk semua i=1,...,m dan °

( )

k k

h x = c

,

untuk semua k= 1,...,l

.

Sebuah solusi fisibel x* dinamakan solusi optimal pada masalah (9) jika f(x*)£ f( )x untuk semua solusi fisibel x pada masalah (9). Setiap menyelesaikan masalah INLP dilakukan relaksasi untuk melepaskan nilai x yang bernilai integer. Penyelesaian masalah relaksasi pada nonlinear programming, di antaranya menggunakan kondisi Karush Kuhn Tucker (KKT)dan metode globaldescent.

2.5 Metode Branch-and-Bound

Dalam penulisan karya ilmiah ini, untuk memperoleh solusi optimum dari masalah INLP digunakan software LINGO 8.0 yaitu sebuah program yang didesain untuk menentukan solusi model linear, nonlinear, dan optimisasi integer. Software LINGO 8.0 ini menggunakan metode branch and bound untuk menyelesaikan masalah IP atau INLP.

Prinsip dasar metode branch and bound adalah memecah daerah fisibel dari masalah (9) dengan memartisi ruang pencarian, dilakukan dengan membagi daerah fisibel ke dalam p himpunan bagian X1, X2,…, Xp

dengan p≥2.

• Branch

Branching (pencabangan) adalah proses membagi-bagi permasalahan menjadi subproblem-subproblem yang mungkin mengarah ke solusi.

• Bound

Bounding (pembatasan) adalah suatu proses untuk mencari atau menghitung batas

atas (dalam masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk solusi optimum pada subproblem yang mengarah ke solusi.

Metode branch-and-bound untuk masalah minimisasi diawali dengan membuat subproblem-subproblem. Sebuah subproblem pada node i, (P(Xi)), i=1,…, p adalah bentuk

dari masalah (9) dengan menggantikan X dengan Xi. Satu atau lebih subproblem dipilih

dari daftar subproblem yang ada. Untuk setiap node dipilih sebuah batas bawah LBi dari nilai

optimal subproblem (P(Xi)) yang

diperkirakan. Jika LBi lebih besar atau sama

dengan nilai fungsi objektif dari nilai awal maka kandidat solusi fisibel terbaik telah ditemukan, kemudian subproblem (P(Xi))

dieliminasi dari pertimbangan selanjutnya. Jika tidak, masalah (P(Xi)) disimpan dalam

daftar subproblem. Nilai awal diperbarui setiap kali sebuah solusi fisibel terbaik

ditemukan. Satu dari node yang tidak

dieliminasi, (P(Xi)), dipilih untuk dilakukan

pencabangan (branching) menjadi subproblem yang lebih kecil. Proses ini diulang sampai tidak ada subproblem yang tersisa dalam daftar.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah minimisasi dengan metode branch-and-bound.

Misalkan diberikan masalah INLP (9).

• Langkah 0 (Inisialisasi)

Didefinisikan L = {P(X)} sebagai subproblem dari fungsi INLP, x* dan v* = f (x) sebagai kandidat solusi optimum masalah INLP. Jika tidak ada solusi fisibel yang tersedia, maka dimisalkan v*= +∞ dan i=0.

• Langkah 1 (Pemilihan node)

Jika L= ∅

,

proses berhenti dan x* adalah solusi optimum INLP. Jika tidak, pilih salah satu atau lebih subproblem {P(X)} dari L sebagai bagian masalah berikutnya untuk diperiksa. Dinotasikan k sebagai banyaknya subproblem yang dipilih dari Ls = {P(X1),... P(Xk)}. MisalkanL:=L L\ s;i=1.

• Langkah 2 (Bounding)

dilanjutkan ke Langkah 5. Jika tidak, proses dilanjutkan ke Langkah 3.

• Langkah 3 (Solusi fisibel)

Simpan solusi fisibel yang ditemukan pada Langkah 2 atau temukan solusi fisibel yang lebih baik dari metode heuristik tertentu. Perbarui kandidat solusi optimal x* dan v*. Jika solusi INLP yang diperoleh lebih baik dari solusi fisibel yang diperoleh sebelumnya, eliminasi P X( _i)dari Lsyang memenuhi

* ;

j

LB ≥v 1≤ <j i.Jika i<k; i= +i 1maka Langkah 2 diulangi. Jika tidak, proses dilanjutkan ke Langkah 4 untuk melakukan pencabangan P X( _i)

.

• Langkah 4 (Branching)

Jika Ls = ∅

,

kembali ke Langkah 1. Jika tidak pilih salah satu subproblem P(Xi) dari

s

L dan X_idibagi menjadi subset yang lebih kecil L_is ={X₁s,...,X_ip}. Eliminasi P(Xi) dari

Ls dan misalkan L:=LULsULs_i. Kembali ke Langkah 1.

• Langkah 5 (Fathoming)

Eliminasi P X( _i) dari Ls

.

Jika i<kdengan

1

i= +i maka kembali ke Langkah 2. Jika

tidak, kembali ke Langkah 4.

(Li & Sun 2006)

Untuk memudahkan pemahaman mengenai metode branch-and-bound diberikan contoh sebagai berikut.

Contoh 2

Misalkan diberikan INLP berikut:

2 2

1 2 1 2 5 1 2 2

min 2v= x +x −2x x − x − x

2 2

1 2

1 2

1 2 1 2

terhadap 16,

5 3 4,

, 0

, .

x x

x x

x x

x x integer

+ ≤

− ≥ −

≥ (10)

Solusi optimum NLP-relaksasi dari

masalah INLP (10) adalah x1=2.57,

2 3.06

x = , dan v= −12.13 (lihat Lampiran 1). Batas atas nilai optimum fungsi objektif masalah (10) adalah v= −12.13. Daerah fisibel masalah (10) ditunjukkan pada Gambar 1. Solusi optimum berada di daerah fisibel yang berasal dari kendala pertidaksamaan masalah (10).

Gambar 1 Daerah fisibel (daerah yang diarsir) untuk NLP-relaksasi dari INLP (10).

Langkah awal metode branch and bound adalah menentukan daftar subproblem L = {P(X)} dari kendala yang ada. Solusi yang didapatkan masalah (10) belum memenuhi syarat integer, maka dimisalkan v*= +∞

.

Karena L≠ ∅ _{maka dibuat}

subproblem-subproblem baru, dimisalkan sebanyak k = 2 yang memenuhi kendala masalah INLP (10). Subproblem-subproblem tersebut dinotasikan Ls={P(X1), P(X2)}, didefinisikan sebagai berikut:

• Subproblem P(X1): masalah INLP (10) ditambah kendala 0≤x₂≤2;

• Subproblem P(X2): masalah INLP (10) ditambah kendala 2≤x2≤4

Hal ini diilustrasikan secara grafis pada Gambar 2.

Gambar 2 Daerah fisibel subproblem P(X1) dan subproblem P(X2)

Langkah selanjutnya adalah menghitung batas atas UBi setiap subproblem. UBi

merupakan pendekatan nilai fungsi objektif yang terdapat pada subproblem (P(Xi)). Jika

subproblem (P(Xi)) memiliki solusi tidak

fisibelmaka UBi = +∞. Penghitungan semua

subproblem menggunakan software LINGO

8.0, ditulis pada Lampiran 2. Hasil semua Daerah fisibel

7

subproblem masalah INLP (10) ditulis dalam Tabel 1 di bawah ini:

Tabel 1 Subproblem-subproblem masalah INLP (10)

No Subproblem x UBi

1 P(X1) (2.25,2) −10.13

2 P(X2) (2.57,3.06) −12.13

Langkah berikutnya adalah bounding dan fathoming. Jika UBi ≥v* maka eliminasi

subproblem P(Xi). Perbarui nilai x* dan v*

dengan solusi fisibel yang memiliki nilai fungsi objektif terkecil dan memenuhi kendala integer. Batas atas yang dihasilkan pada subproblem P(X1), UB1= −10.13 tidak lebih

dari v* dan solusi yang dihasilkan tidak memenuhi kendala integer, maka dipilih salah satu variabel untuk dasar pencabangan. Misalnya dipilihx1sebagai dasar pencabangan

dari subproblem P(X1).

Pencabangan Subproblem P(X1)

menghasilkan 1

s

L ={ 1 1

( ),

P X 2

1

( ),

P X 3

1 ( ), P X 4 1 ( )

P X }, yaitu:

• Subproblem 1

1

( )

P X : Subproblem P(X1) ditambah kendala 0≤x1≤1;

• Subproblem 2

1

( )

P X : Subproblem P(X1) ditambah kendala 1≤ ≤x1 2;

• Subproblem 3

1

( )

P X : Subproblem P(X1) ditambah kendala 2≤x1≤3;

• Subproblem 4

1

( )

P X : Subproblem P(X1) ditambah kendala 3≤x1≤4

Solusi dari hasil pencabangan Subproblem P(X1) ditunjukkan dalam Tabel 2.

Tabel 2 Pencabangan Subproblem P(X1)

No Subproblem x UBi

1 P X( 11) (1,2) −7

2 P X( 12) (2,2) −10

3 P X( 13) (2.25,2) −10.125

4 P X( 14) (3,2) −9

Periksa setiap subproblem baru, jika

*

i

UB ≥v maka eliminasi subproblem(P(Xi)).

Dari Tabel 2, solusi yang dihasilkan

Subproblem 1

1

( )

P X memenuhi kendala

integer dan 1

1 7 *

UB = − <v , maka perbarui x* = (1,2) dan v* = −7 sebagai kandidat solusi optimum.

Langkah selanjutnya adalah memeriksa

Subproblem 2

1

( )

P X . Batas atas yang

dihasilkan Subproblem 2

1

( )

P X yaitu

1

1 10 *

UB = − <v , solusi yang dihasilkan

memenuhi kendala integer dan lebih baik dari

Subproblem 1

1

( )

P X sehingga perbarui x* = (2,2) dan v* = −10 sebagai kandidat solusi optimum INLP.

Dari Tabel 2, batas atas Subproblem

3 1

( )

P X tidak memenuhi syarat eliminasi,

karena 3

1 10.125 *

UB = − <v . Solusi yang

dihasilkan tidak memenuhi kendala integer, maka dipilih salah satu variabel untuk dasar pencabangan. Misalnya x2 sebagai dasar

pencabangan subproblem 3

1

( )

P X .

Pencabangan subproblem 3

1

( )

P X didefinisikan

3. 3.1 3.2

1 { ( 1 ), ( 1 )}

s

L = P X P X , yaitu:

• SubproblemP X( ₁3.1) :SubproblemP X( ₁3)

ditambah kendala 0≤x2≤1;

• Subproblem 3.2

1

( ) :

P X SubproblemP X( ₁3) ditambah kendala 1≤x2 ≤2;

Solusi dari hasil pencabangan Subproblem 3

1

( )

P X ditunjukkan dalam Tabel 3. Tabel 3 Pencabangan Subproblem P X( ₁3)

No Subproblem x UBi

1 P X( 13.1) (2,1) −7

2 P X( 13.2) (2.25,2) −10.125

Dari Tabel 3, batas atas Subproblem

3.1 1

( )

P X memenuhi syarat eliminasi karena

3.1

1 7 *

UB = − >v , sedangkan batas atas

subproblem 3.2

1

( )

P X tidak tereliminasi karena

3.2

1 10.125 *

UB = − <v . Solusi yang dihasilkan

Subproblem 3.2

1

( )

P X tidak diperbarui karena tidak memenuhi kendala integer. Selain dari

itu Subproblem 3.2

1

( )

P X memiliki daerah

fisibel yang tidak dapat dipartisi sehingga tidak dicabangkan lagi.

Selanjutnya diperiksa Subproblem

4 1

( ).

P X Batas atas Subproblem 4

1

( )

P X , yaitu

4

1 9 *

UB = − >v sehingga x* dan v* tidak diperbarui.

Subproblem yang belum diperiksa, yaitu Subproblem P(X2). Batas atas Subproblem P(X2) adalah UB2 = −12.13<v* dan solusi

yang dihasilkan tidak memenuhi kendala integer, maka dilakukan pencabangan. Hasil pencabangan Subproblem P(X2) didefinisikan

1 2 3 4

2 { ( 2), ( 2), ( 2), ( 2)}

s

• Subproblem 1 2

( ) :

P X Subproblem P(X2) ditambah kendala 0≤x1≤1;

• Subproblem 2

2

( ) :

P X Subproblem P(X2) ditambah kendala 1≤ ≤x1 2;

• Subproblem 3

2

( ) :

P X Subproblem P(X2) ditambah kendala 2≤x1≤3;

• Subproblem 4

2

( ) :

P X Subproblem P(X2) ditambah kendala 3≤x1≤4.

Solusi dari hasil pencabangan Subproblem P(X2) ditunjukkan dalam Tabel 4.

Tabel 4 Pencabangan Subproblem P(X2)

No Subproblem x UBi

1 P X( 21) (1,2) −7

2 P X( 22) (2,3.33) −11

3 P X( 23) (2.57,3.06) −12.13

4 P X( 24) (3,2.65) −11.16

Periksa setiap subproblem baru, jika

*

i

UB ≥v maka eliminasi subproblem(P(Xi)).

Dari Tabel 4, batas atas yang dihasilkan

subproblem 2

1

( ),

P X yaitu 1

2 7 *,

UB = − >v

sehingga x* dan v* tidak diperbarui. Batas

atas 2

2

( )

P X , 3

2

( )

P X ,dan 4 2

( )

P X tidak lebih

dari v* dan solusi yang dihasilkan tidak memenuhi kendala integer, maka dilakukan pencabangan dari setiap subproblem. Hasil

pencabangan Subproblem 2

2

( )

P X , yaitu:

• Subproblem 2.1

2

( ) :

P X Subproblem 2

2

( )

P X

ditambah kendala 2≤x2 ≤3;

• Subproblem 2.2

2

( ) :

P X Subproblem 2

2

( )

P X

ditambah kendala 3≤x2 ≤4.

Solusi dari hasil pencabangan Subproblem

2 2

( )

P X ditunjukkan dalam Tabel 5.

Tabel 5 Pencabangan Subproblem 2

2

( )

P X

No Subproblem x UBi

1 P X( 22.1) (2,3) −11

2 P(X22.2) (2,3) −11

Dari Tabel 5, batas atas Subproblem

2.1 2

( )

P X dan 2.2

2

( ),

P X 2

2 11 *

UB = − <v

sehingga perbarui nilai x* dan v*.

Subproblem 2.1

2

( )

P X dan 2.2

2

( )

P X memiliki

daerah fisibel yang tidak dapat dipartisi, maka subproblem ini tidak dicabangkan lagi. Semua variabel subproblem P X( 22.1) dan

2.2 2

( )

P X

bernilai integer (solusinya memenuhi kendala integer) dan solusi yang dihasilkan pada

subproblem ini lebih baik dari batas atas sebelumnya sehingga solusi pada subproblem ini menjadi kandidat batas atas baru dari solusi INLP (10) yaitu x* = (2,3), v*= −11.

Hasil pencabangan subproblem 3

2

( ),

P X

yaitu:

• Subproblem 3.1

2

( ) :

P X Subproblem 3

2

( )

P X

ditambah kendala 2≤x2 ≤3;

• Subproblem 3.2

2

( ) :

P X Subproblem 3

2

( )

P X

ditambah kendala 3≤x2 ≤4.

Solusi dari hasil pencabangan Subproblem

3 2

( )

P X ditunjukkan dalam Tabel 6.

Tabel 6 Pencabangan Subproblem 3

2

( )

P X

No Subproblem x UBi

1 P X( 23.1) (2.65,3) −12.10

2 P X( 23.2) (2.57,3.06) −12.13

Nilai batas bawah Subproblem P(X23.1),

3.1

2 12.10 *

UB = − <v dan Subproblem

P(X23.2), UB23.2= −12.13<v* sehingga

perbarui nilai x* dan v*. Akan tetapi, solusi yang dihasilkan tidak memenuhi kendala integer sehingga x* dan v* tidak diperbarui.

Subproblem 3.1

2

( )

P X dan 3.2

2

( )

P X memiliki

daerah fisibel yang tidak dapat dipartisi lagi, maka subproblem ini tidak dicabangkan.

Langkah selanjutnya adalah memilih masalah yang belum diselesaikan, yaitu

pencabangan Subproblem 4

2

( )

P X . Hasil

pencabangan Subproblem 4

2

( )

P X ,yaitu:

• Subproblem 4.1

2

( ) :

P X Subproblem 4

2

( )

P X

ditambah kendala 2≤x2 ≤3;

• Subproblem 4.2

2

( ) :

P X Subproblem 4

2

( )

P X

ditambah kendala 3≤x2 ≤4.

Solusi dari hasil pencabangan Subproblem

4 2

( )

P X ditunjukkan dalam Tabel 7.

Tabel 7 Pencabangan Subproblem 4

2

( )

P X

No Subproblem x UBi

1 P X( 24.1) (3,2.65) −11.17

2 P X( 24.2) Takfisibel +∞

Nilai batas atas 4.1 2

( ),

P X 4.1

2 11.17 *,

UB = − <v

sehingga tidak memenuhi syarat eliminasi. Akan tetapi, solusi yang dihasilkan tidak memenuhi kendala integer sehingga x* dan

v* tidak diperbarui. Subproblem

4.1 2

( )

9

dapat dipartisi lagi, maka subproblem ini tidak

dicabangkan. Subproblem 4.2

2

( )

P X memenuhi

syarat eliminasi, yaitu UBi ≥v*. Karena

subproblem pada percabangan ini tereliminasi maka x* dan v* tidak diperbarui.

Semua subproblem sudah diperiksa dan tidak ada subproblem tersisa dalam daftar

sehingga L= ∅. Subproblem 2.1

2

( )

P X dan

2.2 2

( )

P X menghasilkan solusi optimal yang

berupa integer. Dengan demikian, solusi optimum pada masalah INLP (10) adalah x1* = 2, x2* = 3, v*= −11.

III PEMODELAN

Model penjadwalan pada karya ilmiah ini menggunakan enam parameter utama sebagai penyusun jadwal yaitu;

1. Hari, yaitu hari di mana kegiatan

perkuliahan diselenggarakan. Hari = {Senin, Selasa, …, Jumat}.

2. Periode waktu, yaitu waktu kuliah di mana mata kuliah diselenggarakan. Periode waktu = {08.00-08.45, 08.45-09.30, …, (t -t+1)}.

3. Kelompok, yaitu kelompok mahasiswa

yang menghadiri mata kuliah yang sama berdasarkan program kuliah yang telah tersedia. Kelompok program regular diselenggarakan pukul 08.00-16.00, sedangkan pukul 17.00-22.00 untuk program ekstensi.

4. Dosen, yaitu orang yang mengajar suatu mata kuliah tertentu dalam suatu kelas. Dosen = {Dosen 1, Dosen 2, …, Dosen l}.

5. Mata kuliah, yaitu pelajaran yang

diajarkan di kelas oleh seorang dosen. Mata kuliah = {mata kuliah 1, mata kuliah 2, …, mata kuliah m}.

6. Ruangan, yaitu tempat berlangsungnya

kegiatan perkuliahan. Ruangan = {ruangan 1, ruangan 2, …, ruangan n}.

Jadwal tersebut dibuat sedemikian rupa sehingga memenuhi kendala utama dan kendala tambahan. Kendala utama dalam penjadwalan, yaitu:

1. Semua mata kuliah terjadwalkan di setiap semesternya.

2. Tidak ada overlapping mata kuliah. 3. Dosen tidak boleh mengajar lebih dari satu

kelas pada periode waktu yang sama. Sedangkan kendala tambahan, yaitu :

1. Untuk mata kuliah yang tediri atas kuliah dan praktikum, jadwal kuliah dilaksanakan lebih dulu dari jadwal praktikum.

2. Setiap mata kuliah diselenggarakan pada periode waktu yang sesuai. Misalkan mata kuliah dengan waktu tatap muka 3 jam tidak boleh diselenggarakan pada waktu tatap muka 2 jam.

3. Setiap dosen tidak mengajarkan mata

kuliah yang bukan bidangnya.

4. Sebagian dosen berharap tidak mengajar pada waktu tertentu.

Dalam model penjadwalan karya ilmiah ini terdapat koefisien (bobot) yang merupakan nilai dari ketidakpuasan yang diberikan oleh mahasiswa program regular dan ekstensi terhadap penjadwalan suatu mata kuliah. Penentuan besar kecilnya bobot ditentukan atas keinginan mahasiswa terhadap suatu mata kuliah yang akan dijadwalkan di awal atau di akhir periode waktu. Semakin kecil bobot maka peluang dijadwalkannya mata kuliah yang sesuai dengan keinginan mahasiswa semakin besar. Penentuan bobot yang disebutkan tidaklah mutlak. Bobot yang ada di sini hanyalah sebagai gambaran saja. Sebagai contoh :

1. Mahasiswa program regular mengharapkan mata kuliah dapat diajarkan di awal periode waktu. Oleh karena itu kepuasan mahasiswa ini diberi bobot (koefisien) yang kecil di awal periode waktu dan bobot yang besar di akhir periode waktu, sehingga mata kuliah ini memiliki peluang yang lebih besar untuk dijadwalkan di awal periode waktu (Gambar 3).

2. Mahasiswa program ekstensi

dapat dipartisi lagi, maka subproblem ini tidak

dicabangkan. Subproblem 4.2

2

( )

P X memenuhi

syarat eliminasi, yaitu UBi ≥v*. Karena

subproblem pada percabangan ini tereliminasi maka x* dan v* tidak diperbarui.

Semua subproblem sudah diperiksa dan tidak ada subproblem tersisa dalam daftar

sehingga L= ∅. Subproblem 2.1

2

( )

P X dan

2.2 2

( )

P X menghasilkan solusi optimal yang

berupa integer. Dengan demikian, solusi optimum pada masalah INLP (10) adalah x1* = 2, x2* = 3, v*= −11.

III PEMODELAN

Model penjadwalan pada karya ilmiah ini menggunakan enam parameter utama sebagai penyusun jadwal yaitu;

1. Hari, yaitu hari di mana kegiatan

perkuliahan diselenggarakan. Hari = {Senin, Selasa, …, Jumat}.

2. Periode waktu, yaitu waktu kuliah di mana mata kuliah diselenggarakan. Periode waktu = {08.00-08.45, 08.45-09.30, …, (t -t+1)}.

3. Kelompok, yaitu kelompok mahasiswa

yang menghadiri mata kuliah yang sama berdasarkan program kuliah yang telah tersedia. Kelompok program regular diselenggarakan pukul 08.00-16.00, sedangkan pukul 17.00-22.00 untuk program ekstensi.

4. Dosen, yaitu orang yang mengajar suatu mata kuliah tertentu dalam suatu kelas. Dosen = {Dosen 1, Dosen 2, …, Dosen l}.

5. Mata kuliah, yaitu pelajaran yang

diajarkan di kelas oleh seorang dosen. Mata kuliah = {mata kuliah 1, mata kuliah 2, …, mata kuliah m}.

6. Ruangan, yaitu tempat berlangsungnya

kegiatan perkuliahan. Ruangan = {ruangan 1, ruangan 2, …, ruangan n}.

Jadwal tersebut dibuat sedemikian rupa sehingga memenuhi kendala utama dan kendala tambahan. Kendala utama dalam penjadwalan, yaitu:

1. Semua mata kuliah terjadwalkan di setiap semesternya.

2. Tidak ada overlapping mata kuliah. 3. Dosen tidak boleh mengajar lebih dari satu

kelas pada periode waktu yang sama. Sedangkan kendala tambahan, yaitu :

1. Untuk mata kuliah yang tediri atas kuliah dan praktikum, jadwal kuliah dilaksanakan lebih dulu dari jadwal praktikum.

2. Setiap mata kuliah diselenggarakan pada periode waktu yang sesuai. Misalkan mata kuliah dengan waktu tatap muka 3 jam tidak boleh diselenggarakan pada waktu tatap muka 2 jam.

3. Setiap dosen tidak mengajarkan mata

kuliah yang bukan bidangnya.

4. Sebagian dosen berharap tidak mengajar pada waktu tertentu.

Dalam model penjadwalan karya ilmiah ini terdapat koefisien (bobot) yang merupakan nilai dari ketidakpuasan yang diberikan oleh mahasiswa program regular dan ekstensi terhadap penjadwalan suatu mata kuliah. Penentuan besar kecilnya bobot ditentukan atas keinginan mahasiswa terhadap suatu mata kuliah yang akan dijadwalkan di awal atau di akhir periode waktu. Semakin kecil bobot maka peluang dijadwalkannya mata kuliah yang sesuai dengan keinginan mahasiswa semakin besar. Penentuan bobot yang disebutkan tidaklah mutlak. Bobot yang ada di sini hanyalah sebagai gambaran saja. Sebagai contoh :

1. Mahasiswa program regular mengharapkan mata kuliah dapat diajarkan di awal periode waktu. Oleh karena itu kepuasan mahasiswa ini diberi bobot (koefisien) yang kecil di awal periode waktu dan bobot yang besar di akhir periode waktu, sehingga mata kuliah ini memiliki peluang yang lebih besar untuk dijadwalkan di awal periode waktu (Gambar 3).

2. Mahasiswa program ekstensi

10

Gambar 3 Bobot suatu mata kuliah yang diharapkan diajarkan di awal periode waktu untuk mahasiswa program regular.

Gambar 4 Bobot suatu mata kuliah yang diharapkan diajarkan di akhir periode waktu untuk mahasiswa program ekstensi.

Variabel-variabel yang digunakan:

Jkr = himpunan periode waktu pada

kelompok mahasiswa regular

Jkx = himpunan periode waktu pada

kelompok mahasiswa ekstensi Jw2 = himpunan periode waktu tatap muka

2 jam

Kr = himpunan mahasiswa regular

Kx = himpunan mahasiswa ekstensi

Mls = himpunan mata kuliah yang bukan

spesialisasi dari dosen

Mp = himpunan mata kuliah berpraktikum

Mw3 = himpunan mata kuliah dengan waktu tatap muka 3 jam

Ltj = himpunan dosen yang tidak dapat

mengajar pada periode waktu tertentu Lts = himpunan dosen yang tidak mengajar

mata kuliah yang bukan spesialisnya

Itl = himpunan hari di mana dosen

berharap tidak mengajar

Jtl = himpunan periode waktu di mana

dosen berharap tidak mengajar Jm2 = himpunan periode waktu untuk mata

kuliah dengan tatap muka 2 jam Nm = himpunan ruangan perkuliahan

Np = himpunan ruangan praktikum

Selain itu, diperlukan pula pendefinisian suatu variabel keputusan:

1 ; jika di hari pada periode kelompok mahasiswa diajar oleh dosen untuk mata kuliah = yang diselenggarakan di ruangan

0 ; selainnya

i j k l m

x_ijklmn ⎧⎪⎨ n

⎪⎩

{

1 ; jika di hari pada periode waktu dosen berharap tidak mengajar =

0 ; selainnya

i j l

b ijl

Model bertujuan meminimumkan ketidakpuasan mahasiswa program regular, ekstensi, dan dosen terhadap penjadwalan

mata kuliah, maka fungsi objektif dari permasalahan ini adalah sebagai berikut:

1 2

min mj( ) mj( ) ijl( )

m j i k l n ijklmn m j i k l n ijklmn i j l k m n ijklmn

a

x

+ a

x

+ b

x

∑∑

∑∑∑∑

∑∑

∑∑∑∑

∑∑∑ ∑∑∑

dengan: 1mj

a = koefisien yang nilainya bersesuaian dengan ketidakpuasan mahasiswa program regular terhadap penjadwalan mata kuliah ,

2mj

a = koefisien yang nilainya bersesuaian dengan ketidakpuasan mahasiswa program ekstensi terhadap penjadwalan mata kuliah.

Kendala yang terkait adalah sebagai berikut:

1. _{Setiap mata kuliah yang diselenggarakan}

hanya dihadiri oleh satu kelompok.  

1, ,

i j l n ijklmn

m k

x

≤ ∀

∑∑∑∑

 

2. Paling banyak satu mata kuliah yang

diselenggarakan di setiap periode waktunya.

1, , ,

k l n ijklmn

i j m

x

≤ ∀

∑∑∑

 

3. Paling banyak satu ruangan yang

dipergunakan dalam suatu periode waktu perkuliahan.

1, , ,

k l m ijklmn

i j n

x

≤ ∀

∑∑∑

4. Setiap periode waktu perkuliahan hanya dihadiri oleh satu kelompok.

1, , ,

m l n ijklmn

i j k

x

≤ ∀

∑∑∑

5. Terpenuhinya jumlah periode waktu yang diperlukan untuk setiap mata kuliah.

( ),

i j k l n ijklmn

h m m

x

= ∀

∑∑∑∑∑

dengan:

( )

h m = total periode waktu selama

seminggu untuk mata kuliah m 6. Jadwal kuliah mata kuliah berpraktikum

harus diselenggarakan sebelum jadwal praktikum.

1 1

/ ( )

/ ( ) 0 , m

p

t i j k l n N

p p

i j k l n N

ijklmn

ijklmn

w m

w m m M

x

x ∈

+ + ∈

− > ∀ ∈

∑∑∑∑ ∑

∑∑∑∑ ∑

dengan: 

( _t)

w m = lamanya waktu kuliah untuk

mata kuliah teori (dalam jam) ( _p)

w m =  _{lamanya waktu kuliah untuk}

mata kuliah praktikum (dalam jam)

7. Tidak ada mata kuliah yang diberikan

setelah pukul 17.00 WIB untuk program regular.

0, k x, r

i l m n ijklmn

j J k K

x

= ∀ ∈ ∈

∑∑∑∑

8. Tidak ada mata kuliah yang diberikan sebelum pukul 17.00 WIB untuk program ekstensi.

0, _{k r}, _x

i l m n ijklmn

j J k K

x

= ∀ ∈ ∈

∑∑∑∑

 

9. Mata kuliah dengan waktu tatap muka 3 jam tidak boleh diselenggarakan pada waktu tatap muka 2 jam.

2 3

0, m , w

i k l n ijklmn

j J m M

x

= ∀ ∈ ∈

∑∑∑∑

10.Setiap dosen tidak mengajarkan mata

kuliah yang bukan spesialisasinya.

0, ls, ts

i j k n ijklmn

m M l L

x

= ∀ ∈ ∈

∑∑∑∑

11.Beberapa dosen berharap tidak mengajar pada waktu tertentu. Jika dosen l berharap tidak mengajar pada hari i periode waktu j,

maka b 1

ijl =

12.Semua variabel keputusan bernilai nol atau satu.

{0,1}, , , , , ,

ijklmn i j k l m n

x

∈ ∀

{0,1}, , ,

ijl

b ∈ ∀i j l

IV STUDI KASUS

Masalah yang akan dicontohkan di sini adalah masalah penjadwalan perkuliahan semester lima di Akademi Manajemen Informatika dan Komunikasi Bina Sarana Informatika (AMIK) BSI Bogor. Hal yang perlu diperhatikan adalah kepuasan dosen dan mahasiswa dalam menyelesaikan kegiatan perkuliahan, ketersediaan ruangan yang terbatas serta preferensi dosen dan mahasiswa berbeda-beda, sehingga kegiatan perkuliahan ini dilakukan lima hari dalam seminggu yang setiap harinya dibagi menjadi dua waktu dengan sejumlah mata kuliah yang dijadwalkan. Pertama, kelompok mahasiswa yang tergolong dalam program regular

melaksanakan kegiatan perkuliahan pada pukul 08.00-16.00 WIB. Kedua, kelompok mahasiswa yang tergolong dalam program ekstensi melaksanakan kegiatan perkuliahan pada pukul 17.00-22.00 WIB.

Di Departemen AMIK, telah ditentukan bahwa satu jam tatap muka di kelas dilakukan selama 45 menit. Untuk mata kuliah yang terdiri dari dua pertemuan yaitu kuliah dan praktikum, jadwal kuliah harus mendahului jadwal praktikum.

Data yang diperlukan untuk memodelkan penjadwalan mata kuliah semester lima untuk mahasiswa program regular dan program ekstensi diberikan sebagai berikut:

Tabel 8 Daftar mata kuliah semester lima di AMIK

Indeks (m) Mata Kuliah (MK) Kode MK Banyaknya periode

waktu Keterangan

1 Pemrograman Visual FOXPRO (K) 735 1 2 jam kuliah

2 Pemrograman Visual FOXPRO (P) 735 1 3 jam praktikum

11

4. Setiap periode waktu perkuliahan hanya dihadiri oleh satu kelompok.

1, , ,

m l n ijklmn

i j k

x

≤ ∀

∑∑∑

5. Terpenuhinya jumlah periode waktu yang diperlukan untuk setiap mata kuliah.

( ),

i j k l n ijklmn

h m m

x

= ∀

∑∑∑∑∑

dengan:

( )

h m = total periode waktu selama

seminggu untuk mata kuliah m 6. Jadwal kuliah mata kuliah berpraktikum

harus diselenggarakan sebelum jadwal praktikum.

1 1

/ ( )

/ ( ) 0 , m

p

t i j k l n N

p p

i j k l n N

ijklmn

ijklmn

w m

w m m M

x

x ∈

+ + ∈

− > ∀ ∈

∑∑∑∑ ∑

∑∑∑∑ ∑

dengan: 

( _t)

w m = lamanya waktu kuliah untuk

mata kuliah teori (dalam jam) ( _p)

w m =  _{lamanya waktu kuliah untuk}

mata kuliah praktikum (dalam jam)

7. Tidak ada mata kuliah yang diberikan

setelah pukul 17.00 WIB untuk program regular.

0, k x, r

i l m n ijklmn

j J k K

x

= ∀ ∈ ∈

∑∑∑∑

8. Tidak ada mata kuliah yang diberikan sebelum pukul 17.00 WIB untuk program ekstensi.

0, _{k r}, _x

i l m n ijklmn

j J k K

x

= ∀ ∈ ∈

∑∑∑∑

 

9. Mata kuliah dengan waktu tatap muka 3 jam tidak boleh diselenggarakan pada waktu tatap muka 2 jam.

2 3

0, m , w

i k l n ijklmn

j J m M

x

= ∀ ∈ ∈

∑∑∑∑

10.Setiap dosen tidak mengajarkan mata

kuliah yang bukan spesialisasinya.

0, ls, ts

i j k n ijklmn

m M l L

x

= ∀ ∈ ∈

∑∑∑∑

11.Beberapa dosen berharap tidak mengajar pada waktu tertentu. Jika dosen l berharap tidak mengajar pada hari i periode waktu j,

maka b 1

ijl =

12.Semua variabel keputusan bernilai nol atau satu.

{0,1}, , , , , ,

ijklmn i j k l m n

x

∈ ∀

{0,1}, , ,

ijl

b ∈ ∀i j l

IV STUDI KASUS

Masalah yang akan dicontohkan di sini adalah masalah penjadwalan perkuliahan semester lima di Akademi Manajemen Informatika dan Komunikasi Bina Sarana Informatika (AMIK) BSI Bogor. Hal yang perlu diperhatikan adalah kepuasan dosen dan mahasiswa dalam menyelesaikan kegiatan perkuliahan, ketersediaan ruangan yang terbatas serta preferensi dosen dan mahasiswa berbeda-beda, sehingga kegiatan perkuliahan ini dilakukan lima hari dalam seminggu yang setiap harinya dibagi menjadi dua waktu dengan sejumlah mata kuliah yang dijadwalkan. Pertama, kelompok mahasiswa yang tergolong dalam program regular

melaksanakan kegiatan perkuliahan pada pukul 08.00-16.00 WIB. Kedua, kelompok mahasiswa yang tergolong dalam program ekstensi melaksanakan kegiatan perkuliahan pada pukul 17.00-22.00 WIB.

Di Departemen AMIK, telah ditentukan bahwa satu jam tatap muka di kelas dilakukan selama 45 menit. Untuk mata kuliah yang terdiri dari dua pertemuan yaitu kuliah dan praktikum, jadwal kuliah harus mendahului jadwal praktikum.

Data yang diperlukan untuk memodelkan penjadwalan mata kuliah semester lima untuk mahasiswa program regular dan program ekstensi diberikan sebagai berikut:

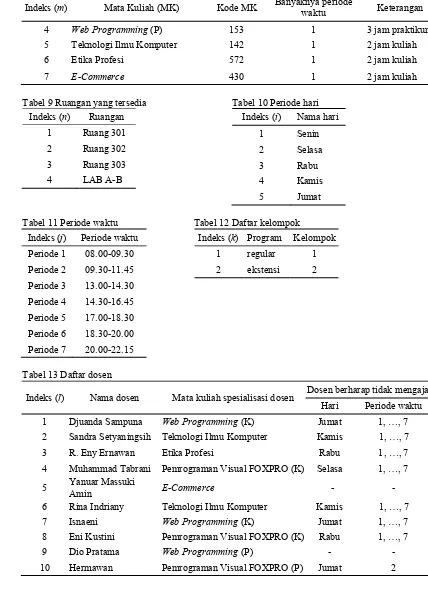
Tabel 8 Daftar mata kuliah semester lima di AMIK

Indeks (m) Mata Kuliah (MK) Kode MK Banyaknya periode

waktu Keterangan

1 Pemrograman Visual FOXPRO (K) 735 1 2 jam kuliah

2 Pemrograman Visual FOXPRO (P) 735 1 3 jam praktikum

Lanjutan Tabel 8

Indeks (m) Mata Kuliah (MK) Kode MK Banyaknya periode

waktu Keterangan

4 Web Programming (P) 153 1 3 jam praktikum

5 Teknologi Ilmu Komputer 142 1 2 jam kuliah

6 Etika Profesi 572 1 2 jam kuliah

7 E-Commerce 430 1 2 jam kuliah

Tabel 9 Ruangan yang tersedia

Indeks (n) Ruangan

1 Ruang 301

2 Ruang 302

3 Ruang 303

4 LAB A-B

Tabel 10 Periode hari Indeks (i) Nama hari

1 Senin 2 Selasa 3 Rabu 4 Kamis 5 Jumat

Tabel 11 Periode waktu Tabel 12 Daftar kelompok

Indeks (j) Periode waktu   Indeks (k) Program Kelompok

Periode 1 08.00-09.30   1 regular 1

Periode 2 09.30-11.45   2 ekstensi 2

Periode 3 13.00-14.30        

Periode 4 14.30-16.45        

Periode 5 17.00-18.30        

Periode 6 18.30-20.00        

Periode 7 20.00-22.15        

Tabel 13 Daftar dosen

Indeks (l) Nama dosen Mata kuliah spesialisasi dosen Dosen berharap tidak mengajar

Hari Periode waktu

1 Djuanda Sampuna Web Programming (K) Jumat 1, …, 7

2 Sandra Setyaningsih Teknologi Ilmu Komputer Kamis 1, …, 7

3 R. Eny Ernawan Etika Profesi Rabu 1, …, 7

4 Muhammad Tabrani Pemrograman Visual FOXPRO (K) Selasa 1, …, 7

5 Yanuar Massuki

Amin E-Commerce - -

6 Rina Indriany Teknologi Ilmu Komputer Kamis 1, …, 7

7 Isnaeni Web Programming (K) Jumat 1, …, 7

8 Eni Kustini Pemrograman Visual FOXPRO (K) Rabu 1, …, 7

9 Dio Pratama Web Programming (P) - -

13

Tujuan karya ilmiah ini adalah membuat penjadwalan terbaik dengan meminimumkan suatu fungsi objektif yaitu penjumlahan dari koefisien-koefisien yang menyatakan ketidakpuasan dari mahasiswa program regular, ekstensi, dan dosen terhadap penjadwalan mata kuliah.

Penentuan koefisien (bobot) yang telah disebutkan pada bagian sebelumnya tidaklah mutlak harus seperti itu. Pada kasus ini hanyalah gambaran saja. Beberapa contoh grafik bobot mata kuliah yang mungkin dapat digunakan diperlihatkan sebagai berikut:

Gambar 5 Bobot mata kuliah Pemrograman Visual FOXPRO (K) yang diharapkan diajarkan di awal periode waktu untuk mahasiswa program regular.

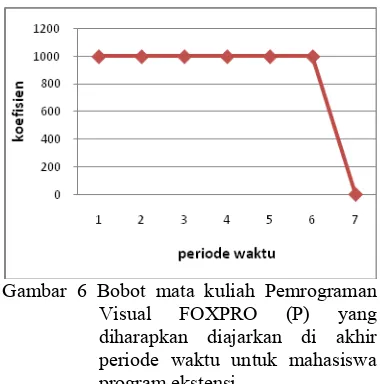
Gambar 6 Bobot mata kuliah Pemrograman Visual FOXPRO (P) yang diharapkan diajarkan di akhir periode waktu untuk mahasiswa program ekstensi.

Untuk memformulasikan penjadwalan mata kuliah ini dalam model INLP, peubah

ijklmn

x

didefinisikan pada setiap periode hari i = 1, 2, …, 5, periode waktu j = 1, 2, …, 7, kelompok mahasiswa k = 1, 2, dosen l = 1, 2, …, 10, mata kuliah m = 1, 2, …, 7, ruangan n = 1, 2, …, 4. Sehingga masalahnya dapat diformulasikan dalam model INLP berikut:

1 2

min mj( ) mj( ) ijl( )

m j i k l n ijklmn m j i k l n ijklmn i j l k m n ijklmn

a

x

+ a

x

+ b

x

∑∑

∑∑∑∑

∑∑

∑∑∑∑

∑∑∑ ∑∑∑

dengan kendala-kendala:

1. Setiap mata kuliah yang diselenggarakan hanya dihadiri oleh satu kelompok.

1, ,

i j l n ijklmn

m k

x

≤ ∀

∑∑∑∑

 

2. Paling banyak satu mata kuliah yang

diselenggarakan di setiap periode waktunya.

      1, , ,

k l n ijklmn

i j m

x

≤ ∀

∑∑∑

 

3. Paling banyak satu ruangan yang

dipergunakan dalam suatu periode waktu perkuliahan.

1, , ,

k l m ijklmn

i j n

x

≤ ∀

∑∑∑

 

4. Setiap periode waktu perkuliahan hanya dihadiri oleh satu kelompok.

1, , ,

m l n ijklmn

i j k

x

≤ ∀

∑∑∑

 

5. Terpenuhinya jumlah periode waktu yang diperlukan untuk setiap mata kuliah.

( ),

i j k l n ijklmn

h m m

x

= ∀

∑∑∑∑∑

 

untuk h(m) = 2, 2, 2, 2, 2, 2, 2.

Misalkan banyaknya periode waktu yang diperlukan untuk mata kuliah Pemrograman Visual FOXPRO per minggu adalah 2, satu periode untuk program regular dan satu periode untuk program ekstensi.

2

i j k l n ijklmn

x

=

∑∑∑∑∑

6. Jadwal kuliah mata kuliah berpraktikum, harus diselenggarakan sebelum jadwal praktikum

a. Program regular

4 3

4 3

1 1 1 1

1 1 1 2 4

/ 2

/ 3 0

i j k l m n

i j k l m n

ijklmn

ijklmn

x

x

= = = =

= = = = =

− >

∑∑∑∑∑∑

4 3

1 1 3 1

4 3

1 1 1 4 4

/ 2

/ 3 0

i j k l m n

i j k l m n

ijklmn ijklmn

x

x

= = = = = = = = = − >

∑∑∑∑∑∑

∑∑∑∑∑∑

  b. Program ekstensi

7 3

5 2 1 1

4 6

1 5 2 2 4

/ 2

/ 3 0

i j k l m n

i j k l m n

ijklmn ijklmn

x

x

= = = = = = = = = − >

∑∑∑∑∑∑

∑∑∑∑∑∑

7 3

5 2 3 1

4 6

1 5 2 4 4

/ 2

/ 3 0

i j k l m n

i j k l m n

ijklmn ijklmn

x

x

= = = = = = = = = − >

∑∑∑∑∑∑

∑∑∑∑∑∑

 

7. Tidak ada mata kuliah yang diberikan

setelah pukul 17.00 WIB untuk program regular.

Untuk k = 1, j = 5, 6, 7 0 i l m n ijklmn

x

=

∑∑∑∑

8. Tidak ada mata kuliah yang diberikan

sebelum pukul 17.00 WIB untuk program ekstensi.

Untuk k = 2, j = 1, 2, 3, 4 0 i l m n ijklmn

x

=

∑∑∑∑

 

9. Mata kuliah dengan waktu tatap muka 3 jam tidak boleh diselenggarakan pada waktu tatap muka 2 jam.

Untuk m = 2, 4, dan j = 1, 3, 5, 6 0

i k l n ijklmn

x

=

∑∑∑∑

10.Setiap dosen tidak mengajarkan mata

kuliah yang bukan spesialisasinya. Untuk l = 1, 7, dan m = 1, 2, 4, 5, 6, 7

0

i j k n ijklmn

x

=

∑∑∑∑

 

Untuk l = 2, 6, dan m = 1, 2, 3, 4, 6, 7

0

i j k n ijklmn

x

=

∑∑∑∑

 

Untuk l = 3, dan m = 1, 2, 3, 4, 5, 7

0

i j k n ijklmn

x

=

∑∑∑∑

 

Untuk l = 4, 8, dan m = 2, 3, 4, 5, 6, 7

0

i j k n ijklmn

x

=

∑∑∑∑

 

Untuk l = 5, dan m = 1, .., 6

0

i j k n ijklmn

x

=

∑∑∑∑

 

Untuk l = 9, dan m = 1, 2, 3, 5, 6, 7

0

i j k n ijklmn

x

=

∑∑∑∑

 

Untuk l = 10, dan m = 1, 3, 4, 5, 6, 7

0

i j k n ijklmn

x

=

∑∑∑∑

11.Beberapa dosen berharap tidak mengajar pada waktu tertentu.

Untuk i = 5, dan l = 1, 7 7

j ijl

b =

∑

Untuk i = 4, dan l = 2, 6 7

j ijl

b =

∑

 

Untuk i = 3, dan l = 3, 8 7

j ijl

b =

∑

 

Untuk i = 2, dan l = 4 7

j ijl

b =

∑

Untuk i = 5, j = 2, dan l = 10 1

b ijl=  

12.Semua variabel keputusan bernilai nol atau satu.

{0,1}, , , , , ,

ijklmn i j k l m n

x

∈ ∀

{0,1}, , ,

ijl

b ∈ ∀i j l

Penyelesaian masalah penjadwalan mata kuliah Akademi Manajemen Informatika dan Komunikasi BSI Bogor pada karya ilmiah ini dilakukan dengan bantuan software LINGO 8.0 menggunakan metode branch and bound. Syntax program dan hasil komputasi dicantumkan pada Lampiran 3. Solusi yang didapat adalah solusi optimal dengan nilai fungsi objektifnya adalah 14080 didapatkan pada iterasi ke 1581. Waktu yang dibutuhkan untuk mendapatkan solusi tersebut sekitar 1 jam 26 menit 41 detik dengan menggunakan komputer Intel Pentium 4 processor komputer 1.34 GHz dengan RAM 1 GB. Hasil komputasi tidak semuanya dicantumkan, karena terlalu banyak. Hasil yang dicantumkan hanya untuk variabel keputusan x (jadwal perkuliahan) dan b (jadwal sebagian dosen tidak bisa mengajar) yang bernilai satu saja, sedangkan jadwal perkuliahan yang terbentuk ditunjukkan dalam Tabel 15 dan Tabel 16.

15

Tabel 15 Jadwal kegiatan belajar mengajar untuk program regular Akademi Manajemen Informatika dan Komunikasi BSI Bogor.

Hari Periode Waktu Mata kuliah Ruangan Dosen

Senin 08.00-09.30 Web Programming (K) 303 Isnaeni

09.30-11.45 Pemrograman Visual FOXPRO (K) 301 Muhammad

Tabrani

Selasa 08.00-09.30 Etika Profesi 302 R. Eny Ernawan

09.30-11.45 Pemrograman Visual FOXPRO (P) Lab A-B Hermawan

Rabu 08.00-09.30 Teknologi Ilmu Komputer 301 Sandra

Setyaningsih

09.30-11.45 Web Programming (P) Lab A-B Dio Pratama

Kamis 08.00-09.30 E-Commerce