ABSTRAK
MODEL MATEMATIKA RANCANG BANGUN WINDFLOW PADA BUNKER DENGAN METODE BEDA HINGGA
Oleh Muzahid Ansori
Model matematika merupakan suatu penggambaran untuk menerjemahkan suatu masalah dalam kehidupan sehari-hari ke dalam bahasa matematika dengan menggunakan persamaan, pertidaksamaan, atau fungsi. Model matematika digunakan untuk mendapatkan model untuk memberikan taksiran dari nilai-nilai kecepatan angin dalam bunker yang dipengaruhi oleh kecepatan, diameter dan banyaknya turbin yang pakai dengan menggunakan metode beda hingga. Diperoleh kesimpulan bahwa model matematika berbentuk f(x) = 0,000034064 x - 0,0000015143 x2 + 0,00000002144 x3 + 0,000000002652 x4.
ABSTRACT
MATHEMATICAL MODEL OF WINDFLOW DESIGN IN THE BUNKER WITH FINITE DIFFERENCE METHOD
By Muzahid Ansori
Mathematical model describes some problems in daily life into mathematics with equality, inequality, or function. Mathematical model is used to get a model to approximate wind speed value in the bunker depends on speed, diameter, and a number of turbines using finite difference method. We conclude that mathematical model is in the form of f(x) = 0,000034064 x - 0,0000015143 x2 + 0,00000002144 x3 + 0,000000002652 x4.
MODEL MATEMATIKA RANCANG BANGUN
WIND FLOW
PADA
BUNKER
DENGAN METODE BEDA HINGGA
(Skripsi)
Oleh
Muzahid Ansori
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
ABSTRAK
MODEL MATEMATIKA RANCANG BANGUN WINDFLOW PADA BUNKER DENGAN METODE BEDA HINGGA
Oleh Muzahid Ansori
Model matematika merupakan suatu penggambaran untuk menerjemahkan suatu masalah dalam kehidupan sehari-hari ke dalam bahasa matematika dengan menggunakan persamaan, pertidaksamaan, atau fungsi. Model matematika digunakan untuk mendapatkan model untuk memberikan taksiran dari nilai-nilai kecepatan angin dalam bunker yang dipengaruhi oleh kecepatan, diameter dan banyaknya turbin yang pakai dengan menggunakan metode beda hingga. Diperoleh kesimpulan bahwa model matematika berbentuk f(x) = 0,000034064 x - 0,0000015143 x2 + 0,00000002144 x3 + 0,000000002652 x4.
ABSTRACT
MATHEMATICAL MODEL OF WINDFLOW DESIGN IN THE BUNKER WITH FINITE DIFFERENCE METHOD
By Muzahid Ansori
Mathematical model describes some problems in daily life into mathematics with equality, inequality, or function. Mathematical model is used to get a model to approximate wind speed value in the bunker depends on speed, diameter, and a number of turbines using finite difference method. We conclude that mathematical model is in the form of f(x) = 0,000034064 x - 0,0000015143 x2 + 0,00000002144 x3 + 0,000000002652 x4.
MODEL MATEMATIKA RANCANG BANGUN
WIND FLOW
PADA
BUNKER
DENGAN METODE BEDA HINGGA
Oleh
Muzahid Ansori
Skripsi
Sebagai Salah Satu Syarat Untuk Memperoleh Gelar
SARJANA SAINS
Pada
Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
RIWAYAT HIDUP
Penulis merupakan anak ketiga dari delapan bersaudara yang dilahirkan di Lampung Selatan pada tanggal 14 April 1996 oleh pasangan Bapak Jadiono dan Ibu Supatmi.
Penulis menempuh pendidikan Sekolah Dasar (SD) di SDN 1 Banjar Agung pada tahun 2001-2007, pendidikan SMP di SMP Tunas Darma Way Galih pada tahun 2007-2010, dan melanjutkan di SMA N 1 Jati Agung pada tahun 2010-2013. Pada tahun 2013 penulis terdaftar sebagai mahasiswa S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung melalui Jalur SBMPTN.
Selama menjadi mahasiswa, Penulis aktif diberbagai organisasi kampus diantaranya pernah menjadi generasi muda BEM, HIMATIKA, dan ROIS FMIPA UNILA Pada periode 2013-2014, Anggota bidang keilmuan HIMATIKA, Anggota departemen ADKESMA dan Anggota Biro BBQ Rois FMIPA pada periode 2014-2015, Kepala Biro Akademik Rois FIMPA pada periode 2015-2016, dan Kepala Departemen HLPM Bem FMIIPA Unila pada periode 2016.
MOTTO
“Sebaik
-baik Kalian adalah yang belajar Al-Quran
dan mengajarkannya”
(Al-Hadist)
“Sebaik
-baiknya manusia adalah yang bermanfaat
bagi manusia lainnya”
“Wahai orang
-orang yang beriman, bersabarlah
kamu dan kuatkanlah kesabaranmu dan tetaplah
bersiap siaga dan bertakwalah kepada Allah,
supaya kamu beruntung.”
(Qs. Ali Imran : 200)
“
Kecerdasan hanya berpengaruh 1% dari
keberhasilan, 99% lah usaha, kerja keras dan
bersungguh
–
sungguh.
”
“barrang siapa bersungguh
-sungguh pasti ia akan
mendapatkannya.”
PERSEMBAHAN
Dengan mengucap puji dan syukur kehadirat Allah SWT yang
memberikan petunjuk dan kemudahan untuk menyelelsaikan studi
Ku ini, Ku persembahkan karya Ku ini untuk:
Bapak dan Ibu Ku tercinta yang selalu mendidik, mendoakan,
memberi semangat dan motivasi, dan hal lain yang tak dapat Ku
ungkapkan dengan kata-kata .
Kakak-kakak dan Adik-adik tercinta yang banyak
membantu,menemani, memotivasi dan memberi kasih sayang
kepadaku agar aku bisa menjadi seseorang yang bermanfaat bagi
kalian dan orang lain.
Dosen Pembimbing dan Penguji yang sangat berjasa dan selalu
memberikan motivasi kepada penulis untuk segera menyelesaikan
tugas-tugasKu.
Sahabat dan teman-teman ku, Terimakasih atas kebersamaan,
keceriaan, canda dan tawa serta doa dan semangat yang telah
diberikan kepadaku
SANWACANA
Alhamdulillahi Robbil ‘alamin, Puji dan syukur Penulis ucapkan kepada Allah
SWT, yang selalu melimpahkan rahmat dan kasih sayang-Nya, sehingga Penulis dapat menyelesaikan skripsi ini. Sholawat serat salam senantiasa tetap tercurah kepada nabi Muhammad SAW, tuntunan dan tauladan utama bagi seluruh umat manusia.
Dalam menyelesaikan skripsi ini, banyak pihak yang teklah membantu Penulis dalam memberikan bimbingan, dorongan, dan saran-saran. Sehingga dengan segala ketulusan dan kerendahan hati pada kesempatan ini Penulis mengucapkan terimakasih yang sebesar-besarnya kepada:
1. Bapak Drs. Tiryono Ruby. M.Sc., Ph.D. selaku Pembimbing utama dan Ketua Jurusan Matematika yang telah meluangkan waktu, memotivasi, dan
membimbing Penulis selama penulisan skripsi.
2. Drs. Suharsono S., M.Sc., Ph.D. selaku pembimbing II yang telah banyak membantu dan memberikan pengarahan dalam proses penyusunan skripsi. 3. Bapak Subian Saidi, S.Si., M.Si., selaku dosen penguji atas kesediaannya
4. Bapak Drs. Rudi Ruswandi selaku pembimbing akademik yang telah membimbing Penulis selama mengikuti perkuliahan di Jurusan Matematika FMIPA Universitas Lampung.
5. Bapak Prof. Warsito, S.Si., DEA.,Ph.D. selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.
6. Bapak dan Ibu Dosen serta Staf Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.
7. Ibu dan Bapak Penulis yang telah memberikan banyak hal yang tidak dapat Penulis nyatakan dalam kata-kata.
8. Kakak-kakak dan Adik-adik Penulis yang telah memberikan dukungan secara finansial dan moril, menghibur, dan memberikan doa, nasihat dan semangat yang sangat membantu Penulis dalam penyusunan skripsi.
9. Bapak Qadar Hasani dan Ibu Dorrah Aziz yang sering membantu dan
memotivasi Penulis untuk terus semangat meraih kesuksesan dan menggapai cita-cita.
10.Teman-teman seperjuangan Matematika angkatan 13: Ali, Haris, Ijal Budi, Dafri, Selma, Tina, dan yang lainnya. Terima kasih atas segala motivasi, bantuan, dan hal lain yang telah kalian berikan kepada Penulis.
11.Keluarga besar HIMATIKA, ROIS, dan BEM FMIPA UNILA atas
kebersamaan dan perjuangan dalam memperbaiki dan mengembangkan diri bersama guna mewujudkan FMIPA yang lebih baik lagi.
Penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan, akan tetapi besar harapan semoga skripsi yang sederhana ini dapat berguna dan bermanfaat bagi kita semua, amiin.
Bandar Lampung, 20 Desember 2016 Penulis
DAFTAR ISI 2.1 Pemodelan Matematika ... 4
2.2 Kemiringan Garis ... 5
2.3 Differensial ... 7
2.4 Persamaan Differensial Biasa ... 8
2.5 Persamaan Differensial Parsial ... 8
2.6 Angin ... 11
2.7 Turbin Ventilator Cyclone ... 13
2.8 Fluida Dinamis ... 14
2.9 Fungsi Polinomial ... 15
2.10 Interpolasi Polinomial (Polinom) Beda Hingga Newton ... 16
III. METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 19
3.2 Alat dan Bahan Penelitian ... 19
ii
3.4 Diagram alir ... 21 IV HASIL DAN PEMBAHASAN
4.1 Hasil Penelitian ... 22 4.2 Pembahasan ... 24 4.2.1 Model Matematika Kecepatan Angin Maksimum yang Dihasilkan dari Setiap Turbin di Dalam Bunker ... 31 4.2.2 Fungsi Kecepatan Angin pada Bunker Terhadap Kecepatan Angin yang Dihasilkan oleh Masing-Masing Turbin... 34 V KESIMPULAN
5.1Kesimpulan ... 38 5.2Saran ... 39
DAFTAR TABEL
Tabel Halaman
2.1 Langkah skematis pembagian beda hingga ... 18
4.1 Data spesifikasi turbin ... 23
4.2 Kecepatan angin yang dihasikan dari setiap turbin di dalam bunker .. 31
4.3 Langkah skematis pembagian beda hingga ... 32
4.4 Nilai pembagian beda hingga kecepatan angin dari setiap tipe ... 32
4.5 Pengaruh kecepatan angin pada turbin terhadap kecepatan di dalam bunker ... 34
4.6 Nilai pembagian beda hingga kecepatan angin dari tipe L45 ... 34
4.7 Nilai pembagian beda hingga kecepatan angin dari tipe L60 ... 35
4.8 Nilai pembagian beda hingga kecepatan angin dari tipe L75 ... 35
DAFTAR GAMBAR
Gambar Halaman
2.1 Garis Sembarang ...5
2.2 Gradien ...6
2.3 Gradien garis pada koordinat kartesius ...6
2.4 Beda hingga pada garis ... 6
2.5 Beda hingga pada batang lurus ...7
2.6 Beda hingga pada bidang empat titik ...11
2.7 Beda hingga pada bidang duabelas titik ...11
2.8 Anemometer ...12
2.9 Wind vane ...12
2.10 Windsock ...13
2.11 Turbin ventilator cyclone ...14
2.12 Contoh grafik polinomial ...17
3.1 Diagram alir penelitian ...21
4.1 Ruang bunker ...22
4.2 Desain turbin ventilator ...24
4.3 Grafik pengaruh kecepatan angin pada bunker terhadap diameter turbin ... ...33
1
I. PENDAHULUAN
1.1 Latar Belakang dan Masalah
Dalam kehidupan sehari-hari manusia tidak dapat terlepas dari permasalahan-permasalahan hidup yang dapat diselesaikan dengan ilmu matematika. Ilmu matematika banyak sekali menghasilkan suatu metode-metode atau formula-formula yang dapat digunakan baik dalam perkembangan ilmu matematika itu sendiri maupun untuk perkembangan ilmu-ilmu lainnya. Salah satu ilmu matematika yang sering digunakan untuk memecahkan permasalahan dalam kehidupan adalah pemodelan matematika.
Matematika terapan merupakan cabang ilmu matematika yang melingkupi penerapan pengetahuan matematika ke bidang-bidang lain, mengilhami dan membuat penggunaan temuan-temuan matematika baru, dan terkadang pada perkembangannya dapat mengarah pada pengembangan disiplin ilmu lainnya.
Angin merupakan salah satu unsur meteorologi yang memiliki peranan penting dalam menentukan kondisi suhu, cuaca dan iklim disuatu tempat. Angin dapat dibatasi sebagai gerakan horizontal udara relatif terhadap permukaan bumi.
2
Penelitian ini membahas tentang perbedaan laju angin pada ketinggian yang berbeda pada suatu tempat dengan menggunakan pemodelan matematika dan juga persamaan differensial parsial. Udara pada suatu tempat yang berada diatas cenderung memiliki kecepatan angin yg lebih cepat jika dibandingkan dengan udara yang ada di bawahnya yang disebabkan karena laju angin yang dibawah lebih banyak mendapati hambatan-hambatan. Oleh karena itu, penulis akan merancang suatu bangun yang dapat memindahkan laju angin yang ada diatas untuk dapat mengalir di dalam ruang bawah tanah sehingga aliran angin (wind flow) yang di atas dapat dirasakan walaupun berada di ruang bawah tanah dengan sirkulasi udara yang baik pula.
1.2 Batasan Masalah
Batasan masalah pada penelitian ini lebih ditekankan pada menghitung beda laju angin yang masuk dan laju angin di dalam bunker dari rancang bangun dengan menggunakan metode beda hingga.
1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah sebagai berikut:
1. Menghitung perbedaan laju angin pada turbin dan di dalam bunker dengan menggunakan teori differensial yaitu metode beda hingga.
2. Pengaplikasian teori differensial khususnya metode beda hingga di kehidupan nyata dalam proses perhitungan beda laju angin.
3
1.4Manfaat Penelitian
Manfaat penelitian ini adalah:
1. Memberikan sumbangan pemikiran dalam memperluas wawasan ilmu matematika.
4
II. TINJAUAN PUSTAKA
2.1 Pemodelan matematika
Pemodelan matematika merupakan proses dalam menurunkan model matematika dari suatu fenomena berdasarkan asumsi-asumsi yang digunakan. Proses ini merupakan langkah awal yang tak terpisahkan dalam menerapkan matematika untuk mempelajari fenomena alam, ekonomi, sosial maupun fenomena-fenomena lainnya. Secara umum dalam menerapkan matematika untuk
mempelajari suatu fenomena meliputi 3 langkah, yaitu:
5
2. Pencarian solusi/kesimpulan matematika. Setelah model matematika diperoleh, solusi atas model tersebut dicari dengan menggunakan metode-metode matematika yang sesuai. Ada kalanya belum terdapat metode-metode
matematika pencarian solusi yang sesuai dengan permasalahan yang dihadapi. Hal ini sering menjadi motivasi para ahli matematika terapan untuk
menciptakan metode matematika baru. Solusi matematika ini sering dinyatakan dalam fungsi-fungsi matematika, angka-angka maupun grafik. 3. Interpretasi solusi/kesimpulan matematika pada fenomena yang dipelajari.
Dalam matematika terapan, solusi yang berupa fungsi, angka-angka maupun grafik tidak berarti banyak apabila solusi tersebut tidak menjelaskan
permasalahan awalnya. Oleh karena itu, interpretasi solusi penting untuk mengerti arti dan implikasi solusi tersebut terhadap fenomena awal dari mana masalahnya berasal (Cahyono, 2013).
Pemodelan matematika adalah penyusunan suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian matematika yang disebut dunia matematika (mathematical world). Pemodelan matematika juga merupakan representasi dari objek, proses, atau hal lain yang diharapkan dapat diketahui polanya sehingga dapat dianalisis (Dym and Ivey, 1990).
2.2 Kemiringan Garis
Sebuah garis sembarang
6
Dimana kemiringan dilambangkan dengan m, sehingga di dapatkan rumus mencari kemiringan = = dimana dapat dilihat grafiknya.
Gambar 2.2 Gradien
Mengukur kemiringan garis dengan alat bantu sebuah penggaris
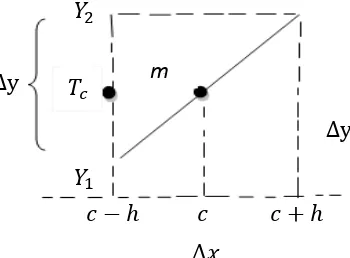
Titik tengah garis atau disebut center dengan menggunakan koordinat cartesius
Gambar 2.3 Gradien Garis Pada Koordinat Kartesius Titik tengah garis yang di lambangkan dengan m dan di dapat persamaannya yakni = = =
Dimana merupakan nilai fungsi = dan merupakan nilai fungsi = (Purcell, 2010).
Laju
7
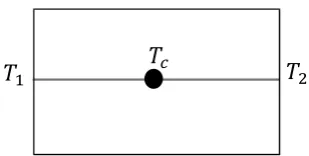
Gambar 2.5 Beda Hingga Pada Batang Lurus
=
= (Soedradjat, 2003).
2.3 Diferensial
a. Kecepatan Rata-rata
Definisi: Misalkan bahwa sebuah benda bergerak disepanjang garis koordinat sehingga posisinya pada saat diberikan oleh = . Pada saat
benda berada di ,pada saat yang berdekatan , benda berada di . Jadi kecepatan rata-rata pada interval ini adalah:
=aaaaaaaaaaaaaaa
b. Kecepatan Sesaat
8
asalkan bahwa limit ini ada dan bukan dan - . c. Diferensial
Definisi Leibniz untuk diferensial: misalkan bahwa variabel bebas berubah dari ke . Perubahan yang berkorespondensi dalam variabel tak bebas
, akan berupa:
=
dan hasil bagi =
Menggambarkan suatu garis sekan yang melalui . Ketika menuju 0, kemiringan garis sekan ini mendekati garis singgung, dan untuk kemiringan garis singgung kita menggunakan lambang . Sehingga:
Aa= aaaaaaa= aaaaaaaaaaaaaaaaaaa aa= (Purcell, 2010).
2.4 Persamaan Diferensial Biasa
Persamaan diferensial biasa adalah persamaan diferensial yang mengandung satu atau lebih fungsi (peubah tak bebas) beserta turunannya terhadap satu peubah bebas. Jika diambil sebagian suatu fungsi satu variabel, dengan dinamakan variabel bebas dan dinamakan variabel tak bebas, maka suatu persamaan
diferensial biasa dapat dinyatakan dalam bentuk = 0 (Ross, 1989).
2.5 Persamaan Diferensial Parsial
Suatu persamaan yang meliputi turunan fungsi dari satu atau lebih variabel terikat terhadap satu atau lebih variabel bebas disebut persamaan diferensial. Jika turunan fungsi itu hanya tergantung pada satu variable bebas maka disebut persamaan
9
diferensial biasa (PDB) dan bila tergantung pada lebih dari satu variabel bebas disebut persamaan diferensial parsial (PDP). Pada PDP, variabel bebas dapat berupa waktu dan satu atau lebih koordinat ruang (Ross, 1989).
Persamaan diferensial parsial merupakan persamaan dengan dua variabel bebas/penentu atau lebih.
10
dan definisi turunan parsial tingkat dua.
Metode beda hingga atau yang lebih dikenal dengan finite difference method adalah metode numerik yang umum digunakan untuk menyelesaikan persoalan teknis dan problem matematis dari suatu gejala fisis. Secara umum metode beda hingga adalah metode yang mudah digunakan dalam penyelesaian problem fisis yang mempunyai bentuk geometri yang teratur, seperti interval dalam satu dimensi, domain kotak dalam dua dimensi, dan kubik dalam ruang tiga dimensi (Li, 2010).
Aplikasi penting dari metode beda hingga adalah dalam analisis numerik, khususnya pada persamaan diferensial biasa dan persamaan diferensial parsial. Prinsipnya adalah mengganti turunan yang ada pada persamaan diferensial dengan diskritisasi beda
- Nilai fungsi di titik
11
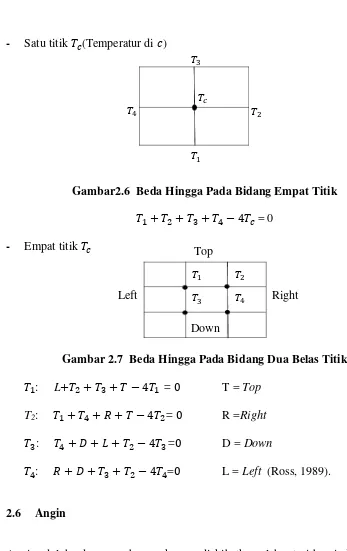
- Satu titik (Temperatur di )
Gambar2.6 Beda Hingga Pada Bidang Empat Titik = 0
- Empat titik
Gambar 2.7 Beda Hingga Pada Bidang Dua Belas Titik : L = T = Top
T2: = R =Right
: = D = Down
: = L = Left (Ross, 1989).
2.6 Angin
Angin adalah udara yang bergerak yang diakibatkan oleh rotasi bumi, dan juga karena adanya perbedaan tekanan udara disekitarnya. Angin bergerak dari tempat bertekanan udara yg tinggi ke tempat yang bertekanan udara rendah. Apabila dipanaskan, udara memuai menjadi lebih ringan sehingga naik. Apabila hal ini terjadi, tekanan udara turun karena udaranya berkurang.
Top
Right
12
Beberapa faktor terjadinya angin diantaranya semakin besar gradien
barometrisnya, semakin cepat tiupan angin, kecepatan angin didekat khatulistiwa lebih cepat dari yang jauh dari garis khatulistiwa, semakin tinggi suatu tempat maka semakin kencang pula angin yang bertiup, hal ini disebabkan oleh pengaruh gaya gesekan yang menghambat laju udara. Dipermukaan bumi, gunung, pohon, dan topografi yang tidak rata lainnya memberikan gaya gesekan yang besar. Semakin tinggi suatu tempat, gaya gesekan ini semakin kecil serta disiang hari angin bergerak lebih cepat dari pada di malam hari (Daryanto, 2000).
Alat untuk mengukur angin antara lain:
1. Anemometer, adalah alat yang mengukur kecepatan angin.
Gambar 2.8 Anemometer
2. Wind Vane, adalah alat untuk mengetahui arah angin.
13
3. Windsock, adalah alat untuk mengetahui arah angin dan memperkirakan besar kecepatan angin, biasanya banyak ditemukan di bandara-bandara.
Gambar 2.10 Windsock
2.7 Turbin Ventilator Cyclone
Turbin ventilator cyclone adalah alat yang berfungsi menghisap udara panas, debu, dan juga berfungsi sebagai alat ventilasi/sirkulasi udara. Turbin ventilator cyclone akan berputar hanya dengan hembusan angin yang sangat lemah
sekalipun, tetapi juga mampu menahan angin berkecepatan tinggi. Berputarnya turbin ventilator cyclone juga disebabkan karena adanya perbedaan tekanan udara didalam dan diluar ruangan, diman secara alamiah udara panas didalam ruangan akan mengalir dan menekan keluar melalui sirip-sirip turbine dan membuat turbin ventilator cyclone otomatis berputar. Dengan demikian ada atau tidak ada angin, turbin ventilator cyclone akan selalu berputar menghisap udara panas dalam ruangan.
14
Gambar 2.11 Turbin Ventilator Cyclone
2.8 Fluida Dinamis
Fluida dinamis adalah fluida (bisa berupa zat cair, gas) yang bergerak. Untuk memudahkan dalam mempelajari, fluida disini dianggap mempunyai kecepatan yang konstan terhadap waktu, tak termampatkan (tidak mengalami perubahan volume), tidak kental, tidak turbulen (tidak mengalami putaran-putaran). Aliran fluida sering dinyatakan dalam debit. Debit adalah banyaknya volume zat cair yang mengalir pada tiap satu satuan waktu, biasanya dinyatakan dalam satuan liter/detik atau dalam satuan meter kubik (m3) per detik.
Q =
Dimana :
Q = debit aliran (m3/s) v = volume (m3)
15
Konsep mekanika fluida berada dalam dua keadaan, yaitu sebagai zat padat dan cair/gas (fluida). Sebuah zat cair dan gas mempunyai bentuk yang ditetapkan oleh wadahnya sendiri (masing-masing). Di sini berlaku persamaan kontinuitas, di mana banyaknya fluida yang masuk sama dengan banyaknya fluida yang keluar, dapat dilihat pada persamaan
v1 x A1 = v2 x A2 Dengan :
v1 = kecepatan fluida pada keadaan awal pipa A1= luas permukaan pada keadaan awal pipa v2= kecepatan fluida diujung pipa
A2= luas pemukaan di ujung pipa
Dengan menganggap bahwa kecepatan fluida pada seluruh penampang sama, maka berlaku persamaan Bernouli :
P1 + ½ ρ v1 = P2 + ½ ρ v2 Dengan :
P = Tekanan fluida v = Kecepatan aliran
ρ = Massa jenis fluida (Sutrisno, 1986).
2.9 Fungsi Polinomial
Fungsi polinomial adalah fungsi yang mengandung banyak suku (polinom) dalam variabel bebasnya. Bentuk umum persamaan polinomial adalah
16
Dengan koefisien tertentu α0, α1, α2, ..., αn. Polinom ini mempunyai derajat
(tepat) sebesar n, jika koefisien penentunya αn ≠ 0 (Conte dan Boor, 1980).
2.10 Interpolasi Polinomial (Polinom) Beda Hingga Terbagi Newton
Interpolasi adalah suatu cara untuk mencari nilai diantara beberapa titik data yang telah diketahui. Interpolasi dapat digunakan untuk memperkirakan suatu fungsi dimana fungsi tersebut tidak terdefinisi dengan suatu formula, tetapi didefinisikan hanya dengan data- data atau tabel yang tersedia. Interpolasi polinomial adalah sebuah metode untuk menaksir (mengestimasi) nilai di antara titik- titik data yang tepat. Persamaan polinomial adalah persamaan aljabar yang hanya mengandung jumlah dari variabel x berpangkat bilangan bulat (integer). Bentuk umum persamaan polinomial order n adalah:
f (x) = a0 + a1x + a2x2+ … +anxn (1.1) dengan a0, a1, a2, …,an adalah parameter yang akan dicari berdasarkan titik data, n adalah derajat (order) dari persamaan polinomial, dan x adalah variabel bebas. Untuk (n + 1) titik data, hanya terdapat satu atau kurang polinomial
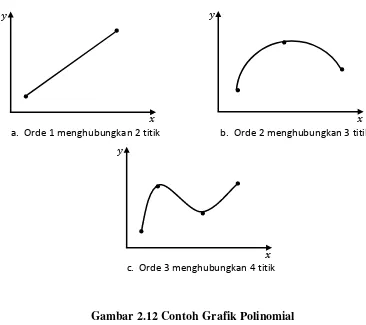
order n yang melalui semua titik. Misalnya, hanya ada satu garis lurus (polinomial order 1) yang menghubungkan dua titik (interpolasi linier) gambar 2.12 a,
demikian juga tiga buah titik dapat dihubungkan oleh fungsi parabola (interpolasi kuadrat) gambar 2.12 b, sedang untuk 4 titik (interpolasi kubik) gambar 2.12 c. Interpolasi polinom terdiri atas penetuan polinom unik orde ke-n yang cocok dengan n+1 titik data. Walaupun terdapat satu, dan hanya satu, polinom orde ke-n yang cocok dengan n+1 titik, terdapat beragam bentuk matematik untuk
17
Gambar 2.12 Contoh Grafik Polinomial
Prosedur seperti dijelaskan diatas dapat digunakan untuk membentuk polinomial order n dari (n + 1) titik data. Bentuk umum polinomial order n adalah:
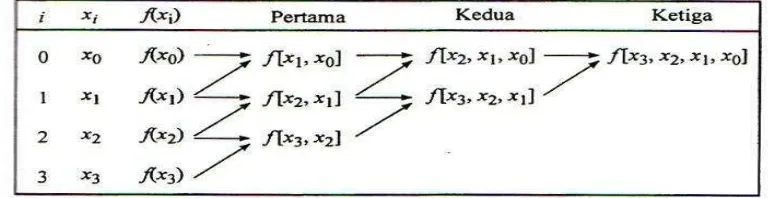
fn(x) = bo + b1(x–x0) + … +bn(x–x0)(x–x1) ... (x–xn 1) (1.2) Seperti yang dilakukan interpolasi linier dan kuadrat, titik-titik data dapat dilakukan dengan evaluasi koefisien b0, b1, ..., bn. Untuk polinomial order n, diperlukan (n + 1) titik data x0, x1, x2, ..., xn. Dengan menggunakan titik-titik data tersebut, maka persamaan berikut digunakan untuk mengevaluasi
koefisien b0, b1, ...,bn. b0 = f (x0) (1.3)
b1 = f [x1, x0] (1.4) b2 = f [x2, x1, x0] (1.5) bn = f [xn, xn – 1, ..., x2, x1,x0] (1.6)
a. Orde 1 menghubungkan 2 titik b. Orde 2 menghubungkan 3 titik
18
Dengan definisi fungsi berkurung ([….]) adalah pembagian beda hingga.
Misalnya, pembagian beda hingga pertama adalah:
f [xi, xj] =
(1.7)
pembagian beda hingga kedua adalah:
f [xi, xj, xk] =
Bentuk pembagian untuk mengevaluasi koefisien-koefisien dalam persamaan (1.3) sampai beda hingga tersebut dapat digunakan persamaan (1.6) yang kemudian disubstitusikan ke dalam persamaan (1.2) untuk mendapatkan interpolasi polinomial order n.
fn(x) = f (x0) + f [x1, x0](x–x0) + f [x2, x1, x0](x–x0)(x–x1) + … + f [xn, xn – 1, ..., x2, x1, x0](x–x0)(x–x1) … (x–xn– 1) (1.10)
Persamaan (1.7) sampai persamaan (1.9) adalah berurutan, artinya pembagian beda yang lebih tinggi terdiri dari pembagian beda hingga yang lebih rendah, secara skematis bentuk yang berurutan tersebut ditunjukkan dalam Tabel 1.
Tabel 2.1 Langkah Skematis Pembagian Beda Hingga
19
III. METODOLOGI PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian ini dilakukan pada semester ganjil tahun ajaran 2016/2017 dengan melakukan penelitian secara studi pustaka dan penelitian lapangan.
3.2 Alat dan Bahan
Bahan yang digunakan berupa buku-buku teks, internet, dan jurnal yang menunjang penelitian. Sedangkan alat yang digunakan adalah laptop, alat ukur (meteran dll), dan alat penunjang lainnya.
3.3 Metode Penelitian
Penelitian ini dilakukan secara studi pustaka yaitu mempelajari buku-buku teks yang terdapat di perpustakaan jurusan matematika, perpustakaan Universitas Lampung dan jurnal yang menunjang proses penelitian dan juga praktek penelitian secara langsung.
Adapun langkah-langkah yang akan dilakukan penulis dalam menyelesaikan penelitian ini adalah sebagai berikut:
20
2. Menuliskan definisi-definisi dan teorema-teorema yang berhubungan dengan penelitian.
3. Mempelajari dan memahami definisi-definisi dan teorema-teorema yang berhubungan dengan penelitian.
4. Menguraikan dan menggunakan definisi-definisi dan teorema-teorema sebagai acuan dalam melakukan penelitian.
5. Pengambilan sampel data kecepatan angin pada lokasi prospek penelitian (Kelurahan Gunung Terang).
6. Pengambilan data ukuran bunker udara. 7. Desain ukuran blower.
21
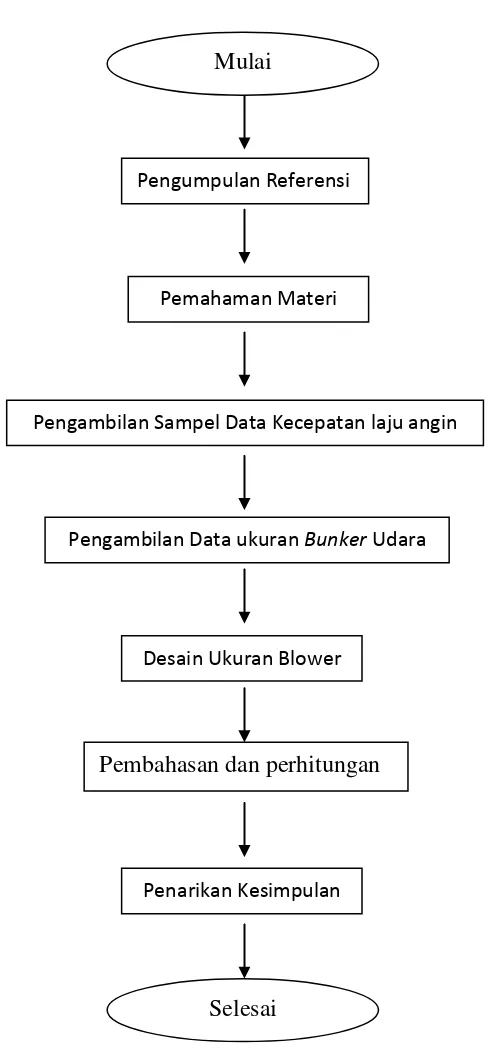
3.4 Diagram Alir
Gambar 3.1 Diagram Alir Penelitian
Pengumpulan Referensi
Pemahaman Materi
Pengambilan Sampel Data Kecepatan laju angin
Pengambilan Data ukuran Bunker Udara
Desain Ukuran Blower
Penarikan Kesimpulan
Pembahasan dan perhitungan Mulai
38
V. KESIMPULAN DAN SARAN
5.1 Kesimpulan
Dari penelitian yang telah dilakukan, dapat diambil kesimpulan antara lain sebagai berikut:
1. Jumlah maksimal orang yang dapat masuk ke dalam bunker adalah 174 orang usia 9 -12 tahun.
2. Kebutuhan minimal pergantian udara dalam bunker saat jumlah orang maksimal di bunker adalah 1,044 m3/ menit.
3. Bunker tipe L45 per satu unit ketika kecepatan udara sedang (antara maksimum dan minimum) sudah mencukupi kebutuhan maksimal udara dalam bunker dengan debit udara 1,0674218 m3/ menit. Untuk mengatasi masalah jika laju angin yang dihasilkan turbin kecil atau mendekati nol, maka digunakan turbin dengan sumber tenaga accu/aki atau listrik tenaga surya yang dapat digunakan setiap saat ketika dibutuhkan.
4. Dengan menggunakan metode pembagian beda hingga didapat model matematika untuk menggambarkan kecepatan angin di dalam bunker yaitu f(x) = 0,000034064 x - 0,0000015143 x2 + 0,00000002144 x3 +
0,000000002652 x4.
39
a. Tipe L45 : y = 0,0025682 x b. Tipe L60 : y = 0,008091 x c. tipe L75 : y = 0,019773 x d. tipe L90 : y = 0,041 x
5.2 Saran
40
DAFTAR PUSTAKA
Cahyono. 2013. Pemodelan Matematika. Graha Ilmu, Bandung.
Carnahan, Brice, H.A. Luther, and James O.Wilkes. 1969. Applied Numerical Methodes. John Willey and Sons, New York.
Conte, S.D. and Carl de Boor. 1980. Dasar-dasar analisis numerik suatu pendekatan algoritma. Edisi Ketiga. Erlangga, Jakarta.
Daryanto. 2000. Fisika Teknik. Rineka Cipta, Jakarta.
Dym and Ivey. 1990. Principles of Mathematical Modelling. Academic Press, New York.
Li, Zhilin. 2010. Finite Difference Methods Basics. Scientic computation and department of Mathematics North Carolina State University
Purcell, Varberg, dan Rigdon. 2010. Kalkulus Jilid 1 Edisi Kedelapan. Erlangga, Jakarta.
Ross, Shepley L. 1989. Intoduction to Ordinary Differential Equations. John Wiley and Sons, New York.
Soedradjat, S. 2003. Fungsi model hidrodinamika estuari dalam pengelolaan ekosistem mangrove (studi kasus pencemaran minyak di estuari sungai donan Cilacap). Berkala Penelitian Hayati, hal: 81-86.
Sutrisno. 1986. Fisika Dasar Mekanika. Jilid 2. Institute Teknologi Bandung, Bandung.