Analisis Rule Evaluation Dalam Fuzzy Inference System (FIS) Mamdani

(1)

ANALISIS

RULE EVALUATION

DALAM

FUZZY

INFERENCE SYSTEM

(FIS) MAMDANI

TESIS

MERRY NAINGGOLAN

117038063

PROGRAM STUDI S2 TEKNIK INFORMATIKA

FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI

UNIVERSITAS SUMATERA UTARA

(2)

ANALISIS

RULE EVALUATION

DALAM

FUZZY

INFERENCE SYSTEM

(FIS) MAMDANI

TESIS

Diajukan sebagai salah satu syarat untuk memperoleh gelar Magister Teknik Informatika

MERRY NAINGGOLAN 117038063

PROGRAM STUDI S2 TEKNIK INFORMATIKA

FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA

2013

(3)

Judul Tesis : ANALISIS RULE EVALUATION DALAM FUZZY INFERENCE SYSTEM (FIS) MAMDANI

Nama Mahasiswa : MERRY NAINGGOLAN Nomor Induk Mahasiswa : 117038063

Program Studi : Magister Teknik Informatika

Fakultas : FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI Universitas Sumatera Utara

Menyetujui Komisi Pembimbing

Pembimbing 2 Pembimbing 1

Dr. Erna Budhiarti Nababan, M.IT Prof. Dr. Tulus, Vordipl.Math.,M.Si.,Ph.D

Diketahui/ Disetujui oleh S2 Teknik Informatika Ketua Program Studi,

Prof. Dr. Muhammad Zarlis NIP: 195707011986011003

(4)

ANALISIS RULE EVALUATION DALAM FUZZY

INFERENCE SYSTEM (FIS) MAMDANI

TESIS

Saya mengakui bahwa tesis ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan

ringkasan yang masing-masing telah disebutkan sumbernya .

Medan, 28 Agustus 2013

Merry Nainggolan NIM : 117038063

(5)

Sebagai sivitas akademika Universitas Sumatera Utara, saya yang bertanda tangan di bawah ini:

Nama : MERRY NAINGGOLAN

Nim : 117038063

Program Studi : Magister ( S2) Teknik Informatika

Jenis Karya Ilmiah : TESIS

Demi pengembangan ilmu pengetahuan, menyetujui untuk memberikan kepada Universitas

Sumatera Utara Hak Bebas Royalti Non-Eksklusif (Non-Exclusive Royalty free Right) atas Tesis

saya yang berjudul:

ANALISIS RULE EVALUATION DALAM FUZZY

INFERENCE SYSTEM (FIS) MAMDANI

Beserta perangkat yang ada (jika diperlukan). Dengan Hak Bebas Royalti Non-Eksklusif ini,

Universitas Sumatera Utara berhak menyimpan, mengalih media, memformat, mengelola dalam

bentuk database, merawat dan mempublikasikan Tesis saya tanpa meminta izin dari saya selama

tetap mencantumkan nama saya sebagai penulis dan sebagai pemegang dan atau sebagai pemilik

hak cipta.

Demikian pernyataan ini dibuat dengan sebenarnya.

Medan, 28 Agustus 2013

Merry Nainggolan

(6)

PANITIA PENGUJI TESIS

KETUA : Prof.Dr. Tulus, Vordipl.math.,M.Si.,Ph.D

Anggota : 1. Dr. Erna Budhiarti Nababan, M.IT

2. Prof. Dr. Opim Salim Sitompul

3. Prof. Dr. Muhammad Zarlis

4. Prof. Dr. Herman Mawengkang

(7)

DATA PRIBADI

Nama lengkap berikut gelar : Merry Nainggolan, S.Kom

Tempat dan Tanggal Lahir : Hutaraja, 21 Desember 1980

Alamat Rumah : Jl. SM.Raja gg.P.Harapan no.31 Ab

Telepon / HP : 0821 6382 1380

Email : [email protected]

Instansi Tempat Bekerja : SMP Negeri 34 Medan

Alamat Kantor : Jl. Brigjen Katamso

Gg. Perbatasan Medan

DATA PENDIDIKAN

SD : SD NEGERI No. 414788 Pangururan Tamat : 1993

SMP : SMP NEGERI 1 Pangururan Tamat : 1996

SMU : SMU NEGERI 1 Sidamanik Tamat : 1999

Strata-1 : STMIK SM. Raja XII Medan Tamat : 2007

AKTA IV : UNIV.DARMA AGUNG MEDAN Tamat : 2008

(8)

Pertama-tama penulis panjatkan puji syukur kehadirat Tuhan Yang Maha Esa atas segala

limpahan rakhmat dan karunia-Nya sehingga Tesis ini dapat diselesaikan.

Dengan selesainya tesis ini, perkenankanlah kami mengucapkan terima kasih yang

sebesar-besarnya kepada :

Rektor Universitas Sumatera Utara, Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc

(CTM), Sp. A(K) atas kesempatan yang diberikan kepada kami untuk mengikuti dan

menyelesaikan pendidikan Program Magister.

Ketua Program Studi Fakultas Ilmu Komputer Universitas Sumatera Utara, Prof. Dr.

Muhammad Zarlis atas bimbingan arahan dan motifasi selama dalam perkuliahan sehingga

penulis dapat menyelesaikan perkuliahan tepat pada waktunya dan juga kepada Sekretaris

Program Studi Magister Teknik Informatika, Muhammad Andri Budiman, S.T, M. Comp. Sc,

M.EM beserta para Staff Pegawai yang telah banyak membantu dalam pengurusan administrasi

serta seluruh Dosen pengajar pada Program Studi Magister Teknik Informatika Program

Pascasarjana Fakultas Ilmu Komputer Universitas Sumatera Utara yang selama duduk dibangku

perkuliahan telah memberikan ilmunya kepada penulis. Terima kasih yang tak terhingga dan

penghargaan setinggi-tingginya penulis ucapkan kepada bapak Prof. Dr. Tulus selaku

Pembimbing Utama yang dengan penuh perhatian dan telah memberikan bimbingan dan

motivasi, demikian juga kepada Ibu Dr. Erna Budhiarti Nababan, M.IT selaku Pembimbing kedua

yang dengan penuh kesabaran menuntun dan membimbing penulis hingga selesainya penulisan

ini.

Terima kasih kepada seluruh keluarga besar saya yang selalu memberikan dukungan

kepada saya, Suami Tommi Simorangkir, Bapak Alm. Gr.MT Nainggolan dan Ibu P.Sibarani,

Penulis juga mengucapkan terima kasih banyak kepada Jaidup Marbun yang telah

membantu dalam penulisan tesis ini seta seluruh teman-teman Kom-A yang telah bersama

berjuang dari awal perkuliahan sampai dalam penyelesaian tesis ini dan sudah banyak

memberikan motifasi dan dapat menjadi tempat berbagi keluh kesah semoga sukses buat kita

(9)

Penulis menyadari masih banyak kekurangan dalam penulisan tesis ini, oleh karena itu

diharapkan saran dan kritik yang sifatnya membangun untuk pengembangan tesis ini, akhir kata

semoga tesis ini bermanfaat bagi pembaca, terima kasih.

Medan, 28 Agustus 2013

(10)

ABSTRAK

Menghitung nilai gizi seseorang berdasarkan Indeks Massa Tubuh secara umum sudah ada, namun penggunaanya sangat kaku, sehingga dengan adanya perubahan kecil saja

sudah mengakibatkan perubahan nilai pada kategori status gizi, berbeda dengan fuzzy

yang memberikan toleransi terhadap perubahan yang kecil tidak akan mempengaruhi tingkat keanggotaan pada variabel gizi. Dalam menentukan status gizi seseorang dengan menggunakan fuzzy Mamdani, ada empat tahapan yang dilakukan, langkah pertama

menentukan himpunan fuzzy dari variabel input dan langkah kedua yaitu menentukan

derajat keanggotaan, langkah ketiga yaitu menghitung predikat aturan (rule evaluation) dengan proses implikasi ada tiga metode yang digunakan yaitu metode Max (maximum); metode Additive (sum) dan metode probabilistik OR (probor) dan langkah terakhir adalah

proses defuzzifikasi yang menggunakan metode bisektor . Penggunaan rule evaluation

dengan ketiga metode tentunya menghasilkan nilai yang berbeda-beda dari masing-masing metode tersebut.

Kata kunci: Sistem Inferensi Fuzzy, Fuzzy Mamdani, Rule Evaluation, Status Gizi

(11)

ABSTRACT

To calculate the nutritional value of a person based on body mass index in general already exists, but It’s use is very stiff, so with only minor changes have resulted in changes in the value of nutritional status categories, in contrast with the fuzzy tolerance of minor changes that will not affect the level of membership in the variable nutrition. In determining a person's nutritional status by using Mamdani fuzzy, there are four steps being taken, the first step determines fuzzy set of input variables and output variables, the second step is to determine the degree of membership, the third step is to calculate the predicate rule (rule evaluation) with the implication there are three method used is the method of Max (maximum); method Additive (sum) and probabilistic methods OR (probor) and the last step is the defuzzification process using the bisector method. The use of rule evaluation with three methods must yield different values of each of these

methods.………..

(12)

HALAMAN JUDUL ... i

PENGESAHAN ... ii

PERNYATAAN ORISINALITAS ... iii

PERSETUJUAN PUBLIKAS ... iv

PANITIA PENGUJI ...v

2.6 Indeks Antropometri 13

2.7 Riset-Riset Terkait 15

2.8 Perbedaan Dengan Riset Yang lain 16

(13)

3.2 Rancangan sistem 19

3.3 Perancangan Inferensi Fuzzy 19

3.3.1 Himpunan fuzzy variabel berat badan

3.3.2 Himpunan fuzzy variabel tinggi badan 21

3.3.3 Himpunan fuzzy variabel nilai gizi 22

3.4 Fungsi Implikasi (Pembentukan aturan) 24

BAB IV HASIL DAN PEMBAHASAN

4.1 Pendahuluan 26

4.2 Pengujian Data 26

4.2.1 Komposisi aturan dengan menggunakan metode MAX 28

4.2.2 Komposisi Aturan dengan menggunakan metode Adaptif(sum) 29

4.2.3 Komposisi aturan dengan menggunakan metode

Probabilistik Or (Probor) 33

4.2.4 Metode MAX dengan BB 55 kg dan TB 146 cm 35

4.2.5 Metode Adaptif (sum)untuk BB 60 dan TB 146 36

4.2.6 Metode Probabilistik (Probor) untuk BB 60 kg dan TB 146 cm39

4.2.7 Metode MAX untuk BB 80 kg dan TB 160 cm 42

4.2.8 Metode Adaptif (sum)untuk BB 80 kg dan TB 146 cm 43

4.2.9 Metode Probabilistik or (Probor)untuk BB 80 kg dan TB 146 cm47

4.2.10 Metode MAX untuk BB 80 kg dan 170 cm 50

4.2.11 Metode Adaptif (sum) untuk BB 80 kg dan TB 170 cm 52

4.2.12 Metode Probabilistik or (Probor) untuk BB 80 kg dan TB 170 55

BAB V KESIMPULAN DAN SARAN

5.1 Kesimpulan 57

5.2 Saran 57

(14)

Nomor

Kategori Ambang Batas IMT

Riset-riset terkait

Variabel dan himpunan fuzzy

Tabel Aturan fuzzy

Variabel berat badan dan tinggi badan

Tabel nilai keanggotaan TB 148 dan BB 60 kg

Variabel TB 148 dan BB 60 kg

Proses defuzzifikasi

Variabel TB 148 dan BB 60 kg dengan metode Probor

Tabel Nilai Keanggotaan

Himpunan keanggotaan TB 146 dan BB 55 kg

Proses defuzzifikasi

Tabel nilai keanggotaan

Variabel nilai BB 80 kg dan TB 160 cm

Proses defuzzifikasi BB 80 kg dan TB 160 cm

Tabel nilai keanggotaan

Nilai Himpunan fuzzy TB 170 dan BB 80 kg

Proses Defuzzifikasi

(15)

Gambar

Tahapan sistem berbasis fuzzy

Flowcart penelitian dengan logika fuzzy

Fungsi keanggotaan berat badan

Fungsi keanggotaan tinggi badan

Himpunan fuzzy nilai gizi

Fungsi keanggotaan BB 60 kg

Fungsi keanggotaan TB 148 kg

Nilai gizi

Nilai gizi dan status gizi

Nilai gizi

Tampilan Program

Import data dari excel

(16)

ABSTRAK

Menghitung nilai gizi seseorang berdasarkan Indeks Massa Tubuh secara umum sudah ada, namun penggunaanya sangat kaku, sehingga dengan adanya perubahan kecil saja

sudah mengakibatkan perubahan nilai pada kategori status gizi, berbeda dengan fuzzy

yang memberikan toleransi terhadap perubahan yang kecil tidak akan mempengaruhi tingkat keanggotaan pada variabel gizi. Dalam menentukan status gizi seseorang dengan menggunakan fuzzy Mamdani, ada empat tahapan yang dilakukan, langkah pertama

menentukan himpunan fuzzy dari variabel input dan langkah kedua yaitu menentukan

derajat keanggotaan, langkah ketiga yaitu menghitung predikat aturan (rule evaluation) dengan proses implikasi ada tiga metode yang digunakan yaitu metode Max (maximum); metode Additive (sum) dan metode probabilistik OR (probor) dan langkah terakhir adalah

proses defuzzifikasi yang menggunakan metode bisektor . Penggunaan rule evaluation

dengan ketiga metode tentunya menghasilkan nilai yang berbeda-beda dari masing-masing metode tersebut.

(17)

ABSTRACT

To calculate the nutritional value of a person based on body mass index in general already exists, but It’s use is very stiff, so with only minor changes have resulted in changes in the value of nutritional status categories, in contrast with the fuzzy tolerance of minor changes that will not affect the level of membership in the variable nutrition. In determining a person's nutritional status by using Mamdani fuzzy, there are four steps being taken, the first step determines fuzzy set of input variables and output variables, the second step is to determine the degree of membership, the third step is to calculate the predicate rule (rule evaluation) with the implication there are three method used is the method of Max (maximum); method Additive (sum) and probabilistic methods OR (probor) and the last step is the defuzzification process using the bisector method. The use of rule evaluation with three methods must yield different values of each of these

methods.………..

(18)

BAB 1

PENDAHULUAN

1.1. Latar Belakang Masalah

Latar belakang munculnya logika fuzzy adalah karena adanya kesenjangan

antara hukum-hukum matematika dengan permasalahan sesungguhnya dikehidupan

nyata (realita), maka perlu suatu metode analisa baru untuk mende kati solusi

yang optimal terhadap permasalahan real. Metode tersebut dikenal sebagai

logika fuzzy (logika kabur /tidak tegas). Konsep baru yang diterapkan dalam

logika fuzzy adalah nilai derajat keanggotaan suatu anggota himpunan tidak hanya 0

dan 1, tetapi bisa antara 0 dan 1. Ini merupakan perbedaan mendasar antara konsep

logika dan konsep logika fuzzy. Konsep logika fuzzy ini didasarkan pada

permasalahan-permasalahan nyata (real) yang kebanyakan bersifat kabur (tidak bisa

didekati dengan logika tegas/tajam).

Secara umum ada tiga metode logika fuzzy yaitu, metode Mamdani, metode

Tsukamoto, dan metode Takagi Sugeno. Namun dalam penelitian ini penulis

menggunakan salah satu metode fuzzy yaitu Metode Mamdani yang juga dikenal

dengan nama metode Max-Min. Metode ini diperkenalkan oleh Ebrahim H. Mamdani

pada tahun 1975. Metode Mamdani sangat cocok digunakan karena menyerupai

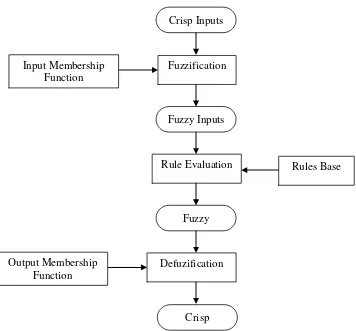
bahasa manusia. Pada sistem Inferensi Fuzzy Metode Mamdani, ada 4 (empat)

tahapan yang digunakan untuk mendapatkan output yaitu, pertama pembentukan

himpunan fuzzy (fuzzification), kedua aplikasi fungsi implikasi, ketiga komposisi

aturan (Rule evaluation) dan yang keempat adalah penegasasan (defuzzy). Dalam

langkah ketiga pemroses logika fuzzy dinamakan rule evaluation (evaluasi aturan),

prosesor fuzzy menggunakan aturan linguistik untuk menentukan aksi kontrol apa

yang harus dilakukan dalam merespon nilai masukan yang diberikan. Rule Evaluation

disebut juga proses pengambilan keputusan (Inference) yang berdasarkan

aturan-aturan yang ditetapkan pada basis aturan-aturan (Rules Base) untuk menghubungkan antar

peubah-peubah Fuzzy masukan dan peubah Fuzzy keluaran. Aturan-aturan ini

berbentuk jika ... maka (IF ... THEN). Ada tiga metode yang digunakan dalam

(19)

melakukan inferensi sistem fuzzy pada metode Mamdani yaitu, Max-min, additive dan

probabilistik OR (probor).

Dalam penelitian ini penulis akan menggunakan metode fuzzy mamdani dari

sudut rule evaluation untuk menentukan status gizi seseorang. Status gizi merupakan

deskripsi keseimbangan antara asupan zat gizi dengan kebutuhan tubuh secara

individual. Keseimbangan antara asupan makanan dengan kebutuhan kalori cenderung

akan menghasilkan gizi baik tapi bila kurang konsumsi makanan yang bergizi

kemungkinan besar akan kurang gizi. Dalam penentuan status gizi dengan parameter

Indeks Massa Tubuh (IMT) menggunakan logika fuzzy, variabel input dibagi menjadi

dua yaitu variabel berat badan dan tinggi badan. Serta satu variabel output, yaitu

variabel nilai gizi. Nilai gizi seseorang akan ditentukan dengan menggunakan tiga

metode yang ada pada rule evaluation yaitu, metode Max, metode additive-sum dan

metode probabilistik OR (probor). Oleh karena itu tesis ini diberi judul “ANALISIS

RULE EVALUATION DALAM FUZZY INFERENCE SYSTEM MAMDANI”.

1.2. Rumusan Masalah

Dari uraian diatas yang menjadi rumusan masalah adalah :

1. Bagaimana pengaruh rule evaluation dalam pengambilan keputusan?

2. Bagaimana fuzzy inference system dalam menganalisis rule

evaluation dalam fuzzy Mamdani?

3. Bagaimana pengaruh metode max, metode sum dan metode

probabilistik or (probor) dalam pengambilan keputusan

1.3 Batasan Masalah

Rumusan masalah diatas, dibatasi dengan beberapa hal sebagai berikut :

1. Metode yang digunakan dalam penelitian ini adalah menggunakan rule

evaluation fuzzy Mamdani.

2. Analisis yang dilakukan hanya sebatas dalam penelitian yang telah

dibuat sebelumnya

3. Permasalahan yang akan dibahas adalah tentang rule evaluation fuzzy

Mamdani untuk menentukan status gizi seseorang berdasarkan IMT .

4. Variabel dalam penentuan status gizi berdasarkan IMT meliputi: berat

(20)

5. Data yang digunakan untuk variabel berat badan hanya sampai 80 kg

dan untuk tinggi badan sampai 180 cm.

1.4. Tujuan Penelitian

Tujuan yang ingin dicapai pada penelitian tesis ini adalah:

1. Dapat mengetahui pengaruh rule evaluation dalam pengambilan

keputusan

2. Dapat mengetahui fuzzy inference system dalam menganalisis rule

evaluation dalam fuzzy Mamdani

3. Dapat mengetahui pengaruh metode max, metode sum dan metode

probabilistik or (probor) dalam pengambilan keputusan

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah:

1. Dapat menambah pengetahuan, wawasan, dan pemahaman penulis tentang

rule evaluation pada fuzzy Mamdani

2. Dapat mengetahui hasil analisis rule evaluation menggunakan metode

max , metode additive dan metode probabilistik pengambilan keputusan .

3. Memberikan kontribusi bagi ilmu pengetahuan khususnya pada bidang

ilmu komputer.

(21)

BAB 2

TINJAUAN PUSTAKA

2.1. Pengertian Fuzzy

Logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input

kedalam suatu ruang output. Titik awal dari konsep modern mengenai ketidakpastian

adalah paper yang dibuat oleh Lofti A Zadeh (1972), dimana Zadeh memperkenalkan

teori yang memiliki obyek-obyek dari himpunan fuzzy yang memiliki batasan yang

tidak presisi dan keanggotaan dalam himpunan fuzzy, dan bukan dalam bentuk logika

benar (true) atau salah (false), tapi dinyatakan dalam derajat (degree). Konsep seperti

ini disebut dengan Fuzziness dan teorinya dinamakan Fuzzy Set Theory. Fuzziness

dapat didefinisikan sebagai logika kabur berkenaan dengan semantik dari suatu

kejadian, fenomena atau pernyataan itu sendiri. Seringkali ditemui dalam pernyataan

yang dibuat oleh seseorang, evaluasi dan suatu pengambilan keputusan.

Fuzzy system (sistem kabur) didasari atas konsep himpunan kabur yang

memetakan domain input kedalam domain output. Perbedaan mendasar himpunan

tegas dengan himpunan kabur adalah nilai keluarannya. Himpunan tegas hanya

memiliki dua nilai output yaitu nol atau satu, sedangkan himpunan kabur memiliki

banyak nilai keluaran yang dikenal dengan nilai derajat keanggotaannya.

Logika fuzzy adalah peningkatan dari logika Boolean yang berhadapan dengan

konsep kebenaran sebagian. Dimana logika klasik (crisp) menyatakan bahwa segala

hal dapat diekspresikan dalam istilah binary (0 atau 1, hitam atau putih, ya atau tidak).

Logika fuzzy menggantikan kebenaran Boolean dengan tingkat kebenaran. Logika

fuzzy memungkinkan nilai keanggotaan antara 0 dan 1, tingkat keabuan dan juga

hitam dan putih, dan dalam bentuk linguistic, konsep tidak pasti seperti “sedikit”, “lumayan”, dan “sangat”. Logika ini diperkenalkan oleh Dr. Lotfi Zadeh dari Universitas California, Barkeley pada tahun 1965. Logika fuzzy telah digunakan pada

bidang-bidang seperti taksonomi, topologi, linguistik, teori automata, teori

pengendalian, psikologi, pattern recognition, pengobatan, hukum, decision analysis,

system theory and information retrieval. Pendekatan fuzzy memiliki kelebihan pada

(22)

melibatkan pembentukan konsep, pengenalan pola, dan pengambilan keputusan dalam

lingkungan yang tidak pasti atau tidak jelas.

Ada beberapa alasan mengapa orang menggunakan logika fuzzy (Kusumadewi

2003) antara lain:

1. Konsep logika fuzzy mudah dimengerti. Konsep matematis yang mendasari

penalaran fuzzy sangat sederhana dan mudah dimengerti.

2. Logika fuzzy sangat fleksibel.

3. Logika fuzzy memiliki toleransi terhadap data-data yang tidak tepat.

4. Logika fuzzy mampu memodelkan fungsi-fungsi nonlinear yang sangat

kompleks.

5. Logika fuzzy dapat membangun dan mengaplikasikan pengalaman-pengalaman

para pakar secara langsung tanpa harus melalui proses pelatihan.

6. Logika fuzzy dapat bekerjasama dengan teknik-teknik kendali secara

konvensional.

7. Logika fuzzy didasarkan pada bahasa alami.

2.2. Konsep Fuzzy Logic

Teori logika fuzzy yang diajukan oleh Zadeh pada pertengahan tahun 1960,

memberikan suatu pemecahan masalah terhadap persoalan yang tidak pasti ini.

Sehingga sistem informasi yang akan dibuat menggunakan model DBMS dan query

yang berbasis fuzzy karena model DBMS konvensional, non fuzzy kurang dapat

memenuhi kebutuhan sistem informasi ini. Banyak model DBMS dan query fuzzy

yang ada, salah satunya adalah model Mamdani yang ditemukan pada tahun 1977.

Prof. Lutfi Zadeh berpendapat bahwa logika benar dan salah dari logika

boolean/konvensional tidak dapat mengatasi masalah gradasi yang ada di dunia nyata.

Untuk mengatasi masalah gradasi tersebut maka ia mengembangkan sebuah himpunan

samar (fuzzy).

2.3. Himpunan Fuzzy

Pada himpunan tegas (crisp), nilai keanggotaan suatu item x dalam suatu himpunan A,

yang sering ditulis dengan µA[x], memiliki 2 yaitu:

1. Satu (1), yang berarti bahwa suatu item menjadi anggota dalam suatu

himpunan, atau

(23)

2. Nol (0), yang berarti bahwa suatu item tidak menjadi anggota dalam suatu

himpunan.

Terkadang kemiripan antara keanggotaan fuzzy dengan probabilitas

menimbulkan kerancuan. Keduanya memiliki nilai pada interval [0,1], namun

interprestasi nilainya sangat berbeda antara kedua kasus tersebut. Keanggotaan fuzzy

memberikan suatu ukuran terhadap pendapat atau keputusan, sedangkan probabilitas

mengindikasikan proporsi terhadap keseringan suatu hasil bernilai benar dalam jangka

panjang. Misalnya, jika nilai keanggotaan bernilai suatu himpunan fuzzy USIA adalah

0,9 maka tidak perlu dipermasalahkan berapa seringnya nilai itu diulang secara

individual untuk mengharapkan suatu hasil yang hampir pasti muda. Di lain pihak,

nilai probabilitas 0,9 usia berarti 10% dari himpunan tersebut diharapkan tidak muda.

Himpunan fuzzy memiliki 2 atribut, yaitu:

1. Linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau

kondisi tertentu dengan menggunakan bahasa alami, seperti: MUDA,

PAROBAYA, TUA

2. Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu

variable seperti: 40, 25, 50, dsb.

Ada beberapa hal yang perlu diketahui dalam memahami sistem fuzzy (Aplikasi

logika fuzzy untuk pendukung keputusan, Sri Kusumadewi,Hari Purnomo, Edisi

kedua, Graha Ilmu, 2010), yaitu:

a. Variable fuzzy

Variable fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem

fuzzy. Contoh: umur, temperature, permintaan, dsb.

b. Himpunan Fuzzy

Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau

keadaan tertentu dalam suatu variabel fuzzy.

c. Semesta Pembicaraan

Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk

dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan

himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari

kiri ke kanan. Nilai semesta pembicaraan dapat berupa bilangan positif

maupun negatif. Ada kalanya nilai semesta pembicaraan ini tidak dibatasi

(24)

Contoh:

a. Semesta pembicaraan untuk variable mahasiswa: [0 50]

b. Semesta pembicaraan untuk variable dosen: [0 50]

d. Domain

Domain himpunan fuzzy adalah keseluruhan nilai yang diijinkan dalam

semesta pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy.

Seperti halnya semesta pembicaraan, domain merupakan himpunan bilangan

real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan. Nilai

domain dapat berupa bilangan positif dan bilangan negatif.

2.4. Fungsi Keanggotaan

Fungsi keanggotaan adalah suatu kurva yang menunjukkan pemetaan titik-titik input

data kedalam nilai keanggotaannya (sering juga disebut dengan derajat keanggotaan)

yang memiliki interval antara 0 sampai 1. Salah satu cara yang dapat digunakan untuk

mendapatkan nilai keanggotaan adalah dengan melalui pendekatan fungsi. Apabila U

menyatakan himpunan universal dan A adalah himpunan fungsi fuzzy dalam U, Then

A dapat dinyatakan sebagai pasangan terurut (Wang, 1997 yang dirujuk Wulandari,

F. 2005). Ada beberapa fungsi yang bisa digunakan.

a. Representasi Linear

Pada representasi linear, pemetaan input ke derajat keanggotaannya

digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan

menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas.

Ada 2 keadaan himpunan fuzzy yang linear. Pertama, kenaikan himpunan

dimulai pada nilai domain yang memiliki derajat keanggotaan nol(0)

bergerak ke kanan menuju ke nilai domain yang memiliki derajat

keanggotaan lebih tinggi (Kusumadewi S, Purnomo H, 2010). Seperti

terlihat pada gambar 2.1

Derajat keanggotaan

µ[x] 1

(25)

Gambar 2.1. Representasi linear naik

Fungsi keanggotaan:

0; x ≤ a

µ[x] = (x-a) / (b-a); a < x < b (2.1)

1; x ≥ b

Kedua, merupakan kebalikan dari yang pertama. Garis lurus dimulai dari nilai

domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak

menurun ke nilai domain yang memiliki derajat keanggotaan lebih pendek.

Seperti terlihat pada gambar 2.2.

Gambar 2.2. Representasi linear turun

Fungsi keanggotaan:

0; x ≥ b

µ[x] = (b-x) / (b-a) a < x < b (2.2)

1; x ≤ a

b. Representasi kurva segitiga

1

0

a _domain b

Derajat keanggotaan

(26)

Kurva segitiga pad dasarnya merupakan gabungan antara 2 garis (linear).

Seperti terlihat pada gambar 2.3.

Gambar 2.3. kurva segitiga

Fungsi Keanggotaan:

0; x ≥ c atau x ≤ a

µ[x] = (x-a) / (b-a) a < x < b (2.3)

(c-x) / (c-b) b < x < c

c. Representase kurva trapezium (Kusumadewi S, Purnomo H, 2010) Kurva trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada titik

yang memiliki nilai keanggotaan 1. Seperti terlihat pada gambar 2.4

asi

Gambar 2.4. Representasi kurva trapezium

(27)

µ[x] = (x-a) / (b-a); a < x < b

(d-x) / (d-c); c < x < d (2.4)

1; b ≤ x ≤ c

2.5. Sistem Inferensi Fuzzy

Salah satu aplikasi logika fuzzy yang telah berkembang amat luas dewasa ini adalah

sistem inferensi fuzzy (Fuzzy Inference System / FIS), yaitu kerangka komputasi yang

didasarkan pada teori himpunan fuzzy, aturan fuzzy berbentuk IF THEN, dan penalaran

fuzzy. Misalnya dalam penentuan status gizi, produksi barang, sistem pendukung

keputusan, penentuan kebutuhan kalori harian, dan sebagainya. Ada tiga metode

dalam sistem inferensi fuzzy yang sering digunakan, yaitu metode Tsukamoto, metode

Mamdani, dan metode Takagi Sugeno. Dalam penelitian ini akan dibahas penentuan

status gizi menggunakan metode Mamdani. Sistem ini berfungsi untuk mengambil

keputusan melalui proses tertentu dengan mempergunakan aturan inferensi

berdasarkan logika fuzzy. Metode Mamdani sering dikenal dengan nama Metode

Min–Max. Metode ini diperkenalkan oleh Ebrahim Mamdani pada tahun 1975. Untuk

mendapatkan output, diperlukan 4 tahapan:

1. Pembentukan himpunan fuzzy

Pada Metode Mamdani, baik variabel input maupun variabel output dibagi

menjadi satu atau lebih himpunan fuzzy.

2. Aplikasi fungsi implikasi

Pada metode Mamdani, fungsi implikasi yang digunakan adalah Max-min.

3. Rule Evaluation (Komposisi Aturan)

Apabila sistem terdiri dari beberapa aturan, maka inferensi diperoleh dari

gabungan antar aturan. Ada tiga metode yang digunakan dalam melakukan inferensi

sistem fuzzy, yaitu: Max-min, additive dan probabilistik OR (probor).

a. Metode Max (Maximum)

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai

maksimum aturan, kemudian menggunakannya untuk memodifikas daerah fuzzy,

dan mengaplikasikannya ke output dengan menggunakan operator OR(union).

(28)

fuzzy yang merefleksikan konstribusi dari tiap-tiap proposisi. Secara umum dapat

dituliskan:

= max ( [xi], (2.5)

keterangan:

= nilai keanggotaan solusi fuzzy sampai aturan ke-i;

= nilai keanggotaan konsekuen fuzzy aturan ke-i.

b. Metode Additive (Sum)

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan

bounded-sum terhadap semua output daerah fuzzy. Secara umum dituliskan:

= min (1, [xi]+ (2.6)

Keterangan:

μsf[xi] = nilai keanggotaan solusi fuzzy sampai aturan ke-i; μkf[xi

c. Metode Probabilistik OR (probor)

product terhadap semua output daerah fuzzy. Secara umum dituliskan:

= [xi]- (2.7)

Keterangan:

= nilai keanggotaan solusi fuzzy sampai aturan ke-i;

= nilai keanggotaan konsekuen fuzzy aturan ke-i.

4. Penegasan (defuzzifikasi)

Input dari proses defuzzifikasi adalah suatu himpunan fuzzy yang diperoleh dari suatu

komposisi aturan – aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu

bilangan pada himpunan fuzzy tersebut. Sehingga jika diberikan suatu himpunan fuzzy

dalam range tertentu, maka harus dapat diambil suatu nilai crisp tertentu sebagai

output.

(29)

Fuzzyfikasi merupakan fase pertama dari perhitungan fuzzy, yaitu mengubah

masukan - masukan yang nilai kebenarannya bersifat pasti ke dalam bentuk fuzzy

input yang berupa tingkat keanggotaan / tingkat kebenaran. Fuzzifikasi adalah proses

perubahan suatu nilai crisp ke dalam variabel fuzzy yang berupa variabel linguistik

yang nantinya akan dikelompokkan menjadi himpunan fuzzy. Dengan demikian, tahap

ini mengambil nilai-nilai crisp dan menentukan derajat di mana nilai-nilai tersebut

menjadi anggota dari setiap himpunan fuzzy yang sesuai.

Ada beberapa metode defuzzifikasi pada komposisi aturan Mamdani, antara

lain:

a. Metode Centroid (Composite Moment)

b. Metode Largest of Maximum (LOM)

c. Metode Mean of Maksimum (MOM)

d. Metode Bisektor

Pada tahap defuzzifikasi penulis menggunakan salah satu metode

defuzzifikasi yaitu Metode Bisektor. Pada metode ini, solusi crisp diperoleh dengan

cara mengambil nilai pada domain fuzzy yang memiliki nilai keanggotaan setengah

dari jumlah total nilai keanggotaan pada daerah fuzzy. Secara umum dituliskan:

(2.8)

Keterangan:

d = nilai hasil penegasan (defuzzifikasi),

di = nilai keluaran pada aturan ke-i,

= derajat keanggotaan nilai keluaran pada aturan ke-i,

(30)

Secara garis besar sistem inferensi fuzzy dapat dilihat pada gambar 2.5

Gambar 2. 5 Tahapan sistem berbasis aturan fuzzy

2.6 Indeks Antropometri

Menurut Supariasa (2001), indeks antropometri adalah kombinasi antara beberapa

parameter antropometri untuk menilai status gizi. Beberapa indeks antropometri yang

sering digunakan yaitu berat badan menurut umur (BB/U), tinggi badan menurut umur

(TB/U), berat badan menurut tinggi badan (BB/TB), dan Indeks Massa Tubuh (IMT).

Indeks BB/U, TB/U, BB/TB digunakan untuk menilai status gizi anak – anak (kurang

dari delapan belas tahun). Sedangkan IMT digunakan untuk menilai status gizi orang

dewasa (lebih dari delapan belas tahun).

1. Berat Badan menurut Umur (BB/U)

Berat badan adalah salah satu parameter yang memberikan gambaran massa

tubuh. Massa tubuh sangat sensitif terhadap perubahan – perubahan yang

mendadak, misalnya karena terserang penyakit infeksi, menurunnya nafsu

makan atau menurunnya jumlah makanan yang dikonsumsi.

Crisp Inputs

Fuzzification Input Membership

Function

Fuzzy Inputs

Rule Evaluation _{Rules Base}

(31)

2. Tinggi Badan menurut Umur (TB/U)

Tinggi badan adalah salah satu ukuran pertumbuhan linier. Pada keadaan

normal, tinggi badan tumbuh seiring dengan pertambahan umur. Pertumbuhan

tinggi badan tidak seperti berat badan, relatif kurang sensitif terhadap masalah

kekurangan gizi dalam waktu yang singkat.

3. Berat Badan menurut Tinggi Badan (BB/TB)

Berat badan memiliki hubungan yang linear dengan tinggi badan. Dalam

keadaan normal, perkembangan berat badan akan searah dengan pertumbuhan

tinggi badan dengan kecepatan tertentu. Indeks BB/TB tidak dipengaruhi oleh

umur.

4. Indeks Massa Tubuh

Indeks Massa Tubuh (IMT) merupakan alat yang sederhana untuk memantau

status gizi orang dewasa, khususnya yang berkaitan dengan kekurangan dan

kelebihan berat badan. Penggunaan IMT hanya berlaku untuk orang dewasa

berumur lebih dari 18 tahun dan tidak dapat diterapkan pada bayi, anak,

remaja, ibu hamil, dan olahragawan. Pada atlet, postur tubuh yang ideal

berbeda antara setiap jenis cabang olah raga. Misalnya postur tubuh yang ideal

bagi atlet petinju atau binaraga, sangat berbeda pada atlet senam atau renang.

Atlet tinju dan binaraga membutuhkan massa tubuh yang besar, otot dan tulang

yang kuat untuk berlatih atau bertanding. Berbeda pada atlet senam atau

renang, yang membutuhkan massa tubuh yang tidak terlalu besar, tetapi tetap

membutuhkan otot dan tulang yang kuat dan lentur. Untuk kondisi ini

diperlukan pengukuran yang khusus,seperti pengukuran tebal lemak untuk

menilai apakah massa tubuh yang besar pada atlet tersebut terdiri dari otot atau

lemak. Rumus perhitungan IMT adalah sebagai berikut:

(32)

Tabel 2.1. Kategori Ambang Batas IMT untuk Indonesia (Supriasa dalam Yogawati)

IMT tidak tergantung pada umur dan jenis kelamin.

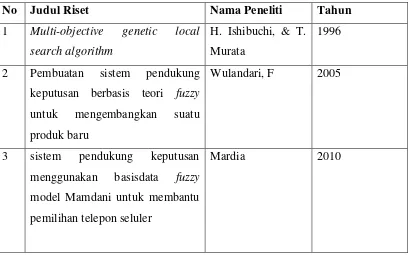
2.7 Riset Terkait

Dalam melakukan penelitian, penulis menggunakan beberapa riset terkait yang

dijadikan acuan dalam melakukan penelitian ini. Adapun riset-riset terkait tersebut

adalah :

Tabel 2.2 Riset terkait

No Judul Riset Nama Peneliti Tahun

1 Multi-objective genetic local

search algorithm

H. Ishibuchi, & T.

Murata

1996

2 Pembuatan sistem pendukung

keputusan berbasis teori fuzzy

untuk mengembangkan suatu

produk baru

Wulandari, F 2005

3 sistem pendukung keputusan

menggunakan basisdata fuzzy

model Mamdani untuk membantu

pemilihan telepon seluler

Mardia 2010

(33)

4 Perbandingan metode

defuzzifikasi aturan Mamdani

dengan beberapa metode

defuzzifikasi, yaitu metode COA

(center of area), bisektor, MOM

(mean of aximum), LOM (largest

of maximum), dan SOM (smallest

of maximum);

Sutikno 2011

5 Penggunaan fuzzy mamdani dalam

menentukan stutus gizi

Yogawati

wulandari

2011

2.8 Perbedaan Dengan Riset Yang Lain

Para peneliti sudah banyak melakukan riset tentang fuzzy Mamdani, namun disini

penulis secara khusus menganalisis rule evaluation yang terdapat pada fuzzy

Mamdani yang terdiri atas tiga metode yaitu metode Max, metode additive-sum dan

(34)

BAB 3

METODE PENELITIAN

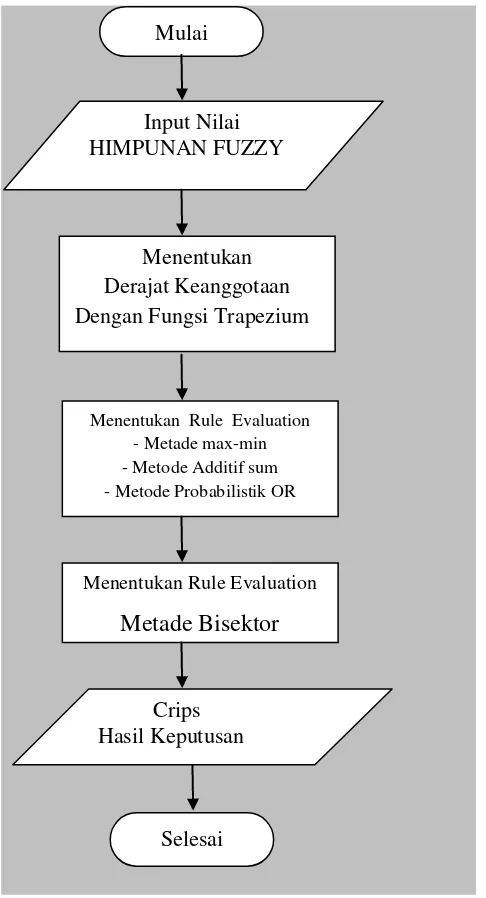
3.1 Rancangan Penelitian

Penelitian yang dilakukan adalah penentuan status gizi seseorang dengan

menggunakan logika fuzzy dengan metode mamdani, dimana untuk penentuan status

nilai gizi seseorang, dapat dilakukan dengan langkah-langkah seperti pada gambar 3.1

Gambar 3.1 Flowchart Penelitian dengan mengunakan logika fuzzy

Input Nilai HIMPUNAN FUZZY

Menentukan Derajat Keanggotaan Dengan Fungsi Trapezium

Mulai

Crips Hasil Keputusan

Menentukan Rule Evaluation - Metade max-min - Metode Additif sum - Metode Probabilistik OR

Menentukan Rule Evaluation

Metade Bisektor

Selesai

(35)

Adapun penjelasan dari flowchart pada gambar 3.1 di atas adalah sebagai

berikut :

1. Himpunan fuzzy

dalam penentuan status gizi dengan parameter Indeks Massa Tubuh (IMT),

variabel input dibagi menjadi dua yaitu variabel berat badan dan tinggi badan.

Serta satu variabel output, yaitu variabel nilai gizi. Variabel nilai gizi ini dibentuk

berdasarkan klasifikasi IMT.

2. Menentukan derajat keanggotaan himpunan fuzzy

Setiap variabel sistem dalam himpunan fuzzy ditentukan derajat keanggotaannya (μ). Dimana derajat keanggotaan tersebut menjadi nilai dalam himpunan fuzzy.

3. Menghitung predikat aturan( rule evaluation) (α)

Variabel-variabel yang telah dimasukkan dalam himpunan fuzzy, dibentuk

aturan-aturan yang diperoleh dengan mengkombinasikan setiap variabel dengan

variabel yang satu dengan atribut lingusitiknya masing-masing. Aturan-aturan

yang telah diperoleh akan dihitung nilai rule evaluation dengan proses implikasi.

Dalam metode Mamdani proses implikasi dilakukan dengan 3 metode yaitu,

a. Metode Max (Maximum)

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai

maksimum aturan, kemudian menggunakannya untuk memodifikas daerah

fuzzy. Metode Max dapat diperoleh dengan menggunakan rumus:

= max ( [xi],

b. Metode Additive (Sum)

bounded-sum terhadap semua output daerah fuzzy

Metode Additive (Sum) dapat diperoleh dengan rumus :

= min (1, [xi]+

c. Metode Probabilistik OR (probor)

(36)

Metode Probabilistik OR (probor) dapat diperoleh dengan rumus :

=

[xi]-4. Defuzzifikasi

Pada tahap defuzIfikasi ini dilakukan penghitungan dengan metode

Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai pada domain

fuzzy yang memiliki nilai keanggotaan setengah dari jumlah total nilai

keanggotaan pada daerah fuzzy

Bisektor dapat diperoleh dengan rumus :

5. Hasil keputusan

Pada bagian ini merupakan hasil keputusan dari rangkaian proses dalam

penegakan status gizi berdasarkan klasifikasi IMT.

3.3 Perancangan Sistem

Dalam perancangan sistem yang akan dibuat menggunakan representasi kurva untuk

mencari derajat keanggotaan pada tiap variabel fuzzy. Representasi kurva yang

digunakan dalam penelitian ini adalah menggunakan kurva bahu dan segitiga

3.4 Perancangan Inferensi Fuzzy

Sebagai langkah awal dari perancangan mesin inferensi fuzzy adalah menentukan

himpunan fuzzy dari tiap-tiap variabel fuzzy. Adapun variabel fuzzy disini yang

digunakan adalah tinggi dan berat badan dengan satu output berupa nilai gizi seperti

dalam Tabel 3.1

(37)

Tabel 3.1 Variabel dan himpunan fuzzy

Variabel Himpunan Domain Fungsi

Keanggotaan

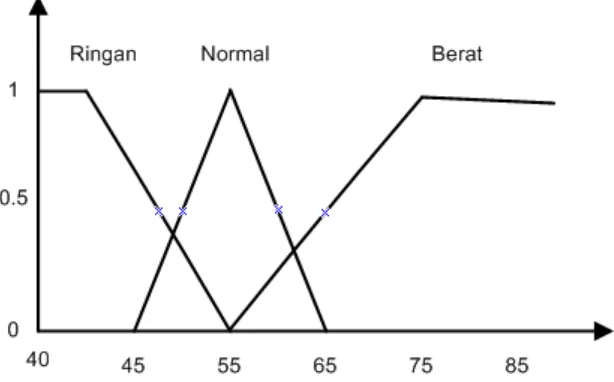
3.4.1 Himpunan fuzzy variabel berat badan

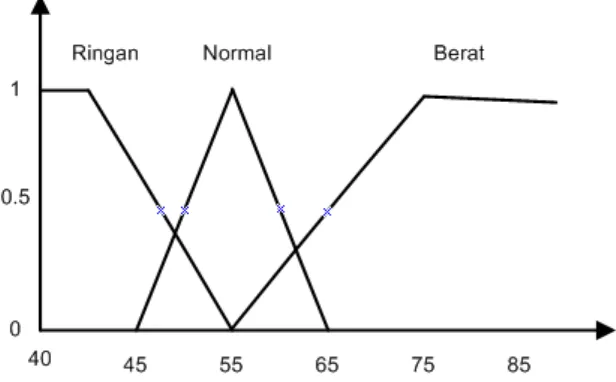
Pada variabel berat badan didefinisikan tiga himpunan fuzzy, yaitu RINGAN,

NORMAL, dan BERAT. Untuk merepresentasikan variabel berat badan digunakan

bentuk kurva bahu kiri untuk himpunan fuzzy RINGAN, bentuk kurva segitiga untuk

himpunan fuzzy NORMAL, dan bentuk kurva bahu kanan untuk himpunan fuzzy

BERAT. Gambar himpunan fuzzy untuk variabel berat badan ditunjukkan pada

Gambar 3.2

(38)

X<=40

40<x<=55

x>55

X<=45 atau x>65

45<x<=55

55<x<65

X<=55

55<x<=75

x>=75

Seseorang dianggap Ringan bila berat badannya antara 40 kg sampai 55 kg,

dianggap Gizi Baik bila berat badannya antara 45 kg sampai 65 kg, dianggap Berat

bila berat badannya antara 55 kg sampai 80 kg, dianggap ringan sekaligus Gizi Baik

bila berat badannya antara 45 kg sampai 55 kg, dan dianggap Gizi Baik sekaligus

Normal bila berat badannya antara 55 kg sampai 65 kg.

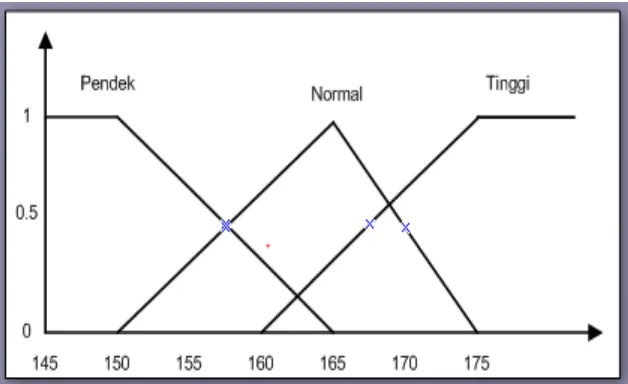
3.4.2 Himpunan fuzzy variabel tinggi badan

Pada variabel tinggi badan didefinisikan tiga himpunan fuzzy, yaitu PENDEK,

NORMAL, dan TINGGI. Untuk merepresentasikan variabel tinggi badan digunakan

bentuk kurva bahu kiri untuk himpunan fuzzy PENDEK, bentuk kurva segitiga untuk

himpunan fuzzy NORMAL, dan bentuk kurva bahu kanan untuk himpunan fuzzy

TINGGI. Representasi himpunan fuzzy untuk variabel tinggi badan ditunjukkan pada

Gambar 3.3

(39)

Gambar 3.3 Fungsi Keanggotaan Tinggi Badan

X<=150

150<x<=165

x>165

X=165

165<x<175

x<=150 atau

x>=175

X<=160

160<x<175

x>=175

Seseorang dianggap Pendek bila tinggi badannya antara 145 cm sampai 165

cm, dianggap normal bila tinggi badannya antara 150 cm sampai 175 cm, dianggap

tinggi bila tinggi badannya antara 160 cm sampai 180 cm, dianggap Pendek

sekaligus Normal bila tingginya antara 150 cm sampai 165 cm, dianggap Normal

sekaligus Tinggi bila tingginya antara 160 cm sampai 175 cm, dan dianggap Pendek

sekaligus Normal dan Sekaligus Tinggi bila tingginya antara 160 cm sampai 165 cm.

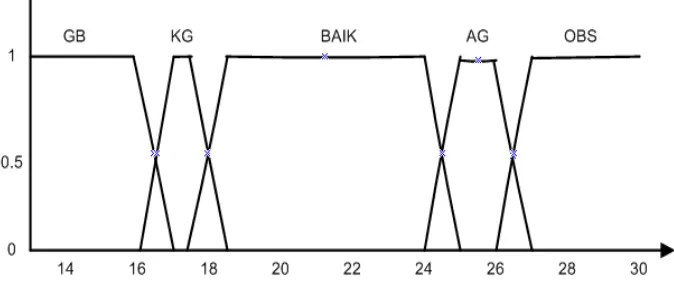
3.4.3 Himpunan fuzzy variabel nilai gizi

Himpunan fuzzy nilai gizi diperoleh berdasarkan klasifikasi pada Indeks Massa Tubuh

(IMT), yang direpresentasikan menggunakan himpunan fuzzy. Pada variabel nilai

(40)

AGAK GEMUK, OBESITAS. Untuk merepresentasikan variabel nilai gizi

digunakan bentuk kurva bahu kiri untuk himpunan fuzzy GIZI BURUK , bentuk

kurva trapesium untuk himpunan fuzzy KURANG GIZI, GIZI BAIK, serta AGAK

GEMUK, bentuk kurva bahu kanan untuk himpunan fuzzy OBESITAS. Gambar

himpunan fuzzy untuk variabel nilai gizi ditunjukkan pada Gambar 3.4.

Gambar 3.4 Himpunan Fuzzy Nilai Gizi dan Status Gizi

Keterangan

GB : GIZI BURUK

KG : KURANG GIZI

BAIK : GIZI BAIK

AG : GEMUK

OBS : OBESITAS (SANGAT GEMUK)

X<16

16<=x<=17

x>17

X<16 atau

x>18.5

16<x<=17

17>x<=17.5

17.5<x<=18.5

(41)

X<17.5 atau

dianggap KURANG GIZI bila nilai gizinya antara 16 sampai 18.5, dianggap Gizi

BAIK bila nilai gizinya antara 17.5 sampai 25, dianggap AGAK GEMUK bila nilai

gizinya antara 24 sampai 27, dianggap OBESITAS bila nilai gizinya antara 26

sampai 33, dianggap GIZI BURUK sekaligus KURANG GIZI bila nilai gizinya antara

16 sampai 17, dianggap KURANG GIZI sekaligus GIZI Baik bila nilai gizinya antara

17.5 sampai 18.5, dianggap GIZI BAIK sekaligus AGAK GEMUK bila nilai gizinya

antara 24 sampai 25, dan dianggap AGAK GEMUK sekaligus OBESITAS bila nilai

gizinya antara 26 sampai 27.

Setelah pembentukan fungsi keanggotaan pada masing – masing variabel, input

yang berupa nilai crisp akan diubah ke dalam fuzzy input yaitu dengan menentukan

derajat keanggotaan nilai input pada sebuah himpunan fuzzy, proses ini disebut

fuzzyfikasi.

3.5 Fungsi Implikasi

Setelah pembentukan himpunan fuzzy, maka dilakukan pembentukan aturan

fuzzy. Aturan - aturan dibentuk untuk menyatakan relasi antara input dan output. Tiap

(42)

antara dua input adalah operator AND, dan yang memetakan antara input-output

adalah IF-THEN. Proposisi yang mengikuti IF disebut anteseden, sedangkan

proposisi yang mengikuti THEN disebut konsekuen.

Berdasarkan kategori dalam IMT, Then dapat dibentuk aturan–aturan sebagai

berikut :

Tabel 3.2 Aturan - aturan dalam penentuan status gizi

Tinggi Badan BERAT BADAN

Ringan Normal Berat

Pendek Baik Agak gemuk Obesitas Normal Kurang Gizi Baik Agak gemuk Tinggi Gizi Buruk Kurang Gizi Baik

Berdasarkan tabel 3.2 Then terbentuklah aturan-aturan fuzzy yang disimbolkan

dengan aturan If –Then

[R1] : If berat badan adalah ringan dan tinggi badan adalah pendek Then status

gizinya adalah Baik.

[R2] : If berat badan adalah ringan dan tinggi badan adalah normal Then status

gizinya adalah Kurang Gizi.

[R3] : If berat badan adalah ringan dan tinggi badan adalah tinggi Then status

gizinya adalah Gizi Buruk.

[R4] : If berat badan adalah normal dan tinggi badan adalah pendek Then status

gizinya adalah Agak Gemuk.

[R5] : If berat badan adalah normal dan tinggi badan adalah normal Then status

[R6] : If berat badan adalah normal dan tinggi badan adalah tinggi Then status

[R7] : If berat badan adalah berat dan tinggi badan adalah pendek Then status

gizinya adalah Obesitas.

[R8] : If berat badan adalah berat dan tinggi badan adalah normal Then status

gizinya adalah Agak Gemuk .

[R9] : If berat badan adalah berat dan tinggi badan adalah tinggi Then status

(43)

BAB 4

HASIL DAN PEMBAHASAN

4.1 Pendahuluan

Dalam bab ini akan dibahas mengenai hasil dan pembahasan bagaimana menentukan

status gizi seseorang berdasarkan tinggi badan dan berat badan, contoh data variabel

yang diuji adalah seperti tabel pada tabel 4.1 .

Tabel. 4.1 variabel Berat badan dan tinggi badan

NO BB TB

1 60 148

2 55 146

3 80 160

4 80 170

4.2 Pengujian Data Contoh kasus 1:

Pada pengujian data ini If seseorang memiliki berat badan 60 Kg dengan tinggi badan

148 cm, Then dapat dihitung

a. Fuzzyfikasi Berat Badan (BB)

(44)

X<45 atau x>65

45<x<=55

55<x<65

µnormal= 0,5

X<=55

55<x<=75

x>=75

µBerat = 0,25

Dari gambar 4.1 dapat disimpulkan bahwa seseorang dengan berat badan 60 kg

dapat dikatakan Gizi Baikdengan nilai keanggotaan 0,5 dan dapat dikatakan gemuk

dengan nilai keanggotaan 0,25

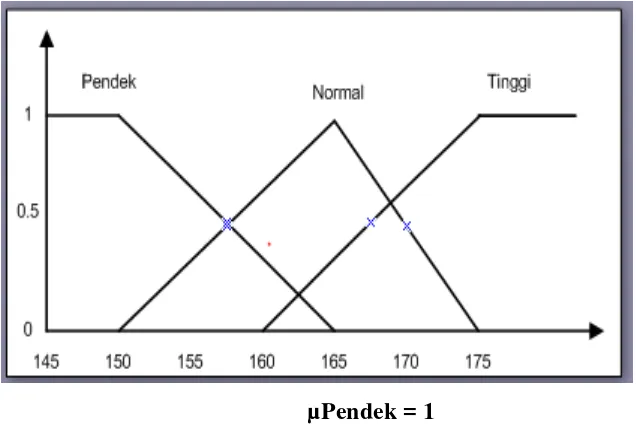
µPendek = 1

Gambar 4.2. Fungsi Keanggotaan Tinggi badan 148 kg

Dari gambar 4.2 dapat disimpulkan bahwa seseorang dengan Tinggi badan

148 kg dapat dikatakan pendek dengan nilai keanggotaan 1.

(45)

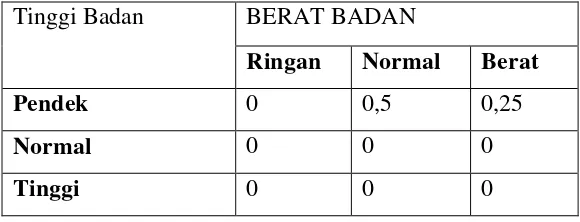
Tabel 4.2 Tabel nilai keanggotaan TB 148 cm dan BB 60 kg

Pendek 0 0,5 0,25

Normal 0 0 0

Tinggi 0 0 0

4.2.1 Komposisi aturan dengan menggunakan metode MAX

Pada metode Max solusi himpunan fuzzy diperoleh dengan cara mengambil

nilai maksimum aturan.

[R4] : If berat badan adalah Normal dan tinggi badan adalah prndek

Then status gizinya adalah agak gemuk.

α- predikat1 = Min (µnormal(60), µpendek(148))

Pendek 0 0,5 0,25

Normal 0 0 0

(46)

Gambar 4.3. Variabel Nilai gizi dan Status Gizi

Pada proses defuzzifikasi dapat dilkukan perhitungan sbb:

xAG = (27-x)/(27-26)=0,5

= 27 – x = 0,5

= 26,5

xAG = (27 – x)/(27-26) = 0.25

= 27 – x = 0.25

= 26.75

Dari gambar 4.3 Pada proses defuzzifikasi metode Max-min dapat disimpulkan

bahwa seseorang yang memiliki tinggi badan 148 dengan berat badan 60 kg

dapat dikatakan agak gemuk dengan fungsi keanggotaan 26.5 dan dapat

dikatakan Obesitasdengan fungsi keanggotaan 26.75. Sehingga nilai gizi dapat

dihitung sebagai berikut:

Nilai gizi =(26.5+26.75)/(0.5+0.25)

= 26,6

Dengan metode max nilai gizi yang diperoleh adalah 26,6

4.2.2 Komposisi Aturan dengan menggunakan metode Adaptif (sum)

bounded-sum terhadap semua output daerah fuzzy.Pada proses metode Adaptif (sum)

untuk memperoleh nilai gizi dapat dilakukan dengan menggunakan rule sebagai

berikut:

(47)

α- predikat1 = Min(1,( (60)+ (148))

α- predikat2 = Min(1,(µringan (60)+ µNormal(148))

α- predikat3 = Min(1,(µringan (60)+ µTinggl(148))

gizinya adalah Agak gemuk .

(48)

[R5] : If berat badan adalah Normal dan tinggi badan adalah Normal Then status

α- predikat5 = Min(1,(Gizi Baik(60)+ µNormal(148))

α- predikat6 = Min(1,(µnormal(60)+ µTinggil(148))

gizinya adalah agak gemuk.

α- predikat8 = Min(1,(µBerat (60)+ µNormal(148))

= min(1,(0,25+0))

= min(1, 0.25)

= 0,25

(49)

Z8 = 18,5 – 0,25

= 18,25

[R9] : If berat badan adalah berat dan tinggi badan adalah tinggi Then status

α- predikat9 = Min(1,(µBerat (60)+ µTTinggi(148))

Pada proses defuzzifikasi dengan metode adaptif sum untuk memperoleh nilai

gizi dapat dilakukan dengan cara menjumlahkan fungsi keanggotaan tiap-tiap

rul, pada metode adaptif sum diperoleh status gizi 26,25 termasuk kategori

status gizi agak gemuk dan sangat gemuk.

Tabel 4.4 variabel TB 148 dan BB 60 kg pada proses Defuzzifikasi

Pendek 1 0 0

Normal 1 0,5 0,5

Tinggi 1 0,25 0,25

4.2.3 Komposisi aturan dengan menggunakan metode Probabilistik Or (Probor)

Pada metode probabilistik, solusi himpunan fuzzy diperoleh dengan cara

melakukan product terhadap semua output daerah fuzzy

[R4] : If berat badan adalah Normal dan tinggi badan adalah pendek Then

status gizinya adalah Agak gemuk

α- predikat = (µnormal(60) + µpendek(148)) - (µnormal(60) *µpendek(148))

(50)

= 1,5 -0,5

Nilai gizi = (25*1 +27,5*1)/(1+1)

= 26,25

Pada metode probabilistik, If seseorang mempunyai berat badan 60 kg, dan

tinggi badan 148 cm, Then nilai gizinya adalah 26,25 termasuk kategori status gizi

agak gemuk dan sangat gemuk.…

Contoh Kasus 2 :

Pada pengujian data ini misalkan seseorang memiliki berat badan 55 Kg dengan tinggi

badan 146 cm, Then dapat dihitung

(51)

Gambar 4.4. Fungsi Keanggotaan Berat badan 55 kg

X<45 atau x>65

45<x<=55

55<x<65

µnormal= 1

X<=40

40<x<=55

x>55

µRingan = 0,5

dapat dikatakan Gizi Baikdengan nilai keanggotaan 1 dan dapat dikatakan kurus

(52)

µPendek = 1

Gambar 4.5. Variabel Tinggi badan 146 kg

146 kg dapat dikatakan pendek dengan nilai keanggotaan 1

X<=150

150<x<=165

x>165

Tabel 4.6 Tabel nilai keanggotaan TB dan BB

Pendek 1 1 0

Normal 0 0 0

Tinggi 0 0 0

4.2.4 Metode MAX dengan BB 55 kg dan TB 146 cm

nilai maksimum aturan

(53)

α- predikat1 = Min(µringan (55), µpendek(146))

= min(0,5 ,1)

= 0,5

[R4] : If berat badan adalah Normal dan tinggi badan adalah pendek Then status

α- predikat1 = Min(µnormal(55), µpendek(146))

= min(1 ,1)

= 1

Tabel 4.7 Himpunan Keanggotaan TB 146 dan BB 55 kg

Kurus Normal Berat

Pendek 1 1 0

Normal 0 0 0

Tinggi 0 0 0

(54)

Nilai gizi = (25+26)/(1+1)

= 25,6

Then status gizinya adalah Gizi Baikdengan nilai gizi 24 dan status gizi agak

gemuk dengan nilai gizi 26, Then kesimpulannya nilai gizi adalah : 25,6

4.2.5 Metode Adaptif (sum)untuk BB 60 dan TB 146

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan

bounded-sum terhadap semua output daerah fuzzy.Pada proses metode Adaptif (sum) untuk

memperoleh nilai gizi dapat dilakukan dengan menggunakan rule sebagai berikut:

α- predikat1 = Min(1,( (55)+ (146))

(55)

α- predikat2 = Min(1,( (55)+ (146))

α- predikat3 = Min(1,( (55)+ (146))

α- predikat4 = Min(1,( (55)+ (146))

(56)

[R6] : If berat badan adalah Normal dan tinggi badan adalah tinggi Then status

α- predikat6 = Min(1,( (55)+ (146))

α- predikat8 = Min(1,( (55)+ (146))

= min(1,(0+0))

= min(1,0)

= 0

[R9] : If berat badan adalah berat dan tinggi badan adalah tinggi Then status gizinya

(57)

Proses Defuzzifikasi

Pada proses defuzzifikasi dengan metode bisektor untuk memperoleh nilai gizi dapat

dilakukan dengan cara menjumlahkan fungsi keanggotaan tiap-tiap rule

Pendek 1 1 1

Normal 1 1 0

Tinggi 1 1 0

4.2.6 Metode Probabilistik (Probor) untuk BB 60 kg dan TB 146 cm

Pada metode probabilistik, solusi himpunan fuzzy diperoleh dengan cara

melakukan product terhadap semua output daerah fuzzy

α- predikat1 = (1,( (55)+ (146)) - ( (55)* (146))

= (0,5 +,1) – (0.5*1)

= (1.5) – (0.5)

= 1

R4] : If berat badan adalah Normal dan tinggi badan adalah pendek Then status

(1,( (55)+ (146)) - ( (55)* (146))

= (1+1) – (1*1)

= 2 - 1

= 1

Tabel 4.9 variabel TB 148 dan BB 80 kg dengan Metode Probor

Pendek 1 1 0

Normal 0 0 0

(58)

xN = 25

xAG = 26

Nilai gizi = (25*1 +27,5*1)/(1+1)

= 25,3

Pada metode probor nilai gizi untuk berat badan 55 kg, dan tinggi badan 146

adalah 25,3

Dari hasil analisis untuk masing-masing metode yaitu metode Max, metode

adaptif sum dan metode probor dapat dilihat nilai gizi yaitu :

Metode Max nilai gizi : 26

Metode Adaptif : 25,2

Metode Probor : 25,3

(59)

X<=80

80

<x<=75

x>=75

µBerat = 1

dapat dikatakan berat dengan nilai keanggotaan 1

µPendek 0,33 µnormal= 0,66 Gambar 4.8. Variabel Tinggi badan 160 cm

160 cm dapat dikatakan pendek dengan nilai keanggotaan 0,33 dan dapat dikatakan

Gizi Baikdengan nilai keanggotaan 0,66

X<=150

150<x<=165

x>165

X=165

165<x<175

x<=150 atau

(60)

Pendek 0 0 0,33

Normal 0 0 0,66

Tinggi 0 0 0

4.2.7 Metode MAX untuk BB 80 kg dan TB 160 cm

nilai maksimum aturan.

[R9] : If berat badan adalah berat dan tinggi badan adalah Normal Then status

α- predikat1 = Min(µberat (80 ), µnormal160))

= min(1 ,0.66)

= 0.66

Tabel 4.11 variabel nilai BB 80 kg TB 160

Pendek 0 0 0,33

Normal 0 0 0,66

Tinggi 0 0 0

(61)

Gambar 4.9. Defuzzifikasi

xAG = (27-x)/(27-26)=0,33

= 27 – x = 0,33

= 26,67

Poses defuzzifikasi:

Maka 26,67

dapat dikatakan agak gemuk dengan fungsi keanggotaan 26,67

4.2.8 Metode Adaptif (sum)untuk BB 80 kg dan TB 146 cm

Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan

bounded-sum terhadap semua output daerah fuzzy.Pada proses metode Adaptif (sum)

untuk memperoleh nilai gizi dapat dilakukan dengan menggunakan rule sebagai

berikut:

α- predikat1 = Min(1,( (80 )+ (160))

= min(1,(0+0,33))

= min (1,0,33)

(62)

Z2 = 25 – 0,33

Z2 = 24,67

[R2] : If berat badan adalah ringan dan tinggi badan adalah NormalThen status

α- predikat2 = Min(1,( (80 )+ (160))

[R3] : If berat badan adalah ringan dan tinggi badan adalah tinggi Then status

α- predikat3 = Min(1,( (80 )+ (160))

[R4] : If berat badan adalah Normal dan tinggi badan adalah Pendek Then status

α- predikat4 = Min(1,( (80 )+ (160))

[R5] : If berat badan adalah Normal dan tinggi badan adalah Normal Then status

(63)

α- predikat5 = Min(1,( (80 )+ (160))

gizinya adalah Obesitas.

(64)

[R9] : If berat badan adalah berat dan tinggi badan adalah tinggi Then status gizinya

Pada proses defuzzifikasi dengan metode bisektor untuk memperoleh nilai gizi

dapat dilakukan dengan cara menjumlahkan fungsi keanggotaan tiap-tiap rule

Pendek 0,33 0,33 1

Normal 0,66 0,66 1

Tinggi 0,66 0 1

4.2.9 Metode Probabilistik or (Probor)untuk BB 80 kg dan TB 146 cm

Pada metode probabilistik, solusi himpunan fuzzy diperoleh dengan cara melakukan

product terhadap semua output daerah fuzzy

= (1,( (80 )+ (160))- (1,( (80 )+ (160))

= (1+1.33) - (1*1.33)

= 2.33-1.33

= 1

(65)

[R7] If berat badan adalah berat dan tinggi badan adalah NormalThen status gizinya

Dari hasil analisis untuk masing-masing metode yaitu metode Max, metode

adaptif sum dan metode probor dapat dilihat nilai gizi yaitu :

Metode Max nilai gizi : 25,26

Metode Adaptif : 24,05

Metode Probor : 24,5

(66)

X<=80

80

<x<=75

x>=75

µnormal= 1

Dari gambar 4.10 dapat disimpulkan bahwa seseorang dengan berat badan 80

kg dapat dikatakan berat dengan nilai keanggotaan 1

µnormal= 0.5 ; µTinggi 0.66

Gambar 4.11. Fungsi keanggotaan Tinggi badan 170 kg cm

(67)

170 cm dapat dikatakan Gizi Baik dengan nilai keanggotaan 0,5 dan dapat

dikatakan tinggi dengan nilai keanggotaan 0,66

X=165

Pendek 0 0 0

Normal 0 0,5 0,66

Tinggi 0 0 0

4.2.10 Metode MAX untuk BB 80 kg dan 170 cm

Pada metode Max solusi himpunan fuzzy diperoleh dengan cara mengambil

nilai maksimum aturan

[R8] : If berat badan adalah berat dan tinggi badan adalah Normal Then status

gizinya adalah agak gemuk .

α- predikat1 = Min(µberat (80 ), µnormal(170 kg))

= min(1 ,0.5) = 0.5

[R9] : If berat badan adalah berat dan tinggi badan adalah tinggi Then tinggi

α- predikat1 = Min(µberat (80 ), µtinggi 170 kg))

= min(1 ,0.66)