TRANSFORMASI LINEAR PADA RUANG BARISAN

TRANSFORMASI MATRIKS PADA RUANG BARISAN

Oleh

NUR ROHMAH

Ruang barisan dengan1 <_∞ merupakan ruang Banach.

1.1 Latar Belakang dan Masalah

Salah satu bahasan tentang ruang barisan adalah teori transformasi matriks. Dalam pembahasan ini lebih difokuskan menganalisa matriks tak hingga, matriks dan masalah kekonvergenan.

Selanjutnya, teorema Banach-Steinhauss dan teorema-teorema yang berkaitan banyak dimanfaatkan untuk mengkaji transformasi matriks tersebut.

Dalam banyak kasus sebagian besar operator linear pada suatu ruang barisan ke ruang barisan lainya, dapat diwakili oleh suatu matriks tak hingga, oleh sebab itu digunakan tranformasi yang diberikan oleh matriks tak hingga, bukan operator linear umum. Sebagai contoh, diambil suatu

ruang barisan .Misal = ; = 1,2, adalah suatu matriks tak

hingga dan = maka

Dengan perkalian matriks biasa diperoleh:

=

Jadi, memetakan barisan ke barisan . Misalkan ( ) = ( ) untuk setiap , dengan

( ) =

Merupakan suatu deret yang konvergen untuk setiap .

Berdasarkan uraian di atas, akan dikaji tentang transformasi matriks pada ruang barisan , dimana matriks yang digunakan adalah matriks tak hingga yang mempunyai sifat sebagai operator linear terbatas. Dalam penelitian ini, penulis membatasi masalah pada ruang barisan , yang selanjutnya akan dikembangkan transformasi matriks pada ruang barisan

.

1.2 Tujuan Penelitian

Tujuan penulisan ini adalah mengetahui cara mentransformasikan matriks

tak hingga sebagai operator linear dengan ruang barisan dengan

1.3 Manfaat Penelitian

Manfaat yang diharapkan dari hasil penulisan ini adalah:

1. Menambah pengetahuan penulis tentang masalah transformasi matriks pada ruang barisan .

2. Dapat memberikan sumbangan pemikiran untuk memperluas dan memperdalam wawasan di bidang analisis khususnya dalam transformasi matriks pada ruang barisan .

Dalam bab ini akan dibahas beberapa konsep mendasar meliputi ruang vektor, ruang Bernorm dan ruang Banach, ruang barisan, operator linear (transformasi linear) serta teorema-teorema yang mendukung. Semua pembicaraan berada dalam bilanganreal .

2.1 Ruang Vektor

Definisi 2.1.1(Maddox, 1970).

Ruang vektor adalah suatu himpunan tak kosong yang dilengkapi dengan fungsi penjumlahan (+): dan fungsi perkalian skalar (. ):

sehingga untuk setiap skalar , dengan elemen , , berlaku:

(1) + = +

(2) ( + ) + = + ( + )

(3)ada sehingga + =

(4)ada sehingga + ( ) =

(5)1. =

(6) ( + ) = +

(7)( + ) = +

2.2 Ruang Bernorm dan Ruang Banach

Definisi 2.2.1(Rudin, 1987)

Fungsi nonnegatif . : disebut norm jika untuk setiap , dan setiap

skalar berlaku

Definisi 2.2.2(Mizrahi dan Sulivan,1949)

Barisan ( ) di dalam ruang Bernorm disebut barisan Cauchy jika untuk setiap bilangan > 0 terdapat bilangan asli N sehingga untuk setiap bilangan asli

, berlaku

| | <

Definisi 2.2.3(Mizrahi dan Sulivan,1949)

Barisan( )di dalam ruang Bernorm disebut barisan konvergen jika untuk setiap bilangan > 0terdapat bilangan asliNsehingga jika berlaku

Definisi 2.2.4(Maddox, 1970)

Suatu ruang vektor bernorm dinamakan ruang Banach jika lengkap. Kelengkapan berarti bahwa setiap barisan Cauchy dalam konvergen jika

( + ) 0 ( , ),

maka terdapat sehingga

( ) 0 ( ).

2.3 Ruang Barisan

Definisi 2.3.1(Soeparna, 2007)

Diberikan yaitu koleksi semua barisan bilangan real, jadi:

= { = { }: }

a. Untuk setiap bilangan realpdengan1 <_∞ didefinisikan

= : ∞ _<

∞ dan norm pada yaitu

‖ ‖ =

∞

b. Untuk = ∞ didefinisikan

= ∈ ∈ : < ∞

dan norm pada yaitu

Definisi 2.3.2(Soeparna, 2007)

Berdasarkan (i), (ii) dan (iii) terbukti bahwa merupakan ruang linear dan

‖ . ‖ norm pada . Dengan kata lain ( ,‖ . ‖ ) ruang bernorma.

b) Untuk1 ≤ < ∞diambil sebarang ̅= { }, = { } ∈ dan skalar α. Diperoleh :

‖ ̅‖ = {∑ | | } = 0 ⇔ | | ≥ 0 untuk setiap

⇔ ̅= {0} = 0.

(ii) ‖ ∝ ̅‖ = {∑ | | } = | |{∑ | | } = ∝‖ ‖

Jelas bahwa ‖ ∝ ̅‖ < ∞ .

(iii) ‖ ̅ + ‖ ≤ ‖ ̅‖ + ‖ ‖ = {∑ | | } + {∑ | | } < ∞. Berdasarkan (i), (ii) dan (iii) terbukti bahwa merupakan ruang linear dan ‖ . ‖

norm pada . Dengan kata lain ( ,‖ . ‖ ) ruang Bernorm.

Teorema 2.3.2(Kreyszig, 1978)

Diberikan ruang barisan dengan1 ≤ ≤ ∞

| | ≤ ‖ ‖ ‖ ‖

b. Akan dibuktikan∑ | | ≤ ‖ ‖ ‖ ‖

Jelas bahwa∑ | | = ∑ | || |

≤ | | | | = ‖ ‖ ‖ ‖

Jika p = q = 2, pertidaksamaan di atas disebut pertidaksamaan Cauchy-Schwarz. Teorima ini sering juga dinamakan PertidaksamaanHolder.

Teorema 2.3.3(Soeparna, 2007)

Jika bilangan real dengan 1 ≤ ≤ ∞ , maka ( ,‖ . ‖ ) merupakan ruang Banach.

Bukti :

Telah dibuktikan bahwa (lp, ‖.‖p) merupakan ruang Bernorm. Jadi tinggal membuktikan bahwa ruang Bernorm itu lengkap.

Dibuktikan dahulu untuk1 ≤ < _∞, diambil sebarang barisan Cauchy

̅( ) ⊂ dengan

a) ̅( ) = ̅( ) = ( ), ( ), ( ), …

Untuk sebarang > 0 terdapat bilangan asli n0sehingga untuk setiap dua bilangan asli , ≥ berlaku

b) ( ) − ( ) < atau ∑ ( ) ₋ ( ) _{< . Hal ini berakibat}

untuk setiap dua bilangan asli m, n > 0 diperoleh ( ) − ( ) <

setiap k. Jadi terdapat bilangan xk sehungga lim → ( ) = atau

lim _→ ( )− = 0. Berdasarkan (b) diperoleh untuk ≥ berlaku

x ( ) − x = lim _→ ( ) − ( ) < . Selanjutnya dibentuk barisan

̅= ( ). Menurut ketidaksamaan Minkowski.

c) {∑ | | } = ∑ − ( ) + ( )

Misalkan merupakan ruang barisan, dikatakan ruang BK (Banach Komplit) jika merupakan ruang Banach dan pemetaan koordinatnya ( ) = , = ( ) ∈ kontinu.

2.4 Operator dan Transformasi Definisi 2.4.1(Kreyszig, 1989)

Suatu pemetaan pada ruang vektor khususnya ruang Bernorma disebut operator.

Definisi 2.4.2(Kreyszig, 1989)

Diberikan ruang Bernorm dan atasfieldyang sama. a. Pemetaan dari dan disebut operator.

b. Operator ∶ → dikatakan linier jika untuk setiap , ∈ dan setiap skalar berlaku ( ) = dan ( + ) = + .

Definisi 2.4.3(Kreyszig, 1989)

Diberikan( , ‖ . ‖ )dan( , ‖ . ‖ ) masing-masing ruang Bernorm.

a. Operator ∶ → dikatakan terbatas jika ada bilangan ∈ dengan

≥ 0sehingga untuk setiap ∈ berlaku‖ ‖ ≤ ‖ ‖ .

b. Operator dikatakan kontinu di ∈ jika diberikan bilangan > 0 ada bilangan > 0 sehingga untuk setiap ∈ dengan‖ − ‖ ≤ berlaku

‖ − ‖ < .

c. Jika kontinu di setiap ∈ , disebut kontinu pada .

Teorema 2.4.1(Ruckle, 1991)

Jika dan masing-masing ruang Bernorm atas field yang sama maka ( , )

Bukti :

Jadi( + ) merupakan operator linear.

Karena A dan B terbatas maka ada bilangan real , ≥ 0 sehingga

Dengan demikian + terbatas (kontinu). Jadi , ∈ ( , ).

Telah dibuktikan bahwa untuk setiap , ∈ ( , ) dan sebarang skalar α, β berlaku , ∈ ( , ). Jadi ( , ) linear.

Teorema 2.4.2 (Maddox, 1970)

Bukti :

Diambil sebarang barisan Cauchy{ } ⊂ ( , ), ‖ . ‖ .

Jadi untuk setiap bilangan terdapat n0 ∈N sehingga jika m, n ∈N dengan

, ≥ berlaku‖ − ‖ < .

Misal untuk setiap x∈X dan , ≥ diperoleh ‖ − ‖ = ‖ ( − ) ‖

≤ ‖ − ‖ ‖ ‖ < ‖ ‖

Jelas untuk setiap bilangan > 0 (dapat dipilih bilangan > 0 sehingga

‖ ‖ < ) ada n0 N sehingga untuk setiap m, n N dengan , ≥

berlaku‖ − ‖ < ‖ ‖ < .

Dengan demikian diperoleh barisan Cauchy { } ⊂ dan Y lengkap, dengan kata lain { }konvergen, katakan ke ∈ .

Jadilim → = danxmenentukan suatu operatorAsehingga = .

Proses di atas dapat diulang untukz Xtetap, denganz≠x.

Jadi diperoleh lim → = dan z menentukan suatu operator A sehingga

= .

Untuk setiap skalaradanb, diperolehax+ bz X.

= +

Jadi operator A bersifat linear. Untuk →∞ diperoleh

‖ ( − ) ‖ = ‖ − ‖ = ‖ − ‖

= ‖ ( − ) ‖ < ‖ ‖

Jadi operator ( − ) dengan ≥ bersifat linear terbatas.

Karena Am dan ( − ) masing-masing terbatas, serta = − ( − )

makaAterbatas (kontinu).

Jadi ∈ ( , ) , ‖ . ‖ dengan kata lain ( , ), ‖ . ‖ ruang Banach.

Definisi 2.4.4(Kreyszig, 1978)

Diberikan ruang Bernorm denganfield .

a. Pemetaan : → disebut fungsi.

b. Himpunan semua fungsi linier kontinu pada disebut ruang dual , biasanya ditulis ∗∈ ( , ).

Teorema 2.4.3 (Ruckle, 1991)

Misal X dan Y ruang BK (Banach Komplit). Jika A matriks tak hingga yang memetakanX keYmakaAkontinu.

Bukti :

Misal =

= ∈

=

Mendefinisikan suatu fungsi linear kontinu padaX. Jelas bahwa setiap :

( ) =

Berdasarkan (i) dan (ii) terbukti merupakan fungsi linear padaX. Selanjutnya akan ditunjukkan kontinu padaX.

Hal ini sama saja membuktikan terbatas padaX.

DiketahuiXruang BK maka terdapatM> 0 sehingga| ( ) | = | | ≤

| ( ) | =

≤

≤

Berdasarkan pembuktian di atas, mendefinisikan fungsi linear kontinu padax

( ) = lim →∞ ( ) Makafjuga kontinu padax. Karenayruang BK diperoleh

Jikay=Axmaka bukti lengkap.

Definisi 2.4.5 (Berberian, 1996)

a. Matriks tak hingga = adalah matriks dengan ∈ dan elemen pada baris dan kolom sebanyak tak hingga.

b. Jika = dan = masing-masing matriks tak hingga dan

skalar maka + = + , = , dan = ∑

3.1 Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester ganjil tahun ajaran 2012/2013 di Jurusan Matematika FMIPA Universitas Lampung.

3.2 Metode Penelitian

Metode penelitian yang digunakan dalam penulisan tugas akhir ini adalah studi pustaka. Hal ini penulis lakukan dengan menggunakan buku-buku yang ada diperpustakaan Universitas Lampung, jurnal-jurnal terakreditasi serta buku-buku yang berkaitan dengan operator linear (transformasi linear), matriks tak hingga dan ruang barisan yang tercantum dalam daftar pustaka.

3.3 Langkah-langkah Penelitian

1. Menyelidiki konsep operator linear kontinu dari ruang barisan ke ruang barisan.

2. Menetapkan ruang barisan yang terlibat meliputi ruang barisan , < <_∞✁

3. Menentukan syarat bagi operator A yang meliputi :

1. A :

2. A :

3. A :

4. A :

5.1 Kesimpulan

Ruang barisan dengan1✧ ✂ ✄merupakan ruang Banach.

Setiap operatorA: ✦ dengan1✧ , ✂✄menentukan suatu matriks tak

hingga dengan syarat-syarat tertentu, dan sebaliknya juga berlaku. Karena

setiap matriks pemetaan bersifat linear maka operatorA: ✦ dengan

1✧ , ✂ ✄bersifat linear. Karena dan terkait dengan matriks tak hingga

makaAkontinu. Oleh karena itu setiap operatorAdari ke dengan

1✧ , ✂ ✄bersifat linear kontinu.

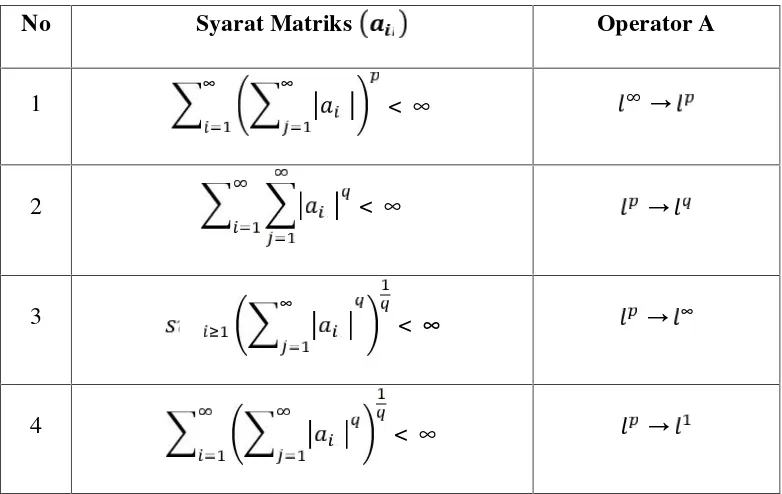
Tabel syarat suatu matriks tak hingga sehingga terkait suatu operator linear

kontinuAdari ke dengan1✧ , ✂ ✄.

No Syarat Matriks Operator A

1 ∞ ∞ < ∞ →

2 < ∞ →

3 ∞ _<

∞ → ∞

5 < ∞ →

5.2 Saran

Oleh Nur Rohmah

0617031052

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

Oleh

NUR ROHMAH

Skripsi

Sebagai Salah Satu Syarat untuk Mencapai Gelar

SARJANA SAINS

Pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

UNIVERSITAS LAMPUNG

BANDAR LAMPUNG

Oleh

NUR ROHMAH

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

Assalamu alaikum wr.wb

Alhamdulillah, puji syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan limpahan rahmat, taufik dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul_“Transformasi Matriks Pada Ruang Barisanlp_{”dengan baik.}

Dalam penyelesaian skripsi ini, tentunya tidak terlepas dari bantuan, dorongan, dan masukan dari berbagai pihak. Oleh karena itu, perkenankanlah penulis memberikan ucapan terimakasih kepada :

1. Bapak Dr. Muslim Ansori, M.Si., selaku pembimbing I yang telah

meluangkan waktunya memberikan bimbingan, dan arahan yang bermanfaat dalam menyelesaikan skripsi.

2. Bapak Amanto, M.Si., selaku pembimbing II yang telah memberi ide, saran, dan membimbing serta membantu penulis dalam menyelesaikan skripsi. 3. Ibu Dorrah Aziz, M.Si., selaku pembahas yang telah memberikan motivasi,

masukan, dan saran kepada penulis dalam menyelesaikan skripsi.

4. Ibu Dr. Ir. Netti Herawati, M.Sc., selaku pembimbing akademik yang telah memberikan masukan dan bimbingan kepada penulis selama menjadi mahasiswa Matematika FMIPA Universitas Lampung.

7. Seluruh dosen, staff, pegawai, penjaga gedung Jurusan Matematika.

8. Keluargaku tercinta, Ayahanda Ahmad Mustofa (alm), Ibunda Siti Rodiyah, mbak pit, mb uut, mas yusuf dan adikku arum. Terima kasih ibu, mbak dan mas berkat do’a serta dorongan moral penuh dengan keharuan dan material yang tiada putusnya sebagai bekal dan motivasi untuk menjadikan hidup lebih bermakna.

9. Teman-teman seperjuangan di Rois FMIPA, keluarga kecilku dan ikhwah di Unila terima kasih atas ukhuwahnya. Semoga kita bisa tetap istiqomah di jalan ini sampai akhir hayat.

10. Teman-teman DT dan An-Nahl Mbak Umil, Mbak Asih, Yuli, Za, Nita, Dudu,

Depol, Ade, Ismi, Dwi, Fe, Au’, Tila, Dedeh, Nining dan Yaya terimakasih

atas waktu yang dilewati bersama dalam berbagi suka maupun duka, berbagi kisah dan tawa, mencoba saling memahami, dalam bingkaian ukhuwah. 11. Sahabatku Yuli Kartika, Atma, Ita, Febri, Uli, Uci, Achmad Rochfi’idan

Seluruh temanCosmic_{terima kasih atas kebersamaannya.}

12. Teman seperjuanganku dalam penyusunan skripsi Anwar Sidiq, dan Pita Rini terimakasih atas kebersamaannya.

13. Teman-teman Jurusan Matematika FMIPA, yang telah memberikan dorongan, semangat, dan inspirasi-inspirasinya. Semoga kita selalu kompak.

Wassalamu alaikum wr.wb

Bandar Lampung, November 2012

Allah SWT,

Keluarga tercinta, ibu yang selalu memberikan kasih

sayangnya dan selalu memberikan do a untuk

keberhasilanku, mbak pit, mbak ut, mas yang selalu

mendorong dan memberi semangat, dan juga adikku arum,

Orang yang menginspirasi dan menjadi teladan bagiku,

Keluarga kecilku,

Adik-adik dan teman seperjuangan dakwah di MIPA,

Judul Penelitian : TRANSFORMASI LINEAR PADA RUANG BARISAN

Nama Mahasiswa : Nur Rohmah

NPM : 0617031052

Jurusan : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam

Menyetujui, Komisi Pembimbing

Pembimbing I Pembimbing II

Dr. Muslim Ansori, M. Si Amanto, M. Si

NIP. 19720227 199802 1 001 NIP. 19730314 200012 1 002

Mengetahui,

Ketua Jurusan Matematika

1. Tim Penguji

Ketua : Dr. Muslim Ansori, M. Si ………...

Sekretaris : Amanto, M. Si …….....

Penguji

Bukan Pembimbing : Dorrah Azis, M. Si ………...

2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Prof. Suharso, Ph. D. NIP. 19690530 199512 1001

Sesungguhnya sesudah kesulitan itu ada kemudahan.

(QS.Al-Insyirah:6)

Penulis dilahirkan di Pelindung Jaya, Lampung Timur pada tanggal 21 Agustus 1988, merupakan anak keempat dari lima bersaudara dari pasangan Bapak Ahmad Mustofa(alm) dan Ibu Siti Rodiyah.

Penulis menyelesaikan Sekolah Dasar di SD Negeri 1 Waymili pada tahun 2000, Sekolah Lanjutan Tingkat Pertama di SMP 1 Muhammadiyah Pelindung Jaya pada tahun 2003, dan Sekolah Menengah Atas di MA Negeri 1 Lampung Timur pada tahun 2006.

Penulis terdaftar sebagai mahasiswi Fakultas Matematika dan Ilmu Pengetahuan Alam Jurusan Matematika Universitas Lampung pada tahun 2006, melalui Seleksi Penerimaan Mahasiswa Baru (SPMB). Selama menjadi mahasiswi penulis pernah menjadi Pengurus Badan Eksekutif Mahasiswa (BEM) FMIPA periode

2006/2007 dan 2007/2008, dan Pengurus Rohani Islam (ROIS) periode