DAFTAR PUSTAKA
Adiwijaya. 2014. Matematika Diskrit Sekolah Tinggi Teknologi Telkom. Bandung: Sekolah Tinggi Teknologi Telkom.
Alavi, N., Nozari, V. & Mazloumzadeh, S. M., 2010. Irrigation water quality evalution using adaptive network-based fuzzy inference system. Paddy Water Environ, Volume 8, pp. 259-266.
Alidoosti, a., Yazdani, M. & Basiri, M. H., 2012. Risk assessment of critical asset using fuzzy inference system. Risk Management, Volume 14, No. 1, pp. 77-91.
Bandar, Z., Fowdar, J., Crockett, K., 2002, Inducing Fuzzy Decision Trees in Non-Deterministic Domains using CHAID. Manchester : Department of Computing and Mathematics, Manchester Metropolitan University.
Budi Nugroho, Didit. 2008. Pengantar Teori Graf. Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana. Salatiga : Universitas Kristen Satya Wacana.
Breiman, L., J.H. Friedman, R.A. Olshen, and C.J. Stone, Classification And Regression Trees, Chapman & Hall, New York, 1993.
Chandrakar, V. K. & Kothari, A. G., 2008. Fuzzy Logic Based Unified Power flow Controllers for improving transient stability. International Journal of power and Energy Systems, Volume 28, p. 2.
http://www.thefreelibrary.com/Credit+scoring+using+data+mining+ techni ques.a0119370565. Tanggal akses : 17 Februari 2016.
Damayanti, Laila Kurnia. 2011. Aplikasi Algoritma Cart untuk Mengklasifika-sikan Data Nasabah Asuransi Jiwa Bersama Bumiputera 1912 Surakarta. Surakarta : Universitas Sebelas Maret. Skripsi Matematika.
Godil, S. S. & Shamim, M. S., 2011. Fuzzy Logic : A"Simple" solution for complexities in neurosciences?. Surgical Neurology International, Volume 2:24.
Han, J., & Kamber, M. 2006. Data Mining Concepts and Techniques. Second Edition. San Fransisco: Morgan Kauffman.
Kusrini & Luthfi, E., T. 2009. Algoritma Data Mining. Yogyakarta: Andi.
Kusumadewi, Sri. 2002. Analisis & Desain Sistem Fuzzy Menggunakan Toolbox Matlab. Yogyakarta: Graha Ilmu.
Kusumadewi, Sri dan Hari Purnomo. 2010. Aplikasi Logika Fuzzy untuk Pendukung Keputusan. Yogyakarta: Graha Ilmu.
Lewis, R.J, An Introduction to Classification And Regression Tree (CART) Analysis, Annual Meeting of the Society for Academic Emergency Medicine in San Fransisco, California, Department of Emergency Medicine, California, 2000. https://www.researchgate.net/publication/
240719582_An_Introduction_to_Classification_and_Regression_Tree_CA RT_Analysis.html. Tanggal Akses : 03 Maret 2016.
Kredit Macet Di BMT El Bummi 372 Yogyakarta. Tesis. FMIPA, Jurusan Statistika, Universitas Islam Indonesia.
Munir, Rinaldi. 2009. Matematika Diskrit (edisi ketiga). Bandung : Penerbit Informatika.
Riyadhi, Slamet., Abdul Syukur. Uji Coba Metode Mamdani untuk Deteksi Penyakit Diabetes di RSUD Dr. H. Soemarno Sosroatmojo Kuala Kapuas.
http://research.pps.dinus.ac.id/jurnal. Tanggal akses : 11 Februari 2016. Sudradjat. 2008. Dasar-dasar Fuzzy Logic. Bandung : Jurusan Matematika
Universitas Padjajaran.
Supardi. 2013. Aplikasi Statistika dalam Penelitian Edisi Revisi. Jakarta: Change Publication.
Tan, PN., M. Steinbach, V. Kumar. 2005. Introduction to Data Mining. Michigan: Michigan State University Publication.
Walpole, R.E dan R.H Myers. 1986. Ilmu Peluang dan Statistika Untuk Insinyur dan Ilmuwan. Terjemahan R.K Sembiring. Bandung: Penerbit ITB.
Wibowo, Ari. 2013. Prediksi Nasabah Potensial Menggunakan Metode Klasifikasi Pohon Biner. Program Studi Teknik Informatika Politeknik Negeri Batam.
http://id.scribd.com/doc/181684943/A152-Prediksi-Nasabah-Pote
nsial-menggunakan-Metode-Klasifikasi-Pohon-Biner-docx#scribd. Tanggal ak-ses : 07 Januari 2016.
0a%20basis%20for%20a%20theory%20of%20possibility-1978.pdf. Tanggal akses : 17 Januari 2016.
Zaki, Mohammed J. And Meira, Wagner. 2014. Data Mining and Analysis: Fundamental Concepts and Algorithms. Cambridge: Cambridge University Press. http://assets.cambridge.org/97805217/66333/frontmatter /9780521766333_frontmatter.pdf. Tanggal akses : 03 Maret 2016.
BAB III
HASIL DAN PEMBAHASAN
3.1. Fuzzy CART
Algoritma CART termasuk dalam anggota analisis klasifikasi yang disebut decision trees karena proses analisis dari CART digambarkan dalam bentuk atau struktur yang menyerupai sebuah pohon, lebih tepatnya pohon klasifikasi yang berbentuk biner (Damayanti, 2011). Algoritma CART dapat mengklasifikasikan data dari semua jenis skala data, baik nominal, ordinal, interval maupun rasio. Algoritma ini menghasilkan output berupa data yang telah terkelompok berdasarkan kesamaan kelas klasifikasi yang tegas (crisp).
Pada himpunan tegas (crisp), nilai keanggotaan yang berbeda sedikit dapat terpisah pada dua kelas klasifikasi. Pengelompokkan variabel dalam analisis klasifikasi sangat tegas, sedikit perbedaan data dapat menyebabkan perbedaan kelas klasifikasi. Misalnya untuk kelas usia dengan rentang 35 – 55 tahun disebut setengah baya, maka 34 tahun dikatakan muda, pendekatan crips ini tidak adil untuk menetapkan hal-hal yang bersifat kontinu (Kusumadewi, 2004).
Bandar (2002) memperkenalkan bahwa fuzzy dapat diinduksikan ke dalam analisis decision tree. Algoritma induksi fuzzy dapat digunakan untuk melunakkan (soften) batasan keputusan yang tajam (sharp) pada algoritma pohon keputusan (decision tree) tradisional.
Fuzzy dapat memperhalus batasan data, khususnya pada data kategorik. Sesuai dengan komponen utama himpunan fuzzy yang memiliki dua atribut (Kusumadewi, 2004); yang pertama linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami, contohnya : muda, parobaya, tua. Yang kedua numerik, yaitu suatu nilai angka yang menunjukkan ukuran dari suatu variabel, contohnya : 3, 4, 17. Oleh karena itu fuzzy hanya dapat digunakan pada data berskala ordinal.
Salah satu jenis Fuzzy Inference System adalah yang dikembangkan oleh Mamdani, yang mampu meningkatkan formulasi awal Zadeh dengan cara yang memungkinkan untuk diterapkan pada sistem kontrol fuzzy. Sistem fuzzy ini juga dikenal sebagai logika fuzzy controller. Seperti sebelumnya, fuzzification memungkinkan FIS metode Mamdani untuk menangani nilai input yang tegas, pemetaan dari nilai tegas untuk himpunan fuzzy didefinisikan dalam semesta pembicaraan. Sistem inferensi menetapkan pemetaan antara himpunan fuzzy dalam domain input dan himpunan fuzzy dalam domain output. Defuzzifikasi mengubah output fuzzy berdasarkan aturan fuzzy menjadi output non-fuzzy (Bandar, 2002).
sebelumnya, dapat diambil pemahaman bahwa FCART hanya dapat diaplikasikan pada data dengan skala ordinal, karena terkait konsep pemikiran dan penilaian manusia dalam batas-batas variabel linguistiknya.
Dalam teknik penggabungan algoritma CART dengan Fuzzy, Fuzzy diinduksikan setelah data melewati seluruh proses klasifikasi pada CART, output algoritma CART tersebut dijadikan rules pada Fuzzy Inference System metode Mamdani. Kemudian melakukan proses inferensi hingga selesai.
Sesuai dengan penelitian yang dilakukan Bandar (2002), langkah-langkah induksi Fuzzy pada algoritma pohon keputusan yang diperkenalkan adalah sebagai berikut :
1. Memisahkan dataset menjadi learning dan testing data;
2. Melakukan Proses analisis CART. Dalam proses ini terdiri atas tiga tahapan yaitu pemecahan node, pelabelan kelas, dan pemangkasan pohon klasifikasi sehingga menghasilkan pohon optimal;
3. Pembentukan aturan (rule) Fuzzy dari Pohon Keputusan CART sebagai Pengetahuan Dasar;
4. Menentukan fungsi keanggotaan (membership function);
Ketika menghitung akurasi persentase untuk dataset di mana variabel target merupakan diskrit, jumlah klasifikasi yang benar dari setiap hasil akan menentukan ukuran keseluruhan kinerja algoritma FCART.
3.2. Uji coba pada Database
Database yang digunakan untuk uji coba pada penelitian ini adalah sebuah database contoh. Database dibagi menjadi dua bagian secara acak, yaitu data learning dan data testing dengan proporsi 80% data learning dan 20% sisanya data testing. Data training digunakan untuk membentuk model klasifikasi, kemudian data testing digunakan untuk menguji akurasi prediksi model terhadap data baru.
Dilakukan analisis data terhadap 686 pasien kanker payudara yang dilakukan oleh German Breast Cancer Study Group. Terdapat enam variabel, yaitu usia pasien (tahun), tsize atau ukuran tumor (mm), pnodes atau banyaknya node positif, kandungan progesteron (ng/dL), kandungan esterogen (pg/dL), dan indikator sensor (0:tersensor, 1:tidak tersensor). Data tersebut terkategorikan dengan dalam variabel seperti pada tabel 2.
Data learning berjumlah 549 dari 686 baris data yang dipilih secara acak, dan sisanya 137 pada data testing. Data learning selanjutnya akan digunakan untuk membuat model klasifikasi dengan algoritma CART sesuai dengan kategorinya.
Tabel 2. Variabel Kategorik Pasien Kanker
Variabel Dependen Kategori
Sensor
1 Tersensor 0
Variabel Independen
Untuk mempermudah penghitungan, data ditabulasikan silang seperti yang terdapat pada lampiran 1. Pemilahan variabel berdasarkan kriteria goodness of split. Suatu split s akan digunakan untuk memecah node t menjadi dua buah node tR dan node tL jika s memaksimalkan nilai ∆i(s,t) = maxs ∆i(s,t). Root
node biasa disebut dengan node 0. Untuk variabel yang lebih dari 2, akan dikombinasikan kategorinya untuk menemukan splitter terbaik. Berikutnya pemilihan split untuk node 1 dan node 2.
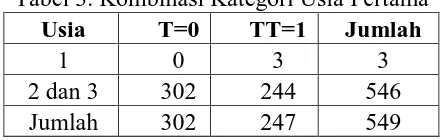
Tabel 3. Kombinasi Kategori Usia Pertama
Usia T=0 TT=1 Jumlah
1 0 3 3
2 dan 3 302 244 546
Jumlah 302 247 549
Impurity Index-nya dihitung sebagai berikut :
∑
{ }
{ }
{ }
Selanjutnya dihitung ∆i(s,t) node tersebut :
Untuk variabel usia yang kedua, kombinasi kategorinya sebagai berikut : Tabel 4. Kombinasi Kategori Usia Kedua
Usia T=0 TT=1 Jumlah
1 dan 2 59 67 126
3 243 180 423
Jumlah 302 247 549
Dengan cara perhitungan yang sama diperoleh sebagai berikut :
∑
{ }
{ }
Untuk variabel tsize yang pertama, kombinasi kategorinya sebagai berikut : Tabel 5. Kombinasi Kategori Tsize Pertama
Tsize T=0 TT=1 Jumlah
Penghitungan ini dilakukan pada semua variabel dan kombinasi kategorinya, sehingga didapatkan seluruh nilai seperti dalam tabel berikut :
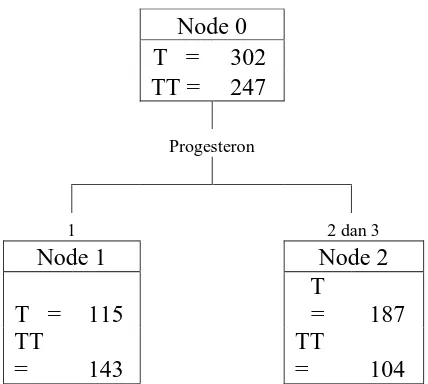
(1) (2) (3) (4) (5) progesteron, sehingga variabel ini terpilih sebagai pemilah terbaik pertama yang membagi node 0 menjadi dua. Node 1 adalah variabel progesteron dengan kategori 1 dan node 2 adalah kategori progesteron dengan kategori 2 dan 3, seperti yang terlihat pada diagram pada gambar 8.
Node 0
Pemberian label kelas pada node-node yang telah terbentuk berdasarkan rumus apabila �� maka . Sebagai contoh, pelabelan node 1 dan node 2 sebagai berikut.
Node 0
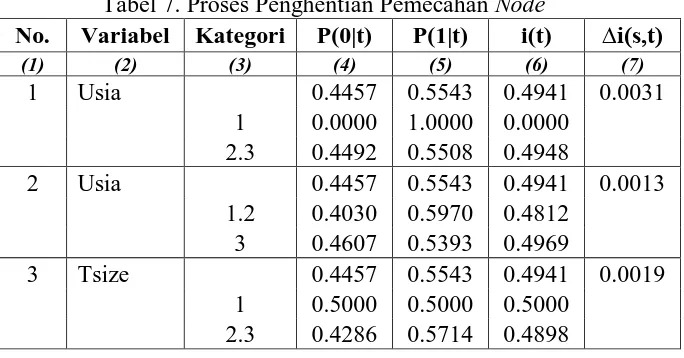
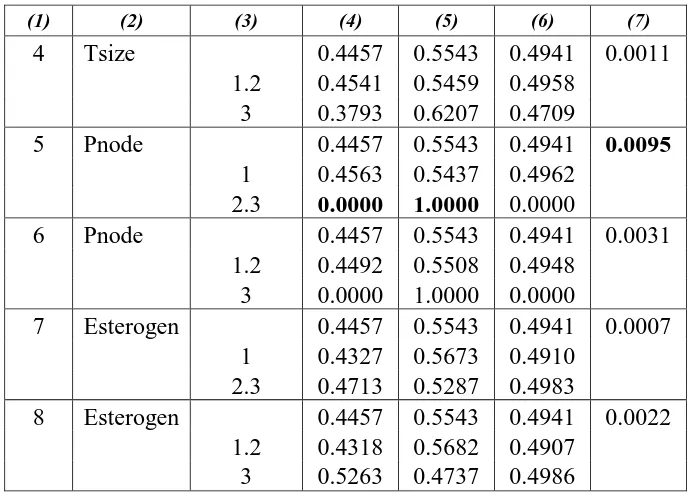
Proses pemecahan yang berulang-ulang akan berhenti dan menghasilkan pohon maksimal. Proses splitting node akan berhenti jika semua variabel telah digunakan. Proses ini juga bisa terhenti jika data dalam kelas telah homogen, atau atau . Contohnya pada pemecahan node 1 dapat terlihat pada tabel 7.
Dari tabel 7, pnode adalah variabel pemilah node 1 menjadi dua node, yaitu node 3 dengan kategori pnode 1 dan node 4 dengan kategori pnode selain 1. Namun karena , maka proses pemecahan node 4 dihentikan, sedangkan node 3 tetap dapat dilanjutkan.
Tabel 7. Proses Penghentian Pemecahan Node
(1) (2) (3) (4) (5) (6) (7)
Proses ini terus dilakukan hingga terbentuk pohon maksimal (Tmax) seperti
terlihat pada lampiran 2 dan lampiran 3. d. Pemangkasan Pohon
Setelah pohon maksimal (Tmax) terbentuk, maka dilakukan proses
pemangkasan pohon klasifikasi. Jika diperoleh dua child node dan parent node yang memenuhi persamaan � � � , maka child node �dan �
dipangkas. Sebagai contoh, berikut proses pemangkasan node 13.
Node 13
� � �
�
��
�
�
��
�
�
��
�
Sehingga diperoleh :
� � �
Karena � � � maka kedua child node dari node 13 (node 23 dan node 24) dipangkas.
Proses pemangkasan ini dilakukan pada setiap subtree dari pohon Tmax
hingga tidak ada lagi node yang bisa dipangkas. Pohon optimal terbentuk setelah proses pemangkasan diakhiri, seperti gambar berikut.
Node 0
Dari diagram di atas dapat disimpulkan bahwa yang mempengaruhi tersensor atau tidaknya adalah variabel kadar progesteron dan variabel usia pasien.
e. Rules untuk Induksi Fuzzy
Dari output pohon klasifikasi CART, terbentuk 3 (tiga) kelas klasifikasi yang berbeda. Tahap selanjutnya, bentuk aturan-aturan fuzzy “IF...THEN...” yang telah dipilih berdasarkan aturan-aturan klasifikasi hasil algoritma CART dalam penelitian ini. Aturan-aturan tersebut diberikan sebagai berikut :
2)If (Usia is MUDA) and (Progesteron is NORMAL) then (Sensor is TERSENSOR)
3)If (Usia is PAROBAYA) and (Progesteron is NORMAL) then (Sensor is TERSENSOR)
4)If (Usia is MUDA) and (Progesteron is BANYAK) then (Sensor is TERSENSOR)
5)If (Usia is PAROBAYA) and (Progesteron is BANYAK) then (Sensor is TERSENSOR)
6)If (Usia is TUA) and (Progesteron is NORMAL) then (Sensor is TERSENSOR)
7)If (Usia is TUA) and (Progesteron is BANYAK) then (Sensor is TERSENSOR)
Operator yang digunakan pada sistem adalah operator standard Zadeh “AND”. Proses defuzzifikasi menggunakan Metode Centroid. Selanjutnya,
aturan-aturan “IF...THEN...” di atas digunakan sebagai input pada tahap inferensi fuzzy.
f. Fungsi Keanggotaan Variabel Fuzzy
Tabel 8. Variabel dalam Induksi Fuzzy Pasien Kanker
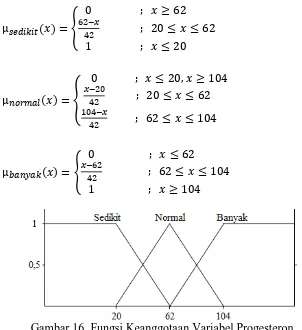
Progesteron [0,+∞] Sedikit [0,62]
Normal [20,104]
Banyak [62,980]
Usia [0,+∞] Muda [0,35]
Parobaya [22,48]
Tua [35,80]
Parameter-parameter tersebut diinput kedalam fungsi keanggotaan yang telah definisikan dan untuk hasilnya dapat dilihat pada fungsi berikut.
a. Variabel Usia
b. Variabel Progesteron
Gambar 17. Fungsi Keanggotaan Variabel Sensor g. Aplikasi Fungsi Implikasi
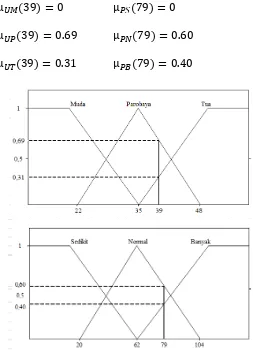
Pada proses aplikasi fungsi implikasi, nilai-nilai dimasukkan pada fungsi implikasi, seperti berikut. Untuk data testing dengan usia 39 tahun dan kandungan progesteron 79 ng/dL. Maka nilai dari fungsi keanggotaannya :
Aplikasi fungsi implikasi sesuai dengan 7 (tujuh) aturan yang telah dibentuk sebelumnya, yaitu :
[R1] If (Progesteron is SEDIKIT) then (Sensor is TIDAK TERSENSOR)
[ ]
[R2] If (Usia is MUDA) and (Progesteron is NORMAL) then (Sensor is TERSENSOR)
[ ] [ ]
[R3] If (Usia is PAROBAYA) and (Progesteron is NORMAL) then (Sensor is TERSENSOR)
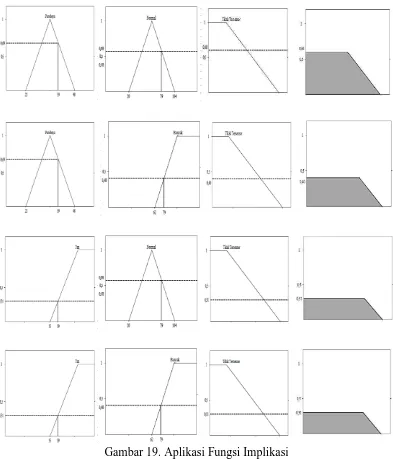
Dari ketujuh aturan di atas, yang memiliki nilai adalah R3, R5, R6 dan R7. Aplikasi fungsi implikasi dari aturan tersebut dapat dilihat juga pada diagram berikut.
Gambar 19. Aplikasi Fungsi Implikasi
kesimpulan masing-masing aturan, sehingga diperoleh daerah solusi fuzzy seperti berikut :
[ ] [ ]
[ ]
[ ]
[ ] [ ]
Gambar 20. Daerah Solusi Fuzzy
Titik potong aturan adalah ketika , maka dapat ditentukan nilai z sebagai berikut :
Sehingga diperoleh fungsi keanggotaan daerah solusi sebagai berikut :
{
h. Defuzzifikasi
Pada tahap ini penegasan dilakukan untuk mengubah himpunan fuzzy menjadi bilangan real. Input proses penegasan adalah suatu himpunan fuzzy, sedangkan output yang dihasilkan merupakan bilangan pada domain himpunan fuzzy tersebut. Defuzzifikasi dilakukan dengan metode centroid, seperti contoh berikut :
Proses implikasi, komposisi dan defuzifikasi ini dilakukan pada setiap data testing, sehingga diperoleh nilai yang mendekati crips, untuk kemudian dilakukan pembulatan ke nilai crips terdekat, yaitu nol dan satu pada database yang digunakan.
i. Uji Akurasi Klasifikasi
Tabel 9. Prediksi Indikator Sensor berdasarkan FCART
No. Usia Progesteron Observasi Prediksi FCART
1 56 61 Tidak Tersensor Tersensor diprediksi indikator sensornya sesuai dengan aturan FCART.
Tabel 10. Akurasi Klasifikasi FCART perbandingan akurasi antara algoritma CART dan algoritma FCART, yaitu dengan melihat perbandingan tingkat akurasi kedua algoritma.
klasifikasi CART. Kemudian dihitung tingkat akurasinya dengan tabulasi silang (confusion matrix 2x2) seperti berikut.
Tabel 9. Akurasi Klasifikasi CART
Algoritma FCART yang telah diperkenalkan dalam penelitian ini mampu meningkatkan kinerja pohon keputusan (decision tree) dengan induksi Fuzzy menggunakan algoritma CART. Penelitian ini juga telah memperlihatkan logika fuzzy untuk melunakkan batas keputusan tajam yang jelas dalam pohon keputusan. Hasil yang diperoleh dari Algoritma FCART menunjukkan adanya peningkatan akurasi kinerja dibandingkan dengan algoritma CART dengan data tegas. Untuk database di mana variabel sasaran merupakan diskrit, peningkatan yang dicapai dengan metode Mamdani adalah hasil dari batas keputusan tajam yang digambarkan sebagai serangkaian daerah fuzzy.
Dari penelitian yang telah dilakukan dengan cara studi literatur dan melakukan uji coba pada database contoh, maka dapat diperoleh beberapa hasil, yaitu :
1) Fuzzy dapat diinduksikan ke dalam algoritma CART;
3) FCART hanya dapat digunakan untuk data dengan skala ordinal, atau data interval dan rasio yang telah dikategorikan menjadi data ordinal;
4) Algoritma FCART memiliki tingkat akurasi yang lebih tinggi dibandingkan dengan Algoritma CART;
BAB IV
PENUTUP
5.1. Kesimpulan
Berdasarkan pembahasan dan hasil penelitian diperoleh kesimpulan bahwa Algoritma CART dengan induksi Fuzzy memiliki tingkat akurasi yang lebih baik daripada Algoritma CART tanpa induksi Fuzzy. Algoritma Fuzzy CART (FCART) dapat digunakan untuk memaksimalkan hasil klasifikasi.
5.2. Saran
Saran yang bisa diberikan peneliti setelah melakukan penelitian pada Algoritma CART dan Algoritma FCART adalah sebagai berikut :
- Untuk mengklasifikasikan data dengan skala interval dan rasio dapat digunakan Algoritma FCART untuk mengurangi ketajaman perbedaan antar kelas klasifikasi;
- Untuk melakukan pengujian kembali pada keakuratan Algoritma FCART dapat digunakan metode-metode lainnya, seperti salah satunya MRE (Magnitude Relative Error) dan MPE (Mean Percentage Error); - Untuk penelitian selanjutnya tentang Algoritma CART, dapat
dikembangkan pada Probabilistic Fuzzy pada CART seperti yang telah diujikan pada Algoritma Decision Tree lainnya;
BAB II
LANDASAN TEORI
2.1. Data
Data adalah bentuk jamak dari datum. Data merupakan keterangan-keterangan tentang suatu hal, dapat berupa sesuatu yang diketahui atau dianggap. Jadi, data dapat diartikan sebagai sesuatu yang diketahui atau yang dianggap atau anggapan. Data juga merupakan sejumlah informasi yang dapat memberikan gambaran tentang suatu keadaan, atau masalah baik yang berbentuk angka-angka maupun yang berbentuk kategori atau keterangan (Supardi, 2013).
Sesuai dengan macam atau jenis variabel, maka data atau hasil pencatatannya juga mempunyai jenis sebanyak variabel. Data dapat dibagi dalam kelompok tertentu berdasarkan kriteria yang menyertainya, misalnya menurut susunan, sifat, waktu pengumpulan, sumber pengambilan dan skala pengukurannya (Supardi, 2013).
a. Pembagian Data Menurut Susunannya 1) Data Acak atau Data Tunggal
Data acak atau data tunggal adalah data yang belum tersusun atau dikelompokkan kedalam kelas-kelas interval.
2) Data Berkelompok
b. Pembagian Data Menurut Sifatnya 1) Data Kualitatif
Data kualitatif adalah data yang tidak berbentuk bilangan. Data kualitatif berbentuk pernyataan verbal, simbol, atau gambar.
Contoh data kualitatif adalah data gender, data golongan darah, data tempat tinggal atau data jenis pekerjaan. Agar dapat dilakukan proses pada data kualitatif atau non metric, data tersebut harus diubah ke dalam bentuk angka, proses ini dinamakan kategorisasi. Data kualitatif dibedakan menjadi dua jenis, yaitu data nominal dan data ordinal.
2) Data Kuantitatif
Data kuantitatif adalah data yang berbentuk bilangan, atau data kualitatif yang diangkakan.
Data kuantitatif dapat disebut sebagai data berupa angka dalam arti sebenarnya. Jadi, berbagai jenis operasi matematika dapat dilakukan pada data kuantitatif. Data kuantitatif merupakan data yang didapat dengan jalan mengukur sehingga bisa mempunyai nilai desimal. Contoh data kuantitatif adalah tinggi badan, usia, penjualan barang, dan sebagainya. Sebagai contoh, tinggi badan seseorang bisa bernilai 165 cm atau 165.5 cm. Seperti pada jenis data kualitatif, jenis data kuantitatif juga terbagi menjadi dua, yaitu data interval dan data rasio.
Data berkala adalah data yang terkumpul dari waktu ke waktu untuk memberikan gambaran perkembangan suatu kegiatan.
2) Data Cross Section
Data cross section adalah data yang terkumpul pada suatu waktu tertentu untuk memberikan gambaran perkembangan keadaan atau kegiatan pada waktu itu.
d. Pembagian Data Menurut Sumber Pengambilannya 1) Data Primer
Data primer adalah data yang diperoleh atau dikumpulkan oleh orang yang melakukan penelitian atau yang bersangkutan yang melakukannya. Data primer disebut juga data asli atau data baru.
2) Data Sekunder
Data sekunder adalah data yang diperoleh atau dikumpulkan dari sumber-sumber yang telah ada. Data itu biasanya diperoleh dari perpustakaan atau dari laporan-laporan/dokumen peneliti yang terdahulu. Data sekunder disebut juga data tersedia.
e. Pembagian Data Menurut Skala Pengukurannya 1) Data Nominal
lainnya dan tidak bisa diurutkan/dibandingkan. Data ini memiliki ciri yaitu kategori data bersifat saling lepas dan kategori data tidak disusun secara logis.
2) Data Ordinal
Data ordinal adalah data yang penomoran objek atau kategori disusun menurut besarnya, yaitu dari tingkat terendah ke tingkat tertinggi atau sebaliknya dengan jarak/rentang yang tidak harus sama. Data ini memiliki ciri seperti ciri data nominal ditambah satu ciri lagi, yaitu kategori data dapat disusun/diurutkan berdasarkan urutan logis dan sesuai dengan besarnya karakteristik yang dimiliki.
3) Data Interval
Data interval adalah data dengan objek/kategori yang dapat dibedakan antara data satu dengan lainnya, dapat diurutkan berdasarkan suatu atribut dan memiliki jarak yang memberikan informasi tentang interval antara tiap objek/kategori sama. Besarnya interval dapat ditambah atau dikurangi. Data ini memiliki ciri sama dengan data ordinal ditambah satu ciri lagi, yaitu urutan kategori data mempunyai jarak yang sama.
4) Data Rasio
2.2. Data Mining
Menurut Han & Kamber (2006), data mining adalah kegiatan yang meliputi pengumpulan dan pemakaian data historis yang menemukan keteraturan, pola dan hubungan dalam set data berukuran besar. Maksud dari pengertian ini yaitu proses pencarian informasi yang tidak diketahui sebelumnya dari sekumpulan data besar. Karakteristik Data mining sebagai berikut (Kusrini & Luthfi, 2009) :
a) Data mining berhubungan dengan penemuan sesuatu yang tersembunyi dan pola data tertentu yang tidak diketahui sebelumnya.
b) Data mining biasa menggunakan data yang sangat besar. Biasanya data yang besar digunakan untuk membuat hasil lebih dipercaya.
c) Data mining berguna untuk membuat keputusan yang kritis, terutama dalam strategi.
Secara umum ada dua jenis metode pada data mining (Kusrini & Luthfi, 2009), yaitu:
a) Metode Prediktive
Proses untuk menemukan pola dari data yang menggunakan beberapa variabel untuk memprediksi variabel lain yang tidak diketahui jenis atau nilainya. Teknik yang termasuk dalam predikative mining antara lain klasifikasi, regresi, dan deviasi.
Proses untuk menemukan suatu karakteristik penting dari data dalam suatu basis data. Teknik data mining yang termasuk dalam descriptive mining adalah clustering, association, dan secuential mining.
2.3. Klasifikasi Data
Klasifikasi data adalah suatu proses yang menemukan properti-properti yang sama pada sebuah himpunan obyek di dalam sebuah basis data, dan mengklasifikasikannya ke dalam kelas-kelas yang berbeda menurut model klasifikasi yang ditetapkan. Tujuan dari klasifikasi adalah untuk menemukan model dari training set yang membedakan atribut ke dalam kategori atau kelas yang sesuai, model tersebut kemudian digunakan untuk mengklasifikasikan atribut yang kelasnya belum diketahui sebelumnya (Zaki & Meira, 2014).
nominal, sedangkan regresi digunakan untuk memprediksi nilai-nilai yang kontinyu. Untuk selanjutnya penggunaan istilah prediction untuk memprediksi kelas yang berlabel disebut classification, dan penggunaan istilah prediksi untuk memprediksi nilai-nilai yang kontinu sebagai prediction (Zaki & Meira, 2014).
a) Model Klasifikasi
Data input untuk klasifikasi adalah koleksi dari record. Setiap record dikenal sebagai instance atau contoh, yang ditentukan oleh sebuah tuple (x,y), dimana x adalah himpunan atribut dan y adalah atribut tertentu, yang dinyatakan sebagai label kelas (juga dikenal sebagai kategori atau atribut target). Klasifikasi adalah tugas pembelajaran sebuah fungsi target f yang memetakan setiap himpunan atribut x ke salah satu label kelas y yang telah didefinisikan sebelumnya. Fungsi target juga dikenal secara informal sebagai model klasifikasi.
b) Pemodelan Deskriptif
Model klasifikasi dapat bertindak sebagai alat penjelas untuk membedakan objek-objek dari kelas-kelas yang berbeda. Sebagai contoh untuk para ahli Biologi, model deskriptif yang meringkas data.
2.4. Teori Graf
noktah, bulatan, atau titik, sedangkan hubungan antara objek dinyatakan dengan garis (Didit Budi Nugroho, 2008).
Secara formal, Graf G didefinisikan sebagai pasangan himpunan (V,E), yang dalam hal ini:
o V = himpunan tidak-kosong dari simpul-simpul (vertices atau node) = { v1 , v2 , ... , vn }
o E = himpunan sisi (edges atau arcs) yang menghubungkan sepasang simpul = {e1 , e2 , ... , en}
atau dapat ditulis singkat notasi G = (V, E).
Definisi diatas menyatakan bahwa V tidak boleh kosong, sedangkan E boleh kosong. Jadi, sebuah graf dimungkinkan tidak mempunyai sisi satu buah pun, tetapi simpulnya harus ada, minimal satu. Graf yang hanya mempunyai satu buah simpul tanpa sebuah sisi pun dinamakan graf trivial. Sedangkan garis yang hanya berhubungan dengan satu simpul disebut loop (Didit Budi Nugroho, 2008). 2.5. Struktur Pohon
a) Misalkan G merupakan suatu graf dengan n buah simpul dan tepat n – 1 buah sisi. Jika G tidak mempunyai sirkuit maka G merupakan pohon. b) Suatu pohon dengan n buah simpul mempunyai n – 1 buah sisi.
c) Setiap pasang simpul di dalam suatu pohon terhubung dengan lintasan tunggal.
d) Misalkan G adalah graf sederhana dengan jumlah simpul n, jika G tidak mengandung sirkuit maka penambahan satu sisi pada graf hanya akan membuat satu sirkuit.
2.5.1 Pohon Berakar
Pada suatu pohon, yang sisi-sisinya diberi arah sehingga menyerupai graf berarah, maka simpul yang terhubung dengan semua simpul pada pohon tersebut dinamakan akar. Suatu pohon yang satu buah simpulnya diperlakukan sebagai akar maka pohon tersebut dinamakan pohon berakar (rooted tree). Simpul yang berlaku sebagai akar mempunyai derajat masuk sama dengan nol. Sementara itu, simpul yang lain pada pohon itu memiliki derajat masuk sama dengan satu. Pada suatu pohon berakar, Simpul yang memiliki derajat keluar sama dengan nol dinamakan daun. Pada Gambar 1 dibawah, a merupakan akar, c, d, f, g, h, i, dan j merupakan daun (Adiwijaya, 2014).
2.5.2 Terminologi Pohon Berakar
Gambar 2. Terminologi Pohon Berakar
a. Anak (child atau children) dan Orangtua (parent) b, c, dan d adalah anak-anak simpul a, a adalah orangtua dari anak-anak itu
b. Lintasan (path). Lintasan dari a ke h adalah a, b, e, h. dengan pnjang lintasannya adalah 3. f adalah saudara kandung e, tetapi, g bukan saudara kandung e, karena orangtua mereka berbeda.
c. Subtree
Gambar 3. Subtree Pohon Berakar d. Derajat (degree)
Derajat sebuah simpul adalah jumlah anak pada simpul tersebut. Contohnya :
o Simpul yang berderajat 2 adalah simpul b dan k. o Simpul yang berderajat 3 adalah simpul a dan e.
Jadi, derajat yang dimaksudkan di sini adalah derajat-keluar.
Derajat maksimum dari semua simpul merupakan derajat pohon itu sendiri. Pohon di atas berderajat 3
e. Daun (leaf)
Simpul yang berderajat nol (atau tidak mempunyai anak) disebut daun. Simpul h, i, j, f, c, l, dan m adalah daun.
f. Simpul Dalam (internal nodes)
Simpul yang mempunyai anak disebut simpul dalam. Simpul b, d, e, g, dan k adalah simpul dalam.
g. Aras (level) atau Tingkat
Gambar 4. Level dalam Pohon Berakar h. Tinggi (height) atau Kedalaman (depth)
Aras maksimum dari suatu pohon disebut tinggi atau kedalaman pohon tersebut. Pohon di atas mempunyai tinggi 4.
disebut pohon n-ary. Jika n = 2, pohonnya disebut pohon biner (binary tree) (Adiwijaya, 2014).
2.5.3 Pohon Keputusan (Decision Tree)
Pohon keputusan adalah model prediksi menggunakan struktur pohon atau struktur berhirarki. Decision tree merupakan metode klasifikasi yang paling popular digunakan. Selain karena pembangunannya relatif cepat, hasil dari model yang dibangun mudah untuk dipahami. Pada decision tree terdapat 3 jenis node (Munir, 2009), yaitu :
a. Root Node, merupakan node paling atas, pada node ini tidak ada input dan bisa tidak mempunyai output atau mempunyai output lebih dari satu. b. Internal Node , merupakan node percabangan, pada node ini hanya
terdapat satu input dan mempunyai output minimal dua.
c. Leaf node atau terminal node , merupakan node akhir, pada node ini hanya terdapat satu input dan tidak mempunyai output.
2.6. Probabilitas
Bila suatu percobaan mempunyai N(S) hasil percobaan yang berbeda dan masing-masing mempunyai kemungkinan yang sama untuk terjadi, dan bila tepat n(A) diantara hasil percobaan itu menyusun kejadian A, maka peluang kejadian A adalah
Menurut Walpole dan Myers (1986) kaidah-kaidah probabilitas ada beberapa macam, antara lain :
1. Kaidah penjumlahan
a. Kaidah penjumlahan dua kejadian yang saling terpisah.
b. Kaidah penjumlahan dua kejadian yang tidak saling bebas.
c. Kaidah penjumlahan n buah kejadian yang saling terpisah. Bila 1, 2, ⋯ , kejadian-kejadian yang saling terpisah, maka
d. Bila A dan ′ adalah dua kejadian yang satu merupakan komplemen lainnya maka
2. Kaidah peluang bersyarat
3. Kaidah Penggandaan
a. Kaidah penggandaan khusus
Bila kejadian A dan B saling bebas maka
b. Jika kejadian-kejadian 1, 2, 3, ⋯ , saling bebas, maka
4. Kaidah Bayes
Jika kejadian-kejadian 1, 2, ⋯ , merupakan partisi dari ruang sampel
S dengan ( ) ≠ 0 untuk = 1, 2, ⋯ , maka untuk sembarang kejadian A yang bersifat ( ) ≠ 0 maka untuk � = 1, 2, ⋯ ,
∑
∑
2.7. Algoritma CART
2.7.1. Partisi Berulang Biner (Binary Recursive Partitioning)
Teknik atau proses kerja dari CART dalam membuat sebuah pohon klasifikasi dikenal dengan istilah Binary Recursive Partitioning. Proses disebut binary karena setiap parent node akan selalu mengalami pemecahan ke dalam tepat dua child node. Sedangkan recursive berarti bahwa proses pemecahan tersebut akan diulang kembali pada setiap child nodes hasil pemecahan terdahulu, sehingga child nodes tersebut sekarang menjadi parent nodes. Proses pemecahan ini akan terus dilakukan sampai tidak ada kesempatan lagi untuk melakukan pemecahan berikutnya. Dan istilah partitioning mengartikan bahwa learning sample yang dimiliki dipecah ke dalam bagian-bagian atau partisi-partisi yang lebih kecil (Damayanti, 2011).
Kriteria pemecahan didasarkan pada nilai-nilai dari variabel independen yang dimiliki. Misalkan dimiliki variabel dependen yang bertipe kategorik dan variabel-variabel independen 1, 2, ⋯ , � . Proses binary recursive partitioning
klasifikasi yang paling besar atau maksimal (proses splitting tidak bisa dilakukan lagi) (Damayanti, 2011).
2.7.2. Langkah Kerja CART
Menurut Lewis (2000) pada dasarnya dalam membuat sebuah pohon klasifikasi, CART bekerja dalam empat langkah utama. Langkah pertama adalah tree building process yaitu proses pembentukan dan pembuatan pohon klasifikasi. Terdiri dari proses splitting nodes yaitu proses pemecahan parent nodes menjadi dua buah child node melalui aturan pemecahan tertentu dan dilakukan secara berulang-ulang serta proses pelabelan kelas yaitu proses mengidentifikasi node-node yang terbentuk pada suatu kelas tertentu melalui aturan pengidentifikasian. Langkah kedua adalah proses penghentian pembuatan atau pembentukan pohon klasifikasi (stopping the trees building process). Pada tahap ini pohon terakhir atau maximal tree (��� ) telah terbentuk. Langkah ketiga adalah pruning yaitu proses pemangkasan atau pemotongan ��� menjadi pohon yang lebih kecil (T). Sehingga proses tersebut menghasilkan optimal tree atau pohon klasifikasi yang optimal.
a. Proses Pemecahan Node
Proses pemecahan pada masing-masing parent node didasarkan pada goodness of split criterion (kriteria pemecahan terbaik). Kriteria pemecahan terbaik ini dibentuk berdasarkan fungsi impurity (fungsi keragaman). Fungsi impurity adalah sebuah fungsi � yang didefinisikan dengan ⋯ dengan ∑ , dimana
Impurity measure (ukuran impurity) dari beberapa node t sebagai berikut (Breiman, et al., 1993) :
� ⋯
maka Gini Diversity Index (Indeks Keragaman Gini) adalah :
∑
Dalam sebuah node t, andaikan terdapat n kelas (1, 2 ⋯ , ). Untuk n = 1 dan i adalah kelas-kelas lainnya maka (2.1) dapat dituliskan sebagai berikut :
Begitu pula untuk n = 2 dan i adalah kelas-kelas lainnya maka (2.1) dapat dituliskan :
∑
∑
Untuk j = 3 dan i adalah kelas-kelas lainnya maka (2.1) dapat dituliskan :
∑
∑
Sehingga untuk n kelas secara umum, didapatkan :
∑
Sehingga berdasarkan (2.1) Gini Diversity Index dapat dituliskan sebagai berikut (Breiman, et al., 1993) : didefinisikan decrease impurity (pengurangan keragaman) :
��
Hal ini berarti splitting (pemecahan) dilakukan untuk membuat dua buah node baru yang keragamannya lebih kecil (homogen) apabila dibandingkan dengan node awalnya (parent node). Misalkan sebuah pohon klasifikasi telah terbentuk dan memiliki sekumpulan atau himpunan terminal nodes �̃ , didefinisikan impurity node I(t), dengan
Didefinisikan pula tree impurity (�) , dengan
� ∑
̃ ∑ ̃
sehingga didapatkan hasil sebagai berikut
b. Pelabelan Kelas
Pelabelan kelas adalah proses pengidentifikasian tiap nodes pada suatu kelas tertentu. Pelabelan kelas tidak hanya diberlakukan untuk terminal nodes saja, non-terminal nodes bahkan root node mengalami proses ini. Hal ini dikarenakan setiap non-terminal nodes memiliki kesempatan untuk menjadi terminal nodes. Sehingga proses pelabelan kelas akan terus dilakukan selama proses splitting masih berlanjut (Breiman, et al., 1993).
Misalkan sebuah pohon klasifikasi telah terbentuk dan memiliki terminal nodes �̃. Class assignment rule mengidentifikasikan sebuah kelas
pelabelan kelas sebagai berikut ; apabila �� maka
(Breiman et al, 1993). c. Proses Penghentian Pemecahan
Menurut Lewis (2000), proses splitting atau pembuatan pohon klasifikasi akan berhenti apabila sudah tidak dimungkinkan lagi dilakukan proses pemecahan. Proses pemecahan akan berhenti apabila hanya tersisa satu objek saja yang ada dalam node terakhir atau semua objek yang berada di dalam sebuah node merupakan anggota kelas yang sama (homogen). Kemudian bernilai 0 atau 1. � , dan resubstitution estimate �(�) untuk nilai misclassification sama dengan 0. Node-node terakhir atau yang tidak mengalami pemecahan lagi sebagai akibat dari kondisi di atas akan menjadi terminal nodes dan diidentifikasikan pada suatu kelas tertentu sesuai dengan class assignment rule yang telah dijelaskan sebelum ini. Pohon klasifikasi yang terbentuk sebagai hasil dari proses ini dinamakan “maximal tree” (��� ).
d. Proses Pemangkasan Pohon
Pohon klasifikasi yang terbentuk dapat berukuran besar dan kompleks dalam mengambarkan struktur data. Sehingga perlu dilakukan suatu pemangkasan, yaitu suatu penilaian ukuran sebuah pohon tanpa mengorbankan kebaikan ketepatan melalui pengurangan simpul pohon sehingga dicapai penghematan gambaran. Pemangkasan dilakukan dengan memangkas bagian pohon yang kurang penting sehingga didapat pohon optimal (Breiman, et al., 1993).
Proses pemangkasan pohon klasifikasi dimulai dengan mengambil � yang merupakan right child node dan � yang merupakan left child node dari ��� yang dihasilkan dari parent node t. Jika diperoleh dua child node dan parent node yang memenuhi persamaan � � � maka hild node � dan � dipangkas. Dimana � dan
�� . Hasilnya adalah pohon �1 yang memenuhi kriteria �(�1) =
�(��� ). Proses tersebut diulang sampai tidak ada lagi pemangkasan yang mungkin terjadi.
2.8. Logika Fuzzy
makna pada ungkapan seperti "sering", "kecil" dan "tinggi". Logika fuzzy memperhitungkan bahwa dunia nyata yang kompleks dan ada ketidakpastian, semuanya tidak dapat memiliki nilai absolut dan mengikuti fungsi linear (Godil & Shamim, 2011)
Pada himpunan tegas setiap elemen dalam semestanya selalu ditentukan secara tegas apakah elemen itu merupakan anggota himpunan tersebut atau tidak. Tetapi dalam kenyataanya tidak semua himpunan terdefinisi secara tegas. Oleh karena itu perlu didefinisikan suatu himpunan Fuzzy yang bisa menyatakan kejadian tersebut. Himpunan Fuzzy memiliki dua atribut (Kusumadewi, 2002), yaitu :
a. Linguistik, yaitu penamaan suatu kelompok yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami, seperti: lambat, sedang, cepat.
b. Numeris, yaitu suatu nilai (angka) yang menunjukkan ukuran dari suatu variabel, seperti: 40, 50, 60, dan sebagainya.
Penerapan logika fuzzy dapat meningkatkan kinerja sistem kendali dengan menekan munculnya fungsi-fungsi liar pada keluaran yang disebabkan oleh fluktasi pada variabel masukan. Pendekatan logika fuzzy secara garis besar diimplementasikan dalam tiga tahapan yaitu :
1. Tahapan pengaburan (fuzzification) yakni pemetaan dari masukan tegas ke himpunan kabur.
3. Tahap penegasan (defuzzification), yakni transformasi keluaran dari nilai kabur ke nilai tegas.
2.8.1. Fungsi Keanggotaan
Fungsi keanggotaan (member function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya (sering juga disebut dengan derajat keanggotaan) yang memiliki interval 0 sampai 1. Salah satu cara yang dapat digunakan untuk mendapatkan nilai keanggotaan adalah menggunakan pendekatan fungsi (Kusumadewi & Purnomo, 2010). Ada beberapa fungsi yang bisa digunakan. Di antaranya, yaitu:
a. Representasi Linear.
Pada representasi linear, pemetaan input ke derajat keanggotannya digambarkan sebagai suatu garis lurus. Bentuk ini paling sederhana dan menjadi pilihan yang baik untuk mendekati suatu konsep yang kurang jelas. Ada dua keadaan himpunan linear, yaitu :
Representasi Linear Naik
Gambar 6. Representasi Linear Naik Fungsi keanggotaan sebagai berikut :
[ ] {
�
�
Representasi Linear Turun
Gambar 7. Representasi Linear Turun Fungsi keanggotaan sebagai berikut :
[ ] {
b. Representasi Kurva Segitiga. Kurva Segitiga pada dasarnya merupakan gabungan antara dua garis (linear).
Gambar 8. Representasi Kurva Segitiga Dengan fungsi keanggotaan sebagai berikut :
[ ] {
� � �
�
c. Representasi Kurva Trapesium. Kurva Trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa titik yang memiliki nilai keanggotaan 1.
Gambar 9. Representasi Kurva Trapesium Dengan fungsi keanggotaan sebagai berikut :
[ ]
{
� � �
�
d. Representasi Kurva Bahu
Gambar 10. Representasi Kurva Bahu 2.8.2. Operator Dasar Fuzzy
Ada beberapa operasi yang didefinisikan secara khusus untuk mengkombinasi dan memodifikasi himpunan Fuzzy. Nilai keanggotaan sebagai hasil dari operasi dua himpunan sering dikenal dengan nama fire strength atau α–
predikat. Ada tiga operator dasar yang diciptakan oleh Zadeh (Kusumadewi & Purnomo, 2010), yaitu:
a. Operator AND
Operator ini berhubungan dengan operasi interseksi pada himpunan. α– predikat sebagai hasil operasi dengan operator AND diperoleh dengan mengambil nilai keanggotaan terkecil antar elemen pada himpunan-himpunan yang bersangkutan.
[ ] [ ]
b. Operator NOT
[ ]
c. Operator OR
Operator ini berhubungan dengan operasi union pada himpunan. α–
predikat sebagai hasil operasi dengan operator OR diperoleh dengan mengambil nilai keanggotaan terbesar antar elemen pada himpunanhimpunan yang bersangkutan.
[ ] [ ]
2.8.3. Fungsi Implikasi
Tiap – tiap aturan (proposisi) pada basis pengetahuan Fuzzy akan berhubungan dengan suatu relasi Fuzzy. Bentuk umum dari aturan yang digunakan dalam fungsi implikasi adalah:
IF x is A THEN y is B
Proposisi yang mengikuti IF disebut sebagai anteseden, sedangkan proposisi yang mengikuti THEN disebut sebagai konsekuen. Secara umum, ada dua fungsi implikasi yang dapat digunakan, yaitu :
a. Min. Pengambilan keputusan dengan fungsi min, yaitu dengan cara mencari nilai minimum berdasarkan aturan ke-i dan dapat dinyatakan dengan :
b. Dot. Fungsi ini akan menskala output himpunan Fuzzy. 2.8. Fuzzy Inference System
melakukan penalaran dengan nalurinya (Alavi, et al., 2010). Langkah pertama dari FIS adalah menetapkan nilai keanggotaan untuk data input dan output (Alidoosti, et al., 2012).
Menurut Kusumadewi & Hartati (2010), sistem inferensi fuzzy merupakan suatu kerangka komputasi yang didasarkan pada teori himpunan fuzzy, aturan fuzzy yang berbentuk IF-THEN, dan penalaran fuzzy.
IF (x1 is A1) (x2 is A2) (x is A1) THEN y is B
dengan adalah operator (misal : OR dan AND)
Sistem inferensi fuzzy didasarkan pada konsep penalaran monoton. Pada metode penalaran secara monoton, nilai crisp pada daerah konsekuen dapat diperoleh secara langsung berdasarkan fire strength pada antesedennya. Salah satu syarat yang harus dipenuhi pada metode penalaran ini adalah himpunan fuzzy pada konsekuennya harus bersifat monoton (baik monoton naik maupun monoton turun). Salah satu inferensi fuzzy adalah Fuzzy Logic Controller.
Fuzzy Logic Controller (FLC) adalah pengendali yang mengendalikan sebuah sistem atau proses dengan menggunakan logika fuzzy sebagai cara pengambilan keputusan. Secara garis besar, terdapat empat komponen utama penyusun FLC, yaitu fuzzification, basis aturan (rule base), modul pengambil keputusan (inference engine), dan modul defuzzifikasi.
2.9.1. Komposisi Aturan
a) Metode Max (Maximum). Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy, dan mengaplikasikannya ke output dengan menggunakan operator OR (union). Jika semua proposisi telah dievaluasi, maka output akan berisi suatu himpunan fuzzy yang merefleksikan kontribusi dari tiap-tiap proposisi. Secara umum dapat dituliskan :
[ ] �� [ ] [ ]
dengan :
[ ] = nilai keanggotaan solusi fuzzy sampai aturan ke – i. [ ] = nilai keanggotaan konsekuen fuzzy aturan ke – i.
b) Metode Additive (Sum). Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan boundedsum terhadap semua output daerah fuzzy. Secara umum dapat dituliskan :
[ ] � [ ] [ ]
dengan :
[ ] = nilai keanggotaan solusi fuzzy sampai aturan ke – i. [ ] = nilai keanggotaan konsekuen fuzzy aturan ke – i.
c) Metode OR (Probor). Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara melakukan product terhadap semua output daerah fuzzy. Secara umum dituliskan :
[ ] [ ] [ ] [ ] [ ]
[ ] = nilai keanggotaan solusi fuzzy sampai aturan ke – i. [ ] = nilai keanggotaan konsekuen fuzzy aturan ke – i.
2.9.2. Metode Mamdani
Salah satu metode FLC yang dapat digunakan untuk pengambilan keputusan adalah metode Mamdani. Metode Mamdani sering juga dikenal dengan nama metode Max-Min. metode ini diperkenalkan oleh Ebrahim Mamdani pada tahun 1975 (Kusumadewi, 2002). Untuk medapatkan output diperlukan beberapa tahapan, antara lain:
a) Pembentukan himpunan fuzzy. Pada metode Mamdani, baik variabel input maupun variabel output dibagi menjadi satu atau lebih himpunan fuzzy. b) Aplikasi fungsi implikasi (aturan). Fungsi implikasi yang digunakan
adalah min.
c) Komposisi aturan. Metode yang digunakan dalam melakukan inferensi sistem fuzzy pada Mamdani adalah max.
2.9.3. Defuzzifikasi
Ada beberapa metode defuzzifikasi pada komposisi aturan Mamdani (Kusumadewi, 2002), antara lain:
b) Metode Bisektor. Pada metode bisektor solusi crisp diperoleh dengan cara mengambil nilai pada domain yang memiliki nilai keanggotaan separo dari jumlah total nilai keanggotaan pada daerah fuzzy. Dapat dituliskan :
zp sedemikian hingga ∫ ∫
c) Metode Mean of Maximum (MOM). Pada metode mean of maximum solusi crisp diperoleh dengan cara mengambil nilai rata-rata domain yang memiliki nilai keanggotaan maksimum.
d) Metode Largest of Maximum (LOM). Pada metode largest of maximumsolusi crisp diperoleh dengan cara mengambil nilai terbesar dari domain yang memiliki nilai keanggotaan maksimum.
e) Metode Smallest of Maximum (SOM). Pada metode smallest of maximumsolusi crisp diperoleh dengan cara mengambil nilai terkecil dari domain yang memiliki nilai keanggotaan maksimum.
2.10. Akurasi Klasifikasi
positif yang diberi label dengan tidak tepat. Istilah-istilah ini berguna ketika menganalisis kemampuan classifier dan diringkas dalam tabel berikut.
Tabel 1. Confusion Matrix
Observasi Prediksi
J1 J2
J1 truepositive falsepositive
J2 falsenegative truenegative
Misalkan terdapat confusion matrix 2×2 seperti pada tabel di atas, maka rumus yang akan digunakan untuk menghitung akurasi adalah sebagai berikut :
� �
� �
Rumus di atas dapat juga didefenisikan seperti pada rumus berikut :
1.1. Latar Belakang
Data mining adalah serangkaian proses untuk menggali nilai tambah berupa informasi yang selama ini tidak diketahui secara manual dari suatu basis data. Informasi yang dihasilkan diperoleh dengan cara mengekstraksi dan mengenali pola yang penting atau menarik dari data yang terdapat dalam basis data. Data mining juga merupakan proses semi otomatik yang memuat teknik statistika dan matematika di dalamnya. Teknik-teknik data mining yang populer ada tiga, yaitu association rules, classification dan clustering.
dan mudah dalam penggunaannya. Dalam proses klasifikasi, metode klasifikasi nonparametrik menggunakan setiap data sebagai dasar penunjukan kelas.
Pada perkembangan terbaru, teknik-teknik yang terdapat di dalam data mining mulai banyak digunakan. Khususnya teknik decision tree telah menjadi teknik yang populer karena pohon yang dihasilkan mudah diinterpretasikan dan divisualisasikan (Chye, 2004). Namun, permasalahan dalam mengklasifikasikan data adalah terjadinya salah klasifikasi, misalnya dalam pengelompokkan data berdasarkan karakteristiknya, terkandung unsur ketidakpastian data terkait dengan pemikiran dan persepsi manusia untuk membaginya.
Ide himpunan fuzzy (fuzzy set) di awali dari matematika dan teori sistem dari L.A Zadeh, pada tahun 1965. Himpunan fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi karakteristik sehingga fungsi tersebut akan mencakup bilangan real pada interval [0,1]. Nilai keanggotaannya menunjukkan bahwa suatu item tidak hanya bernilai benar atau salah. Nilai 0 menunjukkan salah, nilai 1 menunjukkan benar, dan masih ada nilai-nilai yang terletak antara benar dan salah (Sudradjat, 2008). Metode logika fuzzy mempunyai tiga tahapan proses yaitu fuzzifikasi, inferensi dan defuzzifikasi. Dalam teori logika fuzzy sebuah nilai bisa bernilai benar dan salah secara bersamaan tapi berapa besar kebenaran dan kesalahan suatu nilai tergantung dari berapa besar bobot keanggotaan yang dimilikinya
menunjukkan bahwa penggunaan fuzzy pada algoritma tersebut mampu meningkatkan akurasi klasifikasi. Jay Fowdar, Zuhair Bandar, Keeley Crockett dari Departement of Computing and Mathematics Manchester Metropolitan University melakukan penelitian yang berjudul Inducing Fuzzy Decision Trees in Non-Deterministic Domains using CHAID (2002), penelitian ini memperkenalkan bahwa fuzzy dapat diinduksikan ke dalam analisis decision tree. Algoritma induksi fuzzy dapat digunakan untuk melunakkan (soften) batasan keputusan yang tajam (sharp) pada algoritma pohon keputusan (decision tree) tradisional. Muhammad Muhajir (2014) juga telah melakukan penelitian menggunakan fuzzy CHAID, yang memperlihatkan bahwa CHAID yang telah diinduksikan dengan fuzzy memiliki tingkat akurasi yang lebih baik daripada CHAID itu sendiri.
Berdasarkan uraian di atas, peneliti tertarik melakukan penelitian dan selanjutnya melihat hasil akurasi induksi Fuzzy pada Algoritma CART. Sehingga penelitian ini penulis beri judul “Studi Algoritma CART dengan Induksi Fuzzy
dalam Mengklasifikasikan Data”.
1.2. Rumusan Masalah
Perumusan masalah dalam penelitian ini adalah bagaimana hasil akurasi pada Algoritma CART yang telah menggunakan induksi Fuzzy dalam mengklasifikasikan data.
1.3. Batasan Masalah
Penelitian ini dibatasi pada fuzzy yang diinduksikan ke dalam CART merupakan Fuzzy Metode Mamdani.
1.4. Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk mengetahui hasil akurasi dari Algoritma CART yang telah menggunakan induksi Fuzzy dalam mengurangi ketajaman perbedaan antar variabelnya.
1.5. Kontribusi Penelitian
Hasil penelitian ini diharapkan dapat memberikan manfaat, yaitu:
a. Dapat menambah wawasan peneliti dan pembaca tentang Algoritma CART. b. Dapat menambah wawasan peneliti dan pembaca tentang induksi Fuzzy pada
Algoritma CART.
d. Dapat menambah referensi bagi pembaca dalam penelitian sejenis di masa yang akan datang.
1.6. Tinjauan Pustaka
CART (Classification and Regression Trees) adalah salah satu metode atau algoritma dari salah satu teknik eksplorasi data decision tree. Metode ini dikembangkan oleh Leo Breiman, Jerome H. Friedman, Richard A. Olshen dan Charles J. Stone sekitar tahun 1980-an. CART merupakan metodologi statistik non-parametrik yang dikembangkan untuk topik analisis klasifikasi, baik untuk variabel respon kategorik maupun kontinu. CART menghasilkan suatu pohon klasifikasi jika variabel responnya kategorik, dan menghasilkan pohon regresi jika variabel responnya kontinu.
Menurut Ari Wibowo (2013), langkah-langkah penerapan metode CART terdiri atas :
a. Pembentukan pohon klasifikasi, yaitu pemilihan pemilah (classifier), penentuan simpul terminal, dan penandaan label kelas.
b. Pemangkasan pohon klasifikasi, yaitu dengan jalan memangkas bagian tree yang kurang penting sehingga didapatkan pohon optimal.
c. Penentuan pohon klasifikasi optimal.
Langkah-langkah pembentukan pohon klasifikasi pada CART didasarkan pada indeks Gini, dengan perhitungan sebagai berikut :
∑
dimana : i(t) = Indeks Gini
Logika fuzzy adalah bagian atau salah satu metode dalam kecerdasan buatan (Artificial Intelligence). Dalam logika konvensional nilai kebenaran mempunyai kondisi yang pasti yaitu benar atau salah (true or false), dengan tidak ada kondisi di antara. Prinsip ini dikemukakan oleh Aristoteles sekitar 2000 tahun yang lalu sebagai hukum Excluded Middle dan hukum ini telah mendominasi pemikiran logika sampai saat ini (Zhang, 2009).
Proses fuzzy logic melibatkan fungsi keanggotaan, operator logika fuzzy, dan aturan jika-maka (if-then rule). Dalam membangun sistem yang berbasis pada aturan fuzzy maka akan digunakan variabel linguistik. Variabel linguistik adalah suatu interval numerik dan mempunyai nilai-nilai linguistik, yang semantiknya didefinisikan oleh fungsi keanggotaannya (Slamet Riyadhi, 2014).
Metode Mamdani sering juga dikenal dengan nama Metode Max-Min. Metode ini diperkenalkan oleh Ebrahim Mamdani pada tahun 1975. Untuk mendapatkan output, diperlukan 4 tahapan yaitu sebagai berikut (Sri Kusumadewi, 2010) :
a. Pembentukan himpunan fuzzy. Variabel input maupun variabel output dibagi menjadi satu atau lebih himpunan fuzzy.
b. Aplikasi fungsi implikasi (aturan). Fungsi implikasi yang digunakan adalah min.
c. Komposisi aturan. Metode yang digunakan dalam melakukan inferensi sistem fuzzy pada penelitian ini, yaitu max.
Keakurasian fuzzy inference system Mamdani dihitung menggunakan persamaan berikut :
Akurasi=(Jumlah data sesuai)/(Jumlah data) x 100% 1.7. Metodologi Penelitian
1.7.1. Jenis dan Data Penelitian
Penelitian ini termasuk jenis studi literatur dengan mencari referensi teori yang relevan dengan permasalahan yang ditemukan. Referensi teori yang diperoleh dengan jalan penelitian studi literatur dijadikan sebagai fondasi dasar dan alat utama dalam uji coba pengolahan data contoh. Sumber literatur diperoleh dari buku, jurnal, buku dokumentasi, artikel internet dan pustaka yang terkait dengan tema penelitian, yaitu analisis mengenai Fuzzy dan CART. Jenis data yang digunakan sebagai contoh adalah data sekunder, yaitu data yang diperoleh dari data pasien kanker Wisconsin University.
1.7.2. Teknik Penelitian
a. Studi literatur, yaitu mencari dan menghimpun data-data atau sumber-sumber informasi yang berhubungan dengan topik CART dan Fuzzy.
b. Uji coba pengolahan data contoh dengan langkah-langkah berikut :
1) Editing, yaitu mengelompokkan variabel pada database tersebut menjadi variabel kategorik;
2) Membagi data menjadi 2 bagian, yaitu 80% data learning dan 20% data testing;
4) Menentukan rules untuk induksi Fuzzy sesuai dengan output algoritma CART;
5) Menentukan variabel fuzzy; 6) Aplikasi fungsi implikasi; 7) Defuzzifikasi;
8) Uji Akurasi klasifikasi dengan data testing.
STUDI ALGORITMA CART DENGAN INDUKSI FUZZY
DALAM MENGKLASIFIKASIKAN DATA
ABSTRAK
Metode pohon keputusan digunakan untuk mengekstraksi informasi tentang himpunan data dalam masalah klasifikasi, meskipun tidak dapat menangani ketidakpastian yang tertanam dalam data terkait dengan pemikiran dan persepsi manusia. Makalah ini menjelaskan pengembangan algoritma induksi pohon yang meningkatkan akurasi klasifikasi induksi pohon keputusan. Penelitian ini dirancang dengan mengintegrasikan prinsip Algoritma CART (Classification and Regressin Tree) dan konsep himpunan Fuzzy, memungkinkan model untuk menangani data yang tidak pasti dan tidak tepat, serta untuk melunakkan batas keputusan tajam yang melekat dalam algoritma pohon keputusan tegas. CART adalah algoritma pohon keputusan dengan fitur utama pengujian Indeks Gini (indeks keragaman) pada setiap tingkat, yang mengarah ke pembentukan pohon dengan proses pemangkasan untuk menemukan pohon yang optimal. Penerapan logika fuzzy untuk pohon keputusan CART dapat memperlihatkan pengetahuan klasifikasi yang lebih alami dan sejalan dengan pemikiran manusia, serta lebih kuat ketika menangani informasi yang tidak tepat. Hasil penerapan logika fuzzy untuk pohon keputusan CART disajikan dalam makalah ini. Hasil penelitian ini diperoleh dari database nyata, dan menunjukkan bahwa algoritma inferensi fuzzy baru meningkatkan akurasi lebih dari pohon CART tegas.
STUDY OF CART ALGORITHM WITH FUZZY INDUCTION
IN CLASSIFYING DATA
ABSTRACT
Decision tree methods used for extracting information about dataset in classification problems, although unable to deal with uncertainties embedded within the data associated with human thinking and perception. This paper describes the development of a tree induction algorithm which improves the classification accuracy of decision tree induction. The research is designed by integrating the principles of CART (Classification and Regression Tree) algorithm and the fuzzy set-theoretic concepts, enabling the model to handle uncertain and imprecise data, and in order to soften the sharp decision boundaries which are inherent in crisp decision tree algorithms. CART is a decision tree algorithm with the main feature of Gini Index testing (homogenity index) at each level, leading to the production of trees with pruning process to find the optimal tree. The application of fuzzy logic to CART decision trees can represent classification knowledge more naturally and inline with human thinking, and are more robust when it comes to handling imprecise information. The results of applying fuzzy logic to CART decision trees are presented in this paper. These have been obtained from sets of real data, and show that the new fuzzy inference algorithm improves the accuracy over crisp CART trees.
SKRIPSI
OKTAVIYANI DASWATI 1308230003
PROGRAM STUDI S-1 EKSTENSI MATEMATIKA DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan kepada tim penguji skripsi Departemen Matematika sebagai salah satu persyaratan guna memperoleh gelar Sarjana Sains
OKTAVIYANI DASWATI 1308230003
PROGRAM STUDI S-1 EKSTENSI MATEMATIKA DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Studi Algoritma CART dengan Induksi Fuzzy dalam Mengklasifikasikan Data
Kategori : Skripsi
Nama : Oktaviyani Daswati
Nomor Induk Mahasiswa : 130823003
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
(FMIPA) Universitas Sumatera Utara
Disetujui di
Medan, Agustus 2016
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Pangarapen Bangun, M.Si Drs. Partano Siagian, M.Si NIP. 19530303 198303 1 002 NIP.19511227 198003 1 001
Diketahui / Disetujui oleh
Departemen Matematika FMIPA USU Ketua
Prof. Dr. Tulus, M.Si
PERNYATAAN
STUDI ALGORITMA CART DENGAN INDUKSI FUZZY DALAM MENGKLASIFIKASIKAN DATA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan, data dan ringkasan yang masing-masing disebut sumbernya.
Medan, Agustus 2016
PENGHARGAAN
Puji dan syukur ke hadirat Allah SWT yang senantiasa memberikan rahmat dan karunia-Nya, sehingga akhirnya penulis dapat menyelesaikan penulisan skripsi yang berjudul “Studi Algoritma CART dengan induksi Fuzzy dalam Mengklasifikasikan Data” ini. Salawat dan salam selalu terarah kepada junjungan kita Nabi besar Muhammad SAW.
Dengan rasa hormat, penulis mengucapkan terima kasih kepada Bapak Partano Siagian , M.Sc dan Bapak Pangarapen Bangun , M.Si, selaku pembimbing yang telah meluangkan waktu dan menyumbangkan pikiran, saran, nasehat, serta arahan sehingga penulis dapat menyelesaikan skripsi ini. Terimakasih juga kepada Bapak Prof. Dr. Tulus, M.Si dan Ibu Dr. Mardiningsih, M.Si selaku Ketua Departemen Matematika dan Sekretaris Departemen Matematika FMIPA USU, Dekan dan Pembantu Dekan FMIPA USU, seluruh dosen dan civitas akademika Matematika FMIPA USU.
Terima kasih kepada kedua orangtua yang sangat luar biasa, terima kasih buat segala dukungan doa, motivasi, harapan serta kesabarannya. Terima kasih juga buat dukungan kakak satu-satunya, yang tak lupa mengingatkan agar tetap semangat dan tak pernah menyerah. Tak lupa pula untuk sahabat yang bukan kerabat, Rahmyuti, terima kasih untuk dukungannya selalu.
Selanjutnya terima kasih untuk teman seperjuangan di Ekstensi Matematika 2013 dan 2014, terima kasih untuk semua waktu dan dukungannya. Akhir kata, atas perhatian pembaca yang budiman penulis ucapkan terima kasih.
Penulis