Algoritma untuk Dekomposisi Digraph Berbobot dengan Aplikasi Analisis Sikus Kehidupan pada Biota

BIOTA

SKRIPSI

SRI RAFIQOH 060803003

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2010

BIOTA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

SRI RAFIQOH 060803003

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2010

PERSETUJUAN

Judul : ALGORITMA UNTUK DEKOMPOSISI DI-GRAPH BERBOBOT DENGAN APLIKASI ANALISIS SIKLUS KEHIDUPAN PADA BIOTA Kategori : SKRIPSI

Nama : SRI RAFIQOH

Nomor Induk Mahasiswa : 060803003

Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, September 2010

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dr. Saib Suwilo, MSc. Dra. Mardiningsih, MSi NIP. 19640109 198803 1 004 NIP.19630405 198811 2 001

Diketahui oleh

Departemen Matematika FMIPA USU Ketua,

Dr. Saib Suwilo, MSc NIP. 19640109 198803 1 004

PERNYATAAN

ALGORITMA UNTUK DEKOMPOSISI DIGRAPH BERBOBOT DENGAN APLIKASI ANALISIS SIKLUS KEHIDUPAN PADA BIOTA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, September 2010

SRI RAFIQOH 060803003

PENGHARGAAN

Dengan puji dan syukur kepada Allah SWT, karena berkat dan rahmatNya sehingga penulis dapat menyelesaikan skripsi yang berjudul” Algoritma untuk Dekomposisi Digraph Berbobot dengan Aplikasi Analisis Sikus Kehidu-pan pada Biota”ini dengan baik.

Dalam menyelesaikan skripsi ini penulis banyak menerima bantuan dan ma-sukan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terima kasih sebesar-besarnya kepada :

1. Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara. Bapak Dr. Saib Suwilo, M.Sc, dan Bapak Henry Rani S, M.Si selaku Ketua dan Sekretaris Departe-men Matematika di FMIPA USU Medan.

2. Ibu Dra. Mardiningsih, M.Si selaku dosen pembimbing I dan Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing II yang telah memberi dukungan moral, motivasi dan ilmu pengetahuan bagi penulis dalam menyelesaikan penelitian ini.

3. Seluruh Staf Pengajar Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

4. Bapak M. Buyung Akhir dan Ibunda Rohimah tercinta serta Uwakku Hj. Aziah dan Kakakku Hj. Purwati yang selalu memberikan dukungan mo-ril dan materiel maupun doa yang tiada hentinya kepada penulis, serta keponakan-keponakanku tersayang Mutiara Qisthina Hanif dan Nindita Qisthi-na Hanif yang selalu mendoakan penulis dalam penyelesaian skripsi ini.

Tak lupa, penulis juga mengucapkan terima kasih kepada sahabat-sahabatku tersayang yang selalu ada dalam setiap suasana baik suka dan duka Aghni Syah-marani dan Rina Widyasari atas perhatian, dukungan, dan motivasi dalam penger-jaan skripsi ini. Terima kasih juga buat rekan-rekan dilab yaitu Bang Santri, Bang Toni, Bang Radhi, Bang Andhika dan Mizwar. Teman-teman seperjuan-ganku anak Murni’06 Nurul, Ria, dan Mandra. Serta buat anak-anak stambuk ’06, Mahater, Tria, Linda, serta rekan-rekan lainnya yang tidak dapat disebutkan satu-persatu. Juga kepada Mul Kanul Arief yang telah membantu penulis dalam proses penulisan skripsi ini, Rion Siboro, Priskilla Ginting yang selalu berbagi ceri-ta dalam proses penyelesaian skripsi ini serceri-ta adik-adik sceri-tambuk 2007, 2008, dan 2009, terima kasih atas dukungannya. Semoga Allah SWT memberikan balasan atas jasa-jasa mereka yang telah diberikan kepada penulis.

Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta saran dan kritik yang membangun dari pembaca sekalian.

Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini berguna bagi yang membutuhkan.

Medan, Agustus 2010 Penulis,

Sri Rafiqoh

ABSTRAK

Dalam ekologi, analisis siklus kehidupan dapat direpresentasikan dengan digraph. Digraph yang demikian disebut digraph siklus kehidupan yang selanjutnya digraph-digraph tersebut dapat diubah ke dalam matriks-matriks yang berhubungan yaitu matriks elastisitas dan matriks sensitivitas. Dalam penelitian ini digraph yang digunakan adalah digraph berbobot. Partisi suatu matriks elastisitas yang di-gunakan untuk menghitung kontribusi terpisah dari suatu siklus hidup ke laju pertumbuhan populasi ekuivalen dengan dekomposisi suatu digraph siklus kehidu-pan pada populasi. Penelitian ini akan memformulasikan suatu metode dalam proses dekomposisi sehingga mampu mendekomposisikan digraph-digraph siklus hidup yang kompleks menjadi siklus kehidupan individu yang bermakna.

ALGORITHM FOR A DECOMPOSITION OF WEIGHTED DIGRAPHS WITH APPLICATIONS TO LIFE CYCLE ANALYSIS

IN BIOTA

ABSTRACT

In ecology, life cycle analysis can be represented by a digraph. Such digraph called life cycle digraph later on the digraph can be changed to the correspond matrix, sensitivity and elasticity matrix. This research used the weighted digraph. Parti-tioning of the elasticity matrix is used to quantify the separate contributions of life cycle to population growth rate, is equivalent to a weighted life cycle digraph de-composition. This research results a decomposition method which can decompose the complex life cycle digraph to be useful life cycle individual.

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

DAFTAR GAMBAR vii

BAB

1. PENDAHULUAN 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 3

1.3. Tinjauan Pustaka 4

1.4. Tujuan Penelitian 7

1.5. Manfaat Penelitian 7

1.6. Metodologi Penelitian 7

2. LANDASAN TEORI 8

2.1. Graph Berarah (Digraph) 8

2.2. Digraph Terhubung 14

2.3. Digraph Siklus Kehidupan 16

2.4. Matriks Model Populasi 17

2.5. Loop Analysis 20

2.6. Dekomposisi Loop 23

3. HASIL UTAMA 25

3.1. Algoritma untuk Dekomposisi Digraph Berbobot dengan

Aplikasi Analisis Siklus Kehidupan pada Biota 25 3.2. Analisis Siklus Kehidupan pada Caretta caretta 32 4. KESIMPULAN DAN RISET LANJUTAN 40

4.1. Kesimpulan 40

4.2. Riset Lanjutan 40

DAFTAR GAMBAR

Gambar Halaman

1.1 Contoh digraph siklus kehidupan dengan tiga verteks dan empat

arc. 2

1.2 Suatu digraph siklus kehidupan tiga tahap suatu organisme

den-gan dua pilihan untuk proses reproduksi, awal atau akhir (D). 5 1.3 Loop reproduksi awal (D1). 5 1.4 Loop reproduksi akhir (D2). 5

2.1 Graph D(4,6) 9

2.2 (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat 14 2.3 Gambar digraph siklus kehidupan Campanula americana. Ada

tiga tahap yang dilewati yaitu S = biji-biji yang dormant, R =

pembungaan, F = individu yang sudah berbunga. 17 3.1 Gambar digraph siklus kehidupan Caretta caretta dengan laju

pertumbuhan populasi λ=0.945 32 3.2 L1 =1 → 2 → 3 → 4 → 5 → 1. Loop ini menyatakan

kemam-puan Caretta caretta melewati lima tahap dalam kehidupannya. 34 3.3 D1, digraph setelah terdekomposisi satu kali yaitu diperoleh cycle

L1. 34

3.4 L2 =1→2→3→4→5→6→1.KemampuanCaretta caretta

untuk tetap bertahan hidup sampai tahap beremigrasi. 35 3.5 D2, digraph setelah terdekomposisi dua kali yaitu diperoleh cycle

L2. 35

3.6 L3 =1→2→3→4→5→6→7→1. Caretta carettamampu bertahan hidup melalui semua tahap hingga tahap kemampuan

bereproduksi di usia yang dewasa. 36 3.7 D3, digraph setelah terdekomposisi tiga kali yaitu diperoleh cycle

L3. 36

3.8 loop-loop yang merupakan selfloop dari digraph siklus kehidu-pan Caretta caretta masing-masing L4 L5 L6 L7 menyatakan ke-mampuan Caretta caretta untuk tetap bertahan pada satu tahap

tertentu. 37

ABSTRAK

Dalam ekologi, analisis siklus kehidupan dapat direpresentasikan dengan digraph. Digraph yang demikian disebut digraph siklus kehidupan yang selanjutnya digraph-digraph tersebut dapat diubah ke dalam matriks-matriks yang berhubungan yaitu matriks elastisitas dan matriks sensitivitas. Dalam penelitian ini digraph yang digunakan adalah digraph berbobot. Partisi suatu matriks elastisitas yang di-gunakan untuk menghitung kontribusi terpisah dari suatu siklus hidup ke laju pertumbuhan populasi ekuivalen dengan dekomposisi suatu digraph siklus kehidu-pan pada populasi. Penelitian ini akan memformulasikan suatu metode dalam proses dekomposisi sehingga mampu mendekomposisikan digraph-digraph siklus hidup yang kompleks menjadi siklus kehidupan individu yang bermakna.

ALGORITHM FOR A DECOMPOSITION OF WEIGHTED DIGRAPHS WITH APPLICATIONS TO LIFE CYCLE ANALYSIS

IN BIOTA

ABSTRACT

In ecology, life cycle analysis can be represented by a digraph. Such digraph called life cycle digraph later on the digraph can be changed to the correspond matrix, sensitivity and elasticity matrix. This research used the weighted digraph. Parti-tioning of the elasticity matrix is used to quantify the separate contributions of life cycle to population growth rate, is equivalent to a weighted life cycle digraph de-composition. This research results a decomposition method which can decompose the complex life cycle digraph to be useful life cycle individual.

PENDAHULUAN

1.1 Latar Belakang

Siklus kehidupan adalah suatu rangkaian aktivitas secara alami yang dialami oleh individu-individu dalam populasi berkaitan dengan perubahan tahap-tahap dalam kehidupan. Suatu model demografik terdiri dari tahap-tahap dan transisi-transisi antar tahap-tahap tersebut yang mendeskripsikan tentang masa depan suatu in-dividu yang diistilahkan dengan pertumbuhan, kemampuan bertahan hidup, dan proses reproduksi pada rentang waktu berturut-turut (Wardle, 1998). Karena sik-lus kehidupan tersebut selalu melibatkan tahapan-tahapan yang demikian (kelahi-ran, kematian, dan transisi-transisi antar setiap tahap), maka diperlukan suatu metode untuk membandingkan kontribusi-kontribusi relatif dari bentuk-bentuk sejarah kehidupan yang berbeda ke laju pertumbuhan populasi sehingga meng-hasilkan seperangkat loop yang disebut dengan analisis loop (van Groenendael et. al, 1994). Untuk siklus kehidupan yang kompleks, sulit untuk menemukan semua loop yang bermakna dalam siklus kehidupan sehingga diperlukan metode yang relevan.

Dalam ilmu matematika, dikenal istilah tentang graph, yaitu suatu istilah yang menyatakan representasi dari objek diskrit dan hubungan antara objek-objek tersebut. Pada kenyataannya suatu siklus kehidupan individu dalam suatu populasi pada ekologi adalah suatu objek diskrit sehingga untuk mempermudah proses pemahaman terhadap siklus kehidupan itu siklus tersebut direpresentasikan dalam suatu digraph siklus kehidupan.

Suatu digraph siklus kehidupan adalah suatu gambaran secara grafikal menge-nai siklus kehidupan suatu populasi. Verteks-verteks pada digraph menggam-barkan tahap-tahap pada kehidupan, garis penghubung (disebut arc) dari verteks jke verteksimengindikasikan bahwa suatu individu pada tahapj diwaktutdapat mengkontribusi individu ke tahap i pada waktu t+ 1. Representasi lain dari di-graph siklus kehidupan tersebut adalah matriks, yaitu matriks proyeksi populasi. Elemen ke (i, j) pada matriks populasi tidak nol. Oleh karena itu ada hubungan antara suatu matriks proyeksi populasi n tahap dengan suatu digraph siklus ke-hidupan n verteks dimana arc penghubung menghubungkan verteks-verteks yang berkaitan ke elemen-elemen tidak sama dengan nol pada matriks proyeksi (Sun dan Wang, 2007). Hal ini dapat dilihat pada contoh gambar berikut:

t t

t ✒✑ ✓✏

✒✑ ✓✏

✻ ✲ ✲

✻ ✻

v1

11,8

3

v2 3,2

17, 17 v3 47

Gambar 1.1 : Contoh digraph siklus kehidupan dengan tiga verteks dan empat arc.

Siklus kehidupan suatu populasi dapat direpresentasikan dalam digraph ber-bobot. Digraph-digraph tersebut selanjutnya direpresentasikan dalam matriks-matriks yang dapat digunakan untuk mengukur kontribusi terhadap laju pertum-buhan populasi jika matriks-matriks tersebut dipartisi. Partisi matriks-matriks ini menghasilkan sekumpulan loop yang bermakna dalam siklus kehidupan. Proses ini ekuivalen dengan dekomposisi digraph berbobot yang menggambarkan siklus kehidupan. Secara Biologi, dekomposisi itu mengilustrasikan dan memperkirakan kontribusi-kontribusi siklus kehidupan yang berbeda-beda dari individu ke laju pertumbuhan populasi (Casswel, 2001; van Groenendael, 1994; Wardle, 1998).

dengan n − 1 edge yang tidak memuat loop. Loop sendiri terbentuk dengan menambahkan edge kebase tree. Metodespanning treetersebut akan menghasilkan sekumpulan cycle-cycle yang independen. Akan tetapi, metode spanning tree ini akan menimbulkan dua masalah. Pertama, untuk digraph yang cukup rumit bi-asanya sulit bahkan hampir tidak mungkin untuk menemukan suatu tree yang span-nya memuat sekumpulan cycle tanpa arah yang berlawanan. Wardle sendiri menyatakan jika cycle memuat arah yang berlawanan maka tidak mewakili siklus kehidupan individu-individu organisme, yang artinya hal tersebut bertentangan dengan interpretasi secara biologi. Kedua, setiap tree yang merentang sekumpu-lan cycle yang fix; pasangan cycle-cycle yang mungkin penting untuk tujuan per-bandingan mungkin tidak kelihatan di sekumpulan cycle yang sama.

Karena masih adanya kendala-kendala pada hasil Wardle maka pada tahun 2007 Sun dan Wang menentukan suatu metode baru. Sun dan Wang menge-mukakan suatu metode dekomposisi melalui suatu algoritma pendekatan teori graph. Digraph didekomposisi menjadi dua bagian, bagian pertama merupakan sekumpulan cycle sederhana yang tidak memuat arah berlawanan dan terdiri dari arc-arc dengan bobot yang sama. Bagian kedua adalah subgraph-subgraph tanpa cycle-cycle sederhana seperti yang terdapat sebelumnya. Karena algoritma untuk dekomposisi ini tidak tunggal maka perlu dilakukan riset lanjutan sehingga dapat ditentukan cycle-cycle mana yang lebih berarti yang seharusnya menjadi prioritas utama untuk dipilih. Pada penelitian ini akan ditentukan suatu metode dekom-posisi melalui pendekatan algoritma untuk mendekomdekom-posisi digraph berbobot ter-hubung. Riset utama akan difokuskan untuk menemukan algoritma yang relevan sehingga menghasilkan sekumpulan cycle yang bermakna dalam analisis siklus ke-hidupan.

1.2 Perumusan Masalah

biologi.

1.3 Tinjauan Pustaka

Berikut akan diberikan kajian pustaka mengenai graph, digraph, maupun hal-hal yang berkaitan dengan analisis siklus kehidupan.

1.3.1 Digraph.

Istilah-istilah mengenai digraph diambil dari Brualdi dan Ryser (1991). Suatu di-graph adalah himpunan titik-titik yang tidak kosong yang unsurnya disebut nodes atau verteks, dan himpunan garis-garis berarah yang menghubungkan verteks-verteks tersebut disebut arc.

Suatu digraph berbobot (D, W) adalah suatu digraphDyang memiliki bobot numerik yang ditandai pada setiap directed edgenya. Digraph-digraph berbobot memiliki suatu representasi matriks sebagai berikut:

dari verteks

ke verteks

   

w11 w12 ... w1n w21 w22 ... w2n

..

. ... ... ... wn1 wn2 ... wnn

   

wij adalah bobot arc dari verteksvi ke verteksvj.

Suatu cycle atau simple cycle adalah suatu perjalanan tertutup dari barisan arc-arc diD yang menghubungkan verteksvi1, vi2, ..., vik, vi1 secara berurutan,vi1, vi2,

..., vik masing-masing berbeda kecuali verteks awal dan verteks akhir. Dalam

tulisan ini, simple cycle atau cycle diistilahkan dengan loop sebagaimana diambil dari literatur-literatur ekologi.

1.3.2 Dekomposisi Analisis Siklus Kehidupan dalam Ekologi.

Secara Biologi dekomposisi menggambarkan dan menghitung kontribusi-kontribusi berbeda dari siklus kehidupan individu ke laju pertumbuhan populasi. Sedangkan secara matematis dekomposisi disini didefinisikan sebagai partisi atau pembagian

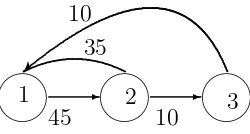
dari matriks-matriks representasi digraph berbobot menjadi submatriks-submat-riks yang apabila disatukan akan membentuk digraph siklus kehidupan itu sendiri. Akan tetapi dekomposisi bukanlah satu-satunya cara untuk menghitung kontri-busi-kontribusi berbeda dari siklus kehidupan. van Groenendael (1994) sebelum-nya telah menemukan analisis loop (loop analysis) sebagai metode yang sesuai un-tuk membagi matriks-matriks elastisitas unun-tuk menenun-tukan kontribusi-kontribusi yang dimaksud. Analisis loop berimplikasi pada suatu kalkulasi kontribusi relatif dari loop sejarah kehidupan ke kemampuan berdasarkan elastisitas elemen-elemen transisi matriks proyeksi. Berikut diberikan contoh gambar analisis loop seperti yang dikemukakan oleh van Groenendael.

✖✕ ✗✔

✖✕ ✗✔

✖✕ ✗✔

✻

✲ ✲

1 10

2 35

45 10 3

Gambar 1.2 : Suatu digraph siklus kehidupan tiga tahap suatu organisme dengan dua pilihan untuk proses reproduksi, awal atau akhir (D).

✒✑ ✓✏

✒✑ ✓✏

✻ ✲

1 2

35

35

Gambar 1.3 : Loop reproduksi awal (D1).

✒✑ ✓✏

✒✑ ✓✏

✒✑ ✓✏

✻ ✲ ✲ 1

10 2

10 10 3

Gambar 1.4 : Loop reproduksi akhir (D2).

Berdasarkan gambar (1.2), (1.3), dan (1.4) diketahui bahwa D = D1 ∪D2, yang artinya dekomposisi merupakan partisi digraph menjadi subgraph-subgraph yang jika dihubungkan dengan matriks, matriks-matriks tersebut diubah menjadi sub-matriks-submatriks.

ditunjukkan oleh graph siklus kehidupan (Caswell, 1989). Suatu karakteristik penting dari graph ini adalah kenyataan bahwa graph siklus kehidupan tersebut dapat didekomposisi menjadi sekumpulan loop, masing-masing kontribusi tersebut berhubungan dengan eigenvalue dominan pada matriks proyeksi yang berkaitan pada suatu penambahan cara yang sederhana (de Kroon, 1987; Caswell, 1989).

Dasar matematik dari kalkulasi elastisitas loop didasarkan pada dua sifat berikut (van Groenendael et. al, 1994):

1. Untuk setiap tahap pada graph siklus hidup, jumlah elastisitas dari transisi yang masuk sama dengan jumlah elastisitas transisi yang keluar. Transisi masuk dan transisi keluar sama dengan definisi derajat verteks pada graf berarah yang menyatakan bahwa derajat masuk (id(vi)) sama dengan derajat

keluar (od(vi))

n X

i=1

id(vi) = n X

i=1

od(vi).

2. Elastisitas suatu loop sama dengan karakteristik elastisitas dikali oleh jumlah transisi-transisi pada loop.

Suatu langkah penting dari analisis loop adalah bahwa analisis loop tersebut meru-pakan langkah dasar untuk mendekomposisi graph siklus kehidupan suatu populasi menjadi sekumpulan siklus kehidupan yang diikuti oleh individu-individu populasi.

1.3.3 Sensitivitas Demografik dan Analisis Elastisitas.

Sensitivitas demografi berarti sensitivitas λ (pertumbuhan populasi) untuk beru-bah pada laju demografik yang partikular. Sensitivitas mengukur pengaruhλdari perubahan simpangan yang absolut dari suatu laju vital relatif yang partikular ke perubahan laju vital yang lainnya. Suatu tambahan dari analisis sensitivitas adalah analisis elastisitas, yang menilai sensitivitas proporsional λke dalam suatu laju yang vital.

1.4 Tujuan Penelitian

Penelitian ini bertujuan untuk menentukan sekumpulan loop yang bermakna dalam siklus kehidupan dengan pendekatan matematis, yaitu algoritma yang didasarkan pada teori graph sehingga dapat diinterpretasikan dengan baik secara biologi.

1.5 Manfaat Penelitian

Penelitian ini bermanfaat untuk memperkaya literatur dalam teori graph khusus-nya aplikasi teori graph ini dalam bidang Biologi sehingga diharapkan dapat mem-permudah pekerjaan yang biasa dilakukan oleh para ahli ekologi.

1.6 Metodologi Penelitian

Metode penelitian ini bersifat literatur atau kepustakaan. Untuk menentukan su-atu metode baru dalam proses dekomposisi dilakukan pendekatan sebagai berikut:

1. Mempelajari literatur-literatur yang berkaitan dengan graph siklus kehidu-pan, analisis loop, serta literatur-literatur yang berkaitan dengan penelitian ini.

2. Menentukan matriks transisi dan matriks elastisitas berdasarkan graph siklus kehidupan (yang merupakan digraph berbobot) yang diketahui serta menen-tukan λ untuk mengetahui laju pertumbuhan populasi.

3. Mendekomposisi graph siklus kehidupan menjadi sekumpulan loop yang ber-makna (tidak memuat arah berlawanan).

4. Menentukan algoritma untuk proses dekomposisi digraph berbobot yang menggambarkan siklus kehidupan hingga menjadi sekumpulan loop yang bermakna dalam siklus kehidupan, yaitu sekumpulan loop yang dapat di-interpretasikan dengan baik secara biologi.

LANDASAN TEORI

Pada bab ini akan diperlihatkan teori-teori yang berhubungan dengan penelitian ini sehingga dapat dijadikan sebagai landasan berpikir dalam melakukan peneli-tian ini dan akan mempermudah dalam hal pembahasan hasil utama pada bab berikutnya. Teori tersebut mencakup pengertian dari digraph, contoh digraph, dan aplikasi digraph pada analisis siklus kehidupan.

2.1 Graph Berarah (Digraph)

Suatu graph berarah (digraph)Dadalah himpunan berhingga tak kosongV bersama suatu himpunanAyang terdiri dari pasangan berurut dengan unsur diV. Sehing-ga berdasarkan uraian di atas suatu digraphD terdiri dari dua himpunan yaitu:

1. Himpunan berhingga tak kosong V. Unsur dari V disebut verteks dari D.

2. Himpunan A yang merupakan himpunan bagian dari pasangan tak berurut dari unsur-unsur di V. Unsur dari A disebut arc dari D (Chartrand dan Lesniak, 1986 ).

Digraph D dengan himpunan verteksV dan himpunan arc A dinotasikan dengan D(V, A). Andaikan vi dan vj adalah dua verteks di D. Suatu arc vi, vj atau juga

dapat dinotasikan denganvi →vj adalah suatu arc diD yang menghubungkan vi

dan vj.

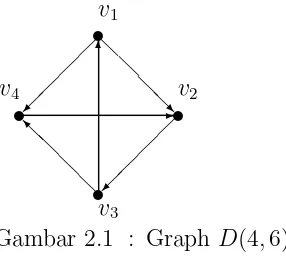
Contoh 1 : Himpunan verteksV ={v1, v2, v3, v4}bersama dengan himpunan arc A={v1 → v2, v1 → v4, v2 →v3, v3 →v4, v3 → v1, v4 →v2} adalah suatu digraph dengan 4 verteks dan 6 arc, dinotasikan dengan D(4,6).

Suatu digraph biasanya direpresentasikan secara grafis dengan cara setiap verteks pada digraph tersebut direpresentasikan sebagai suatu titik atau lingkaran kecil dan setiap arc (vi → vj) yang terdapat dalam digraph itu direpresentasikan

sebagai suatu garis berarah darivi kevj. Representasi grafis digraph pada contoh

1 diperlihatkan seperti gambar (2.1) dibawah ini.

t

t

t

t

✲ ✠

❅ ❅

❅ ❅ ❘

✠ ❅ ❅ ❅ ❅ ■

✻ v1

v2

v3 v4

Gambar 2.1 : Graph D(4,6)

Suatu representasi lain dari suatu digraph D dapat dituliskan dalam bentuk matriks adjacency sebagai berikut:

aij =

1, jika terdapat arc dari verteks j ke i 0 jika sebaliknya

maka untuk digraph pada gambar (2.1) di atas memiliki representasi matriks se-bagai berikut:

  

0 0 1 0 1 0 0 1 0 1 0 0 1 0 1 0

  

Suatu digraph berbobot adalah suatu pasangan (V, w) dimana V adalah su-atu himpunan berhingga verteks-verteks danwadalah suatu fungsi yang memeta-kan setiap pasangan verteks (x, y) ke nilai integer positif atau tak berhingga (∞). Fungsiw disebut fungsi bobot dan nilainya dapat diinterpretasikan sebagai suatu harga, jarak, atau waktu, dan lain sebagainya dalam bentuk fungsi sebagai berikut w:V(D)→R. Digraph berbobot memiliki representasi matriks sebagai berikut:

ke verteks

   

dari verteks w11 w12 ... w1n w21 w22 ... w2n

..

. ... ... ... wn1 wn2 ... wnn

   

Andaikan u, v∈V. Suatu walk dariu kevdinotasikan dengan (u, v). Suatu walk dari u ke v disingkat sebagai uv-walk atau luv (untuk selanjutnya dipakai

notasi (luv)). Suatu walk dariukev yang panjangnyam adalah suatu barisan arc

dalam bentuk

(u=v0, v1),(v1, v2), ...,(vm−2, vm−1),(vm−1, vm =v)

(Chartrand dan Lesniak, 1986 ). Walk di atas juga dapat direpsentasikan sebagai berikut

u=v0 →v1 →v2· · ·vm−1 →vm =v

(Chartrand dan Lesniak, 1986). Suatu path puv adalah suatu luv tanpa ada

pe-rulangan verteks kecuali mungkin verteks awal dan verteks akhir dan panjangnya dinotasikan denganℓ(puv). Suatu cycle adalah path dengan verteks awal sama

den-gan verteks akhir atau denden-gan perkataan lain cycle adalah path tertutup. Selain beberapa istilah yang telah ditunjukkan di atas, masih ada beberapa istilah lain yang berkaitan dengan digraph yang akan dijelaskan pada bagian-bagian berikut.

2.1.1 Nilai Eigen (Eigenvalue).

MisalkanAadalah suatu matriksn×n. Suatu skalarλdisebut sebagai suatu nilai eigen atau nilai karakteristik dariA jika terdapat suatu vektor tak nol xsehingga

Ax=λx

PersamaanAx=λx dapat dituliskan dalam bentuk

adalah N(A−λI)x yang merupakan ruang bagian dari Rn_{. Jadi, jika λ adalah}

nilai eigen dari A, maka N(A−λI) 6= {0} dan sembarang vektor tak nol dalam N(A −λI) adalah vektor eigen milik λ. Ruang bagian N(A −λI) dinamakan ruang eigen yang berhubungan dengan nilai eigen λ.

Persamaan (2.1) akan mempunyai penyelesaian nontrivial jika dan hanya jika A−λI singular, atau secara ekuivalen

det(A−λI) = 0. (2.2)

Jika determinan pada persamaan (2.2) diuraikan, akan kita dapatkan suatu poli-nom berderajat n dalam peubah λ.

p(λ) =det(A−λI). (2.3)

Polinom ini disebut polinom karakteristik (characteristic polynomial) dan per-samaan (2.3) disebutpersamaan karakteristik (characteristic equation)untuk mat-riksA. Akar dari polinom karakteristik adalah nilai eigen dariA(Horn dan John-son, 1985 ).

2.1.2 Pohon (Tree).

Definisi. Pohon adalah suatu graph terhubung yang tidak memiliki sirkuit. Proposisi. Anggap G adalah suatu graph. Pernyataan berikut ekuivalen.

(1). Gadalah tree.

(2). Gterhubung dan tak memuat cycle.

(3). Diantara dua verteks sebarang di G pasti ada suatu path.

Bukti: (1)⇒ (2): Karena suatu cycle adalah suatu sirkuit, pernyataan (1) ber-akibat ke pernyataan (2).

dariP1 dan kemudianP2 pada order yang berlawanan akan memuat sebuah cycle, kontradiksi dengan (2).

(3)⇒(1): Karena ada suatu path antara dua verteks sebarang di G, pastilah G terhubung. Selanjutnya, G tidak memuat sirkuit. Sebaliknya, itu akan memuat sebuah cycle dan sebuah cycle akan menentukan dua path antara dua verteks sebarang pada graph tersebut.

Implikasi-implikasi yang terbentuk adalah (1)⇒(2)⇒(3)⇒(1)

memberikan keekuivalenan antara (1), (2), dan (3), (Goodaire dan Parmenter, 1998).

Pohon yang terdiri atas satu verteks disebut pohon yang menyusut atau pohon yang mengalami degenerasi atau pohon yang trivial.

2.1.3 Pohon Perentang (Spanning Tree).

Definisi. Suatu edge e∈EG adalah suatu bridge dari graph G jika G−e

memi-liki komponen terhubung yang lebih banyak dari G, yaitu jika c(G−e) > c(G). Definisi. Suatu (spanning tree) dari suatu graph Gterhubung adalah suatu sub-graph yang merupakan suatutree dan memuat semua verteks di G(Goodaire dan Parmenter, 1998).

Teorema 2.1 Setiap graph terhubung memiliki suatu spanning tree, oleh karena itu suatu spanning graph adalah tree.

Bukti: Anggap H ⊆ G adalah suatu spanning subgraph terhubung minimal, ada suatu spanning subgraph terhubung dari G sedemikian hingga H − e tidak terhubung untuk setiape ∈EH. Subgraph yang demikian diperoleh dariGdengan

menghapusnonbridges seperti pada langkah berikut:

(a.) Anggap H0 =G.

(b.) Untuk i≥0 anggap Hi+1 =Hi−ei, dimana ei bukanlah suatu bridge, Hi+1 adalah suatu spanning subgraph dari Hi dan sekaligus dari G.

(c.) H =Hk jika hanya bridges yang tetap ada.

Berdasarkan pernyataan yang menyatakan bahwa suatu graph terhubung adalah tree jika dan hanya jika semua edges adalah bridges, maka H adalah suatu tree (Harju, 2007).

Suatu edge dalam suatu spanning tree disebut cabang (branch) sedangkan edge yang tidak terdapat pada spanning tree tersebut tapi terdapat pada graph semula disebut tali hubung (chord). Graph yang tidak terdapat pada pohon perentang disebut cotree. Pada graph terhubung dengan m buah sisi dan n buah verteks terdapatn−1 buah cabang danm−n+1 buah tali. Himpunan tali hubung dengan verteks yang bersisian dengannya disebut komplemen pohon. Untuk graph terhubungGdengan nbuah verteks danm buah sisi, kita dapat menghitung jum-lah cabang dan tali hubungnya (chord) dengan rumus sebagai berikut:

jumlah cabang =n−1 jumlah tali hubung (chord) =m−n+ 1

Jumlah cabang pada pohon perentang dari sebuah graph G disebut rank graph G, dan jumlah tali hubung (chord) pada graph Gdisebutnullity graph G. Dapat dilihat bahwa

rank+nullity= jumlah sisi graph G (Goodaire dan Parmenter, 1998).

2.1.4 Gabungan Graph (Union) dan Join Graph.

Gabungan (Union) G = G1 ∪G2 memiliki V(G) = V(G1) ∪V(G2) dan E(G) = E(G1)∪E(G2), jika suatu graph G terdiri dari n ≥ 2. Join G = G1 + G2 memiliki V(G) = V(G1)∪ V(G2) dan E(G) = E(G1) ∪ E(G2) ∪ {uv|u ∈ V(G1) dan v∈V(G2)} (Chartrand dan Lesniak, 1986).

2.2 Digraph Terhubung

Suatu digraph dikatakan terhubung jika untuk setiap sebarang dua verteksnya terhubung oleh suatu arc. Dalam tulisan ini yang dibicarakan adalah digraph ter-hubung kuat mengingat matriks proyeksi populasi adalah suatu matriks nonnegatif dan diasumsikan bahwa matriks proyeksi populasi tersebut irreducible (Adams, 2008).

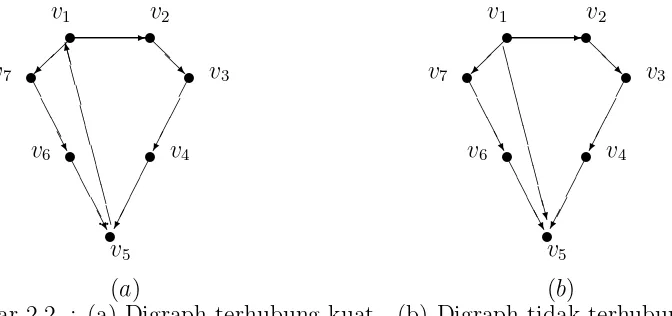
DefinisiSuatu digraph D dikatakan terhubung kuat (strongly connected) jika un-tuk setiap pasangan verteksu danv di D terdapat suatuuv−walk danvu−walk. Berikut akan diberikan contoh digraph terhubung kuat dan digraph tidak ter-hubung kuat beserta matriks adjacency-nya.

t v1 t v2 t v7 t v6 t v5

t v4

t v3 ✲ ❅ ❅ ❘ ✁ ✁ ✁ ✁☛ ..❈❈ ❈ ❈ ❈ ❈ ❈ ❈ ❈❈❖ ✁ ✁ ✁ ✁☛ ✠ ❆ ❆ ❆ ❆❯ ❆ ❆ ❆ ❆❯

(a)

t v1 t v2 t v7 t v6 t v5

t v4

t v3 ✲ ❅ ❅ ❘ ✁ ✁ ✁ ✁☛ ✁ ✁ ✁ ✁☛ ✠ ❆ ❆ ❆ ❆❯ ❆ ❆ ❆_❆❯ ❈ ❈ ❈ ❈ ❈ ❈ ❈ ❈ ❈❲

(b)

Gambar 2.2 : (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat

A=        

0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0

        B =        

0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0

       

A adalah matriks untuk digraph terhubung kuat sedangkan B adalah matriks untuk digraph tidak terhubung kuat.

DefinisiMatriks A berorder n disebut reducible jika dengan permutasi yang simul-tan pada barisnya kita memperoleh suatu matriks berbentuk

A1 O A21 A2

dimana A1 dan A2 adalah matriks bujur sangkar berorder paling tidak 1. Jika A tidak reducible maka A disebut irreducible. Matriks berorder satu adalah matriks irreducible.

Teorema 2.2 Diketahui A suatu matriks berorder n. A disebut irreducible jika dan hanya jika digraphD tersebut terhubung kuat.

Bukti : Pertama asumsikan bahwa A reducible. Selanjutnya himpunan verteks V dari D dapat dibagi menjadi dua himpunan tak kosong V1 dan V2 sedemikian hingga tidak ada arc dari suatu verteks di V1 ke suatu verteks di V2. Jika a adalah suatu verteks di V1 dan b adalah suatu verteks di V2 tidak ada walk yang menghubungkan dariakeb. Oleh karena ituDbukanlah suatu digraph terhubung kuat.

Sekarang asumsikan bahwaD tidak terhubung kuat. Kemudian ada verteks-verteks berbeda a dan b di D dimana tidak ada walk yang menghubungkan dari a ke b. Anggap W1 terdiri dari b dan semua verteks D yang darinya terdapat walk yang menghubungkan ke b, dan anggap W2 terdiri dari a dan semua verteks yang menujunya terdapat walk yang menghubungkan dari a. Himpunan W1 dan W2 tak kosong dan disjoint. Anggap W3 adalah himpunan yang setiap verteksnya tidak berada di W1 maupun di W2. Secara simultan permutasikan baris-baris A sedemikian hingga baris-baris tersebut berhubungan ke verteks-verteks di W2

pertama kali diikuti oleh hubungan lainnya ke verteks-verteks di W3:

     

W2 W3 W1

W2 X11 X12 X13

W3 X21 X22 X23

W1 X31 X32 X33

     

Karena tidak ada walk yang menghubungkan dari a ke b maka tak ada arc dari suatu verteks di W2 ke suatu verteks di W1. Juga tak ada arc dari suatu verteks c di W3 ke suatu verteks di W1, karena arc yang demikian berimplikasi bahwa c berada diW1. Oleh karena itu X13 =O dan X23 =O, dan A reducible (Brualdy dan Ryser, 1991).

2.3 Digraph Siklus Kehidupan

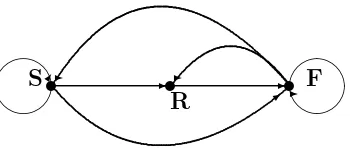
Siklus kehidupan adalah suatu rangkaian aktivitas secara alami yang dialami oleh individu-individu dalam populasi berkaitan dengan perubahan-perubahan tahap dalam kehidupan. Verteks-verteks pada digraph menggambarkan tahap-tahap pada kehidupan, garis penghubung (disebut arc) dari verteksj ke verteks i mengindikasikan bahwa suatu individu pada tahapj diwaktu t dapat mengkon-tribusi individu ke tahap i pada waktu t+ 1.

t ✲t ✲t ✚✙

✛✘

✚✙ ✛✘

✲

✣ ✲ ✲

✸ S

R F

Gambar 2.3 : Gambar digraph siklus kehidupanCampanula americana. Ada tiga tahap yang dilewati yaitu S = biji-biji yang dormant, R = pembungaan, F = individu yang sudah berbunga.

Digraph siklus kehidupan akan memiliki suatu representasi matriks. Matriks-matriks tersebut selanjutnya akan disebut dengan Matriks-matriks proyeksi populasi, ma-triks sensitivitas dan mama-triks elastisitas. Mama-triks-mama-triks ini selanjutnya akan dipartisi hingga akhirnya apabila diubah kembali ke dalam representasi digraph menghasilkan cycle-cycle yang bermakna.

2.4 Matriks Model Populasi

Matriks model populasi dapat mengklasifikasikan siklus kehidupan baik menggu-nakan usia atau tahap-tahap dalam kehidupan yang dilaluinya. Model pengklasi-fikasian berdasarkan usia menyatakan dinamika populasi dengan membagi vari-abel usia yang kontinu menjadi stadium-stadium usia yang diskrit, masing-masing dalam rentang yang sama. Model pengklasifikasian berdasarkan tahapan yang dilaluinya biasanya lebih fleksibel, dan memungkinkan analisis untuk pola siklus kehidupan yang lebih kompleks. Tahap-tahap tersebut mungkin menggambar-kan status sosial (seperti keturunan dengan kemapanan), tahapan-tahapan yang terus berkembang atau lokasi-lokasi yang renggang (seperti daerah dengan kual-itas tinggi dengan daerah kualkual-itas rendah). Transisi-transisi antar tahap-tahap tersebut dikembangkan oleh laju vital yang menggambarkan proses-proses seperti pertumbuhan, fertilitas, kemampuan bertahan hidup bahkan peluang menjadi su-atu yang menghasilkan keturunan atau memperoleh susu-atu daerah dengan kualitas tinggi. Berikut diberikan matriks-matriks yang berkaitan dengan gambar 1.1 yang menggambarkan posisi setiap arc-nya yang merupakan matriks model populasi.

     

1 2 3

1 0.2 0.6 1.1 2 0.3 0 0 3 0 0.6 0.8

     

     

1 2 3

1 3 3.2 11.8 2 17 0 0 3 0 17 47

     

Matriks Transisi Matriks Elastisitas

Pada model matriks yang didasarkan pada tahap yang dilaluinya (stage based matrix model), ukuran suatu populasi dihitung dari waktu t ke waktu t+ 1 de-ngan mengalikan suatu matriksA dengan suatu vektorn (dalam hal ini n adalah populasi mula-mula) dengan persamaan

n(t+ 1) =A×n(t). (2.4)

Matriks model populasi adalah suatu tipe matriks transisi untuk proses Markov. Eigenvalueλpada matriks proyeksi populasi merupakan istilah untuk laju pertum-buhan dalam populasi, yaitu eigenvalue yang diperoleh setelah tahapan-tahapan yang dilalui mencapai kestabilan dimana nilai λ tetap dari satu waktu ke waktu berikutnya setelah sebelumnya dilakukan proses menghitung λ secara berulang-ulang.

Setiap entri pada matriks transisi berkaitan dengan matriks Leslie yang biasanya menggunakan parameter usia untuk mengklasifikasikan individu serta berdasarkan kelamin untuk model demografiknya sedangkan matriks elastisitas biasanya dinyatakan dalam persentasi. Pada analisis siklus kehidupan, matriks elastisitas dapat dianggap sebagai suatu jumlah konservatif yang alurnya mele-wati digraph siklus kehidupan (bobot pada setiap arc-nya).

" _F

1 F2 F3 P1 0 0

0 P2 P3

#

Matriks Leslie

Fx = kesuburan spesifik berdasarkan usia pada tahap x

Px = peluang bertahan hidup spesifik berdasarkan usia pada tahap x

2.4.1 Matriks Sensitivitas dan Matriks Elastisitas.

Matriks elastisitas merupakan matriks yang tersusun dari elemen-elemen yang menggambarkan sensitivitas proporsional dari λ yang berkaitan dengan elemen-elemen pada matriks proyeksi populasi. Matriks transisi menyatakan peluang per-pindahan tahap-tahap dalam siklus kehidupan dari satu tahap ke tahap berikut-nya atau meberikut-nyatakan parameter-parameter siklus kehidupan seperti tingkat ke-mampuan untuk bertahan hidup, laju pertumbuhan dan laju kelahiran individu-individu. Perubahan-perubahan kecil yang terjadi pada elemen-elemen matriks transisi tersebut akan berpengaruh terhadapλ. Untuk mengetahui seberapa jauh perubahan-perubahan itu berpengaruh dilakukan analisis sensitivitas (dalam hal ini matriks diubah ke dalam matriks sensitivitas) dengan persamaan:

sij =

viwj

< wv > (2.5)

dimana,

sij = entri pada matriks sensitivitas.

w= right eigenvector (vektor dimana tahap yang dilalui telah stabil). v= left eigenvector (vektor nilsi reproduktif).

vi = elemen ke idari vektor nilai reproduktif.

wj = elemen ke j dari vektor dimana tahap yang dilalui telah stabil. < wv >= vektor produk w dan v.

Sensitivitas proporsional disebut sebagai nilai elastisitas. Analisis elastisi-tas mengestimasi pengaruh dari suatu perubahan proporsional pada laju vital pertumbuhan populasi. Hubungan antara s dan e adalah (Caswell, 2001):

eij = aij

λ sij. (2.6)

dimana,

eij= entri pada matriks elastisitas. aij= entri pada matriks model populasi.

Elastisitas total (jumlah elemen-elemen di matriks elastisitas) adalah 1, atau 100% (Sun dan Wang, 2007). Sebagai tambahan, elastisitas diamati pada setiap tahap adalah:

n X

j=1 eij =

n X

j=1

eji∀i...n. (2.7)

Dengan perkataan lain, matriks elastisitas memenuhi sifatflow conservation (Sun dan Wang, 2007).

Dalam analisis siklus kehidupan, elastisitas dapat dipandang sebagai suatu jumlah konservatif yang mengalir melalui digraph siklus kehidupan. Ketika po-pulasi yang digambarkan oleh digraph siklus kehidupan itu didekomposisi menjadi siklus-siklus yang menggambarkan alur kehidupan yang diikuti oleh organisme-organisme individu yang berbeda, elastisitas total dari setiap siklus kehidupan menggambarkan sensitivitas proporsional dari laju pertumbuhan populasi λ ke alur kehidupan partikular. Dengan perkataan lain, elastisitas dapat digunakan untuk menggambarkan kontribusi relatif dari alur hidup alternatif ke variasi-variasi dalam laju pertumbuhan populasi (Sun dan Wang, 2007).

2.5 Loop Analysis

Suatu model demografik terdiri dari tahapan-tahapan dan transisi-transisi antar tahap-tahap tersebut yang menggambarkan nasib suatu individu dalam istilah-istilah yang biasa disebut dengan pertumbuhan, kemampuan bertahan hidup, reproduksi dalam suatu interval waktu yang berturut-turut. Tahap-tahap dan transisi-transisi masing-masing digambarkan dalam verteks dan arc pada digraph siklus kehidupan. Suatu demografik digraph siklus kehidupan menyatakan bahwa transisi-transisi adalah peluang suatu individu berpindah secara tak langsung dari satu tahap ke tahap berikutnya (Wardle, 1998).

takan bahwa loop-loop tersebut menahan arah yang sama sebagai aliran individu-indvidu dari satu tahap ke tahap berikutnya melalui siklus kehidupan. Analisis loop merupakan suatu tipe analisis sensitivitas untuk suatu model demografik (Wardle, 1998). Elastisitas atau sensitivitas proporsional (de Kroon et.al, 1986) dihitung dari matriks elemen transisi dan nilai-nilai elastisitas tersebut nantinya akan menjadi bobot pada arc suatu digraph siklus kehidupan.

Jumlah elastisitas untuk suatu transisi yang masuk ke suatu verteks sama dengan jumlah elastisitas suatu transisi yang meninggalkan suatu verteks. Keke-kalan elastisitas pada suatu verteks ini berimplikasi bahwa elastisitas-elastisitas menggambarkan aliran dalam suatu jumlah yang tetap pada suatu digraph. Akan tetapi, pada kenyataannya individu-individu dalam suatu siklus kehidupan tidak kekal, beberapa dari individu-individu tersebut mungkin mati dan meninggalkan sistem tersebut. Oleh karena itu, karena elastisitas-elastisitas menggambarkan kontribusi elemen-elemen matriks yang terpisah untuk menigkatkan laju pertum-buhan populasi, elastisitas-elastisitas tersebut harus melakukan hal yang demikian sehingga melalui efek-efek individu akhirnya melengkapi siklus kehidupan (Wardle, 1998).

Metode umum dari analisis loop demografik ditemukan oleh van Groenendael et.al (1994) yang melibatkan empat langkah sebagai berikut:

1. Bentuk suatu digraph siklus kehidupan dan matriks proyeksi populasi. 2. Hitung nilai elastisitas dari matriks berdasarkan persamaan (2.6).

3. Dekomposisi digraph siklus kehidupan menjadi loop-loop yang tak bercabang sedemikian hingga semua transisi termasuk setidaknya satu kali ke bebera-pa loop (van Groenendael et.al, 1994). Elastisitas karakteristik loop sama dengan elastisitas elemen-elemen yang tunggal ke loop tersebut.

4. Elastisitas loop diperoleh dengan mengalikan elastisitas karakteristiknya de-ngan jumlah elemen-elemen transisi yang terdapat di loop. Jumlah total elastisitas loop sama dengan 1 (Wardle, 1998).

2.5.1 Menentukan Banyaknya Loop.

Jumlah loop pada suatu digraph siklus kehidupan ekuivalen dengan nulitasL, L=b−n+c

b = Jumlah arc pada digraph; n = Jumlah verteks; c = Komponen (suatu subset digraph terhubung yang memuat jumlah maksimal arc). Untuk demografik digraph siklus kehidupan nilaicselalu 1 karena setiap tahap suatu siklus kehidupan dapat dicapai dari setidaknyai tahap lainnya.

2.5.2 Menentukan Sekumpulan Loop-Loop Independen dalam Suatu Digraph Siklus Kehidupan.

yang tunggal. Jumlah loop akan berhubungan dengan jumlah chord pada cotree (Wardle, 1998).

2.5.3 Menghitung Elastisitas Loop.

Nilai elastisitas adalah bobot-bobot di arc dalam digraph, dan elastisitas pada chord mendefinisikan elastisitas karakteristik dari loop. Karena sifat kekekalan elastisitas pada suatu verteks menyatakan bahwa peluang yang memasuki suatu verteks sama dengan elastisitas yang meninggalkan verteks tersebut. Oleh karena itu, elastisitas karakteristik juga mendefinisikan elastisitas semua arc dalam loop (Wardle, 1998).

2.6 Dekomposisi Loop

Anggap A adalah suatu matriks proyeksi populasi berorder n. Untuk menghin-dari terjadinya kasus trivial atau kasus terdegenerasi, asumsikan n ≥ 2. Matriks tersebut merupakan matriks nonnegatif dan akan diasumsikan juga bahwa matriks tersebut tidak tereduksi, meskipun tidak selalu primitif. Laju pertumbuhan popu-lasi berhinggaλ adalah eigenvalue real dominan dari A. Eigenvalue real dominan adalah nilai eigenλ1 yang memenuhi |λ1| >|λi| untuki = 2,3, .., n. Suatu benda

yang berhubungan dengan A adalah suatu digraph siklus kehidupan berorder n, yang setiap verteksnya berhubungan dengan kelas-kelas usia atau tahapan dalam suatu kehidupan populasi dan arc nya berhubungan dengan transisi dari satu kelas ke kelas berikutnya. Anggap 1,2,3, ..., n sebagai verteks-verteks di D, ada suatu arc (i, j) yang berarah dari verteks i ke verteks j jika dan hanya jika aj,i > 0.

AnggapE(D) sebagai himpunan arc dengan m=|E(D)|. Karena A tak tereduk-si, makaA terhubung kuat (Adams, 2008).

Suatu loop di D dengan panjang k adalah suatu barisan tak kosong (i1, i2), (i2, i3), ...,(ik, il) dari arc-arc dimana verteks-verteksi1, i2, ...ik berbeda. Anggap L(D) ={L1, L2, ..., Ll}sebagai himpunan semua loop diD dengan l=|L(D)|dan

anggap li sebagai panjang dari loop Li dengan i = 1,2, ..., l. Definisikan suatu

setiap loop Lk suatu bilangan nonnegatif g(Lk) yang memenuhi ej,i= P Lk∃(i,j)

g(Lk)

untuk setiap (i, j)∈E(D). Bilangang(Lk) adalah karakteristik elastisitas dariLk

yaitu lkg(Lk). Oleh karena itu elastisitas karakteristik tersebut bisa saja bernilai

0 (Adams, 2008).

HASIL UTAMA

Pada bab ini akan diperlihatkan hasil utama dari penelitian ini. Hasil utama yang diperoleh berdasarkan penjelasan-penjelasan yang telah dipaparkan pada bab-bab sebelumnya. Hasil utama dari penelitian ini yaitu algoritma untuk dekomposisi digraph berbobot dengan aplikasi analisis siklus kehidupan pada ekologi.

3.1 Algoritma untuk Dekomposisi Digraph Berbobot dengan Aplikasi Analisis Siklus Kehidupan pada Biota

Input: Digraph berbobot terhubung dan repesentasi matriks dari digraph tersebut. Output: Cycle-cycle tanpa arah berlawanan.

Berdasarkan hasil yang diperoleh oleh Sun dan Wang (2007), maka diperoleh al-goritma sebagai berikut:

1. Diketahui sebuah digraph berbobot terhubung beserta representasi matriks berbobotnya yang merupakan matriks elastisitasW = (wij).

2. Tentukan semua cycle yang mungkin, kemudian cari cycle tanpa arah berla-wanan dengan catatan cycle dicari melalui suatu titik tertentu yang meru-pakan titik awal dan akhir. Proses ini dapat dipaparkan sebagai berikut:

a. Tentukan suatu verteks sebagai verteks awal sekaligus verteks akhir, anggapv1 dengan syarat setidaknya ada satu arc dariv1dan setidaknya ada satu arc menuju v1.

b. Pilih i1 sebagai verteks yang akan dikunjungi dengan syarat ada arc dari verteks awal ke verteks i1 (v1 →vi1, wi1,1 >0).

c. Jika terdapat arc dari verteks vi1 ke v1, maka suatu cycle telah

dite-mukan yaitu v1 → vi1 → v1. Selanjutnya, cari verteks lain yang akan

dikunjungi berikutnya dariv1ke{v2, ..., vn} \ {vi1}, yakni suatu verteks

i2 sedemikian hingga ada arc dari vi1 ke vi2 (wi2,i1 >0).

d. Jika tidak terdapat arc dari vi1 ke setiap vj (wj,i1 = 0), kembali ke

langkah b untuk memilih i1 yang lain dari v1 sehingga ada arc dari v1 kevi1 tersebut (wi1,1 >0) dan lanjutkan langkah-langkah berikutnya.

e. Jika terdapat arc dari verteks vi2 ke v1 maka suatu cycle ditemukan

yaitu v1 → vi1 → vi2 → v1. Ulangi langkah c untuk menentukan

verteks lain yang mungkin bisa dikunjungi (masih dengan verteks awal dan verteks akhir yang sama yaitu v1), {v2, ..., vn} \ {vi1, vi2}. Pilih

verteksi3 sedemikian hingga ada arc dari v12 ke v13, (wi3,i2 >0).

f. Jika tidak terdapat arc dari vi2 ke setiap vj maka kembali ke langkah

c untuk menentukan i2 lain dari vi1 sedemikian hingga ada arc dari vi1

kevi2 (wi2,i1 >0) lalu lanjutkan langkah-langkah berikutnya.

g. Jika cycle tidak dapat dilengkapi untuk setiap j sedemikian hingga wj,i>0 maka tidak ada lagi cycle yang berawal dan berakhir di verteks v1.

3. Jika suatu cycleL1 diperoleh maka setiap arc pada cycle tersebut akan diberi bobot yang sama yang merupakan bobot terkecil diantara semua arc pada L1.

4. D telah terdekomposisi menjadiD =D1∪L1 dan banyaknya arc diD1 lebih kecil daripada arc di D. Bobot pada digraph berhubungan dengan elemen-elemen pada matriks sehingga jika digraph terdekomposisi maka representasi pada matriksnya adalah:

(wD

ij)n×n= (wDij1)n×n+ (wLij1)n×n

dengan wD ij,w

D1

ij ,w L1

ij adalah bobot pada setiap arc di D,D1, dan L1.

5. Ulangi semua langkah di atas pada D1 hingga ditemukan suatu cycle baru L2 di D1.

6. Akhir dari proses ini adalah

D =Dr∪(∪ri=1Li) i= 1,2, ..., r

dimana Li adalah cycle tanpa arah berlawanan, Dr merupakan subdigraph

tanpa cycle-cycle.

7. Berdasarkan langkah-langkah di atas maka telah diperoleh cycle-cycle tan-pa arah berlawanan sehingga cycle-cycle tersebut datan-pat diaplikasikan tan-pada analisis siklus kehidupan yang dapat diikuti sebagai alur kehidupan oleh makhluk hidup. Dengan perkataan lain, cycle-cycle yang dihasilkan dapat diinterpretasikan dengan baik dalam ekologi.

Algoritma di atas menghasilkan dua corollary berdasarkan sifat-sifat dari dekomposisi tersebut. Corollary tersebut berkaitan dengan konsep kekekalan aliran yang dideskripsikan pada definisi berikut.

DefinisiSuatu digraph berbobot memenuhi flow conservation condition jika ∀i,

n X

j=1 wij =

n X

j=1 wji

dengan n adalah jumlah arc di D.

Jika wij dianggap sebagai jumlah aliran dari verteks j ke verteks i, maka P

j wij

adalah jumlah total aliran ke verteks i, P j

wji adalah jumlah total aliran yang

keluar dari verteks i. Flow conservation condition menyatakan kesamaan jumlah aliran yang masuk dan aliran yang keluar pada setiap verteks.

Corollary 3.1. Jika D memenuhi flow conservation condition, maka graph sisa Dr adalah null graph.

Bukti: Setiap cycle pada dekomposisi memenuhi flow conservation condition. Flow conservation condition tersebut adalah additive. Oleh karena itu digraph sisa Dr harus memenuhi kondisi tersebut, dan karena Dr tidak memiliki cycle, maka

dapat dipastikan Dr kosong (selain verteks tanpa arc). Corollary ini didasarkan

1. Sebarang simple cycleLdariD dengan bobot arc yang sama memenuhiflow conservation condition untuk setiap verteks vi ∈ D. Asumsikan bahwa L

memiliki path sebagai berikut vi1 → vi2 → ... → vik → vi1, dimana im,

m= 1,2,3, ..., k berbeda, dan setiap arc di L memiliki bobot yang sama w. AnggapwL

ij bobot dari arc untuk digraph berbobotL. Maka untuk sebarang

verteksvi ∈D. X j wL ij =    wL

im,im₋1 =w=w

L

im+1,im =

P j

wL

ji, jika verteks vi =vim ∈L

0 =P j

wL

ji jika verteks vi ∈/ L

dimana secara umum digunakanim−1 =ik jikaim=i1,im+1=i1jikaim =ik

dan wL

ij = 0 jika arc berarah yang berhubungan tidak berada di L. Jumlah

keseluruhan meliputi semuavj ∈ D. Persamaan masih berlaku jika jumlah

keseluruhan vj ∈ L. Dengan perkataan lain, flow conservation condition

dipenuhi oleh L yang berkaitan keD dan berkaitan juga keL.

2. D \L memenuhi flow conservation condition pada setiap verteks vi ∈ D.

Anggap wij bobot arc untuk D, w′ij bobot arc untuk D\L, wijL=w sebagai

bobot arc untukL. Berdasarkan hal di atas, untuk sebarang verteksvi ∈D, X

j

w′ij =   

P j

wij −w=P j

wji−w=P j

wji′ , jika verteks vi =vim ∈L

P j

wij = P

j

wji = P

j w′

ji jika verteks vi ∈/ L

Sebagai akibat dari kedua fakta di atas, Dr = D \ ∪ri=1L memenuhi flow conservation condition. Anggap wDr

ij sebagai bobot arc untuk digraph sisa Dr.

Berdasarkan definisi,Drtidak memiliki cycle, baik cycle dengan panjang satu atau

disebut juga self loop dengan bentuk vi ↔ vi. Oleh karena itu, wD

r

ii = 0, untuk

setiapi. Dr juga tidak mengandung cycle dengan panjang dua vi →vj →vi, yang

berakibat wDr

ij = 0 jika w Dr

ji 6= 0. Anggap bahwa w Dr

ij ≡0. Asumsikan setidaknya

ada satu wDr

ij >0 terdapat diDr. Anggap wo=wD

r

r2,r1 =mini6=j{w

Dr

ij :w Dr

ij >0}

merupakan bobot terkecil yang tak nol diDr, dimana wo = wr1,r2 berarti bahwa

arc dari verteks vr1 ke verteks vr2 6=vr1 adalah bobot wo. Karena Dr memenuhi

flow conservation condition pada verteksvr2

X j

wj,r2

Dr

=X

j wr2,j

Dr

≥wDr

r2,r1 =wo >0.

Pasti ada suatu verteksvr3 sedemikian hingga w

Dr

r3,r2 ≥wo >0, dengan perkataan

lain ada suatu verteks dengan bobot wDr

r3,r2 dari verteks vr2 ke verteks vr3, dan

vr1, vr2, vr3 berbeda karena Dr tidak memuat cycle yang lain lagi. Pada verteks

vr3,Dr memenuhiflow conservation condition,

X j

wDr

j,r3 =

X j

wDr

r3,j ≥w

Dr

r3,r2 ≥wo >0

dan demikian seterusnya. Karena tidak ada cycle dengan panjang sebarang di Dr, langkah-langkah ini akan membentuk suatu path vr1 →vr2 → ...→vrm yang

berakhir pada suatu verteksvrm untuk 1< m < n arc pada path tersebut. Hal ini

berakibat

X j

wj,rm

Dr

= 06=X

j

wrm,j

Dr

≥wrm,rm₋1 ≥wo >0.

Kondisi kekekalan tidak dipenuhi pada verteks akhirvrm. Hal ini merupakan suatu

kontradiksi. Oleh karena itu pasti adawDr

ij ≡0. AkibatnyaDr tidak memiliki arc

sehingga digraph sisaDr merupakan nullgraph.

Corollary 3.2Untuk digraph sisaDr, semua eigenvalue dari matriks berbobotnya

(wDr

ij )n×n adalah 0.

Bukti Anggap suatu kasus nontrivial Dr bukan nullgraph. Suatu eigenvalue λ

dari (wDr

ij )n×n membuat fungsi karakteristik yang berhubungan menjadi nol,

de-ngan perkataan lain,det{λIn−(wD

r

ij )}n×n= 0, denganInadalah matriks identitas

berordern. Anggap suatu ekspansi dari fungsi karakteristik

det{λIn−(wD_ijr)n×n}=λn+c1λn−1+c2λn−2+...+cn

dengan

c1 =w11Dr +wD

r

22 +...+wD

r

nn

c2 =−

X

sign σ 2

Y i=1

wiσ(i)

c3 =−

X

sign σ 3

Y i=1

wiσ(i)

.. . cn=−

X

sign σ n Y i=1

wiσ(i)

dimana P

sign σ n Q i=1

wiσ(i) adalah penjumlahan yang yang berlaku untuk semua n! permutasiσ darinbilangan{1,2,...,n}dansign σ(sgn σ) dari suatu permutasi σ adalah (+1) atau (-1) bergantung pada banyaknya transposisi atau pasangan bilangan yang saling bertukar posisi pada {1,2,...,n} apakah genap atau ganjil. Oleh karena itu, setiap bentuk perkalian

w1σ(1)w2σ(2)....wnσ(n)

yang merupakan determinan akan bertanda (+)sign jika permutasi σ genap dan bertanda (-)signjika permutasiσ ganjil.

Karena tidak ada cycle di Dr, maka tidak ada cycle dengan panjang satu

atau self loop vi ↔vi. Oleh karena itu wDr

ii ≡0 ∀i= 1, ..., n

yang berakibat

c1 = 0. Akibatnya, jika terdapat

X

sign σ k Y i=1

wiσ(k), 1≤k ≤n yang berhubungan dengan istilah

wDr

1,σ(1)w

Dr

2,σ(2)...w

Dr

k,σ(k)= 0.

Untukk = 2, pernyataan di atas berimplikasi bahwa istilah-istilah pada c2 harus memiliki bentuk

c2 =−

X

sign σ 2

Y i=1

wiσ(i)

karena istilah-istilahwDr

1,σ(1)wDr2,σ(2)yang berhubungan dengan permutasi

1 2 1 2

adalah 0. Selanjutnya, tidak ada cycle dengan panjang duavi1 →vi2 →vi1 diDr,

oleh karena itu

w₁Dr,σ(1)w

Dr

2,σ(2)≡0 yang berakibat

c2 = 0.

Dan, sebagai akibatnya, jika terdapat

X

sign σ n Y i=1

wiσ(i),1≤k ≤n

kemudian berhubungan dengan istilah

wDr

1,σ(i)w

Dr

2,σ(i)w

Dr

m′_,σ(i)w

Dr

k,σ(k) =w

Dr

1,σ(1)w

Dr

m,σ(i)w

Dr

m,σ(i)w

Dr

k,σ(i)= 0 untuk setiapi= 1,2, ...m, ...m′_{, ...k...n.}

Pernyataan yang sama pada cycle dengan panjang k

wDr

k,σ(k) ≡0 ∀k = 3,4, ..., n. Oleh karena itu fungsi karakteristik menjadi

λn+c1λn−1+c2λn−2 +...+cn =λn = 0⇒λ= 0.

3.2 Analisis Siklus Kehidupan pada Caretta caretta

Caretta caretta(Logger Head Sea Turtle) memiliki karakteristik kepala yang besar, dengan dagu dan otot yang lebih berat dari jenis kura-kura laut lainnya. Spesies ini merupakan kura-kura bercangkang keras terbesar di dunia. Caretta caretta banyak dijumpai di laut-laut yang dekat ke kutub seperti Alaska, bagian paling timur Rusia dan Norway, sepanjang Australia Selatan dan Afrika Selatan.

Hewan ini mencapai kematangan seksual ketika cangkang-cangkangnya ber-ukuran kurang dari 50 cm. Telur-telur dengan besar diameter 40-42 mm diletakkan di daerah-daerah pasang. Telur-telur ditempatkan di sarang yang biasanya dipilih di daerah yang tenang dengan drainase baik atau vegetasi yang berumput. Karena tidak ada metode yang ditemukan untuk menentukan usia yang pasti dariCaretta caretta, data pada kasus ini didasarkan pada kelas-kelas ukuran. Contoh siklus ke-hidupanCaretta carettadiambil dari Course et.al (1987). Caretta caretta memiliki 7 tahapan kelas dan dapat digambarkan dalam digraph siklus kehidupan sebagai berikut, dimana

1)telur, menetas (<1 tahun); 2)Hewan muda yang kecil (1-7 tahun); 3)Hewan muda yang besar (8-15 tahun); 4)subadult (16-21 tahun); 5)ternak baru (22 tahun); 6)remigrant tahun pertama (23 tahun); 7)ternak dewasa (24-54 tahun).

t ✲ t ✲ t ✲t ✲ t ✲ t ✲ t

✒✑ ✓✏

✒✑ ✓✏

✒✑ ✓✏

✒✑ ✓✏

✐ ✛

✐

✸

✸ ✸ ✸

1 2 3 4 5 6 7

Gambar 3.1 : Gambar digraph siklus kehidupanCaretta caretta dengan laju per-tumbuhan populasi λ=0.945

.

Selanjutnya akan diberikan matriks proyeksi populasi dari digraph siklus kehidupan tersebut. Dari matriks proyeksi populasi ini akan dihasilkan matriks sensitivitas dan matriks elastisitas yang dihitung berdasarkan persamaan (2.5) dan

(2.6). A=        

0 0 0 0 127 4 80

0,6747 0,7370 0 0 0 0 0 0 0,0486 0,6610 0 0 0 0 0 0 0,0147 0,6907 0 0 0

0 0 0 0,0518 0 0 0

0 0 0 0 0,8091 0 0

0 0 0 0 0 0,8091 0,8091

       

Matriks proyeksi populasi

S =        

0,0223 0,0724 0,0123 0,0007 0,00004 0,00003 0,0012 0,0312 0,1013 0,0173 0,0009 0,00006 0,000045 0,0017 0,1339 0,4344 0,0743 0,0042 0,0002 0,00019 0,0076 2,5859 8,3872 1,4351 0,0826 0,005 0,0037 0,1477 12,6968 41,1801 10,4281 0,6005 0,0245 0,0272 671,1604 11,3259 36,7333 6,2855 0,3619 0,0219 0,0164 0,6471 13,1185 42,5477 7,2802 0,4192 0,0254 0,0190 0,7496

        Matriks Sensitivitas E =        

0 0 0 0 1,2 0,03 3,9 5,1 18,1 0 0 0 0 0

0 5,1 11,9 0 0 0 0 0 0 5,1 3,9 0 0 0 0 0 0 5,1 0 0 0 0 0 0 0 3,9 0 0 0 0 0 0 0 3,9 23,0

        Matriks Elastisitas

Berdasarkan persamaan (2.1)maka dapat dihitung jumlah loop yang dihasilkan yaitu:

L= 13−7 + 1 L= 7

Langkah-langkah dekomposisi digraph siklus kehidupan padaCaretta carettaadalah sebagai berikut:

t ✲t ✲ t ✲ t ✲ t ✲t ✲ t ✐ ✛ ✐ ✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✲ ✸ ✸ ✸ ✸

1 2 3 4 5 6 7

1. Digraph berbobot yang merupakan digraph siklus kehidupan pada Caretta caretta

Bobot setiap arc dalam contoh ini dilihat pada matriks elastisitas yang telah diketahui sebelumnya.

2. Ambil verteks 1 sebagai verteks awal sekaligus verteks akhir, himpunan arc yang diperoleh adalah 1→2 →3→ 4→ 5→ 1 sebagai L1. Karena bobot terkecil pada cycle ini adalah (1,2) (dilihat pada matriks elastisitas) yaitu bobot pada arc (5→1) maka elastisitas loop adalah 1,2×5 = 6,0.

t ✲ t ✲ t ✲t ✲ t

✲

5

1 2 3 4

Gambar 3.2 : L1 =1 →2→ 3→ 4→5 →1. Loop ini menyatakan kemampuan Caretta caretta melewati lima tahap dalam kehidupannya.

Selanjutnya, dekomposisiL1 dari D sehingga diperoleh digraph D1 sebagai berikut:

t ✲ t ✲ t ✲t ✲ t ✲ t ✲ t

✐ ✐ ✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✲ ✸ ✸ ✸ ✸

1 2 3 4 5 6 7

Gambar 3.3 : D1, digraph setelah terdekomposisi satu kali yaitu diperoleh cycle L1.

Adapun representasi matriks dari proses di atas adalah:

D1 =

       

0 0 0 0 0 0,03 3,9 3,9 18,9 0 0 0 0 0 0 3,9 11,9 0 0 0 0 0 0 3,9 13,9 0 0 0 0 0 0 3,9 0 0 0 0 0 0 0 3,9 0 0 0 0 0 0 0 3,9 23,0

       

L1 =

       

0 0 0 0 1,2 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

D=D1 ∪L1

D=D1 ∪(1→2→3→4 →5→1)

       

0 0 0 0 0 0,03 3,9 3,9 18,9 0 0 0 0 0 0 3,9 11,9 0 0 0 0 0 0 3,9 13,9 0 0 0 0 0 0 3,9 0 0 0 0 0 0 0 3,9 0 0 0 0 0 0 0 3,9 23,0

        +        

0 0 0 0 1,2 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

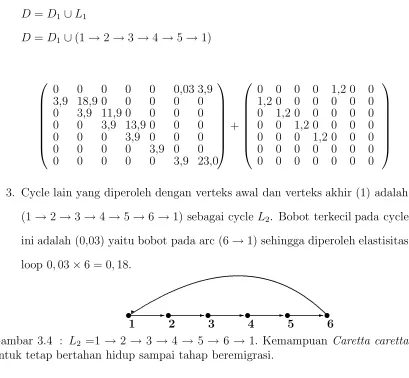
3. Cycle lain yang diperoleh dengan verteks awal dan verteks akhir (1) adalah (1→2→3→4→5→6→1) sebagai cycle L2. Bobot terkecil pada cycle ini adalah (0,03) yaitu bobot pada arc (6→1) sehingga diperoleh elastisitas loop 0,03×6 = 0,18.

t ✲ t ✲ t ✲t ✲ t ✲ t

✲

[image:47.612.116.525.74.452.2]

1 2 3 4 5 6

Gambar 3.4 : L2 =1 → 2 → 3 → 4→ 5→ 6 → 1. Kemampuan Caretta caretta untuk tetap bertahan hidup sampai tahap beremigrasi.

Selanjutnya, dekomposisi L2 dari digraph D1 hingga diperoleh digraph D2 sebagai berikut:

t ✲ t ✲ t ✲t ✲ t ✲ t ✲ t

✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✲ ✸ ✸ ✸ ✸

1 2 3 4 5 6 7

Gambar 3.5 : D2, digraph setelah terdekomposisi dua kali yaitu diperoleh cycle L2.

Representasi matriks dari proses di atas

D2 =

       

0 0 0 0 0 0 3,9 3,87 18,9 0 0 0 0 0 0 3,87 11,9 0 0 0 0 0 0 3,87 13,9 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,9 23,0

       

L2 =        

0 0 0 0 0 0,03 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0 0

       

D=D2 ∪L2

D1 =D2∪(1 →2→3→4→5→6→1)

       

0 0 0 0 0 0 3,9

3,87 18,9 0 0 0 0 0 0 3,87 11,9 0 0 0 0 0 0 3,87 13,9 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,9 23,0

        +        

0 0 0 0 0 0,030 0,030 0 0 0 0 0 0 0,030 0 0 0 0 0 0 0,030 0 0 0 0 0 0 0,030 0 0 0 0 0 0 0,030 0 0 0 0 0 0 0 0

       

4. Cycle terakhir yang diperoleh dengan verteks awal dan verteks akhir 1 adalah L3 yaitu (1 → 2 → 3 → 4 → 5 → 6 → 7 → 1). Bobot terkecil pada cycle ini adalah (3,87) yaitu bobot pada arc (1→2) sehingga diperoleh elastisitas loop 3,87×7 = 27,09.

t ✲ t ✲ t ✲t ✲ t ✲ t ✲ t

✲

[image:48.612.138.522.77.310.2]

1 2 3 4 5 6 7

Gambar 3.6 : L3 =1 → 2→ 3→ 4 → 5→ 6 →7 → 1. Caretta caretta mampu bertahan hidup melalui semua tahap hingga tahap kemampuan bereproduksi di usia yang dewasa.

Selanjutnya, dekomposisiL3 dari D2 sehingga diperolehD3 sebagai berikut:

t t t t t t ✲ t

✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✒✑ ✓✏ ✲ ✸ _{✸ ✸ ✸ ✸}

1 2 3 4 5 6 7

Gambar 3.7 : D3, digraph setelah terdekomposisi tiga kali yaitu diperoleh cycle L3.

Representasi matriks dari proses di atas

D3 =

       

0 0 0 0 0 0 0,03 0 18,9 0 0 0 0 0 0 0 11,9 0 0 0 0 0 0 0 13,9 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0,03 23,0

       

L3 =

       

0 0 0 0 0 0 3,87 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0

       

D2 =D3∪L3

D2 =D3∪(1 →2→3→4→5→6→7→1)

       

0 0 0 0 0 0 0,03 0 18,9 0 0 0 0 0 0 0 11,9 0 0 0 0 0 0 0 13,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,03 23,0

        +        

0 0 0 0 0 0 3,87 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0

       

5. Dekomposisi semua cycle dengan panjang 1 (selfloop) yaitu L4(2 → 2), L5(3→3),L6(4 →4) dan L7(7 →7) dariD3 sehingga diperolehD4 sebagai digraph sisa yaitu digraph yang tak memuat cycle lagi sehingga tak dapat didekomposisi. ✉ ✉ ✉ ✉ ✖✕ ✗✔ ✖✕ ✗✔ ✖✕ ✗✔ ✖✕ ✗✔ ✸ ✸ ✸ ✸

2 3 4 7

Gambar 3.8 : loop-loop yang merupakan selfloop dari digraph siklus kehidu-panCaretta caretta masing-masing L4 L5 L6 L7 menyatakan kemampuan Caretta caretta untuk tetap bertahan pada satu tahap tertentu.

Representasi matriksnya adalah sebagai berikut:

D4 =

       

0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,03 0

       

L4 =

       

0 0 0 0 0 0 0 0 18,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

L5 =

       

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

L5 =

       

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

L6 =

       

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

L7 =

       

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 23

       

D3 =D4∪L4∪L5∪L6∪L7

D3 =D4∪(2 →2)∪(3→3)∪(4 →4)∪(7→7)

       

0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,03 0

        +        

0 0 0 0 0 0 0 0 18,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

       

+        

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 23

       

Hasil dekomposisi itu secara utuh adalah:

D =D4 ∪L1∪L2∪L3∪L4∪L5∪L6∪L7

       

0 0 0 0 1,2 0,03 3,9 5,1 18,1 0 0 0 0 0

0 5,1 11,9 0 0 0 0 0 0 5,1 3,9 0 0 0 0 0 0 5,1 0 0 0 0 0 0 0 3,9 0 0 0 0 0 0 0 3,9 23,0

        =        

0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,03 0

        +        

0 0 0 0 1,2 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 1,2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0,03 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0,03 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0 3,87 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0 0 0 0 0 0 0 3,87 0

        +        

0 0 0 0 0 0 0 0 18,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 13,9 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

        +        

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 23

       

KESIMPULAN DAN RISET LANJUTAN

Pada bab ini akan diberikan kesimpulan yang diperoleh dari hasil penelitian pada bab sebelumnya. Selanjutnya akan ada saran untuk penelitian lebih lanjut. 4.1 Kesimpulan

Telah diketahui bahwa sebelumnya metode dalam proses dekomposisi telah dite-mukan, yaitu suatu metode menggunakanspanning tree. Metode ini sulit diterap-kan jika dekomposisi dilakuditerap-kan untuk analisis sejarah kehidupan yang kompleks ( ditemukan cycle yang memuat arah berlawanan). Cycle-cycle yang memuat arah berlawanan tidak dapat didimterpretasikan dengan baik secara biologi karena se-cara umum cycle-cycle tersebut tidak dapat menggambarkan alur kehidupan yang diikuti oleh individu-individu. Oleh karena itu, algoritma yang dihasilkan pa-da penelitian ini pa-dapat diaplikasikan dengan baik karena algoritma ini menjamin bahwa cycle yang dihasilkan tidak lagi memuat arah berlawanan.

4.2 Riset Lanjutan

Penelitian ini telah menunjukkan algoritma untuk mendekomposisi digraph berbo-bot yang dapat diaplikasikan pada siklus kehidupan di ekologi. Penelitian lebih lanjut diperlukan untuk menentukan suatu program sederhana proses dekompo-sisi berdasarkan algoritma pada penelitian ini sehingga menjadi lebih efisien bila digunakan para ahli ekologi.

DAFTAR PUSTAKA

Adams, M. J. 2008. Graph decompositionfor Demographic Loop Analysis. Mathematical Biology57: hal. 209-221.

Adams, M. J. dan Vollmer, J. 23 Februari 2010. DLA GUI Documentation. http://www2.truman.edu/ ˜mjadams/ReadMe.pdf

Brualdi, R. A. dan Ryser, H. J. 1991. Combinatorial Matrix Theory. Cam-bridge: Cambridge University Press.

Bang-Jensen, J. dan Gutin, G. 2007. Digraphs: theory, algorithms and appli-cations. Springer: Berlin Heidelberg New York.

Chartrand, G. dan Lesniak, L. 1986. Graph & Digraph, 2nd edn. The Wodsworth & Brooks: USA.

Caswell, H. 2001. Matrix population models: construction, analysis, and in-terpretation, 2nd edn. Sunderland: Sinauer.

Deborah, T., Caswell, H., Larry, B.C. 1987. stage based population model for loggerhead sea turtles and implications for conservation. Ecology 68: hal. 1412-1423.

Harju, T. 2007.Lectures Note on Graph Theory, Finland: University of Turku. Hayward, G. D. dan McDonald, D. B. 23 Februari 2