I. BAB 1 KESEBANGUNAN & KONGRUEN
Bab ini memperkenalkan konsep keseimbangan dan kekongruenan bangun datar, khususnya segitiga dan persegi panjang. Konsep keseimbangan menekankan perbandingan sisi-sisi yang bersesuaian pada bangun yang memiliki sudut-sudut yang sama besar. Hal ini penting dalam pemahaman skala dan pengukuran dalam berbagai konteks, termasuk pembuatan peta, model, dan perancangan bangunan. Sementara itu, kekongruenan menjelaskan tentang kesamaan ukuran dan bentuk dua bangun datar, di mana sisi-sisi dan sudut-sudut yang bersesuaian memiliki ukuran yang sama. Pemahaman konsep ini melatih kemampuan siswa dalam menganalisis dan membandingkan bentuk-bentuk geometri.
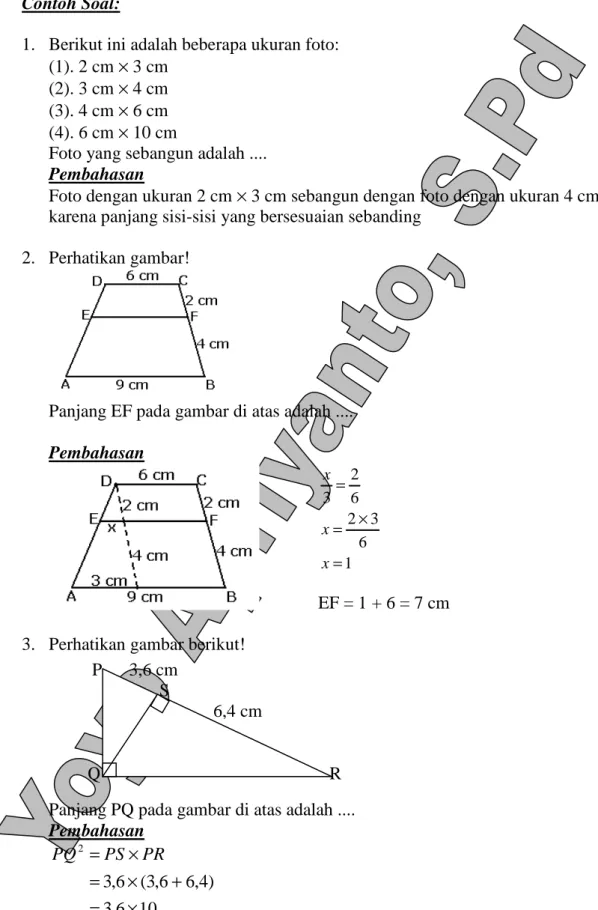
1.1 KESEBANGUNAN
Subbab ini mendalami definisi bangun sebangun, syarat-syarat dua bangun dikatakan sebangun (sudut-sudut bersesuaian sama besar dan sisi-sisi bersesuaian sebanding), dan cara menghitung panjang sisi bangun sebangun dengan menggunakan perbandingan. Contoh soal dan latihan soal yang diberikan melatih siswa dalam mengaplikasikan konsep perbandingan dan proporsi dalam memecahkan masalah geometri. Diagram dan ilustrasi yang terdapat dalam bab ini membantu visualisasi konsep keseimbangan. Nilai akademisnya terletak pada penguatan kemampuan pemecahan masalah matematis dan aplikasi dalam kehidupan nyata, misalnya dalam teknik sipil dan arsitektur.
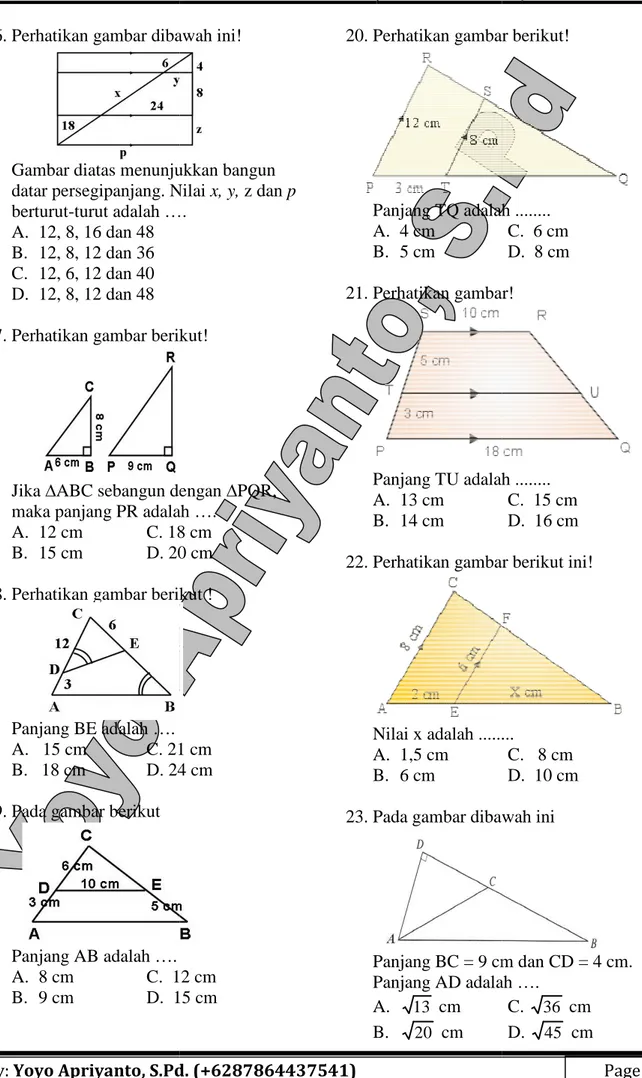
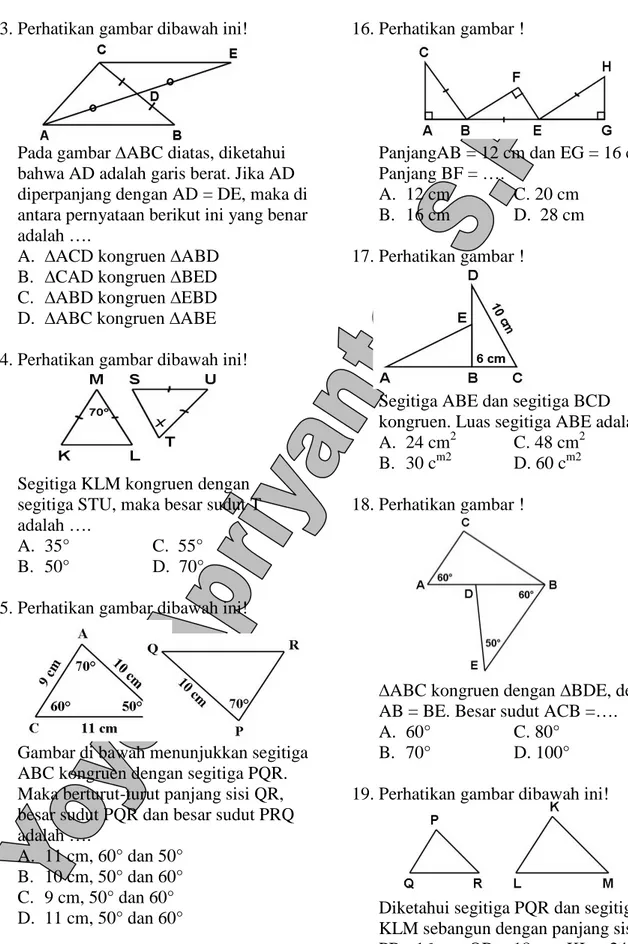
1.2 KEKONGRUENAN
Subbab ini membahas definisi bangun kongruen dan syarat-syarat dua bangun dikatakan kongruen (sudut-sudut dan sisi-sisi bersesuaian sama besar dan sama panjang). Berbeda dengan keseimbangan yang fokus pada perbandingan, kekongruenan menekankan pada kesamaan absolut ukuran. Contoh soal dan latihan soal yang diberikan melatih siswa untuk mengidentifikasi bangun kongruen dan mengaplikasikan pengetahuan mereka dalam masalah geometri. Nilai pedagogisnya terletak pada pengembangan kemampuan berpikir kritis dan analitis siswa dalam menganalisis sifat-sifat geometri.
II. BAB 2 TABUNG, KERUCUT & BOLA
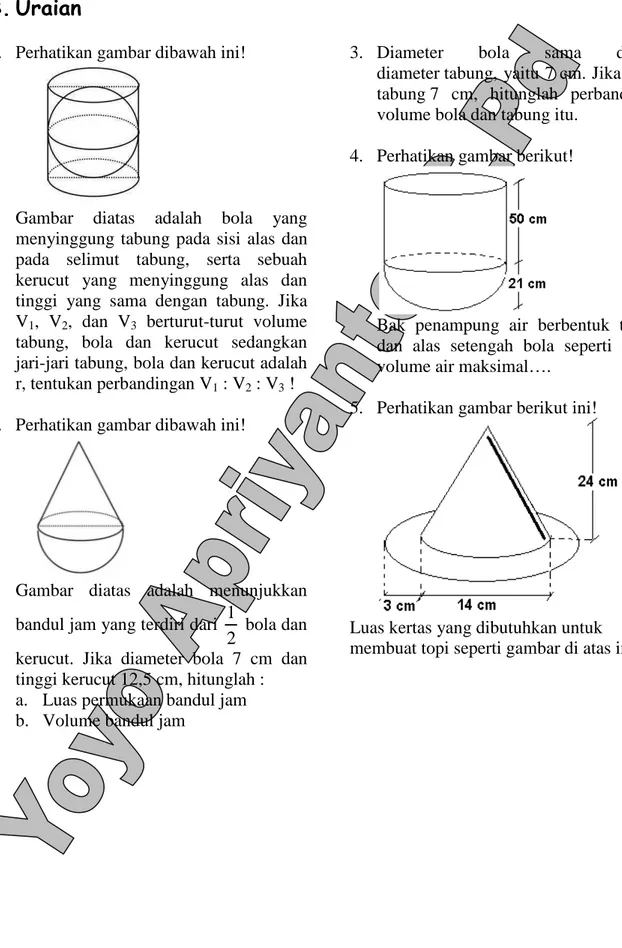
Bab ini memfokuskan pada pengukuran dan perhitungan bangun ruang, meliputi tabung, kerucut, dan bola. Siswa akan mempelajari unsur-unsur bangun ruang tersebut, seperti jari-jari, tinggi, garis pelukis, serta rumus untuk menghitung luas permukaan dan volume. Pemahaman bab ini penting dalam penerapan matematika dalam kehidupan sehari-hari dan berbagai disiplin ilmu, misalnya dalam bidang teknik dan arsitektur.
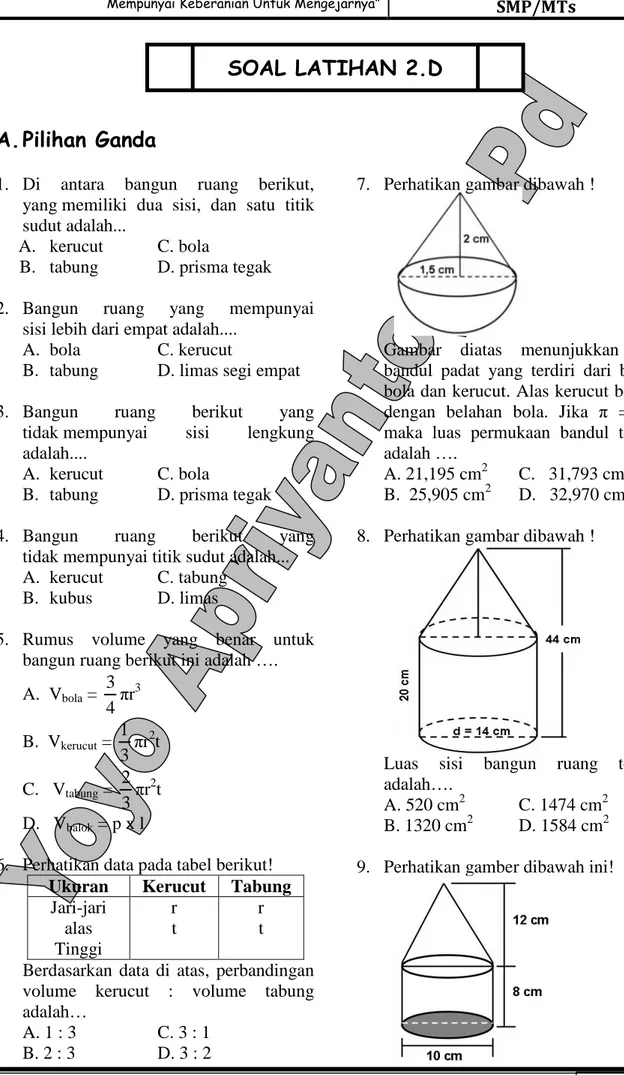
2.1 TABUNG
Subbab ini membahas unsur-unsur tabung, jaring-jaring tabung, rumus luas permukaan tabung (termasuk tabung tanpa tutup), dan rumus volume tabung. Contoh soal yang beragam, mulai dari menghitung volume hingga menyelesaikan masalah kontekstual, melatih siswa untuk mengaplikasikan rumus dan konsep secara tepat. Diagram jaring-jaring tabung membantu siswa memvisualisasikan bentuk tiga dimensi dan hubungan antara luas permukaan dan volume. Nilai aplikatifnya terlihat dalam perhitungan kapasitas dan bahan baku dalam berbagai industri.
2.2 KERUCUT
Subbab ini menjelaskan unsur-unsur kerucut, jaring-jaring kerucut, rumus luas permukaan kerucut (termasuk selimut kerucut), dan rumus volume kerucut. Soal-soal latihan menekankan pada pemahaman hubungan antara jari-jari, tinggi, dan garis pelukis. Visualisasi jaring-jaring kerucut memperkuat pemahaman siswa tentang bentuk tiga dimensi. Penerapan konsep ini penting dalam perhitungan kapasitas dan desain berbagai produk, seperti topi dan corong.
2.3 BOLA
Subbab ini membahas unsur-unsur bola, rumus luas permukaan bola, dan rumus volume bola. Soal-soal yang diberikan melatih kemampuan siswa dalam menghitung luas permukaan dan volume bola serta menyelesaikan masalah kontekstual yang melibatkan bola. Pemahaman konsep ini penting dalam berbagai bidang, seperti ilmu fisika, astronomi, dan teknik.
2.4 CAMPURAN TABUNG, KERUCUT & BOLA
Subbab ini menggabungkan konsep tabung, kerucut, dan bola dalam satu permasalahan. Siswa akan diajak menyelesaikan soal-soal yang melibatkan kombinasi bangun ruang tersebut, misalnya menghitung volume gabungan bangun ruang atau luas permukaan bangun gabungan. Hal ini meningkatkan kemampuan berpikir kritis dan analitis siswa dalam mengaplikasikan pengetahuan mereka dalam situasi yang lebih kompleks.
III. BAB 3 STATISTIKA
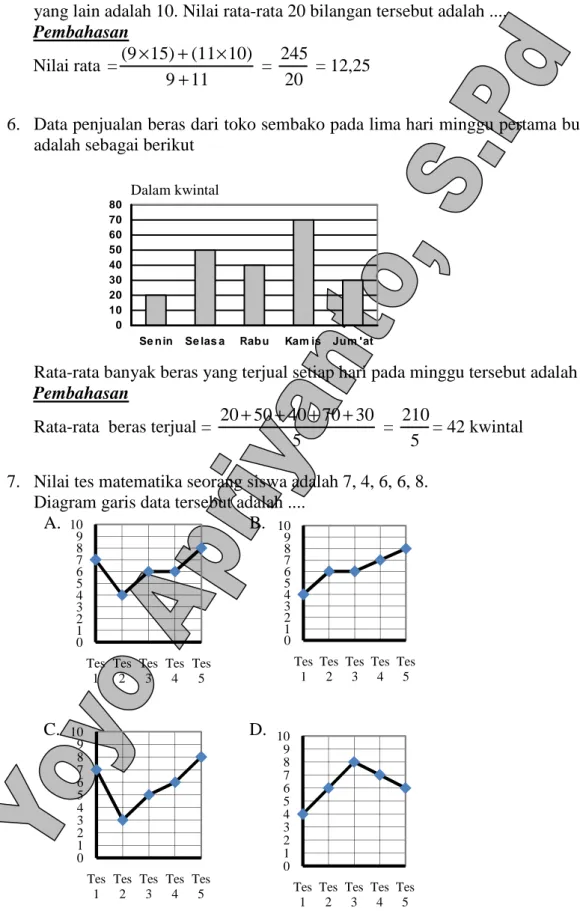
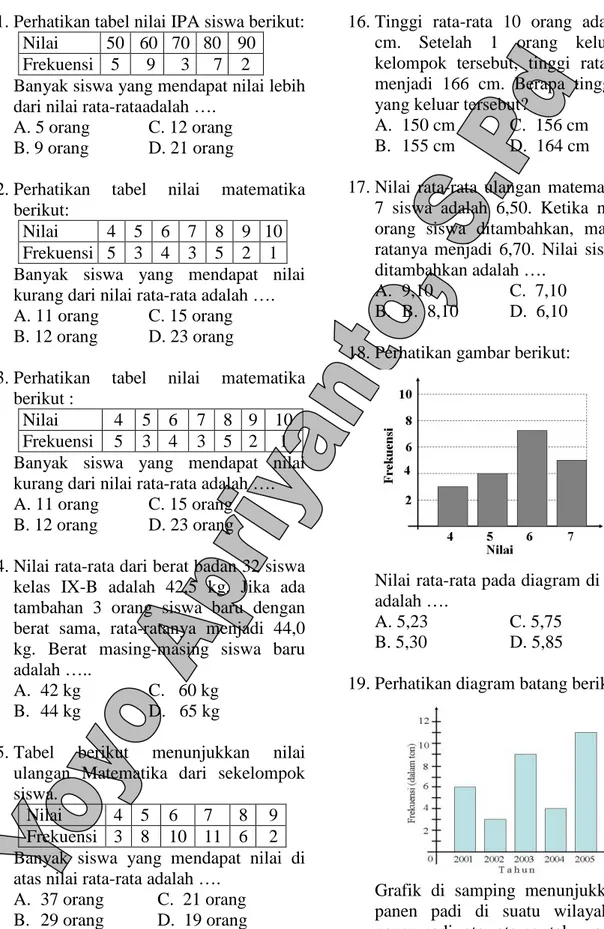
Bab ini memperkenalkan dasar-dasar statistika deskriptif. Siswa akan belajar tentang pengumpulan data, penyajian data dalam berbagai bentuk diagram (diagram batang, diagram garis, dan diagram lingkaran), dan perhitungan rata-rata (mean). Pemahaman konsep ini penting dalam menganalisis data dan menarik kesimpulan.
3.1 PENGUMPULAN DATA
Subbab ini membahas tentang pengertian statistika, populasi, dan sampel. Konsep ini penting sebagai landasan dalam memahami proses pengumpulan data yang representatif dan akurat. Pentingnya memilih sampel yang tepat untuk mewakili populasi dijelaskan secara rinci.
3.2 PENYAJIAN DATA
Subbab ini membahas cara menyajikan data dalam bentuk diagram batang, diagram garis, dan diagram lingkaran. Siswa diajarkan untuk memilih jenis diagram yang paling tepat untuk menyajikan data tertentu. Contoh soal dan latihan soal yang diberikan melatih siswa untuk menginterpretasi dan menganalisis informasi yang disajikan dalam berbagai bentuk diagram.
3.3 MEAN (RATA-RATA)
Subbab ini membahas perhitungan mean atau rata-rata hitung suatu data. Berbagai contoh soal dan latihan soal diberikan untuk melatih siswa menghitung mean dari data tunggal dan data kelompok, termasuk soal-soal yang melibatkan analisis data dan penarikan kesimpulan sederhana. Pemahaman mean sebagai ukuran kecenderungan pusat data sangat penting dalam analisis data.
IV. BAB 4 PELUANG (Tidak Tercakup dalam Text)
Bab ini akan membahas tentang konsep dasar peluang, ruang sampel, kejadian, dan perhitungan peluang suatu kejadian. Ini termasuk peluang kejadian saling lepas, peluang kejadian bersyarat, dan teorema Bayes. Penerapan konsep ini akan mencakup berbagai contoh, dari soal-soal sederhana hingga masalah-masalah yang lebih kompleks. Pemahaman ini memberikan dasar untuk statistika inferensial.
V. BAB 5 POLA BILANGAN, BARISAN DAN DERET BILANGAN (Tidak Tercakup dalam Text)
Bab ini akan membahas tentang pola bilangan, barisan aritmatika dan geometri, serta deret aritmatika dan geometri. Siswa akan belajar bagaimana mengidentifikasi pola, menentukan rumus umum suatu barisan dan deret, serta menyelesaikan masalah yang berkaitan dengan barisan dan deret. Ini melatih kemampuan berpikir logis dan analitis.