PENYELESAIAN MASALAH NILAI BATAS ORDE DUA MENGGUNAKAN METODE BEDA HINGGA
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Imelda Pa’dai NIM: 163114008
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2022
NUMERICAL SOLUTIONS OF SECOND ORDER BOUNDARY VALUE PROBLEMS USING A FINITE DIFFERENCE METHOD
Final Project
Presented as a Partial Fulfillment of the Requirements To Obtain the Degree of Sarjana Mathematics
Mathematics Study Program
By:
Imelda Pa’dai
Student Number: 163114008
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
2022
iii
iv
v
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa tugas akhir yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 18 Januari 2022 Penulis,
Imelda Pa’dai
vi MOTTO
“Sebab TUHAN, Dia sendiri akan berjalan di depanmu, Dia sendiri akan menyertai engkau, Dia tidak akan membiarkan engkau dan tidak akan
meninggalkan engkau; janganlah takut dan janganlah patah hati.”
Ulangan 31:8
vii
HALAMAN PERSEMBAHAN
Karya ini kupersembahkan untuk:
Tuhan Yesus Kristus yang selalu setia menyertaiku, kedua orang tua dan keluargaku yang selalu mendukung, serta almamaterku.
viii
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Imelda Pa’dai NIM : 163114008
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
PENYELESAIAN MASALAH NILAI BATAS ORDE DUA MENGGUNAKAN METODE BEDA HINGGA
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Dibuat di Yogyakarta
pada tanggal 18 Januari 2022 Yang menyatakan,
Imelda Pa’dai
ix
KATA PENGANTAR
Ucapan puji dan syukur kepada Tuhan Yesus Kristus atas segala berkat, hikmat, dan penyertaanNya sehingga tugas akhir ini dapat diselesaikan dengan baik. Tugas Akhir ini dibuat dengan tujuan memenuhi syarat untuk memperoleh gelar Sarjana Matematika pada Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma.
Penulis menyadari bahwa penulis melibatkan banyak pihak yang bersedia membantu dalam berbagai macam kesulitan, tantangan, dan hambatan. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih kepada.
1. Bapak Prof. Ir. Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku Dekan Fakultas Sains dan Teknologi sekaligus dosen pembimbing tugas akhir penulis yang selalu sabar dalam memberikan arahan dan telah meluangkan waktu, tenaga, dan pikiran kepada penulis.
2. Bapak Hartono, S.Si., M.Sc., Ph.D., selaku Ketua Program Studi Matematika.
3. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku Dosen pembimbing akademik.
4. Romo Prof. Dr. Frans Susilo, SJ., Bapak Dr. ret. nat. Herry Pribawanto Suryawan, S.Si., M.Si., Bapak Ricky Aditya, M.Sc., Ibu Maria Vianney Any Herawati, S.Si., M.Si., Ibu Dr. Lusia Krismiyati Budiasih selaku Dosen program studi Matematika.
5. Romo/Bapak/Ibu dosen/karyawan Fakultas Sains dan Teknologi yang telah berdinamika bersama selama penulis berkuliah.
6. Bapak, Mama, Kakak, Adek, dan Nenek yang selalu percaya, mendukung, dan memdoakan penulis.
7. Gembala dan Jemaat Gereja KIBAID Jemaat Yogyakarta yang senantiasa mendukung dan mendoakan penulis.
8. Teman-teman Prodi Matematika Angkatan 2016, terkhusus STUDY SOFT (Vanes, Diani, Lusi, Rika, Lydia, Devita, Yesi, Arnel, Tia, Cilla, Feli, Yuni).
x
9. Fritz dan Jerry yang meminjamkan laptop. Kak Lona dan Kak Selmi yang selalu memberikan semangat dan motivasi.
10. Semua pihak yang tidak dapat disebutkan satu per satu dalam proses penulisan Tugas Akhir ini.
Semoga segala perhatian, dukungan, bantuan dan cinta yang telah diberikan mendapatkan balasan dari Tuhan Yang Maha Esa. Penulis menyadari bahwa masih banyak kekurangan dalam penulisan Tugas Akhir ini. Oleh karena itu, penulis mengharapkan kritik yang membangun dan saran demi penyempurnaan Tugas Akhir ini. Harapan penulis, semoga Tugas Akhir ini bermanfaat bagi pembaca dan menjadi referensi belajar yang baik.
Yogyakarta, 18 Januari 2022 Penulis,
Imelda Pa’dai
xi ABSTRAK
Masalah nilai batas banyak muncul dalam bidang teknik, misalnya teknik sipil terkait bentuk dan kekuatan bangunan. Tugas akhir ini membahas masalah nilai batas yang berupa persamaan diferensial biasa orde dua, yang selanjutnya disebut masalah nilai batas orde dua. Masalah tersebut diselesaikan secara numeris menggunakan metode beda hingga. Skema numeris beda hingga dan hasil-hasil perhitungannya disajikan. Dari hasil pengamatan error metode beda hingga, diperoleh bahwa metode beda hingga dapat menyelesaikan masalah nilai batas orde dua secara akurat.
Kata kunci: persamaan diferensial biasa orde dua, masalah nilai batas, metode beda hingga.
xii ABSTRACT
Boundary value problems often arises in the field of engineering, for example, civil engineering related to the shape and strength of buildings. This final project discusses boundary value problems in the forms of second-order ordinary differential equations, hereinafter referred to as second-order boundary value problems. The problems are solved numerically using a finite difference method.
The finite difference numerical scheme and the results of its calculations are presented. From the observation of the finite difference method errors, it is found that the finite difference method solves second-order boundary value problems accurately.
Keywords: Second-order ordinary differential equations, boundary-value problems, finite-difference methods.
xiii DAFTAR ISI
HALAMAN JUDUL ... i
TITLE PAGE ... ii
LEMBAR PERSETUJUAN ... iii
LEMBAR PENGESAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
MOTTO ... vi
HALAMAN PERSEMBAHAN ... vii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ... viii
KATA PENGANTAR ... ix
ABSTRAK ... xi
ABSTRACT ... xii
KATA PENGANTAR ... xiii
DAFTAR ISI ... xiv
DAFTAR TABEL ... xv
DAFTAR GAMBAR ... xvi
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Rumusan Masalah ... 2
C. Batasan Masalah ... 3
D. Tujuan Penulisan ... 3
E. Manfaat Penelitian ... 3
F. Metode Penulisan ... 3
G. Sistematika Penulisan ... 3
BAB II PERSAMAAN DIFERENSIAL DAN HAL-HAL TERKAIT ... 5
A. Turunan ... 5
B. Persamaan Diferensial ... 6
C. Masalah Nilai Awal ... 8
D. Masalah Nilai Batas ... 10
E. Aproksimasi Beda Hingga ... 11
xiv
BAB III METODE BEDA HINGGA UNTUK MASALAH NILAI BATAS
LINEAR ... 12
A. Pengenalan Masalah ... 12
B. Metode Beda Hingga untuk Masalah Nilai Batas Linear ... 13
BAB IV METODE BEDA HINGGA UNTUK MASALAH NILAI BATAS NONLINEAR ... 22
A. Iterasi Metode Newton ... 23
B. Algoritma Beda Hingga Nonlinear ... 24
C. Ekstrapolasi Richardson ... 30
BAB V PENUTUP ... 32
A. Kesimpulan ... 32
B. Saran ... 32
DAFTAR PUSTAKA ... 33
LAMPIRAN ... 34
xv
DAFTAR TABEL
Tabel 3.1 Hasil perhitungan contoh 3.1 ... 18
Table 3.2 Hasil perhitungan ekstrapolasi Richardson untuk contoh 3.2 ... 21
Table 4.1 Hasil perhitungan contoh 4.1 ... 28
Tabel 4.2 Hasil perhitungan ekstrapolasi Richardson untuk contoh 4.1 ... 31
xvi
DAFTAR GAMBAR
Gambar 3.1 Defleksi balok persegi panjang ... 12
Gambar 3.2 Hasil perhitungan menggunakan MATLAB contoh 3.1 ... 19
Gambar 3.3 Grafik simulasi numeris contoh 3.1 ... 19
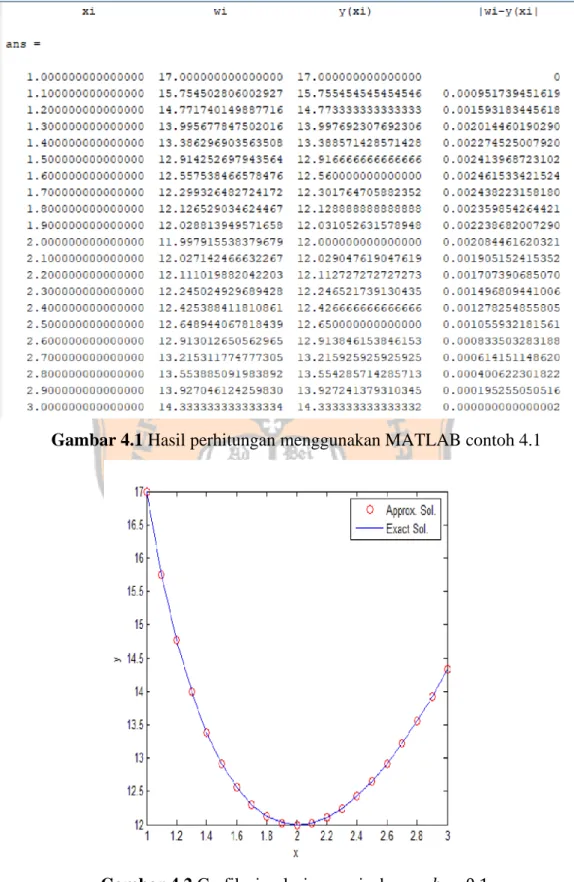
Gambar 4.1 Hasil perhitungan menggunakan MATLAB contoh 4.1 ... 29
Gambar 4.2 Grafik simulasi numeris contoh 4.1 ... 29
1 BAB I PENDAHULUAN
A. Latar Belakang
Persamaan diferensial adalah persamaan yang memuat turunan sekurang- kurangnya satu turunan dari suatu fungsi yang tidak diketahui (varibel terikat) terhadap satu atau lebih variabel bebas. Menyelesaikan persamaan diferensial berarti mencari fungsi yang tidak diketahui tersebut. Bentuk umum persamaan diferensial orde satu yaitu:
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦)
dengan 𝑡 adalah variabel bebas dan 𝑦 adalah variabel terikat.
Secara umum, persamaan diferensial dibagi menjadi dua yaitu persamaan diferensial biasa (PDB) dan persamaan diferensial parsial (PDP). PDB adalah persamaan diferensial yang hanya mengandung satu variabel bebas, sedangkan PDP adalah persamaan diferensial yang mengandung dua atau lebih variabel bebas (Zill, 2016). Persamaan diferensial mempunyai peranan yang penting dalam kehidupan, banyak permasalahan dalam bidang ilmu pengetahuan yang dapat diformulasikan ke dalam bentuk persamaan diferensial. Selain itu, persamaan diferensial juga digunakan sebagai model matematika dalam berbagai bidang sains dan teknik (Burden and Faires, 2011).
Terdapat dua macam cara dalam menyelesaikan persamaan diferensial yaitu secara analitik (biasanya digunakan untuk menyelesaikan masalah persamaan diferensial bentuk sederhana) dan numerik (biasanya digunakan untuk menyelesaikan persamaan diferensial yang sulit diselesaikan secara analitik).
Metode numerik adalah metode yang digunakan untuk menyelesaikan masalah matematika dengan operasi aritmetika (Chapra and Canale, 2015). Penyelesaian persamaan diferensial menggunakan metode numerik dibagi menjadi dua yaitu penyelesaian masalah nilai awal dan penyelesaian masalah nilai batas.
Masalah nilai awal biasa ditulis dengan
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦), untuk 𝑎 ≤ 𝑡 ≤ 𝑏, dengan kondisi awal
𝑦(𝑎) = 𝛼,
dan akan dicari pendekatan 𝑦(𝑡) untuk penyelesaian masalah nilai awal tersebut.
Selanjutnya, bentuk umum dari masalah nilai awal akan menjadi:
𝑑𝑛𝑦
𝑑𝑡𝑛 = 𝑓(𝑡, 𝑦, 𝑦′, 𝑦′′, … , 𝑦(𝑛−1)), untuk 𝑎 ≤ 𝑡 ≤ 𝑏, dengan sebanyak 𝑛 kondisi awal
𝑦(𝑎) = 𝛼1, 𝑦′(𝑎) = 𝛼2, …, 𝑦(𝑛−1)= 𝛼𝑛.
Dalam tugas akhir ini, masalah nilai batas orde dua dapat diselesaikan secara numeris yang akan ditentukan:
𝑦" = 𝑓(𝑥, 𝑦, 𝑦′), untuk 𝑎 ≤ 𝑥 ≤ 𝑏, dengan kondisi batas
𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽.
Salah satu cara untuk menyelesaikan masalah tersebut adalah dengan menggunakan metode beda hingga. Metode beda hingga lebih mudah dari segi pemrograman dengan komputer dan konsepnya mudah dipahami (Burden and Faires, 2011).
B. Rumusan Masalah
Berdasarkan latar belakang diatas, dapat dikemukakan beberapa masalah yang akan dikaji dalam tulisan ini, yaitu sebagai berikut:
1. Bagaimana bentuk skema numerik dan algoritma penyelesaian masalah nilai batas dengan metode beda hingga?
2. Bagaimana hasil perhitungan penyelesaian masalah nilai batas dengan metode beda hingga?
C. Batasan Masalah
Masalah yang dibahas dalam tugas akhir ini terbatas pada penyelesaian masalah nilai batas orde dua dalam suatu persamaan diferensial biasa dengan menggunakan metode beda hingga.
D. Tujuan Penulisan
Tujuan yang ingin dicapai dalam penulisan tugas akhir ini adalah sebagai berikut:
1. Menentukan bentuk skema numerik dan algoritma penyelesaian masalah nilai batas dengan metode beda hingga.
2. Menentukan hasil perhitungan penyelesaian masalah nilai batas dengan metode beda hingga.
E. Manfaat Penulisan
Manfaat penulisan yang diharapkan adalah pembaca dapat mengetahui dan memahami persamaan diferensial orde dua dan metode penyelesaiannya secara numeris.
F. Metode Penulisan
Metode penulisan yang digunakan dalam tugas akhir ini yaitu metode telaah pustaka dengan mempelajari berbagai buku-buku dan jurnal-jurnal yang berkaitan dengan materi yang dikaji dan menganalisanya untuk dijadikan bahan dalam pembuatan tugas akhir ini.
G. Sistematika Penulisan
Sistematika penulisan tugas akhir adalah sebagai berikut:
BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan
E. Manfaat Penelitian F. Metode Penulisan G. Sistematika Penulisan
BAB II PERSAMAAN DIFERENSIAL DAN HAL-HAL TERKAIT A. Turunan
B. Persamaan Diferensial C. Masalah Nilai Awal D. Masalah Nilai Batas E. Aproksimasi Beda Hingga
BAB III METODE BEDA HINGGA UNTUK MASALAH NILAI BATAS LINEAR
A. Pengenalan Masalah
B. Metode Beda Hingga untuk Masalah Nilai Batas Linear
BAB IV METODE BEDA HINGGA UNTUK MASALAH NILAI BATAS NONLINEAR
A. Iterasi Metode Newton
B. Algoritma Beda Hingga Nonlinear C. Ekstrapolasi Richardson
BAB V PENUTUP A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
5 BAB II
PERSAMAAN DIFERENSIAL DAN HAL-HAL TERKAIT
Pada bab ini, penulis membahas landasan teori yang digunakan dalam menyelesaikan masalah nilai batas orde dua dengan menggunakan metode beda hingga. Landasan teori yang digunakan dalam tugas akhir ini antara lain: turunan, persamaan diferensial, masalah nilai awal, masalah nilai batas, dan aproksimasi beda hingga.
A. Turunan
Dalam subbab ini akan dijelaskan definisi turunan dan contoh dari turunan.
Definisi 2.1
Fungsi 𝑓 didefinisikan dengan rumus 𝑓′(𝑥) = lim
ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ
disebut turunan dari 𝑓 terhadap fungsi 𝑥. Domain dari 𝑓 terdiri dari semua 𝑥 dalam domain 𝑓 dengan syarat limitnya ada (Anton dkk, 2012).
Contoh 2.1
Contoh ini diambil dari buku Stewart (2012).
Tentukan turunan 𝑓′(𝑥) apabila diketahui 𝑓(𝑥) = 𝑥3− 𝑥.
Penyelesaian:
𝑓′(𝑥) = lim
ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥)
ℎ = lim
ℎ→0
[(𝑥 + ℎ)3− (𝑥 + ℎ)] − [𝑥3− 𝑥]
ℎ
= lim
ℎ→0
𝑥3+ 3𝑥2ℎ + 3𝑥ℎ2+ ℎ3 − 𝑥 − ℎ − 𝑥3+ 𝑥 ℎ
= lim
ℎ→0
3𝑥2ℎ + 3𝑥ℎ2 + ℎ3− ℎ ℎ
= lim
ℎ→0(3𝑥2+ 3𝑥ℎ + ℎ2− 1)
= 3𝑥2− 1
Contoh 2.2
Tentukan turunan 𝑓′(𝑥) apabila diketahui 𝑓(𝑥) =1−𝑥
2+𝑥. Penyelesaian:
𝑓′(𝑥) = lim
ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥)
ℎ = lim
ℎ→0
1 − (𝑥 + ℎ)
2 + (𝑥 + ℎ)−1 − 𝑥 2 + 𝑥 ℎ
= lim
ℎ→0
(1 − 𝑥 − ℎ)(2 + 𝑥) − (1 − 𝑥)(2 + 𝑥 + ℎ) ℎ(2 + 𝑥 + ℎ)(2 + 𝑥)
= lim
ℎ→0
(2 − 𝑥 − 2ℎ − 𝑥2 − 𝑥ℎ) − (2 − 𝑥 + ℎ − 𝑥2− 𝑥ℎ) ℎ(2 + 𝑥 + ℎ)(2 + 𝑥)
= lim
ℎ→0
−3ℎ
ℎ(2 + 𝑥 + ℎ)(2 + 𝑥)
= lim
ℎ→0
−3
ℎ(2 + 𝑥 + ℎ)(2 + 𝑥)
= −3
(2 + 𝑥)2
B. Persamaan Diferensial
Dalam subbab ini akan dibahas tentang persamaan diferensial berdasarkan acuan dari buku Ross (1989). Persamaan diferensial yang akan dibahas yaitu definisi dan beberapa contoh persamaan diferensial.
Definisi 2.2 (Persamaan Diferensial)
Persamaan yang memuat turunan sekurang-kurangnya satu variabel terikat terhadap satu atau lebih variabel bebas disebut persamaan diferensial.
Contoh 2.3
Persamaan berikut merupakan contoh persamaan diferensial
𝑑2𝑦
𝑑𝑥2+ 𝑥𝑦 (𝑑𝑦
𝑑𝑥)2 = 0, (2.1)
𝑑4𝑥
𝑑𝑡4 + 5𝑑2𝑥
𝑑𝑡2 + 3𝑥 = sin 𝑡, (2.2)
𝜕𝑣
𝜕𝑠+𝜕𝑣
𝜕𝑡= 𝑣, (2.3)
𝜕2𝑢
𝜕𝑥2+𝜕2𝑢
𝜕𝑦2+𝜕2𝑢
𝜕𝑧2 = 0. (2.4)
Definisi 2.3 (Persamaan Diferensial Biasa)
Persamaan diferensial yang memuat sekurang-kurangnya satu variabel terikat terhadap satu variabel bebas disebut persamaan diferensial biasa.
Contoh 2.4
Persamaan (2.1) dan (2.2) adalah persamaan diferensial biasa. Pada persamaan (2.1) 𝑥 adalah variabel bebas tunggal dan 𝑦 adalah variabel terikat. Pada persamaan (2.2) variabel bebasnya adalah 𝑡 sedangkan 𝑥 adalah variabel terikat.
Definisi 2.4 (Persamaan Diferensial Parsial)
Persamaan diferensial yang memuat sekurang-kurangnya satu variabel terikat terhadap lebih dari satu variabel bebas disebut persamaan diferensial parsial.
Contoh 2.5
Persamaan (2.3) dan (2.4) adalah persamaan diferensial parsial. Pada persamaan (2.3) variabel 𝑠 dan 𝑡 adalah variabel bebas dan 𝑣 adalah variabel terikat. Pada persamaan (2.4) ada 3 variabel bebas yaitu 𝑥, 𝑦, dan 𝑧; dan 𝑢 adalah variabel terikatnya.
Definisi 2.5 (Orde Persamaan Diferensial)
Tingkat tertinggi dari turunan yang muncul dalam persamaan diferensial disebut orde dari suatu persamaan diferensial.
Contoh 2.6
Persamaan (2.1) merupakan persamaan diferensial berorde satu dan persamaan (2.2) merupakan persamaan diferensial berorde empat. Persamaan (2.3) dan (2.4) berturut-turut merupakan persamaan diferensial parsial berorde satu dan dua.
Definisi 2.6 (Persamaan Diferensial Biasa Linear)
Persamaan diferensial biasa linear berorde 𝑛 dengan 𝑦 variabel terikat dan 𝑥 variabel bebas adalah persamaan yang dapat ditulis dalam bentuk
𝑎0(𝑥)𝑑𝑑𝑥𝑛𝑦𝑛 + 𝑎1(𝑥)𝑑𝑑𝑥𝑛−1𝑛−1𝑦+ ⋯ + 𝑎𝑛−1(𝑥)𝑑𝑦𝑑𝑥+ 𝑎𝑛(𝑥)𝑦 = 𝑏(𝑥), (2.5) dimana 𝑎0 ≠ 0.
Contoh 2.7
Persamaan diferensial biasa berikut keduanya memiliki variabel terikat 𝑦, dapat dilihat bahwa turunan-turunannya berpangkat satu, tidak ada perkalian terhadap turunannya.
𝑑2𝑦
𝑑𝑥2+ 5𝑑𝑦
𝑑𝑥+ 6𝑦 = 0, (2.6)
𝑑4𝑦
𝑑𝑥4+ 𝑥2 𝑑3𝑦
𝑑𝑥3+ 𝑥3 𝑑𝑦
𝑑𝑥= 𝑥𝑒2. (2.7)
Definisi 2.7 (Persamaan Diferensial Biasa Nonlinear)
Persamaan diferensial biasa dikatakan nonlinear jika minimal salah satu dari persamaan diferensial biasa yang membentuknya merupakan persamaan diferensial biasa tidak linear.
Contoh 2.8
𝑑2𝑦
𝑑𝑥2+ 5𝑑𝑦
𝑑𝑥+ 6𝑦2 = 0, (2.8)
𝑑2𝑦
𝑑𝑥2+ 5 (𝑑𝑦
𝑑𝑥)3+ 6𝑦 = 0, (2.9)
𝑑2𝑦
𝑑𝑥2+ 5𝑦𝑑𝑦
𝑑𝑥+ 6𝑦 = 0. (2.10)
C. Masalah Nilai Awal Contoh 2.9
Tentukan penyelesaian 𝑓 dari persamaan diferensial
𝑑𝑦
𝑑𝑥 = 2𝑥 (2.11)
dengan 𝑥 = 1 sehingga 𝑓 bernilai 4.
Penjelasan:
Cari fungsi 𝑓 yang memenuhi dua syarat beriku:
1. Fungsi 𝑓 harus memenuhi persamaan (2.11). Fungsi 𝑓 harus sedemikian rupa sehingga 𝑓’(𝑥) = 2𝑥 untuk setiap 𝑥 dalam interval 𝐼.
2. Fungsi 𝑓 harus bernilai 4 di 𝑥 = 1. Fungsi 𝑓 harus sedemikian rupa sehingga 𝑓(1) = 4.
Notasi:
Masalah dapat diperlihatkan dalam notasi yang sederhana seperti berikut:
𝑑𝑦
𝑑𝑥= 2𝑥, 𝑦(1) = 4.
Notasi 𝑦(1) = 4 menyatakan bahwa penyelesaian yang diinginkan 𝑦 harus bernilai 4 pada 𝑥 = 1 yaitu 𝑦 = 4 pada 𝑥 = 1.
Penyelesaian:
𝑦 = 𝑥2+ 𝑐, (2.12) dimana 𝑐 sebarang bilangan konstan dan masing-masing penyelesaian memenuhi persyaratan 1. Selanjutnya akan ditentukan konstanta 𝑐 sehingga (2.12) memenuhi persyaratan 2 yaitu 𝑦 = 4 pada 𝑥 = 1. Substitusi 𝑥 = 1 dan 𝑦 = 4 pada persamaan (2.12) sehingga diperoleh 4 = 1 + 𝑐 pindah ruas menjadi 𝑐 = 3. Selanjutnya kembali pada persamaan (2.12) diperoleh
𝑦 = 𝑥2+ 3,
yang merupakan penyelesaian dari persamaan diferensial (2.11) yang bernilai 4 pada 𝑥 = 1. Dengan kata lain, fungsi 𝑓 didefinisikan sebagai
𝑓(𝑥) = 𝑥2+ 3,
memenuhi kedua persyaratan yang ditetapkan dalam masalah.
Dalam penerapan persamaan diferensial orde pertama dan yang lebih tinggi, masalah yang sering ditemui serupa dengan contoh 2.9 di atas yang melibatkan persamaan diferensial dengan satu atau lebih syarat batas yang harus dipenuhi oleh penyelesaian persamaan diferensial yang diberikan. Masalah nilai awal adalah persamaan diferensial yang hanya mengandung satu nilai 𝑥 atau biasa juga disebut sebagai masalah nilai batas satu titik.
Contoh 2.10
𝑑2𝑦
𝑑𝑥2+ 𝑦 = 0, 𝑦(1) = 3, 𝑦′(1) = −4.
Tentukan penyelesaian dari persamaan diferensial 𝑑2𝑦
𝑑𝑥2+ 𝑦 = 0,
Asumsikan jika 𝑥 = 1, maka nilai 𝑦 = 3 dan asumsikan turunan pertama 𝑦 bernilai −4 dengan 𝑥 = 1. Kedua syarat ini berhubungan dengan satu nilai 𝑥 yaitu 𝑥 = 1 yang disebut dengan masalah nilai awal.
D. Masalah Nilai Batas
Masalah nilai batas adalah persamaan diferensial biasa yang mengandung dua nilai fungsi 𝑥 yang berbeda.
Contoh 2.11
𝑑2𝑦
𝑑𝑥2+ 𝑦 = 0, 𝑦(0) = 1, 𝑦 (𝜋
2) = 5.
Dari contoh 2.11 di atas akan dicari penyelesaian dengan persamaan diferensial yang sama dengan contoh 2.10, tetapi memiliki dua nilai 𝑥 yang berbeda yaitu yang pertama saat 𝑥 = 0 maka nilai 𝑦 = 1 dan yang kedua saat 𝑥 = 𝜋/2 maka nilai 𝑦 = 5. Disebut masalah nilai batas karena memiliki dua syarat batas yang berbeda yaitu 0 dan 𝜋
2.
E. Aproksimasi Beda Hingga
Salah satu cara menyelesaikan persamaan diferensial adalah dengan menggunakan metode beda hingga. Metode beda hingga menggunakan ekspansi deret Taylor maju dan mundur 𝑓(𝑥) di titik 𝑥 sedemikian sehingga
𝑓(𝑥 + ℎ) = 𝑓(𝑥) + ℎ𝑓′(𝑥) +ℎ2
2!𝑓′′(𝑥) +ℎ3
3!𝑓′′′(𝑥) +ℎ4
4!𝑓4(𝑥) + ⋯ (2.11) 𝑓(𝑥 − ℎ) = 𝑓(𝑥) − ℎ𝑓′(𝑥) +ℎ2
2!𝑓′′(𝑥) −ℎ3
3!𝑓′′′(𝑥) +ℎ4
4!𝑓4(𝑥) + ⋯ (2.12) 𝑓(𝑥 + 2ℎ) = 𝑓(𝑥) + 2ℎ𝑓′(𝑥) +(2ℎ)2
2! 𝑓′′(𝑥) +(2ℎ)3
3! 𝑓′′′(𝑥) +(2ℎ)4
4! 𝑓4(𝑥) + ⋯ (2.13) 𝑓(𝑥 − 2ℎ) = 𝑓(𝑥) − 2ℎ𝑓′(𝑥) +(2ℎ)2
2! 𝑓′′(𝑥)
−(2ℎ)3
3! 𝑓′′′(𝑥) +(2ℎ)4
4! 𝑓4(𝑥) − ⋯ (2.14) Apabila (2.11) dijumlahkan dan dikurangkan dengan (2.12) akan diperoleh
𝑓(𝑥 + ℎ) + 𝑓(𝑥 − ℎ) = 2𝑓(𝑥) + ℎ2𝑓′′(𝑥) +ℎ124𝑓(4)(𝑥) + ⋯ (2.15) 𝑓(𝑥 + ℎ) − 𝑓(𝑥 − ℎ) = 2𝑓ℎ′(𝑥) +ℎ3
3 𝑓′′′(𝑥) + ⋯ (2.16) Apabila (2.3) dijumlahkan dan dikurangkan dengan (2.4) akan diperoleh
𝑓(𝑥 + 2ℎ) + 𝑓(𝑥 − 2ℎ) = 2𝑓(𝑥) + 4ℎ2𝑓′′(𝑥) +4ℎ4
3 𝑓(4)(𝑥) + ⋯ (2.17) 𝑓(𝑥 + 2ℎ) − 𝑓(𝑥 − 2ℎ) = 4ℎ𝑓′(𝑥) +8ℎ3
3 𝑓′′′(𝑥) + ⋯ (2.18) Dapat dilihat ketika persamaan (2.11) dan (2.12) dijumlahkan akan menghasilkan turunan genap, ketika dikurangkan akan menghasilkan turunan ganjil.
12 BAB III
METODE BEDA HINGGA UNTUK MASALAH NILAI BATAS LINEAR
Dalam bab ini akan dibahas pengenalan masalah dan metode beda hingga untuk masalah nilai batas linear.
A. Pengenalan Masalah
Masalah umum dalam teknik sipil adalah tentang defleksi sebuah balok persegi panjang yang dikenai muatan seragam sedangkan ujung balok ditopang sehingga tidak mengalami defleksi.
Gambar 3.1 Defleksi balok persegi panjang (Burden and Faires, 2011).
Misalkan 𝑙, 𝑞, 𝐸, 𝑆, dan 𝐼 masing-masing melambangkan panjang balok, intensitas dari muatan seragam, modulus elastisitas, tegangan pada titik akhir, dan momen inersia pusat. Persamaan diferensial yang mendekati situasi fisika dapat ditulis dalam bentuk:
𝑑2𝑤(𝑥) 𝑑𝑥2 = 𝑆
𝐸𝐼𝑤(𝑥) + 𝑞𝑥
2𝐸𝐼(𝑥 − 𝑙),
dimana 𝑤(𝑥) adalah defleksi pada posisi sejauh 𝑥 dari ujung kiri balok. Karena tidak terjadi defleksi di ujung balok, maka terdapat dua syarat batas, yaitu:
𝑤(0) = 0 dan 𝑤(𝑙) = 0.
Ketika balok memiliki ketebalan yang seragam, maka 𝐸𝐼 bersifat konstan.
Ketika ketebalan balok tidak seragam, momen inersia 𝐼 adalah fungsi dari 𝑥.
Masalah fisika bergantung posisi daripada bergantung waktu yang sering dideskripsikan dalam bentuk persamaan diferensial dengan kondisi dikenakan pada
lebih dari satu titik. Masalah nilai batas dua titik dalam penulisan ini menggunakan persamaan diferensial biasa orde dua yang berbentuk:
𝑦′′ = (𝑥, 𝑦, 𝑦′), untuk 𝑎 ≤ 𝑥 ≤ 𝑏 (3.1) dengan kondisi batas
𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽 (3.2)
B. Metode Beda Hingga untuk Masalah Nilai Batas Linear 1. Pendekatan Diskrit
Dipandang masalah nilai batas orde dua linear,
𝑦′′= 𝑝(𝑥)𝑦′+ 𝑞(𝑥)𝑦 + 𝑟(𝑥), untuk 𝑎 ≤ 𝑥 ≤ 𝑏, dengan 𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽. (3.3) Akan digunakan metode beda hingga untuk mengaproksimasi 𝑦’ dan 𝑦’’. Pertama, pilih bilangan bulat 𝑁 > 0 dan bagi [𝑎, 𝑏] sebanyak (𝑁 + 1) subinterval yang sama panjang yang titik akhirnya adalah titik penghubung 𝑥𝑖 = 𝑎 + 𝑖ℎ, untuk 𝑖 = 0,1, … , 𝑁 + 1, dimana ℎ =𝑏−𝑎
𝑁+1.
Dalam titik penghubung, 𝑥𝑖 untuk 𝑖 = 1,2, … , 𝑁, persamaan diferensial yang akan didekati dengan bentuk
𝑦′′(𝑥𝑖) = 𝑝(𝑥𝑖)𝑦′(𝑥𝑖) + 𝑞(𝑥𝑖)𝑦(𝑥𝑖) + 𝑟(𝑥𝑖). (3.4) Dengan mengekspansikan 𝑦 ke dalam polinomial Taylor berderajat empat di sekitar 𝑥𝑖 yang dinilai di 𝑥𝑖+1, diperoleh
𝑦(𝑥𝑖+1) = 𝑦(𝑥𝑖 + ℎ)
= 𝑦(𝑥𝑖) + ℎ𝑦′(𝑥𝑖) +ℎ2
2 𝑦′′(𝑥𝑖) +ℎ3
6 𝑦′′′(𝑥𝑖) +ℎ4
24𝑦(4)(𝜉𝑖+), untuk 𝜉𝑖+ pada (𝑥𝑖, 𝑥𝑖+1), dan dinilai di 𝑥𝑖−1, diperoleh
𝑦(𝑥𝑖−1) = 𝑦(𝑥𝑖 − ℎ)
= 𝑦(𝑥𝑖) − ℎ𝑦′(𝑥𝑖) +ℎ2
2 𝑦′′(𝑥𝑖) −ℎ3
6 𝑦′′′(𝑥𝑖) +ℎ4
24𝑦(4)(𝜉𝑖−), untuk 𝜉𝑖− pada (𝑥𝑖−1, 𝑥𝑖).
Jika persamaan di atas dijumlahkan, maka diperoleh 𝑦(𝑥𝑖+ 1) + 𝑦(𝑥𝑖−1) = 2𝑦(𝑥𝑖) + ℎ2𝑦′′(𝑥𝑖) +ℎ4
24[𝑦(4)(𝜉𝑖+) + 𝑦(4)(𝜉𝑖−)],
dan penyelesaian untuk 𝑦′′(𝑥𝑖) adalah 𝑦′′(𝑥𝑖) = 1
ℎ2[𝑦(𝑥𝑖+1) − 2𝑦(𝑥𝑖) + 𝑦(𝑥𝑖−1)] −ℎ2
24[𝑦(4)(𝜉𝑖+) + 𝑦(4)(𝜉𝑖−)].
Dengan demikian diperoleh 𝑦′′(𝑥𝑖) = 1
ℎ2[𝑦(𝑥𝑖+1) − 2𝑦(𝑥𝑖) + 𝑦(𝑥𝑖−1)] −ℎ2
12𝑦(4)(𝜉𝑖), (3.5) untuk 𝜉𝑖 pada (𝑥𝑖−1, 𝑥𝑖+1). Disebut Rumus Beda Pusat untuk 𝑦′′(𝑥𝑖).
Rumus Beda Pusat untuk 𝑦′(𝑥𝑖) berbentuk
𝑦′(𝑥𝑖) =2ℎ1 [𝑦(𝑥𝑖+1) − 𝑦(𝑥𝑖−1)] −ℎ62𝑦′′′(𝜂𝑖), (3.6) untuk 𝜂𝑖 pada (𝑥𝑖−1, 𝑥𝑖+1).
Dengan menggunakan skema beda pusat pada persamaan (3.4) akan menghasilkan persamaan
𝑦(𝑥𝑖+1) − 2𝑦(𝑥𝑖) + 𝑦(𝑥𝑖−1)
ℎ2 = 𝑝(𝑥𝑖) [𝑦(𝑥𝑖+1) − 𝑦(𝑥𝑖−1)
2ℎ ] + 𝑞(𝑥𝑖)𝑦(𝑥𝑖) +𝑟(𝑥𝑖) −ℎ2
12[2𝑝(𝑥𝑖)𝑦′′′(𝜂𝑖) − 𝑦(4)(𝜉𝑖)].
Metode beda hingga dengan galat pemotongan menghasilkan orde 𝑂(ℎ2) menggunakan persamaan dengan syarat batas 𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽 untuk mendefinisikan sistem persamaan linier
𝑤0 = 𝛼, 𝑤𝑁+1= 𝛽 dan
(−𝑤𝑖+1+2𝑤𝑖−𝑤𝑖−1
ℎ2 ) + 𝑝(𝑥𝑖) (𝑤𝑖+1−𝑤𝑖−1
2ℎ ) + 𝑞(𝑥𝑖)𝑤𝑖 = −𝑟(𝑥𝑖), (3.7) untuk setiap 𝑖 = 1,2, … , 𝑁.
Dalam bentuk yang akan ditinjau, persamaan (3.7) menjadi
− (1 +ℎ
2𝑝(𝑥𝑖)) 𝑤𝑖−1+ (2 + ℎ2𝑞(𝑥𝑖))𝑤𝑖 − (1 −ℎ
2𝑝(𝑥𝑖)) 𝑤𝑖+1= −ℎ2𝑟(𝑥𝑖), dan sistem persamaan yang dihasilkan dapat ditulis dalam bentuk matriks 𝑁 × 𝑁 tridiagonal
𝑨𝒘 = 𝒃, (3.8)
dimana
[
2 + ℎ2𝑞(𝑥1) −1 +ℎ
2𝑝(𝑥1) 0 ⋯ 0
−1 −ℎ
2𝑝(𝑥2) 2 + ℎ2𝑞(𝑥2) ⋮ ⋱ ⋮
0 ⋱ ⋱ ⋱ 0
⋮ ⋱ ⋱ ⋱ −1 +ℎ
2𝑝(𝑥𝑁−1)
0 ⋯ 0 −1 −ℎ
2𝑝(𝑥𝑁) 2 + ℎ2𝑞(𝑥𝑁) ] ,
𝒘 = [
𝑤1 𝑤2
⋮ 𝑤𝑁−1
𝑤𝑁 ]
, dan b=
[
−ℎ2𝑟(𝑥1) + (1 +ℎ
2𝑝(𝑥1)) 𝑤0
−ℎ2𝑟(𝑥2)
⋮
−ℎ2𝑟(𝑥𝑁−1)
−ℎ2𝑟(𝑥𝑁) + (1 −ℎ2𝑝(𝑥𝑁))𝑤𝑁+1] .
Teorema berikut memberikan syarat dimana sistem linear tridiagonal (3.8) memiliki penyelesaian yang tunggal.
Teorema 3.1
Misalkan 𝑝, 𝑞,dan 𝑟 kontinu pada [𝑎, 𝑏]. Jika 𝑞(𝑥) ≥ 0 pada [𝑎, 𝑏], maka sistem linear (3.8) mempunyai penyelesaian yang tunggal dengan syarat ℎ <2
𝐿, dimana 𝐿 = max
𝑎≤𝑥≤𝑏|𝑝(𝑥)|.
Harus diingat bahwa hipotesis Teorema 3.1 menjamin penyelesaian yang tunggal untuk masalah nilai batas (3.3). Algoritma berikut ini mengimplementasikan metode Beda Hingga Linear.
2. Algoritma Beda Hingga Linear
Untuk pendekatan penyelesaian masalah nilai batas
𝑦′′ = 𝑝(𝑥)𝑦′+ 𝑞(𝑥)𝑦 + 𝑟(𝑥), untuk 𝑎 ≤ 𝑥 ≤ 𝑏, dengan 𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽 ∶
MASUKAN titik akhir 𝑎, 𝑏; dengan syarat batas 𝛼, 𝛽; bilangan bulat 𝑁 ≥ 2.
KELUARAN pendekatan 𝑤𝑖 terhadap 𝑦(𝑥𝑖) untuk setiap 𝑖 = 0,1, … 𝑁 + 1.
Langkah 1 tetapkan ℎ =𝑏−𝑎
𝑁+1;
𝑥 = 𝑎 + ℎ;
𝑎1 = 2 + ℎ2𝑞(𝑥);
𝑏1= −1 + (ℎ
2) 𝑝(𝑥);
𝑑1 = −ℎ2𝑟(𝑥) + (1 + (ℎ
2) 𝑝(𝑥)) 𝛼.
Langkah 2 Untuk 𝑖 = 2, … , 𝑁 − 1 tetapkan 𝑥 = 𝑎 + 𝑖ℎ;
𝑎𝑖 = 2 + ℎ2𝑞(𝑥);
𝑏𝑖 = −1 + (ℎ
2) 𝑝(𝑥);
𝑐𝑖 = −1 − (ℎ
2) 𝑝(𝑥);
𝑑𝑖 = −ℎ2𝑟(𝑥).
Langkah 3 tetapkan 𝑥 = 𝑏 − ℎ;
𝑎𝑁= 2 + ℎ2𝑞(𝑥);
𝑐𝑁 = −1 − (ℎ
2) 𝑝(𝑥);
𝑑𝑁 = −ℎ2𝑟(𝑥) + (1 − (ℎ
2) 𝑝(𝑥)) 𝛽.
Langkah 4 tetapkan 𝑙1 = 𝑎1; (Gunakan Langkah 4-8 untuk menyelesaikan sistem linier tridiagonal)
𝑢1 = 𝑏1/𝑎1; 𝑧1 =𝑑1
𝑙1.
Langkah 5 Untuk 𝑖 = 2, … , 𝑁 − 1 tetapkan 𝑙𝑖 = 𝑎𝑖− 𝑐𝑖𝑢𝑖−1; 𝑢𝑖 =𝑏𝑖
𝑙𝑖 ;
𝑧𝑖 = 𝑑𝑖 − 𝑐𝑖𝑧𝑖−1 𝑙𝑖 .
Langkah 6 tetapkan 𝑙𝑁= 𝑎𝑁−𝑐𝑁𝑢𝑁−1; 𝑧𝑁= (𝑑𝑁− 𝑐𝑁𝑧𝑁−1)
𝑙𝑁 .
Langkah 7 tetapkan 𝑤0 = 𝛼;
𝑤𝑁+1= 𝛽.
𝑤𝑁= 𝑧𝑁.
Langkah 8 Untuk 𝑖 = 𝑁 − 1, … ,1 tetapkan 𝑤𝑖 = 𝑧𝑖 − 𝑢𝑖 𝑤𝑖+1.
Langkah 9 Untuk 𝑖 = 0, … , 𝑁 + 1 tetapkan 𝑥 = 𝑎 + 𝑖ℎ;
OUTPUT(𝑥, 𝑤𝑖).
Langkah 10 STOP (Prosedur selesai)
Contoh 3.1
Gunakan Algoritma di atas dengan 𝑁 = 9 untuk menyelesaikan masalah nilai batas 𝑦′′ = −2
𝑥𝑦′+ 2
𝑥2𝑦 +sin(ln𝑥) 𝑥2 , untuk 1 ≤ 𝑥 ≤ 2, dengan 𝑦(1) = 1 dan 𝑦(2) = 2.
Penyelesaian:
Untuk contoh ini, gunakan 𝑁 = 9, jadi ℎ = 0.1. selanjutnya bandingkan hasilnya dengan penyelesaian eksak
𝑦 = 𝑐1𝑥 + 𝑐2 𝑥2− 3
10sin (ln 𝑥) − 1
10cos(ln 𝑥),
dimana
𝑐2 = 1
70[8 − 12 sin(ln 2) − 4 cos(ln 2)] ≈ −0.03920701320, dan
𝑐1= 11
10− 𝑐2 ≈ 1.13920701320.
Hasil lengkapnya dapat dilihat pada Tabel 3.1.
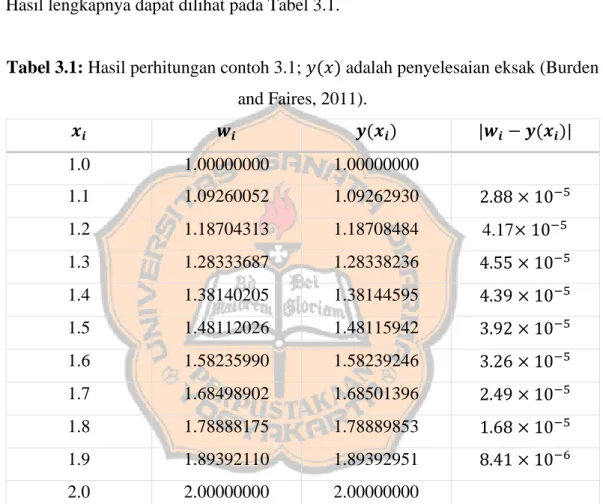
Tabel 3.1: Hasil perhitungan contoh 3.1; 𝑦(𝑥) adalah penyelesaian eksak (Burden and Faires, 2011).
𝒙𝒊 𝒘𝒊 𝒚(𝒙𝒊) |𝒘𝒊− 𝒚(𝒙𝒊)|
1.0 1.00000000 1.00000000
1.1 1.09260052 1.09262930 2.88 × 10−5
1.2 1.18704313 1.18708484 4.17× 10−5
1.3 1.28333687 1.28338236 4.55 × 10−5
1.4 1.38140205 1.38144595 4.39 × 10−5
1.5 1.48112026 1.48115942 3.92 × 10−5
1.6 1.58235990 1.58239246 3.26 × 10−5
1.7 1.68498902 1.68501396 2.49 × 10−5
1.8 1.78888175 1.78889853 1.68 × 10−5
1.9 1.89392110 1.89392951 8.41 × 10−6
2.0 2.00000000 2.00000000
Dapat dilihat dari tabel dimana galatnya cukup kecil sehingga algoritma beda hingga linear dapat digunakan untuk menyelesaikan masalah nilai batas.
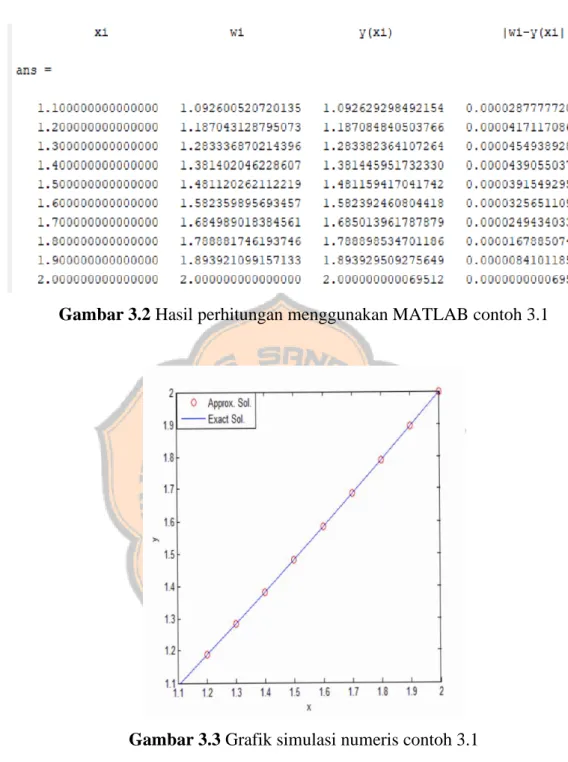
Gambar 3.2 Hasil perhitungan menggunakan MATLAB contoh 3.1
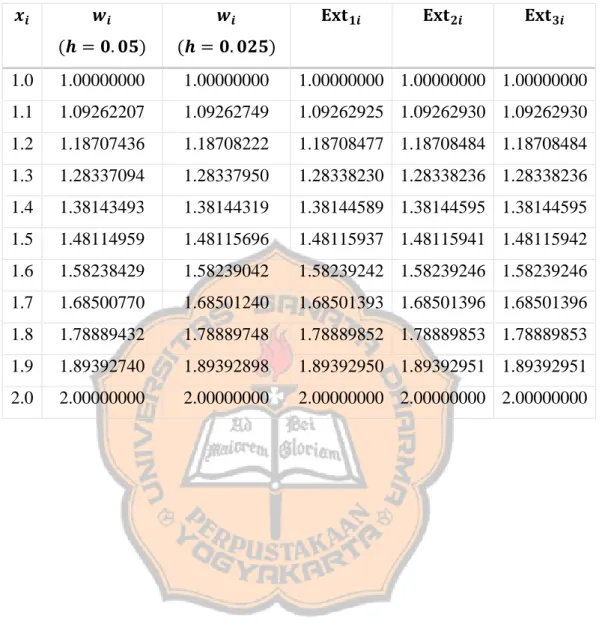
Gambar 3.3 Grafik simulasi numeris contoh 3.1
3. Menggunakan Ekstrapolasi Richardson
Untuk memperoleh metode beda hingga dengan galat pemotongan dengan orde yang tinggi, lebih baik memperhitungkannya dengan mengurangi langkah- langkahnya. Sebagai tambahan, teknik ekstrapolasi Richardson dapat digunakan secara efektif untuk metode ini karena galatnya berupa pangkat genap dari ℎ dengan koefisien tidak bergantung pada ℎ, asalkan 𝑦 terdiferensiasi.
Contoh 3.2
Terapkan ekstrapolasi Richardson untuk memperkirakan penyelesaian masalah nilai batas
𝑦′′ = −2
𝑥𝑦′+ 2
𝑥2𝑦 +sin(ln𝑥)
𝑥2 , untuk 1 ≤ 𝑥 ≤ 2, dengan 𝑦(1) = 1 dan 𝑦(2) = 2, gunakan ℎ = 0.1, 0.05, dan 0.025.
Jawab:
Penyelesaiannya dapat dilihat pada Tabel 3.2. Ekstrapolasi pertama adalah Ext1𝑖 = 4𝑤𝑖(ℎ = 0.05) − 𝑤𝑖(ℎ = 0.1)
3 ;
ekstrapolasi kedua adalah
Ext2𝑖 =4𝑤𝑖(ℎ = 0.025) − 𝑤𝑖(ℎ = 0.05)
3 ;
dan ekstrapolasi terakhir adalah
Ext3𝑖 =16Ext2𝑖− Ext1𝑖
15 .
Tabel 3.2: Hasil perhitungan ekstrapolasi Richardson untuk contoh 3.2
𝒙𝒊 𝒘𝒊
(𝒉 = 𝟎. 𝟎𝟓)
𝒘𝒊 (𝒉 = 𝟎. 𝟎𝟐𝟓)
𝐄𝐱𝐭𝟏𝒊 𝐄𝐱𝐭𝟐𝒊 𝐄𝐱𝐭𝟑𝒊
1.0 1.00000000 1.00000000 1.00000000 1.00000000 1.00000000 1.1 1.09262207 1.09262749 1.09262925 1.09262930 1.09262930 1.2 1.18707436 1.18708222 1.18708477 1.18708484 1.18708484 1.3 1.28337094 1.28337950 1.28338230 1.28338236 1.28338236 1.4 1.38143493 1.38144319 1.38144589 1.38144595 1.38144595 1.5 1.48114959 1.48115696 1.48115937 1.48115941 1.48115942 1.6 1.58238429 1.58239042 1.58239242 1.58239246 1.58239246 1.7 1.68500770 1.68501240 1.68501393 1.68501396 1.68501396 1.8 1.78889432 1.78889748 1.78889852 1.78889853 1.78889853 1.9 1.89392740 1.89392898 1.89392950 1.89392951 1.89392951 2.0 2.00000000 2.00000000 2.00000000 2.00000000 2.00000000
22 BAB IV
METODE BEDA HINGGA UNTUK MASALAH NILAI BATAS NONLINEAR
Dalam bab ini akan dibahas iterasi Newton, algoritma beda hingga nonlinear, dan ekstrapolasi Richardson untuk masalah nilai batas nonlinear.
Secara umum, masalah nilai batas nonlinear berbentuk
𝑦′′ = 𝑓(𝑥, 𝑦, 𝑦′), untuk 𝑎 ≤ 𝑥 ≤ 𝑏, dengan 𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽, Metode beda hingga untuk masalah nilai batas nonlinear hampir sama dengan metode beda hingga yang diterapkan untuk menyelesaikan masalah nilai batas linear. Namun karena sistem persamaan diferensialnya tidak linear, sehingga diperlukan proses iterasi untuk menyelesaikannya.
Dipandang 𝑓 memenuhi syarat berikut:
• 𝑓 dan turunan parsial 𝑓𝑦 dan 𝑓𝑦′ kontinu pada
𝐷 = {(𝑥, 𝑦, 𝑦′ )│𝑎 ≤ 𝑥 ≤ 𝑏, dengan −∞ < 𝑦 < ∞ dan −∞ < 𝑦′ < ∞};
• 𝑓𝑦(𝑥, 𝑦, 𝑦′) ≥ 𝛿 pada 𝐷, untuk 𝛿 > 0;
• 𝑘 konstan dan 𝐿 ada, dengan 𝑘 = max
(𝑥,𝑦,𝑦′)∈𝐷|𝑓𝑦(𝑥, 𝑦, 𝑦′)| dan 𝐿 = max
(𝑥,𝑦,𝑦′)∈𝐷|𝑓𝑦′(𝑥, 𝑦, 𝑦′)|.
Seperti pada masalah linear, selang [𝑎, 𝑏] dibagi sebanyak (𝑁 + 1) subinterval yang sama panjang yang titik akhirnya adalah titik penghubung 𝑥𝑖 = 𝑎 + 𝑖ℎ, untuk 𝑖 = 0,1, … , 𝑁 + 1. Asumsikan bahwa penyelesaian eksak memiliki batas turunan keempat sehingga dapat mengganti 𝑦"(𝑥𝑖) dan 𝑦′(𝑥𝑖) di setiap persamaan
𝑦"(𝑥𝑖) = 𝑓(𝑥𝑖, 𝑦(𝑥𝑖), 𝑦′(𝑥𝑖))
dengan menggunakan Rumus Beda Pusat yang diberikan dalam persamaan (3.5) dan (3.6) untuk setiap 𝑖 = 1,2, … , 𝑁, akan menghasilkan
𝑦(𝑥𝑖 + 1) − 2𝑦(𝑥𝑖) + 𝑦(𝑥𝑖−1) ℎ2
= 𝑓 (𝑥𝑖, 𝑦(𝑥𝑖),𝑦(𝑥𝑖+1) − 𝑦(𝑥𝑖−1)
2ℎ −ℎ2
6 𝑦′′′(𝜂𝑖)) +ℎ2
12𝑦(4)(𝜉𝑖), untuk 𝜉𝑖 dan 𝜂𝑖 pada interval (𝑥𝑖−1, 𝑥𝑖+1).
Seperti pada masalah linear, metode beda hingga yang dihasilkan yaitu dengan menghapus suku galat dan menggunakan syarat batas:
𝑤0 = 𝛼, 𝑤𝑁+1= 𝛽, dan
𝑤𝑖+1− 2𝑤𝑖+ 𝑤𝑖−1
ℎ2 + 𝑓 (𝑥𝑖, 𝑤𝑖,𝑤𝑖+1− 𝑤𝑖−1 2ℎ ) − 0, untuk setiap 𝑖 = 1,2, … , 𝑁.
Sistem nonlinear 𝑁𝑥𝑁 diperoleh dengan menggunakan metode, 2𝑤1− 𝑤2+ ℎ2𝑓 (𝑥1, 𝑤1,𝑤2− 𝛼
2ℎ ) − 𝛼 = 0, −𝑤1+ 2𝑤2− 𝑤3+ ℎ2𝑓 (𝑥2, 𝑤2,𝑤3−𝑤1
2ℎ ) = 0,
⋮ (4.1)
−𝑤𝑁−2+ 2𝑤𝑁−1− 𝑤𝑁+ ℎ2𝑓 (𝑥𝑁−1, 𝑤𝑁−1,𝑤𝑁− 𝑤𝑁−2
2ℎ ) = 0, −𝑤𝑁−1+ 2𝑤𝑁+ ℎ2𝑓 (𝑥𝑁, 𝑤𝑁,𝛽 − 𝑤𝑁−1
2ℎ ) − 𝛽 = 0 memiliki penyelesaian yang tunggal jika ℎ <2
𝐿.
A. Iterasi Metode Newton
Metode Newton digunakan untuk sistem nonlinear. Barisan dari iterasi {(𝑤1(𝑘), 𝑤2(𝑘), … , 𝑤𝑁(0))𝑡} adalah pusat yang dihasilkan untuk penyelesaian (4.1) jika pendekatan awal (𝑤1(0), 𝑤2(0), … , 𝑤𝑁(0))𝑡 cukup dekat untuk penyelesaian (𝑤1, 𝑤2, … , 𝑤𝑁)𝑡 dan matriks Jacobi digunakan untuk sistem nonsingular. Untuk sistem (4.1), matriks Jacobi 𝐽(𝑤1, 𝑤2, … , 𝑤𝑁) tridiagonal dengan entri-𝑖𝑗
𝐽(𝑤1, … , 𝑤𝑁)𝑖𝑗
= {
−1 +ℎ
2𝑓𝑦′(𝑥𝑖, 𝑤𝑖,𝑤𝑖+1− 𝑤𝑖−1
2ℎ ) , untuk 𝑖 = 𝑗 − 1 dan 𝑗 = 2, … , 𝑁, 2 + ℎ2𝑓𝑦(𝑥𝑖, 𝑤𝑖,𝑤𝑖+1− 𝑤𝑖−1
2ℎ ) , untuk 𝑖 = 𝑗 dan 𝑗 = 1, … , 𝑁,
−1 −ℎ
2𝑓𝑦′(𝑥𝑖, 𝑤𝑖,𝑤𝑖+1− 𝑤𝑖−1
2ℎ ) , untuk 𝑖 = 𝑗 + 1 dan 𝑗 = 1, … , 𝑁 − 1, dimana 𝑤0 = 𝛼 dan 𝑤𝑁+1 = 𝛽.
Metode Newton untuk sistem nonlinear memiliki syarat bahwa iterasi 𝑁𝑥𝑁 sistem nonlinear
𝐽(𝑤1, … , 𝑤𝑁)(𝑣1, … , 𝑣𝑁)𝑡
= − (2𝑤1− 𝑤2− 𝛼 + ℎ2𝑓 (𝑥1, 𝑤1,𝑤2− 𝛼 2ℎ ), −𝑤1+ 2𝑤2− 𝑤3+ ℎ2𝑓 (𝑥2, 𝑤2,𝑤3− 𝑤1
2ℎ ) , …,
−𝑤𝑁−2+ 2𝑤𝑁−1− 𝑤𝑁+ ℎ2𝑓 (𝑥𝑁−1, 𝑤𝑁−1,𝑤𝑁− 𝑤𝑁−2 2ℎ ),
−𝑤𝑁−1 + 2𝑤𝑁+ ℎ2𝑓 (𝑥𝑁, 𝑤𝑁,𝛽 − 𝑤𝑁−1
2ℎ ) − 𝛽)
𝑡
diselesaikan untuk 𝑣1, 𝑣2, … , 𝑣𝑁, jika
𝑤𝑖(𝑘) = 𝑤𝑖(𝑘−1)+ 𝑣𝑖, untuk setiap 𝑖 = 1,2, … , 𝑁.
B. Algoritma Beda Hingga Nonlinear
Untuk pendekatan penyelesaian masalah nilai batas nonlinear 𝑦′′ = 𝑓(𝑥, 𝑦, 𝑦′), untuk 𝑎 ≤ 𝑥 ≤ 𝑏,
dengan 𝑦(𝑎) = 𝛼 dan 𝑦(𝑏) = 𝛽 ∶
INPUT titik akhir 𝑎, 𝑏; syarat batas 𝛼, 𝛽; bilangan bulat 𝑁 ≥ 2; toleransi 𝑇𝑂𝐿; bilangan maksimum iterasi 𝑀.
OUTPUT pendekatan 𝑤𝑖 terhadap 𝑦(𝑥𝑖) untuk setiap 𝑖 = 0,1, . . . , 𝑁 + 1 atau jumlah maksimum iterasi melebihi.
Langkah 1 Tetapkan ℎ =𝑏−𝑎
𝑁+1; 𝑤0 = 𝛼;
𝑤𝑁+1= 𝛽.
Langkah 2 Untuk 𝑖 = 1, … , 𝑁 tetapkan 𝑤𝑖 = 𝛼 + 𝑖 (𝛽−𝛼
𝑏−𝑎) ℎ.
Langkah 3 Tetapkan 𝑘 = 1.
Langkah 4 Saat 𝑘 ≤ 𝑀, gunakan Langkah 5-16.
Langkah 5 Tetapkan 𝑥 = 𝑎 + ℎ;
𝑡 =𝑤2− 𝛼 2ℎ ;
𝑎1 = 2 + ℎ2𝑓𝑦(𝑥, 𝑤1, 𝑡);
𝑏1 = −1 + (ℎ
2) 𝑓𝑦′(𝑥, 𝑤1, 𝑡);
𝑑1 = −(2𝑤1− 𝑤2− 𝛼 + ℎ2𝑓(𝑥, 𝑤1, 𝑡)).
Langkah 6 Untuk 𝑖 = 2, … , 𝑁 − 1 tetapkan 𝑥 = 𝑎 + 𝑖ℎ;
𝑡 =𝑤𝑖+1− 𝑤𝑖−1
2ℎ ;
𝑎𝑖 = 2 + ℎ2𝑓𝑦(𝑥, 𝑤1, 𝑡);
𝑏𝑖 = −1 + (ℎ
2) 𝑓𝑦′(𝑥, 𝑤1, 𝑡);
𝑐𝑖 = −1 − (ℎ
2) 𝑓𝑦′(𝑥, 𝑤1, 𝑡);
𝑑𝑖 = −(2𝑤𝑖− 𝑤𝑖+1− 𝑤𝑖−1+ ℎ2𝑓(𝑥, 𝑖, 𝑡)).
Langkah 7 Tetapkan 𝑥 = 𝑏 − ℎ;
𝑡 =𝛽 − 𝑤𝑁−1
2ℎ ;
𝑎𝑁 = 2 + ℎ2𝑓𝑦(𝑥, 𝑤𝑁, 𝑡);
𝑐𝑁= −1 − (ℎ
2) 𝑓𝑦′(𝑥, 𝑤𝑁, 𝑡);
𝑑𝑁 = −(2𝑤𝑁− 𝑤𝑁−1− 𝛽 + ℎ2𝑓(𝑥, 𝑤𝑁, 𝑡)).
Langkah 8 Tetapkan 𝑙1 = 𝑎1; 𝑢1 = 𝑏1
𝑎1; 𝑧1 = 𝑑1
𝑙1.
Langkah 9 Untuk 𝑖 = 2, … , 𝑁 − 1 tetapkan 𝑙𝑖 = 𝑎𝑖 − 𝑐𝑖𝑢𝑖−1; 𝑢𝑖 = 𝑏𝑖
𝑙𝑖 ;
𝑧𝑖 = 𝑑𝑖 − 𝑐𝑖𝑧𝑖−1 𝑙𝑖 .
Langkah 10 Tetapkan 𝑙𝑁 = 𝑎𝑁−𝑐𝑁𝑢𝑁−1; 𝑧𝑁 =(𝑑𝑁− 𝑐𝑁𝑧𝑁−1)
𝑙𝑁 .
Langkah 11 Tetapkan 𝑣𝑁 = 𝑧𝑁
𝑤𝑁= 𝑤𝑁+ 𝑣𝑁.
Langkah 12 Untuk 𝑖 = 𝑁 − 1, … ,1 tetapkan 𝑣𝑖 = 𝑧𝑖 − 𝑢𝑖 𝑣𝑖+1; 𝑤𝑖 = 𝑤𝑖+ 𝑣𝑖.
Langkah 13 Jika ‖𝑣‖ ≤ 𝑇𝑂𝐿 maka gunakan Langkah 14 dan 15.
Langkah 14 Untuk 𝑖 = 0, … , 𝑁 + 1 tetapkan 𝑥 = 𝑎 + 𝑖ℎ;
OUTPUT(𝑥, 𝑤𝑖).
Langkah 15 STOP. (Prosedur berhasil.)
Langkah 16 Tetapkan 𝑘 = 𝑘 + 1.
Langkah 17 OUTPUT (‘Jumlah maksimum iterasi melebihi’) (Prosedur tidak berhasil.)
STOP.
Contoh 4.1
Dengan menggunakan algoritma di atas dengan ℎ = 0.1, masalah nilai batas nonlinear
𝑦′′= 1
8(32 + 2𝑥3 − 𝑦𝑦′), untuk 1 ≤ 𝑥 ≤ 3, dengan 𝑦(1) = 17 dan 𝑦(3) =43
3. Penyelesaian:
Prosedur yang digunakan dalam algoritma di atas akan berhenti jika iterasi yang berurutan berbeda kurang dari 10−8 dan akan tercapai dengan empat iterasi.
Hasilnya dapat dilihat dalam Tabel 4.1.
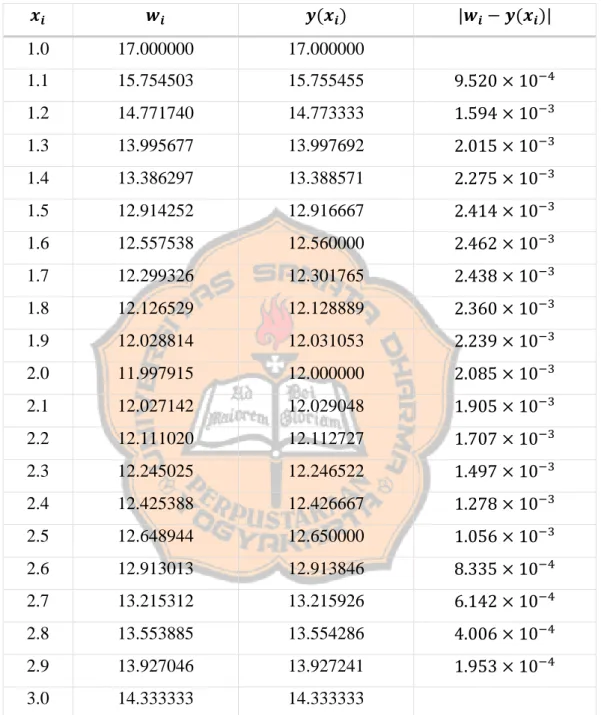
Tabel 4.1: Hasil perhitungan contoh 4.1; 𝑦(𝑥) adalah penyelesaian eksak (Burden and Faires, 2011).
𝒙𝒊 𝒘𝒊 𝒚(𝒙𝒊) |𝒘𝒊− 𝒚(𝒙𝒊)|
1.0 17.000000 17.000000
1.1 15.754503 15.755455 9.520 × 10−4
1.2 14.771740 14.773333 1.594 × 10−3
1.3 13.995677 13.997692 2.015 × 10−3
1.4 13.386297 13.388571 2.275 × 10−3
1.5 12.914252 12.916667 2.414 × 10−3
1.6 12.557538 12.560000 2.462 × 10−3
1.7 12.299326 12.301765 2.438 × 10−3
1.8 12.126529 12.128889 2.360 × 10−3
1.9 12.028814 12.031053 2.239 × 10−3
2.0 11.997915 12.000000 2.085 × 10−3
2.1 12.027142 12.029048 1.905 × 10−3
2.2 12.111020 12.112727 1.707 × 10−3
2.3 12.245025 12.246522 1.497 × 10−3
2.4 12.425388 12.426667 1.278 × 10−3
2.5 12.648944 12.650000 1.056 × 10−3
2.6 12.913013 12.913846 8.335 × 10−4
2.7 13.215312 13.215926 6.142 × 10−4
2.8 13.553885 13.554286 4.006 × 10−4
2.9 13.927046 13.927241 1.953 × 10−4
3.0 14.333333 14.333333
Dapat dilihat dari tabel dimana galatnya cukup kecil sehingga algoritma beda hingga nonlinear dapat digunakan untuk menyelesaikan masalah nilai batas.
Gambar 4.1 Hasil perhitungan menggunakan MATLAB contoh 4.1
Gambar 4.2 Grafik simulasi numeris dengan ℎ = 0.1.
C. Menggunakan Ekstrapolasi Richardson
Prosedur ekstrapolasi Richardson dapat digunakan untuk metode beda hingga nonlinear juga. Pada Tabel 4.2 memperlihatkan hasil ketika metode diterapkan untuk contoh dengan ℎ = 0.1, 0.05, dan 0.025, dengan empat iterasi untuk setiap nilai ℎ. Nilai dari 𝑤𝑖(ℎ = 0.25) akan akurat dengan galat sekitar 1.5 × 10−4. Tetapi, nilai dari Ext3𝑖 semuanya akurat pada tabel yang sudah terdaftar dengan galat maksimum yang sebenarnya yaitu 3.68 × 10−10.
Tabel 4.2: Hasil perhitungan ekstrapolasi Richardson untuk contoh 4.1 𝒙𝒊 𝒘𝒊(𝒉
= 𝟎. 𝟎𝟓)
𝒘𝒊(𝒉
= 𝟎. 𝟎𝟐𝟓)
𝐄𝐱𝐭𝟏𝒊 𝐄𝐱𝐭𝟐𝒊 𝐄𝐱𝐭𝟑𝒊
1.0 17.00000000 17.00000000 17.00000000 17.00000000 17.00000000 1.1 15.75521721 15.75539525 15.75545543 15.75545460 15.75545455 1.2 14.77293601 14.77323407 14.77333479 14.77333342 14.77333333 1.3 13.99718996 13.99756690 13.99769413 13.99769242 13.99769231 1.4 13.38800424 13.38842973 13.38857346 13.38857156 13.38857143 1.5 12.91606471 12.91651628 12.91666881 12.91666680 12.91666667 1.6 12.55938618 12.55984665 12.56000217 12.56000014 12.56000000 1.7 12.30115670 12.30161280 12.30176684 12.30176484 12.30176471 1.8 12.12830042 12.12874287 12.12899094 12.12888902 12.12888889 1.9 12.03049438 12.03091316 12.03105457 12.03105275 12.03105263 2.0 11.99948020 11.99987013 12.00000179 12.00000011 12.00000000 2.1 12.02857252 12.02892892 12.02902924 12.02904772 12.02904762 2.2 12.11230149 12.11262089 12.11272872 12.11272736 12.11272727 2.3 12.24614846 12.24642848 12.24652299 12.24652182 12.24652174 2.4 12.42636789 12.42658702 12.42666773 12.42666673 12.42666667 2.5 12.64973666 12.64993420 12.65000086 12.65000005 12.65000000 2.6 12.91362828 12.91379422 12.91384683 12.91384620 12.91384615 2.7 13.21577275 13.21588765 13.21592641 13.21592696 13.21592593 2.8 13.55418579 13.55426075 13.55428603 13.55428573 13.55428571 2.9 13.92719268 13.92722921 13.92724153 13.92724139 13.92724138 3.0 14.33333333 14.33333333 14.33333333 14.33333333 14.33333333
32 BAB V
KESIMPULAN DAN SARAN
A. Kesimpulan
Tugas Akhir ini telah membahas metode numerik untuk menyelesaikan masalah nilai batas linear dan nonlinear. Metode beda hingga telah berhasil menyelesaikan masalah-masalah tersebut. Sebagai suatu metode numerik, metode beda hingga menghasilkan penyelesaian hampiran yang mempunyai galat. Dari hasil pembahasan Tugas Akhir ini, galat tersebut cukup kecil.
B. Saran
Penelitian lebih lanjut, masalah nilai batas linear dan nonlinear dapat diselesaikan dengan metode-metode lain yang lebih akurat yaitu metode yang menghasilkan penyelesaian dengan galat yang lebih kecil.