A A BB 25 kN sin wt 25 kN sin wt 2m 2m 4m4m a a bb A A BB P P a a bb SOAL SOAL Keterangan: Keterangan: 1.
1. Material Material A A = = Beton Beton bertulang bertulang 30 30 x x 50 50 cmcm
Eb = Eb =
√
√
= 23500 Mpa = 2,35 x 10 = 23500 Mpa = 2,35 x 1055 kg/cm kg/cm22 f’c f’c = 25 Mpa= 25 Mpa fy fy = = 400 400 MpaMpa ζζ = = 0,050,05 BJ BJ = = 2,4 2,4 T/mT/m33 2.2. Material Material B B = = Struktur Struktur baja baja WF WF 300 300 x x 150150 fy fy = = 250 250 MpaMpa ζζ = = 0,020,02 Diketahui Diketahui : : w/wn w/wn = = 0,2; 0,2; 0,4; 0,4; 0,6; 0,6; 0,8; 0,8; 1,01,0 Diminta : Diminta : a.
a. Hitung perpindahan, gaya geser, momen akibat dynamic untuk berbagai macam Hitung perpindahan, gaya geser, momen akibat dynamic untuk berbagai macam w/wnw/wn yang diminta!
yang diminta! b.
b. Hitung tulangan yang dibutuhkanHitung tulangan yang dibutuhkan c.
c. Hitung stress ratio!Hitung stress ratio! PENYELESAIAN
PENYELESAIAN 1.
1. Untuk material A dengan beton bertulang 30 x 50 cmUntuk material A dengan beton bertulang 30 x 50 cm Muatan
Muatan balok balok (q) (q) = = (30 (30 x x 50) 50) x x 2,4.102,4.1033 = 3,6 kg/cm = 3,6 kg/cm Berat
Berat balok balok = = (30 (30 x x 50 50 x x 600) 600) x x (2,4x (2,4x 101033) = 2160 kg) = 2160 kg Berat
Berat Fo Fo = = 25 25 kN kN = = 2500 2500 kgkg Inersia
Inersia beton beton ==
= 312.500 cm = 312.500 cm44 KekakuanKekakuan Balok Balok di di titik titik C C ==
Pembuktian rumus kekakuan balok di titik C
Pembuktian rumus kekakuan balok di titik C dengan metode bidang momen sebagaidengan metode bidang momen sebagai muatan sebagai berikut.
L A B
Momen di titik C:Maka lendutan di titik C menjadi:
Maka, untuk kekakuan baloknya:
∑MB = 0 RA(L) – P(b) = 0
∑MA = 0 -RB(a+b) + P(a) = 0
(
)
(
)(
)
A C B 2m 4m Fs
Oleh karena itu, simpangan statik ystmenjadi = Fo/Kl
= 2500/20654,30 = 0,1210 cm
a. Menghitung perpindahan, gaya geser, momen akibat beban dinamik untuk berbagai macam w/wn yang diminta.
Untuk ratio frekuensi r = w/wn = 0,2 Amplitudo gerakan:
√
√
(dynamic load factor) :
√
Perbesaran gaya Fo menjadi (Fs) = Fo x DLF = 2500 x 1,041 = 2603,60 kg Reaksi perletakan:
Gaya geser maksimum menjadi RA = 2815,73 kg dan
Momen maksimum berada di titik C = RA(200) – 3,6(200)(100) = 491146 kgcm
Untuk ration frekuensi r = w/wn = 0,4
√
∑MB = 0
RA(600) – Fs(400) – 3,6(600)(300) = 0 RA = 2815,73 kg
√
Fs = Fo x DLF = 2500 x 1,189 = 2972,82 kg Reaksi Perletakan: RA = 3061,88 kg RB = 2070,94 kg Gaya geser = RA = 3061,88 kg Momen = RA(200) – 3,6(200)(100) = 540376 kg.cmUntuk ration frekuensi r = w/wn = 0,6
√
√
Fs = Fo x DLF = 2500 x 1,556 = 3889,196 kg Reaksi Perletakan: RA = Fs(400) + q(600)(300)/600 = 3672,80 kg RB = 2376,40 kg Gaya geser = RA = 3672,80 kg Momen = MC = RA(200) – 3,6(200)(100) = 662560 kg.cmUntuk ration frekuensi r = w/wn = 0,8
√
√
Fs = Fo x DLF = 2500 x 2,712 = 6779,08 kg Reaksi Perletakan: RA = Fs(400) + q(600)(300)/600 = 5599,38 kg RB = 3339,69 kg Gaya geser = RA = 5599,38 kgMomen = MC = RA(200) – 3,6(200)(100) = 1047876 kg.cm
Untuk ration frekuensi r = w/wn = 1,0
√
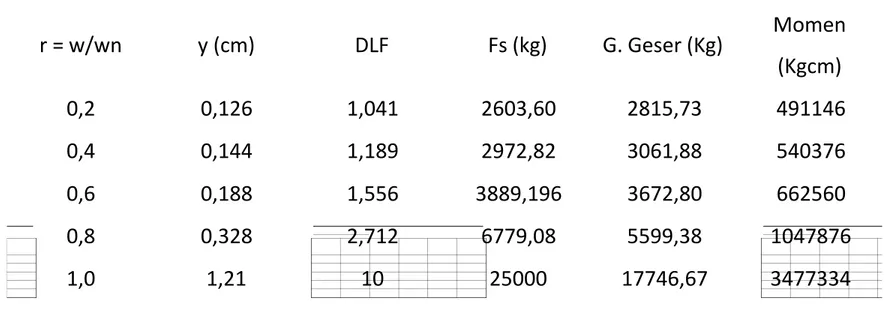
Fs = Fo x DLF = 2500 x 10 = 25000 kg Reaksi Perletakan: RA = 17746,67 kg RB = 9413,33 kg Gaya geser = RA = 17746,67 kg Momen = MC = 3477334 kg.cmTABEL : Amplitudo Gerakan, Dynamic Load Factor (DLF), Gaya Fs, Gaya Geser, dan Momen untuk berbagai macam w/wn
r = w/wn y (cm) DLF Fs (kg) G. Geser (Kg) Momen (Kgcm) 0,2 0,126 1,041 2603,60 2815,73 491146 0,4 0,144 1,189 2972,82 3061,88 540376 0,6 0,188 1,556 3889,196 3672,80 662560 0,8 0,328 2,712 6779,08 5599,38 1047876 1,0 1,21 10 25000 17746,67 3477334
b. Perhitungan tulangan yang dibutuhkan untuk balok beton (30 x 50 cm) Eb = 2,35 x 105 Mpa
f’c = 25 Mpa fy = 400 Mpa q = 3,6
Es (Modulus elastisitas tulangan) = 2 x 105 Mpa b = 30 cm
Menghitung Rasio Penulangan (
):
(
)
(
)
Ambil
Menghitung tinggi efektif balok (d) :
(
)
Karena d>h, maka solusi lain dalam mencari nilai d, digunakan ukuran ideal
, sehingga:
...(persamaan A )Anggap :
Dimana m dan Rn menjadi:
Persamaan A menjadi :
Dengan Rumus ABC, menjadi:
√
√
√
Ambil tulangan 6D25
...(Ok!)Berikut Gambar Perencanaan Tulangan :
2. Untuk Material A dengan baja profil 300 x 150, h = 300 ; b = 150 ; kf = 9 ; tw = 6,5
Diketahui: Berat profil = 36,7 kg/m Jari-jari girasi = 13 mm Luas penampang = 46,78 cm2 Ix = 7210 cm4 Iy = 508 cm4 fy =250 Mpa ζ = 0,02
Modulus elastik baja =200000 Mpa Kekakuan baja di titik C :
Oleh karena itu, simpangan statik Yst yang seterusnya menjadi:
a. Menghitung perpindahan, gaya geser, momen akibat beban dinamik untuk berbagai macam w/wn yang diminta:
-
⁄
√
√
√
√
Reaksi Perletakan:
Gaya geser =
= 1846,77 kg
-
⁄
√
√
√
√
Reaksi Perletakan:
Gaya geser =
= 2093,87 kg
-
⁄
√
√
√
√
Reaksi Perletakan:
Gaya geser =
= 2711,77 kg
-
⁄
√
√
√
√
Reaksi Perletakan:
Gaya geser =
= 4721,55 kg
-
⁄
Reaksi Perletakan:
Gaya geser =
= 41776,77 kg
TABEL. Amplitudo Gerakan Dynamic Load Factor (DLF), Gaya Fs, Gaya Geser, dan Momen untuk berbagai macam
⁄
⁄
y (cm) DLF Fs (kg) Gaya Geser (kg) Momen (kg.cm) 0,2 0,4 0,6 0,642 0,733 0,962 1,042 1,190 1,561 2605,00 2975,65 3902,50 1846,77 2093,87 2711,77 362014 411434 5350140,8 1,0 1,704 15,400 2,767 25,000 6917,17 62500,00 4721,55 41776,77 936970 8348014
b. Perhitungan stress ratio, sebagai berikut: tf = 9 mm tw = 6,5 mm b = 300 mm h = 500 mm bf = 150 mm E = 200000 Mpa fy = 250 Mpa Pengecekan Penampang:
IWF merupakan penampang yang dikategorikan sebagai penampang yang compact:
Component A (mm2) Y from top (mm) Ay (mm3) Flange Web 1350 1833 4,5 75,0 6075 137475 SUM 3183 143550
Perhitungan momen nominal baja dengan menganggap sudah berada pada zona plastis atau batas maksimum zona elastis.
Sehinga stress ratio:
Berarti beban yang dipikul terlalu besar, sehingga baja profil WF 300x150 tidak akan mampu menopang beban tersebut.