BAB II LANDASAN TEORI

BAB II

LANDASAN TEORI

2.1 Pengenalan Kecerdasan Buatan (Artificial Intelligence)

Kecerdasan buatan atau artificial intelligence merupakan salah satu bagian dari ilmu komputer yang membuat agar mesin (komputer) dapat melakukan pekerjaan seperti dan sebaik yang dilakukan oleh manusia. Seiring dengan perkembangan jaman, maka peran komputer semakin mendominasi kehidupan manusia, komputer tidak lagi digunakan hanya sebagai alat hitung, lebih dari itu komputer digunakan untuk dapat diberdayakan untuk mengerjakan segala sesuatu yang dapat dikerjakan manusia.

Manusia dapat menjadi pintar dan mampu menyelesaikan bebagai permasalahan yang ada karena manusia memiliki pengetahuan dan pengalaman yang diperoleh dari proses belajar, selain itu manusia juga diberi akal untuk dapat melakukan penalaran dan mengambil kesimpulan berdasarkan pengetahuan dan pengalaman yang mereka miliki.

Agar komputer bisa bertindak seperti dan sebaik manusia, maka komputer harus diberi bekal pengetahuan, dan mempunyai kemampuan menalar. Untuk itu pada kecerdasan buatan atau artificial intelligence, akan mencoba untuk memberikan beberapa metoda untuk membekali komputer dengan kedua komponen tersebut agar komputer bisa menjadi mesin yang pintar.

2.1.1 Perbedaan Kecerdasan Buatan Dan Kecerdasan Alami

Jika dibandingkan dengan kecerdasan alami (kecerdasan yang dimiliki oleh manusia), kecerdasan buatan memiliki beberapa kelebihan secara komersial antara lain :

a. Kecerdasan buatan lebih bersifat permanen. Kecerdasan alami akan cepat mengalami perubahan. Hal ini dimungkinkan karena kemampuan manusia untuk mengingat sesuatu cukup terbatas. Kecerdasan buatan tidak akan berubah sepanjang sistem komputer dan program tidak di ubah.

b. Kecerdasan buatan lebih mudah diduplikasi dan disebarkan. Menduplikasikan pengetahuan manusia dari satu orang ke orang lain membutuhkan proses yang sangat lama, dan juga suatu keahlian itu tidak akan pernah dapat diduplikasi dengan lengkap. Oleh karena itu, jika pengetahuan terletak pada suatu sistem komputer, pengetahuan tersebut dapat disalin dari komputer tersebut dan dapat dengan mudah dipindahkan ke komputer yang lain.

c. Kecerdasan buatan akan lebih murah dibanding dengan kecerdasan alami. Menyediakan layanan komputer akan lebih mudah dan lebih murah dibandingkan dengan harus mendatangkan seseorang untuk mengerjakan sejumlah perkerjaan dalam jangka waktu yang sangat lama

d. Kecerdasan buatan besifat konsisten. Hal ini disebabkan karena kecerdasan buatan adalah bagian dari teknologi komputer sedangkan kecerdasan alami akan senantiasa mengalami perubahan.

e. Kecerdasan buatan dapat didokumentasikan. Keputusan yang dibuat oleh komputer dapat didokumentasikan dengan mudah dengan melacak setiap aktivitas dari sistem tersebut.

f. Kecerdasan buatan dapat mengerjakan perkerjaan lebih cepat dibanding kecerdasan alami.

g. Kecerdasan buatan dapat mengerjakan pekerjaan lebih teliti dan lebih baik dibanding kecerdasan alami.

Sedangkan keuntungan dari kecerdasan alami adalah :

a. Kreatif. Kemampuan untuk menambah ataupun memenuhi pengetahuan itu sangat melekat pada jiwa manusia. Pada kecerdasan buatan, untuk menambah pengetahuan harus dilakukan melalui sistem yang dibangun.

b. Kecerdasan alami memungkinkan seseorang untuk menggunakan pengalaman secara langsung. Sedangkan pada kecerdasan buatan harus bekerja dengan input-input simbolik.

c. Pemikiran manusia dapat digunakan secara luas, sedangkan kecerdasan buatan sangat terbatas.

2.1.2 Sejarah Kecedasan Buatan

Kecerdasan buatan termasuk bidang ilmu yang relatif muda. Pada tahun 1950-an para ilmuwan dan peneliti mulai memikirkan bagaimana caranya agar mesin dapat melakukan perkerjaannya seperti yang dikerjakan oleh manusia. Alan Turing, seorang matematikawan dari inggris pertama kali mengusulkan adanya tes untuk melihat bisa tidaknya sebuah mesin dikatakan cerdas. Hasil tes tersebut kemudian dikenal dengan Turing Test.

Kecerdasan buatan itu atau “artificial intelligence” itu sendiri muncul dari seorang profesor dari Massachusetts Institute of Technology yang bernama John McCarthy pada tahun 1956 pada Dartmouth Conference yang dihadiri oleh para peneliti AI. Pada konferensi tersebut juga didefinisikan tujuan dari kecerdasan buatan, yaitu:

mengetahui dan memodelkan proses-proses berpikir manusia dan mendesign mesin agar dapat menirukan kelakuan manusia tersebut. Beberapa program AI yang mulai dibuat pada tahun 1956-1966, antara lain :

1. Logic Theorist, diperkenalkan pada Dartmouth Conference, program ini dapat membuktikan teori-teori matematika.

2. Sad Sam, diprogram oleh Robert K. Lindsay (1960). Program ini dapat mengetahui kalimat-kalimat sederhana yang ditulis dalam bahasa inggris dan mampu memberikan jawaban dari fakta-fakta yang didengar dalam sebuah percakapan.

3. ELIZA, diprogram oleh Joseph Weizenbaum (1967). Program ini mampu melakukan terapi terhadap pasien dengan memberikan beberapa pertanyaan.

2.1.3 Lingkup Kecerdasan Buatan Pada Aplikasi Komersial

Makin pesatnya perkembangan teknologi menyebabkan adanya perkembangan dan perluasan lingkup yang membutuhkan kehadiran kecerdasan buatan. Karakteristik ‘cerdas’ sudah mulai dibutuhkan tidak hanya dibidang ilmu komputer (informatika), namun juga sudah merambah diberbagai disiplin ilmu yang lain. Lingkup utama dalam kecerdasan buatan adalah :

1. Sistem Pakar (Expert System). Disini komputer digunakan sebagai sarana untuk menyimpan pengetahuan para pakar. Dengan demikian komputer akan memiliki keahlian untuk menyelesaikan permasalahan dengan meniru keahlian yang dimiliki oleh pakar.

2. Pengolahan Bahasa Alami (Natural Language Processing). Dengan pengolahan bahasa alami ini diharapkan user dapat berkomunikasi dengan komputer dengan menggunakan bahasa sehari-hari.

3. Pengenalan Ucapan (Speech Recognition). Melalui pengenalan ucapan diharapkan manusia dapat berkomunikasi dengan komputer dengan menggunakan suara

4. Robotika dan Sistem Sensor (Robotics And Sensory System).

5. Computer Vision, mencoba untuk dapat menginterpretasikan gambar atau obyek-obyek tampak melalui komputer.

6. Intelligent Computer-aided Instruction. Komputer dapat digunakan sebagai

tutor yang dapat melatih dan mengajar.

7. Game Playing, mencoba agar komputer dapat melakukan keputusan dalam

bermain game sesuai dengan pemikiran manusia.

Beberapa karakteristik yang ada pada sistem yang menggunakan artificial

intelligence adalah pemrogramannya yang cenderung bersifat simbolik ketimbang

algoritmik, bisa mengakomodasi input yang tidak lengkap, bisa melakukan inferensi, dan adanya pemisahan antara kontrol dengan pengetahuan. Namun, seiring dengan perkembangan teknologi, muncul beberapa teknologi yang juga bertujuan untuk membuat agar komputer menjadi cerdas sehingga dapat menirukan kerja manusia sehari-hari.

Teknologi ini juga mampu mengakomodasikan adanya ketidakpastian dan ketidaktepatan data input, dengan didasari pada teori himpunan, maka pada tahun 1965 muncul Logika Fuzzy. Kemudian pada tahun 1975 John Holland mengatakan bahwa setiap problem berbentuk adaptasi (alami maupun buatan) secara umum dapat

diformulasikan dalam terminologi genetika. Algoritma genetika ini merupakan simulasi proses evolusi Darwin dan operasi genetika atas kromosom.

2.1.4 Soft Computing

Soft computing adalah koleksi dari beberapa metodologi yang bertujuan untuk

mengeksploitasi adanya toleransi terhadap ketidakpastian, ketidaktepatan, dan kebenaran parsial untuk dapat diselesaikan dengan mudah, robustness, dan biaya penyelesaiannya murah. Definisi ini pertama kali diungkapkan oleh Prof. Lotfi A. Zadeh pada tahun 1992.

Soft computing merupakan inovasi baru dalam membangun sistem cerdas. Sistem

cerdas ini merupakan sistem yang memiliki keahlian seperti manusia pada domain tertentu, mampu beradaptasi dan belajar agar dapat bekerja lebih baik jika terjadi perubahan lingkungan. Unsur-unsur pokok dalam Soft Computing, adalah :

1. Sistem Fuzzy (mengakomodasi ketidaktepatan). 2. Jaringan Syaraf (menggunakan pembelajaran).

3. Probabilistic Reasoning (mengakomodasi ketidakpastian). 4. Evolutionary Computing (optimasi).

Keempat unsur tersebut bukan merupakan pesaing antara satu dengan yang lain, namun diantaranya bisa saling melengkapi, biasanya unsur-unsur pokok tersebut akan digunakan secara sinergis ketimbang dikerjakan secara sendiri-sendiri. Selain itu Soft

Computing memiliki beberapa karakteristik, antara lain :

1. Soft Computing memerlukan keahlian manusia, apabila direpresentasikan dalam bentuk aturan (IF – THEN).

3. Soft Computing merupakan teknik optimasi baru. 4. Soft Computing menggunakan komputasi numeris. 5. Soft Computing memiliki toleransi kegagalan.

2.2 Mendefinisikan Masalah Sebagai Suatu Ruang Keadaan

Seperti yang telah kita ketahui bahwa, pada sistem yang menggunakan kecerdasan buatan, akan mencoba untuk memberikan output berupa solusi dari suatu masalah berdasarkan kumpulan pengetahuan yang ada. Secara umum, untuk membangun suatu sistem yang mampu menyelesaikan masalah, perlu dipertimbangkan 4 hal :

1. Mendefinisikan masalah dengan tepat. Pendefinisian ini mencakup spesifikasi yang tepat mengenai keadaan awal dan solusi yang diharapkan.

2. Menganalisis masalah tersebut serta mencari beberapa teknik penyelesaian masalah yang sesuai.

3. Merepresentasikan pengetahuan yang perlu untuk menyelesaikan masalah tersebut.

4. Memlilih teknik penyelesaian masalah yang terbaik.

Untuk menyelesaikan suatu masalah diperlukan representasi masalah tersebut kedalam ruang keadaan (State Space), yaitu suatu ruang yang berisi semua keadaan yang mungkin. Sehingga secara umum, untuk mendeskripsikan masalah dengan baik, harus :

1. Mendefinisikan suatu ruang keadaan. 2. Menetapkan satu atau lebih keadaan awal. 3. Menetapkan satu atau lebih tujuan.

Ada beberapa cara untuk merepresentasikan Ruang Keadaan, antara lain :

2.2.1 Graph Keadaan

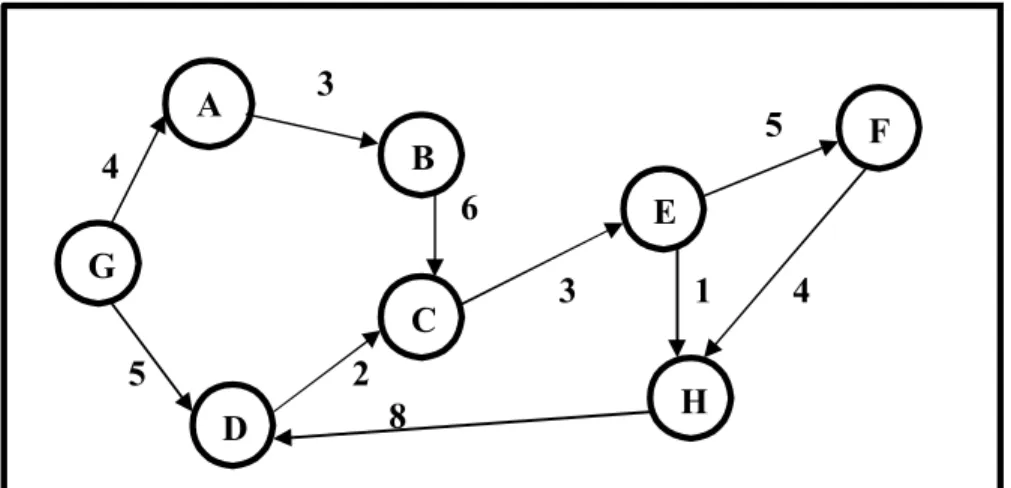
Graph terdiri dari node-node yang menunjukan keadaan yaitu keadaan awal dan keadaan baru yang akan dicapai dengan menggunakan operator. Node-node dalam graph keadaan saling dihubungkan dengan menggunakan arc (busur) yang diberi panah untuk menunjukan arah dari suatu keadaan ke keadaan berikutnya.

Gambar 2.1 Graph Keadaan

2.2.2 Pohon Pelacakan

Untuk menghindari kemungkinan adanya proses pelacakan suatu node secara berulang, maka digunakan struktur pohon.

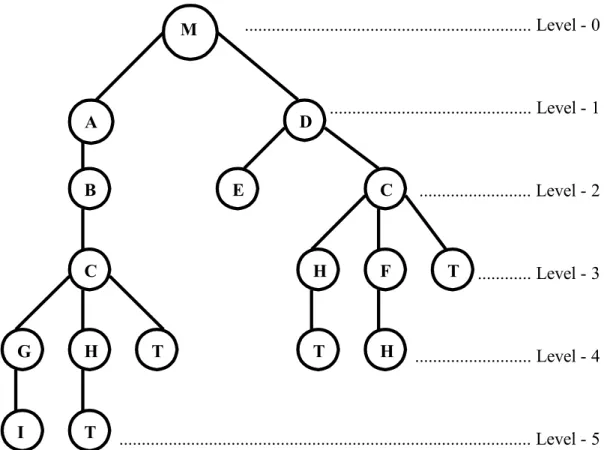
Struktur pohon digunakan untuk menggambarkan keadaan secara hirarkis. Pohon juga terdiri dari beberapa node. Node yang terletak pada level-0 disebut dengan nama “akar”. Node akar menunjukan keadaan awal yang biasanya merupakan topik atau obyek. Node akar memiliki beberapa percabangan yang terdiri atas beberapa node successor

3 5 4 6 3 1 4 5 2 8 A B C D E F G H

yang sering disebut dengan nama “anak” dan merupakan node-node perantara. Namun jika dilakukan pencarian mundur, maka dapat dikatakan bahwa node tersebut memiliki

predecessor. Node-node yang tidak memiliki anak sering disebut dengan nama node

“daun” yang menunjukan akhir dari suatu pencarian, dapat berupa tujuan yang diharapkan (goal) atau jalan buntu (dead end).

... Level - 0 ... Level - 1 ... Level - 2 ... Level - 3 ... Level - 4 ... Level - 5

Gambar 2.2 Struktur Pohon

2.3 Metode Pencarian dan Pelacakan

Hal penting dalam menentukan keberhasilan sistem berdasarkan kecerdasan adalah kesuksesan dalam pencarian dan pencocokan. Pada dasarnya ada 2 teknik

A B C D E C G H M I T F H T H T T

pencarian dan pelacakan yang digunakan, yaitu pencarian buta (blind search) dan pencarian terbimbing (heuristic search).

2.3.1 Pencarian Buta (Blind Search)

Pada metode pencarian buta (blind search) ada 2 metode yang umum digunakan, antara lain :

1. Pencarian Melebar Pertama (Breadth-First Search)

Pada metode Breadth-First Search, semua node pada level n akan dikunjungi terlebih dahulu sebelum mengunjungi node-node pada level n+1. Pencarian dimulai dari node akar terus ke level ke-1 dari kiri ke kanan, kemudian berpindah ke level berikutnya demikian pula dari kiri ke kanan hingga ditemukannya solusi.

2. Pencarian Mendalam Pertama (Depth-First Search)

Pada metode Depth-First Search, proses pencarian akan dilakukan pada semua anaknya sebelum dilakukan pencarian ke node-node yang selevel. Pencarian dimulai dari node akar ke level yang lebih tinggi. Proses ini diulangi terus hingga ditemukannya solusi.

2.3.2 Pencarian Heuristik (Heuristic Search)

Pencarian buta tidak selalu dapat diterapkan dengan baik, hal ini disebabkan waktu aksesnya yang cukup lama serta besarnya memori yang diperlukan. Kelemahan ini sebenarnya dapat diatasi jika ada informasi tambahan dari domain yang bersangkutan. Ada 4 metode pencarian heuristik :

1. Pembangkit dan penggujian (Generate and Test)

Pada prinsipnya metode ini merupakan penggabungan antara depth-first

search dengan pelacakan mundur (backtracking), yaitu bergerak ke belakang

menuju pada suatu keadaan awal. Nilai pengujian berupa jawaban ‘ya’ atau ‘tidak’.

2. Pendakian bukit (Hill Climbing)

Metode ini hampir sama dengan metode pembangkitan dan pengujian, hanya saja proses pengujian dilakukan dengan fungsi heuristik. Pembangkitan keadaan berikutnya sangat tergantung pada feedback dari prosedur pengetesan. Tes yang berupa fungsi heuristik ini akan menunjukan seberapa baiknya nilai terkaan yang diambil terhadap keadaan-keadaan lainnya yang mungkin.

3. Pencarian terbaik pertama (Best First Search)

Metode best-first search ini merupakan kombinasi dari metode depth-first

search dan metode breadth-first search dengan mengambil kelebihan dari

kedua metode tersebut. Apabila pada pencarian dengan metode hill climbing tidak diperbolehkan untuk kembali ke node pada level yang lebih rendah meskipun node pada level yang lebih rendah tersebut memiliki nilai heuristik yang lebih baik, lain halnya dengan metode best-first search ini. Pada metode

best-first search, pencarian diperbolehkan mengunjungi node yang ada dilevel

yang lebih rendah, jika ternyata node pada level yang lebih tinggi ternyata memiliki nilai heuristik yang lebih buruk.

4. Simulated Annealing

Ide dasar simulated annealing terbentuk dari pemrosesan logam. Annealing (memanaskan kemudian mendinginkan) dalam pemrosesan logam ini adalah suatu proses bagaimana membuat bentuk cair berangsur-angsur menjadi bentuk yang lebih padat seiring dengan penurunan temperatur. Simulated

annealing biasanya digunakan untuk penyelesaian masalah yang mana

perubahan keadaan dari suatu kondisi ke kondisi yang lainnya membutuhkan ruang yang sangat luas, misalkan perubahan gerakan dengan menggunakan permutasi pada masalah Travelling Salesman Problem.

2.4 Reduksi Masalah

Pada algoritma-algoritma terdahulu, kita mencari solusi menggunakan pohon OR, dimana lintasan dari awal sampai tujuan tidak terletak pada satu cabang. Apabila lintasan dari keadaan awal sampai tujuan dapat terletak pada satu cabang, maka kita akan dapat menemukan tujuan lebih cepat. Ada beberapa algoritma untuk mereduksi masalah, antara lain :

1. Graph AND-OR

Algoritma Graph AND-OR ini pada dasarnya sama dengan Best-First Search, dengan mempertimbangkan adanya arc AND.

2. Algoritma AO*

Algoritma AO* menggunakan struktur Graph. Tiap-tiap node pada graph tersebut akan memiliki nilai h’ yang merupakan biaya estimasi jalur dari node itu sendiri sampai suatu solusi.

2.5 Representasi Pengetahuan

Dalam menyelesaikan masalah kecerdasan buatan dibutuhkan pengetahuan yang cukup. Tidak hanya itu, sistem juga harus memiliki kemampuan untuk menalar. Basis pengetahuan dan kemampuan untuk melakukan penalaran merupakan bagian terpenting dari sistem yang mengunakan kecerdasan buatan.

2.5.1 Logika

Logika adalah bentuk representasi pengetahuan yang paling tua. Proses logika adalah proses membentuk kesimpulan atau menarik suatu inferensi berdasarkan fakta yang telah ada. Input dari proses logika berupa premis atau fakta-fakta yang diakui kebenarannya sehingga dengan melakukan penalaran pada proses logika dapat dibentuk suatu inferensi atau kesimpulan yang benar pula.

Ada 2 penalaran yang dapat dilakukan untuk mendapat kesimpulan, antara lain : penalaran deduktif dan penalaran induktif. Penalaran deduktif adalah penalaran yang dimulai dari prinsip umum untuk mendapatkan kesimpulan yang lebih khusus, sedangkan penalaran induktif adalah penalaran yang dimulai dari fakta-fakta khusus untuk mendapatkan kesimpulan umum. Logika terbagi menjadi beberapa logika, antara lain :

1. Logika Proposisi

Proposisi adalah sutau pernyataan yang dapat bernilai benar (B) atau salah (S). Simbol-simbol seperti P dan Q menunjukkan proposisi. Dua atau lebih proposisi dapat digabungkan dengan menggunakan operator logika :

Operator NOT digunakan untuk memberikan nilai negasi (lawan) dari pernyataan yang telah ada.

b. Operator Konjungsi : ^ (AND)

Operator AND digunakan untuk mengkombinasikan 2 buah proposisi. Hasil yang diperoleh akan bernilai benar jika kedua proposisi bernilai benar, dan akan bernilai salah jika salah satu dari kedua proposisi bernilai salah.

c. Operator Disjungsi : v (OR)

Operator OR digunakan untuk mengkombinasikan 2 buah proposisi. Hasil yang diperoleh akan bernilai benar jika salah satu dari kedua proposisi bernilai benar, dan akan bernilai salah jika kedua proposisi bernilai salah.

d. Operator Implikasi : → (if-then)

Implikasi: Jika P maka Q akan menghasilkan nilai salah jika P benar dan Q salah, selain itu akan selalu bernilai benar.

e. Operator Ekuivalensi : <=>

Ekuivalensi akan menghasilkan nilai benar jika P dan Q keduanya benar atau keduanya salah.

2. Logika Predikat

Logika predikat digunakan untuk merepresentasikan hal-hal yang tidak dapat direpresentasikan dengan menggunakan logika proposisi. Pada logika predikat kita dapat merepresentasikan fakta-fakta sebagai suatu pernyataan yang disebut dengan wff (well-formed formula).

1. Representasi Fakta Sederhana

Merepresentasi fakta sederhana dapat dilakukan melalui 3 cara :

a. Kita bisa menggunakan beberapa urutan aturan-aturan yang ada untuk memutuskan bahwa jawaban mana yang lebih mendekati, kemudian kita coba untuk membuktikan jawaban tersebut. Apabila gagal, kita coba untuk membuktikan aturan yang lainnya.

b. Kita coba buktikan kedua jawaban secara simultan dan berhenti apabila salah satu jawaban telah sukses dibuktikan.

c. Kita coba buktikan salah satu jawaban (terbukti atau tidak terbukti). Informasi yang diberikan (terbukti maupun tidak terbukti) bisa kita gunakan untuk menguatkan jawaban yang lainnya.

2. Representasi Hubungan Instance Dan Isa

Predikat Instance adalah predikat dengan argumen pertama berupa obyek dan argumen kedua berupa klas dimana obyek terdapat. Predikat Isa adalah predikat yang menunjukkan hubungan antar sub-klas.

3. Computable Function

Jika fakta yang akan disajikan jumlahnya sangat banyak, maka kita tidak mungkin mengekspresikannya secara individu. Untuk itu diperlukan computable function. Computable function biasanya juga digunakan sebagai computable predicates , sehingga kita dapat mengevaluasi predikat.

4. Resolusi

Resolusi merupakan suatu teknik pembuktian yang lebih efisien, sebab fakta-fakta yang akan dioperasikan terlebih dahulu dibawa kebentuk standar yang sering disebut dengan nama klausa. Pembuktian suatu pernyataan menggunakan resolusi ini dilakukan dengan cara menegasikan pernyataan tersebut, kemudian dicari kontradiksinya dari pernyataan-pernyataan yang sudah ada.

2.5.2 Pohon

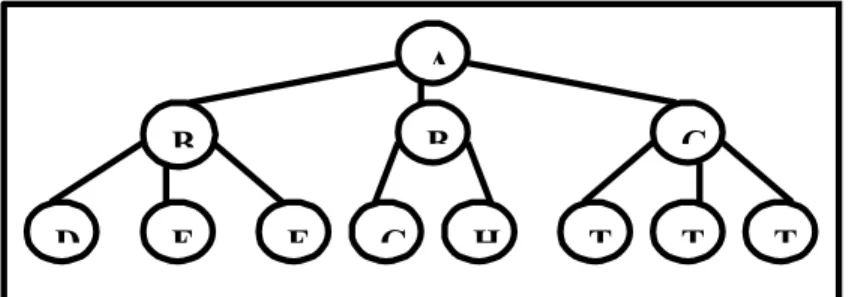
Pohon merupakan struktur penggambaran pohon secara hirarkis. Struktur pohon terdiri dari node-node yang menunjukkan obyek, dan arc (busur) yang menunjukkan hubungan antar obyek.

Gambar 2.3 Contoh Struktur Pohon

2.5.3 Jaringan Semantik

Jaringan semantik merupakan gambaran pengetahuan grafis yang menunjukan hubungan antar berbagai obyek. Jaringan semantik terdiri dari lingkaran-lingkaran yang menunjukkan obyek dan informasi tentang obyek-obyek tersebut. Obyek disini bisa

B D E B F C A H G T T T

berupa benda atau peristiwa. Antara 2 obyek dihubungkan dengan arc yang menunjukkan hubungan antar obyek.

2.5.4 Frame

Frame merupakan kumpulan pengetahuan tentang suatu obyek tertentu, peristiwa, lokasi, situasi, dll. Frame memiliki slot yang menggambarkan rincian (atribut) dan karakteristik obyek, frame biasanya digunakan untuk merepresentasikan pengetahuan yang didasarkan pada karakteristik yang sudah dikenal, yang merupakan pengalaman-pengalaman. Dengan menggunakan frame, sangatlah mudah untuk membuat inferensi tentang obyek, peristiwa atau situasi baru, karena frame menyediakan basis pengetahuan yang ditarik dari pengalaman.

2.5.5 Naskah (Script)

Script adalah skema representasi pengetahuan yang sama dengan frame, yaitu

merepresentasikan pengetahuan berdasarkan karakteristik yang sudah dikenal sebagai pengalaman-pengalaman. Perbedaannya, frame menggambarkan obyek sedangkan script menggambarkan urutan peristiwa, dalam menggambarkan urutan peristiwa, script menggunakan slot yang berisi informasi tentang orang, obyek, dan tindakan-tindakan yang terjadi dalam suatu peristiwa.

2.5.6 Sistem Produksi

Sistem produksi secara umum terdiri dari beberapa komponen-komponen antara lain ruang keadaan, yang berisi keadaan awal, tujuan dan kumpulan aturan yang

digunakan untuk mencapai tujuan. Dan strategi kontrol, yang berguna untuk mengarahkan bagaimana proses pencarian akan berlangsung dan mengendalikan arah eksplorasi.

Sistem produksi ini merupakan salah satu bentuk representasi pengetahuan yang sangat populer dan banyak digunakan adalah sistem produksi. Representasi pengetahuan dengan sistem produksi, pada dasarnya berupa aplikasi aturan (rule) yang berupa:

1. Antecendent, yaitu bagian yang mengekspresikan situasi atau premis (pernyataan berawalan IF).

2. Konsekuen, yaitu bagian yang menyatakan suatu tindakan tertentu atau konklusi yang diterapkan jika suatu situasi atau premis bernilai benar (penyataan berawalan THEN).

Apabila pengetahuan direpresentasikan dengan aturan, maka ada 2 metode penalaran yang dapat digunakan, yaitu :

1. Forward Reasoning (penalaran maju). Pelacakan dimulai dari keadaan awal (informasi atau fakta yang ada) dan kemudian dicoba untuk mencocokkan dengan tujuan yang diharapkan.

2. Backward Reasoning (penalaran mundur). Pada penalaran ini dimulai dari tujuan atau hipotesa, baru dicocokkan dengan keadaan awal atau fakta-fakta yang ada.

2.6 Pengenalan Logika samar

Sekitar 2000 tahun yang lalu, Aristoteles mengemukakan suatu hukum yang dikenal dengan hukum “Execludec Middle“. Dalam hukum ini diperkenalkan suatu

prinsip logika, yang disebut logika konvensional, atau lebih dikenal dengan logika boolean atau logika klasik atau logika digital biasa. Dalam logika boolean, nilai kebenaran mempunyai kondisi yang sudah pasti, dengan tidak adanya kondisi antara, sehingga segala hal hanya dapat diekspresikan dalam istilah binary, yaitu : Ya – Tidak atau ON – OFF atau High – Low atau “1“ – “0“ atau Hitam – Putih. Memang tidak dapat dipungkiri, hukum ini telah mendominasi pemikiran logika di dunia sampai sekarang. Namun, yang harus juga disadari, pemikiran mengenai logika boolean ini dengan nilai kebenaran yang pasti yaitu benar atau salah dalam kehidupan yang nyata sangatlah tidak mungkin. Oleh karena itu dibentuklah Logika samar.

Logika samar atau yang disebut juga dengan kekaburan menawarkan logika yang dapat merepresentasi keadaan sebenarnya, mengatasi masalah gradasi yang tak terhingga, yang berada pada dunia nyata. Logika samar merupakan peningkatan dari logika boolean yang berhadapan dengan konsep kebenaran sebagian.

Sejarah Logika samar:

 Tahun 1965, Prof. Zadeh dari California Univ. menulis paper yang sangat terkenal dan menjadi bahan referensi utama dunia Fuzzy.

 Tahun 1974, Prof Mandani dari London Univ. menerapkan teori Fuzzy untuk mengendalikan steam engine.

 Tahun 1970-an, Institusi Ilmiah mengenai Logika samar terbentuk dan teori mengenai Fuzzy berkembang pesat.

 Tahun 1980-an, Fuzzy masuk pada dunia terapan seperti industri semen, IC fuzzy, komputer fuzzy, kendali fuzzy, dsb.

Kebenaran boolean oleh Logika samar dinyatakan dalam tingkat/derajat kebenaran, yang dapat memberikan suatu nilai dari nol secara kontinu sampai nilai satu, tingkat keabuan dan juga hitam dan putih, dan dalam bentuk linguistik, konsep yang tidak pasti seperti “sedikit“,“lumayan“, dan “sangat“. Itulah sebabnya suatu hal dalam Logika samar dapat saja dikatakan memiliki nilai sebagian benar dan sebagian salah pada waktu yang sama.

Logika samar telah mengadopsi penilaian yang dilakukan oleh manusia terhadap kebenaran, dimana dalam penilaian manusia tersebut seringkali terdapat suatu kebimbangan terhadap benar dan salah. Dengan kata lain Logika samar telah berhasil meniru cara berpikir manusia dengan menggunakan konsep sifat kesamaran atau kekaburan suatu nilai. Kenyataan yang terjadi sekarang ini, semakin banyak orang yang menggunakan Logika samar untuk membuat berbagai aplikasi yang berkaitan dengan

Artificial Inteligence. Adapun beberapa alasan mengapa orang menggunakan Logika

samar antara lain :

 Konsep Logika samar mudah dimengerti, karena konsep matematik yang mendasari penalaran Logika samar sangat sederhana dan mudah dimengerti.

 Logika samar sangat fleksibel.

 Logika samar memiliki toleransi terhadap data – data yang tidak tepat.  Logika samar mampu memodelkan fungsi – fungsi nonlinear yang sangat

kompleks.

 Logika samar dapat membangun dan mengaplikasikan pengalaman – pengalaman para pakar langsung tanpa harus melalui proses pelatihan.

 Logika samar dapat bekerja sama dengan teknik – teknik kendali secara konvensional.

 Logika samar didasarkan pada bahasa alamiah.

Konsep Logika samar direpresentasikan oleh suatu pengetahuan yang direkonstruksikan dengan if – then rules. Contoh : Jika mesin panas dan dinyalakan terus menerus maka matikan mesin tersebut. Contoh tersebut adalah pengaplikasian logika samar dalam bentuk controller/pengatur.

Beberapa aplikasi logika logika samar, antara lain :

 Pada tahun 1990 pertama kali dibuat mesin cuci dengan logika samar di Jepang (Matsushita Electic Industrial Company). Sistem fuzzy digunakan untuk menentukan putaran yang tepat secara otomatis berdasarkan jenis banyaknya kotoran serta jumlah yang akan dicuci. Input yang digunakan adalah : seberapa kotor, jenis kotoran dan banyaknya yang dicuci. Mesin ini menggunakan sensor optik, mengeluarkan cahaya ke air dan mengukur bagaimana cahaya tersebut sampai ke ujung lainnya. Makin kotor, maka sinar yang sampai akan semakin redup. Selain itu sistem juga dapat menentukan jenis kotoran (daki atau minyak).

 Transmisi otomatis pada mobil. Mobil Nissan telah menggunakan sistem fuzzy pada transmisi otomatis, dan mampu menghemat bensin 12 - 17%.  Kereta bawah tanah Sendai mengontrol pemberhentian otomatis pada area

 Ilmu kedokteran dan biologi, seperti sistem diagnosis yang didasarkan pada logika fuzzy, penelitian kanker, manipulasi peralatan prostetik yang didasarkan pada logika fuzzy,dll.

 Manajemen dan pengambilan keputusan, seperti manajemen basisdata yang didasarkan pada logika fuzzy untuk menganalisa keadaan pasar yang berubah-ubah sehingga bisa menghasilkan suatu keputusan yang akurat.

2.7 Teori Fuzzy Set

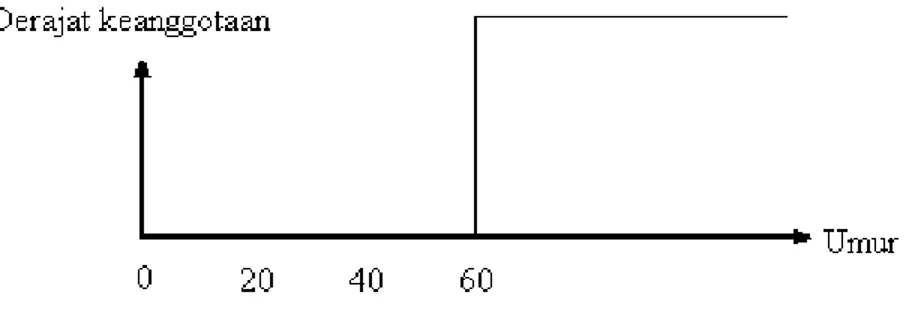
Teori Fuzzy Set merupakan suatu teori tentang konsep penilaian, dimana segala sesuatu merupakan persoalan derajat atau diibaratkan bahwa segala sesuatu memiliki elastisitas. Dengan nilai/derajat elastisitas ini Fuzzy Set mempertegas sesuatu yang Fuzzy. Contoh berikut ini akan menjelaskan bagaimana konsep “umur” yang digolongkan “tua” dalam pengertian Fuzzy Set dan Crisp Set. Misal, diberikan suatu definisi bahwa setiap orang yang berumur 60 tahun atau lebih adalah “tua”.

Gambar 2.4 Konsep “Tua” Dalam Pengertian Crisp Set

Dari grafik di atas dapat terlihat jelas bahwa dalam crisp set, batas – batas antara “tua” dan “tidak tua” sangat jelas. Setiap orang yang berumur > 60 dikatakan “tua”,

sedangkan yang lainnya (40,…,55) termasuk dalam anggota “tidak tua”. Dengan kata lain, dalam crisp set tidak dikenal adanya derajat ketuaan.

Sedangkan dalam Fuzzy Set, setiap anggota memiliki nilai berdasarkan pada derajat keanggotaan. Adapun konsep “umur” yang digolongkan “tua” dalam pengertian

Fuzzy Set dinyatakan dalam grafik di bawah ini.

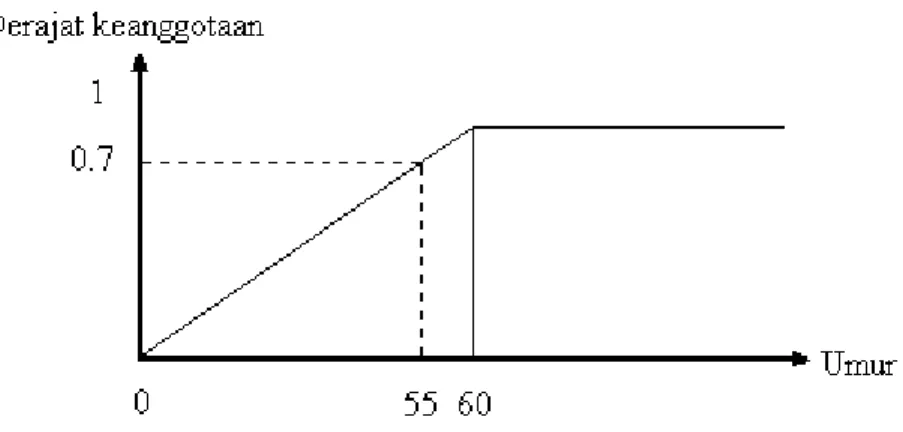
Gambar 2.5 Konsep “Tua” Dalam Pengertian Fuzzy Set

Grafik di atas secara jelas memperlihatkan bahwa anggota yang berumur 55 tahun, derajat keanggotaannya adalah 0,7, sedangkan anggota yang berumur 60 tahun derajat keanggotaannya 1. Untuk yang berumur > 60 tahun mewakili secara tepat konsep “tua” yaitu berderajat 1, sedangkan yang berumur < 60 tahun memiliki derajat berlainan, yang nilainya berkisar kurang dari 1. Derajat keanggotaan ini berfungsi untuk menunjukkan seberapa dekat nilai tiap – tiap umur dalam anggota himpunan itu dengan konsep “tua”. Bisa dikatakan bahwa anggota yang berumur 55 tahun adalah 70 % (0,7) “mendekati tua”, atau dengan bahasa alami “hampir“ atau “mendekati tua“.

Fuzzy Set dinyatakan melalui sekumpulan obyek x dengan masing – masing

dengan μ atau disebut juga dengan nilai kebenaran dan nilai ini dipetakan ke dalam range (0,1). Jika x adalah sekumpulan obyek dengan anggotanya dinyatakan dengan x maka himpunan fuzzy dari A di dalam x adalah himpunan dengan sepasang anggota.

A = {(x,μA(x))|x X}

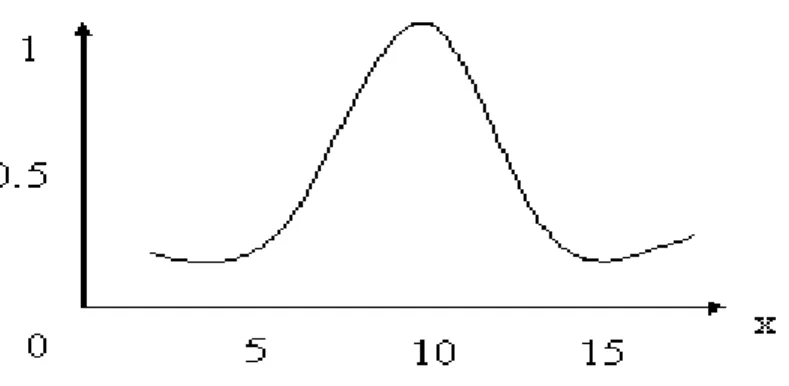
Sebagai contoh, jika A = “bilangan yang mendekati 10“ dengan : A = {(x,μA(x))|μA(x) = (1+(x – 10)2)-1}

A = {(0.0.01),…,(5,0.04),…,(10,1),…,(15,0.04),…} Maka grafik yang mewakili nilai μA(x) adalah:

Gambar 2.6 Grafik Fuzzy Untuk Bilangan Yang Mendekati 10

Dalam pembentukan suatu fuzzy set, terdapat dua atribut yang memegang peranan penting, yakni :

 Nilai linguistik, yaitu penamaan suatu grup yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami. Misal : “cepat”, ”sedang”, atau “lambat”, dan sebagainya.

 Nilai numeris, yaitu suatu nilai berupa angka yang menunjukkan nilai suatu variabel. Misal : 5, 10, 15, dan sebagainya.

2.7.1 Variabel Fuzzy (Variabel Linguistik)

Inti dari teknik pemodelan fuzzy adalah nama suatu fuzzy set yang disebut variabel linguistik. Variabel linguistik merupakan variabel yang bernilai kata/kalimat, bukan angka. Sebagai alasan menggunakan kata/kalimat daripada angka karena informasi yang disampaikan akan menjadi lebih informatif, meskipun kenyataannya peranan linguistik kurang spesifik dibandingkan dengan angka. Variabel linguistik merupakan konsep penting dalam Logika samar dan memegang peranan penting dalam beberapa aplikasi.

Misal, jika “kecepatan” adalah suatu variabel linguistik, maka nilai linguistik untuk variabel kecepatan tersebut antara lain “lambat”, “sedang”, dan “cepat“. Hal ini seusai dengan kebiasaan manusia sehari – hari dalam menilai sesuatu, misalnya : “Ia mengendarai mobil dengan cepat“, tanpa memberikan nilai berapa kecepatannya.

Konsep tentang variabel linguistik ini juga pertama kali diperkenalkan oleh Prof. Lofti Zadeh. Variabel linguistik ini menurut Zadeh dikarakteristikkan dengan :

(X, T(x), U, G, M) dimana :

X = Nama variabel (variabel linguistik).

T(x) = Semesta pembicaraan untuk x atau disebut juga nilai linguistik dari x. U = Jangkauan dari setiap nilai fuzzy untuk x yang dihubungkan dengan

variabel dasar U.

G = Aturan sintaksis untuk memberikan nama (x) pada setiap nilai X. M = Aturan semantik yang menghubungkan setiap X dengan artinya.

Sebagai contoh, jika :

X = “kecepatan”, U [0,100], dan T(kecepatan) = {lambat, sedang, cepat} Maka M untuk setiap X adalah :

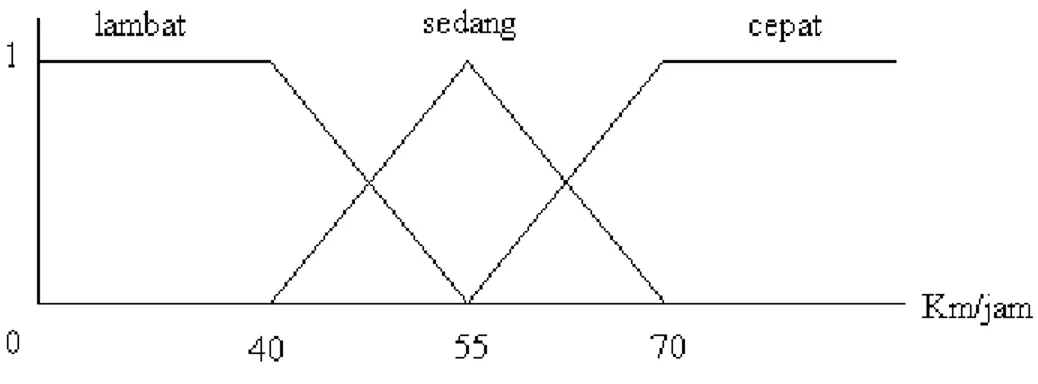
M(lambat) = Fuzzy setnya “kecepatan dibawah 40 km/jam” dengan fungsi keanggotaan lambat.

M(sedang) = Fuzzy setnya “kecepatan mendekati 55 km/jam” dengan fungsi keanggotaan sedang.

M(cepat) = Fuzzy setnya „“kecepatan diatas 70 km/jam“ dengan fungsi keanggotaan cepat.

Gambar grafik fungsi keanggotaannya sebagai berikut :

Gambar 2.7 Grafik Fungsi Keanggotaan Kecepatan

2.7.2 Operasi Fuzzy Set

Misalkan himpunan A dan B adalah dua nilai dari Fuzzy Set pada semesta pembicaraan U dengan fungsi keanggotaan dan , maka μA dan μB, maka operasi – operasi

 Union (Penggabungan)

Gabungan Fuzzy set A dan B adalah Fuzzy set C. C = A B atau C = A ATAU B

Dengan derajat keanggotaan C adalah : μC(x) = max (μAx) , μB(x))

= (μA(x) v (μB(x))

 Intersection (Irisan)

Irisan Fuzzy set A dan B adalah Fuzzy set C. C = A B atau A DAN B

Dengan derajat keanggotaan C adalah : μC(x) = min (μAx) , μB(x))

= (μA(x) ^ (μB(x))

 Complement (Ingkaran)

Komplemen Fuzzy set A diberi tanda A’ (NOT A), dan didefinisikan

sebagai berikut :

μA’(x) = 1 - μA(x)

2.7.3 Fungsi Keanggotaan

Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik – titik input data ke dalam derajat keanggotaannya yang memiliki interval antara 0 sampai 1. Pada dasarnya ada dua cara mendefinisikan keanggotaan dari Fuzzy

Set, yaitu secara numeris dan fungsional. Definisi numeris menyatakan fungsi derajat

jumlah elemen diskret dalam semesta pembicaraan. Definisi fungsional menyatakan derajat keanggotaan sebagai batasan ekspresi analitis yang dapat dihitung. Standar atau ukuran tertentu pada fungsi keanggotaan secara umum berdasar atas semesta X bilangan

real.

Fungsi keanggotaan (membership function) yang sering digunakan terdiri dari beberapa jenis, yaitu :

 Fungsi Linear

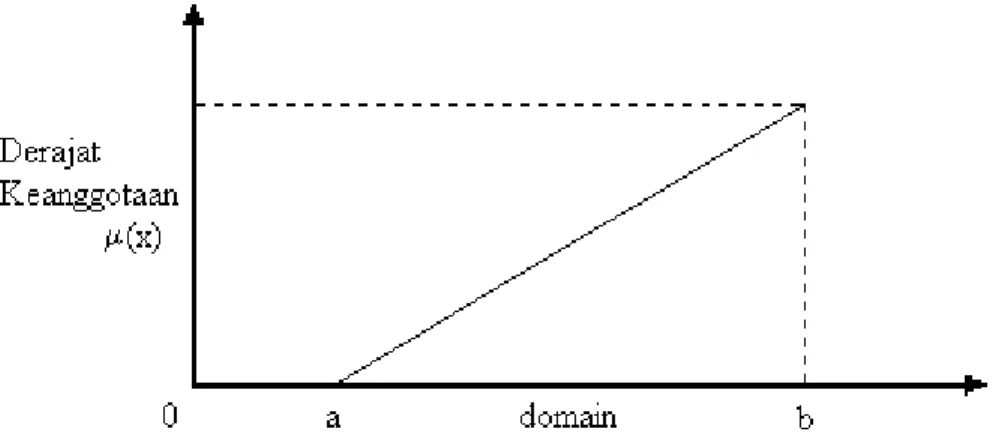
Fungsi keanggotaan dari fungsi linear adalah :

0 jika x < a , x > c μ(x) = (x – a)/(b – a) jika a < x < b

1 jika x > b

Gambar grafik fungsi keanggotaannya adalah :

Gambar 2.8 Grafik Fungsi Keanggotaan Linear

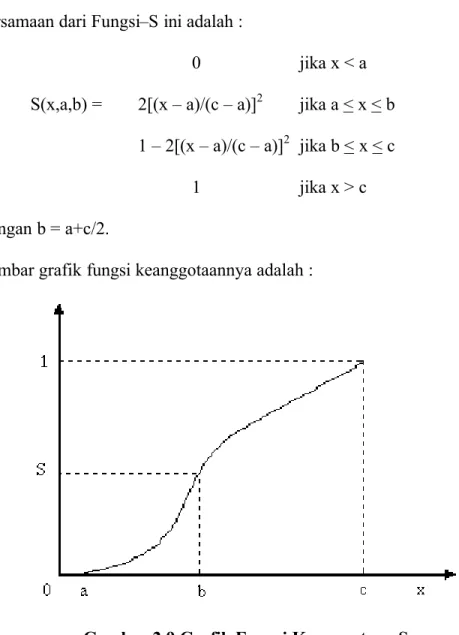
 Fungsi-S (S-function)

Fungsi–S atau Sigmoid merupakan kurva yang dibentuk sehubungan dengan kenaikan dan penurunan nilai yang tidak linear. Fungsi

keanggotaannya akan tertumpu pada 50% nilai keanggotaan yang sering disebut dengan titik infleksi.

Persamaan dari Fungsi–S ini adalah :

0 jika x < a S(x,a,b) = 2[(x – a)/(c – a)]2 jika a < x < b

1 – 2[(x – a)/(c – a)]2 jika b < x < c 1 jika x > c Dengan b = a+c/2.

Gambar grafik fungsi keanggotaannya adalah :

. Gambar 2.9 Grafik Fungsi Keanggotaan S

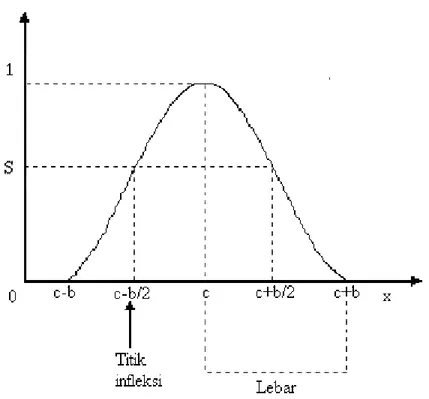
 Fungsi-PI (PI-function)

Fungsi-PI merupakan salah satu kurva berbentuk lonceng, di mana derajat keanggotaan yang bernilai 1 tepat terletak pada pusat domain c (lihat gambar).

PI(x,b,c) = S(x,c – b,c – b/2,c) jika x < c 1 – S(x;c,c + b/2,c + b) jika x > c

Gambar grafik fungsi keanggotaannya adalah :

Gambar 2.10 Grafik Fungsi Keanggotaan PI

Fungsi keanggotaan segitiga (Triangular membership function) Persamaan untuk bentuk segitiga ini adalah :

0 jika x < a, x > c T(x;a.b.c) = (x – a)/(b – a) jika a < x < b

Gambar grafik fungsi keanggotaannya adalah :

Gambar 2.11 Grafik Fungsi Keanggotaan Segitiga

Fungsi keanggotaan trapesium (Trapezoidal membership function) Persamaan untuk bentuk trapezium ini adalah :

0 jika x < a , x > d Z(x;a,b,c,d) = 1 jika b < x < c

(x – a)/(b – a) jika a < x < b (d – x)/(d – c) jika c < x < d

Gambar 2.12 Grafik Fungsi Keanggotaan Trapesium

2.7.4 Diagram Alir Fuzzy Set

Dalam teori Fuzzy Set untuk mendapatkan solusi yang eksak, maka ada tiga langkah umum yang dapat dilakukan :

 Fuzzifikasi (fuzzification)

Fuzzifikasi adalah fase pertama dari perhitungan fuzzy yaitu pengubahan nilai tegas ke nilai fuzzy. Proses fuzzifikasi dapat dinyatakan sebagai berikut :

x = fuzzifier (xo)

dengan xo adalah sebuah vektor nilai tegas dari satu variabel input, x

adalah vektor fuzzy set yang didefinisikan sebagai variabel, dan fuzzifier adalah sebuah operator fuzzifikasi yang mengubah nilai tegas ke fuzzy set.  Penalaran/Evaluasi Kaidah (rule evaluation)

Aturan pada suatu model fuzzy menunjukkan bagaimana suatu sistem beroperasi. Secara umum aturan dituliskan sebagai :

IF ( X1is A1) * ( X2is A2) * ( X3 is A3) * ... * ( Xn is An ) THEN Y is B Dengan * adalah operator ( misal : OR atau AND ), X1 adalah skalar dan A1 adalah variabel linguistik. Apabila sistem tidak menggunakan hedge, maka variabel linguistiknya sama dengan himpunan fuzzy.

Untuk menulis aturan perlu diperhatikan hal-hal berikut ini :

o Kelompokkan semua aturan yang memiliki solusi pada variabel yang sama.

o Urutkan aturan sehingga mudah dibaca.

o Gunakan identitas untuk memperlihatkan struktur aturan.

o Gunakan penamaan yang umum untuk mengidentifikasikan variabel-variabel pada kelas yang berbeda.

o Gunakan komentar untuk mendeskripsikan tujuan dari suatu atau sekelompok aturan.

o Berikan spasi antar aturan.

o Tulis variabel dengan huruf besar-kecil, himpunan fuzzy dengan huruf besar, dan elemen-elemen bahasa lainnya dengan huruf kecil.  Defuzzifikasi (Defuzzification)

Input dari proses defuzzifikasi adalah suatu fuzzy set yang diperoleh dari komposisi aturan – aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu bilangan pada domain fuzzy set tersebut. Sehingga jika

diberikan suatu fuzzy set dalam range tertentu, maka harus dapat diambil suatu nilai crisp tertentu sebagai output.

Pengendali logika fuzzy harus mengubah variabel keluaran kabur menjadi nilai-nilai tegas yang dapat digunakan untuk mengendalikan sistem. Proses ini disebut penegasan (Defuzzification). Telah dikembangkan banyak metode untuk melakukan penegasan ini, diantaranya adalah :

2. Metode Centroid (CompositeMoment )

Pada metode ini, solusi crisp diperoleh dengan cara mengambil titik pusat daerah fuzzy, dirumuskan:

Dengan di adalah nilai domain ke-i dan μ( di ) adalah nilai keanggotaan titik tersebut.

3. Metode Bisektor

Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai pada domain fuzzy yang memiliki nilai keanggotan separuh dari jumlah total nilai keanggotaan pada daerah fuzzy. Secara umum dituliskan:

Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai rata-rata domain yang memiliki nilai keanggotaan maksimum, dirumuskan sebagai berikut:

5. Metode Largest Of Maximum (LOM)

Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai terbesar dari domain yang memiliki nilai keanggotaan maksimum, dapat dirumuskan :

6. Metode Smallest Of Maximum (SOM )

Pada metode ini, solusi crisp diperoleh dengan cara mengambil nilai terkecil dari domain yang memiliki nilai keanggotaan maksimum, dirumuskan :

Diagram alir proses pengaturan dalam teori fuzzy set dapat digambarkan sebagai berikut:

Gambar 2.13 Diagram Alir Proses Pengaturan Himpunan Fuzzy Crisp Input

Fuzzification

Penalaran

Defuzzifikasi

2.8 Sistem Visual

Sistem visual buatan atau vision system (computer vision) adalah suatu sistem yang mempunyai kemampuan untuk menganalisa obyek secara visual, setelah data obyek yang bersangkutan dimasukkan dalam bentuk citra (image).

Secara umum tujuan dari sistem visual adalah untuk membuat model nyata dari sebuah citra. Citra yang dimaksud adalah citra digital hasil konversi suatu obyek menjadi citra melalui suatu sensor yang prosesnya disebut digitasi. Dengan demikian citra lain seperti foto, gambar cetak, gambar sketsa, dan lain-lain yang berada pada media cetak seperti kertas atau media lainnya baru dapat diproses setelah dikonversi ke dalam citra digital melalui proses digitasi.

Sebuah sistem visual mempunyai kemampuan untuk memperbaiki informasi yang berguna dari sebuah pemandangan (scene) hasil proyeksi dua dimensi. Citra merupakan hasil proyeksi dua dimensi dari obyek atau benda tiga dimensi, sehingga informasi tidak bisa didapatkan begitu saja, melainkan harus diperbaiki karena sesungguhnya ada bagian informasi yang hilang setelah benda diproyeksikan ke dalam citra.

2.9 Citra Digital 2.9.1 Definisi Citra

Sebuah citra adalah kumpulan piksel-piksel yang disusun dalam dua dimensi. Piksel adalah sampel dari pemandangan yang mengandung intensitas citra yang dinyatakan dalam bilangan bulat. Indeks baris dan kolom (x,y) dari sebuah piksel dinyatakan dalam bilangan bulat. Piksel (0,0) terletak pada sudut kiri atas pada citra,

indeks x bergerak ke kanan dan indeks y bergerak ke bawah. Konvensi ini dipakai merujuk pada cara penulisan larik yang digunakan dalam pemrograman komputer.

(a) (b)

Gambar 2.14 Perbedaan Letak Titik Origin Pada Kordinat Grafik Dan Pada Citra (a) koordinat pada grafik matematika (b) koordinat pada citra

2.9.2 Tipe Citra

Menurut Chastain et al (2000), ada dua tipe dasar citra berdasarkan cara penyimpanannya, yaitu :

a. Raster atau Bitmap Format

Citra yang disimpan dengan format bitmap atau raster memiliki karakteristik menyimpan setiap piksel dari sebuah citra. Format ini biasa digambarkan dengan bentuk matriks berukuran panjang piksel x lebar piksel, yang masing masing dari piksel tersebut berisi nilai rgb dari piksel tersebut. Contoh : BMP, JPG, GIF, dll.

b. Vector Format

Citra yang disimpan dengan format vektor memiliki karakteristik menyimpan konstruksi dari suatu titik, garis, ukuran, warna dan sebagainya yang dapat membentuk suatu citra. Contoh penyimpanan yang menggunakan format ini adalah PS, PDF, WMF, CDM, dll.

2.9.3 Piksel

Gambar yang bertipe bitmap tersusun dari piksel-piksel. Piksel disebut juga dengan dot. Piksel berbentuk bujursangkar dengan ukuran relatif kecil yang merupakan penyusun atau pembentuk gambar bitmap.

Banyaknya piksel tiap satuan luas tergantung pada resolusi yang digunakan. Keanekaragaman warna piksel tergantung pada bit depth yang dipakai. Semakin banyak jumlah piksel tiap satu satuan luas, semakin baik kualitas gambar yang dihasilkan dan tentu akan semakin besar ukuran file-nya.

Sebuah piksel pada titik P memiliki koordinat (x, y) memiliki empat hubungan titik vertikal dan horisontal dimana koordinat itu adalah :

K u

Kumpulan dari piksel-piksel ini disebut dengan 4 neighbours of P, yang dituliskan dengan N4(P). Setiap piksel merupakan suatu unit yang terletak tepat disamping titik P(x,

y). Selain itu juga terdapat empat diagonal neighbours terhadap titik P, empat titik diagonal itu adalah:

( x – 1, y – 1 ) ( x – 1, y + 1 ) P( x, y ) ( x – 1, y + 1 ) ( x + 1, y + 1 ) (x, y – 1) (x – 1, y) P(x, y) (x + 1, y) (x, y + 1)

Empat diagonal neighbours ini dituliskan dengan ND(P). Titik-titik ini bersama

dengan N4(P), disebut dengan 8 neighbours dari P, yang biasa dituliskan dengan N8(P).

(x – 1, y – 1) (x, y – 1) (x + 1, y – 1)

(x – 1, y) P(x, y) (x + 1, y)

(x – 1, y + 1) (x, y + 1) (x + 1, y + 1)

2.9.4 Relasi Antar Piksel

Menurut Parker (1993), hubungan antar piksel berperan dalam menentukan karakteristik suatu citra, hubungan yang paling mendasar ini disebut dengan connectivity.

Hubungan antar piksel tersebut dapat digambarkan sebagai berikut : 0 (i-1,j-1) 1 (i,j-1) 2 (i+1,j-1) 3 (i-1,j) 4 (i,j) 5 (i+1,j) 6 (i-1,j+1) 7 (i,j+1) 8 (i+1,j+1) Gambar 2.15 Relasi Antar Piksel

Ada dua aturan utama dalam relasi antar piksel, yaitu :

a. Dua piksel dikatakan 4-adjacent jika bersebelahan secara horisontal atau vertikal saja. Contoh untuk piksel 4 maka 4-adjacent-nya adalah 1,3,5,7.

b. Dua piksel dikatakan 8-adjacent jika bersebelahan secara diagonal atau piksel-piksel tersebut juga bersebelahan secara 4-adjacent. Contoh untuk piksel 4 maka 8-adjacent-nya adalah 0,1,2,3,5,6,7,8.

2.10 Pengolahan Citra 2.10.1 Geometri Citra

Untuk dapat mengerti dan melakukan operasi pengolahan citra, pertama-tama harus memahami dengan baik apa dan bagaimana sifat citra itu sendiri. Ada dua hal penting yang sangat mendasar pada proses pembentukan citra yang harus dipahami dan selanjutnya sangat perlu untuk terus diingat, yaitu :

a. Geometri formasi citra yang menentukan lokasi suatu titik dalam pemandangan yang diproyeksikan pada bidang citra.

b. Fisik cahaya yang menentukan kecerahan suatu titik pada bidang citra sebagai fungsi pencahayaan pemandangan dan sifat-sifat permukaan.

2.10.2 Definisi Pengolahan Citra

Image processing atau pengolahan citra adalah bidang tersendiri yang sudah

cukup berkembang sejak orang mengerti bahwa komputer tidak hanya dapat menangani data teks, melainkan juga data citra.

Teknik-teknik pengolahan citra biasanya digunakan untuk melakukan transformasi dari satu citra kepada citra yang lain, sementara tugas perbaikan informasi terletak pada manusia melalui penyusunan algoritmanya. Bidang ini meliputi penajaman

citra, penonjolan tertentu dari suatu citra, kompresi citra dan koreksi citra yang tidak fokus atau kabur.

Pengertian pengolahan citra sedikit berbeda dengan pengertian mesin visual (machine vision), meskipun keduanya seolah-olah dapat dipergunakan dengan maksud yang sama. Terminologi pengolahan citra digunakan bila hasil pengolahan data yang berupa citra adalah juga berbentuk citra yang lain, yang mengandung atau memperkuat informasi khusus pada citra hasil pengolahan sesuai dengan tujuan pengolahannya. Sedangkan terminologi mesin visual digunakan bila data hasil pengolahan citra langsung diterjemahkan dalam bentuk lain, misalnya grafik yang siap diinterpretasikan untuk tujuan tertentu, gerak peralatan atau bagian dari peralatan mekanis, atau aksi lainnya yang berarti bukan merupakan citra lagi. Dengan demikian jelaslah bahwa pengolahan citra merupakan bagian dari mesin visual, karena untuk menghasilkan keluaran selain citra, informasi dari citra yang ditangkap oleh kamera juga perlu diolah dan dipertajam pada bagian-bagian tertentu.

2.11 Citra SPOT (Satellite Pour l'Observation de la Terre)

Citra SPOT (Satellite Pour l'Observation de la Terre) adalah citra dengan resolusi tinggi yang menggambarkan permukaan bumi yang diambil dari sistem satelit dan diambil dari luar angkasa. Sistem citra SPOT ini diciptakan untuk meningkatkan pengetahuan dan menejemen dari keadaan bumi untuk mengeksplorasi kekayaan alam bumi, menganalisa dan meprediksi fenomena alam termasuk iklim dan keadaan laut, serta memantau aktifitas manusia dan fenomena alam yang terjadi.

Perusahaan SPOT Image memasarkan citra dengan resolusi tinggi yang mampu diambil dari setiap sudut dari bumi. Sejarah dari satelit SPOT sebagai berikut :

 SPOT 1 diluncurkan tanggal 22 Februari 1986  SPOT 2 diluncurkan tanggal 22 Januari 1990  SPOT 3 diluncurkan tanggal 26 September 1993  SPOT 4 diluncurkan tanggal 24 Maret 1998  SPOT 5 diluncurkan tanggal 4 Mei 2002

2.12 Metode Konvensional (K-Means Clustering)

Metode K-Means Clustering adalah salah satu dari metode statistik yang digunakan sebagai metode konvensional untuk melakukan proses segmentasi citra. Metode ini bisa dideskripsikan sebagai metode partisi, yaitu metode ini akan membagi data menjadi cluster-cluster tersendiri berdasarkan sampel atau inputan yang diberikan. Metode ini menempatkan setiap titik pada cluster dimana titik tengah yang terdekat. Titik tengah adalah rata-rata dari semua titik yang terdapat dalam suatu cluster. Langkah-langkah yang dilakukan adalah :

1. Memilih jumlah cluster yang diinginkan, k.

2. Secara acak membuat k clusters dan menentukan titik tengah setiap cluster. 3. Mengambil sampel dari data untuk menentukan titik tengah dari setiap cluster. 4. Menentukan titik-titik ke titik tengah terdekat setiap cluster.

5. Menghitung ulang titik tengah cluster.

6. Mengulang langkah ketiga dan keempat sampai kriteria yang ditentukan tercapai.

Keuntungan utama dari metode ini adalah metode ini simpel dan cepat untuk proses pada data yang besar. Tetapi, kekurangan dari metode ini adalah ketidakstabilan hasil dari setiap proses. Hal ini terjadi karena metode ini termasuk sebagai metode

supervised learning, dimana dibutuhkan sampel atau input untuk mampu melakukan

proses. Perbedaan input dalam setiap proses akan menghasilkan output yang berbeda-beda.

2.13 Model Logika Samar (Fuzzy Logic) Untuk Pengolahan Citra

Dalam proses pengenalan pola atau computer vision sering terjadi ketidakpastian atau keraguan yang diakibatkan oleh informasi input yang tidak lengkap, informasi samar dari citra, batasan-batasan area yang berlebihan dan pola-pola yang belum di kenali dan hubungan antar sesama pola. Hal ini dapat menyebabkan terjadi pengambilan keputusan yang salah.

2.13.1 Hubungan Ketidakpastian Dalam Pengolahan Citra dan Logika Samar

Masalah dalam mengolah dan menganalisa suatu image adalah kerancuan pada nilai piksel terhadap tingkat nilai keterangan cahaya. Pendekatan konvensional dalam menganalisa dan pengenalan pola terdiri dari membagi citra secara kasar menjadi beberapa segmen area dan mengolah segmen tersebut dan hubungan antar segmen lalu men-interpretasikan atau mengklasifikasi citra. Secara batas-batas area citra tidak selalu terlihat jelas, maka akan muncul banyak ketidakpastian dan keakuratan data dalam proses pengolahan citra tersebut. Kesalahan dalam mengolah citra akan mempengaruhi dalam pengambilan keputusan.

Dari pembahasan diatas maka, menjadi sangat penting untuk menghindari terjadinya kesalahan pengolahan data dari citra. Untuk mendeskripsikan dan interpretasi informasi yang tidak akurat pada suatu pola adalah menentukan dasar-dasar dari pola tersebut (garis, sudut, kurva, dsb) dan hubungannya dengan menggunakan fuzzy sets.

2.13.2 Ketidakpastian Citra dan Kekaburan Masalah

Suatu citra X(MxN) bisa dianggap sebgai suatu array dari himpunan fuzzy yang memiliki derajat keanggotaan (membership degree) dalam notasi himpunan fuzzy dapat ditulis sebagai :







x m M n N



X  x mn : 1,2,..., ; 1,2,... ,

dimana _x(x_mn)menyatakan nilai proses citra μ dengan (m,n) sebagai piksel.

2.13.3 Ketidakpastian Dalam Tingkat Keabu-abuan

Definisi dari masalah diformulasikan untuk menggambarkan ketidakpastian tingkat keabu-abuan dalam suatu citra X dengan dimensi M x N dengan level L adalah sebagai berikut :

Rth order fuzzy entropy:





( )log ( )





1 ( )



log



1 ( )



) / 1 ( ) ( ' r i r i r i i r i s s s s k X H  

_

     i=1,2,…k

Dimana s mengambarkan ith kombinasi dari r piksel dalam X; k adalah jumlah dari _ir

kombinasi dan (s_ir) menggambarkan derajat dari kombinasi s ._ir Hybrid Entropy:

. ,..., 2 , 1 , ,... 2 , 1 ) ( exp ) 1 ( ) / 1 ( ) 1 exp( ) / 1 ( log log ) ( N n M m MN E MN E with E P E P X H mn m n mn b m n mn mn w b b w w hy         





   

Dimana _mn menggambarkan derajat “keputihan” dari (m,n) piksel. P_w dan P_b

menggambarkan probabilitas terjadinya warna putih (_mn=1) dan hitam (_mn=0) piksel. Dan E_w dan E menggambarkan rata-rata kemungkinan interpretasi piksel sebagai putih _b

dan hitam. Correlation:





/( ) 4 1 ) , ( 1 2 2 2 1 2 1 X X C m n mn mn          



    = 1 if X1+ X2= 0 With









. ,... 2 , 1 : ,..., 2 , 1 1 2 1 2 2 2 2 2 1 1 N n M m X X m n mn m n mn      





 

Dimana _1mndan _2mnmenggambarkan derajat proses dari μ1dan μ2 dengan (m,n) piksel

2.13.4 Flexibilitas Dalam Derajat Keanggotaan (Flexibility in Membership

Functions)

Karena teori himpunan logika samar (Fuzzy Logic) adalah generalisasi dari teori himpunan konvensional, teori himpunan logika samar memiliki flexibilitas yang lebih besar untuk menangkap beberapa aspek terhadap ketidaklengkapan dan ketidaksempurnaan informasi. Flexibilitas dari teori himpunan logika samar ditunjang oleh konsep dari fungsi keanggotaan (membership function). Derajat keanggotaan

(membership degree) adalah yang menghubungkan antara data dengan konsep himpunan

logika samar. Semakin besar derajat keanggotaan maka, semakin tinggi kedekatannya dengan data tersebut.

Karena derajat keanggotaan harus didapat secara subjektif dan bergantung pada data yang ada. Terjadi beberapa masalah dalam menentukan nilai suatu himpunan. Masalahnya adalah bagaimana mengolah suatu derajat keanggotan data menjadi suatu himpunan. Pada saat mengolah data tersebut sering terjadi masalah-masalah utama, yaitu ketidakpastian dan ketidaklengkapan data serta batas-batas yang tidak jelas.

Terdapat dua operator yang dapat digunakan “Bound Function” dan “Spectral

Fuzzy Sets” untuk menganalisa flexibilitas dan ketidakpastian dalam evaluasi fungsi

keanggotaan. Konsep dari spectral fuzzy sets digunakan pada sebuah fungsi keanggotaan yang unik, yang menghubungkan setiap elemen dengan derajat keanggotaannya masing-masing, hal ini mengurangi kesulitan (ketidakpastian) dalam memilih sebuah fungsi. Sebuah himpunan spectral fuzzy F dapat diformulasikan dalam:





n j r i x x x U U F j j j i F i j ,..., 2 , 1 ; ,..., 2 , 1 , , / ) (      

Konsep ini ditemukan untuk berguna dalam segmentasi terhadap batas-batas yang tidak jelas.

2.14 Fuzzy Clustering

Fuzzy clustering adalah salah satu teknik untuk menentukan cluster optimal dalam

suatu ruang vektor yang didasarkan pada bentuk normal Euclidian untuk jarak antar vektor. Fuzzy clustering sangat berguna bagi pemodelan fuzzy terutama dalam mengidenifikasi aturan aturan fuzzy.

Cluster dikatakan fuzzy jika tiap-tiap objek dihubungkan dengan menggunakan derajat keanggotaan (bukan dengan keanggotaan crisp). Pada prakteknya biasanya perlu dilakukan preprocessing ter-lebih dahulu. Akan lebih menguntungkan apabila data yang akan diolah dalam keadaan normal, misalkan berada pada interval [0 1]. Dengan demikian kita perlu melakukan normalisasi untuk suatu nilai u, menjadi u normal (ΰ) dengan rumus: ύ = min min u u u u maz 

dengan umin adalah nilai terkecil yang terukur dan umax adalah nilai terbesar yang terukur.

Dengan melakukan standarisasi, dapat mentransformasikan nilai rata-rata (mean) tiap variabel menjadi nol, dan deviasi standar menjadi 1. Jika data terdistribusi normal dengan mean m dan deviasi standar σ, maka akan didapatkan nilai standar:

u* =

 m u 

Kita juga perlu melakukan penskalaan nilai pada interval tertentu. Apabila penskalaan dilakukan secara linear pada interval [u1u2], maka:

U’ = _{2 1 1} 1 2 1 ) (u u u u u u u    

Setelah melakukan preprocessing, variabel-variabel yang relevan dapat segera dipilih, tentu saja dengan bantuan para ahli. Untuk sekumpulan data u = (u1,u2,…,uN) dapat

dicari:  mean :

_

  N i i u N m 1 1  variansi:



    N i i m u N v 1 2 ) ( 1 1  deviasi standar:   v

 range: su_maxu_min

 koefisien korelasi:







        N i N i i i N i i i m y m x m y m x r 1 1 2 2 2 1 1 2 1 ) ( ) ( ) )( (

dengan m1adalah mean dari X, dan m2adalah mean dari Y.

Koefisien korelasi akan bernilai pada interval [-1 1]. Jika r = -1, berarti ada korelasi negatif yang kuat antara X dan Y. Jika r = 1, berarti ada korelasi positif yang kuat antara X dan Y. Namun jika r = 0, berarti tidak ada korelasi antara X dan Y. Dua variabel yang terkorelasi kuat mengindikasikan bahwa keduanya tergantung secara linear. Jika dua variabel tergantung secara linear berarti terjadi redundancy (ketidakperluan). Sehingga jika hal ini terjadi, kita cukup memilih salah satu variabel saja.

2.14.1 Ukuran Fuzzy

Ukuran fuzzy menunjukkan derajat kekaburan dari himpunan fuzzy. Secara umum ukuran kekaburan dapat ditulis sebagai suatu fungsi:

f:P(X) R

dengan P(X) adalah himpunan semua subset dari X. f(A) adalah suatu fungsi yang memetakan subset A ke karakteristik derajat kekaburannya.

Dalam mengukur nilai kekaburan, fungsi f harus mengikuti hal-hal sebagai berikut:

1. f(A) = 0 jika dan hanya jika A adalah himpunan crisp.

2. Jika A<B, maka f(A) ≤ f(B). Disini, A<B berarti B lebih kabur disbanding A (atau A lebih tajam disbanding B). Relasi ketajaman A<B didefinisikan dengan:

μA[x] ≤ μB[x], jika μB[x] ≤ 0,5; dan

μA[x] ≥ μB[x], jika μB[x] ≥ 0,5;

3. f(A) akan mencapai maksimum jika dan hanya jika A benar-benar kabur secara maksimum. Tergantung pada interpretasi derajat kekaburan, nilai fuzzy maksimal biasanya terjadi pada saat μA[x] = 0,5 untuk setiap x.

2.15 Indeks Kekaburan

Indeks kekaburan adalah jarak antara suatu himpunan fuzzy A dengan himpunan crisp C yang terdekat. Himpunan crisp C terdekat dari himpunan fuzzy A dinotasikan

sebagai μC[x] = 0, jika μA[x] ≤ 0,5, dan μC[x] = 1, jika μA[x] ≥ 0,5. Ada 3 kelas yang

paling sering digunakan dalam mencari indeks kekaburan, yaitu: 1. Hamming distance. f(A) = ∑│ μA[x] - μC[x] │ atau f(A) = ∑ min [ μA[x], 1 - μA[x] ] 2. Euclidean distance. f(A) = {∑ [ μA[x] - μC[x] ]2}1/2 3. Minkowski distance. f(A) = {∑ [ μA[x] - μC[x] ]w}1/w dengan w ε [1,~]. 2.16 Fuzzy Entropy

Fuzzy entropy didefinisikan dengan fungsi:

f(A) = - ∑{ μA[x] log μA[x] + [ 1 - μA[x] ] log [ 1 - μA[x] ] }

2.17 Ukuran Kesamaan

Ukuran kesamaan digunakan untuk menunjukkan derajat perbedaan antara 2 himpunan fuzzy. Perbedaan antara premis suatu aturan dengan input fuzzynya kemudian dapat digunakan untuk menentukan nilai α pada suatu aturan.

2.18 Fuzzy C-Means (FCM)

Fuzzy C-Means (FCM) adalah suatu teknik pengclusteran data yang mana keberadaan tiap-tiap titik data dalam suatu cluster ditentukan oleh derajat keanggotaan. Teknik ini pertama kali diperkenalkan oeh Jim Bezdek pada tahun 1981.

Konsep dasar FCM, pertama kali adalah menentukan pusat cluster, yang akan menandai lokasi rata-rata untuk tiap-tiap cluster. Pada kondisi awal, pusat cluster ini masih belum akurat. Tiap-tiap titik data memiliki derajat keanggotaan untuk tiap-tiap cluster. Dengan cara memperbaiki pusat cluster dan derajat keanggotaan tiap-tiap cluster akan bergerak menuju lokasi yang tepat. Perulangan ini didasarkan pada minimisasi fungsi obyektif yang menggambarkan jarak dari titik data yang diberikan ke pusat cluster yang terbobot oleh derajat keanggotaan titik data tersebut.

Output dari FCM bukan merupakan fuzzy inference system, namun merupakan deretan pusat cluster dan beberapa derajat keanggotaan untuk tiap-tiap titik data. Informasi ini dapat digunakan untk membangun suatu fuzzy inference system.

Apabila terdapat suatu himpunan data (input atau output data dari sistem fuzzy) sebagai berikut :

U = (u1, u2, u3, …, uN)

Derajat keanggotaansuatu titik data ke-k di cluster ke-I adalah : μik(uk) [0,1] dengan (1 ≤ i ≤ c; 1 ≤ k ≤ N)

                     . ] [ . . . ] [ ] [ . . . . . . . . . . . . . ] [ . . . ] [ ] [ ] [ . . . . ] [ ] [ ) ( 2 1 2 2 2 21 2 12 1 1 1 21 1 11 N cN N N N N c c f c                    Dengan



  1 1 i ik  ,

yang berarti bahwa jumlah nilai keanggotaan suatu data pada semua cluster harus sama dengan 1.

Fungsi obyektif iterasi ke-t P(c) pada matriks partisi adalah:



    N k c i i f k w ik t c u v P 1 1 2 | | ) ( ) (  ,

dengan vfiadalah pusat vektor pada cluster fuzzy ke-i,





   _N k w ik N k k w ik fi u v 1 1 ) ( ) (   ,

dengan w adalah bobot pada nilai-nilai keanggotaan, | uk - vfi | adalah bentuk normal