Fakultas Ilmu Komputer
Universitas Brawijaya 2791
Optimasi
Fuzzy Time Series
Menggunakan Algoritma
Particle Swarm
Optimization
Untuk Peramalan Jumlah Penduduk Di Kabupaten
Probolinggo
Cahyo Adi Prasojo1 , Budi Darma Setiawan 2, Marji3
1,2,3Program Studi Teknik Informatika Fakultas Ilmu Komputer Universitas Brawijaya
Email: 1[email protected], 2 [email protected] , 3[email protected]
Abstrak
Pertumbuhan penduduk terjadi dikarenakan meningkatnya jumlah kelahiran. Dampak pertumbuhan penduduk ini berpengaruh terhadap kesejahteraan manusia, baik dalam bidang ekonomi, kesehatan, sosial, politik dan budaya. Oleh karena itu diperlukan peramalan jumlah penduduk, untuk mengetahui seberapa pesat laju pertumbuhan penduduk. Salah satu metode peramalan yang digunakan yaitu Fuzzy Time Series (FTS). Namun, metode ini masih memiliki kekurangan yaitu pada penentuan nilai interval yang kurang tepat. Maka diperlukan algoritma optimasi untuk mencari nilai yang optimal dari interval tersebut. Penelitian ini bertujuan untuk melakukan peramalan jumlah penduduk pada Kabupaten Probolinggo dengan menggunakan metode FTS yang di optimasi menggunakan algoritma Particle Swarm Optimization (PSO). Optimasi yang dilakukan untuk mendapatkan nilai interval optimal pada FTS dan nilai parameter optimal pada PSO. Parameter pada PSO yang di optimasi adalah 𝑤 (Bobot Inersia), 𝑐1 (konstanta kecepatan 1)dan 𝑐2 (konstanta kecepatan 2). Hasil dari pengujian tersebut, yaitu didapatkan nilai fitness 𝒘, 𝒄𝟏 dan 𝒄𝟐 terbaik, adalah 0,559140, 0,535084 dan 0,621134 dan nilai parameternya 0,6, 1,8 dan 2,4. Didapatkan nilai fitness terbaik dari peramalan tersebut, yaitu: 0,445334.
KataKunci : Jumlah Penduduk, Peramalan, Fuzzy Time Series (FTS), Particle Swarm Optimization (PSO).
Abstract
Population growth occurs due to the increasing number of births. The impact of population growth is affecting human welfare, Both in the economic, health, social, politic and cultural fields. Therefore it is necessary to forecast the population, to know how fast the rate of population growth. One of the most commonly used forecasting methods is the Fuzzy Time Series (FTS). However, this method still has a deficiency that is on the determination of the value of the interval that is less precise. therefore it is necessary the optimization algorithm to find the optimal value of the interval. This study aims to perform population forecasting in Probolinggo District by using FTS method which will be optimized using Particle Swarm Optimization (PSO) algorithm. Optimization is performed to obtain optimal interval value on FTS and optimal parameter value on PSO. The parameters in the optimized PSO are
𝑤 (Inertial Weight), 𝑐1 (velocity constant 1) and 𝑐2 (velocity constant 2). The result of the test, that is got the best fitness 𝒘, 𝒄𝟏and 𝒄𝟐 value, is 0,559140, 0,535084 and 0.621134 and parameter value are
0,6, 1.8 and 2.4. Get the best fitness value of the forecasting, is 0.445334.
Keywords : Population, Forecasting, Fuzzy Time Series (FTS), Particle Swarm Optimization (PSO).
1. PENDAHULUAN
Perkembangan zaman semakin pesat pada saat ini, seiring dengan pertumbuhan penduduk yang begitu derastis naik dari waktu kewaktu. Akibatnya terjadinya krisis moneter dan krisis moral yang diikuti dengan penurunan kualitas bangsa Indonesia. Kondisi ini dapat membawa banyak dampak permasalahan antara lain: pengangguran, tindakan kriminal, bangunan
sebagai tempat tinggal, dan kurangnya investasi. Angka pengangguranpun meningkat yang membuat bangsa Indonesia semakin miskin. Selain itu, masalah yang dihadapi bangsa Indonesia seiring dengan permasalahan yang ada adalah kepadatan penduduk yang meningkat, sedangkan pendapatan yang terus menurun (As’ad et All, 2013). Dari peristiwa tersebut diperlukan adanya upaya untuk menangani
bersangkutan dengan permasalahan-permasalahan tersebut dengan mengetahui seberapa besar pertumbuhan penduduk.
Bertambahnya jumlah penduduk yang sangat luas dapat berdampak pada kehidupan sosial, ekonomi, karena setiap orang memerlukan makanan, pakaian pendidikan, tempat tinggal dan kebutuhan lain-lain, sehingga terjadi tidak seimbangan antara pertumbuhan penduduk dan pendapatan masyarakat Ratnaningrum (2007). Oleh karena itu perlunya untuk melakukan, peramalan jumlah penduduk sehingga dapat mengontrol pertumbuhan penduduk dan kesejahteraan penduduk secara berkala, berdasarkan hasil peramalan yang dilakukan.
Menururt penelitian sebelumnya Ratnaningrum (2007), yang berjudul “Tingkat Pertumbuhan Penduduk Periode 1995-2005 Kabupaten Kudus dan Ramalan Jumlah penduduk Tahun 2008 dengan Metode Smoothing”, yaitu untuk meramalkan jumlah penduduk Kabupaten Kudus diperlukan metode peramalan, salah satunya adalah Double Exponential Smothing. Dari perhitungan nilai kesalahan menggunakan Mean Square Error (MSE) memiliki nilai kesalahan yang cukup kecil, jika menggunakan nilai 𝛼 = 0,1.
Berdasarkan penelitian yang sebelumnya telah dilakukan oleh Wangren Q. Et. all (2015) yang berjudul “Generalized Fuzzy Time Series Forecasting Model Enhanced with Particle Swarm Optimization”, yaitu peramalan yang dilakukan menggunakan metode Fuzzy Time Series memiliki hasil yang kurang baik, dari kekurangan itu kemudian dilakukan optimasi menggunakan algoritma Particle Swarm Optimization. Setelahdilakukan optimasi, hasilnya terlihat perbedaan nilai RMSE nya yaitu 72,99833333 dan 5,162333333.
Penelitian selanjutnya oleh Tarokh dan Koochakpour (2015) yang berjudul “Designing Budget Forecasting anf Revision System Using Optimization Methods” mengatakan bahwa untuk melakukan prediksi pada anggaran penjualan barang dapat meningkatkan kinerja perusahaan secara keseluruhan dari suatu organisasi dan keefektifitasanya tergantung dari validitas dan nilai akurasi dari prediksi yang dihasilkan. Untuk mencapai tingkat akurasi yang lebih maksimum mereka menerapkan salah satu algoritma yaitu Particle Swarm Optimization. Perbandingan antara hasil prediksi dengan hasil prediksi yang menggunakan Particle Swarm Optimization lebih tinggi, oleh karena itu dengan
melakukan optimasi dapat meningkatkan anggaran penjualan dan nilai peramalan secara signifikan.
Penelitian selanjutnya oleh Khoslah, at.all (2012) yang berjudul “Identification of Type-2 Fuzzy Models for Time-series Forecasting using Particle Swarm Optimization” pada data Mackey-Glass Time Series telah di lakukan empat percobaan yang berbeda dengan data set Time Series yang tidak berpola. Desain kerangka dususun secara generik dan dapat memodifikasi parameternya. Fakta bahwa kinerja dari algoritma evolusioner tergantung pada pemilihan parammeter. Dari semua percobaan tersebut, Particle Swarm Optimization dapat mengoptimalkan fungsi parameter yang ada sehingga dapat mencapai nilai akurasi dan konvergensi yang lebih baik.
Pada skripsi ini penulis menggunakan metode Fuzzy Time Series untuk melakukan peramalan dan nantinya akan di optimasi menggunakan metode Particle Swarm Optimization pada derajat keanggotaaanya. Peramalan dilakukan pada data jumlah penduduk kabupaten probolinggo perkecamatan selama 4 tahun terakhir 2013-2016. Hasil dari penelitian ini nantinya diharapkan menghasilkan nilai prediksi yang optimum untuk data jumlah penduduk kabupaten probolinggo.
2. DATASET
Data yang digunakan pada penelitian ini adalah data jumlah penduduk Kabupaten Probolinggo yang didapat dari Dinas Kependudukan dan Pencatatan Sipil Kabupaten Probolinggo. Data yang digunakan dibagi menjadi dua yaitu data training dan data testing. Data tersebut tersusun dari data jumlah penduduk perkecamatan setiap bulan dan setiap tahunya dari 4 tahun terakhir mulai tahun 2013-2016.
3. PERAMALAN
faktor lain yang dapat mempengaruhi perkembangan data di masa yang mendatang dapat diartikan sebagai peramalan (Sofian Assauri, 1984). Untuk memperkirakan suatu kebutuhan dimasa mendatang dengan memperhatikan kebutuhan dalam ukuran lokasi, waktu, kualitas, dan kuantitas yang dibutuhkan dibutuhkan proses peramalan. Salah satu cara untuk menentukan ukuran kesalahan secara statistik yaitu dengan Root Mean Squared Error (RMSE) yang ditunjukkan pada Persamaan 1.
𝑅𝑀𝑆𝐸 = √𝑀𝑆𝐸 = √∑𝑛𝑡=1𝑒𝑡2
𝑛 (1)
Dimana dijelaskan :
𝑒𝑡 = Nilai error pada t tertentu
𝑛 = Jumlah Data Uji
4. FUZZY TIME SERIES (FTS)
Menurut Barry Render (2003) metode time series merupakan salah satu metode peramalan/prediksi nilai utuk masa mendatang dengan menggunakan data historis/runtut waktu. Dalam model ini dapat diasumsikan bahwa apa yang terjadi dimasa depan dapat disebabkan oleh kejadian masa lalu. Dengan kata lain metode ini melihat apa yang telah terjadi elama periode waktu tertentu dan menggunakan serangkaian data masa lalu untuk melakukan prediksi. Pengertian lain menurut Mey dan Isa (2014) Fuzzy Time Series adalah salah satu metode peramalan yang menggunakan fungsi-fungsi nilai Fuzzy sebagai dasarnya. Sistem peramalan ini menggunakan pola dari data masa lalu yang nantinya digunakan untuk memprediksikan data dimasa yang mendatang.
Menurut Song dan Chissom (1993), beberapa diantaranya dari proses Fuzzy Time Series yang nantinya penting untuk melakukan peramalan, yaitu:
1. Definisi 1. Dimana 𝑌(𝑡) untuk 𝑡 =
(… , 0, 1, 2, … ), yang merupakan potongan dari bilangan Real (𝑅1), yang menjadi bagian dari himpuanan semesta dari Fuzzy set 𝑓𝑖(𝑡) untuk 𝑖 = (1, 2, 3, … , … ), jika 𝑓(𝑡) adalah himpunan 𝑓1(𝑡), 𝑓2(𝑡), … Maka 𝑓(𝑡) merupakan himpunan Fuzzy dari fungsi
𝑌(𝑡).
2. Definisi 2. Jika 𝐹(𝑡) hanya disebebkan oleh
𝐹(𝑡 − 1) dan ditunjukkan dengan 𝐹(𝑡 −
1) → 𝐹(𝑡) maka ada Fuzzy Relation antara
𝐹(𝑡) dan 𝐹(𝑡 − 1).
Tahapan-tahapan dalam peramalan FTS dapat dilihat dibawah ini (Cheng et all, 2008):
Tahapan dalam melakukan proses peramalan menggunakan algoritma Fuzzy Time Series Cheng sebagai berikut (Cheng et all, 2008):
1. Mendefinisikan nilai Semesta, kemudian membaginya berdasarkan interval yang sudah di tentukan terlebih dahulu. Apabila terdapat data yang nilainya lebih tinggi dibandingkan dengan rata-rata dari jumlah data tiap interval, maka interval tersebut dapat dibuat interfal baru dengan membagi 2 data tersebut.
2. Mendefinisikan himpunan Fuzzy pada Semesta dan melakukan Fuzzyfikasi pada data historis yang diamati. Contoh:
𝐴1, 𝐴2, 𝐴3, … , … , 𝐴𝑛 adalah nilai himpunan Fuzzy dari A. Fuzzyfikasi yang didapat dari himpunan A, ditunjukkan oleh Persamaan 2 bibawah ini: 3. menentukan relasi Fuzzy Logic berdasarkan
data sebelumnya. Pada langkah ke-2 kemudian dibentuk dua himpunan Fuzzy secara berurutan 𝐴𝑖(𝑡 − 1) 𝑑𝑎𝑛 𝐴𝑗 (𝑡) yang dinyatakan sebagai 𝐴𝑖 → 𝐴𝑗.
4. Mengklasifikasikan relasi-relasi tersebut menjadi grup Fuzzy Logic Relation. Logic Relation. Contoh:
(𝑡 = 1) 𝐴1 → 𝐴1, dengan bobot 1, (𝑡 = 2) 𝐴2 → 𝐴1, dengan bobot 1, (𝑡 = 3) 𝐴2 → 𝐴3, dengan bobot 2, (𝑡 = 4) 𝐴3 → 𝐴1, dengan bobot 3,
6. Membentuk persamaan matriks dari
7. Menghitung hasil peramalan. Dengan cara mengkalikan matrik sebelumya dengan matriks defuzzyfikasi 𝐿𝑑𝑓 dimana 𝐿𝑑𝑓 =
[𝑚1, 𝑚2, … , 𝑚1𝑘] sedangkan 𝑚𝑘 adalah
nilai tengah dari tiap-tiap interval cara untuk menghitung Peramalan seperti pada persamaan 4 sebagai berikut:
𝑭𝒕 = 𝑳𝒅𝒇(𝒕−𝟏)𝑾𝒏(𝒕 − 𝟏)
(4)
5. PARTICLE SWARM OPTIMIZATION
( PSO )
Kennedy dan Eberhart (1995) meneliti dan mengenbangkan metode Particle Swarm Optimization sebagai salah satu metode optimasi. Algoritma ini berbasis populasi yang mengeksploitasi individu dalam suatu popoulasi menuju daerah penyelesaian dalam daerah pencarianya (Dian et. All, 2011). Algoritma PSO diambil dari penelitian perilaku sekawanan hewan, yaitu: burung dan ikan yang bergarak menuju titik tertentu dalam mencari posisi terbaik dalam suatu ruang tertentu (Rachmat et. all , 2016). Dapat diasumsikan bahwa burung-burung tersebut adalah partikel dan di setiap partikel memiliki memori untuk mengingat posisi dan kecepatan terbang mereka. Untuk setiap pencarian nantinya akan menjadi sebuah iterasi, sedangkat partikel yang mengetahui lokasi atau posisi makanan atau pusatnya akan menjadi nilai fetness terbaik dari iterasi tersebut (Rachmat et. all , 2016).
Tahapan-tahapan proses Particle Swarm Optimization yang telah dijabarkan sebagai berikut (Hu et al., 2014):
Tahap 1 :
Inisialisasi awal partikel, yang didalamnya memiliki jumlah populasi, posisi awal dan kecepatan sawal etiap partikel.
Tahap 2 :
Melakukan perhitungan fitness pada setiap partikel yang ada. Kemudian posisi partikel terbaik disimpan sebagai
(pBest) beserta fitness-nya dari setiap partikel. Kemudian global optimal (gBest) untuk menyimpan posisi terbaik dengan nilai Fitness tertinggi.
Tahap 3 :
Kecepatan dan posisi dari setiap partikel akan di update. Proses update kecepatan dengan menggunakan Persamaan 5
𝒗𝒊,𝒋𝒕+𝟏= 𝒘. 𝒗
𝑐 = konstanta kecepatan
𝑟 = nilai acak ∈ [0,1] Persamaan 6 akan digunakan untuk proses update posisi setiap partikel
𝒙𝒊,𝒋𝒕+𝟏= 𝒙𝒊,𝒋𝒕 + 𝒗𝒊,𝒋𝒕+𝟏 (6)
Melakukan pembaruan pBest. Dengan ketentuan jika fitness baru lebih besar dari fitness yang lama, partikel yang baru akan menggantikan partikel yang lama sebagai pbest yang baru.
Tahap 6 :
fitness tertinggi dari pbest yang sudah diperbarui sebelumnya akan diguunakan untuk gbest yang baru.
Tahap 7 :
6. PERANCANGAN DAN IMPLEMENTASI
Perancangan Sistem akan menjelaskaan analisis dan perancangan peramalan jumlah penduduk dengan menggunakan algoritma FTS-PSO. Adapaun tahapan-tahapan dari analisis dan perancangan sistem dapat dilihat dari Gambar 1.
Gambar 1. Diagram Alir Kombinasi FTS dan PSO
Langkah-langkah yang dilakukan dalam implementasi antara lain:
1. Implementasi Optimasi Fuzzy Time Series Menggunakan Algoritma Particle Swarm Optimization Untuk Peramalan Jumlah Penduduk Di Kabupaten Probolinggo 2. Output yang diperoleh berupa hasil
peramalan dan RMSE.
Representasi partikel yang digunakan dalam PSO adalah interval FTS yang akan dioptimasi. dalam PSO ditunjukkan pada Tabel berikut:
Tabel 1. Representasi partikel IPSO
Partikel 1 2 3 4 5
X1 -156 -81 -22 10 48
X2 -156 -76 -35 15 48
X3 -156 -73 -23 30 48
Kemudian perhitungan yang digunakan sebagai fitness partikel adalah nilai error (RMSE) dari peramalan dengan menggunakan FTS yang ditunjukkan pada Persamaan 7.
𝑓𝑖𝑡𝑛𝑒𝑠𝑠 = 1+𝑅𝑀𝑆𝐸1 (7)
7. PENGUJIAN DAN ANALISIS
7.1. Pengujian dan Analisis Nilai Parameter
𝒘 Pada PSO
Pengujian nilai parameter w dilakukan untuk mendapatkan nilai w yang optimal dalam eramalan jumlah penduduk menggunakan metode FTS – PSO. Data yang digunakan dalam pengujian ini yaitu data jumlah penduduk kabupaten probolinggo perkecamatan selama 4 tahun terakhir. Parameter-parameter yang digunakan untuk uji coba batas parameter 𝑤 adalah sebagai berikut:
Jumlah Data : 48
Jumlah Iterasi PSO : 1000
Jumlah Partikel PSO : 10
Nilai Parameter 𝐶1 : 1,5
Nilai Parameter 𝐶2 : 1,5
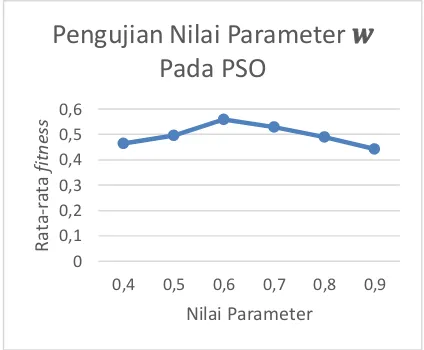
Hasil uji coba pengujian nilai parameter 𝑤 pada PSO dapat dilihat pada Gambar 2.
Gambar 2. Grafik Pengujian Nilai Parameter 𝒘 Pada
PSO 0
0,1 0,2 0,3 0,4 0,5 0,6
0,4 0,5 0,6 0,7 0,8 0,9
R
at
a
-r
at
a
fi
tn
e
ss
Nilai Parameter
Pengujian Nilai Parameter
𝒘
Pada PSO
Start
Data Jumlah Penduduk
Optimasi Interval Dengan PSO
Iterasi == n & JmlPartikel == n
Yes No
Pengujian Fuzzy Time Series
Hasil peramalan jumlah penduduk
Didapatkan bahwa nilai parameter w yang optimal adalah 0,6 yang memiliki nilai fitness tertinggi dengan nilai 0,559140. Nilai paramaeter ini akan digunakan untuk mencari nilai optimal parameter c1 dan c2 pada PSO.
7.2. Pengujian dan Analisis Nilai Parameter
𝑪𝟏 Pada PSO
Pengujian nilai parameter c1 dilakukan untuk mendapatkan nilai w yang optimal dalam Peramalan jumlah penduduk menggunakan metode FTS – PSO. Data yang digunakan dalam pengujian ini yaitu data jumlah penduduk kabupaten probolinggo perkecamatan selama 4 tahun terakhir. Parameter-parameter yang digunakan untuk uji coba batas parameter 𝑤
Hasil uji coba pengujian nilai parameter 𝐶1 pada PSO dapat dilihat pada Gambar 3
Gambar 3. Grafik pengujian Nilai Parameter 𝐶1 Pada PSO
Ditunjukkan bahwa nilai fitness tertinggi adalah 0,535084 dengan nilai parameter c1 1,8 yang ditunjukan oleh Gambar 3 dan nantinya nilai in akan digunakan sebagai nilai parameter terbaik untuk c1 dan digunakan untuk melakukkan optimasi untuk parameter berikutnya.
7.3. Pengujian dan Analisis Nilai Parameter
𝑪𝟐 Pada PSO
Pengujian nilai parameter 𝐶2 dilakukan untuk mendapatkan nilai 𝐶2 yang optimal dalam peramalan jumlah penduduk menggunakan metode FTS – PSO. Data yang digunakan dalam pengujian ini yaitu data jumlah penduduk kabupaten probolinggo perkecamatan selama 4 tahun terakhir. Parameter-parameter yang digunakan untuk uji coba batas parameter
𝐶2adalah sebagai berikut:
Jumlah Data : 48
Jumlah Iterasi PSO : 10.000
Jumlah Partikel PSO : 10
Nilai Parameter 𝑤 : 0,6
Nilai Parameter 𝐶1 : 1,8
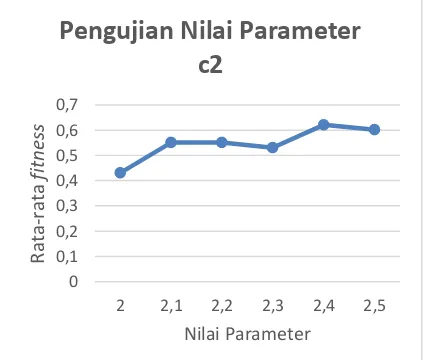
Hasil uji coba pengujian nilai parameter 𝐶2 pada PSO dapat dilihat pada Tabel Hasil uji coba pengujian nilai parameter 𝐶2 pada PSO dapat dilihat pada Gambar 4.
Gambar 4. Grafik pengujian Nilai Parameter 𝐶2 Pada PSO
Ditunjukkan bahwa nilai fitness cenderung naik dengan nilai fitness yang cenderug naik dengan nilai fitness tertinggi adalah 0,621134 dan dengan nilai parameter 2,4. Nilai ini akan digunakan sebagi nilai parameter c2 yang optimal.
7.4. Pengujian dan Analisis Nilai Jumlah Iterasi PSO
Pengujian jumlah Iterasi PSO ini dilakukan dengan menentukan jumlah iterasi yang digunakan untuk peramalan. Data yang digunakan diambil dari data perkecamatan hingga 4 tahun terakhir mulai dari tahun 2013
Pengujian Nilai Parameter
c1
hingga tahun 2016. Tercatat jumlah data 48 dengan parameter jumlah penduduk setiap bulannya selama 4 tahun tersebut. Hasil dari pengujian nilai parameter sebelumnya akan digunakan sebagai nilai parameter dari PSO yang optimal. Parameter-parameter yang digunakan untuk uji coba batas parameter 𝑤 dilihat pada Gambar 5.
Gambar 5. Grafik Pengujian Jumlah Iterasi Pada PSO
Didapatkan bahwa jumlah iterasi yang semakin banyak mengindikasikan nilai fitness yang semakin baik dan menunjukkan jumlah iterasi yang dibutuhkan untuk mencapai konvergensi. Dari pengujian tersebut didapatkan nilai fitness yang optimal yaitu, 0,566826 dengan jumlah iterasi sebanyak 1000.
7.5. Pengujian dan Analisis Jumlah Data
Pengujian jumlah data ini dilakukan dengan menentukan jumlah data yang digunakan untuk peramalan sebagai data latih dan data uji. Data tersebut diambil dari data perkecamatan hingga 4 tahun terakhir mulai dari tahun 2013 hingga tahun 2016. Tercatat jumlah data 48 dengan parameter jumlah penduduk setiap bulannya selama 4 tahun tersebut. Hasil dari pengujian nilai parameter sebelumnya akan digunakan sebagai nilai parameter dari PSO yang optimal.
Parameter-parameter yang digunakan untuk uji coba batas parameter 𝑤 adalah sebagai berikut:
Jumlah Iterasi PSO :1.000 dilihat pada Gambar 6.
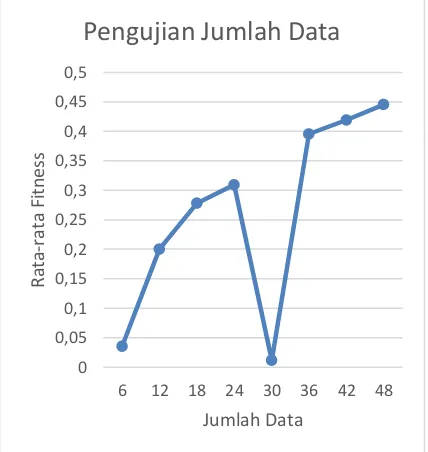
Gambar 6. Grafik Pengujian Jumlah Data
Dituunjukkan bahwa jumlah data dapat mempengaruhi hasil peramalan yang terlihat pada fitness, semakin banyak jumlah data, semakin baik nilai fitnessnya.nilai fitnes terbaik adalah 0,445334 dengan jumlah data 48.
7.6. Analisis Global Hasil Pengujian
Berdasarkan dari hasil pengujian sebelumnya yang telah dilakukan didapatkan nilai parameter dengan nilai fitness yang terbaik. Pada pengujian nilai parameter 𝒘 didapatkan nilai fitness terbaik, yaitu 0,559140 dan nilai parameternya 0,6. Sedangkan pada nilai parameter 𝐶1 dan 𝐶2 masing-masing memiliki nilai didapatkan nilai fitness terbaik, yaitu 0,535084 dan 0,621134 dan nilai parameternya 1,8 dan 2,4.
Pengujian lain yang dilakukan adalah pengujian jumlah iterasi PSO dan jumlah Data yang digunakan. Jumlah iterasi PSO yang digunakan dalam pengujian yaitu: 10, 20, 30, 40,
50, 1.00, 1.000, 10.000, 100.000. Sedangkan untuk pengujian jumlah data, jumlah data yang digunakan yaitu: 6, 12, 18, 24, 30, 36, 42, 48. Dari pengujian iterasi didapatkan nilai fitness terbaik yaitu: 0,566826 dengan jumlah iterasi sebanyak 1.000. Sedangkan untuk pengujian jumlah data didapatkan nilai fitness terbaik yaitu: 0,445334 dengan jumlah data sebanyak 48.
Untuk mengetahui tingkat keakuratan dari peramalanmenggunakan FTS dan FTS-PSO dilakukan percobaan dengan mengguanakan data jumlah penduduk dari bulan Juli tahun 2016 – Desember 2016. Hasil percobaan yang dilakukan dapat dilihat dari Tabel 2 serta pada Gambar 7 Dan 8.
Tabel 2. Perbandingan Nilai RMSE FTS dan PSO-FTS
Metode RMSE
PSO-FTS 14,50370333
FTS 52,05198333
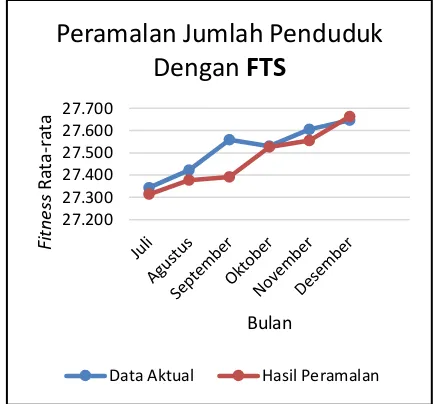
Gambar 7. Grafik Peramalan Jumlah Penduduk Dengan FTS-PSO
Berdasarkan grafik pada Gambar 7, didapatkan nilai fitness rata-rata peramalan jumlah penduduk yang membandingkan data aktual dengan data peramalan mendekati nilai dari data aktual, dengan rata-rata RMSE 14,50370333. Peramalan ini dilakukan dengan menggunakan metode FTS-PSO.
Gambar 8. Grafik Peramalan Jumlah Penduduk Dengan FTS
Berdasarkan grafik pada Gambar 8, didapatkan nilai fitness rata-rata peramalan jumlah penduduk yang membandingkan data aktual dengan data peramalan tidak mendekati nilai dari data aktual, dengan rata-rata RMSE 52,05198333. Peramalan ini dilakukan dengan menggunakan metode FTS.
8. KESIMPULAN
Dari hasil penelitian tentang peramalan jumlah penduduk menggunakan metode Fuzzy Time Series yang dioptimasi menggunakan Particle Swarm Optimization, maka dapat diambil kesimpulan sebagai berikut:
1. Metode Fuzzy Time Series (FTS) dapat digunakan untuk melakukan peramalan. peramalan yang dilakukan menggunakan metode FTS memeberikan nilai RMSE, yaitu: 52,05198333. Metode Particle Swarm Optimization (PSO) dapat digunakan untuk melakukan optimasi metode FTS. Langkah pertama dengan melakukan optimasi interval FTS dengan PSO. Interval pada FTS tersebut akan digunakan sebagai partikel pada PSO yang nantinya memiliki fitness yang tinggi sebagai penentu partikel yang optimal, dimana semakin tinggi fitness semakin baik nilai akurasinya. Nilai interval dilakukan dengan mengambil nilainya secara acak dengan batasan tertentu. Langkah kedua akan dilakukan perhitungan peramalan menggunakan metode FTS dengan interval yang optimal untuk mendapatkan nilai peramalan yang lebih akurat dan baik. Sehingga didapatkan nilai RMSE, yaitu:
14,50370333. Dapat dilihat dari perbandingan peramalan menggunakan FTS dan FTS-PSO, RMSE yang lebih baik menggunakan metode FTS-PSO.
2. Hasil dari pengujian yang dilakukan dengan menggunakan data jumlah penduduk Kabupaten Probolinggo pada setiap kecamatan mulai tahun 2013 sampai 2016, didapatkan nilai paramater terbaik yaitu: 𝑤 = 0,6, 𝑐1= 1,8 dan 𝑐2= 2,4. Sehingga diperoleh nilai fitness terbaik dari peramalan tersebut, yaitu: 0,445334.
Pada penelitian jumlah penduduk dengan menggunakan metode Fuzzy Time Series yang diptimasi dengan metode Particle Swarm Optimization masih terdapat banyak kekurangan. Kekurangan tersebut dapat dikembangkan dengan melakukan penelitian yang lebih baik lagi. Saran yang dapat dilakukan untuk penelitian selanjutnya, yaitu:
1. Diharapakan untuk penelitian yang dilakukan berikutnya, optimasi metode FTS dapat dilakukan dengan menggunakan metode optimasi yang lain selain PSO. 2. Diharapkan untuk penelitian selanjutnya,
melibatkan faktor lain selain jumlah penduduk, misal jumlah kelahiran, kematian, migrasi dan lain sebagainya.
9. DAFTAR PUSTAKA
Assauri S. 1984. Teknik dan Model Peramalan. Jakarta: Fakultas Ekonomi Universitas Indonesia
As’ad, Made I.T., Yulianisetia D. 2013. “Peramalan Pertumbuhan Penduduk Kabupaten Situbondo Dengan Model Arima, Deret Aritmatik, Deret Geometri
Dan Deret Eksponensial “The
Forecasting Growth Of The Population In Situbondo By Using Arima, Aritmatics,
Geometrics And Exponential””.
Kadikma, Vol. 4, No. 1, Hal 141-152. Universitas Jember.
Dukcapil. 2014. Data Kependudukan. [Online]
Tersedia di:
<http://dukcapil.kemendagri.go.id/detail/ data-kependudukan>. [Diakses 4 Januari 2017]
Hansung S. 2012. Peramalan Data AHSG Menggunakan Fuzzy Time Series. IJCCS. Vol.6, No.2, July 2012, pp. 79-88. Universitas Multimedia Nusantara.
Huang Y-L., Hong S-J, Kuo I-H, Kao T-W, Takao T. 2012. A hybrid forecasting model based on adaptive fuzzy time Series and particle swarm optimization. International Symposium on Biometrics and Security Technologies. Pp. 66-70.
Kennedy, J. & Eberhart, R.C., 1995. Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks, pp.1942-1948.
Khosla M., Kumar R.S., Uddin M. 2012. Identification of Type-2 Fuzzy Models Time-Series Forecasting Using Particle Swarm Optimization. IEEE. 2012
Internasional Coferance on
Communication Systems and Network Technologyes.
Qiu W., Zhang C., Zang P. 2015. Generalized Fuzzy Time Series Forecasting Model Enhanced with Particle Swarm Optimization. International Journal of u- and e- Service, Science and Technology. Vol.8, No.5.
Rachmat Z.Y., Ratnawati D.E., Arwan A. 2016. Optimasi Komposisi Makanan Untuk Atlet Endurance Menggunakan Metode Particle Swarm Optimization. JTIIK Vol. 3, No.2,. Pp . 103-109.
Ratnaningrum D. 2007. Tingkat Pertumbuhan Penduduk Periode 1995-2005 Kabupaten Kudus dan Ramalan Jumlah penduduk Tahun 2008 dengan Metode Smoothing. D3. Universitas Negeri Semarang.
Render, B., Stair Jr., R.M. dan Hanna, M.E., 2003, Quantitative Analysis for Management, 8th edition. New Jersey: Pearson Education, Inc.
Song Q. Dan Chissom B.S.. 1993. Fuzzy time Series and Its Models. Fuzzy Set and System Vol. 54. Pp. 269-277.