ON A PERTURBATION OF THE STUDENT
t
DISTRIBUTION
Katsuo Takano
Abstract. This paper is to prove the infinite divisibility of atdistribution with
the odd degrees of freedom2n+ 1without using of Bessel functions. The Laplace-Stieltjes transform of an infinitely divisible probability distribution is concentrated on the interval[0,1). A simple expression of the Laplace-Stieltjes transform is made by using of hypergeometric function. The L´evy measure of the Student t distribution obtained from the L´evy mesure of the distribution with the density functon.
1. INTRODUCTION
A probability distribution functionF(x) is called an infinitely divisi-ble probability distribution if for each integer n > 1 there is a probability distributionFn(x) such that the following relation holds,
F(x) = (Fn∗ · · · ∗Fn)(x),
where * denotes the convolution. If a probability distribution functionF(x) is concentrated on the interval [0,∞) and an infinitely divisible probability distribution, and if we set
η(s) =
Z ∞
0
e−sxdF(x), ηn(s) = Z ∞
0
e−sxdFn(x),
Received 28-11-2011, Accepted 05-12-2011.
2010 Mathematics Subject Classification: 60E07; 40A25; 46F12.
Key words and Phrases: probability distribution function; infinitely distribution function; density function.
the following relation
η(s) = (ηn(s))n
holds. It is known that the Laplace-Stieltjes transform of an infinitely di-visible probability distribution F(x) which is concentrated on the interval [0,∞) can be written as follows:
η(s) = exp{−ds+
Z ∞
+0
(e−sx−1)1
xdK(x)}
where
(c1) K(x) is nondecreasing, (c2) K(−0) = 0,
(c3) R∞
1 1/x dK(x)<∞.
Here, let us assume d= 0 in what follows. If an infinitely divisible proba-bility distribution F(x) which is concentrated on the interval [0,∞) and if the probability distribution function F(x) has a density function f(x), the density funcionf(x) satisfies the following integral equation:
xf(x) =
Z x
0
f(x−t)dK(t), x >0.
If dK(t) =k(t)dt we have
xf(x) =
Z
(0,x)
f(x−t)k(t)dt, x >0.
We will discuss about the Student t distribution. The density function of the Student tdistribution with degrees of freedom r is as follows:
T(t) = Γ((√r+ 1)/2))
πr Γ(r/2)
1
(1 +t2/r)(r+1)/2
Ifr is an odd integer,r= 2n+ 1 for a nonnegative integernand if we make change of variable, t/√r=x, we have the density function
Γ(n+ 1)
√
πΓ(n+ 1/2) 1 (1 +x2)n+1.
use of the Bessel functons (cf. [3]). We will make use of the fact that if
h tends to +0 the density function of the Student t distribution can be obtained by the following relation
f(x; 1, h) = c
(1 +x2)((1 +h)2+x2)· · ·((1 +nh)2+x2) → (1 +cx02)n+1,
wherec and c0 are normalised constants.
2. THE HYPERGEOMETRIC FUNCTION
Let a be a positive constant. In what follows, suppose that a1 = a, a2 =
a+h, ..., an+1=a+nh.Let us consider the following density function
f(x;a, h) = c Πn+1j=1(a2
j +x2)
(1)
wherec is a normalized constant. It holds that
f(x;a, h) =c n+1 X
j=1
1 Πn+1l=1,l6=j(−a2
j +a2l)(a2j +x2)
. (2)
From the relation 1
a2 j +x2
=
Z ∞
0
e−t(a2j+x2)dt
=
Z ∞
0
1
√ πve
−x2/v√
π e−a2j/vv−3/2dv
we obtain the following equality
f(x;a, h) =
Z ∞
0
1
√ πve
−x2/v
n+1 X
j=1
c√π
Πn+1l=1,l6=j(−a2 j +a2l)
e−a2j/vv−3/2dv. (3)
Let us denote the mixing density function in the integrand of (3) byg(v).The mixing densityg(v) is positive on [0,∞) and a probability density function. We take the Laplace transform of g(v).Since it holds that
Z ∞
0
e−sve−a2j/vv−3/2dv= √
π aj
we obtain
η(s) =c√π n+1
X
j=1
1 Πn+1l=1,l6=j(−a2
j +a2l) Z ∞
0
e−sve−a2j/vv−3/2dv
=cπ n+1 X
j=1
1
ajΠn+1l=1,l6=j(−a2j +a2l)
e−2aj√s. (4)
For n= 3 we obtain
η(s) = cπ
a3!h3(2a+h)(2a+ 2h)(2a+ 3h)e− 2a√s
·1 +(−3)(2m)z (2m+ 4) +
(−3)(−2)(2m)(2m+ 1)z2
(2m+ 4)(2m+ 5)2!
+(−3)(−2)(−1)(2m)(2m+ 1)(2m+ 2)z
3
(2m+ 4)(2m+ 5)(2m+ 5)3!
. (5)
Making use of hypergeometric function we obtain the simple expression
η(s) = 2cπ
n!h2n+1(2m) n+1
zmF(−n,2m; 2m+n+ 1;z) (6)
where we letz=e−2h√sandm=a/h.Concerning the roots of the hyperge-ometric functionF(−n,2m; 2m+n+ 1;z) the author obtained the following result (cf.[11]).
Theorem 2.1 If m is a positive constant and n is a natural number the hypergeometric functionF(−n,2m; 2m+n+ 1;z)has roots outside the unit disk.
3. THE STUDENT t DISTRIBUTIONS
We show that the probability distribution with density function (2) is in-finitely divisible and obtain the L´evy measure of the Studentt distribution from the L´evy mesure of the distribution with the density functon (2).
Proof 3.1
Let us show that the density functiong(v) is an infinitely divisible density for every positive integer n. To show the infinite divisibility of the distribution withg(v),it suffices to show that ifdK(x) =k(x)dxthe following relation
−η′(s) =η(s)
Z ∞
0
e−sxk(x)dx
holds and k(x) is a nonnegative function and satisfies the conditions (c1), (c2), (c3) imposed on an infinitely divisible probability distribution. From (6) we have
η(s) = 2cπ
n!h2n+1(2m) n+1
zm n X
j=0
(−n)j(2m)j
(2m+n+ 1)jj!z
j, (7)
where we set z=e−2h√s and m=a/h.From this we obtain
η′(s) =− 2cπh
n!h2n+1(2m) n+1√s n
X
j=0
(−n)j(2m)j(m+j)
(2m+n+ 1)jj!
zm+j (8)
and hence
−ηη′((ss)) = √h
s Xn
j=0
(−n)j(2m)j(m+j)
(2m+n+ 1)jj!
zm+j
/ n X
j=0
(−n)j(2m)j(m+j)
(2m+n+ 1)jj!
zm+j. (9)
If we setz=e−2h√s and ℜ{√s} ≥0,then|z| ≤1.
We note that
F(−n,2m; 2m+n+ 1;z)6= 0.
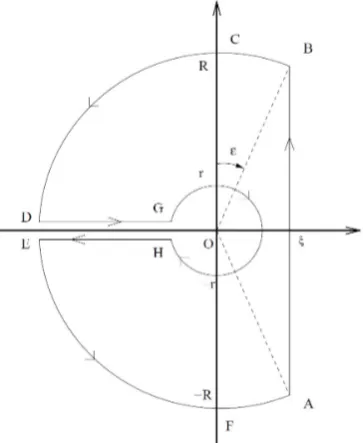
The denominator of (9) does not vanish in the whole complex plane except at the origin. By the contour integration of the figure after the reference we can calculate the inverse Laplace transform of the following formula
k(t) = lim
R→∞
1 2πi
Z ξ+iR1
ξ−iR1
ets(−1)η′(s)
Figure 1: Contour of integration
(ξ >0, t >0, R1=Rcosǫ).
Let
D=√s 3 X
j=0
(−3)j(2m)jzj
(2m+ 4)jj! ,
N =h 3 X
j=0
(−3)j(2m)j(m+j)zj
(2m+ 4)jj! .
(A) The integral along a small circle with the center at O.
Froms=reiθ,√s=√r(cosθ/2 +isinθ/2) for−π < θ < π,we see that
I estN
Dds=− Z π
−π ereiθt
hn h
3 X
j=0
(−3)j(2m)j(m+j)e−j2h
√
reiθ/2
(2m+ 4)jj!
o
/n 3 X
j=0
(−3)j(2m)je−j2h
√reiθ/2
(2m+ 4)jj!
oi√
Since for every 0< r≤1 and 0≤θ≤π
We see that
asR→+∞.We show that
Z π2
π 2−ǫ
|√Reiθ/2eReiθt|dθ→0 (12)
asR→ ∞. From the fact that
cosθ= cos(φ+π
2 −ǫ) = sinφ, 0≤φ≤ǫ, sinǫ= ξ
R ≥sinφ≥0,
we see that
Z π2
π 2−ǫ
√
R|eiθ/2eReiθt|dθ =
Z π2
π 2−ǫ
√
RetRcosθdθ
=
Z ǫ
0 √
RetRsinφdφ≤ Z ǫ
0 √
RetRξ/Rdφ=√Retξǫ
= etξ(√Rsinǫ) ǫ sinǫ =e
tξ(√Rξ R)
ǫ
sinǫ →0 (13)
asR→ ∞.
(C) The integrals alongD→Gand H →E.
=−
Therefore we see that
For the general case nwe obtain
k(t) = 1
π Z ∞
0
e−ty2hn n X
j=0
(−n)j(2m)j(m+j)e−j2hyi
(2m+n+ 1)j
o
/n n X
j=0
(−n)j(2m)je−j2hyi
(2m+n+ 1)j o
+n
n X
j=0
(−n)j(2m)j(m+j)e+j2hyi
(2m+n+ 1)j
o
/n n X
j=0
(−n)j(2m)je+j2hyi
(2m+n+ 1)j oi
hdy. (16)
To show the infinite divisibility it is necessary to show that the following function
ℜn n X
j=0
(−n)j(2m)j(m+j)e−j2hyi
(2m+n+ 1)j
o
·n n X
j=0
(−n)j(2m)je+j2hyi
(2m+n+ 1)j o
is nonnegative for y≥0.Let 2hy=θin the above and let
A = ℜn
n X
j=0
(−n)j(2m)j(m+j)e−i(m+j)θ
(2m+n+ 1)j
o
·n n X
j=0
(−n)j(2m)je+i(m+j)θ
(2m+n+ 1)j o
.
If n= 0 we obtain
A= (1/m2)(cosθ·mcosθ+msinθ·sinθ) = 1/m.
If n= 1 we obtain
A= 2m(2m+ 1)
2m+ 2 (1−cosθ). For the generalnwe obtain
A= 2
n−1(2m) n+1
(2m+n+ 1)n
Let
distribution with the density function (2) is infinitely divisible since it is a mixture density of the normal distributions.
Let us denote the characteristic fuction of the probability distribution with the density function (2) in the following form
φ(t) = exph
In what follows we will obtain the measurel(x)dx/x. We have
φ(t) =
Using the following equality
We see that the function l(x) can be given in the following form
l(x) = (sgn x)
Z ∞
0
e−2√w|x|U(w)dw
= (sgn x)
Z ∞
0
e−|x|v 22n−1
h
(2m)n+1h(sin(hv/2))2n/
π n X
j=0
(2m)j 22j
(2m+n+ 1)n−j
n j
2n−j n
(2(n−j))!(sin(hv/2))2jidv. (22)
Let us denote the characteristic function of the Student tdistribution with odd degrees of freedom in the following form
φ(t) = exph
Z
R−{0}
eitx−1− itx 1 +x2
lst(x) x dx
i .
Theorem 3.2 The function lst(x) can be given in the explicit form lst(x) = (sgn x)
Z ∞
0
e−|x|v
(2a)2n+1v2ndv/
2π n X
j=0
(2a)2j
n j
2n−j n
(2(n−j))!v2j}. (23)
We take a= 1 for the Student t distribution.
Proof 3.2
By (22) andhm=awe see that
l(x) = (sgn x)
Z ∞
0
e−|x|v
h
22n−1(2m)n+1h(sin(hv/2))/(hv/2)2n
(hv/2)2n/nπ n X
j=0
(2m)j 22j
(2m+n+ 1)n−j
n j
2n−j n
From the above we see that
lst(x) = (sgn x) Z ∞
0
e−|x|v h(2a)2n+1v2n/
2π n X
j=0
(2a)2j
n
j
2n−j n
(2(n−j))!v2jidv
ash tends +0 and we obtain (23). Ifa= 1 we have
lst(x) = (sgn x) Z ∞
0
e−|x|yh2(2y)2n/
n
2π n X
j=0
n j
2n−j n
(2(n−j))!(2y)2joidy.
(25)
In order to show that the results here coincide with those formulae of which have been already obtained we write down the several cases (cf. [1]). If n= 1
lst(x) = (sgn x) Z ∞
0
e−|x|y y 2 π(1 +y2)dy.
If n= 2
lst(x) = (sgn x) Z ∞
0
e−|x|y y 4
π(32+ 3y2+y4)dy.
If n= 3
lst(x) = (sgn x) Z ∞
0
e−|x|y y 6
π(225 + 45y2+ 6y4+y6)dy.
If n= 4
lst(x) = (sgn x) Z ∞
0
e−|x|y
y8
π(11025 + 1575y2+ 135y4+ 10y6+y8)dy. (26)
From the above we see that the function lst(x) can be decomposed to the
If n= 1
lst(x) =
1
πx −(sgn x) Z ∞
0
e−|x|y 1 π(1 +y2)dy
= 1
πx − sgn x
π h
cos|x| Z →∞
|x|
siny
y dy−sin|x| Z →∞
|x|
cosy y dy
i ,
(x6= 0). (27)
If n= 2
lst(x) =
1
πx −(sgn x) Z ∞
0
e−|x|y 3 2+ 3y2
π(32+ 3y2+y4)dy.
If n= 3
lst(x) =
1
πx
−(sgn x)
Z ∞
0
e−|x|y 225 + 45y
2+ 6y4
π(225 + 45y2+ 6y4+y6)dy.
References
[1] M. Abramowitz and I. A. Stegun, Handbook of Mathematical Func-tions, New York, Dover, 1970.
[2] L. Bondesson, Generalized Gamma Convolutions and Related Classes of Distributions and Densities,Lecture Note in Statistics,76, Springer-Verlag, 1992
[3] E. Grosswald, The Student t-distribution of any degree of freedom is infinitely divisible, Z. Wahrscheinlichkeitstheorie verw. Gebiete, 36 (1976), 103–109.
[4] C. Halgreen, Self-decomposability of the generalized inverse Gaussian distribution and hyperbolic distributions,Z. Wahrscheinlichkeitstheorie verw. Gebiete,47 (1979), 13–17.
[5] D. H. Kelker, Infinite divisibility and variance mixtures of the normal distribution, Ann. Math. Statist.,42 (1971), 802–808.
[7] L. J. Slater, Generalized hypergeometric functions, Cambridge Univ. Press, Cambridge, 1966.
[8] F. W. Steutel, Preservation of infinite divisibility under mixing and related topics, Math. Centre Tracts, Math. Centre, Amsterdam, 33. 1970
[9] F.W.Steutel, K.van Harn, Infinite divisibility of probability distribu-tions on the real line, Marcel Dekker, 2004
[10] K. Takano, On infinite divisibility of normed product of Cauchy densi-ties,J. Comput.Applied Math., 150(2003), 253-263.
[11] K. Takano & H. Okazaki, The Gauss hypergeometric series with roots outside of the unit disk, Proceedings of the 8-th international conference on difference equations and applications, Edited by S. Elaydi, G. Ladas et all, (Held at Czech) (2005), 265-272.
[12] K. Takano, Hypergeometric functions and infinite divisibility of prob-ability distributions consisting of Gamma functions, International J. Pure and Applied Math., 20 no.3 (2005), 379-404.
[13] O. Thorin, On the infinite divisibility of the Pareto distribution,Scand. Acturial. J.,(1977), 31–40.
[14] G. N. Watson, A Treatise on the Theory of Bessel Functions, Second Edition, Cambridge University Press, 1966
Katsuo Takano: Department Mathematics, Faculty of Science, Ibaraki University,
Mito-city, Ibaraki 310 Japan