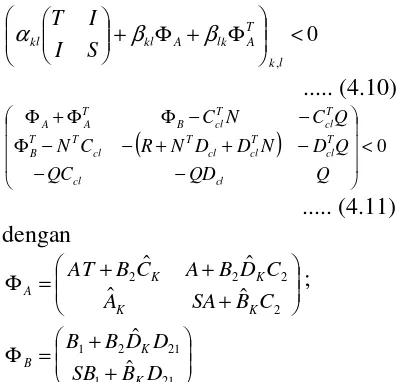Sintesis Sistem Kendali Linier Invarian

SINTESIS SISTEM KENDALI LINIER INVARIAN

WAKTU DISIPATIF DENGAN PELETAKAN KUTUB

MELALUI PENDEKATAN PERTIDAKSAMAAN

MATRIKS LINIER

Aciek Ida Wuryandari1

ABSTRACT

In this paper, we address the synthesis of dissipative controllers for linear time invariant (LTI) systems to render the closed loop system dissipative and to locate the closed-loop poles in a specified region in the complex plane. Such control design criteria is aimed at guaranteeing some robustness properties of the closed-loop system and providing transient nominal performance. Characterizations of dissipative systems and pole location can be expressed as linear matrix inequality (LMI). This expression is utilized to derive LMI conditions from which the controller achieving the design objective can be constructed. The LMI conditions can be solved effectively using interior point algorithm.

Keywords: dissipative systems, linear time invariant systems, dissipative controllers, pole placement, linear matrix inequality.

ABSTRAK

Dalam naskah ini, akan dirancang suatu pengendali disipatif untuk sistem linier invarian waktu (LIW) untuk membuat sistem lingkar tertutup disipatif dan meletakkan kutub-kutub lingkar tertutupnya pada suatu daerah tertentu dalam bidang kompleks. Hal ini sesuai dengan kriteria perancangan sistem kendali yang menjamin sifat kekokohan sistem lingkar tertutup dan kinerja tanggapan peralihan yang baik. Karakterisasi dari sistem disipatif dan peletakan kutub dapat diekspresikan sebagai pertidaksamaan matriks linier (PML). Ekspresi ini digunakan untuk menurunkan kondisi-kondisi PML sehingga pengendali yang diinginkan dapat dibangun. Kondisi-kondisi PML dapat diselesaikan secara efektif dengan menggunakan algoritma yang dibuat.

Kata kunci: sistem-sistem disipatif, sistem linier invarian waktu, pengendali disipatif, peletakan kutub, pertidaksamaan matriks linier.

1

1. PENDAHULUAN

Tujuan para perancang sistem kendali adalah untuk membangun sistem yang dapat digunakan pada lingkungan riel (dunia nyata) dengan spesifikasi yang dinginkan. Dalam praktek, selalu terdapat kemungkinan ketidakpastian yang bersumber pada ketidak-tepatan pemodelan, variasi parameter sistem, gejala non-linier dan lain-lain. Sistem kendali yang memiliki kemampuan untuk beroperasi pada situasi yang realistis adalah sistem kendali kokoh. Secara matematis berarti bahwa pengendali harus mampu melayani tidak hanya sebuah kendalian, tetapi untuk suatu himpunan kendalian.

Kestabilan sistem lingkar tertutup yang dihasilkan harus dipertimbangkan dalam perancangan sistem kendali. Kestabilan itu sendiri mengacu kepada konsep kestabilan Lyapunov yang dipusatkan pada tingkah laku trayektori dari sistem dengan keadaan awal (initial state) berada dekat titik keseimbangan (equilibrium). Hal ini penting karena gangguan eksternal selalu hadir dalam sistem nyata yang dapat menyebabkan trayektori keluar dari keseimbangannya. Gagasan dari kestabilan Lyapunov berasal dari energi yang ditinjau ketika adanya gangguan pada titik keseimbangannya. Bila dinamika sistem setelah gangguan sedemikian rupa sehingga tingkat energi sistem tidak bertambah terhadap waktu, atau tingkat energinya tidak pernah melebihi nilai awal, atau menurun menuju nol, maka sistem stabil.

Gagasan Lyapunov tersebut diterapkan pada konsep kedisipatifan suatu sistem. Sistem yang mengalami disipasi energi akan kehilangan energinya secara perlahan menuju nol, atau apabila ada supply energi, maka

akumulasi energi dalamnya akan sama atau lebih kecil dari supply energi yang diterimanya (Gupta, 1996).

Pendekatan PML dalam perancangan pengendali memberikan manfaat untuk menangani spesifikasi-spesifikasi perancangan yang dianggap tidak mudah untuk dikerjakan. Dalam naskah ini, konsep sistem disipatif dan formulasi PML akan dikembangkan untuk menghasilkan metodologi perancangan pengendali yang mengantisipasi ketidakpastian pada penguatan (gain) dan/atau fasa.

Masalah sistem kendali disipatif dalam penelitian ini adalah mencari suatu pengendali K sehingga sistem kendali yang dirancang merupakan suatu sistem lingkar tertutup yang stabil, bersifat disipatif dan kutub-kutub sistem lingkar tertutupnya terletak disuatu daerah tertentu dalam bidang kompleks. Tujuannya adalah sistem kendali yang dihasilkan bersifat kokoh dan memiliki tanggapan peralihan yang baik. Sifat kokoh diperoleh dari kedisipatifan sistem lingkar tertutup, sedangkan tanggapan peralihan yang baik dapat diperoleh dengan cara meletakkan kutub-kutub lingkar tertutup pada daerah yang tepat pada bidang kompleks.

Dalam perhitungan fungsi energi yang disimpan (atau tersimpan) memang seringkali ditemukan banyak kesulitan, tetapi dapat diatasi, yaitu dengan kenyataan tidak terdapatnya fungsi energi tersimpan yang unik, melainkan senantiasa berada dalam suatu rentang fungsi energi, yang dapat digambarkan sebagai hubungan masukan/keluaran. Terminologi disipatif digunakan secara umum dalam konsep kepasifan dan fungsi energi sebagai konsep dari energi yang disimpan atau entropi (Willems, 1972).

Dengan menggunakan abstraksi matematis dari pengertian daya dan energi, konsep energi disipasi telah digunakan untuk mengembangkan kondisi-kondisi yang cukup untuk kestabilan sistem disipatif. Hasil-hasil perhitungan numerik dari kestabilan (dalam literatur) seperti kondisi-kondisi penguatan kecil, kondisi-kondisi kepasifan (passivity), kondisi-kondisi sektor, secara alami mengikuti aturan sistem-sistem disipatif (Gupta, 1996).

Definisi 2.1: Misalkan persamaan ruang keadaan, x= g x u t y

(

, , ,

)

=h x u t

(

, ,

)

, dengan x, u dan y menyatakan keadaan, masukan dan keluaran sistem; g dan h merupakan fungsi-fungsi nonlinier yang menggambarkan dinamika sistem.

Sistem ini disebut disipatif, jika terdapat suatu fungsi daya, p y u

( )

, , yang terintegralkan, dan suatu fungsi dari keadaan sistem, yaitu fungsi energi,

( )

E x , sehingga berlaku pertidaksamaan berikut.

( ) ( )

(

)

∫

1 ≥ −

0

)) ( ( )) ( (

, _{1 0}

t

t p yt u t dt E x t E x t

untuk semua masukan yang dapat diterima, u(t), dalam interval waktu

[

t0,t1

]

, dan y(t) suatu keluaran dari

sistem dinamis.

Pertidaksamaan dalam Definisi 2.1 menjamin bahwa untuk suatu sistem linier disipatif, integral waktu dari daya masukan di dalam interval, yaitu energi total masukan ke sistem, adalah lebih besar atau sama dengan perubahan bersih dalam energi total sistem. Selisih antara energi total yang masuk ke sistem dan perubahan bersih dalam energi sistem adalah energi yang didisipasikan oleh sistem. Hal inilah yang menyebabkan mengapa sistem-sistem yang memenuhi pertidaksamaan di atas disebut sistem-sistem disipatif.

2.1. Sistem LIW Disipatif

Perhatikan suatu sistem LIW, Σ, seperti berikut (Gupta, 1996).

( ) ( ) ( )

x t = Ax t +Bu t

y t( )=Cx t( )+Du t( ) ..… (2.1) dengan

y(t) : vektor keluaran px1

(

y t( )∈ℜp

)

u(t) : vektor masukan mx1

(

u t m

)

( )∈ℜ

x(t) : vektor keadaan nx1

(

x t_{( )∈ℜ}n

)

A, B, C, D matriks-matriks sistem yang menggambarkan dinamika sistem.

Matriks fungsi alih pxm dari sistem ini adalah

( )

G s( )=C sI−A −1B+D

Suatu fungsi daya kuadratis dari masukan dan keluaran diekspresikan sebagai

( )

[

]

p y u y u Q N

N R

y

u

T T

T

, = 



 

 

  



 ..… (2.2)

dengan

Q₌QT _{: matriks simetris pxp}

(

Q₌QT _∈ℜpxp

)

R= RT : matriks simetris mxm

(

R= RT ∈ℜmxm

)

N : matriks riel pxm

(

N pxm

)

∈ℜ

dengan

(

A B C D, , ,

)

adalah suatu realisasi

minimal dari sistem, adalah disipatif yang berkaitan dengan fungsi daya kuadratis (2.2) jika terdapat suatu fungsi energi kuadratis definit positif

E x( )= x PxT , dengan P= PT >0, yang memenuhi pertidaksamaan disipatif (2.3).

(

)

∫

T ≥ −

0 p y,u dt E(x(T)) E(x(0)) … (2.3)

untuk semua T∈

[

0,∞

)

dan semua m e u∈L2

menyatakan ruang yang kuadratnya terintegralkan dalam selang 0 sampai ∞. Kondisi pertidaksamaan (2.3) ekivalen dengan Definisi 2.1.

Sistem LIW riel terbatas memenuhi pertidaksamaan

yT t y t dt u t u t dt T

T T

( ) ( ) ( ) ( )

0 0

∫

≤

∫

untuk semua T∈

[

0,∞

)

dan 2 . m

e

u∈L

Sama dengan pertidaksamaan (2.4).

{

uT t u t yT t y t dt

}

T

( ) ( )− ( ) ( ) ≥

∫

₀ 0 ... (2.4) Terlihat bahwa sistem riel terbatas

adalah sistem LIW disipatif dengan fungsi daya kuadratis

p y u( , )=uT( ) ( )t u t −yT( ) ( )t y t , merupakan fungsi daya kuadratis persamaan (2.2), dengan R = I, Q = -I

dan N = 0.

Secara umum norm sistem riel terbatas dengan G s( )_∞ ≤γ , atau H∞, memenuhi pertidaksamaan berikut.

yT t y t dt u t u t dt

T

T T

( ) ( ) ( ) ( )

0

2 0

∫

≤γ

∫

untuk semua T∈

[

0,∞

)

dan 2 .

m e

u∈L

Jadi sistem ini adalah disipatif yang berkaitan dengan

p y u( , )=γ2uT( ) ( )t u t −yT( ) ( )t y t _{, yaitu}

fungsi daya kuadratis persamaan (2.2), dengan R = γ2I, Q = -I dan N = 0.

Sistem-sistem pasif ditentukan oleh karakteristik sifat masukan-keluaran

seperti terlihat dalam pertidaksamaan (2.5).

yT t u t dt

T

0 0

∫

( ) ( ) ≥ ..… (2.5)

untuk semua T∈

[

0,∞

)

dan ₂m.

e

u∈L

Kondisi ini adalah disipatif yang berkaitan dengan suatu fungsi daya kuadratis

p y u yT t u t uT t y t ( , )= ( ) ( )+ ( ) ( )

atau bentuk umum fungsi daya kuadratis persamaan (2.2), dengan R = 0, Q = 0 dan N = I. Sistem seperti ini biasa dikenal sebagai sistem riel positif ketat (strictly positive real).

2.1.1. Karakterisasi Sistem LIW Disipatif

Dalam bagian ini dibahas syarat perlu dan cukup bahwa suatu sistem bersifat disipatif yang dituangkan dalam

lemma kedisipatifan, yang merupakan generalisasi lemma Kalman-Yakubovich untuk sistem riel positif, dan bounded realness lemma untuk sistem penguatan terbatas.

Kondisi-kondisi untuk lemma

kedisipatifan ekivalen dengan ekspresi dalam bentuk suatu PML. Karakterisasi PML dari sistem penguatan terbatas, riel positif dan sektor terbatas, diturunkan langsung dari karakterisasi PML disipatif sistem LIW, dengan mensubstitusikan fungsi dayanya masing-masing.

Teorema 2.1.: Misalkan Σ =

(

A B C D, , ,

)

suatu realisasi minimal dari suatu sistem LIW stabil. Pernyataan-pernyataan berikut adalah ekivalen. a. Sistem LIW, Σ, bersifat disipatif

berkaitan dengan suatu fungsi daya kuadratis

p y u

( )

[

y u

]

Q N

N R

y

u

T T

T

, = 



 

 

  

b. (Karakterisasi PML) Terdapat suatu matriks simetris, definit positif,

P= PT >0, yang memenuhi pertidaksamaan matriks linier berikut.

( )

( ) <0

 

 

− − − − +

−

+ −

− +

QD D N D D N R C N QD P B

N QD C PB QC

C P A PA

T T T T

T

T T

T

Secara umum hasil-hasil dalam Teorema 2.1 untuk sistem-sistem LIW disipatif menegaskan adanya kaitan untuk sistem-sistem penguatan terbatas, riel positif dan sektor terbatas, yaitu dengan mensubstitusikan fungsi daya masing-masing dalam hasil-hasil yang umum.

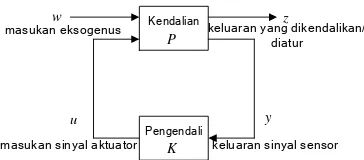
3. SISTEM KENDALI DISIPATIF Model matematis sistem yang dikendalikan dibentuk dari hubungan sinyal masukan dan keluaran ke kendalian maupun pengendali.

P

K

w z

y u

Gambar 1. Diagram blok sistem lingkar tertutup

Variabel-variabel bebas dari model adalah sinyal-sinyal masukan, dan variabel-variabel tak bebas berupa sinyal-sinyal keluaran.

3.1. Sistem Kendali LIW Disipatif Dalam perancangan sistem kendali selalu diinginkan memperoleh kinerja sistem kokoh terhadap ketidakpastian. Sistem M dengan masukan berupa gangguan d dan kinerja keluaran e, serta

blok ketidakpastian ∆ dihubungkan ke sistem melalui sinyal w dan z.

∆

e

M d

w z

Gambar 2. Diagram blok sistem kendali dengan blok ketidakpastian

Masalah kestabilan kokoh adalah menentukan apakah sistem stabil untuk ketidakpastian ∆ yang diijinkan.

Suatu sistem dinamis M dalam bentuk (Willems, 1972)

( )

t g

(

x

( ) ( )

t wt

)

x = , ... (3.1)

( )

t h

(

x

( ) ( )

t wt

)

z = , ... (3.2) dengan w

( )

t ∈ℜm,z

( )

t ∈ℜl, dan x

( )

t ∈ℜn.

Dalam kasus khusus dari suatu sistem LIW, M direpresentasikan sebagai

( )

t Ax

( )

t Bw

( )

t

x = + ... (3.3)

( )

t Cx

( )

t Dw

( )

t

z = + ... (3.4) dengan fungsi alih linier:

( )s C(sI A) B D M = − −1 + _.

(Sesuai dengan sistem LIW, maka M dan ( )s

M dapat dipertukarkan).

Untuk sistem dinamis M, suatu fungsi kuadratis r(t) disebut sebagai suatu supply rate. Supply rate dipilih berdasarkan pada sifat-sifat sistem. Sebagai contoh, apakah itu norm terbatas atau pasif.

Definisi 3.1 (Willems, 1972): Suatu sistem M dari bentuk persamaan (3.1) dan (3.2), dengan keadaan x∈ℜn

disebut disipatif terhadap supply rate

( )

⋅,⋅

r jika terdapat suatu fungsi definit positif ℜn →ℜ

M

V : , disebut suatu fungsi

( )

(

xt

)

V

(

x

( )

t

)

r

(

w

( ) ( )

ξ zξ

)

dξ V

t

t M

M ≤ +

∫

2

1

,

1

2

..… (3.5)

untuk semua t₁,t₂ dan untuk semua

( ) ( )

⋅ z ⋅ w

( )

⋅

x , dan yang memenuhi (3.1)

dan (3.2).

Jika V_M

( )

x adalah suatu fungsi yang dapat didiferensialkan, maka suatu pernyataan kedisipatifan sistem M

terhadap supply rate r adalah

( )

(

x t

)

≤r

(

w

( ) ( )

t ,z t

)

, t≥0

V_M … (3.6)

dengan V_M menotasikan total turunan

dari V_M

( )

x sepanjang trayektori x

( )

t

(Willems, 1972).

Untuk suatu sistem disipatif kuat (strongly dissipative systems), (3.6) diubah dengan kondisi

( )

(

xt

)

r

(

w

( ) ( )

t z t

)

VM < , ; x≠0

dengan suatu modifikasi yang sama untuk (3.5).

Diasumsikan bahwa fungsi-fungsi

storage dapat didiferensialkan sehingga kondisi dalam (3.6) dapat digunakan. Sebagai suatu contoh yang umum, suatu sistem mekanik dengan masukan gaya dan keluaran kecepatan; fungsi storage

nya adalah energi yang disimpan atau yang tersedia dalam sistem.

Secara umum, sistem-sistem norm terbatas H∞ adalah disipatif terhadap

supply rate dari bentuk

z z w w

r = T − T

Lemma 3.1 (Willems, 1972):

Anggap dua sistem dinamis M₁dan M₂ dengan representasi ruang keadaan seperti dalam (3.1) dan (3.2), dan pasangan masukan-keluaran

(

w₁,z₁

)

dan

(

w₂,z₂

)

.

Asumsikan bahwa kedua sistem dihubungkan seperti terlihat dalam

Gambar 3., sehingga w₁ = z₂ dan

1

2 z

w = . Selanjutnya kaitkan sistem-sistem ini dengan keadaan-keadaan

1

M

2

M

1

w z1

2

z w2

Gambar 3. Diagram blok interkoneksi umpan balik dari sistem LIW

2 1,x

x ; supply rate r₁

(

w₁,z₁

)

dan

(

2 2

)

2 w ,z

r ; dan fungsi storage _{( )1} 1 x

VM dan

( )

2 2 x

VM . Anggap bahwa VM1

( )

x1 dan

( )

2

2 x

V_M adalah definit positif, dan supply

rate memenuhi r₁

(

w₁,z₁

)

+r₂

(

w₂,z₂

)

=0, untuk semua w₁ = z₂ dan w₂ =z₁, maka solusi

(

x1,x2

)

=0 untuk interkoneksi

umpan balik dari M₁dan M₂ adalah stabil

Lyapunov dengan fungsi Lyapunov

2 1 M

M V

V

V = + .

Teorema kepasifan berimplikasi bahwa suatu pengendali positif riel ketat akan menuju ke suatu sistem persamaan tertutup yang stabil. Sistem pasif dapat didefinisikan sebagai suatu sistem yang menghabiskan energi.

Sistem kendali disipatif yang ketat didefinisikan sebagai sistem kendali yang mendisipasikan energinya hampir disepanjang trayektorinya. Energi harus didisipasikan oleh suatu sistem kendali LIW disipatif ketat hampir disepanjang perjalanan sistem tersebut, dan disipasi energi hanya mungkin sama dengan nol untuk suatu trayektori eksponensial stabil.

interkoneksi sistem adalah penjumlahan dari fungsi-fungsi storage dari dua subsistem (Willems, 2002).

Dengan demikian dapat dikatakan bahwa teorema kestabilan sama dengan teorema kepasifan. Kunci idenya adalah bahwa interkoneksi dari dua sistem disipatif adalah stabil.

( )s

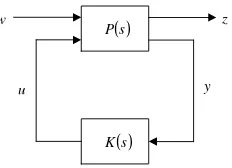
Gambar 4. Diagram blok masalah sistem kendali disipatif

Perhatikan sebuah sistem lingkar tertutup pada Gambar 4.

P s( )adalah kendalian kontinyu LIW dan layak (proper).

w = masukan-masukan eksogenus

u = masukan-masukan kendali

z = keluaran-keluaran yg dikendalikan

y = keluaran-keluaran yang diukur Sehingga berlaku



Bila diberikan hukum keluaran umpan balik u=K s y( ) dan dengan Biasanya, dalam pendekatan ruang keadaan terhadap sistem kendali, digunakan beberapa realisasi minimal (dapat dikendalikan (controllable) dan diamati (observable)) dari kendalian

( )

s

P , seperti terlihat pada persamaan (3.7) berikut.

( ) ( 1 2) Persamaan (3.7) berkaitan dengan persamaan ruang keadaan

u

dan diasumsikan bahwa

(A1).

(

A B C, 2, 2

)

dapat distabilkan dan

dapat dideteksi; (A2). D₂₂ =0

Asumsi pertama perlu dan cukup untuk stabilisasi kendalian oleh keluaran umpan balik dinamis.

Dengan asumsi (A2) dan sebuah realisasi pengendali rasional riel yang layak, maka K(s) dapat dituliskan seperti persamaan (3.8).

(

)

K s( )= D_K +C_K sI − A_K −1B_K;

A_K ∈ℜkxk ..… (3.8) Dengan demikian suatu realisasi (tidak perlu minimal) dari fungsi alih lingkar tertutup dari w ke z diperoleh sebagai persamaan (3.9).

tunggal, yang didefinisikan sebagai

dan didefinisikan

A A

Yang selanjutnya dapat diperoleh

;

Diberikan suatu matriks simetris

Ψ ∈ℜmxm

dan dua matriks P, Q dengan kolom berdimensi m; masalahnya adalah mencari beberapa matriks Θ dengan dimensi yang cocok (kompatibel) sehingga diperoleh pertidaksamaan

(3.14).

Ψ+PTΘTQ+QTΘP<0 … (3.14)

WP dan WQ adalah matriks-matriks yang

masing-masing kolomnya merupakan basis ruang nol dari P dan Q. Sehingga pertidaksamaan (3.14) dapat diselesaikan untuk Θ, jika dan hanya

komplemen Schur dari Q.

Perhatikan suatu sistem LIW, Σ (2.1) dan suatu fungsi daya kuadratis sehingga Teorema 2.1. dapat dituliskan sebagai berikut.

Misalkan Σ =

(

A B C D, , ,

)

suatu realisasi minimal dari suatu sistem LIW stabil. Pernyataan-pernyataan berikut adalah ekivalen.

1. Sistem LIW, Σ, bersifat disipatif berkaitan dengan suatu fungsi daya kuadratis

2. (Karakterisasi PML) Terdapat suatu matriks simetris, definit positif,

,

pertidaksamaan matriks linier berikut. 3.

Selanjutnya (3.17) dapat dituliskan sebagai pertidaksamaan (3.18).

(

)

<0

3.2.1. Penyelesaian Masalah

Lemma 3.4: Anggap suatu fungsi alih realisasi waktu kontinyu (tidak perlu minimal), T s( )=D+C sI( −A)−1B_.

Pernyataan-pernyataan berikut adalah ekivalen.

a. T(s) bersifat disipatif terhadap fungsi daya p(y,u) persamaan (2.2)

b. Terdapat sebuah solusi X simetris definit positif ke PML (3.18).

Sesuai dengan persamaan (3.7) dan asumsi (A1) - (A2) serta notasi persamaan (3.12), didefinisikan (3.19) seperti berikut.

(

T

)

masing-masing kolomnya membangun ruang nol dari P dan Q, maka himpunan dari pengendali disipatif orde-k adalah tidaorde-k orde-kosong, jiorde-ka dan hanya jika terdapat beberapa (n+k) x (n+k) matriks X_cl definit positif, sehingga

diperoleh pertidaksamaan (3.20) seperti berikut.

Karakterisasi yang lebih sederhana didapatkan dengan memisahkan X_cl dan

Xcl

−1 _{yang sesuai untuk Acl, menghitung}

P

W dan W_Qsecara tegas dan menghasilkan blok matriks.

Perumusan dan perhitungan akan lebih sederhana bila menggunakan definisi-definisi berikut.

: ; Teorema 3.1 (Pengendali sistem kendali LIW disipatif): Anggap suatu kendalian yang layak orde n, P(s), dengan realisasi minimal persamaan

(3.7) dan asumsi (A1) - (A2). Sebut W12 dan W21 masing-masing menyatakan basis ruang nol

₍

I D D

₎

BT

− +

12 12 2dan

(

I−D D21 21+

)

C2. Dengan menggunakan

notasi-notasi definisi (3.22) dan (3.23), maka masalah sistem kendali disipatif dapat diselesaikan, jika dan hanya jika a. 1>max

(

( 11), ( 11

)

~ ) ,

max max

σ D σ D

b. terdapat pasangan-pasangan matriks simetris _T,S∈ℜnxn _sehingga berlaku PML berikut.

0

Selanjutnya, himpunan pengendali disipatif orde-k tidak kosong, jika dan hanya jika (ii) memuat beberapa T, S yang memenuhi batasan rank (3.27).

( )

dinyatakan sebagai matriks identitas.

3.2.2. Perumusan PML dan Sifat- Sifat Konveksitas

0

ekivalen dengan pertidaksamaan berikut

0

Sedangkan batasan (3.26) yaitu T>0; S>0; λmin(TS)≥1

ekivalen dengan

T I

sehingga Teorema 3.1 dapat dirumuskan kembali sebagai berikut.

Sistem kendali disipatif dapat diselesaikan jika dan hanya jika terdapat matriks simetris T, S yang memenuhi terdapat pengendali-pengendali disipatif orde k<n (orde direduksi) jika dan hanya jika (3.28) - (3.30) memuat beberapa T, S yang memenuhi (3.31).

( )

Rank I−TS ≤k ..… (3.31) Untuk kestabilan numerik, N _Tdan

S

N dapat dipilih orthonormal. Dihitung dengan mudah melalui Singular Value Decompotation dari

B TAKAN KUTUB

Kestabilan sistem lingkar tertutup merupakan syarat minimum dalam sistem kendali. Selain dari pada itu, suatu pengendali yang baik, seharusnya juga dapat memberikan tanggapan yang cepat dan redaman yang baik. Hal ini dapat dicapai antara lain dengan

meletakkan kutub-kutub lingkar tertutup pada suatu lokasi tertentu dalam bidang kompleks, untuk menjamin tanggapan peralihan yang memuaskan. Kondisi penurunan yang cepat, redaman yang baik dan pengendali yang dinamis dapat ditentukan oleh keberadaan kutub-kutub dan interseksinya dengan bidang di sebelah kiri sumbu khayal bidang kompleks. Daerah ini merupakan daerah stabil, dan interseksinya dapat berbentuk strip vertikal/horizontal, cakram, sektor kerucut dan lain-lain, dapat diekspresikan sebagai PML. Sebagai contoh, tanggapan undak dari suatu sistem orde 2 dengan pole λ=−ζω_n ± jω_d sepenuhnya dikarakterisasi dalam bentuk-bentuk frekuensi alami tak teredam ω = λ, rasio redaman ζ , dan

( )s ≤−α

Re . Hal menarik lainnya adalah himpunan S(α,r,θ) dari bilangan

kompleks x+ jy sehingga

y x r

jy x

x<−α<0, + < , tanθ <−

Letak kutub-kutub lingkar tertutup pada daerah ini menjamin suatu laju penurunan minimum α, suatu rasio redaman yang minimum ζ =cosθ dan maksimum frekuensi alami tak teredam

θ

ω_n =rsin . Batas-batas ini menentukan

overshoot maksimum, frekuensi osilasi, waktu tunda, waktu naik dan waktu tenang dari tanggapan peralihan suatu sistem (Chilali, 1996).

α θ r

Gambar 5. Daerah PML S

(

_α,r,_θ

)

(Chilali, 1996)

4.1. Daerah-Daerah PML dalam Bidang Kompleks

Suatu daerah PML adalah suatu bagian dari bidang kompleks yang didefinisikan dalam persamaan (4.1).

{

∈ : + + <0

}

= T

z z

z C α β β

D … (4.1)

Dengan

[ ]

mxm

kl ∈ℜ

= α

α adalah suatu

matriks simetris dan

[ ]

mxm kl ∈ℜ = β β

adalah suatu matriks riel.

Fungsi matriks (4.2) berikut disebut fungsi karakteristik .

( )

[

kl kl lk

]

kl m

T

z z z

z z

fD :=α+ β+ β =α +β +β 1_≤ ,_≤

..… (4.2) Dengan kata lain, suatu daerah PML adalah suatu bagian (subset) dari bidang kompleks yang direpresentasikan oleh

suatu PML dalam z dan z, atau ekivalen dengan suatu PML dalam x=Re

( )

z dan

( )

. Im z

y= Sebagai suatu hasil, maka daerah PML adalah konveks. Selain dari pada itu, daerah PML adalah simetris terhadap sumbu riel karena untuk semua

( )

=

( )

<0.

∈ z f z

z D, f_{D D}

Khususnya, lokasi kutub yang diberikan dalam daerah PML dapat dikarakterisasi dalam bentuk blok matriks mx , seperti terlihat pada m

persamaan (4.3) berikut.

(

)

(

)

T

(

)

T

AX XA

X X

A

M_D , :=α⊗ +β⊗ +β ⊗

[

T

]

_{kl m} lk

kl

klX+ AX + XA ≤ ≤

= α β β _{1 ,}

..… (4.3) Matriks A adalah stabil ↔ terdapat suatu matriks simetris X sehingga (Polderman, 1998)

(

A,X

)

<0, X >0 MD

Terlihat bahwa MD

(

A,X

)

dalam (4.3)

dan fD

( )

z dalam (4.2) dikaitkan oleh

substitusi

(

X AX XAT

)

(

z z

)

, , 1 ,

, ↔ .

4.2. PML Pengendali Disipatif dengan Peletakan Kutub

Diinginkan merancang suatu pengendali K

( )

s , sehingga sistem kendali akan memiliki sistem lingkar tertutup stabil, sistem lingkar tertutup

(PK)

F , bersifat disipatif terhadap suatu fungsi daya p

(

w,z

)

, dan kutub-kutub sistem lingkar tertutup terletak di suatu daerah tertentu dalam bidang kompleks

.

Batasan peletakan kutub dipenuhi jika dan hanya jika terdapat XD >0

sehingga diperoleh pertidaksamaan (4.4) berikut.

(

+ + T

)

_1≤k,l≤m<0

cl lk cl

kl

klXD β A XD β XDA

α

Sistem disipatif memiliki solusi

tentunya harus dapat memenuhi

pertidaksamaan (4.4) dan

pertidaksamaan (4.5). Konveksitas dapat dilaksanakan dengan mencari suatu solusi bersama, yaitu

0

> =XD

X

untuk pertidaksamaan (4.4) dan

pertidaksamaan (4.5).

Diasumsikan kendalian strictly

proper : D22=0.

Pengendali K

( )

s dapat

direpresentasi kan dalam bentuk ruang keadaan seperti berikut.

y adalah persamaan (3.9).

Untuk merancang pengendali K( )s ,

langkahnya adalah sebagai berikut.

Katakan A∈ℜnxn danD p xm

22∈ℜ 2 2,

dan k adalah orde dari pengendali

(A_K ∈ℜkxk).

Perubahan variabel pengendali

secara mutlak didefinisikan dalam

bentuk-bentuk matriks Lyapunov X

(yang tidak diketahui) (Polderman, 1998).

Didefinisikan variabel-variabel

pengendali baru sebagai berikut.

( )

(diperoleh) matriks pengendali

K K K

K B C D

A , , , yang memenuhi

persamaan-persamaan dalam (4.8). Jika

M dan L adalah matriks persegi (k = n) dan invertible, makaA_K,B_K,C_K,D_K adalah unik.

Dalam perancangan orde penuh,

selalu dapat diasumsikan bahwa M dan L

mempunyai rank baris penuh. Jadi

variabel A_K,B_K,C_K,D_K dapat digantikan

oleh Aˆ_K,Bˆ_K,Cˆ_K,Dˆ_Ktanpa kehilangan

bentuk umumnya.

0

Sistem Riel Terbatas:

0

Sistem Riel Positif Ketat

(

)

<0 Riel Positif Ketat:

( ) ( )

Seringkali diambil κ =1

5. SIMULASI DAN ANALISIS HA SIL SIMULASI KENDAL.I DISI- PATIF DENGAN PELETAKAN KUTUB

5.1. Perancangan Pengendali Disipa- tif dengan Peletakan Kutub

adalah fungsi sensitivitas; sedangkan

( )

s

W2 adalah sebuah filter high pass,

yang berkaitan dengan

(

G K

)

K G

T = ₀ /1+ ₀ , T adalah fungsi alih

lingkar tertutup, yang merupakan

complementary sensitivity. Adapun

hubungan antara S dan T adalah

S I T= − .

Selanjutnya menghitung matriks dari sistem P

( )

s yang berdasarkan G_{0( )}s ,

( )

s

W1 dan W2

( )

s yang telah diketahui.

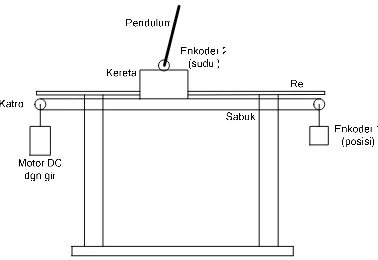
5.2. Studi Kasus untuk Pendulum Terbalik

Pemilihan contoh penggunaan pada

sistem kendali pendulum terbalik

mengingat bahwa sistem ini cenderung memiliki sifat yang kurang stabil, artinya kestabilannya mudah sekali terganggu. Dengan meletakkan kutub-kutubnya di lokasi tertentu, khususnya disebelah kiri sumbu khayal bidang kompleks akan

Gambar 8. Sistem pendulum terbalik

menyebabkan sistem bersifat stabil. Studi kasus pendulum terbalik ini untuk memeriksa apakah kutub-kutubnya berada disebelah kiri sumbu khayal dan tanggapan peralihannya baik (berarti waktu peralihannya cukup singkat) setelah diberikan suatu pengendali K

( )

s .

Dalam pemodelan pendulum terbalik, variabel masukannya adalah gaya dan variabel keluarannya adalah perubahan posisi. Hasil yang diharapkan adalah menjaga pendulum stabil dalam posisi tegak (ke atas) meskipun gaya diberikan kepadanya.

Suatu model pendulum terbalik, dengan matriks-matriks dinamiknya adalah

   

 

   

 

− =

   

 

   

 

− − −

=

42 . 2 496 , 0 0 0

;

354 . 0 4 . 40 6 . 48 0

0010 . 0 26 . 8 136 . 0 0

1 0 0 0

0 1 0 0

B A

     

=

   

 

=

0 0 ; 0 0 1 0

0 0 0 1

D C

Batasan yang diambil adalah model akar-akar disebelah kiri sumbu khayal dengan α<−0,1 dan interseksinya berbentuk sektor kerucut.

Hasil simulasi memberikan nilai kutub-kutub lingkar terbukanya adalah s

= 0, s = 6,7717, s = 6.8506 dan s = -8.5351 (Gambar 9.). Terlihat bahwa terdapat kutub yang berada di kanan sumbu khayal bidang kompleks, yaitu s = 6,7717. Dalam keadaan seperti ini, dipastikan bahwa sistem tidak stabil.

Sedangkan hasil simulasi untuk kutub lingkar tertutupnya, dimana sudah terdapat pengendali K( )s , adalah s = -47.167, s = -161±59i, s = 0, s = -3±2i, s = -7 dan s = -9 (Gambar 10.). Terlihat bahwa semua kutub terletak disebelah kiri sumbu khayal pada bidang kompleks s. Hal ini menyatakan bahwa sistem tersebut stabil.

Pada keluaran, solusi obyektif dari ketelitian yang diinginkan adalah γ = 2,9044 (setelah menjalani 42 kali iterasi), sedangkan γopt (penguatan RMS terbaik yang dapat diperoleh) adalah 2,8461. Hal ini sesuai dengan kinerja pengendali yang dirancang, dimana γ≥ γopt.

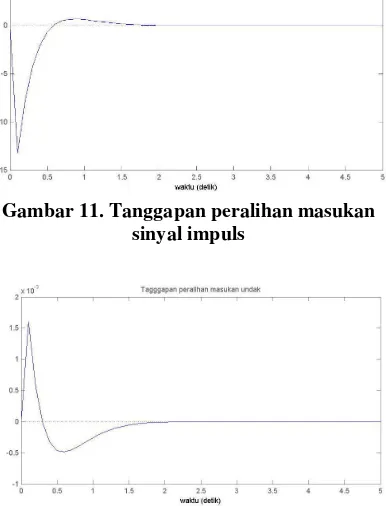
Dari kedua tanggapan peralihan (Gambar 11 dan Gambar 12) terlihat bahwa untuk mencapai keadaan tunak diperlukan waktu yang tidak terlalu lama, ± 1,9 detik. Waktu puncak ± 0,15 detik. Sehingga dapat diketahui bahwa ωn = 3,6056 rad/dtk, ωd = 2, 0003

Gambar 10. Letak kutub-kutub lingkar tertutup

Gambar 11. Tanggapan peralihan masukan sinyal impuls

Gambar 12. Tanggapan peralihan masukan undak

rad/dtk, ζ = 0,832 dan sudut θ = 33,695o. Hal ini memperlihatkan bahwa sistem memberikan tanggapan peralihan yang baik. Secara teoritis, tanggapan peralihan terbaik diberikan oleh sistem

dengan sudut 40o ≤ θ ≤ 60o dan 0,4 ≤ ζ ≤ 0,8. Dengan demikian, hasil simulasi mendekati keadaan terbaik secara teoritis.

6. KESIMPULAN

Karakterisasi PML untuk sintesis pengendali disipatif dengan peletakan kutub diperoleh dari penggabungan antara syarat yang harus dipenuhi bagi peletakan kutub di sebelah kiri sumbu khayal bidang kompleks dan PML sistem LIW disipatif, sehingga diperoleh PML yang nantinya memenuhi kriteria yang telah ditetapkan.

Hasil-Hasil khusus PML pengen dali disipatif dengan peletakan kutub diperoleh untuk sistem riel terbatas, sistem riel positif ketat dan sistem campuran, yang merupakan campuran antara sistem H∞ dan sistem riel positif ketat.

Hasil simulasi model sistem pen dulum terbalik yang berupa pengujian sistem LIW disipatif dengan peletakan kutub, memperlihatkan bahwa terdapat kutub yang berada di kanan sumbu khayal bidang kompleks. Dalam keadaan seperti ini, dipastikan bahwa sistem tidak stabil. Sedangkan untuk kutub-kutub lingkar tertutupnya, dimana sudah terdapat pengendaliK

( )

s , terlihat bahwa semua kutub terletak disebelah kiri sumbu khayal pada bidang kompleks s. Tanggapan peralihan memperlihat kan bahwa untuk mencapai keadaan tunak cukup singkat.

tertutup stabil dan disipatif, dapat saja terjadi dengan letak kutub-kutub lingkar tertutupnya berada dimana saja, sehingga belum tentu memberikan tanggapan peralihan yang baik.

DAFTAR PUSTAKA

Apkarian, P. et. al. (1996), LMI Techniques in Control Engineering from Theory to Practice, Workshop Notes CDC 1996, Kobe, Japan. Chilali, Mahmoud and Pascal Gahinet

(1996), H∞ Design with Pole Placement Constraints : An LMI Approach, IEEE Transactions on Automatic Control, 41, 358 - 367. Chilali, M., P. Gahinet, and P.

Apkarian, (1999), Robust Pole Placement in LMI Regions, IEEE Transactions on Automatic Control, 44, 2257 - 2267.

Gahinet, P & P. Apkarian (1994), “A Linear Matrix Inequality Approach to H∞ Control,” Int. Journal Robust and Nonlinear Control, 4, 421 - 448. Gahinet, P., Arkadi Nemirovski, Alan J. Laub, dan Mahmoud Chilali, (1995), LMI Control Toolbox : For Use with MATLAB, The MATH WORKS Inc..

Gupta, Sandeep (1996), Robust Stabilization of Uncertain Systems Based on Energy Dissipation Concepts, NASA Contractor Report 4713.

Haddad, W. M., and D. S. Bernstein (1992), “Controller Design with Regional Pole Constraints,” IEEE Transaction on Automatic Control, 37, 54 - 69.

Polderman, J. W., and J. C. Willems (1998), Introduction to Mathematical Systems Theory : A Behavioral Approach, Springer-Verlag.

Willems, Jan C. (1972), Dissipative Dynamical Systems Part I : General Theory, Archive for Rational Mechanics and Analysis, 45, No. 5, 321 - 351.

Willems, Jan C. (1972), Dissipative Dynamical Systems Part II : Linear Systems with Quadratic Supply Rates, Archive for Rational Mechanics and Analysis, 45, No. 5, 352 – 393.