Diajukan Sebagai Salah Satu Syarat Guna Mengikuti Ujian Skripsi untuk Memperoleh Gelar Strata Satu pada Jurusan Matematika. Oleh

SKRIPSI

PENERAPAN TEOREMA KARAKTERISASI

PADA DISTRIBUSI POISSON DALAM MENENTUKAN PELUANG MEMENANGKAN SUATU PERMAINAN

Diajukan Sebagai Salah Satu Syarat Guna Mengikuti Ujian Skripsi

untuk Memperoleh Gelar Strata Satu pada Jurusan Matematika

Oleh

LA ASRIMA BUTON

F1A1 11 070

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HALU OLEO

KENDARI 2016

iii KATA PENGANTAR

Puji syukur penulis panjatkan kehadirat Allah SWT, sehingga penyusunan

tugas akhir dengan judul “Penerapan Teorema Karakterisasi pada Distribusi

Poisson dalam Menentukan Peluang Memenangkan Suatu Permainan”.

Dapat terselesaikan dan tersusun sebagaimana mestinya. Penulis sepenuhnya menyadari bahwa seluruh rangkaian kegiatan, dimulai dari tahap awal penyusunan hingga penyelesaian penulis tugas akhir ini, senantiasa mendapat bantuan dan petunjuk-petunjuk dari berbagai pihak. Oleh karena itu penulis mengucapkan

terima kasih dan penghargaan yang setinggi-tingginya kepada Bapak Rasas Raya,

S.Si., M.Si., selaku dosen pembimbing I dan Bapak Dr.Makkulau, S.Si., M.Si

selaku dosen pembimbing II, yang dengan penuh keiklasan dan kesungguhan telah meluangkan waktunya, memberikan petunjuk, arahan dan bimbingan sejak awal penyusunan hingga selesainya tugas akhir ini.

Melalui hasil karya ini secara khusus dan dengan hati yang tulus penulis

mempersembahkan untuk Ayahanda tercinta Lambori dan Ibunda tersayang Wa

Piu yang telah memberikan do’a restu, pengorbanan, kasih sayang dan perhatian

yang tidak terhingga. Dan untuk saudara-saudaraku tersayang adik Arisa dan

Adirman yang selalu memberikan dukungan dan do’a serta kasih sayangnya.

Ucapan terima kasih juga penulis haturkan kepada:

iv

2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Halu

Oleo, Bapak Dr. Muh. Zamrun F., S.Si., M.Si., M.Sc

3. Wakil Dekan I, II, dan III Fakultas MIPA Universitas Halu Oleo.

4. Segenap Staf Administrasi di lingkungan Fakultas MIPA Universitas Halu

Oleo.

5. Ketua Jurusan Matemaika Fakultas MIPA Universitas Halu Oleo, Bapak

La Gubu, S.Si., M.Si.

6. Kepala Laboratorium Komputasi Matematika Fakultas MIPA Universitas

Halu Oleo, Ibu Norma Muhtar, S.Si., M.Si.

7. Kepala Warintek Fakultas MIPA Universitas Halu Oleo, Bapak L.M.

Umar Recky, R., S.Si., M.Si.

8. Tim Penguji Bapak La Gubu, S.Si., M.Si., Bapak Muksar, S.Si., M.Si., Ibu

Agusrawati S.Si., M.Si, yang telah memberikan saran dan kritikan, sehingga skripsi ini dapat menjadi lebih baik.

9. Seluruh staf pengajar pada Jurusan Matematika Fakultas MIPA

Universitas Halu Oleo.

10.Teman-temanku Math-011: Amal, Asran, Arfan, Agus(Pepes), Jefri, Irul,

Randy, Hasrun, Syafar Kasim, Siti Sartina, Cici, Rita Rukaya, Asmarita, Nurlita, Nisfa, Juri, serta teman-teman yang lain yang tidak sempat disebutkan namanya satu persatu terima kasih atas bantuan dan kebersamaannya selama ini.

11.Teman-teman Asramaku: Ardi, Yano, Konu, Ejon, Ucu, Sam, Kahar,

teman-v

teman yang lain yang tidak sempat disebutkan namanya satu persatu terima kasih atas supportnya serta kebersamaannya selama ini.

12.Teristimewa Istri yang Paling saya cintai dan sayangi Halmatia yang selalu

membantu saya, serta memberikan support baik lisan maupun tulisan.

Akhirnya penulis hanya bisa memanjatkan do’a semoga Allah SWT memberikan balasan yang setimpal kepada semua pihak yang telah membantu penulis, Amin.

Kendari, April 2016

vi DAFTAR ISI

HALAMAN JUDUL………...i

HALAMAN PENGESAHAN...……….………...ii

KATA PENGANTAR ………..…….iii

DAFTAR ISI………..………...vi

ABSTRAK..………...………viii

ABSTRACT ………...……ix

BAB I PENDAHULUAN 1.1Latar Belakang Masalah………...………..1

1.2Rumusan Masalah………..………3

1.3Tujuan Penelitian ………..………3

1.4Manfaat Penelitian………...4

BAB II TINJAUAN PUSTAKA 2.1 Permainan………...………....5

2.2 Distribusi Poisson………...…....5

2.3 Karakterisasi Distribusi Poisson………..…..9

BAB III METODE PENELITIAN 3.1 Waktu dan Tempat………..….12

vii

3.2 Prosedur Penelitian………...…..……….12

BAB IV HASIL PENELITIAN

4.1 Bukti-bukti Teorema karakterisasi………...…………14

4.2 Skor Berdistrbusi Posson………...19

4.3 Penerapannya ke Data Sepak Bola………...………21

BAB V PENUTUP

5.1 Kesimpulan………..………24 5.2 Saran………..………..………24 DAFTAR PUSTAKA

viii PENERAPAN TEOREMA KARAKTERISASI

PADA DISTRIBUSI POISSON DALAM MENENTUKAN PELUANG MEMENANGKAN SUATU PERMAINAN

OLEH

LA ASRIMA BUTON F1A1 11 070

Abstrak

Dalam tulisan ini dibahas bukti-bukti teorema karakterisasi serta penerapan teorema karakterisasi yang erat kaitannya dengan distribusi Poisson

pada penerapan data sepak bola. Peluang P() suatu tim dengan skor rata-rata

mengalahkan tim lainnya Q() yang memiliki skor rata-rata  dihitung

ketika skor masing-masing tim berdstribusi Poisson. Teorema karakterisasi

mengatakan, jika persamaan p



p

 

Q



p



p

 

Q



d d      

 berlaku untuk setiap

distribusi, skor dari tim dengan rata-rata , maka skor tim dengan rata-rata  berdistribus Poisson.

Kata kunci: Teorema Karakterisasi, Peluang, Distribusi Poisson, dan Permainan.

ix APPLICATION OF THE CHARACTERIZATION THEOREM ON

POISSON DISTRIBUTION IN

DETERMINING THE OPPORTUNITY OF WINNING A GAMES By:

LA ASRIMA BUTON F1A1 11 070

Abstract

In this paper we discuss the application of the characterization theorem, which has close relation with Poisson distribution, to some soccer data. The probability P() that a team with mean score beats a team Q() with mean score  is calculated when the score of each team is Poisson distributed. The

characterization theorem states if p



p

 

Q



p



p

 

Q



d

d _{    }



 holds for any

score distribution of the team with mean , then the score of the team with mean

must be Poisson distributed.

1 BAB I

PENDAHULUAN

1.1 Latar Belakang Masalah

Dalam pertandingan sepak bola, terutama dalam babak final, dukungan terhadap tim-tim yang diprediksi akan menang dalam suatu pertandingan seringkali dijadikan ajang untuk menjagokan salah satu tim favoritnya. Oleh karena itu pertimbangan pengambilan keputusan terhadap tim mana yang akan layak didukung untuk memenangkan pertandingan merupakan hal yang cukup penting. Besarnya peluang suatu tim dalam memenangkan suatu pertandingan merupakan salah satu alat dalam pengambilan keputusan untuk memilih tim mana yang layak mendapat dukungan. Apabila peluang suatu tim untuk memenangkan pertandingan semakin besar, maka kemungkinan tim tersebut didukung akan semakin besar, karena kemungkinan memenangkan taruhan akan semakin besar.

Salah satu faktor yang digunakan untuk menghitung peluang suatu tim untuk memenangkan pertandingan adalah hasil akhir yang dicapai oleh suatu tim pada pertandingan-pertandingan sebelumnya (kualifikasi) dan mempunyai tiga kemungkinan, yaitu kalah, menang, dan seri. Faktor tersebut dapat direpresentasikan dalam bentuk perolehan skor, dimana skor tersebut adalah gol-gol yang diraih oleh suatu tim dari beberapa pertandingan. Salah satu metode yang digunakan untuk menghitung peluang menang suatu tim adalah dengan menggunakan teorema karakterisasi pada distribusi Poisson.

2

Andaikan A dan B adalah dua tim yang bertanding, dengan skor A

dan B saling bebas. Misalkan tim A memperoleh skor n dengan peluang untuk

menang P_n dan tim B memperoleh skor m dengan peluang untuk menang q_m.

Tim A dikatakan menang atas tim B apabila skor tim A lebih besar dari skor tim B. Sedangkan, tim A dan tim B dikatakan seri apabila skor tim A lebih besar dari skor tim B. Dalam teori peluang, dapat ditentukan besarnya peluang tim A menang atas tim B yang diberi notasi P[n>m]dan besarnya peluang jika tim B

menang atas tim B yang diberi notasi P[m>n] dan besarnya peluang jika tim dan

tim B seri dengan notasi P[n=m].

Misalkan tim A merupakan lawan dengan skor tertinggi dengan

peluang untuk menang 𝑃_𝑛 dimana 𝑃_𝑛 berdistribusi poisson dengan rerata λ, maka

untuk setiap 𝑞𝑚:

_𝑑𝑑

λ𝑃 𝐴 𝑚𝑒𝑛𝑎𝑛𝑔 = 𝑃[𝐴 𝑑𝑎𝑛 𝐵 𝑠𝑒𝑟𝑖] (1)

Persamaan (1) merupakan bentuk persamaan dari teorema karakterisasi yang berhubungan erat dengan distribusi Poisson.

Penerapan teorema karakterisasi distribusi Poisson ini, seringkali digunakan oleh para pengamat pertandingan untuk menentukan peluang menang atau seri dari tim yang akan bertanding dalam babak final suatu pertandingan berdasarkan hasil perolehan skor pada pertandingan-pertandingan sebelumnya (kualifikasi).

3

Berdasarkan uraian diatas dibahas persamaan teorema dari karakterisasi pada distribusi Poisson beserta dengan pembuktian, penjabaran dan penerapannya pada data-data hasil perolehan skor dari suatu pertandingan sepak

bola. Untuk selanjutnya tugas akhir ini diberi judul “Penerapan Teorema

Karakterisasi pada Distribusi Poisson dalam Menentukan Peluang Memenangkan Suatu Permainan”.

1.2 Rumusan Masalah

Berdasarkan latar belakang masalah yang telah dipaparkan, maka permasalahan dalam tugas akhir ini dapat dirumuskan sebagai berikut:

1. Bagaimanakah teorema karakterisasi yang berdistribusi poisson?

2. Bagaimanakah penerapan teorema karakterisasi pada data-data hasil

perolehan skor suatu pertandingan untuk penentuan peluang menang atau seri dari suatu tim?

1.3 Tujuan Penelitian

Adapun tujuan dari penelitian ini adalah:

1. Memperlihatkan bukti-bukti matematis dari teorema karakterisasi pada

distribusi Poisson.

2. Mengetahui penerapan teorema karakterisasi dalam menentukan peluang

4 1.4 Manfaat Penelitian

Manfaat dari penelitian ini yaitu memberikan wawasan baru dalam perhitungan peluang menang atau seri suatu tim berdasarkan skor-skor yang didapatkan dari hasil pertandingan sebelumnya agar pengambilan keputusan tidak bersifat spekulatif yang cenderung subyektif.

5 BAB II

TINJAUAN PUSTAKA

2.1. Permainan

Usaha olah diri (olah pikiran dan olah fisik) yang sangat bermanfaat bagi

peningkatan dan pengembangan motivasi, kinerja, dan prestasi dalam melaksanakan tugas dan kepentingan organisasi dengan lebih baik (Muhammad, 2009).

Permainan merupakan sebuah aktivitas rekreasi dengan tujuan bersenang-senang, mengisi waktu luang, atau berolahraga ringan. Permainan biasanya dilakukan sendiri atau bersama-sama (Riyanto. 2006).

2.2. Distribusi Poisson

Distribusi Poisson adalah percobaan yang menghasilkan nilai numerik

pada suatu variabel acak x, jumlah keluaran yang terjadi selama suatu selang

waktu yang diketahui atau di dalam suatu daerah (ruang) yang ditentukan disebut

sebagai percobaan Poisson, sehingga sebuah percobaan Poisson dapat memunculkan pengamatan untuk variabel acak x. Distribusi Poisson menggambarkan probabilitas pada peristiwa acak (random) yang akan terjadi pada jeda (interval) waktu atau ruang dengan kondisi probabilitas sangat kecil, meskipun jumlah percobaan yang dilakukan besar tetapi hasilnya tidak berarti

(Manurung, 2013).

Distribusi Poisson pertama kali diperkenalkan oleh Siméon-Denis Poisson (1781–1840) dan diterbitkan bersama teori peluangnya, pada tahun 1838 dalam

6

karyanya: Recherches sur la probabilité des jugements en matière criminelle et en

matière civile (“Penelitian Peluang Hukum Masalah Pidana dan Perdata”).

Karyanya memfokuskan variabel acak yang menghitung antara lain jumlah kejadian diskret (kadang juga disebut "kedatangan") yang terjadi selama interval

waktu tertentu. Apabila nilai harapan kejadian pada suatu interval adalah , maka

peluang terjadi peristiwa sebanyak x kali adalah:

! ) ; ( x e x f x     (2) dengan x adalah bilangan bulat non negatif dan  adalah bilangan riil positif. (Mukid, 2011).

Distribusi poisson merupakan sebuah distribusi probabilitas diskrit yang sering menjelaskan tingkat kedatangan pada teori antrian. Kedatangan dianggap sebagai kedatangan yang acak apabila kedatangan tersebut tidak terikat satu sama lain dan kejadian kedatangan tersebut tidak dapat diramalkan secara tepat. Banyaknya kedatangan pada setiap unit waktu dapat diperkirakan oleh sebuah

distribusi probabilitas yang dikenal sebagai distribusi poisson (Poisson

distribution). Hal ini dikarenakan jika tingkat kedatangan mengikuti distribusi

poisson dengan tingkat kedatangan rata-rata , maka waktu antar kedatangan

mengikuti distribusi eksponensial negatif dengan waktu antar kedatangan rata-rata 1

. Distribusi eksponensial negatif juga merupakan perwakilan dari distribusi

poisson, tetapi menjelaskan waktu antar kedatangan dengan menentukan bahwa waktu antar kedatangan ini benar-benar acak.

7

dimana: P (x) = probabilitas kedatangan sejumlah x X = jumlah kedatangan per satuan waktu  = tingkat kedatangan rata-rata

e = 2,71828 dasar logaritma

Hubungan antara  dengan

1 dijelaskan dalam teorema berikut ini yaitu jika

kedatangan mengikuti distribusi poisson maka, suatu variabel random waktu antar kedatangan mengikuti distribusi eksponensial negatif. Pembuktiannya yaitu:

) (t

f = fungsi densitas probabilitas dari interval waktu t antar pemunculan

kejadian yang berturut-turut, t 0. F(t)= fungsi distribusi kumulatif dari t.

Jika suatu kumpulan variabel acak, waktu antar kedatangan berurutan dimisalkan T, maka (Jay dan Barry, 2006):

{ }

{T t P

P   tidak ada kedatangan dalam waktu t}

_P

_e

t

O t     ()



    T t O

e

P

t dt t f() () 

Proses poisson adalah suatu proses pemecahan {N(t),t 0disebut proses poisson dengan laju , 0,

Jika dipenuhi tiga syarat berikut:

1. N(0) = 0

2. Proses tersebut memiliki inkremen bebas

3. Banyaknya kejadian pada sembarang interval waktu dengan panjang t,

8

Jadi untuk semua , 0,1,..

! ) ( ) ) ( ) ( ( , 0 ,       k k t e k s N s t N P s t k t  

Dari syarat (3) dapat dilihat bahwa proses poisson memiliki inkremen yang stasioner (Ross,2009).

Dari syarat ini juga dapat diperoleh E(N(t))t

Suatu variabel acak X, dengan parameter  0, dan mempunyai fungsi

kepadatan peluang diskrit dengan bentuk:

,... 3 , 2 , 1 , ! ) , (    x x e x f x    dan > 0 (3) Dikatakan mempunyai fungsi peluang poisson. Suatu peristiwa dikatakan mengikuti distribusi poisson jika:

a. Kemungkinan terjadinya peristiwa dalam suatu waktu adalah rata-rata

kedatangan yang di notasikan dengan sebagai .

b. Banyaknya peristiwa yang terjadi dalam suatu waktu tertentu adalah tidak

tergantung pada banyaknya peristiwa yang terjadi dalam satuan waktu yang lain.

c. Jumlah peristiwa rata-rata yang terjadi pada suatu satuan waktu adalah

sebanding terhadap ukuran satuan waktu tersebut.

dimana  _{adalah suatu parameter yang menyatakan rata-rata banyaknya kejadian}

dalam selang atau interval tertentu. Distribusi poisson dengan parameter  biasa

dinotasikan denganP().

2.3Karakterisasi Distribusi Poisson

9

1. Banyaknya hasil yang terjadi dalam suatu interval tertentu tidak terpengaruh oleh apa yang terjadi pada interval lain yang terpisah (tidak berpotongan dan independen) dalam kaitan ini, proses Poisson dikatakan tidak punya ingatan). 2. Peluang terjadi suatu hasil (tunggal) dalam selang tertentu yang amat pendek

sebanding dengan panjang selang dan tidak tergantung pada banyaknya hasil yang terjadi di luar selang.

3. Peluang terjadinya lebih dari satu hasil dalam selang waktu yang pendek (sempit) dapat diabaikan.

Distribusi poisson memiliki suatu karakteristik yaitu nilai mean dan variansi yang sama. Nilai mean dan variansi dari variabel acak Y yang

berdistribusi poisson dengan parameteradalah:



   0 ) , ( . ) ( y y f y Y E  =



   0 ! . y y y e y   =



   1 ! . y y y e y   =



     1 1 )! 1 ( .! . y y y y e y    =



     1 1 )! 1 ( y y y e  

Misalkan x = y – 1, maka didapat:



    0 ( )! . ) ( x x x e y Y E  

10 ) (Y E =



 0 ) , ( . x x f   y = .1,

sehingga mean dari distribusi poisson parameternya yaitu . Selanjutnya dihitung

nilai variansi dari distribusi poisson, yaitu:

) , ( . ) ( 0 2 2  E Y y f y y



   = ! . 0 2 y e y y y     



=



   0 2 ! . y y y e y   =



     0 1 2 )! 1 .( . y y y y e y    =



       1 1 )! 1 ( ). 1 ) 1 (( y y y e y    =                            



( 1)._{( 1)! ( 1)!} 1 1 1 2 y e y e y y y y y   _   =           







       1 1 1 2 )! 1 ( )! 2 )( 1 ( ). 1 ( y y y y y e y y e y   _    _         





        1 1 1 2 )! 1 ( )! 2 ( . y y y y y e y e      

11          





        1 1 1 2 2 2 )! 1 ( )! 2 ( ) ( y y y y e y e Y E      _       







   1 1 ) , ( ) , ( y y x f z f     E(Y2) 



.11



2  2 2 )] ( [ ) ( ) (y E Y E Y Var   22  

sehingga variansi dari distribusi poisson juga merupakan parameternya dan

12 BAB III

METODE PENELITIAN 3.1 Waktu dan Tempat

Penelitian ini berlangsung dari bulan November 2015 sampai hasil penelitian selesai. Penelitian ini berlokasi di Jurusan Matematika, Fakultas MIPA Universitas Halu Oleo Kendari Sulawesi Tenggara.

3.2 Prosedur Penelitian

Pada penelitian ini, peneliti menggunakan metode kepustakaan dan simulasi data. Dengan tahapan sebagai berikut:

1. Tahap awal adalah menghitung peluang suatu tim untuk memenangkan

pertandingan yang dicapai oleh suatu tim pada pertandingan-pertandingan sebelumnya (kualifikasi) dan mempunyai tiga kemungkinan, yaitu kalah, menang, dan seri.

2. Faktor tersebut dapat direpresentasikan dalam bentuk perolehan skor,

dimana skor tersebut adalah gol-gol yang diraih oleh suatu tim dari beberapa pertandingan.

3. Salah satu metode yang digunakan untuk menghitung peluang menang

suatu tim adalah dengan menggunakan teorema karakterisasi pada distribusi Poisson.

13

Untuk lebih jelasnya dapat dilihat pada flow chart di bawah ini:

Gambar: 1. Flo Chart prosedur penelitian

KUALIFIKASI SERI TEOREMA KARAKTERISASI DISTRIBUSI POISSON SELESAI KALAH MENANG PELUANG

14 BAB IV

HASIL DAN PEMBAHASAN

Hasil yang diperoleh dari penelitian ini berupa bukti-bukti tentang teorema karakterisasi distribusi Poisson dan bagaimana penerapannya dalam permainan sepak bola untuk menghitung peluang untuk memenangkan suatu pertandingan.

4.1 Bukti-bukti Teorema Karakterisasi.

Teorema:

Jika P() suatu variabel acak berdistribusi Poisson dengan rata-rata   0

dan Q variabel acak bernilai bilangan bulat nonnegatif yang saling bebas dengan

P(), maka berlaku:

 



p Q



p



p

 

Q



p d d        (5)

Sebaliknya, misalkan p

 

 variabel acak bernilai bilangan bulat

nonnegatif yang memiliki rata-rata  0 dengan

p

 

p



p

 

n



n     yang

dapat diturunkan terhadap dan Q adalah variabel acak bernilai bilangan bulat nonnegatif yang saling bebas dengan p

 

 . Jika persamaan (5) dipenuhi untuk semua variabel acak Q, maka p

 

 berdistribsi Poisson.

Bukti:

Jika p

 

 berdistribusi Poisson dengan

p

 

P



p

 

n



n     diberikan oleh

15

 





_

     0 ! m m m m e q Q p P    (6)

Dan ruas kiri dari persamaan (5) ialah:

 





_{ }



 

      0 1 m n m m p d d q Q p P d d _   

 

             0 1 ! m n m n m n e d d q   

 

              0 1 1 ! ! m n m n n m n n n e q   



    0 ! m m m m e q   (7)

Untuk memperoleh bentuk terakhir dari persamaan (7), gunakan kenyataan

bahwa penjumlahan terhadap n akan divergen. Karena ruas kanan dari persaman

(6)dan (7) identik, maka persamaan (5)terbukti. Untuk membuktikan sebaliknya,

di mulai dengan: p



p

 

 Q



1 p



p

 

 Q



. Dengan demikian, persamaan (5) dapat dituliskan dalam bentuk:

 





p



p

 

Q



d d Q p p d d _      {1 p



p

 

Q



d d _   

 

_       





  m m n m m P q d d 0 0 1  





 

    m n n m m P q 0 . 0 

16 _m

 

 m mp q



   0 (8) Persamaan (8) memberikan:

 

 







       m n m m m n m m P q p q 0 0 . 0   maka:

 



( ) ( )



( ) ) ( 1 1 . 1 . 1 .      p q P P q p q p q o o o o o     



( ) 1.( ) ... . ( )



( ) .     m m m o m P P p q p q     diperoleh: ) ( ) ( ) ( ) ( ) ( . 1 . 1 . . .      p P P P P o o o     ) ( ) ( ... ) ( . . .    m m o P p P    jadi,



   m n m n P P 0 . ) ( ) (  (9) Jika m = 0, maka: ) ( ) ( . .   o o p P  (10) 1. Persamaan (10) memberikan: P_o.()p_o.()

dari persamaan (9) untuk m = 1 diperoleh:

) ( ) ( ) ( ₁. ₁. .    p P P_o   P₁.()P₁.() p_o.()

17 Subtitusikan P_o.()p_o.()diperoleh:



( )



) ( ) ( ₁. . 1  p  Po  P    p₁.()P_o()

Jadi, pernyataan di atas benar untuk m = 1.

2. Misalkan pernyataan berikut benar untuk m = k,

Maka P_k.()p_k.()P_k1().

Akan dibuktikan untuk m = k + 1 berlaku: P_k._1()p_k._1()P_k() Perhatikan: P_k.()p_k.()P_k1() karena P₀.() p₁.()...P_k()P_k.(), maka:



( ) ( ) ... ( )



( ) ) ( ₀. ₁. . ₁ .            _{k k} k P p P P P

kemudian kedua ruas ditambahkan P_k._1() diperoleh:



( ) ( ) ... ( )



( ) ( ) ) ( ) ( _{1 0}. ₁. .₁ .₁ .                  _{k k k k} k P P p P P P P



( ) ( ) ... ( ) ( )



( ) ) ( ) ( _{1 0}. ₁. . ₁ .₁ .                  _{k k k k} k P P p P P P P Karena P₀.() p₁.()...P_k()P_k._1()P_k._1(), maka: ) ( ) ( ) ( ) (  _k._1   _k._1   _k._1  k P P P P P_k._1()P_k._1()



P_k._1()P_k.()



karena P_k._1()P_k._1()P_k.(), maka: P_k._1()P_k._1()P_k.()

Jadi , terbukti bahwa -P_m.()P_m.()P_m._1()m

18

Persamaan (10) dan (11) merupakan persamaan diferensial biasa linear.

Karenaialah rata-rata dari P()maka



    0 , ) ( ) ( m m mp m E    sehingga pada = 0 diperoleh:



   0 ) 0 ( ) ( m m mp m E  0P0(0)1P1(0)2P2(0)3P3(0)...0 (12) dan 0 (0) 0(0) 1 1(0) 2 2(0) 3 3(0) ... 1      



  P P P P p m m (13)

Solusi dari kedua persamaan (12) dan (13) di atas adalah: 1 ) 0 ( 0  P dan P₁(0)P₂(0)P₃(0)...0. Jadi, P₀(0)1; P_m(0)0

Dengan syarat awal pada persamaan (10)dan (11)mempunyai solusi unik,

dan dapat dibuktikan bahwa distribusi Poisson persamaan (1)adalah solusinya. Ini

menyempurnakan bukti dari teorema karakterisasi distribusi Poisson, karena

persamaan (5) dipenuhi maka P.()berdistribusi Poisson. Kemudian ruas kiri dan

ruas kanan dari (5)diintegralkan terhadap  dengan batas bawah = 0.



 





_





 



0 . . . ) ( ) ( Q PP Q P P (14)

19 4.2 Skor Berdistribusi Poisson

Beberapa rumus yang digunakan untuk menghitung skor yang berdistribusi Poisson agar bisa mendapatkan nilai peluang menang, dan seri, dari suatu pertandingan.

Diasumsikan Q() juga berdistribusi Poisson dengan rata-rata 0

maka:

 

 



P Q 



P 



     0 ! ! n n n n e n e  

 

 



     0 2 ! n n n e   







  2   e (15) Di sini Persamaan (14) memberikan:

 



P Q()



P 

 







    0 ) ( Q P P







     _ 0 2 e







     _ 0 2 e e (16)

Persamaan (16)juga dapat diturunkan dari persamaan (14)secara langsung

dengan memperhatikan ruas kiri, yang dapat dinyatakan sebagai penjumlahan ganda.

20

Jadi, jika skor P dan Q berdistribusi Poisson dengan P() dan Q

 

 ,

maka persaman (16) adalah peluang P menang dan persamaan (15) adalah

peluang P dan Q seri. Untuk pertandingan yang seimbang, dengan  = ,

persamaan (15) menjadi:

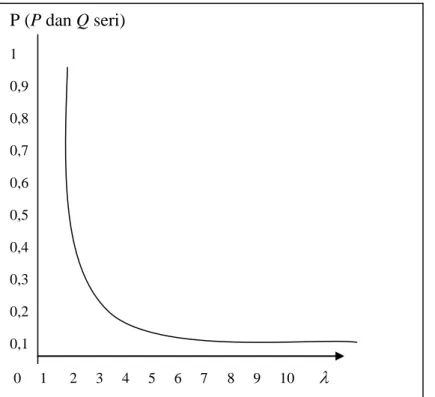
P[ P dan Q seri]e2(2)] (17) Fungsi ini seperti ditunjukkan pada Gambar 4.1 monoton turun dari satu untuk

0



 dan menuju ke nol untuk  menuju untuk besar.

Gambar 4.1. Peluang seri jika skor kedua tim berdistribusi Poisson dengan

rata-rata sama,  dihitung dari persamaan (17)

Gambar 1 menunjukkan bahwa peluang seri lebih mungkin terjadi antara lawan dengan skor rendah daripada antara lawan dengan skor tinggi. Dari

kenyataan bahwa



 





1



( ) ( )





, 2 1 ) ( ) ( ) ( Q  PQ  P P  Q  P P      diperoleh: P (P dan Q seri) 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 1 2 3 4 5 6 7 8 9 10 

21







(2 )



2 1 .menang  e2  P P (18)

Untuk besar, fungsi ini konvergen secara asimtotik ke .

4 2 1 2 1  

4.3Penerapanya ke Data Sepak Bola

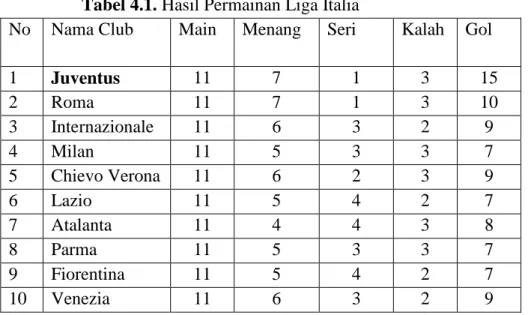
Misalkan hasil pertandingan permainan sepak bola Liga Italia adalah sebagai berikut:

Tabel 4.1. Hasil Permainan Liga Italia

No Nama Club Main Menang Seri Kalah Gol

1 Juventus 11 7 1 3 15 2 Roma 11 7 1 3 10 3 Internazionale 11 6 3 2 9 4 Milan 11 5 3 3 7 5 Chievo Verona 11 6 2 3 9 6 Lazio 11 5 4 2 7 7 Atalanta 11 4 4 3 8 8 Parma 11 5 3 3 7 9 Fiorentina 11 5 4 2 7 10 Venezia 11 6 3 2 9

Dalam Tabel 4.1 ditunjukkan hasil-hasil permainan sepakbola yang

dimainkan di Liga Sepakbola Italia (data diambil dari Lembaran Khusus Olahraga Pikiran Rakyat, Gelora). Untuk masing-masing pasangan tim, Tabel 4.1 menunjukkan jumlah permainan antara satu tim melawan tim lainnya, jumlah keseluruhan gol yang dicetak, jumlah permainan yang dimenangkan masing-masing tim, dan jumlah seri dari keseluruhan permainan tersebut. Hasil bagi gol-gol tiap permainan ialah rata-rata jumlah gol-gol tiap permainan yang dicetak oleh masing-masing tim melawan tim lainnya. Misalkan jumlah gol yang dicetak oleh

22

masing-masing tim berdistribusi Poisson dengan parameter yang bergantung

kepada tim lawan.

Sebagai contoh, pada permainan antara Juventus dan AS Roma, ada

parameter untuk Juventus dan parameter untuk AS Roma. Untuk menaksir

parameter-parameter ini digunakan maximum likelihood method. Statistik penaksir

dari λ dan μ ialah:

! ! ) , ( 1 1 1 m e n e L i i m N i n    



      



        N i i i mi N ni N m n e e N i N i 1 ! ! 1 ) )( (  1  1



    N i i i S N S N m n e e 1 ! ! 1 ) )( ( 1  2 ₍₁₉₎

Disini N = 11 ialah jumlah permainan, S1 = 15 ialah jumlah keseluruhan gol yang

dicetak oleh Juventus, dan S2 = 10 ialah jumlah keseluruhan gol yang dicetak oleh

AS Roma. ln L(,) = -N +S₁1 ln  - N + S₂ ln



  N i In 1 



  N i i In n 1 i m (20) Dengan menurunkan   InL dan   InL

sama dengan nol, dan mencari

penyelesaian untuk  dan , diperoleh taksiran maximum likelihood.

N S₁ ˆ _  dan N S₂ ˆ   (21)

Taksiran-taksiran ini ditunjukkan dalam kolom Tabel 1 berjudul “Gol tiap

23 364 . 1 11 15 ˆ_{ }  dan 0.909 11 10 ˆ   

Sekarang, nilai ˆdan ˆ digunakan pada persamaan (15) untuk menaksir

peluang seri dan persamaan (16) untuk menaksir peluang suatu tim dengan

parameter mengalahkan tim dengan parameter .

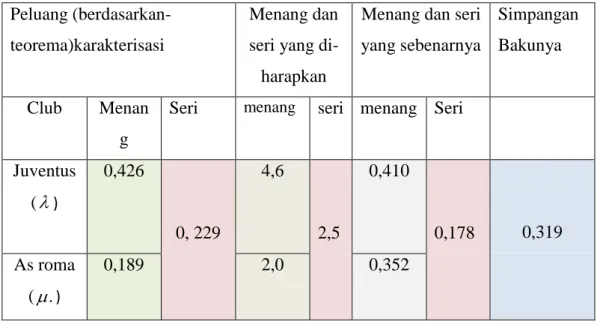
Peluang kemenangan antara Juventus dan As Roma ditampilkan pada Tabel 4.2 berikut:

Tabel 4.2. Peluang yang dihasilkan oleh Kedua Tim Peluang (berdasarkan-

teorema)karakterisasi

Menang dan seri yang di- harapkan

Menang dan seri yang sebenarnya

Simpangan Bakunya

Club Menan

g

Seri menang seri menang Seri

Juventus () 0,426 0, 229 4,6 2,5 0,410 0,178 0,319 As roma (.) 0,189 2,0 0,352

Taksiran peluang-peluang tersebut ditunjukkan dalam kolom Tabel 4.2 berjudul “Peluang (berdasarkan teorema Karakterisasi)”. Dengan menggunakan

perangkat lunak Maple13 dapat dihitung peluang menang, peluang kalah, dan

peluang seri masing-masing tim. Pada permainan antara Juventus melawan AS Roma, peluangnya adalah 0,426 untuk kemenangan Juventus yang didapat dengan

24

kemenangan AS Roma, yang didapat dengan menggunakan nilaiˆdan ˆ, _pada

persamaan (16), dan 0,229 bahwa kedua tim ini seri yang didapat dengan

menggunakan nilaiˆdan ˆ, _{pada persamaan (15). Kemudian mengalikan}

masing-masing peluang dengan jumlah permainan, sehingga menghasilkan nilai ditunjukkan dalam kolom “Menang dan seri yang diharapkan”. Maka, jumlah menang yang diharapkan untuk Juventus menang atas As Roma ialah (0,426)11 = 4,6; dan AS Roma menang atas Juventus ialah (0,189)11 = 2,0; serta seri ialah (0,229)11 = 2,5. Kolom berikutnya menunjukkan jumlah “Menang dan seri yang sebenarnya”. Maka jumlah menang dan seri yang sebenarnya untuk Juventus

menang atas As Roma ialah: 0,410; yang didapat dengan menggunakan nilaiˆdan

, ˆ

 _{pada persamaan (18), dan 0,352 untuk kemenangan As Roma yang didapat}

dengan menggunakan nilaiˆdan ˆ, _{pada persamaan (18), sedangkan seri ialah:} 0,178 yang didapat dengan menggunakan nilaiˆdan ˆ, _{pada persamaan (17),} ditunjukkan dalam kolom ketiga tabel 4.2.

Jumlah seri yang diharapkan ialah pN, dan simpangan baku ialah

, ) 1

( P N

P

p  yang ditunjukkan pada kolom terakhir. Jumlah menang yang

diharapkan dan simpangan baku untuk tim-tim lainnya dihitung dengan cara yang sama, menggunakan peluang yang tepat.. Hal ini menunjukkan bahwa model sesuai dengan data yang diberikan.

25 BAB V

PENUTUP 5.1 Kesimpulan

Berdasarkan pembahasan yang terdapat di dalam tugas akhir ini, dapat disimpulkan bahwa:

1. Distribusi Poisson adalah syarat utama dalam pembuktian teorema dasar

karakterisasi yang mempunyai persamaan

! ) ; ( x e x f x     untuk X = 0, 1, 2,

2. Bukti dari teorema karakterisasi Jika P() suatu variabel acak

berdistribusi Poisson dengan rata-rata   0 dan Q variabel acak bernilai bilangan bulat nonnegatif yang saling bebas dengan P(), maka berlaku:

 



p Q



p



p

 

Q



p d d      

 Sebaliknya, misalkan p

 

 variabel

acak bernilai bilangan bulat nonnegatif yang memiliki rata-rata  0

dengan

p

 

p



p

 

n



n     yang dapat diturunkan terhadap dan Q adalah

variabel acak bernilai bilangan bulat nonnegatif yang saling bebas dengan

 



p .

3. Untuk mengetahui penerapan teorema karakterisasi dalam menentukan

peluang menang atau seri dari suatu tim, ada beberapa persamaan yang di bahas disini, P



P

   

 Q









  2   e

26 P



P

 

 Q()









    d e e



  0

2 , peluang bahwa tim A menang atas tim B.

5.2 Saran

Penulis menyadari dalam penyusunan tugas akhir ini, masih banyak kekurangan, selain itu masalah yang dibahas dalam tugas akhir ini dibatasi pada faktor perolehan skor dari masing-masing tim dalam menghitung besarnya peluang menang dan seri masing-masing tim. Oleh karena itu, diharapkan pada penulis berikutnya yang ingin membahas mengenai estimasi peluang suatu tim dalam memenangkan suatu pertandingan agar lebih menambah dan mengkaji lebih dalam faktor-faktor yang menjadi penentu keberhasilan suatu tim agar peluang yang dihasilkan menjadi lebih objektif.

27

DAFTAR PUSTAKA

Abramowitz, M. dan Stegun, I.A.1965. Handbook of MathematicalFunctions. New York :Dover

Handoko, M. & Riyanto, T 2006. permainan Penyegar Pertemuan. Yogyakarta: Kanisius.

Hasan, M.I. 2001. Pokok-pokok Materi Statistika 1. Jakarta: Bumi Aksara. Manurung. 2013. Metode Statistik. Bandung: Tarsito.

Muhammad, 2009. Pengantar Metode Statistika I. Jakarta: LP3ES.

Mukid. 2011. Probabilitas dan Statistika untuk Teknik dan Sains. Jakarta: Esis erlangga.

Sjamsul.1994. Statistik Teori dan Aplikasi Edisi ke Enam. Jakarta: Erlangga.

Walpole, R.E & Myers, R.H. 1995. Ilmu peluang dan Statistik untuk Insiyur dan Ilmuwan. Bandung: ITB.

29 Lampiran: Hasil peluang menang, dan Seri antara Juventus melawan As Roma.

>

>

>

>

>

>

>

>

>

=

>

>

>

>

>

>

>

30

>

 

>

>

>

>

>

>

>

>

>

>

>

>

>

>

>

31

>

>

>

>

>

>

>

>

>