DIKTAT
DASAR SISTEM KONTROL
EE-3133
Oleh : BASUKI RAHMAT
Jurusan Teknik Elektro
SEKOLAH TINGGI TEKNOLOGI TELEKOMUNIKASI
Daftar Isi
I. SISTEM KONTROL
1. Konsep dan Pengertian Sistem Kontrol 2. Control Problem
3. Transformasi Laplace
4. Persamaan Differensial dan Fungsi Transfer II. MODEL SYSTEM
1. Model Persamaan differensial 2. Model Diagram dan Fungsi Transfer 3. Model Ruang Keadaan
4. Model Flow Diagram III. TANGGAPAN SYSTEM
1. Respon Time system Orde I 2. Respon Time System Orde II 3. Time respon spesifikasi 4. Frekuensi Respon system
5. Karakteristik Tanggapan Steady State ( Mantap ) IV. ANALISA SISTEM KONTROL
1. Kestabilan Sistem
2. Kriteria Kestabilan Routh-Hurwitz V. PERFORMANSI SITEM KONTROL
1. Respon Frekuensi 2. Diagram Bode 3. Diagram Nyquist
4. Kriteria stabilitas Nyquist 5. Gain Margin & Phase Margin VI. METODE ROOT LOCUS
1. Diagram Tempat Kedudukan akar 2. Tempat Kedudukan Penguatan Konstan 3. Prosedur membuat diagram Root Locus VII. DESAIN SISTEM KONTROL
1. Spesifikasi Desain System Kontrol 2. Jenis Kontroller / kompensator
I. SISTEM KONTROL I.Konsep dan Penegrtian Sistem Kontrol
Cerita kasus : kehidupan sehari-hari, - Kasus Pendingin - Kasus kecepatan - Kasus pemanas
- Kasus lainnya ( Sistem Komunikasi ) I.1. System terkontrol/terkendali ( Controlled system ).
System terkontrol/terkendali : system yang dapat dikontrol/dikendalikan baik secara langsung maupun tak langsung.
a. System terkendali langsung ( on-line controlled system ) loop terbuka
b. System terkendali langsung loop tertutup, dengan umpan balik
Set point
Latar belakang kontrol / kendali :
Terjadinya keluaran/hasil yang menyimpang dari harapan Diperlukan dinamika output sesuai dengan harapan
Tujuan kontrol / kendali :
Untuk mendapatkan keluaran/hasil dengan criteria : a. Sesuai dengan harapan.
b. Peningkatan qualitas output 1.1. CONTROL PROBLEM
Pada dasarnya masalah kontrol/kendali adalah masalah menentukan/seting nilai parameter sistem/input agar diperoleh output yang sesuai dengan harapan. Untuk menentukannya diperlukan pemahaman karakteristik fisis dari sistem.
Karakteristik sistem didapatkan dari model sistem, dan keluaran sistem funsi waktu. Controller Plant/Obyek
controller Plant/Obyek
Keluaran sistem sebagai fungsi waktu ( solusi persamaa differensial lengkap)
Model sistem ( model dinamika sistem ) biasanya di nyatakan dalam bentuk –bentuk : a. Pesamaan differensial-Solusinya
b. Fungsi transfer c. Diagram blok
d. Diagram aliran sinyal ( Signal Flow diagram )
Representasi Control Problem ;
Formulasi Problem
Tranlasi
1.2.Persamaan Diferensial
Sistem dinamis biasa dimodelkan secara matematik dengan bentuk persamaan differensial.
x sebagai variable keadaan sistem, y atau u biasanya input keadaan sistem
x adalah solusi persamaan differensial/respon sistem/output sistem terhadap suatu input. 1.3.Transformasi Laplace
Transformasi Laplace dalam sistem kontrol digunaan untuk : a. Memodelkan sistem dalam variable laplace( P Diff laplace)
b. Memudahkan solusi lengkap pesamaan differensial, karena solusi pers. Diff dapat dengan mudah dengan bantuan tranformasi Laplace.
Problem Fisik/teknis
Theory Concept
Formulasi Matematik ( P dif & Laplace trsf )
Matematik
Problem/Solusi ( P dif & Laplace trsf )
Definisi :
F(s) = L f(t); L= operator Transformasi Laplace
F(t) = L-1 [F(s)]; L-1 = operator Transformasi Laplace balik
Bentuk umum
F(s) = ∫ f(t) e-st dt ; Transformasi Laplace
F(t) = ∫ F(s) est ds ; Transformasi Laplace balik Penggunaan trasformasi Laplace :
1. model sistem .
Sistem dinamik dalam sistem persamaan differensial:
Model sistem dalam variable laplace : [aos2 + a1s + a2] . x(s) = b u(s)
Model sistem tersebut dapat dinyatakan sebagai fungsi transfer : x(s) = output ; u(s) = input
ao,a1,a2 dan b = konstanta 2, dari sistem
2. Solusi pesamaan diferensial dengan transfomasi Laplace.
Output sistem :
1
X(s)= --- x b.U(s) [aos2 + a1s + a2]
X(s) merupakan bentuk output( solusi pers. diff), dan x(t) dicari dengan transformasi Lapalce balik dari X(s), dengan bantuan tabel laplace.
1.4. Fungsi Transfer (FT)
Fungsi Transfer ( FT ) adalah perbandingan Output terhadap Input dalam variable Laplace
Sistem dalam variable laplace, yang telah diturunkan dari persamaan differensial sistem : [aos2 + a1s + a2] . X(s) = b U(s)
maka fungsi Transfer sistem adalah :
X(s) 1
G(s) = --- = --- U(s) [aos2 + a1s + a2]
1.4.1 Fungsi Transfer sistem Loop terbuka dan Loop tertutup Loop terbuka
R(s) C(s)
Fungsi Transfer loop terbuka dinyatakan dengan bentuk ; C(s) T(s)= --- = G(s) R(s) Loop tertutup R(s) + C(s) -
Fungsi Transfer loop tertutup dinyatakan dengan bentuk
C(s) G(s) T(s) =--- = --- R(s) 1 + G(s) H(s) G(s) G(s) H(s)
II. MODEL SISTEM Model Sistem Kontrol digambarkan dengan :
II.1. Model Persamaan Differensial
Model ini merupakan model sistem dinamik bentuk persamaan diferensial :
an yn + an-1 yn-1 +…….. +ao = bmxm + bm-1xm-1 +…+ b0 dengan yn = dny/dtn dan xm = dmx/dtn
y = output ( respon ) ; x = input
dalam bentuk laplace yn = dny/dtn = sn y(s)
II.2. Model Fungsi Transfer dan Diagram Blok
Fungsi tranfer sistem menggambarkan hubungan input dan output sistem
Fungsi tranfer sistem : perbandingan antara Output fungsi laplace terhadap input fungsi laplace
[aos2 + a1s + a2] . X(s) = b U(s)
maka fungsi Transfer sistem adalah :
X(s) 1
G(s) = --- = --- U(s) [aos2 + a1s + a2]
1.4.1 Fungsi Transfer sistem Loop terbuka dan Loop tertutup Loop terbuka
R(s) C(s)
Fungsi Transfer loop terbuka dinyatakan dengan bentuk ; C(s)
T(s)= --- = G(s) R(s)
Loop tertutup
R(s) + C(s)
-
Fungsi Transfer loop tertutup dinyatakan dengan bentuk
C(s) G(s)
T(s) =--- = --- R(s) 1 + G(s) H(s) II.3. Model Ruang keadaan
X’ = AX + BU Y = CX + DU
X matrik kolom varisbel keadaan Y variabel output
U Variabel input
A = Matrik keadaan (bujur sangkar ); B dan D = matrik Input ; C = Matrik output
II.4. Model Grafik aliran sinyal
G4
R G1 G2 G3 c
H1
R = sinyal input dan C = sinyal output
III. TANGGAPAN/RESPON SYSTEM Respon system adalah tanggapan system terhadap sinyal input
Respon sistem dapat diketahui dari output sistem, setelah mendapatkan sinyal input. Tinjauan Respon system ada dua kawasan :
G(s)
a. Kawasan waktu ( Time respon )
b. Kawasan frekuensi ( Frekuensi respon )
Respon transient ( peralihan ) ….(1)
Respon Steady State
( mantap )…….(2)
R(s)
Magnitude …(3)
Phasa……….(4)
Bentuk/kurva respon output sistem menggambarkan karakteristik sistem, dan secara teori dapat diketahui secara empiris dari solusi persamaan diferensial system.
Input sinyal test
Sinyal test biasa digunakan dalam melihat respon sistem terhadap masukan. Sinyal tersebut dapat menggambarkan keadaan :
(1). Adanya gangguan sesaat berupa impulse, ( dengan unit impulse ) (2). Adanya input sinyal tetap-DC, secara mendadak , ( dengan unit Step) (3). Adanya input sinyal yang berubah, secara mendadak, (dengan unit Ramp) Sinyal test
1. Unit impulse : δ(t)
2. Unit Step : r(t) = u(t) = 1………….t > 0 3. Unit Ramp : r(t) = t………t > 0 III.1. Tangapan (Respon) Transient sistem
III.1.1. Sistem Orde 1
1. Sistem Orde 1, dengan unit unit impuls
1
G(s) = --- ; input : r(t) = δ(t) = 1 ……t = to ; τs + 1 = 0…….t ≠ to dlm bentuk laplace R(s) = 1 ; τ = konstanta waktu
Tangapan sistem orde 1 terhadap input Unit impulse.
1
C(s) = G(s) .R(s) = --- ; C(t) = e-(1/ τ) t … t >0 ; (τs+1)
Kurva respon sistem orde 1 terhadap input unit Impuls G(s)
Time respon [ c(t) ].I
c(t)
t 2. Sistem Orde I, dengan input unit step
1 1
G(s) = --- ; input : r(t) = 1….t > 0 ; dlm bentuk laplace R(s) = --- τs + 1 s Tangapan sistem orde 1 terhadap input Unit Step.
1
C(s) = --- ; C(t) = [1 – e-(1/ τ) t ] … t >0 ; τ = konstanta waktu s (τs+1)
Kurva respon sistem orde 1 terhadap input unit step c(t)
1
t
2. Sistem Orde 1, dengan input unit Ramp sistem orde 1:
1 G(s) = ---
τs + 1
1
input unit Ramp : r(t) = t ; dlm bentuk laplace : R(s) = --- s2
Tanggapan sistem orde I, terhadap input unit Ramp 1
C(s) = G(s) . U(s) = ---; c(t) = t – τ + τe-(1/τ) t …..t >0 s2(τs + 1)
Kurva respon sistem orde 1 terhadap input unit Ramp
c(t)
t
III.1.2 Sistem Orde 2 Sistem orde 2 : 1 ωn G(s) = --- ; atau G(s) = --- Js2 + Fs + K s2 + 2ζωns + ω2 ωn = K/J ; 2ζωn = F/J = 2σ σ = atenuasi wn = Frekuensi natural ζ = Rasio redaman sistem Persamaan karakteristik sistem orde 2 s2 + 2ζωns + ω2 = 0
akar2 persamaan karakteristik sistem :
s1, s2 = - ζωn + V (ζωn)2 - ωn = -ζωn + ωn Vζ2 −1 σ = ζωn dan ωd = ωn Vζ2 −1
disini koefisien factor redaman : 0< ζ < 1, sehingga menjadi bentuk imajiner Æ jωd = j ωn V(1 - ζ2)
maka s1, s2 = - σ + jωd bentuk komplek untuk sistem orde 2 diatas, G(s) dapat dinyatakan :
ωn
G(s) =--- ; (s – s1 ) ( s – s2 )
III.2.1 Respon sistem orde II
Respon sistem orde 2 untuk 3 macam input seperti pada orde 1dapat digambarkan sebagai berikut:
(1). Respon sistem orde 2 terhadap input unit impuls r(t) =δ(t) input unit impulse dalam bentuk laplace : R(s) = 1
ωn
maka outputnya C(s) = R(s).G(s) = --- ; (s – s1 ) ( s – s2 )
dengan mencari faktornya didapat : A B
C(s) = R(s).G(s) = --- + --- ; (s – s1 ) ( s – s2 )
dengan transformasi laplace balik maka output dalam fungsi waktu : c(t) = A es1t + B es2t
= A e (- σ + j ωd )t + B e(- σ − j ωd ) t
nilai A dan B, didapat dari syarat batas ( awal dan akhir ), atau gunakan pecahan parcial.
(2). Respon sistem orde 2 terhadap input unit Step 1 input unit Step dalam bentuk laplace : R(s) = ---
s
ωn
maka outputnya C(s) = R(s).G(s) = --- ; s (s – s1 ) ( s – s2 ) dengan mencari faktornya didapat :
A B C
C(s) = R(s).G(s) = --- + --- + --- ; s (s – s1 ) ( s – s2 ) output dalam fungsi waktu : c(t) = A +B es1t + C es2t
= A + B e (- σ + jωd )t + C e(- σ − jωd ) t
nilai A, B dan C didapat dari syarat batas ( awal dan akhir )
untuk kedua bentuk respon masukan impulse dan Unit step, terjadi bentuk output exponensial komplek yang dapat di uraikan menjadi bentuk sinusoid : jumlahan (sin w t dan Cos wt ), dan perkalian dengan factor redaman e (- σ) t .
Note :
e (- σ + jωd )t = e - σ t . e j ωd t
= e - σ t ( Cos ωdt +j Sin ωd t )
Karakteristik respon sistem orde 2 terhadap input unit Impuls dan Unit Step dipengaruhi oleh, keadaan nilai ( ζ ).
a. Jika ζ = 0 , maka redaman sistem α = 0, sehingga sistem akan mengalami osilasi terus dengan ωd = ωn , hal ini dapat ditunjukkan dengan bentuk
C(t) = ( Cos ωnt + j Sin ωnt )
Sistem dinamakan dalam kondisi tanpa redaman Un-damp
b. Jika : 0 < ζ < 1 , maka redaman sistem σ = ζ ωn > 0, sehingga sistem akan mengalami osilasi teredam dengan ωd = ωn V(1 - ζ2 ), hal ini dapat ditunjukkan dengan bentuk
Sistem dinamakan dalam kondisi underdamp
c. Jika : ζ = 1 , maka redaman sistem σ = ωn > 0, sehingga sistem akan mengalami redaman tanpa osilasi , dengan ωd = ωn V1 - ζ2 = 0, sehingga output menjadi bentuk
C(t) = e - σ t = e - ωnt
Sistem dinamakan dalam kondisi Critical damp
III.2 KARAKTERISTIK TANGGAPAN STEADY STATE (Mantap)
Saat steady state(mantap) pada suatu sistem, ada dua hal penting yang perlu diperhatikan, dalam sistem kontrol :
a. Steady state Error
b. Besar nilai steady state Error
Karena keluaran kondisi mantap inilah yang, dibutuhkan oleh subsistem yang ada di belakangnya
Kedua hal tersebut nilainya ditentukan oleh koefisien Error III.2.1. Koefissien Error tergantung pada dua hal , yaitu :
1. Type sistem 2. Input sistem 1. Type sistem:
Type digunakan untuk memberikan ciri karakteristik sistem terhadap jumlah akar persamaan karakteristik pada titik Nol ( nilai Nol ) pada bidang komplek.
(a). Type 0 ( Nol ) jika, akar persamaan karakteristik bernilai nol tidak ada ( tak terdapat s = 0, dari akar persamaan karakteristik )
K(s+z1)(s+z2) …. G’(s) =---
(s+p1)(s+p2)(s+p3)…
(b) Type 1 ( satu ) jika, akar persamaan karakteristik bernilai nol berjumlah 1 ( satu ) atau ada satu buah, akar persamaan karakteristik s = 0
K(s+z1)(s+z2) …. G’(s) =---
s(s+p1)(s+p2)(s+p3)…
(c) Type n, jika akar persamaan karakteristik bernilai nol berjumlah n, atau ada n buah, akar persamaan karakteristik s = 0
K(s+z1)(s+z2) …. G’(s) =---
sn(s+p1)(s+p2)(s+p3)… n = type sistem ( 0,1,2,3,…. ) bilangan bulat.
Error Steady state pada berbagai type sistem Koefisien Error sistem, meliputi :
1. koefisien error posisi/static error (Kp), terhadap input unit step 2. Koefisien error kecepatan/Velocity error (Kv), terhadap input Ramp
3. Koefisien error percepatan/Acceleration error ( Ka), terhadap input Parabolic. c(t)ss Kp = --- = lim G(s) e(t)ss s Æ 0 (dc(t)/dt)ss Kv = ---= lim s G(s) e(t)ss s Æ 0 (d2c(t)/dt2)ss Ka = ---= lim s2 G(s) e(t)ss s Æ 0
a. untuk Type 0 (nol),
k.z1.z2… Kp = lim G(s) = ---= k’ sÆ 0 P1.p2.p3…. Kv = lim s G(s) = 0 s Æ 0 Ka = lims2G(s) = 0 s Æ 0
b. untuk Type 1 (satu),
k.z1.z2… Kp = lim G(s) = ---= ~ sÆ 0 s (P1.p2.p3…). k.z1.z2… Kv = lim s G(s) = ---= k’ sÆ 0 (P1.p2.p3…).
s k.z1.z2…
Ka = lim s2 G(s) = ---= 0 sÆ 0 (P1.p2.p3…). c. untuk Type-2 (dua),
k.z1.z2… Kp = lim G(s) = ---= ~ sÆ 0 s2 (P1.p2.p3…). k.z1.z2… Kv = lim s G(s) = ---= ~ sÆ 0 s (P1.p2.p3…). k.z1.z2… Ka = lim s2 G(s) = ---= k’ sÆ 0 (P1.p2.p3…)
a.2. STEADY STATE ERROR R(s) Error = E(s) = R(s) – C(s) = ---
1 + G(s) Error steady state :
s R(s)
e(t)ss =lim sE(s) = lim --- s Æ0 sÆ0 1 + G(s)
Error steady state untuk berbagi type a. Type 0 (nol)
K ( s+z1)(s+z2)…. G(s) =--- (s+p1)(s+p2)(s+p3)...
1
1. Type sistem 0, dengan input unit step: R(s) =---- S s( 1/s) 1
e(t)ss = lim --- = --- sÆ0 1 + G(s) 1 + Kp
1 2. Type sistem 0, dengan input unit Ramp: R(s) =----
S2 s( 1/s2) 1/s
e(t)ss = lim --- = lim ---= ~ sÆ0 1 + G(s) sÆ0 1 + G(s)
2 3. Type sistem 0, dengan input unit Parablic: R(s) =----
S3 s( 2/s3) 2/s2
e(t)ss = lim --- = lim ---= ~ sÆ0 1 + G(s) sÆ0 1 + G(s) b. Type sistem 1, k ( s+z1)(s+z2)…. G(s) =--- S (s+p1)(s+p2)(s+p3)... 1
1. Type sistem 1, dengan input unit step: R(s) = ---- S s( 1/s) 1
e(t)ss = lim --- = --- = 0 sÆ0 1 + G(s) 1 +
~
1
2. Type sistem 1, dengan input unit Ramp: R(s) =---- S2
s( 1/s2) 1 1 e(t)ss = lim --- = limit --- = ---
sÆ0 1 + G(s) sÆ0 s(1 + G(s)) Kv 2
3. Type sistem 1, dengan input unit Parablic: R(s) =--- S3 s( 2/s3) 2/s2
e(t)ss = limit --- = limit ---=
~
sÆ0 1 + G(s) sÆ0 1 + G(s)c. Type 2
Dengan cara sama untuk type 2 akan didapatkan hasil berikut : a. Type 2, input unit step, maka e(t)ss = 0
b. Type 2, input unit ramp, maka e(t)ss = 0
c. Type 2, input unit parabolic, maka e(t)ss = 1/ Ka
III. 3. Spesifikasi tanggapan waktu ( Time Respon spesifikasi ) sistem orde 2. Spesifikasi tanggapan waktu sistem orde 2, merupakan sifat yang dimiliki oleh sistem orde 2. sifat tersebut sbb :
a. Rise Time ( waktu naik )
Rise time = waktu respon ( 10 s/d 90 )% dari nilai/kondisi akhir untu redaman lebih, dan ( 0 s/d 100 ) % untuk redaman kurang.
Tr = (1/ωd) tan –1(ωd /-σ).
b. Percent Overshoot (lewatan maksimum), Mpt = c(tp) –1 = - e - ζ ωn(π/ωd ) (Cos π + (σ/ωd)Sin π ), ζ dengan (σ/ωd ) = --- V(1 - ζ2 ) Mpt - Css Percent Overshoot = e - (σ/ωd )π x 100 % = --- x 100 % Css Css = C (tss)
c. Setling Time (Waktu tetapan) : Ts Waktu mencapai set output beberapa percent
Untuk 2 % maka Ts = 4 T = (4/σ)
Untuk 5 % maka Ts = 3 T = (3/σ)
d. Peak Time ( waktu puncak ) : tp
Peak time adalah waktu untuk mencapai puncak Overshoot. Waktu puncak berkaitan dengan terjadinya puncak pertama kali.
Maka : tp = (π/ωd )
III. 4. Respon frekuensi sistem .
Respon frekuensi sistem, merupakan gambaran tanggapan sistem terhadap input sinusoida pada kondisi mantap.
Jika r(t) = A cos ωt, atau R(s) = As/(s2 +ω2)
dan C(s) = G(s) R(s) = G(s) [ As/(s2 +ω2)]
dengan mengubah bentuk tersebut kedalam pecahan parcialnya : C(s) = k1/(s-jω) + k2/(s-jω) + Cg(s)
Untuk t Æ ~ maka suku Cg(s) akan konvergen menuju nol (sistem stabil ), sehingga C(s) hanya dipengaruhi oleh sinusoida pada kondisi mantapnya.
sebab
G(jω) merupakan bentuk komplek = | G(jω)| e jθ Dengan : k1 = (1/2) AG(jω) dan k2 = (1/2) AG(-jω)
Maka c(t) = k1 e - jωt + k2 e - jωt atau
= (A/2) | G(jω)| e jθ e - jωt + (A/2) | G(jω)| e -jθ e - jωt = A | G(jω)| cos (ωt + θ )
IV. ANALISA SISTEM IV.1. KESTABILAN SISTEM
Kestabilan system : sifat stabilitas suatu sistem Definisi :
Sistem linier stabil, Jika sistem linier mendapatkan input terbatas ( bounded ), maka outputnya juga terbatas ( bounded ).
[ Bouded input, bouded output ] = BIBO Sifat kestabilan :
- Dapat ditentukan / dicari dari akar2 persamaan karakteristik.
- Ada kaitan antara nilai & tanda akar2 persamaan karakteristik dengan kestabilan.
1V.1. Sifat Kestabilan Sistem loop tertutup.
R(s) C(s)
C G T =--- = ---
R 1 + GH
Bentuk umum fungsi transfer :
C(s) k(s-z1)(s-z2)(s-z3)…. --- = --- R(s) (s – p1 ) (s – p2) (s – p3 ).. Atau G ( s ) H(s)
C(s) Ao A1 An --- = --- + --- + ……… + ---
R(s) s – p1 s – p2 s – p3
Persamaan karakteristik sistem :
a3s3
– a2s
2- a1s - ao = (s – p1) ( s – p2) ( s – p3 ) = 0
s1 = p1, s2 = p2 dan s3 = p3
s1, s2 dan s3
, biasanya bentuk komplek α + j ω keluaran sistem saat transient/peralihan :c(t) = k est
Cara menentukan kestabilan sistem dengan mencari akar2 persamaan karakteristik
Kondisi stabil dapat dipenuhi, jika akar persaman karakteristik sistem bagian riil bertanda negatif ( stabil ), jika bertanda positif tak terpenuhi ( tak stabil ).
akar2 persamaan karakteristik sistem : si = αi + jϖi
αi = bagian riil; ϖi =bagian Imajiner Secara matematik untuk t Æ ~,
jika :
αi < 0, maka | c(t) | = berhingga, sehingga sistem stabil dan
αi > 0, maka | c(t) | = tak berhingga, sistem tak stabil
namun cara menentukan kestabilan sistem dengan mencari akar persamaan karakteristik, jika dilakukan secara manual untuk sistem dengan orde tinggi perlu waktu lama dan sulit. Cara yang cepat dengan metode Routh-Hurwitz
Metode Routh-Hurwitz untuk menentukan keastabilan : Perhatikan sistem dengan persamaan polinom :
Q(s) = ansn + an-1 sn-1 +….+ ao
Deret Routh :
Sn an an-2 an-4 an-6 Sn-1 an-1 an-3 an-5 an-7 Sn-2 B1 b2 b3 b4 … … l1 l2 So M1 1 an an-2 b1 = - ----
an-1 an-1 an-3
1 an an-4 b2 = - ---- an-1 an-1 an-5 1 an-1 an-3 c1 = - ---- b1 b1 b2
V. PERFORMANSISISTEM KONTROL V1. Respon Frekuensi Sistem
• Analisa sistem orde tinggi, sukar dilalukan dengan metode klasik ( time respon ). Maka respon frekuensi dapat digunakan sebagai alat penting untuk analisa sistem. • Respon frekuensi : Respon terhadap input sinusoida tungal pada daerah frekuensi
sangat luas ( sehingga didekati dengan nilai f atau ω = 0 s/d ~ ) . • Respon sistem dapat dicari dari respon elemen-elemen penyusunnya.
• Respon sistem linier terhadap sinyal sinusoida terdiri dari respon ‘transient’ dan steady state ( mantap ).
• Respon mantap berupa sinusoida dengan frekuensi sama dengan sinyal input. • Perbedaan yang terjadi antara Input-Output hanya pada Rasio Amplitudo serta
Phasa Input-Output.
• Untuk sistem G(s) = G(jω), maka
Magnitude ( rasio amplitudo input-output ) = | G(jω) | = √(Re)2 + (Im)2
Re = bagian riil dari G(jω) dan Im = bagian Imajiner dari G(jω) Phase = ∅( jω) = ∠ G(jω) = arc.tan ( Im/Re)
u(t) ∆t
Periode
time Gambar.5.1 Respon Sinusoida sistem orde-1
Respon sistem dapat dituliskan sebagai :
y(t) = |G(jw)| ∠ G(jω) = |G(jw)| (- arc.tan (Im/Re)) = |G(jw)| Sin (ωt - arc.tan (Im/Re))……….(5.5)
Untuk frekuensi input yang sangat rendah, magnituda output mendekati K kali magnitude input.
Beda phasa adalah kecil untuk ω kecil. Beda sudut phasa bagi sistem orde-satu selalu negatif.
• Diagram Bode.
• Diagram Bode menunjukkan ratio magnituda output-input serta sudut phasa suatu sistem terhadap ferkuensi.
• Sistem orde-dua sebagai fungsi frekuensi : |G(jω)| = 1/ √ ((1 – j(ω/ωn)2
)2 + 4 ζ2 ((ω/ωn)2)2
(jω) = - tan –1 { 2(ω/ωn)/(1- (ω/ωn)2)
Dengan diagram Bode dapat diketahui performansi suatu sistem dalam domain frekuensi :
- Maksimum dari perubahan input diijinkan agar sistem tetap pada performansi . - Daerah kerja gain serta phasa terhadap frekuensi .
DIAGRAM NYQUIST
Diagram Nyquist menyatakan Gain dan Phasa sebagai fungsi frekuensi dalam satu bidang.
Stabilitas absolut sistem kontrol loop tertutup dapat ditentukan dari kurva respon frekuensi sistem loop terbukanya, tanpa mencari pole sistem.
Sistem kontrol loop tertutup, stabil jika pole dari (1 + G(s)H(s)) = 0, terletak seluruhnya disebelah kiri sumbu khayal.
Kriteria Stabilitas Nyquist menyatakan hubungan respon frekuensi G(jw) dengan jumlah zero dan pole, dari 1 + G(s)H(s), dikiri sumbu khayal.
Kriteria Stabilitas Nyquist :
1). Kurva G(jw) tidak mengelilingi titik (-1 +j0 ) : sistem stabil jika tidak terdapat pole dari G(s) yang berada di sebelah kanan sumbu khayal, sebaliknya sistem tidak stabil. 2). Kurva G(jw) mengelilingi titik (-1 + j0 ) satu atau lebih melawan arah jarum jam:
sistem stabil jika jumlah putaran adalah sama dengan jumlah pole sistem G(s)’ yang berada di sebalah kanan sumbu khayal, dan sebaliknya sistem tak stabil.
3). Kurva G(jw) mengelilingi titik ( -1 + j0 ), satu atau lebih searah putaran jarum jam : sistem tdk stabil.
• Hubungan ketiga kondisi diatas dinyatakan : Z = N + P
Z : Jumlah Zero dari [1 + G(s)] disebalah kanan sumbu khayal
N : Jumlah kali kurva G(jω) mengelilingi titik(- 1 + j 0 )searah putaran jarum jam P : Jumlah pole dari sistem G(s) di sebelah kanan sumbu khayal.
• Jika P tdk sama dengan nol , untuk sistem stabil, haruslah Z = 0,atau N = -P, kurva mengelilingi titik ( -1 + j0 ) berlawana arah jarum jam.
• Jika P = 0 maka Z = N , untuk sistem stabil, kurva G(jω) mengelilingi titik ( -1 + j 0 ). GAIN MARGIN dan PHASE MARGIN
• Gain Margin dan Phase Margin adalah dua parameter penting untuk menyatakan performansi sistem dari repon frekuensi.
•
Gain Margin : Faktor yang menyatakan seberapa besar gain suatu kontroller dapat dinaikkan sebelum mencapai kondisi tak stabil, pada suatu fekuensi dimana sudut fasanya : -180o .
•
Gain margin : kebalikan dari |G(jω)| pada frekuensi dimana sudut fasa : -180o 1
• Kg = --- | G( jωc ) |
• Phase Margin :
• Factor sudut seberapa besar sudut phasa dapat membesar sebelum mencapai kondisi tdk stabil, pada gain frekuensi ‘ Crossover ’ agar sistem tetap stabil.
γ = 180o + ∅
• Gain Margin dan Phase Margin yang sangat besar menunjukkan sistem kontrol loop tertutup adalah sangat stabil ( umumnya kondisi sistem kontrol yang juga tidak baik ). •Gain margin yang sedikit lebih besar dari satu , dan phase margin yang positif dan
kecil menunjukkan bahwa sistem sangat dekat dengan kondisi tidak stabil.
•Gain margin disekitar angka 3, dan phase margin diantara 30o – 35o umumnya akan menghasilkan sistem yang cukup baik .
VI. METODE ROOT LOCUS ( Tempat kedudukan akar )
Metode ini, metode grafis untuk mencari akar2 persamaan karakteristik, (akar2 polinom). Grafik keadaan akar persamaan karakteristik berguna untuk analisa sistem fisis (melihat sifat kestabilan, performance ) sistem.
Mencari pole2 loop tertutup dari pole dan zero lup terbuka dengan penguatan (k) sebagai parameter .
Dalam desain sistem kontrol linier, metode ini berguna untuk menunjukkan cara modifikasi pole dan zero / rekayasa sistem kontrol linier, untuk memenuhi spesifikasi peformance sistem, yang diinginkan.
VI.1. Diagram tempat kedudukan akar ( diagram root locus).
Sistem fungsi transfer lup tertutup ;
R(s) C(s)
Gambar. VII.1. diagram sistem lup tertutup C(s) G(s)
--- = --- R(s) 1 + G(s)H(s) Dengan pesamaan karakteristik ;
1 + G(s) H(s) = 0 atau G(s)H(s) = -1
G(s) H(s) merupakan besaran komplek, maka dapat dipisahkan jadi : a. besaran Sudut G(s)H(s) = +180o(2k +1) b. besaran Magnitude | G(s)H(s) | = 1 G ( s ) H(s)
Nilai2 “s” yang memenuhi syarat dua besaran, adalah pole2 lup tertutup ( akar2 persamaan karakteristik). Nilai tersebut merupakan diagram titik2 pada bidang komplek.
Tempat kedudukan akar sistem orde kedua
Tinjau sistem yang ditunjukkan fungsi transfer lup terbuka : k
G(s)H(s) =--- s(s+1)
fungsi transfer lup tertutupnya: C(s) k --- = --- R(s) s2 +s + k
Persamaan karakteristiknya : s2 +s + k = 0
Jika k diubah dari nol (0) sampai tak hingga bagaimana tempat kedudukan akar2 persamaan tsb. ?
Gambar diagram tempat kedudukan akar.
Akar2 persamaan karakteristik ;
S1 = -1/2 +1/2 V1- 4k, dan S1 = -1/2 -1/2 V1- 4k Akar2 tersebut, real jika k< ¼ dan Imajiner, jika k > ¼.
Tempat kedudukan akar2 tersebut diberikan dengan skala k, dan akan membesar sesuai dengan arah anak panah.
Secara grafik dapat dianalisa sbb:
a. jika k = 0 maka maka pole lup tetutup, sama dengan pole G(s)H(s), yaitu 0 dan -1
b. jika k = diperbesar dari nol sampai ¼ maka pole2 bergerak menuju titik (-1/2 , 0 ), semua pole terletak pada sb nyata, dan sistem mempunyai redaman lebih, shg tanpa osilasi. c. Jika k = ¼ , kedua pole ( -1/2 ) nyata dan bersatu,
d. jika k > ¼ , diperbesar terus, maka kedudukan pole meninggalkan sumbu nyata bergerak sepanjang s = -(1/2) menuju s = -1/2 + j ~ dan s = ½ -j ~ ; bernilai komplek, dengan redaman kurang.
e. Tiap titik pada kedudukan akar memenuhi syarat sudut :
= -< s - < s + 1 = + 180o (2k+1) ; dengan ( k =1,2,3…...)
Catatan : titik2 diluar tempat kedudukan akar ( bukan pole ) tidak memenuhi syarat sudut tersebut.
f. Jika pole2 lup tertutup ditentukan tempat kedudukan akar, maka nilai k yang berkaitan dihitung dari syarat besar/magnitude.
Misalnya jika pole dipilih s1 = -(1/2) + j2 maka harga “ k ” untuk kondisi ini diperoleh dari : k | G(s) H(s) | = | --- | = 1 s(s+1) maka k = | s(s + 1 ) | ( s = - ½ +j 2 ) = (17/ 4) Catatan:
1. ada pengaruh perubahan harga k terhadap perilaku respon transient sistem orde 2.
2. kenaikan k memperkecil nilai koefisien rasio redaman, memperbesar lewatan maksimum, memperbesar frekuensi alamiah teredam dan tak teredam.
VI.2 Tempat kedudukan penguatan konstan
Tempat kedudukan penguatan konstan dari sistem diperoleh dari syarat besar, magnitude. k | G(s) H(s) | = | --- | = 1 s(s+1) atau | s(s+1) | = k
VI.3 Ortogonalitas tempat kedudukan akar dan tempat kedudukan penguatan konstan.
Tempat kedudukan akar dan tempat kedudukan penguatan konstan pada bidang s adalah pemetaan konformal dari tempat kedudukan :
< G(s)H(s) = + 180o(2k+1) dan |G(s)H(s)| = konstan pada bidang G(s)H(s).
Tempat kedudukan fasa konstan dan penguatan konstan saling orthogonal, maka tempat kedudukan akar dan tempat kedudukan peguatan konstan pada bidang s saling
orthogonal.
VI.4 Prosedur umum membuat diagram Root locus : Contoh : untuk sistem
K
G(s) = --- s(s+1)(s+2)
1.Cari persamaan karakteristik loop tertutup 1 + G(s)H(s) = 0,
dari contoh sistem s(s+1)(s+2)+K=0
2.Cari titik awal dan titik akhir serta banyaknya cabang tempat kedudukan :
Titik awal : titik awal akar persamaan karakteristik adalah titik2 pole dari lup terbuka/ akar persamaan karakteristik lop tertutup dengan K=0 .
Dari contoh sistem :
s = 0, s = -1 dan s = -2
Titik akhir : titik akhir adalah salah satu zero lup terbuka atau suatu zero lup terbuka di tak terhingga.
Dari contoh ini titik akhir berada di titik tak hingga / tak ada zero
3. Tentukan tempat kedudukan akar pada sumbu nyata,
Tempat kedudukan akar pada sumbu nyata, dengan syarat sudut < G(s)H(s) = -180o Jika antara titik 0 dan –1 letakkan titik uji maka syarat sudut:
<s=180o, <s+1 = <s+2 = 0o
sehingga : -< s -<s+1 - <s+2 = -180o, antara 0 dan –1 Æ syarat sudut terpenuhi, maka daerah ini merupakan tempat kedudukan akar.
Jika antara –1 dan –2 diletakkan titik uji, maka syarat sudut jadi : < s = < s+1 = 180o , dan <s+2 = 0o
sehingga : -<s-<S+1 = -180o-180o-0o =0o, Æ daerah ini tak memenuhi syarat sudut, maka daerah ini bukan merupakan tempat kedudukan akar.
3. Tentukan tempat kedudukan akar asymtot, dan sudut Asymtot Dengan titik uji s Æ ~ ( tak hingga )
K
Lim G(s) = limit --- = Lim K / s3 sÆ~ sÆ~ s(s+1)(s+2) sÆ ~ + 180o(2k+1) sudut asymtot = --- n – m n = banyak pole m = banyak zero
maka dari sistem diatas n ( pole ) = 3
m(zero) = 0
sudut asymtot masing-masing : ( + 180o ) / 3 ; diperoleh : 60o, - 60o
4. Tentukan perpotongan asymtot dengan sumbu nyata : Σ pole – Σ zero ( p1+p2+…+pn) – (z1+z2+…+zm) σ = - ---= - --- n-m n-m -2-1-0 σ = - --- = - 1 3
atau dengan asumsi titik s Æ ~, maka persamaan karakteristik sistem (s+1)3 = 0 dan akarnya s = σ= -1
5. Tentukan titik “breakway” dan titik “Break-In”;
Titik “ Beakway” adalah titik berangkat dari sumbu nyata ke bidang complex, terletak antara 2 pole
Titik “ Beak-in” adalah titik masuk dari dari bidang complex ke sumbu nyata, terletak antara 2 zero,
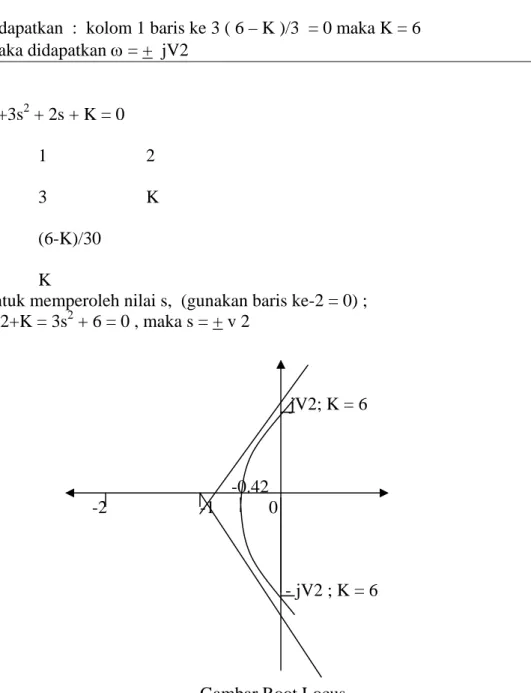
Keduanya di dapatkan dengan bentuk : dK --- = 0 ; ds dengan s3+3s2 + 2s= - K maka : 3s2+6s + 2 = 0 didapatkan s1 = -0.42 dan s2 = -1. 57
Titik “ breakway” terletak pada daerah akar, berada antara 0 dan –1; sehingga titik tersebut adalah: s1 = -0.42
Selajutnya pada, titik s1= - 0.42 ; maka nilai K = 0.385
6. Tentukan titik potong kurva dengan sumbu Imajiner; Dengan s = jω , maka persamaan karakteristik menjadi ; (jω)3 + 3(jω)2 + 2(jω) + K = 0
(K – 3 ω 2) +j (2ω – ω 3 ) = 0
kedua bagian ( riil dan Imajiner ) = 0 (K – 3 ω 2) = 0 ; (2ω – ω 3
) = 0; dari 2 persamaan ini,
maka ω = + V 2 ( titik potong kurva root locus pada sumbu imajiner ), sehingga nilai K = 6 .
atau gunakan metode Routh
didapatkan : kolom 1 baris ke 3 ( 6 – K )/3 = 0 maka K = 6 maka didapatkan ω = + jV2 s3+3s2 + 2s + K = 0 s3 1 2 s2 3 K s1 (6-K)/30 s0 K
untuk memperoleh nilai s, (gunakan baris ke-2 = 0) ; 3s2+K = 3s2 + 6 = 0 , maka s = + v 2
jV2; K = 6
-0.42 -2 -1 0
- jV2 ; K = 6
Contoh : 2
Sistem loop tertutup dengan penguat lingkar : K( s + 3 )
KG(s)H(s) = ---; jika : H(s) =1 ( s + 2 )2
dari sistem tersebut maka :
1. persamaan karakteristik loop tertutup: ( s + 2 )2 + K ( s + 3 ) = 0
2. Titik awal & titik akhir:
Titik awal : K = 0 didapatkan pada pole : Æ s = -2 Titik akhir : K =0 didapatkan pada zero : Æ s = -3
3. Asymtot : Sudut Asymtot : + 180o + 180o + 180o = --- = ---= --- = ~ n – m 1 – 1 0 Perpotongan asymtot : Σ pole – Σ zero ( p1+p2+…+pn) – (z1+z2+…+zm) σ = - ---= - --- n-m n-m -2 – (- 3 ) 1 --- = --- = ~ 1 – 1 0
dari dua syarat asymtot maka tidak ditemukan asymtot, sehingga kurvanya tidak mengikuti asymtot, tetapi berbentuk lingkaran .
4. Titik breakway & Break-in dari pers. karakeristik didapatkan
( s + 2 )2 K = - ---;
( s + 3 )
(dK/ds ) = 0, (2s+4)(s+3) – (s+2)2 = s2+6s +8 = (s+2)(s+4) = 0 maka S1 = -2 ( breakway ) dan s2 = -4 ( break-in )
4. Titik potong dengan sumbu imajiner tidak ada Im
-4 -3 -2 -1 Re
VII. DESAIN SISTEM KONTROL
Sasaran sistem Kontrol :Menentukan sinyal kontrol u(s) yang dapat memberikan output sistem y(s), sesuai dengan spesifikasi yang telah ditentukan, apapun yang terjadi dengan dinamika proses maupun gangguan.
R(s) C(s)
P(s) = Proses; C(s) = Kontroller Masalah Desain/Perancangan.
Secara teknis apa sih pertimbangan desain itu ? : Desain sistem bertujuan agar,
“Dengan suatu plant ( obyek kontrol ) dan spesifikasi yang telah ada ( kurang memenuhi syarat),
Kemudian lakukan desain dengan menambahkan kompensator agar dapat memenuhi spesifikasi yang diharapkan”.
Ada 2 macam pendekatan dalam desain :
1. Pilih konfigurasi, seluruh sistem mulai dari kompensator dengan memilih parameter kompensator untuk memenuhi spesifikasi kinerja sistem.
2. Dengan plant yang ada, cari sistem seluruhnya sehingga diperoleh spesifikasi dan kemudian tentukan kebutuhan kompensator yang harus di berikan/tambahkan pada sistem tersebut.
Atau :
i. Diberikan plant, cari sistem tersebut agar optimum terhadap criteria perfomace yang diberikan.
ii. Hitung Compensator untuk memenuhi / mendapatkan tahap (i).
Perancangan sistem kontroller :
1. mencari/memilih kontroller. 2. Seting ( tuning ) sistem kontrol.
Keduanya bertujuan mencari/menentukan sinyal kontrol u(t) yang akan diumpankan ke proses.
Jenis Kontroller/Kompensator.
Beberapa jenis kontroller yang digunakan keperluan automatik di industri : a. Kontroller dua posisi ( “on-Off ”)
On……. M1 > 0 M1;On U(t) = ⎨ Off…… M2 < 0 M2; Off e(t) u(t) b. Kontroller Proporsional Contoh : Kontroller C(s) = Kp = Proporsional
c. Kontroller Proporsional + Diferensial (PD) Contoh :
Kontroller ; C(s) = kp + Kds ) …….. (1) Berapa parameter : kp dan Kd……….. (2)
d.Kontroller Proporsional + Integral (PI) Contoh : C(s) = Kp + Ki/s
e.Kontroller Proporsional + Integral + Differensial (PID) C(s)
Contoh : C(s) = Kp + Kd s + Ki/s Cara kompensasi :
1). serie ( umpan maju ) 2). Paralel ( umpan balik )
Beberapa macam jenis Kontroller, yang sering digunakan selain kompensator diatas : b. Jaringan Phase - Lead
c. Jaringan Phase – Lag d. Jaringan Phase Lead-Lag
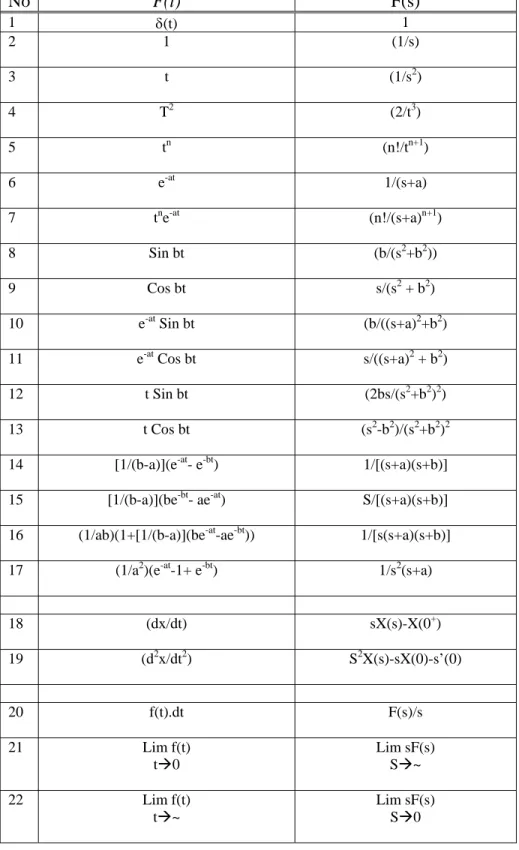
Tabel Transformasi Laplace No F(t) F(s) 1 δ(t) 1 2 1 (1/s) 3 t (1/s2) 4 T2 (2/t3) 5 tn (n!/tn+1) 6 e-at 1/(s+a) 7 tne-at (n!/(s+a)n+1) 8 Sin bt (b/(s2+b2)) 9 Cos bt s/(s2 + b2)
10 e-at Sin bt (b/((s+a)2+b2)
11 e-at Cos bt s/((s+a)2 + b2)
12 t Sin bt (2bs/(s2+b2)2)
13 t Cos bt (s2-b2)/(s2+b2)2
14 [1/(b-a)](e-at- e-bt) 1/[(s+a)(s+b)]
15 [1/(b-a)](be-bt- ae-at) S/[(s+a)(s+b)]
16 (1/ab)(1+[1/(b-a)](be-at-ae-bt)) 1/[s(s+a)(s+b)]
17 (1/a2)(e-at-1+ e-bt) 1/s2(s+a)
18 (dx/dt) sX(s)-X(0+) 19 (d2x/dt2) S2X(s)-sX(0)-s’(0) 20 f(t).dt F(s)/s 21 Lim f(t) tÆ0 Lim sF(s) SÆ~ 22 Lim f(t) tÆ~ Lim sF(s) SÆ0