BAB II
LANDASAN TEORI
2.1. Dasar – Dasar Peluang
Program stokastik adalah salah satu cabang matematika yang berhubungan dengan keputusan optimal dalam keadaan tidak pasti yang dinyatakan dengan distribusi peluang. Ruang sampel yang dinotasikan dengan Ω adalah himpunan dari hasil pengamatan yang mungkin terjadi.
Definisi 2.1.1. 𝑃 . adalah fungsi peluang jika untuk setiap 𝐴 ∈ 𝛺 dihubungkan dengan sebuah bilangan 𝑃 𝐴 sedemikian hingga 𝑃 𝐴 ≥ 0 𝑑𝑎𝑛 𝑃 𝛺 = 1.
Ruang sampel (Ω) dikatakan diskrit jika hanya mengandung terhingga banyaknya titik – titik yang dapat disusun menurut barisan sederhana 𝜔1,𝜔2,𝜔3,…. Peluang kejadian 𝐴𝑖 = 𝜔𝑖 ditulis sebagai 𝑃(𝜔1). Pada saat pengamatan dilakukan
terhadap suatu nilai berarti kita sedang mengamati sebuah variabel acak. Di dalam notasi variabel acak ditulis dengan huruf kapital, misalkan X.
Definisi 2.1.2. Suatu peubah acak X adalah suatu fungsi bernilai riil yang dihubungkan dengan daerah definisi 𝛺 untuk setiap 𝜔 ∈ 𝛺; X(𝜔) 𝜖 𝑅 = {𝑦: −∞ < 𝑦 + ∞}
Definisi 2.1.3.Jika X adalah peubah acak maka fungsi distribusinya didefinisikan sebagai berikut: 𝐹𝑥 𝑋 = 𝑃 𝑥 ≤ 𝑋 ; 𝑢𝑛𝑡𝑢𝑘 𝑠𝑒𝑡𝑖𝑎𝑝 𝑥 ∈ (−∞, +∞).
Definisi 2.1.4. Suatu peubah acak yang diskrit yang mendapat nilai
𝑥1, 𝑥2, 𝑥3, … , 𝑥𝑛 mempunyai fungsi peluang 𝑝 𝑥1), 𝑝(𝑥2 , 𝑝 𝑥3 , … , 𝑝(𝑥𝑛) dengan
𝑝 𝑥𝑖 = 𝑃 𝑋 = 𝑥𝑖 ; 𝑖 = 1,2, … , 𝑛.
2.2.Distribusi Peluang
Dalam melakukan sebuah pengamatan akan dicari nilai harapan yang dikenal dengan istilah nilai ekspektasi dari peubah acak.
Definisi 2.2.1. Nilai ekspektasi dari sebuah peubah acak adalah:
𝐸(𝑋) = 𝜇𝑥 = 𝑥𝑃𝑥(𝑥)
Penyebaran nilai dari pengamatan terhadap rata – ratanya disebut varians. Definisi 2.2.2. Varians dari sebuah peubah acak didefinisikan adalah:
𝑉𝑎𝑟(𝑋) = 𝜍2 = 𝐸((𝑋 − 𝜇𝑥)2)
Akar kuadrat nilai varians disebut sebagai deviasi standar. Definisi 2.2.3. Deviasi standar dari sebuah peubah acak adalah:
Pengamatan tidak terbatas hanya pada satu peubah acak. Misalkan dua peubah acak X dan Y memiliki rata – rata 𝐸(𝑋) = 𝜇x dan 𝐸(𝑌) = 𝜇y maka kovarians dari
peubah acak tersebut adalah:
𝐶𝑜𝑣 𝑋, 𝑌 = 𝐸((𝑋 − 𝜇𝑥)(𝑌 − 𝜇y)) = 𝐸(𝑋𝑌) −𝜇x 𝜇
y
Kovarians merupakan ukuran tentang bagaiman dua variabel bergerak atau berubah bersama – sama. Kovarians dapat bernilai positip (bergerak searah), negatif (bergerak berlawanan arah) dan nol (tidak ada hubungan antara kedua peubah acak).
2.3.Proses Stokastik
Proses stokastik berhubungan dengan waktu dari fungsi acak. Proses stokastik menunjukkan barisan waktu suatu kejadian.
Definisi 2.3.1. Proses stokastik X(t) terdiri dari sebuah pengamatan dengan peluang P(.) yang didefinisikan pada ruang sampel Ω dan dihubungkan dengan fungsi waktu 𝑥 𝑡, 𝑠 terhadap setiap ruang sampel hasil pengamatan.
Proses stokastik dapat dikategorikan menjadi dua bagian yaitu proses stokastik waktu diskrit dan proses stokastik kontinu. Proses stokastik waktu diskrit X(t) jika himpunan semua nilai yang mungkin dari X(t) sepanjang waktu t adalah himpunan berhingga, sebaliknya X(t) adalah proses stokastik waktu kontinu. Pada tulisan ini proses stokastik untuk alokasi aset multi-period terjadi pada waktu diskrit.
Keputusan penting dalam melakukan investasi baik individu maupun institusi adalah untuk memilih kelas aset yang berbeda dan keuntungan investasi. Dasar pertimbangannya adalah tingkat pengembalian (return) dan resiko dari
portfolio. Nilai return yang merupakan motivasi bagi investor untuk berinvestasi. Nilai return diperoleh dari perubahan harga aset di awal investasi terhadap harga aset di akhir periode investasi. Nilai return pada waktu t yaitu 𝑅𝑡 didefenisikan sebagai berikut:
𝑅𝑡 = ln Xt Xt−1
dengan Xt adalah harga aset pada waktu t.
2.4. Alokasi Aset Single-Period dan Multi-Period 2.4.1. Alokasi Aset Single-Period
Keputusan untuk menentukan jumlah alokasi aset dalam sebuat portfolio sangat penting bagi setiap investor. Portfolio adalah gabungan dua atau lebih kelas aset yang dipilih dalam berinvestasi. Besar modal yang diinvestasikan dalam tiap sekuritas tentu akan menentukan besar keuntungan yang akan diperoleh sesuai dengan resiko yang ditanggungnya. Kebijakan untuk menentukan portfolio optimal dengan waktu satu periode (single-period) diselesaikan dengan menggunakan metode mean-varians yang ditemukan oleh Harry Markowitz.
Harry Markowitz (1952) mengatakan return sebuah portfolio bersifat acak dan untuk mengevaluasinya perlu diperhatikan dua hal penting yakni return harapan dan resikonya. Dalam hal ini resiko direpresentasikan dengan menggunakan varians portfolio. Tingkat pengembalian (return) dari sebuah portfolio didefenisikan sebagai berikut:
𝑅𝑝𝑡 = 𝑛𝑖=1𝑊𝑖𝑅𝑖,𝑡
dengan 𝑖 = jenis aset dalam portfolio dan 𝑅𝑖,𝑡= return pada waktu t sedangkan 𝑊𝑖
Andaikan 𝑥 = 𝑥1, 𝑥2, … , 𝑥𝑛 adalah n kelas aset yang dipertimbangkan untuk sebuah portfolio dan andaikan 𝑅 = 𝑅1, 𝑅2, … , 𝑅𝑛 nilai acak return dari masing –masing kelas aset dengan rata – rata return 𝑟 = (𝑟1, 𝑟2, … , 𝑟𝑛) dan kovarians matriks = [𝜍𝑖,𝑗] dengan 𝜍𝑖,𝑗 = 𝐸(𝑅𝑖 − 𝑟𝑖) 𝑅𝑗 − 𝑟𝑗 untuk i,j = 1, 2, ..., n. Model mean – varians Markowitz situlis sebagai berikut:
Min Var (𝑅𝑇𝑥) =𝑥𝑇 𝑥 𝑒𝑇𝑥 = 1
𝑟𝑇𝑥 ≥ 𝜌 𝑥 ≥ 0
Varians dari return portfolio diminimalkan pada tingkat return harapan sebesar
𝜌.
2.4.2. Alokasi Aset Multi-Period
Investasi sering dilakukan untuk waktu jangka panjang. Waktu perencanaan investasi yang panjang dibagi dalam beberapa periode (multi-period). Kebijakan dibuat pada setiap periode sampai keseluruhan periode dalam waktu perencanaan. Kebijakan yang diambil dalam satu periode akan dipengaruh oleh kebijakan yang sebelumnya. Pada sebuah masalah alokasi aset multi-period, investasi dikategorikan dalam aset 𝑖 = 1, 2, … , 𝑛. Pengambil keputusan harus menentukan jumlah modal yang akan diinvestasikan pada setiap aset i, yaitu
𝑥𝑖,𝑡 untuk setiap periode 𝑡 = 1, 2, … , 𝑇.
Setiap periode t investor dapat membeli atau menjual aset i. Jumlah aset i yang dijual maupun yang dibeli pada saat t masing-masing dinotasikan dengan
𝑦𝑡𝑖 dan 𝑧
𝑡𝑖. Setiap investasi 𝑥𝑖,𝑡 memberikan return sebesar 𝑅𝑡 𝑖 sehingga
tidak diketahui dengan pasti. Akan tetapi distribusi peluang 𝑅𝑡 𝑖 diketahui.
Masalah ini dikenal dengan istilah “wait-and-see”.
Keputusan yang akan diambil dipengaruhi oleh proses diskrit 𝜉𝑡 𝑡=0𝑇 yang
tidak diketahui dengan pasti pada waktu keputusan tersebut diambil. Pada waktu t pengambil keputusan mengetahui 𝜔0, 𝜔1, … , 𝜔𝑡 dengan mendistribusikan peluangnya masing – masing 𝑃0, 𝑃1, … , 𝑃𝑡 dan tt=0𝑃𝑡 = 1 . Variabel keputusannya bergantung pada proses stokastik {𝜔0, 𝜔1, … , 𝜔𝑡} dan nilai ekspektasinya.
Model stokastik multi-period dapat diselesaikan dengan strategi tradisional yang dikenal dengan strategi fixed – mix dan strategi buy and hold (V. V. Kolbin, 1977). Pada strategi buy and hold tidak ada rebalancing portfolio sehingga keputusannya dititikberatkan pada keputusan awal yang dibuat. Persamaanya adalah:
𝑥0𝑖 1 + 𝑏𝑡𝑐𝑖 + 𝑥0𝑐𝑎𝑠
𝑛 −1
𝑖=1
= 𝑊0
dengan 𝑊0 adalah modal awal, 𝑛 − 1 adalah banyaknya jenis aset dalam pasar
modal dan 𝑏𝑡𝑐𝑖 adalah biaya transaksi untuk investasi pada aset i. Nilai 𝑥
𝑡𝑖 yang
diinvestasikan pada waktu t tentunya akan memberikan return sehingga antara waktu t dan t+1 diperoleh:
𝑥𝑡−1𝑖,𝜔1,…,𝜔𝑡−1𝑅 𝑡 𝑖,𝜔𝑡 = 𝑥 𝑡 𝑖,𝜔1,…,𝜔𝑡 untuk 𝑖 = 1, … , 𝑛 − 1 dan t = 1, … , T − 1
Variabel acak 𝑅𝑡 𝑖,𝜔𝑡
adalah vektor acak return dari aset jenis i antara periode waktu t dan t+1 dengan skenario 𝜔𝑡. Maka di akhir periode akan diperoleh:
𝑥𝑇−1𝑖,𝜔1,…,𝜔𝑇−1𝑅 𝑇 𝑖,𝜔𝑇 1 − 𝑠𝑡𝑐𝑖 + 𝑥 𝑇−1 𝑐𝑎𝑠 ,𝜔1,…,𝜔𝑇−1 = 𝑛−1 𝑖=1 𝑊𝑇𝜔1,…,𝜔𝑇
dengan 𝑠𝑡𝑐𝑖 adalah biaya transaksi untuk menjual aset i dan 𝑊 𝑇
𝜔1,…,𝜔𝑇
adalah hasil akhir yang diperoleh dalam skenario sepanjang waktu T. Fungsi utilitas dinyatakan dengan slack variables 𝑢𝑇𝜔1,…,𝜔𝑇 untuk tujuan yang diinginkan G dan
𝜐𝑇𝜔1,…,𝜔𝑇 untuk pengurangan tujuan sehingga:
𝑢𝑇𝜔1,…,𝜔𝑇 − 𝜐
𝑇
𝜔1,…,𝜔𝑇 = 𝑊
𝑇
𝜔1,…,𝜔𝑇 − 𝐺
Maka fungsi objektif akhir Z adalah:
𝑍 = 𝜔1,…,𝜔𝑇 𝜖Ω1×…×ΩT[𝑢𝑇𝜔 1,…,𝜔 𝑇−𝜓𝜐𝑇𝜔 1,…,𝜔 𝑇]
[ Ω1 ×…× ΩT ] ; 𝜓 adalah slope fungsi utilitas.
Pada strategi fixed – mix ada tambahan kendala pada saat pengalokasian kembali modal pada waktu t. Jadi harus ada tambahan variabel untuk menyatakan jumlah aset yang dibeli yakni 𝑦𝑖 dan jumlah aset yang dijual yakni 𝑧𝑖. Maka modal awal dapat ditulis sebagai berikut:
𝑥0𝑖 1 + 𝑏𝑡𝑐𝑖 + 𝑥0𝑐𝑎𝑠
𝑛 −1
𝑖=1
= 𝑊0
dan bagian fix – mix yakni 𝑥𝐹𝑀𝑖 :
𝑥𝐹𝑀𝑖 = 𝑥0 𝑖 𝑥0𝑖 𝑛 𝑖=1 ; 𝑖 = 1, … , 𝑛
Dalam satu tenggang waktu diperoleh: 𝑥𝑡−1𝑖,𝜔1,…,𝜔𝑡−1𝑅 𝑡 𝑖,𝜔𝑡 + 𝑦 𝑡 𝑖,𝜔1,…,𝜔𝑡 − 𝑧 𝑡 𝑖,𝜔1,…,𝜔𝑡 = 𝑥 𝑡 𝑖,𝜔1,…,𝜔𝑡; 𝑖 = 1, … , 𝑛 − 1
Maka di akhir periode akan diperoleh:
𝑥𝑐𝑎𝑠 𝑖,𝜔1,…,𝜔𝑡−1𝑅 𝑡 𝑖,𝜔𝑡 − 𝑦 𝑡 𝑖,𝜔1,…,𝜔𝑡 1 + 𝑏𝑡𝑐𝑖 + 𝑧 𝑡 𝑖,𝜔1,…,𝜔𝑡 𝑛−1 𝑖=1 1 − 𝑠𝑡𝑐𝑖 𝑛−1 𝑖=1 = 𝑥𝑡𝑐𝑎𝑠 ,𝜔1,…,𝜔𝑡
dengan 𝑦𝑡𝑖,𝜔1,…,𝜔𝑡 adalah jumlah aset i yang dibeli dengan skenario (𝜔
1,
… , 𝜔𝑡) dan 𝑧𝑡𝑖,𝜔1,…,𝜔𝑡
adalah jumlah aset i yang dijual dengan skenario (𝜔1, … , 𝜔𝑡). Selain itu, kendala fixed – mix: 𝑥𝑡𝑖,𝜔 1,…,𝜔 𝑡
𝑥𝑡𝑖,𝜔 1,…,𝜔 𝑡
𝑛 𝑖=1
= 𝑥𝐹𝑀𝑖 ; 𝑖 = 1, … , 𝑛
Persamaan akhirnya adalah:
𝑥𝑇−1𝑖,𝜔1,…,𝜔𝑇−1𝑅 𝑇 𝑖,𝜔𝑇 𝑛−1 𝑖=1 1 − 𝑠𝑡𝑐𝑖 + 𝑥 𝑇−1 𝑐𝑎𝑠 ,𝜔1,…,𝜔𝑇−1𝑅 𝑇 𝑐𝑎𝑠 ,𝜔𝑇 = 𝑊 𝑇 𝜔1,…,𝜔𝑇; 𝑢𝑇𝜔1,…,𝜔𝑇 − 𝜐 𝑇 𝜔1,…,𝜔𝑇 = 𝑊 𝑇 𝜔1,…,𝜔𝑇 − 𝐺; dan 𝑍 = 𝜔1,…,𝜔𝑇 𝜖Ω1×…×ΩT[𝑢𝑇𝜔 1,…,𝜔 𝑇−𝜓𝜐𝑇𝜔 1,…,𝜔 𝑇] [ Ω1 ×…× ΩT ]
2.5. Model Dasar Program Stokastik
Program stokastik merupakan kerangka yang umum dalam model optimasi dengan ketidakpastian. Dalam model optimasi deterministik parameter diasumsikan dengan pasti namun kenyataan yang sebenarnya di waktu yang akan datang tidak dapat ditentukan dengan pasti sehingga parameter bersifat acak.
Ketidakpastian tersebut dinyatakan dalam sebuah distribusi peluang. Model program stokastik yang umum digunakan dalam bidang keuangan adalah model program stokastik rekursif. Model program stokastik rekursif merupakan kombinasi dari model antisipatif dan adaptif (Yu, Ji dan Wang, 2003).
2.5.1. Model Antisipatif
Model antisipatif merupakan model statis yang keputusannya tidak bergantung pada pengamatan keadaan masa yang akan datang. Perencanaanya memperhitungkan semua kemungkinan yang akan terjadi di masa yang akan datang oleh karena tidak ada kesempatan untuk memperbaikinya nanti. Kelayakan model antisipatif dinyatakan dalam kendala probabilistik. Misalkan tingkat keandalan 𝛼 dinyatakan dengan 0 < 𝛼 ≤ 1, dan kendala ditulis dalam bentuk:
𝑃 𝜔 𝑓𝑗 𝑥, 𝜔 = 0, 𝑗 = 1,2, … , 𝑛 ≥ 𝛼,
Dalam hal ini x merupakan vektor variabel keputusan berdimensi m dan 𝑓𝑗: ℝ𝑚 × Ω → ℝ, 𝑗 = 1, 2, … , 𝑛. Fungsi objektifnya dapat berupa keandalan dengan tipe seperti 𝑃 𝜔 𝑓0 𝑥, 𝜔 ≤ 𝛾 , dengan 𝑓0: ℝ𝑚 × Ω → ℝ ∪ +∝ dan 𝛾 adalah
konstanta. Model antisipatif memilih kebijakan yang memenuhi karakteristik dari kendala dan fungsi tujuan.
2.5.2. Model Adaptif
Pada model adaptif, informasi yang berhubungan dengan ketidakpastian muncul secara parsial sebelum keputusan dibuat sehingga proses optimasi memerlukan pembelajaran. Misalkan 𝒜 adalah kumpulan semua informasi relevan yang tersedia dalam pengamatan yang merupakan sub bagian dari kejadian yang mungkin. Variabel keputusan x bergantung pada kejadian yang dapat diamati dan x disebut dengan istilah 𝒜 − 𝑎𝑑𝑎𝑝𝑡𝑒𝑑 (teradaptasi 𝒜) atau 𝒜 − 𝑚𝑒𝑎𝑠𝑢𝑟𝑎𝑏𝑙𝑒
Minimum 𝐸[𝑓0(𝑥 𝜔 , 𝜔)| 𝒜]
Kendala 𝐸[𝑓𝑗(𝑥 𝜔 , 𝜔)| 𝒜] = 0 𝑗 = 1, 2, … , 𝑛 𝑥 𝜔 𝜖 𝑋 hampir pasti
Pemetaan 𝑥: Ω → 𝑋 sedemikian hingga 𝑥 𝜔 menjadi 𝒜 − 𝑚𝑒𝑎𝑠𝑢𝑟𝑎𝑏𝑙𝑒. Masalah ini dapat dinyatakan dengan menyelesaikan persamaan deterministik berikut untuk semua 𝜔:
Minimum 𝐸[𝑓0(𝑥, . )| 𝒜] 𝜔
Kendala 𝐸[𝑓𝑗(𝑥, . )| 𝒜] 𝜔 = 0 𝑗 = 1, 2, … , 𝑛
𝑥 𝜖 𝑋
Ada 2 kasus ekstrim yang terjadi yakni informasi lengkap dan tidak ada informasi. Kasus pertama menghasilkan model antisipatif sedangkan kasus kedua dikenal sebagai model distribusi. Akan tetapi yang menarik adalah jika hanya sebagian informasi yang tersedia.
2.6. Model Program Stokastik Rekursif
Model rekursif yang merupakan model yang sering digunakan dalam membentuk kerangka matematika. Model ini tidak hanya mengantisipasi pengamatan di masa yang akan datang tetapi juga mempertimbangkan informasi yang ada untuk membentuk keputusan yang rekursi. Misalnya, seorang manajer portfolio mempertimbangkan pergerakan harga saham (antisipatif) sekaligus meyeimbangkan posisi portfolio dalam perubahan harga (adaptif) (Yu, Ji dan Wang, 2003).
2.6.1. Model Program Stokastik Rekursif Dua Tahap
Masalah perencanaan dan manajemen dalam ketidakpastian resiko biasanya diselesaikan dengan program stokastik dua tahap. Solusi dari program stokastik
dua tahap terdiri dari vektor deterministik dan vektor acak. Pada tahap pertama dibuat solusi tahap awal 𝑥0 kemudian vektor acak 𝜔0 ditentukan pada tahap kedua.
Fungsi program stokastik rekursif dua tahap (Two-Stage Stochastic Programming with Recourse) dapat ditulis sebagai berikut:
Minimum 𝑓 𝑥 +Ε[𝒬(𝑥, 𝜔) ]
Kendala 𝐴𝑥 = 𝑏 untuk 𝑥 ∈ ℝ+𝑚0
dengan x adalah keputusan antisipatif pada tahap pertama yang dibuat dan
𝒬 𝑥, 𝜔 adalah nilai optimal untuk semua Ω dari program non linier:
Minimum 𝓆 𝑥, 𝜔
Kendala 𝑊 𝜔 𝑦 = 𝜔 − 𝑇 𝜔 𝑥 𝑦 ∈ ℝ+𝑚1
dengan y adalah keputusan adaptive pada tahap kedua yang bergantung pada kenyataan dari vector acak tahap pertama. 𝓆 𝑥, 𝜔 dinotasikan sebagai fungsi biaya tahap kedua dan { 𝑇 𝜔 , 𝑊 𝜔 , 𝜔 | 𝜔 ∈Ω} adalah parameter model. Parameternya adalah vector acak 𝜔 yang merupakan parameter acak. T adalah matriks teknologi yang terdiri dari koefisien teknologi yang mengubah keputusan pada tahap pertama x menjadi rekursif pada masalah tahap kedua. W adalah matriks rekursif dan h adalah vektor rekursif pada tahap kedua. Secara umum model rekursif dua tahap diformulasikan sebagai berikut:
Minimum 𝑓 𝑥 +Ε min{𝓆 𝑥, 𝜔 |𝑇 𝜔 𝑥 + 𝑊 𝜔 𝑦 = 𝜔 }
Kendala 𝐴𝑥 = 𝑏 untuk 𝑥 ∈ ℝ+𝑚0 dan 𝑦 ∈ ℝ
+ 𝑚1
Model program stokastik akan lebih mudah diselesaikan bila diubah ke dalam persamaan deterministik ekuivalen.
2.6.2. Formulasi Deterministik Ekuivalen
Andaikan model program stokastik linier sebagai berikut: Minimum 𝑔0 𝑥, 𝜔
Kendala 𝑔𝑖 𝑥, 𝜔 ≤ 0, 𝑖 = 1,2, … , 𝑚 𝑥 ∈ 𝑋 ⊂ ℝ𝑛
Vektor 𝜔 adalah vektor acak yang bervariasi pada himpunan Ξ ⊂ ℝk. Lebih tepatnya lagi, andaikan ℱ adalah sebuah family dari “kejadian” yang merupakan himpunan bagian dari Ξ dan distribusi peluangnya 𝑃 pada ℱ diketahui. Akibatnya untuk setiap himpunan bagian 𝐴 ⊂ Ξ merupakan kejadian dengan 𝐴 ∈ ℱ dan peluang 𝑃 𝐴 diketahui. Selain itu, diasumsikan bahwa fungsi 𝑔𝑖 𝑥, . : Ξ → ℝ ∀𝑥, 𝑖 adalah variabel acak dan distribusi peluang 𝑃 bebas terhadap 𝑥. Akan tetapi persamaan tersebut tidak didefinisikan dengan baik dalam pengertian minimum dan kendala juga tidak jelas jika dipertimbangkan untuk mengambil keputusan 𝑥
sebelum mengetahui realisasi 𝜔. Oleh karena itu, diperlukan proses revisi model yang dikenal dengan istilah “deterministic equivalents”. Proses pembentukan model analog dengan program stokastik linier rekursif.
Prosesnya sebagai berikut:
𝑔𝑖+ 𝑥, 𝜔 = 0 jika 𝑔𝑖 𝑥, 𝜔 ≤ 0 𝑔𝑖 𝑥, 𝜔 yang lainnya
Kendala i dilanggar jika dan hanya jika 𝑔𝑖 𝑥, 𝜔 > 0 untuk keputusan x yang diberikan dan realisasi 𝜔 dari 𝑊. Akan tetapi untuk setiap kendala disediakan sebuah rekursif atau aktivitas tahap kedua yakni 𝑦𝑖 𝜔 sehingga setelah mengamati realisasi 𝜔, dipilih semacam pengganti kerugian akibat pelanggaran
kendala jika ada yang memenuhi 𝑔𝑖 𝑥, 𝜔 − 𝑦𝑖 𝜔 ≤ 0 . Usaha tersebut mengakibatkan biaya tambahan atau penalty 𝑞𝑖 untuk setiap unit. Biaya tambahan ini disebut fungsi rekursif dihitung sebagai berikut:
𝒬 𝑥, 𝜔 = min𝑦 𝑚𝑖=1𝑞𝑖𝑦𝑖 𝜔 ≥ 𝑔𝑖+ 𝑥, 𝜔 , 𝑖 = 1, 2, … , 𝑚 ,
yang menghasilkan total biaya pada tahap pertama dan biaya rekursif:
𝑓0 𝑥, 𝜔 = 𝑔0 𝑥, 𝜔 +𝒬 𝑥, 𝜔
Dalam kasus terapan, pengambil keputusan yang akan meminimumkan total biaya harapan (tahap pertama dan biaya rekursif) cukup mempertimbangkan persamaan ekuivalen deterministik program stokastik dua tahap berikut:
Minimum 𝐸[𝑓0 𝑥, 𝜔 ] = Minimum 𝐸[{𝑔0 𝑥, 𝜔 +𝒬 𝑥, 𝜔 }]
Masalah dua tahap di atas dapat diperluas menjadi model program stokastik multi tahap.
2.6.3. Model Program Stokastik Rekursif Multi Tahap
Model program stokastik tidak terbatas hanya pada formulasi dua tahap. Dalam kenyataan pengamatan sering dilakukan dalam banyak tahapan. Hal ini memungkinkan pengamatan dilakukan untuk T tahap yang berbeda. Istilah tahap menginterpretasikan periode waktu. Program stokastik menggunakan pohon skenario untuk menyatakan kejadian yang mungkin di masa akan datang. Program stokastik efektif digunakan untuk menyelesaikan model umum dengan mempertimbangkan biaya transaksi.
Pengamatan dilakukan terhadap masalah stokastik dengan T tahap yang berbeda terdapat di dalam sekumpulan informasi {𝒜𝑡}𝑡=1𝑇 dan 𝒜𝑡 ⊂ 𝒜𝑡… ⊂ 𝒜𝑡.
Andaikan vektor random Ω= Ω1xΩ2x … xΩT. Pengembangan model program stokastik rekursif multi tahap diformulasikan sebagai berikut:
Minimum 𝑓 𝑦0 + E min 𝓆1 𝑦1, 𝜔1 + ⋯E[min𝓆𝑇 𝑦𝑇, 𝜔𝑇 ]…
Kendala 𝑇1 𝜔1 𝑦0+ 𝑊1 𝜔1 𝑦1 = 1 𝜔1 ,
𝑇𝑇 𝜔𝑇 𝑦𝑇−1+ 𝑊𝑇 𝜔𝑇 𝑦𝑇 = 𝑇 𝜔𝑇
𝑦0 ∈ ℝ+𝑚0
Keputusan optimal yang diambil pada tahap 𝑡 yaitu 𝑥 𝑡 bergantung pada keputusan
pada tahap sebelumnya dan realisasi pengamatan dilakukan sampai tahap 𝑡.
Fungsi biaya pada stage 𝑡 ≥ 1 adalah:
𝒬𝑡 𝑥0, 𝑥1,…,𝑥𝑇−1, 𝜔1, … , 𝜔𝑇 = min{𝓆𝑇 𝑥𝑇 |𝑔𝑇(𝑥0, 𝑥1,…,𝑥𝑇, 𝜔1, … , 𝜔𝑇) ≤ 0}
Jadi, total biaya untuk multi-tahap
𝑓0 𝑥0, 𝜔1, … , 𝜔𝑇 =𝑔0 𝑥0 + 𝑇𝑡=1𝒬𝑡 𝑥0, 𝑥 1, … , 𝑥 𝑡−1, 𝜔1, … , 𝜔𝑇
menghasilkan persamaan deterministik ekuivalen yang menggambarkan keputusan dinamik untuk masalah program stokastik rekursif multi-tahap adalah:
2.7. Fungsi Utilitis
Fungsi utilitis merupakan ukuran integrasi nilai terhadap kemungkinan. Menurut teori utilitis Bernouli (1738) dan Von Neumann dan Morgenstern (1944), ketidakpastian dihubungkan dengan nilai rata-rata. Konsep ini umumnya diterima dalam bidang keuangan. Investor menilai kuantitas ketidakpastian berdasarkan fungsi utilitis dan maksimum utilitis harapan. Fungsi utilitis Von Neumann dan Morgenstern dari seorang investor penghindar resiko adalah fungsi konkaf. Maksimum utilitis harapan didefenisikan sebagai berikut:
Max 𝐸𝑢[𝑅𝑇𝑥] untuk 𝑥 ≥ 0
dengan 𝑢(𝑊) adalah fungsi utilitis konkaf. Fungsi utilitis dimaksimumkan pada akhir periode dan kekayaan di akhir periode adalah 𝑊 = 𝑅𝑇𝑥. Misalkan 𝑢 𝑊 =
−𝑒(−𝜆𝑊 ) (fungsi utilitis dengan resiko 𝜆) dan diasumsikan aset berdistribusi
normal multivariat (𝑅 = 𝑁 𝑟, dengani 𝑟 sebagai vektor mean 𝑟𝑒𝑡𝑢𝑟𝑛 dan
matriks kovarians). Dengan menggunakan transformasi eksponensial maka diperoleh 𝐸 −𝑒(−𝜆𝑊 ) = −𝑒(𝜆𝐸𝑊 −
𝜆 2
2 var 𝑊 ).
Fungsi utilitis Von Neumann dan Morgenstern 𝑢(𝑊) merupakan representasi perilaku investor terhadap resiko. Menurut Arrow (1971) dan Pratt (1964) koefisien resiko absolut dan relatif adalah:
ARA 𝑊 = − 𝑢′′ 𝑊
𝑢′ 𝑊 dan RRA 𝑊 = − 𝑊
𝑢′′ 𝑊
𝑢′ 𝑊
Lemma 2.7.1 Untuk suatu waktu perencanaan t dari sebuah investasi I berdistribusi normal dengan mean 𝜇 dan standard deviasi 𝜍. Andaikan U adalah fungsi utilitas eksponensial negatif dengan koefisien resiko 𝜆 > 0: 𝑈 𝑊 = −𝑒(−𝜆𝑊 ). Andaikan 𝑤
0 adalah kekayaan investor di awal periode. Maka
Bukti: Untuk investasi I berdistribusi normal dengan mean 𝜇 dan standar deviasi
𝜍 selama waktu t dan kekayaan awal 𝑊0, nilai akhir 𝑊𝑡 adalah variabel acak berdistribusi normal: 𝑊𝑡 = 𝑊0 𝜍𝑋 + 1 + 𝜇 dengan X~N[0,1] 𝐸 𝑈 𝑊𝑡 = 𝑈( ∞ −∞ 𝑊0 𝜍𝑥 + 1 + 𝜇 ) 1 2𝜋e −𝑥22 𝑑𝑥 = −e −λW0 𝜍𝑥 +1+𝜇 ∞ −∞ 1 2𝜋e −𝑥22 𝑑𝑥 = −𝑒 −λW0 1+𝜇 1 2𝜋e −𝑥22 −λW0𝜍𝑥 𝑑𝑥 ∞ −∞ = −𝑒 −λW0 1+𝜇 1 2𝜋𝑒 −12 𝑥+λW0𝜍 2+21𝜆2W02𝜍2𝑑𝑥 ∞ −∞ = −𝑒 −λW0 1+𝜇 +12𝜆2W02𝜍2 1 2𝜋𝑒 −12 𝑥+λW0𝜍 2 ∞ −∞ 𝑑𝑥 Substitusi 𝑦 = 𝑥 + λW0𝜍 = −𝑒 −λW0 1+𝜇 +12𝜆2W02𝜍2 1 2𝜋 ∞ −∞ 𝑒−12𝑦2𝑑𝑦 = −𝑒−λW0(1+𝜇−12λW0𝜍2)
Dalam melakukan investasi perlu diperhatikan efisiensi aset pada portfolio.
Teorema 2.7.1 Andaikan 𝐼1𝑑𝑎𝑛 𝐼2 adalah dua investasi dengan return berdistribusi normal sepanjang waktu t dengan mean return 𝜇1 𝑑𝑎𝑛 𝜇2 dan
standard deviasi dari return adalah 𝜍1𝑑𝑎𝑛 𝜍2 dengan kekayaan awal W0 untuk kedua kelas investasi. Maka 𝐼1𝑙𝑒𝑏𝑖 𝑒𝑓𝑖𝑠𝑖𝑒𝑛 𝑑𝑎𝑟𝑖𝑝𝑎𝑑𝑎 𝐼2 jika dan hanya jika:
Bukti: Untuk investasi I berdistribusi normal dengan mean 𝜇 dan standar deviasi
𝜍 selama waktu t dan kekayaan awal 𝑊0, nilai akhir 𝑊𝑡 adalah variabel acak berdistribusi normal:
𝑊𝑡 = 𝑊0 𝜍𝑋 + 1 + 𝜇 dengan X~N[0,1]
Untuk fungsi utilitis yang didefenisikan sebagai berikut:
𝑢 𝜇, 𝜍 = 𝐸 𝑈 𝑊𝑡 = 𝑈(𝑊0(𝜍𝑥 + 1 + 𝜇)) ∞ −∞ 1 2𝜋𝑒 −12𝑥2𝑑𝑥
Pembuktiannya dilakukan dengan menunjukkan bahwa 𝜕𝑢
𝜕𝜇 > 0 dan 𝜕𝑢 𝜕𝜍 < 0 untuk 𝜍 > 0. 𝜕𝑢 𝜕𝜇 = 𝑈 ′ ∞ −∞ 𝑊0 𝜍𝑥 + 1 + 𝜇 𝑊0 1 2𝜋𝑒 −12𝑥2 𝑑𝑥 > 0 karena 𝑈′ > 0 𝜕𝑢 𝜕𝜍= 𝑈 ′ ∞ −∞ 𝑊0 𝜍𝑥 + 1 + 𝜇 𝑊0𝑥 1 2𝜋𝑒 −12𝑥2𝑑𝑥 = 𝑈′ 0 −∞ 𝑊0 𝜍𝑥 + 1 + 𝜇 𝑊0𝑥 1 2𝜋𝑒 −12𝑥2 𝑑𝑥 + 𝑈′ ∞ 0 𝑊0 𝜍𝑥 + 1 + 𝜇 𝑊0𝑥 1 2𝜋𝑒 −12𝑥2𝑑𝑥 = 𝑈′ ∞ 0 𝑊0 𝜍 −𝑥 + 1 + 𝜇 𝑊0 −𝑥 1 2𝜋𝑒 −12 −𝑥 2 𝑑𝑥 + 𝑈′ ∞ 0 𝑊0 𝜍𝑥 + 1 + 𝜇 𝑊0𝑥 1 2𝜋𝑒 −12𝑥2 𝑑𝑥 = [𝑈′ 𝑊0 𝜍𝑥 + 1 + 𝜇 − 𝑈′ 𝑊 0 −𝜍𝑥 + 1 + 𝜇 𝑊0𝑥] ∞ 0 1 2𝜋𝑒 −12𝑥2 𝑑𝑥
𝑈′′ < 0, sehingga 𝑈′ adalah fungsi menurun maka jika 𝑎 > 𝑏 diperoleh 𝑈′ 𝑎 −
𝑈′ 𝑏 < 0. Akibatnya untuk setiap 𝜇 > 0 dan 𝜍 > 0 maka nilai dalam kurung menjadi negatif dan jika integralnya bernilai negatif maka kita telah memperoleh hasilnya.
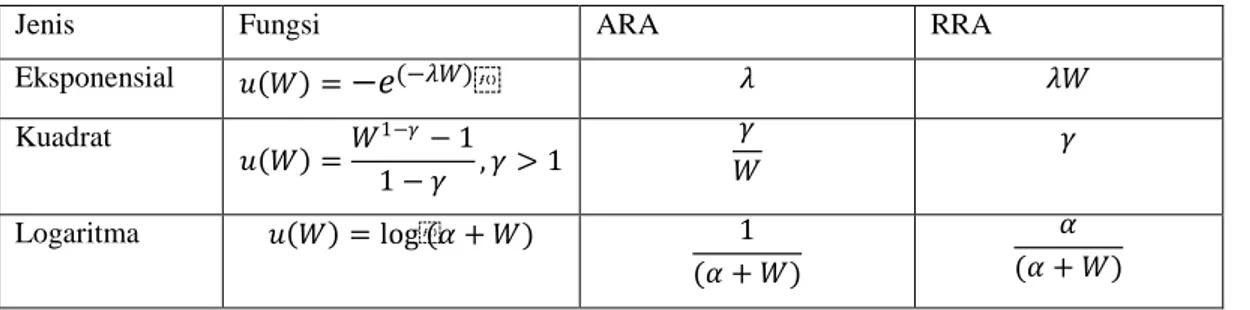
Tabel 2.7.1: Fungsi Utilitis yang umumnya digunakan (HARA)
Jenis Fungsi ARA RRA
Eksponensial 𝑢 𝑊 =−𝑒(−𝜆𝑊) 𝜆 𝜆𝑊 Kuadrat 𝑢 𝑊 =𝑊 1−𝛾− 1 1 − 𝛾 , 𝛾 > 1 𝛾 𝑊 𝛾 Logaritma 𝑢 𝑊 = log(𝛼 + 𝑊) 1 (𝛼 + 𝑊) 𝛼 (𝛼 + 𝑊)