Hello! am Fazatia Aidila I am here to give presentation as a requirement for my final project

Hello!

I am Fazatia Aidila 1212100095

I am here to give presentation as a requirement for my final project

Supervisor

Drs. M. Setijo Winarko, M.Si Drs. Lukman Hanafi, M.Sc

Jurusan Matematika

Fakultas MIPA Institut Teknologi Sepuluh Nopember Surabaya 2016

Analisa Kualitatif

pada Model SIR

dengan Fungsi

Latar Belakang

Campak, Gondong, Cacar, Polio,

Influenza Model Matematika

SIR Keterlambatan

Pengobatan

Analisa Kualitatif pada Model SIR dengan

Fungsi Pengobatan Saturasi

“

▧ Bagaimana menentukan bilangan reproduksi dasar, kestabilan dari titik kesetimbangan bebas penyakit dan endemik dari model dan adanya bifurkasi mundur serta menganalisa bifurkasi terutama bifurkasi Hopf?

▧ Bagaimana intepretasi hasil analisis dari model epidemik tipe SIR dan penyelesaian numerik dari model tersebut serta simulasinya

Batasan Masalah

Permasalahan yang dibahas pada Tugas Akhir ini akan dibatasi pada model epidemi SIR dengan fungsi pengobatan saturasi yang dinyatakan dengan 𝑇 𝐼 = _𝛼+𝐼𝑟𝐼

1. Menentukan bilangan reproduksi dasar, kestabilan dari titik kesetimbangan bebas penyakit dan kesetimbangan endemik dari model dan adanya bifurkasi mundur serta menganalisa bifurkasi terutama bifurkasi Hopf

Tujuan

2. Mengintepretasikan hasil analisis model epidemi tipe SIR dan penyelesaian numerik dari

model tersebut serta

1. Mengetahui dinamika penyebaran penyakit model epidemi tipe SIR yang dipengaruhi fungsi pengobatan saturasi

Manfaat

2. Diperoleh pengetahuan dalam mengintrepetasikan hasil analisis dan simulasi pada model epidemi tipe SIR

Penelitian Terkait

Analisa Kualitatif pada Model SIS dengan Pengobatan (2013)

Pada penelitian tersebut terjadi bifurkasi mundur pada saat 𝑅₀ < 1 yang menunjukkan bahwa pada saat 𝑅0 < 1

kapasitas pengobatan yang diberikan kurang efektif sehingga menyebabkan masih ada individu yang terinfeksi dan penyakit akan menjadi endemik

Analisis Kestabilan dan Bifurkasi Mundur pada Model Infeksi Virus Hepatitis B dan C pada Tubuh Pasien (2015)

Pada Tugas Akhir tersebut terjadi bifurkasi mundur pada saat 𝑅₀ < 1 yang menunjukkan bahwa transplantasi hati sebagai bentuk pengobatan ternyata

kurang efektif dalam

menghilangkan virus hepatitis dalam tubuh

Bilangan reproduksi dasar (𝑅0) merupakan suatu parameter

yang digunakan untuk mengetahui tingkat penyebaran suatu penyakit. Kondisi yang akan timbul sebagai berikut

▧ Jika 𝑅₀ < 1 , maka penyakit akan menghilang dalam populasi

▧ Jika 𝑅₀ = 1, maka penyakit akan menetap dalam populasi ▧ Jika 𝑅₀ > 1 , maka penyakit akan meningkat menjadi

wabah dalam populasi

Titik Kesetimbangan

Pandang persamaan diferensial sebagai berikut:

𝑑𝑥

𝑑𝑡 = 𝑓(𝑥, 𝑦) 𝑑𝑦

𝑑𝑡 = 𝑔(𝑥, 𝑦)

(2.1)

Sebuah titik 𝑥0, 𝑦0 merupakan titik kesetimbangan dari persamaan

(2.1) jika memenuhi 𝑓 𝑥0, 𝑦0 = 𝑔 𝑥0, 𝑦0 = 0 . Karena turunan

suatu konstanta sama dengan nol, maka sepasang fungsi konstan. 𝑥 𝑡 = 𝑥₀

dan

𝑦 𝑡 = 𝑦₀

adalah penyelesaian kesetimbangan dari persamaan (2.1) untuk semua 𝑡.

Kestabilan Asimtotik Lokal

Kestabilan asimtotik lokal merupakan kestabilan dari sistem linear atau kestabilan dari linearisasi sistem tak linear. Kestabilan asimtotik lokal pada titik kesetimbangan ditentukan oleh tanda pada bagian real dari akar-akar karakteristik sistem.

Persamaan Karakteristik

𝜆2 − 𝜆 𝑎 + 𝑑 + 𝑎𝑑 − 𝑏𝑐 = 0 (2.2)

Diperoleh nilai eigen sebagai berikut

𝜆_1,2 = 𝑎+𝑑 ± 𝑎+𝑑 2−4 𝑎𝑑−𝑏𝑐 . 2

Dalam hal ini 𝜆₁ + 𝜆₂ = 𝑇𝑟 𝐽 , 𝜆₁. 𝜆₂ = 𝑑𝑒𝑡(𝐽) dan ∆ = 𝑇𝑟 𝐽 − 4 det(𝐽) sehingga persamaan (2.2) dapat dinyatakan sebagai

𝜆2 − 𝑇𝑟(𝐽)𝜆 + 𝑑𝑒𝑡(𝐽) = 0 (2.3)

Tabel Kriteria Kestabilan

Nilai Eigen 𝑇𝑟 𝐽 , det 𝐽 ,Kriteria dan ∆ Nama Kestabilan 𝜆₁ > 𝜆₂ > 0 𝜆₁ < 𝜆₂ < 0 𝜆₁ = 𝜆₂ > 0 𝜆₁ = 𝜆₂ < 0 𝑇𝑟 𝐽 > 0 atau 𝑇𝑟 𝐽 < 0 𝑑𝑒𝑡(𝐽) > 0 ∆≥ 0

simpul Stabil asimtotis jika semua nilai eigen negatif,

Tidak stabil jika semua nilai eigen positif.

𝜆1 > 0 > 𝜆2

𝜆₁ < 0 < 𝜆₂

det(J) < 0

∆> 0 Sadel Tidak stabil. 𝜆₁ = 𝑎 + 𝑖𝑏

𝜆₂ = 𝑎 − 𝑖𝑏

𝑇𝑟 𝐽 > 0 atau 𝑇𝑟 𝐽 < 0

𝑑𝑒𝑡(𝐽) > 0

spiral Stabil asimtotis jika bagian real nilai eigen negatif,

Tidak stabil jika bagian real nilai eigen positif.

𝜆₁ = 𝑖𝑏 𝜆₂ = −𝑖𝑏 𝑇𝑟 𝐽 = 0 𝑑𝑒𝑡(𝐽) = 0 ∆≤ 0 Pusat Stabil.

Bifurkasi Mundur

Kurva Bifurkasi Mundur mempunyai titik kesetimbangan bebas penyakit yang stabil serta 2 titik kesetimbangan endemik yang tidak stabil dan stabil ketika 𝑅0 < 1 .

Sedangkan ketika 𝑅0 > 1

kurva mempunyai titik kesetimbangan bebas penyakit tidak stabil dan titik kesetimbangan endemik yang stabil.

Bifurkasi Hopf

Teorema 2.2

Diberikan suatu sistem dinamik

𝑥 = 𝑓 𝑥, 𝑦, 𝜇

𝑦 = 𝑔 𝑥, 𝑦, 𝜇 (2.4)

dimana μ merupakan parameter dengan 𝑓 0,0, 𝜇 = 0 dan 𝑔 0,0, 𝜇 = 0

andaikan syarat berikut terpenuhi Matriks Jacobian 𝐽 = 𝜕𝑓 𝜕𝑥 𝜕𝑓 𝜕𝑦 𝜕𝑔 𝜕𝑥 𝜕𝑦 𝜕𝑦

yang dihitung pada titik kesetimbangan x, y = (0,0) pada saat μ = 0

mempunyai sepasang eigen value imaginer murni.

Jika eigen value 𝜆 𝜇 = 𝑎 𝜇 ± 𝑖𝛽(𝜇) dengan 𝑎 0 = 0 dan 𝛽(0) ≠ 0) dari

titik (0,0) berlaku syarat transversal sebagai berikut

𝑑

Indeks Stabilitas

Stabilitas dari orbit priodik dicari dengan menggunakan rumus berikut

𝛤 = 1 16 𝜕3𝑓 𝜕𝑥3 + 𝜕3𝑔 𝜕𝑥2𝜕𝑦 + 𝜕3𝑓 𝜕𝑥𝜕𝑦2 + 𝜕3𝑔 𝜕𝑦3 + 1 16𝐷 𝜕2𝑓 𝜕𝑥𝜕𝑦 𝜕2𝑓 𝜕𝑥2 + 𝜕2𝑓 𝜕𝑦2 − 𝜕2𝑔 𝜕𝑥𝜕𝑦 𝜕2𝑔 𝜕𝑥2 + 𝜕2𝑔 𝜕𝑦2 − 𝜕2𝑓 𝜕𝑥2 𝜕2𝑔 𝜕𝑥2 + 𝜕2𝑓 𝜕𝑦2 𝜕2𝑔 𝜕𝑦2

yang disebut indeks stabilitas dan dihitung pada titik (0,0) dengan μ = 0. Jika Γ > 0 orbit periodik tak stabil dan jika Γ < 0 maka orbit periodik stabil.

Metode Runge Kutta

Persamaan diferensial (2.1) 𝑑𝑥 𝑑𝑡 = 𝑓 𝑥, 𝑦 𝑑𝑦 𝑑𝑡 = 𝑔 𝑥, 𝑦

dapat diselesaikan dengan metode numerik Runge-Kutta, sehingga didapat penyelesaian numerik dalam bentuk persamaan (i) dan (ii) sebagai berikut

𝑥_𝑛+1 = 𝑥_𝑛+1 6(𝑘1,𝑥 + 2𝑘2,𝑥+ 2𝑘3,𝑥 + 𝑘4,𝑥) (i) dengan 𝑘1,𝑥 = 𝑕𝑓 (𝑡𝑛, 𝑥𝑛) 𝑘2,𝑥 = 𝑕𝑓(𝑡𝑛+ 𝑕 2, 𝑥𝑛 + 𝑘1,𝑥 2 ) 𝑘_3,𝑥 = 𝑕𝑓(𝑡_𝑛+𝑕 2, 𝑥𝑛 + 𝑘_2,𝑥 2 ) 𝑘_4,𝑥 = 𝑕𝑓(𝑡_𝑛 + 𝑕, 𝑥_𝑛 + 𝑘_3,𝑥) 𝑦𝑛+1 = 𝑦𝑛 + 1 6(𝑘1,𝑦 + 2𝑘2,𝑦+ 2𝑘3,𝑦 + 𝑘4,𝑦) (ii) dengan 𝑘_1,𝑦 = 𝑕𝑓 (𝑡_𝑛, 𝑦_𝑛) 𝑘_2,𝑦 = 𝑕𝑓(𝑡_𝑛+𝑕 2, 𝑦𝑛 + 𝑘_1,𝑦 2 ) 𝑘_3,𝑦 = 𝑕𝑓(𝑡_𝑛 +𝑕 2, 𝑦𝑛 + 𝑘2,𝑦 2 ) 𝑘_4,𝑦 = 𝑕𝑓(𝑡_𝑛 + 𝑕, 𝑦_𝑛 + 𝑘_3,𝑦)

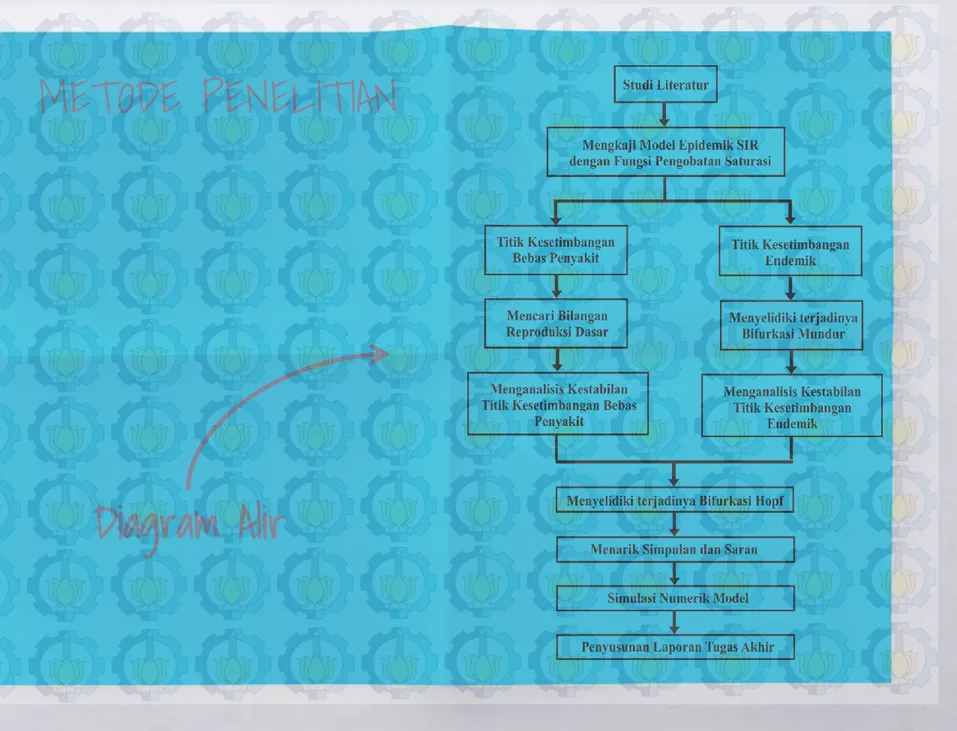
Diagram Alir

Model Epidemi SIR dengan Fungsi Pengobatan

Saturasi

Model epidemi setelah direduksi

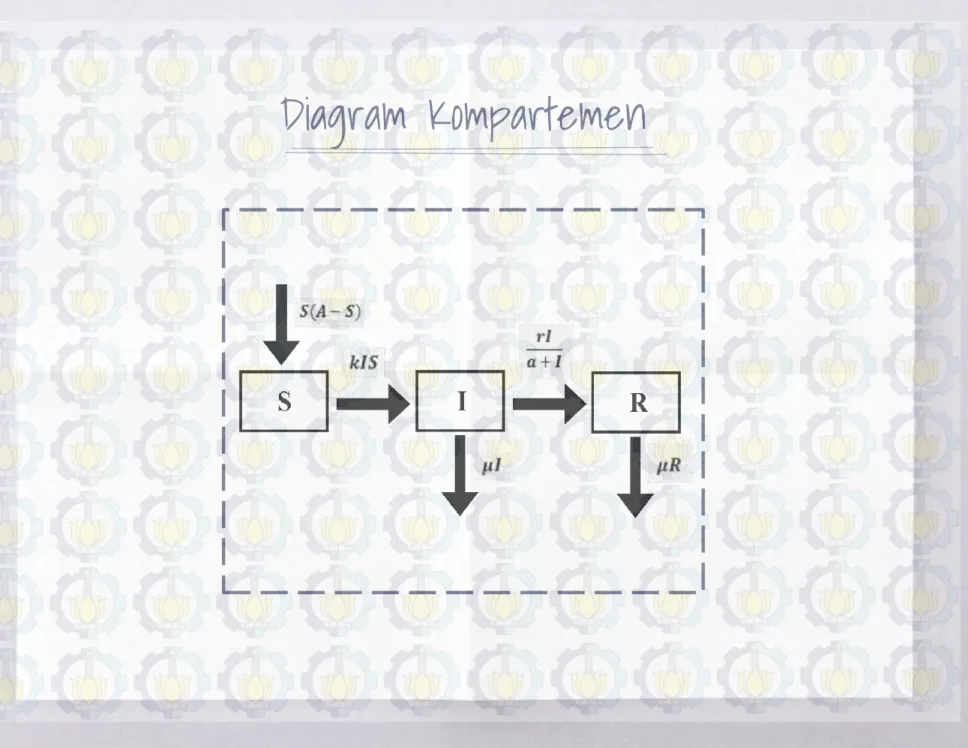
𝑑𝑆 𝑑𝑡 = 𝑆 𝐴 − 𝑆 − 𝑘𝐼𝑆 𝑑𝐼 𝑑𝑡 = 𝑘𝐼𝑆 − 𝜇𝐼 − 𝑟𝐼 𝑎+𝐼 (4.2) dengan kondisi awal

𝑆 0 > 0, 𝐼 0 > 0 Model epidemi SIR dengan fungsi

pengobatan saturasi 𝑑𝑆 𝑑𝑡 = 𝑆 𝐴 − 𝑆 − 𝑘𝐼𝑆 𝑑𝐼 𝑑𝑡 = 𝑘𝐼𝑆 − 𝜇𝐼 − 𝑟𝐼 𝑎+𝐼 (4.1) 𝑑𝑅 𝑑𝑡 = 𝑟𝐼 𝑎+𝐼 − 𝜇𝑅

Daerah Penyelesaian

Daerah untuk sistem Persamaan (4.1) adalah

𝛺 = 0 ≤ 𝑆 𝑡 ≤ 𝑀1, 0 ≤ 𝑆 𝑡 + 𝐼 𝑡 + 𝑅 𝑡 ≤ 𝐴+𝜇

𝜇 𝑀1, 𝐼 𝑡 ≥ 0, 𝑅(𝑡) ≥ 0

karena kondisi awal bernilai positif maka 𝛺 merupakan daerah invarian positif yang artinya semua penyelesaian berada di dalam 𝛺.

Titik Kesetimbangan Bebas Penyakit dan Bilangan

Reproduksi Dasar

Titik Kesetimbangan Bebas Penyakit

𝐸₁ = 𝑆₀, 𝐼₀ = 𝐴, 0

Bilangan Reproduksi Dasar

𝑅0 = 𝑘𝐴 𝜇+𝑟

𝛼

Kestabilan Titik Kesetimbangan Bebas Penyakit

Teorema 4.3.1

Titik bebas penyakit 𝐸₁ stabil asimtotis lokal jka 𝑅₀ < 1 dan tidak stabil

jika 𝑅₀ > 1. Bukti :

Berdasarkan nilai eigen yang telah diperoleh pada sistem (4.2)

𝜆₃ < 0 , dan 𝜆₄ < 0 ⟺ 𝜇 + 𝑟 𝛼 𝑅0 − 1 < 0 ⟺ 𝑅₀ − 1 < 0 ⟺ 𝑅₀ < 1

hal ini membuktikan jika 𝑅0 < 1 maka titik kesetimbangan bebas

penyakit 𝐸1= 𝐴, 0 stabil asimtotis lokal, sebaliknya jika 𝑅0 > 1 titik

Titik Kesetimbangan Endemik

Titik Kesetimbangan Endemik

Berdasarkan Persamaan (4.2) diperoleh

𝑆2 − 𝛼𝑘 + 𝐴 +𝑢 𝑘 𝑆 + 𝑢 𝑘 𝛼𝑘 + 𝐴 + 𝑟 = 0 (4.20) dengan 𝑅₀ ≥ 1 − 𝛼2𝑘2+𝑟 𝜇𝛼+𝑟 + 2𝛼𝑘 𝑟 𝜇𝛼+𝑟 ≔ 𝑝0

diperoleh penyelesaian positif dari (4.20)

𝑆₁ = 𝛼𝑘+𝐴+ 𝑢 𝑘+ ∆ 2 dan 𝑆2 = 𝛼𝑘+𝐴+𝑢 𝑘− ∆ 2

Selanjutnya jika 𝑆₁ < 𝐴 maka 𝑅₀ > 1 + 𝛼2𝑘2−𝑟

𝜇𝛼+𝑟 ≔ 𝑝1 dan 𝑅0 < 1

dan jika 𝑆₂ < 𝐴 maka 𝑅₀ > 1 + 𝛼2𝑘2−𝑟

Titik Kesetimbangan Endemik

Perhatikan bahwa 𝛼𝑘 < 𝑟 ekivalen dengan 𝑝₁ < 1.

Sehingga ketika 𝑅₀ ≥ 𝑝₀, dapat disimpulkan

▧ Jika 𝛼𝑘 < 𝑟, maka sistem (4.2) memiliki dua titik kesetimbangan

endemik 𝐸₁ = (𝑆₁, 𝐼₁) dan 𝐸₂ = (𝑆₂, 𝐼₂) pada saat 𝑅₀ < 1.

▧ Jika 𝛼𝑘 < 𝑟, maka sistem (4.2) memiliki titik kesetimbangan endemik

tunggal 𝐸₂ = (𝑆₂, 𝐼₂) pada saat 𝑅₀ > 1, dan titik kesetimbangan

endemik 𝐸₁ tidak ada karena 𝑝₁ < 𝑅₀ < 1 tidak berlaku.

▧ Misalkan 𝛼𝑘 ≥ 𝑟, maka 𝑝₁ ≥ 1, sehingga titik kesetimbangan

endemik 𝐸₁ tidak ada. Kemudian ketika 𝑅₀ > 1 terdapat titik

kesetimbangan endemik tunggal 𝐸₂ = 𝑆₂, 𝐼₂ dan tidak ada titik

Teorema 4.4.1

Pada sistem Persamaan (4.2) terjadi bifurkasi mundur dengan titik kesetimbangan endemik 𝑬𝟏 dan 𝑬𝟐 pada saat 𝑹𝟎 < 𝟏 dan

𝜶𝒌 < 𝒓

Kestabilan Titik Kesetimbangan Endemik

▧ Kestabilan Titik Kesetimbangan Endemik untuk 𝑅₀ = 𝑅_𝑐 𝐸₀ = 𝑆₀, 𝐼₀ = 𝐴+𝛼𝑘+ 𝜇 𝑘 2 , 𝐴−𝛼𝑘−𝜇 𝑘 2

diperoleh 𝑑𝑒𝑡(𝐽(𝐸₀) < 0 sehingga 𝐸₀ tidak stabil (saddle)

▧ Kestabilan Titik Kesetimbangan Endemik untuk 𝑅_𝑐 < 𝑅₀ < 1 𝐸1 = (𝑆1, 𝐼1) = 𝐴+𝛼𝑘+𝜇 𝑘+ ∆ 2 , 𝐴−𝛼𝑘−𝜇 𝑘− ∆ 2𝑘

diperoleh 𝑑𝑒𝑡(𝐽(𝐸1) < 0 sehingga 𝐸1 tidak stabil (saddle)

𝐸₂ = 𝑆₂, 𝐼₂ = 𝐴+𝛼𝑘+ 𝜇 𝑘− ∆ 2 , 𝐴−𝛼𝑘−𝜇 𝑘+ ∆ 2𝑘

diperoleh 𝑑𝑒𝑡(𝐽 𝐸₂ > 0 sehingga 𝐸₂ merupakan simpul atau spiral.

Kemudian didapat 𝑡𝑟 𝐽 𝐸₂ = 𝑟𝐼2

Kestabilan Titik Kesetimbangan Endemik

selanjutnya misalkan (𝐻₁) ∆₄₄= 𝑘 − 1 𝐴 − 𝜇 + 𝛼𝑘 2 +4𝛼𝐴 1 − 𝑘 𝑘 > 0 dan didefinisikan 𝐻 ≜ 𝛼𝑘2 𝑘−1− 𝜇 𝑘 𝑘−1 − 𝑘−1 𝐴−𝜇+𝛼𝑘_(𝑘−1)2+4𝛼𝐴 1−𝑘 𝑘

maka kestabilan titik kesetimbangan endemik 𝐸2 dinyatakan dalam

teorema berikut

Teorema 4.4.2 misalkan

𝛼𝑘 < 𝑟, 𝑝₁ < 𝑅₀ < 1 dan (𝐻₁) ada, maka untuk sistem

Persamaan (4.2) mempunyai ▧ 𝐸₂ stabil jika 𝑘 − 1 𝐴 − 𝜇 + 𝛼𝑘 ≤ 0 atau 𝑘 − 1 𝐴 − 𝜇 + 𝛼𝑘 > 0 𝑟 < 1 4 𝐴 + 𝛼𝑘 − 𝜇 𝑘 2 − 𝐻2 ▧ 𝐸₂ tidak stabil jika

𝑘 − 1 𝐴 − 𝜇 + 𝛼𝑘 > 0 𝑟 > 1 4 𝐴 + 𝛼𝑘 − 𝜇 𝑘 2 − 𝐻2

Bifurkasi Hopf

Teorema 4.4.3

Misalkan 𝑎𝑘 < 𝑟, 𝑝₁ < 𝑅₀ < 1. Maka pada sistem (4.2) terjadi

bifurkasi Hopf jika 𝐻1 , 𝑘 − 1 𝐴 − 𝜇 + 𝛼𝑘 > 0, dan

𝐼₂ = 𝑘−1 𝐴−𝜇+𝛼𝑘

2𝑘(𝑘−1) 1 − 1 +

4𝛼𝐴 1−𝑘 𝑘

𝑘−1 𝐴−𝜇+𝛼𝑘 2 berlaku Selanjutnya jika

𝜎 < 0 orbit periodik dari sistem (4.2) stabil sehingga terjadi bifurkasi

Hopf superkritikal. Dan jika 𝜎 > 0, orbit periodik dari sistem (4.2)

Bifurkasi Hopf

Bukti Bedasarkan sistem (4.2) 𝑑𝑆 𝑑𝑡 = 𝑆 𝐴 − 𝑆 − 𝑘𝐼𝑆 𝑑𝐼 𝑑𝑡 = 𝑘𝐼𝑆 − 𝜇𝐼 − 𝑟 𝛼+𝐼

didapatkan salah satu titik kesetimbangan 𝐸₂ = (𝑆₂, 𝐼₂) dan matriks

Jacobian 𝐸₂ diketahui sebagai berikut 𝐽 𝐸₂ = −𝑆2 −𝑘𝑆2 𝑘𝐼₂ 𝑟𝐼2 𝛼+𝐼₂ 2 Selanjutnya diperoleh 𝜆_1,2 = 𝑡𝑟(𝐽(𝐸2) ± 𝑡𝑟(𝐽(𝐸2) 2−4𝑑𝑒𝑡(𝐽(𝐸2)) 2

Bifurkasi Hopf

Bifurkasi Hopf terjadi apabila matriks Jacobian mempunyai sepasang nilai eigen yang imajiner murni. Kedua nilai eigen imajiner murni jika dan hanya jika 𝑡𝑟(𝐽(𝐸₂) = 0. Pada pembahasan sebelumnya diketahui

bahwa 𝑡𝑟(𝐽 𝐸₂ ) = 0 jika hanya jika (𝐻₁), 𝑘 − 1 𝐴 − 𝜇 + 𝛼𝑘 > 0, dan 𝐼2 =

𝑘−1 𝐴−𝜇+𝛼𝑘

2𝑘(𝑘−1) 1 − 1 +

4𝛼𝐴 1−𝑘 𝑘

𝑘−1 𝐴−𝜇+𝛼𝑘 2 berlaku. Maka terjadi

bifurkasi Hopf dengan syarat transversal

𝑑 𝑑𝑟 𝑅𝑒 𝜆 𝐽(𝐸2) _𝑟=1 4 𝛼𝑘+𝐴− 𝑢 𝑘 2 −𝐻2 = 𝐼₂ 2 𝛼+𝐼₂ 2 ≠ 0

Bifurkasi Hopf

Selanjutnya ditentukan bentuk normal bifurkasi Hopf dengan melakukan translasi titik kesetimbangan (𝑆₂, 𝐼₂) ke titik (0,0) dengan melakukan

transformasi 𝑥 = 𝑆 − 𝑆₂, 𝑦 = 𝐼 − 𝐼₂ dan 𝑑𝜏 = 𝑑𝑡 𝛼+𝑦+𝐼2 , sehingga diperoleh 𝑑𝑥 𝑑𝜏 = 𝛼 + 𝑦 + 𝐼2 [(𝐴 − 2𝑆2 − 𝑘𝐼2)𝑥 − 𝑘𝑆2𝑦 − 𝑘𝑥𝑦 − 𝑥 2_] 𝑑𝑦 𝑑𝜏 = 𝑘𝑥𝑦 + 𝑘𝑆2 − 𝑢 𝑦 + 𝑘𝐼2𝑥 𝛼 + 𝑦 + 𝐼2 − 𝑟𝛼𝑦 𝛼+𝐼2

Kemudian untuk memudahkan, maka dimisalkan 𝑥 = 𝑆, 𝑦 = 𝐼 dan 𝜏 = 𝑡,

didapat 𝑑𝑆 𝑑𝑡 = 𝛼 + 𝐼 + 𝐼2 [(𝐴 − 2𝑆2 − 𝑘𝐼2)𝑆 − 𝑘𝑆2𝐼 − 𝑘𝑆𝐼 − 𝑆 2_] 𝑑𝐼 𝑑𝑡 = 𝑘𝑆𝐼 + 𝑘𝑆2 − 𝑢 𝐼 + 𝑘𝐼2𝑆 𝛼 + 𝐼 + 𝐼2 − 𝑟𝛼𝐼 𝛼+𝐼₂

Bifurkasi Hopf

Berdasarkan Persamaan (4.2) dan 𝑡𝑟 𝐽 𝐸2 = 0, diperoleh

𝐴 − 𝑆₂ − 𝑘𝐼₂ = 0, 𝑘𝑆₂ − 𝑢 − 𝑟

𝛼+𝐼₂ = 0, dan 𝑟𝐼2 − 𝑆2 𝛼 + 𝐼2

2 _{= 0}

sehingga persamaan 𝑑𝑆_𝑑𝑡 dan 𝑑𝐼_𝑑𝑡 menjadi

𝑑𝑆 𝑑𝑡 = −𝑆2 𝛼 + 𝐼2 𝑆 − 𝑘𝑆2 𝛼 + 𝐼2 𝐼 − 𝑘𝛼 + 𝐴 𝑆𝐼 − 𝛼 + 𝐼2 𝑆 2 −𝑘𝑆2𝐼2 − 𝑘𝑆𝐼2 − 𝑆2𝐼 (4.58) 𝑑𝐼 𝑑𝑡 = 𝑘𝐼2 𝛼 + 𝐼2 𝑆 + 𝑆2 𝛼 + 𝐼2 𝐼 + 𝑘 𝛼 + 2𝐼2 𝑆𝐼 + 𝑟𝐼2 𝛼+𝐼2+ 𝑘𝑆𝐼 2 (4.59)

Bifurkasi Hopf

Kemudian membentuk persamaan (4.58) dan (4.59) dalam bentuk matriks

𝑑𝑆 𝑑𝑡 𝑑𝐼 𝑑𝑡 = −𝑚 −𝑘𝑚 𝑝 𝑚 𝑆 𝐼 + 𝑔 𝑕 (4.60) dengan 𝑚 = 𝑆₂ 𝛼 + 𝐼₂ 𝑝 = 𝑘𝐼₂ 𝛼 + 𝐼₂ 𝑔 = − 𝑘𝛼 + 𝐴 𝑆𝐼 − 𝛼 + 𝐼₂ 𝑆2 − 𝑘𝑆₂𝐼2 − 𝑘𝑆𝐼2 − 𝑆2𝐼 𝑕 = 𝑘 𝛼 + 2𝐼₂ 𝑆𝐼 + 𝑟𝐼2 𝛼+𝐼2+ 𝑘𝑆𝐼 2

Bifurkasi Hopf

Selanjutnya dengan mencari matriks Jacobian dari persamaan (4.58) dan (4.59) dan subtitusi titik kesetimbangan (0,0) diperoleh matriks

Jacobian

𝐽 = −𝑚 −𝑘𝑚 𝑝 𝑚

dari matriks Jacobian di atas diperoleh nilai persamaan karakteristik

𝜆 2 − 𝑚2 + 𝑝𝑘𝑚 = 0 𝜆 2 + 𝑑𝑒𝑡 𝐽 𝐸₂ = 0

𝜆 = ±𝑖 𝑑𝑒𝑡 𝐽 𝐸2 = ±𝑖𝜔

dengan permisalan

Bifurkasi Hopf

Berikutnya dengan subtitusi

𝑆 = 𝑥 𝑝− 𝑚𝑦 𝑝𝜔 dan 𝐼 = 𝑦 𝜔

ke matriks (4.60) maka matriksnya menjadi 𝑑𝑥 𝑑𝑡 𝑑𝑦 𝑑𝑡 = 0 −𝜔 𝜔 0 𝑥 𝑦 + 𝑓(𝑥, 𝑦) 𝑔(𝑥, 𝑦)

dan bentuk Normal Bifurkasi Hopf sebagai berikut 𝑑𝑥 𝑑𝑡 = −𝜔𝑦 + 𝑓(𝑥, 𝑦) 𝑑𝑦 𝑑𝑡 = 𝜔𝑥 + 𝑔(𝑥, 𝑦) dengan 𝑓 𝑥, 𝑦 = 2𝑚 𝛼+𝐼₂ −𝑝 𝑘𝛼+𝐴 −𝑚𝑘 𝛼+2𝐼₂ 𝑝𝜔 𝑥𝑦 + 𝑝𝑚 𝑘𝛼+𝐴 −𝑘𝑆₂𝑝2− 𝛼+𝐼₂ 𝑚2−𝑘𝐼₂𝑚2 𝑝𝜔2 𝑦 2 ₋ 𝛼+𝐼2 𝑝 𝑥 2₋ 1 𝑝𝜔𝑥 2_{𝑦 +} 2𝑚−𝑝𝑘+𝑚𝑘 𝑝𝜔2 𝑥𝑦 2 ₊ 𝜔2−𝑘𝑚2 𝑝𝜔3 𝑦 3 dan 𝑔 𝑥, 𝑦 = 𝑘 𝛼+2𝐼₂ 𝑝 𝑥𝑦 − 𝑘𝑚𝐼₂ 𝑝𝜔 𝑦 2₊ 𝑘 𝑝𝜔𝑥𝑦 2 ₋ 𝑘𝑚 𝑝𝜔2𝑦 3

Bifurkasi Hopf

Untuk menyelidiki jenis bifukasi Hopf yang terjadi menggunakan indeks stabilitas Γ = 1 16 𝑓𝑥𝑥𝑥 + 𝑓𝑥𝑦𝑦 + 𝑔𝑥𝑥𝑦 + 𝑔𝑦𝑦𝑦 + _16𝜔1 𝑓_𝑥𝑦 𝑓_𝑥𝑥 + 𝑓_𝑦𝑦 − 𝑔_𝑥𝑦 𝑔_𝑥𝑥 + 𝑔_𝑦𝑦 − 𝑓_𝑥𝑥𝑔_𝑥𝑥 + 𝑓_𝑦𝑦𝑔_𝑦𝑦 (0.0) dan diperoleh Γ = 2𝑘 𝑎+𝐼2 3𝑆2𝐼2 16𝑝2𝜔4 𝜎 dengan 𝜎 = [ 𝑎 + 𝐼₂ (𝑆₂ 2𝑘2 + 𝑘 + 2 + 𝑘3𝐼₂) − 𝑘2𝐼₂ 𝑘𝑎 + 𝐴 −2𝑘2𝑆₂𝐼₂] −𝑘𝐼₂ + 𝑎 + 𝐼₂ −2 − 𝑎𝑘 + 𝑆₂ 𝑘𝑆₂ − 2𝑆₂2) + 𝑘𝑎 + 𝐴 𝑆₂ −2𝑎 − 2𝐼₂ + 𝑎𝑘 −2𝑘𝑆22 𝑎 + 2𝐼2 + 2𝑘𝑆 𝐼22 2

Berdasarkan Gambar dengan parameter 𝐴 = 2.6, 𝜇 = 0.2, 𝑘 = 2, 𝑎 = 0.05, 𝑟 = 0.11 terlihat adanya orbit periodik stabil dengan

nilai Γ = −0.9891 < 0, sehingga dapat disimpulkan terjadi bifurkasi

Hopf superkritikal.

Analisis Kestabilan Titik Kesetimbangan ketika 𝑅0 < 1.

𝐴 = 2, 𝜇 = 0.2, 𝑘 = 0.8, 𝑎 = 0.55, 𝑟 = 1.2

Analisis Kestabilan Titik Kesetimbangan ketika 𝑅0 > 1.

𝐴 = 2, 𝜇 = 0.2, 𝑘 = 2, 𝑎 = 0.9, 𝑟 = 0.25

KESIMPULAN

▧ Pada saat terjadi Bifurkasi Maju, Bilangan Reproduksi Dasar adalah 𝑅₀ = 𝑘𝐴

𝜇+𝑟 𝛼

dengan titik kesetimbangan bebas penyakit 𝐸₁ = 𝑆₀, 𝐼₀ = 𝐴, 0

dan titik kesetimbangan endemik yang stabil 𝐸₂ = 𝑆₂, 𝐼₂ = 𝐴+𝛼𝑘+ 𝜇 𝑘− ∆ 2 , 𝐴−𝛼𝑘−𝜇 𝑘+ ∆ 2𝑘

Titik kesetimbangan bebas penyakit stabil asimtotik ketika 𝑅0 < 1, dan

KESIMPULAN

▧ Pada saat terjadi Bifurkasi Mundur, Bilangan Reproduksi Dasar adalah 𝑅𝑐 =

𝑘𝐴𝑐 𝜇+𝑟

𝛼

dengan titik kesetimbangan bebas penyakit 𝐸1 = 𝑆0, 𝐼0 = 𝐴, 0

dan titik kesetimbangan endemik sebagai berikut: Pada saat 𝑅0 = 𝑅𝑐 𝐸₀ = 𝑆₀, 𝐼₀ = 𝐴+𝛼𝑘+ 𝜇 𝑘 2 , 𝐴−𝛼𝑘−𝜇 𝑘 2

yang merupakan titik pelana (saddle point) yang tidak stabil.

. Pada saat 𝑅𝑐 < 𝑅0 < 1 𝐸₁ = 𝑆₁, 𝐼₁ = 𝐴+𝛼𝑘+𝜇 𝑘+ ∆ 2 , 𝐴−𝛼𝑘−𝜇 𝑘− ∆ 2𝑘

𝐸₁ merupakan titik pelana (saddle point) yang tidak stabil,

𝐸₂ = 𝑆₂, 𝐼₂ = 𝐴+𝛼𝑘+𝜇 𝑘− ∆ 2 , 𝐴−𝛼𝑘−𝜇 𝑘+ ∆ 2𝑘 𝐸₂ stabil jika 𝑟 < 1 4 𝛼𝑘 + 𝐴 − 𝑢 𝑘 2 − 𝐻2 dan tidak stabil jika 𝑟 > 1₄ 𝛼𝑘 + 𝐴 −𝑢 𝑘 2 − 𝐻2 .

KESIMPULAN

▧ Pada saat laju pengobatan 𝑟 = 1

4 𝛼𝑘 + 𝐴 −

𝑢 𝑘

2

− 𝐻2 terdapat sepasang nilai eigen yang imajiner murni yang menyebabkan adanya bifurkasi Hopf. Untuk σ < 0 terjadi bifurkasi Hopf superkritikal dan pada saat σ > 0 terjadi bifurkasi Hopf subkritikal.

▧ Dengan metode Numerik Runge-Kutta orde 4 menggunakan software MATLAB diperoleh hasil bahwa jika 𝑅0 < 1, maka terjadi keadaan

bebas penyakit karena kestabilan sistem menuju titik kesetimbangan bebas penyakit 𝐸1. Kemudian jika 𝑅0 > 1, maka penyakit menjadi

endemik karena kestabilan sistem menuju titik kesetimbangan endemik.

Daftar Pustaka

[1] Nugroho, Susilo. (2009). “pengaruh Vaksinasi Terhadap Penyebaran Penyakit dengan Model Epidemik SIR”. Tugas Akhir S1 Jurusan Matematika Unversitas Sebelas Maret.

[2] WHO(World Health Organization), Country Health Profile, http://www.who.int/countries/idn/en/. Diakses pada tanggal 4 September 2015, pukul 00.18 WIB.

[3] Iktisholiyah. (2010). “Analisis Stabilitas dan Optimal Kontrol pada Model Epidemik Tipe SIR dengan Vaksinasi”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[4] Zhang,X,dkk. (2008). “Backward Bifurcation of an Epidemik Model with Saturated Treatment Function”. Journal of Mathematical Analysis and Application, Vol 340, No. 1, pp 433-443.

[5] Lestari, Intan P. (2012). “Eksistensi Bifurkasi Mundur pada Model Penyebaran Penyakit Menular dengan Vaksinasi”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[6] Iswahyuni, N. (2013). “Analisa Kualitatif pada Model Epidemik SIS dengan Pengobatan”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[7] Musa, M. (2015). “Analisis Kestabilan dan Bifurkasi Mundur pada Model Infeksi Virus Hepatitis B dan C pada Tubuh Pasien”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[8] Jordan, D. W and Smith P. 2007. “Nonlinier Ordinary Differential Equations”. NewYork: Oxford University Press.

Daftar Pustaka

[9] Subiono. 2013. Sistem Linear dan Kontrol Optimal. Surabaya. Subiono Jurusan Matematika ITS Surabaya.

[10] Anton H, Rorres C. 2005. Elementary Linear Algebra 9th _{edition. John Wiley & Sons, Inc.}

[11] Nara. (2014). “Analisa Kualitatif pada Model Penyakit Parasitosis”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[12] Castilo, C. dan Chavez. (2004). “Dynamical Models of Tubercolosis and Their Aplications”. [13] Zulminarni. (2007). “Analisa Kualitatif pada Model Penyakit Parasitosis”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[14] Novitasari, Y. (2009). “Menunjukan Eksistensi Orbit Periodik dari Sistem dinamik dengan menggunakan Bifurkasi Hopf”. Tugas Akhir S1 Jurusan Matematika ITS Surabaya.

[15] Hirsch, M. (2004). “Diffrential Equations Dynamical Systems and an Introduction to Chaos” [16] Wang, J,dkk. (2011). “Qualitative and Bifurcation Analysis Using an SIR Model with a Saturated Treatment Function”. Journal of Mathematicaland Computer Modelling, Vol 55, pp 710-722.