Mendeskripsikan Himpunan

3

Himpunan

• Himpunan adalah koleksi tak terurut dari obyek, yang disebut anggota himpunan

• Notasi.

– aA : a adalah anggota himpunan A – aA : a bukan anggota himpunan A

• Contoh 1.

– Himpunan bilangan bulat yang terdiri dari 1 digit – Himpunan bilangan bulat tak negatif

– Himpunan muka dadu

– Himpunan muka uang logam

– Himpunan mahasiswa yang terdaftar di MA2151 K-01

Notasi Himpunan

• N = {0,1, 2, 3, . . .}, himpunan bilangan cacah • Z = {. . . ,−2,−1, 0, 1, 2, . . .}, himpunan bilangan

bulat

• Z+ _{= {1, 2, 3, . . .}, himpunan bilangan bulat positif}

• Q = {p/q | p ∈ Z, q ∈ Z, dan q  0}, himpunan bilangan rasional

• R, himpunan bilangan real

• R+_{, himpunan bilangan real positif}

5

Mendeskripsikan Himpunan

• Metoda roster: Mendaftarkan semua anggota himpunan

Contoh 2.

1. V: himpunan semua huruf vokal dapat dideskripsikan sebagai V = {a, e, i, o, u}.

2. O: Himpunan semua bilangan ganjil positif lebih kecil dari 10 dapat dideskripsikan sebagai 0 = {1, 3, 5, 7, 9}.

3. Himpunan bilangan bulat positif lebih kecil dari 100 dapat dideskripsikan sebagai {1, 2, 3, . . . , 99}.

• Notasi pembangun himpunan

Contoh 3.

O: Himpunan semua bilangan ganjil positif lebih kecil dari 10

dapat ditulis sebagai O = {x | x adalah bilangan ganjil positif lebih kecil dari 10} atau O = {x ∈ Z+ _{| x ganjil dan x < 10}.}

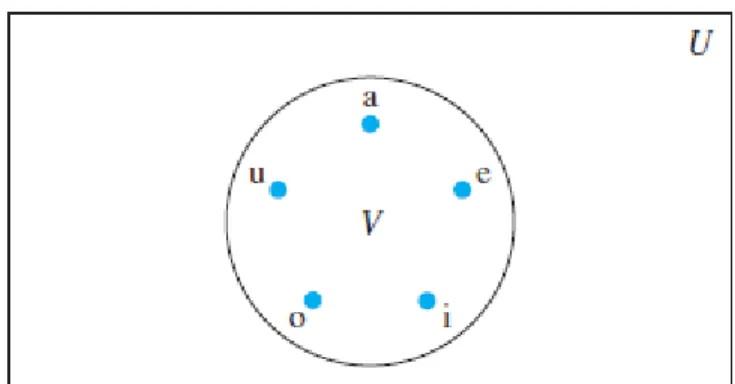
Diagram Venn

Himpunan semesta: himpunan semua objek yang dibicarakan.

Contoh 4.

V: himpunan semua huruf vokal dapat dideskripsikan dengan diagram Venn.

Kesamaan Himpunan

Definisi 1

Dua himpunan adalah

sama

jika dan hanya jika

mereka memiliki anggota yang sama.

A,B: himpunan

A dan B dikatakan

sama

, dinotasikan

A = B

,

jika dan hanya jika ∀x(x ∈ A ↔ x ∈ B).

Himpunan Kosong dan Singleton

• Himpunan yang tidak memiliki anggota

disebut

himpunan kosong

, dinotasikan dengan

∅

atau

{ }

.

• Himpunan dengan satu anggota disebut

himpunan singleton

.

Contoh 5.

9

Himpunan vs Himpunan dari Himpunan

Contoh 6.

• {1,2} vs {{1},{2}}

• {} vs {{}} = {



}

10

Himpunan Bagian

Definisi 2.

A, B: himpunan.

A adalah himpunan bagian B, dinotasikan A  B, jika dan hanya jika setiap anggota A juga merupakan anggota B.

A  B: x ( x  A  x  B)

Teorema 1. Untuk setiap himpunan S, berlaku   S dan S  S. Untuk menunjukkan A = B, tunjukkan A ⊆ B dan B ⊆ A.

Himpunan bagian sejati A  B:

Himpunan Kuasa

Himpunan kuasa P(S): himpunan semua himpunan bagian S.

P(S) memuat S, .

Soal 1. Apakah himpunan kuasa dari {0, 1, 2}? Contoh 7. Apakah P() dan P({})?

P() = {}

12

Kardinalitas

S: himpunan.

Kardinalitas dari S, dinotasikan |S|, adalah banyaknya anggota S yang berbeda.

Contoh 8.

• Misalkan A himpunan bilangan ganjil positif lebih kecil dari 10. Maka |A| = 5.

• Misalkan S himpunan alfabet. Maka |S| = 26.

Himpunan hingga adalah himpunan dengan kardinalitas suatu bilangan bulat positif.

Suatu himpunan dikatakan tak hingga jika himpunan tersebut bukan hingga.

13

Hasil Kali Kartesius

A,B: himpunan

Hasil kali Kartesius A dan B, dinotasikan A x B,

adalah himpunan semua pasangan terurut (a, b), di mana a ∈ A dan b ∈ B.

A × B = {(a, b) | a ∈ A ∧ b ∈ B}.

Soal 2.

Himpunan dan Kuantifikasi

∀x∈S(P(x)) berarti ∀x(x ∈ S → P(x)).

∃x∈S(P(x)) berarti ∃x(x ∈ S ∧ P(x)).

Soal 3.

Himpunan Kebenaran

P: predikat, D: domain

Himpunan kebenaran dari P adalah himpunan bagian dari D yang mengakibatkan P(x) benar.

Himpunan kebenaran dari P(x) dinotasikan dengan {x ∈ D | P(x)}.

Soal 4.

Apakah himpunan kebenaran dari predikat P(x), Q(x), dan R(x), di mana domain adalah himpunan bilangan bulat

17

Operasi Himpunan

• Gabungan

A



B

= { x | (x



A)



(x



B)}

• Irisan

A



B

= { x | (x



A)



(x



B)}

A, B dikatakan

saling lepas

jhj A



B =



Prinsip inklusi-eksklusi:

|A ∪ B| = |A| + |B| − |A ∩ B|.

• Selisih

A – B

= {x | (x



A)



(x



B)}

Bukti Identitas Himpunan

• Diagram Venn

• Himpunan bagian

• Ekivalensi logika

• Tabel keanggotaan

Soal 5.

Tunjukkan A ∩ B = A ∪ B.

22

Fungsi

Fungsi dari A ke B adalah pemasangan setiap anggota A ke tepat satu anggota B.

Notasi. f: A  B dan f (a) = b

A disebut domain dan B disebut kodomain dari f b disebut peta dari a dan a disebut prapeta dari b

Range atau peta dari f adalah himpunan peta dari semua anggota A,

Range(f) = {y|  x  A f(x) = y}  B

Contoh 9.

Manakah yang merupakan fungsi?

(1) A = B = Z, f(x) = x+10 (2) A = B = Z, f(x) = x2

23

Terminologi

• Dua fungsi dikatakan sama jika mereka memiliki domain, kodomain, dan aturan pemetaan yang sama.

• Fungsi f dikatakan satu-satu atau injektif, jika dan hanya jika f (a) = f (b) mengakibatkan a = b untuk setiap a and b di domain f.

• Fungsi f dari A ke B dikatakan pada atau

surjektif, jika dan hanya jika untuk setiap b ∈ B ada anggota a ∈ A sehingga f (a) = b.

• Fungsi f dikatakan korespondensi satu-satu atau bijektif, jika fungsi tersebut satu-satu dan pada.

Contoh 10.

Injektif, Surjektif, Bijektif

1. Apakah fungsi f(x) = x + 1 dari R ke R

satu-satu?

2. Apakah fungsi f(x) = x

2

_{dari Z ke Z pada?}

3. Misalkan f fungsi dari {a, b, c, d} ke {1, 2, 3, 4}

dengan f (a) = 4, f (b) = 2, f (c) = 1, dan f (d) =

3. Apakah f bijektif?

25

Invers dan Komposisi

Misalkan f korespondensi satu-satu dari A ke B. Fungsi invers dari f adalah fungsi yang

memetakan b ∈ B ke a ∈ A sedemikian sehingga f (a) = b.

Fungsi invers dari f dinotasikan dengan f-1 f-1_{(b) = a jhj f(a) = b}

Catatan. f-1_(x)  _1/f(x)

Jika f: A  B dan g: C  A, maka komposisi dari fungsi f dan g, f ° g: C  B, adalah f°g(x) = f(g(x))

26

Beberapa Fungsi Penting

Fungsi identitas (x)=x f ° f –1 = _f -1 _{° f =} 

Fungsi floor memetakan bilangan real x ke bilangan bulat terbesar yang lebih kecil atau sama dengan x.

Notasi.  x 

Fungsi ceiling memetakan bilangan real x ke bilangan bulat terkecil yang lebih besar atau sama dengan x.

28

Barisan

Barisan adalah fungsi dari himpunan bagian Z (biasanya {0, 1, 2, . . .} atau {1, 2, 3, . . .}) ke himpunan S.

Notasi. a_n adalah peta dari n dan {a_n} barisan

Barisan aritmetika adalah barisan dalam bentuk a, a + d, a + 2d, . . . , a + nd, . . .

dengan suku awal a dan beda d merupakan bilangan real.

Barisan geometri adalah barisan dalam bentuk a, ar, ar2_{, . . . , ar}n_{, . . .}

Relasi Recurrence

Relasi recurrence untuk barisan {a_n} adalah persamaan yang

menyatakan a_n dalam satu atau lebih suku sebelumnya dalam

barisan, yaitu, a₀, a₁, . . . , a_n−1, untuk semua bilangan bulat n dengan n ≥ n₀, di mana n₀ bilangan bulat tak negatif.

Suatu barisan disebut solusi dari relasi recurrence jika

suku-sukunya memenuhi relasi recurrence tersebut.

Soal 6.

Apakah {a_n}, dengan a_n = 3n untuk setiap bilangan bulat tak

negatif n, adalah solusi dari relasi recurrence a_n = 2a_n−1 − a_n−2 for n = 2, 3, 4, . . . . ? Bagaimana dengan a_n = 2n _{dan a}

Contoh. Barisan Fibonacci

Barisan Fibonacci, f

₀

, f

₁

, f

₂

, . . . , didefinisikan

dengan kondisi awal

f

₀

= 0, f

₁

= 1,

dan relasi recurrence

33

Kardinalitas

Suatu himpunan hingga jika kardinalitasnya adalah suatu bilangan bulat n.

Dua himpunan A, B dikatakan memiliki

kardinalitas yang sama, dinotasikan|A| = |B|, jhj terdapat korespondensi satu-satu dari A ke B.

Himpunan tak hingga.

Berapa kardinalitasnya? Apakah semua

himpunan tak hingga memiliki kardinalitas yang sama?

34

Himpunan Terhitung

Definisi.

Suatu himpunan dikatakan terhitung jika himpunan tersebut hingga atau memiliki kardinalitas yang sama dengan himpunan bilangan bulat positif.

Himpunan yang bukan terhitung dikatakan tak terhitung.

Jika himpunan tak hingga S terhitung, kardinalitas dari S dinyatakan oleh ℵ₀ (aleph null), dan ditulis |S| = ℵ₀

Soal 7.

Tunjukkan bahwa himpunan bilangan ganjil positif terhitung.