Regresi Logistik 4.1 INTERPRETING THE LOGISTIC REGRESSION MODEL 4.2 INFERENCE FOR LOGISTIC REGRESSION

(1)

(2)

(3)

Regresi Logistik

4.1 INTERPRETING THE LOGISTIC REGRESSION MODEL

4.2 INFERENCE FOR LOGISTIC REGRESSION

(4)

Model regresi logistik menggunakan peubah

penjelas, baik kategorik atau kontinu, untuk

memprediksi peluang dari hasil yang spesifik.

Dengan kata lain, regresi logistik dirancang untuk

menggambarkan peluang yang terkait dengan

nilai-nilai peubah respon.

(5)

(6)

(7)

• β>0 maka kurva akan naik

• β<0 maka kurva akan turun

• Jika β= 0 maka nilai π (x) tetap pada

berapapun nilai x kurva akan menjadi

garis horisontal

(8)

• X  Peubah penjelas kuantitatif

• Y  Peubah respon biner

• π(x)  peluang sukses peubah X

• Model Logit (log odds)

(9)

Interpretasi β

• Odds akan meningkat secara multiplikatif

sebesar e

β

_{untuk setiap kenaikan 1 unit x}

• e

β

_{ rasio odds}

)

(

1 )

(

x

X

odds

X

x

odds

RasioOdds







logit akan meningkat sebesarβ untuk setiap kenaikan 1 cm x

Interpretasi alternatif Not familiar

(10)

What Is an Odds Ratio?

An odds ratio indicates how much more likely,

with respect to odds, a certain event occurs in

one group relative to its occurrence in another

group.

Example: How much more likely are females

to purchase 100 dollars or more in

products compared to males?

(11)

(12)

4.1.1 Linear Approximation Interpretations β→ 0, kurva datar horizontal

β = 0 , Y bebas terhadap X

Β > 0, kurva π(x) membentuk fkp sebaran logistik

Kemiringan curam terjadi pada x yang π (x) = 0,50. Nilai x tersebut berhubungan dengan p arameter regresi logistik dengan x =-α / β.

nilai x ini disebut tingkat median efektif (EL₅₀).

(13)

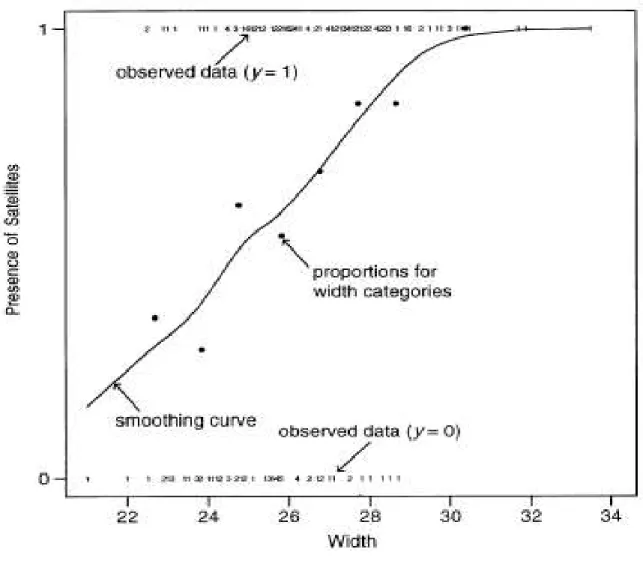
4.1.2 Horseshoe Crabs: Viewing and Smoothing a Binary Outcome

The study investigated factors that affect whether the female crab had any other males, called satellites, residing nearby her. The response outcome for each female crab is her number of satellites. An explanatory variable thought possibly to affect this was the female crab’s shell width, which is a summary of her size. In the sample, this shell width had a mean of 26.3 cm and a standard deviation of 2.1 cm.

Y indicate whether a female crab has any satellites (other males who could mate with her). That is, Y = 1 if a female crab has at least one satellite, and Y = 0 if she has no satellite.We first use the female crab’s width (in cm) as the sole predictor.

(14)

• Suatu penelitian mengenai faktor-faktor yang

mempengaruhi banyaknya satellite yang

dipunyai kepiting betina (Y)

• Y= 1 jika kepiting betina memiliki paling tidak

1 satellite

Y=0 jika tidak memiliki satellite.

• X= lebar cangkang kepiting betina (dalam cm)

(15)

(16)

Syntax SAS

Data crab;

input width sat;

datalines;

28.3

1

26.0

1

25.6

0 .

.

24.5

0 ;

proc logistic data=crab descending;

model sat=width/expb;

(17)

Output

At the minimum width in this sample of 21.0 cm, the estimated probability is exp(−12.351 + 0.497(21.0))/[1 + exp(−12.351 + 0.497(21.0))] = 0.129

At the maximum width of 33.5 cm, the estimated probability equals exp(−12.351 + 0.497(33.5))/[1 + exp(−12.351 + 0.497(33.5))] = 0.987

(18)

• lebar minimum x= 21 cm,

= 0.129

• lebar maksimum x= 33.5 cm

= 0.987

(19)

Interpretasi Output

• Dugaan π(x) =0.5 saat

• Dugaan odds =

 kepiting betina yang memiliki lebar 1 cm

lebih besar, memiliki kecenderungan 1.64 kali

mempunyai satelit

8 .

24

497 .

0 /

351 .

12 ˆ

/

ˆ











x

 

ˆ

exp



0 .

497 

1 .

64 exp





(20)

• Pada mean sampel lebar 26,3 cm, π (x) = 0,674.

• (Bab 4.1.1), perubahan kenaikan peluang pada titik mean

• Untuk kepiting betina dengan lebar badan dekat lebar rata-rata,

peluang kenaikan satelit pada tingkat 0,11 per 1 cm peningkatan

lebar.

• tingkat dugaan perubahan terbesar pada nilai x (24,8) di mana π (x)

= 0,50; peluang diperkirakan meningkat pada tingkat (0,497) (0,50)

(0,50) = 0,12 per 1 cm peningkatan lebar

 



1 ˆ

 



0.497 (0.674)

(0.326)

=

0.11 ˆ

ˆ

_

_x

_{ x}

_

_

(21)

Berbeda dengan model peluang linier,

model regresi logistik

memungkinkan laju perubahan

bervariasi sebagaimana perubahan x

(22)

Regression Fit

• Model paling sederhana untuk interpretasi

adalah model peluang π(x) = α + βx.

• Menggunakan pendekatan OLS (software GLM

dengan asumsi respon normal dengan fungsi

penghubung identitas) menghasilkan model

(23)

Proc GLM

proc genmod data=crab;

model sat=width/ dist = nor

link = identity

lrci;

run;

(24)

4.1.3 Horseshoe Crabs: Interpreting the Logistic Regression Fit

• π(x) adalah peluang kepiting betina memiliki

satelit dengan lebar badan x cm

• Dugaan peluang (adanya) satelit akan

meningkat 0.092 untuk setiap peningkatan 1

cm lebar badan kepiting

• Interpretasi  lebih sederhana, namun

tidak

sesuai untuk nilai ekstrim

• Misalkan pada contoh ini lebar badan

maksimal 33.5 cm. Dugaan peluangnya=

−1.766 + 0.092(33.5) =

1.3 .

(25)

Grouping

Untuk mendapatkan gambar dengan bentuk yang

lebih jelas, dilakukan pengelompokan untuk lebar

badan kepiting betina sbb:

Lalu hitung rataan contoh di masing-masing

kategori

(26)

Figure 4.2 contains eight dots representing the sample proportions of

female crabs having satellites plotted against the mean widths for the eight categories.

(27)

4.1.4 Odds Ratio Interpretation

Odds

Odds sukses

(respon =1)

However, this is a 64% increase;

 

2 .

07

674 .

0

1

0 .

674 ;

674 .

0 ˆ

;

3 .

26 





x

odds

x



 

3 .

40

773

1

0 .

773 ;

773 .

0 ˆ

;

3 .

27 





x

odds

x



64 .

1

07 .

2

3 .

4

3 . 26.3 27



RasioOdds

(28)

(29)

4.1.5 Logistic Regression with Retrospective Studies

• Regresi logistik juga dapat digunakan pada data hasil

studi restrospektif  Peubah X yang acak (bukan

peubah Y)

• Dapat digunakan bila salah satu respon kategori

jarang terjadi, dan sebuah studi prospektif mungkin

memiliki terlalu sedikit kasus untuk untuk dapat

menduga pengaruh dari prediktor dengan baik.

(30)

Retros

pective

Case-control

biomedis

Y1(kasus) dan 0(kontrol)

X  diamati

(31)

(32)

4.2 INFERENCE FOR LOGISTIC REGRESSION

• 4.2.1 Binary Data can be Grouped or Ungrouped

(33)

Data crab grup

data crab2;

input width y n;

cards;

22.69 5

14 23.84 4

14 24.78 17

28 25.84 21

39 26.79 15

22 27.74 20

24 28.67 15

18 30.41 14

14 ;

proc logistic data=crab2;

model y/n=width/influence stb expb;

output out=predict p=pi_hat lower=LCL upper=LCL;

run;

(34)

confidence interval for effect

A large-sample Wald confidence interval for the

parameter β in the logistic regression model,

logit[π(x)] = α + βx, is

 

SE

z

₂

ˆ

_

(35)

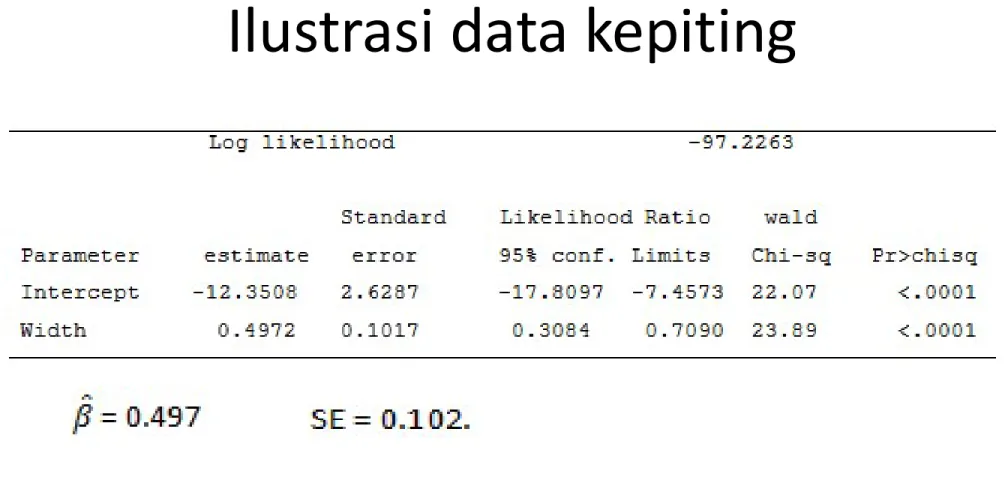
Ilustrasi data kepiting

• Selang kepercayaan 95% untuk β adalah

0.497± 1.96(0.102) = [0.298, 0.697]

(36)

• Selang kepercayaan berdasarkan likelihood

ratio = (0.308, 0.709).

• Interval likelihood ratio untuk pengaruh pada

odds setiap kenaikan 1 cm lebar cangkang =

(e

308 , e

709 )= (1.36, 2.03).

• Berarti setiap kenaikan 1 cm lebar cangkang,

akan menaikkan odds satellite paling sedikit

1.36 kali dan paling banyak 2 kali

(37)

Hypothesis Testing about Effect of X

• Test for parameter model ().

• Simultanious test G-test

(38)

Uji Simultan

Statistik uji-G adalah uji rasio kemungkinan (likelihood ratio

test) yang digunakan untuk menguji peranan variabel

penjelas di dalam model secara bersama-sama (Hosmer &

Lemeshow, 1989). Rumus umum uji-G untuk menguji

hipotesis :

H0 : 1 = 2 = … = k = 0

H1 : minimal ada satu  yang tidak sama dengan 0

adalah

Statistik G ini, secara teoritis mengikuti sebaran 

2

_dengan

derajat bebas k.

       bebas peubah dengan

likelihoodlikelihood pa peubah bebas G 2ln tan

(39)

Partial Test

Sementara itu, uji Wald digunakan untuk menguji

parameter i secara parsial. Hipotesis yang diuji

adalah:

H0 : 

_i

= 0

H1 : 

_i

 0

Formula statistik Wald adalah:

Secara teori, statistik Z ini mengikuti sebaran

normal baku jika H0 benar.

Atau menggunakan statistik uji yang

mengikuti sebaran dengan db=1

)

ˆ

(

ˆ

i i

SE

Z





(40)

Uji Hipotesi Data Kepiting

• Hipotesis  H

₀

: = 0 vs H

₁

:   0

• Statistik Uji : Z= 0.497/0.102 = 4.9.

(This shows strong evidence of a positive effect of width on the

presence of satellites (P <0.0001))

• The equivalent chi-squared statistic, z

2

_{= 23.9, has df = 1.}

• Software reports that the maximized log likelihoods equal L0 =

−112.88 under H0: β = 0 and L1 = −97.23 for the full model. The

likelihood-ratio statistic equals −2(L0 − L1) = 31.3, with df = 1.

• This also provides extremely strong evidence of a width effect (P <

0.0001).

(41)

Confidence Intervals for Probabilities

• Ilustrasi dengan memperkirakan probabilitas dari satelit untuk

kepiting betina lebar x = 26,5, yang dekat lebar rata-rata

• Persamaan regresi logistiknya:

πˆ = exp(−12.351 + 0.497(26.5))/[1 + exp(−12.351 + 0.497(26.5))] =

0.695 • Output software: selang kepercayaan 95% untuk probability

sesungguhnya (0.61, 0.77).

(42)

Kenapa menggunakan

model untuk menduga

(43)

X=26,5 cm

6 kepiting, 4

memiliki satelit

Binom

p= 4/6=0.67

(44)

Reality is more complicated. In

practice, any model will not

exactly represent the

true relationship between π(x)

and x.

(45)

Ilustrasi

(46)

Data CHD; input age $ CHD @@; cards; <=55 1 <=55 1 >55 1 >55 0 >55 0 <=55 1 <=55 0 >55 1 >55 0 >55 0 <=55 1 <=55 0 >55 1 >55 0 >55 0 <=55 1 <=55 0 >55 1 >55 0 >55 0 <=55 1 <=55 0 >55 1 >55 0 >55 0 <=55 1 <=55 0 >55 1 >55 0 >55 0 <=55 1 <=55 0 >55 1 >55 0 >55 0 <=55 1 >55 1 >55 1 >55 0 >55 0 <=55 1 >55 1 >55 1 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 <=55 1 >55 1 >55 0 >55 0 >55 0 ;