Teori posibilitas - USD Repository

Diajukan untuk memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh:

Nama : Andreana Ika Nurinasari NIM : 02 3114 017

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

Presented as Partial Fulfillment to Obtain the Sarjana Sains Degree

in Mathematics Study Program

By

Name : Andreana Ika Nurinasari Student Number: 02 3114 017

MATHEMATICS STUDY PROGRAM

SCIENCE AND TECHNOLOGY FACULTY SANATA DHARMA UNIVERSITY

DIA membuat segala sesuatu indah pada waktunya….

Skripsi ini ku persembahkan untuk : Yesus Kristus dan Bunda Maria yang senantiasa menyertaiku. Albertus Galih suami, teman, sahabat dan segala – galanya,

terimakasih untuk cinta, perhatian dan segala dukungan moral maupun spiritualnya,

disusun untuk memenuhi salah satu syarat memperoleh gelar Sarjana Sains di Program Studi Matematika Jurusan Matematika Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.

Dalam penyusunan skripsi ini penulis mendapatkan bantuan dari berbagai pihak. Oleh karena itu dalam kesempatan ini perkenankanlah penulis menghaturkan terima kasih yang sebesar – besarnya kepada pihak yang telah memberikan bantuan ini, antara lain:

1. Romo Dr. Frans Susilo, SJ selaku dosen pembimbing yang telah dengan sabar membimbing dan mendampingi penulis sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Terima kasih Romo……

2. Bapak Y. G. Hartono, S.Si, M.Sc selaku Kepala Program Studi Matematika. 3. Ibu Lusia Krismiyati Budiasih, S.Si, M.Si, terimakasih atas masukan –

masukannya.

4. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc selaku dosen pembimbing akademik atas segala bimbingan dan perhatian yang diberikan kepada penulis.

5. Romo Ir. Gregorius Heliarko S.J., S.S., B.S.T., M.A., M.Sc selaku Dekan Fakultas Sains dan Teknologi.

6. Segenap Bapak dan Ibu Dosen Program Studi Matematika atas segala ilmu, bimbingan, perhatian yang penulis dapatkan selama menimba ilmu di bangku kuliah ini.

7. Segenap karyawan Universitas Sanata Dharma khususnya perpustakaan Paingan atas segala pelayanan yang telah diberikan

berikan.

11.Saudara - saudara sepupuku Dek Dian, Dek Nana, dll termakasih atas segala dukungan yang telah diberikan.

12.Teman – teman seperjuanganku di Matematika 2002: Priska (thanks buat semuanya ya…), Retno (ayo Ret, kamu pasti bisa..), Lili, Vida, Lia, Ijup, Aan, Galih, Bani, Markus, Taim, Lenta, Debby, Felix, Tato, Archy, Ika, Cia, Aning, Dani, Rita, Nunung, Asih, Desy, Wuri, Deon, Palma terimakasih atas kebersamaannya selama ini. Dan juga kakak – kakak dan adik – adik atas segala bantuannya.

13.Berbagai pihak yang tidak dapat penulis sebutkan satu persatu, terima kasih atas segala bantuannya.

Walaupun telah diusahakan sebaik mungkin namun dalam penulisan ini skripsi ini tentu masih banyak kekurangan, kekeliruan dan masih jauh dari sempurna. Oleh karena itu penulis mengharapkan saran dan kritik yang bersifat membangun demi kemajuan yang akan dating.

Semoga skripsi ini dapat memberikan tambahan wawasan dan pengetahuan bagi pembaca.

Yogyakarta, ………... 2007

HALAMAN PENGESAHAN……….. iii

HALAMAN PERSEMBAHAN………... iv

HALAMAN MOTTO……….. v

HALAMAN PERNYATAAN KEASLIAN KARYA……….. vi

HALAMAN ABSTARK……….. vii

HALAMAN ABSTRACK……… viii

KATA PENGANTAR……….. ix

DAFTAR ISI………. xi

BAB I PENDAHULUAN……… 1

A. Latar Belakang Masalah………. 1

B. Perumusan Masalah……… 4

C. Pembatasan Masalah………... 4

D. Tujuan Penulisan………. 4

E. Manfaat Penulisan………... 4

F. Metode Penulisan………. 5

G. Sistematika Penulisan………... 5

BAB II TEORI HIMPUNAN KABUR……….……… 7

A. Himpunan Kabur……….………. 7

B. Operasi pada Himpunan Kabur………... 11

C. Relasi Kabur………. 16

D. Proposisi Kabur……… 17

BAB III TEORI POSIBILITAS……… 20

A. Pendekatan Intuitif Posibilitas……….. 20

B. Pendekatan Aksiomatis Posibilitas………22

PENUTUP……… 65 A. Kesimpulan……… 65

Tabel 3.2.2.3 Badan Evidensi Marginal………. 39 Tabel 3.2.2.4 Hubungan antara pemetaan dasar, ukuran kepercayaan, dan ukuran

Gambar 2.1.2.2 Grafik fungsi keanggotaan himpunan kabur A∩B………… 14

Gambar 2.1.2.3 Grafik fungsi keanggotaan himpunan kabur A~∪B~………… 15

Gambar 3.2.3.1a Barisan lengkap himpunan-himpunan bagian tersarang dari X.... 50

Gambar 3.2.3.1b Ukuran posibilitas yang didefinisikan pada X……… 50

Gambar 3.2.3.2 Badan evidensi tersarang marginal……… 57

Gambar 3.2.3.3 Badan evidensi tersarang bersama……… 58

Gambar 3.2.3.4 Distribusi posibilitas marginal……… 59

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Teori himpunan kabur pertama kali diperkenalkan oleh Prof. L.A. Zadeh

pada tahun 1965. Teori ini berlandaskan pada himpunan kabur yang dipakai untuk

menyelesaikan suatu permasalahan optimasi yang memuat kekaburan dalam

perumusannya. Teori himpunan kabur merupakan perluasan dari teori himpunan

klasik atau tegas. Himpunan tegas A didefinisikan dengan menggunakan suatu

fungsi χ_A yang nilainya dalam {0,1}. Fungsi keanggotaan dari himpunan A

didefinisikan sebagai berikut :

⎩

Keunggulan dari teori himpunan kabur adalah kemampuannya

memodelkan secara lebih mendekati kenyataan. Sebab dari permasalahan yang

terjadi dalam kehidupan nyata diubah ke dalam bahasa matematis supaya

mempermudah penyelesaiannya dan kemudian penyelesaian tersebut

dikembalikan ke dalam permasalahan nyata. Salah satu cara pemodelannya adalah

penentuan fungsi keanggotaan himpunan kabur dimana setiap anggota

mempunyai derajat keanggotaan. Fungsi keanggotaan dari suatu himpunan kabur

à dalam semesta X adalah pemetaan A ~

μ dari X ke selang tertutup [0,1], yaitu :

Teori himpunan kabur adalah alat yang dapat digunakan untuk

memodelkan suatu permasalahan dalam proses ukuran untuk memperoleh

penyelesaian yang sesuai dengan realita.

Dalam kehidupan, kita sering berjumpa dengan gejala kekaburan. Ambil

suatu contoh. Dalam suatu kelas seorang guru menyuruh para siswanya yang

mempunyai sepeda untuk mengangkat tangannya. Maka dalam seketika kelas itu

terbagi menjadi dua kelompok (himpunan) secara tegas, yaitu kelompok para

siswa yang mengangkat tangannya (mempunyai sepeda) dan kelompok para siswa

yang tidak mengangkat tangannya (tidak mempunyai sepeda). Lain halnya dengan

contoh tentang suatu bentuk percobaan kejahatan yang belum tentu kesalahan dari

tersangka. Himpunan orang-orang yang bersalah dalam kejahatan dan himpunan

orang-orang yang tidak bersalah, dianggap mempunyai batasan-batasan yang

sangat jelas. Di dalam contoh kedua ini, yang diperhatikan bukan derajat dimana

tersangka bersalah melainkan derajat dimana bukti-bukti menunjukkan

keanggotaan tersangka di dalam himpunan orang-orang yang bersalah maupun

dalam himpunan orang-orang yang tidak bersalah. Bersalah di sini mengandung

unsur ketidaktegasan karena bersalah menurut pandangan orang yang satu dengan

yang lain bisa berbeda. Bukti-bukti yang sempurna akan menunjukkan pada

keanggotaan penuh di dalam suatu himpunan dan hanya satu dari himpunan ini.

Tetapi, bukti yang sempurna jarang ditemukan.

Untuk melihat jenis ketidakpastian akan ditunjuk suatu nilai pada suatu

himpunan. Nilai ini menunjukkan derajat bukti atau kepastian dari keanggotaan

sudah kita kenal, suatu angka ditunjukkan pada masing-masing elemen dari

himpunan universal, yang berarti derajat keanggotaannya dalam suatu himpunan

khusus dengan batas-batas yang tidak jelas (kabur). Sebaliknya, ukuran kabur

menunjuk suatu nilai dalam interval [0,1] pada masing-masing himpunan tegas

dari himpunan universal yang berarti derajat kepercayaan atau kepastian dari

suatu elemen khusus x yang ada dalam himpunan itu.

Ketidakpastian adalah fokus utama dari teori posibilitas. Konsep pokok

dari teori posibilitas adalah distribusi posibilitas. Guna mendefinisikan distribusi

probabilitas lebih dahulu kita akan mengenal pembatasan kabur. Ambil x adalah

suatu variabel linguistik dan à adalah suatu himpunan kabur yang dikaitkan

dengan nilai linguistik A. Maka proposisi kabur x adalah A dapat diinterpretasikan

sebagai pembatasan kabur pada x dan pembatasan ini dikarakteristikan dengan

fungsi keanggotaan ~(x) A

μ . Dengan kata lain, kita dapat menginterpretasikan

) ( ~ x A

μ sebagai derajat posibilitas dengan x = u. Sebagai contah, misalkan x adalah

umur seseorang dan à adalah himpunan kabur muda. Orang itu adalah muda (x

adalah A) maka μ_A(30) dapat diinterpretasikan sebagai derajat posibilitas bahwa

umur orang itu adalah 30.

Dari masalah ukuran tersebut, kita dapat membuat model matematika

yang sesuai dengan permasalahan yang melibatkan unsur-unsur tidak tegas di

dalamnya, kemudian mencari solusi atau penyelesaian dari model matematika

B. Rumusan Masalah

Berdasarkan latar belakang di atas, pokok-pokok permasalahan yang akan dibahas dalam penulisan ini adalah sebagai berikut :

Bagaimana membuat model yang cocok untuk masalah ukuran posibilitas yang

erat hubungannya dengan teori himpunan kabur?

C. Batasan Masalah

Dalam penulisan ini, penulis membatasi suatu metode atau cara dalam teori himpunan kabur yang berkaitan masalah ukuran kabur yaitu dengan teori

posibilitas. Dalam penulisan ini, penulis tidak akan membahas teori probabalitas.

D. Tujuan Penulisan

Tujuan penulisan yang akan dicapai dalam penulisan ini adalah :

1. Merumuskan model matematika yang sesuai dengan pengukuran kabur

yang melibatkan unsur-unsur yang tidak tegas.

2. Merumuskan penyelesaian ukuran kabur.

3. Menerapkan model matematika yang telah dibuat dalam satu masalah

kongret di lingkungan kabur

E. Manfaat Penulisan

Tulisan ini diharapkan dapat berguna untuk menambah wawasan tentang matematika, terutama tentang posibilitas kabur suatu teori yang erat hubungannya

F. Metode Penulisan

Metode yang digunakan dalam penulisan ini adalah studi pustaka yaitu dengan mempelajari beberapa materi yang berkaitan dengan pemakaian teori

himpunan kabur dalam ukuran kabur.

G. Sistematika Penulisan

BAB I PENDAHULUAN

Bab ini berisi tentang latar belakang penulisan tentang masalah ukuran

posibilitas. Tentang bagaimana masalah ketidakpastian yang merupakan fokus

utama dari teori posibilitas. Selain itu, terdapat tujuan penulisan, metode penulisan

dan manfaat penulisan bagi penulis. Selanjutnya diberikan pula sistematika

penulisan dalam masalah ukuran posibilitas ini.

BAB II TEORI HIMPUNAN KABUR

Bab ini berisi landasan teori dalam penulisan ini, yaitu teori himpunan

kabur. Kemudian disinggung pula tentang operasi pada himpunan kabur dan relasi

kabur.

BAB III TEORI POSIBILITAS

Bab ini berisi tentang teori posibilitas baik melalui pendekatan intuitif

maupun secara aksiomatis. Selain itu dibahas juga teori ukuran kabur dan teori

BAB V PENUTUP

Bab ini berisi tentang kesimpulan dari penulisan tentang masalah ukuran

BAB II

TEORI HIMPUNAN KABUR

A. Himpunan Kabur

Secara intuitif himpunan adalah suatu kumpulan atau koleksi

obyek-obyek (konkret maupun abstrak) yang mempunyai kesamaan sifat tertentu. Suatu

himpunan haruslah terdefinisi secara tegas, dalam arti bahwa untuk setiap obyek

selalu dapat ditentukan secara tegas apakah obyek tersebut merupakan anggota

himpunan itu atau tidak. Dengan perkataan lain, untuk setiap himpunan terdapat

batas yang tegas antara obyek-obyek yang merupakan anggota himpunan dan

obyek-obyek yang tidak merupakan anggota dari himpunan tersebut. Oleh

karenanya himpunan semacam itu seringkali juga disebut himpunan tegas.

Himpunan tegas dapat dinyatakan dengan menggunakan fungsi karakteristik, yaitu

suatu fungsi dari semesta X ke himpunan {0,1}. Suatu himpunan A dalam semesta

X dapat dinyatakan dengan fungsi karakteristik χ_A: X→ {0,l}.

fungsi keanggotaan dari himpunan kaburA~, dan nilainya menyatakan derajat

keanggotaan unsur-unsur di dalam himpunan kaburA~. Derajat keanggotaan sama

dengan 1, yaitu A ~

μ (x) = 1 untuk suatu x∈X, menyatakan keanggotaan penuh

dengan 0, yaitu μ_A~(x) = 0 untuk suatu x∈X , menyatakan bahwa unsur x tersebut

sama sekali bukan anggota himpunan kabur A~.

Definisi 2.1.1

Himpunan kabur A~ dalam X dapat dinyatakan sebagai pasangan terurut

{

x x x X

}

A~= ( ,μ_A~( )) ∈ ,

di mana μ_A~ adalah fungsi keanggotaan dari himpunan kabur A~.

Bila semesta X kontinu, maka himpunan kabur A~ dapat dinyatakan dengan

∫ =

∈X

x A

x x A~ μ~( )/

di mana lambang

∫

di sini bukan merupakan lambang operator integral,

melainkan melambangkan keseluruhan x∈X bersama dengan derajat

keanggo-taannya di dalam himpunan kabur A~ . Jika semesta X adalah himpunan yang

diskret, maka himpunan kabur A~ dapat dinyatakan dengan

∑ =

∈X

x A

x x

A~ μ~( )/

di mana lambang ∑ di sini bukan merupakan lambang operator jumlah,

melainkan melambangkan keseluruhan x∈X bersama dengan derajat

Contoh 2.1.1

Dalam semesta X = {1,2,3,4,5,6,7}, A~ adalah himpunan "bilangan bulat yang

dekat dengan empat". Maka himpunan kabur tersebut dapat dituliskan sebagai

berikut:

∑ =

∈X

x A

x x

A~ μ~( )/

= 0,06/1 + 0,10/2 + 0,50/3 + 1/4 + 0,50/5 + 0,10/6 + 0,06/7.

Definisi 2.1.2

Pendukung dari suatu himpunan kabur A~, yang dilambangkan dengan Pend(A~),

adalah himpunan tegas yang memuat semua unsur dari semesta yang mempunyai

derajat keanggotaan taknol dalam A~ , yaitu

Pend(A)= {x∈X ~(x)>0}

A

μ .

Definisi 2.1.3

Tinggi (height) dari suatu himpunan kaburA~, yang dilambangkan dengan

Tinggi(A~), didefinisikan sebagai

Tinggi(A~) = sup

{

~(x)

}

A X x

μ ∈

.

Definisi 2.1.4

Titik silang dari suatu himpunan kabur A~ adalah elemen dari semesta yang

Definisi 2.1.5

Teras (core) dari suatu himpunan kabur A~, yang dilambangkan dengan

Teras(A~), adalah himpunan semua unsur dari semestanya yang mempunyai

derajat keanggotaan sama dengan 1, yaitu

Teras(A~) =

{

x∈X ~(x)=1

}

A

μ .

Definisi 2.1.6

Pusat dari suatu himpunan kabur didefinisikan sebagai berikut : Jika nilai purata

dari semua titik dimana fungsi keanggotaan himpunan kabur itu mencapai nilai

maksimum adalah berhingga, maka pusat himpunan kabur itu adalah nilai purata

tersebut. Jika nilai purata itu takhingga positif (negatif), maka pusat himpunan

ka-bur itu adalah yang terkecil (terbesar) di antara semua titik yang mencapai nilai

fungsi keanggotaan maksimum.

Contoh 2.1.2

Untuk himpunan kabur A~ dalam Contoh 2.1.1.1 di atas :

Pend(A~) = {1,2,3,4,5,6,7}

Tinggi(A~) = 1

Titik silang dari A~ adalah 3 dan 5

Teras(A~) = {4}

Definisi 2.1.7

Dua buah himpunan kabur A~ dan B~ dalam semesta X dikatakan sama, dengan

lambang A~ = B~, bila dan hanya bila

) ( )

( ~

~ x x

B

A μ

μ =

untuk setiapx∈X .

Definisi 2.1.8

Himpunan kabur A~ dan B~disebut himpunan bagian dari himpunan kabur B~,

dengan lambang A~⊆ B~, bila dan hanya bila

) ( )

( ~

~ x x

B

A μ

μ ≤

untuk setiapx∈X .

Contoh 2.1.3

Dalam semesta X = {l,2,3,4,5,6,7}

A~ = 0,06/1 + 0,10/2 + 0,50/3 + 1/4 + 0,50/5 + 0,10/6 + 0,06/7 dan

B~ = 0,10/2 + 0,4/3 + 1/4 + 0,5/5 + 0,1/6

Maka B~⊆ A~.

B. Operasi pada Himpunan Kabur

A' =

{

x∈X x∈A

}

.

Kalau himpunan tegas A adalah himpunan semua bilangan positif dalam

semesta himpunan semua bilangan bulat, maka A' adalah himpunan semua

bilangan bulat negatif atau nol.

Gabungan dua buah himpunan tegas A dan himpunan tegas B, dengan

notasi A∪B, adalah himpunan semua elemen dalam semesta yang merupakan

anggota himpunan A atau anggota himpunan B, yaitu

A∪B =

{

x x∈A∨x∈B

}

.

Irisan dua buah himpunan tegas A dan himpunan tegas B, dengan notasi

A∩B, adalah himpunan semua elemen semesta yang merupakan anggota

him-punan A dan sekaligus anggota himpunan B, yaitu

A∩B =

{

x x∈A∧x∈B

}

.

Karena fungsi keanggotaan suatu himpunan kabur adalah perampatan

dari fungsi karakteristik himpunan tegas, maka operasi-operasi pada himpunan

kabur dapat kita definisikan sesuai dengan operasi-operasi pada himpunan tegas.

Misalkan A~ dan B~adalah himpunan kabur dalam semesta X.

Definisi 2.2.1

Komplemen dari suatu himpunan kabur A~ adalah himpunan kabur A' dengan

fungsi keanggotaan

) ( 1 )

( ~

~ x x

A

A μ

μ _′ = −

Definisi 2.2.2

Diketahui dua buah himpunan kabur A dan B dengan fungsi keanggotaan sebagai

Maka grafik fungsi keanggotaan himpunan kabur A′~ adalah sebagai berikut

2 1

0 3 4 5 6

1

A ~

X A~′

Gambar 2.2.1. Grafik fungsi fungsi keanggotaan himpunan kabur A′~

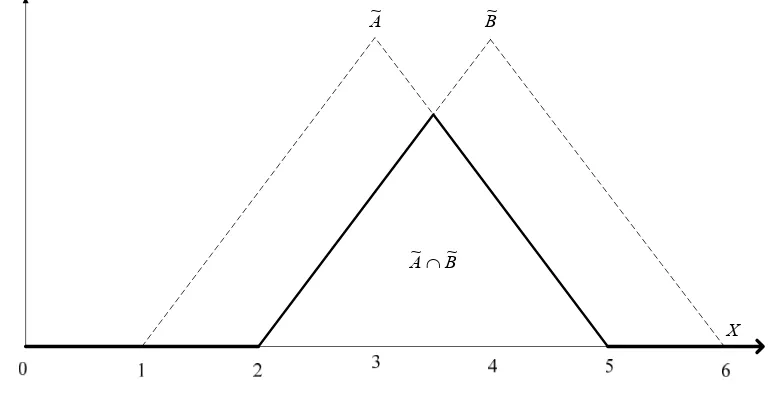
Grafik fungsi keanggotaan himpunan kabur A~∩B~ adalah sebagai berikut:

B~ A ~_∩

A~ B~

X

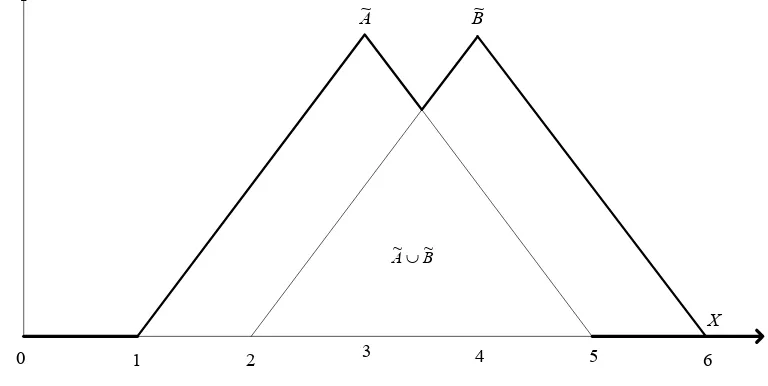
Grafik fungsi keanggotaan himpunan kabur A~∪B~ adalah sebagai berikut:

2 1

0 3 4 5 ₆

1

B A~∪~

A~ B~

X

Gambar 2.2.3. Grafik fungsi keanggotaan himpunan kabur A~∪B~

Contoh 2.2.2

Dalam semesta X ={ 1,2,3,4,5,6,7}

A~ = 0,6/1 + 0,1/2 + 0,5/3 + 1/4 + 0,5/5 + 0,1/6 + 0,6/7

B~ = 0,2/2 + 0,5/3 + 0,7/4 + 0,5/5.

Maka

A~ ' = 0,4/1 + 0,9/2 + 0,5/3 + 0,5/5 + 0,9/6 + 0,4/4

B~' = 1/1 + 0,8/2 + 0,5/3 + 0,3/4 + 0,5/5 + 1/6 + 1/7

A~ ∪ B~ = 0,6/1 + 0,2/2 + 0,5/3 + 1/4 + 0,5/5 + 0,1/6 + 0,6/7

C. Relasi Kabur

Definisi 2.3.1

Relasi kabur (biner) R~ antara elemen-elemen di himpunan X dan elemen-elemen

di himpunan Y adalah suatu himpunan bagian kabur dari darab Cartesius X × Y,

yaitu himpunan kabur :

R~=

{

(x,y), ~(x,y) (x,y) X Y)

}

R ∈ ×

μ .

Dengan melihat definsi relasi kabur di atas, dapat disimpulkan bahwa

sebuah himpunan kabur A~ dalam semesta X dengan fungsi keanggotaan μ_A~dapat

dipandang sebagai sebuah relasi kabur uner.

Contoh 2.3.1

Misalkan X = {40, 87, 314} dan Y = {10, 36, 228}, kemudian didefinisikan relasi

kabur R~, yaitu relasi "jauh lebih besar" antara elemen-elemen X dan Y. Maka

relasi tersebut dapat ditulis sebagai berikut: R~ = 0,3 / (40,10) + 0,1 / (40,36) +

0,5 / (87,10) + 0,3 / (87,36) + 0,9 / (314,10)+ 0,7 / (314,36) + 0,4 / (314,228).

Atau dengan matriks relasi sebagai berikut:

Definisi 2.3.2

Bila R~ adalah suatu relasi kabur pada semesta X × Y, maka invers dari R~, yang

dinyatakan dengan R~-1, adalah relasi kabur pada semesta Y × X dengan fungsi

keanggotaan

) , ( ) ,

( ~

~1 y x _R x y

R μ

μ − =

untuk setiap (y,x) ∈ Y × X.

Matriks dari invers relasi kabur R~, yaitu R~-1, adalah transpose dari matriks dari

relasi R~.

D. Proposisi Kabur

Proposisi kabur adalah kalimat yang memuat predikat kabur, yaitu

predikat yang dapat direpresentasikan dengan suatu himpunan kabur. Proposisi

kabur yang mempunyai nilai kebenaran tertentu disebut pernyataan kabur. Nilai

kebenaran dari suatu pemyataaan kabur disajikan dengan suatu bilangan real

dalam selang [0,1]. Nilai kebenaran itu disebut juga derajat kebenaran dari

pernyataan kabur itu. Bentuk umum dari proposisi kabur adalah

x adalah A

di mana x adalah suatu variabel linguistik dan predikat A adalah suatu nilai

linguistik dari x. Misalkan proposisi kabur "x adalah A" dilambangkan dengan

p(x), dan derajat kebenaran dari p(x0) dengan τ(p(x0)), maka

p

(

Contoh 2.4.1

Dalam proposisi kabur

Badan anak itu gemuk

Predikat "gemuk" dapat dikaitkan dengan himpunan kabur S~ dengan fungsi

keanggotaan S~

μ . Derajat kebenaran dari pernyataan kabur

Badan anak yang beratnya 90 kg itu adalah gemuk

sama dengan dereajat keanggotaan 90 kg dalam himpunan kabur " gemuk",

misalnya S~

μ (90) = 0,8.

Predikat "benar" adalah suatu predikat kabur yang dapat dinyatakan

dengan suatu himpunan kabur B~, dengan derajat keanggotaan bilangan real dalam

semesta [0,1], sedangkan predikat "salah" adalah S~ = B~'.

Definisi 2.4.1

Fungsi keanggotaan himpunan kabur B~ tersebut didefinisikan sebagai fungsi

identitas, yaitu

x x

B~( )=

μ

untuk setiap x∈[0,1], di mana x adalah derajat kebenaran suatu pernyataan kabur.

Definisi 2.4.2

Fungsi keanggotaan himpunan kabur S~ =B~' adalah

μ_S~(x) = k(μ

untuk setiap x∈ [0,1], di mana k adalah suatu komplemen kabur.

Contoh 2.4.2

Dalam contoh 2.1.4.1 pernyataan kabur

Badan anak yang beratnya 90 kg itu adalah gemuk

mempunyai derajat kebenaran 0,8. Maka pernyataan kabur

"Badan anak yang beratnya 90 kg itu adalah gemuk" adalah benar

mempunyai derajat kebenaran ~(80)=0,8 B

BAB III

TEORI POSIBILITAS

A. Pendekatan Intuitif Posibilitas

Tidak lama setelah Zadeh memperkenalkan teori himpunan kabur pada

akhir tahun enam puluhan, ia mengembangkan konsep posibilitas secara intuitif

melalui penelitiannya yang dipublikasikan dalam artikel yang berjudul "Fuzzy

Sets as a Basic for a Theory of Possibility" pada tahun 1978. Sesuai judul

karangannya itu, Zadeh membangun teori posibilitas atas dasar teori himpunan

kabur. Teori posibilitas adalah teori yang melengkapi teori probabilitas dalam

menangani masalah - masalah yang berhubungan dengan ketidakpastian. Misalkan

x adalah suatu variabel dalam semesta U dan A~ adalah himpunan kabur dalam U

dengan fungsi keanggotaan A~

μ , di mana ~(x) A

μ menyatakan derajat keanggotaan

elemen x ∈ U dalam himpunan kabur A. Maka predikat kabur A dalam proposisi

"x adalah A " dapat diinterpretasikan sebagai suatu pembatasan kabur pada

variabel x.

Definisi 3.1.1

Diberikan himpunan kabur A~ dalam U dan proposisi "x adalah A", maka

distribusi posibilitas yang berkaitan dengan x, yang dinyatakan dengan notasi πx,

secara numerik didefinisikan sama dengan fungsi keanggotaan A~ , yaitu

untuk setiap x ∈ U.

Contoh 3.1.1

Himpunan kabur "bilangan bulat kecil" didefinisikan sebagai

A~ = 1/1 + 1/2 + 0.8/3 + 0.6/4 + 0.4/5 + 0.2/6.

Maka distribusi posibilitas yang berkaitan dengan x jika diketahui bahwa "x

adalah bilangan bulat kecil” secara numerik adalah

πx = 1/1 + 1/2 + 0.8/3 + 0.6/4 + 0.4/5 + 0.2/6.

Posibilitas bahwa x adalah 3, jika diberikan "x adalah bilangan bulat kecil”,

adalah 0.8, yaitu πx (3) = μ_A~(3) = 0.8.

Definisi 3.1.2

Jika C adalah himpunan tegas dalam semesta U dan πx adalah distribusi posibilitas

yang berkaitan dengan x, maka ukuran posibilitas dari C, yang dinotasikan dengan

Posx(C), yang menyatakan posibilitas bahwa "x adalah anggota C" didefinisikan

sebagai berikut

Posx(C) = supmin _x( )

U u

u π

∈ .

Definisi 3.1.3

Jika A~ adalah suatu himpunan kabur dalam U, dan πx adalah distribusi posibilitas

yang berkaitan dengan x, maka ukuran posibilitas dari A~, dengan notasi Posx(A

~ ),

Posx(A

~

) = supmin{ ~(u), _x(u)} A

U u

π μ

∈ .

Contoh 3.1.2

Lihat contoh 3.1.1

πx = 1/1 + 1/2 + 0.8/3 + 0.6/4 + 0.4/5 + 0.2/6

dan himpunan tegas C = {3,4,5}. Maka ukuran posibilitas (C) adalah

Posx(C) = supmin x( ) }

5 , 4 , 3 {

u

u

π ∈

= max [0.8, 0.6, 0.4]

= 0.8.

B. Pendekatan Aksiomatis Posibilitas

Selanjutnya akan dibahas teori posibilitas yang dibangun dengan

pendekatan aksiomatis dalam kerangka teori yang lebih luas yaitu ukuran kabur.

Zadeh mengakui bahwa pendekatan intuitif yang dipakainya dalam

mengembangkan teori posibilitas itu tidak sepenuhnya dapat diandalkan. la

menyarankan diadakannya penelitian lanjutan untuk mengembangkan pendekatan

aksiomatis yang akan meletakkan teori posibilitas itu di atas dasar matematis yang

lebih kokoh. Pendekatan terakhir ini menempatkan teori posibilitas dalam

1. Ukuran kabur

Definisi 3.2.1.1

Andaikan X adalah suatu himpunan semesta pembicaraan dan P(X) adalah

keluarga semua himpunan bagian dari X. Suatu ukuran kabur adalah suatu fungsi

g : P(X) → [0,1] yang memenuhi syarat-syarat berikut:

1. g (φ) = 0 dan g (X) = 1 (syarat batas)

2. Untuk setiap A,B ∈ P(X), bila A ⊆B, maka g (A) ≤g (B) (sifat monoton)

Untuk himpunan semesta takhingga ditambahkan syarat :

3. Bila A1 ⊂ A2 ⊂... adalah barisan naik himpunan - himpunan dalam P(X),

tian berdasarkan keterbatasan informasi yang tersedia bahwa suatu elemen

tertentu dari X adalah anggota himpunan A tersebut. Dalam hal ini informasi yang

tersedia tidak memungkinkan untuk memperoleh kepastian sepenuhnya mengenai

keanggotaan elemen tersebut dalam himpunan A. Sebagai contoh, misalnya kita

kita akan mencoba untuk menentukan apakah pasien ini termasuk himpunan

orang-orang penderita pneumonia, bronchitis, emphysema, atau penyakit panas

biasa. Pemeriksaan fisik dapat membantu seorang dokter untuk mendiagnosa

pen-yakit namun ini kurang meyakinkan. Sebagai contoh, kita menetapkan nilai yang

tinggi yaitu 0,75 untuk bronchitis dan nilai yang lebih rendah untuk kemungkinan

yang lain, seperti 0,45 untuk pneumonia dan emphysema dan 0 untuk penyakit

panas biasa. Di sini kita berhadapan dengan jenis ketidakpastisan yang secara

fundamental berbeda dengan ketidakpastian yang muncul sebagai akibat kaburnya

suatu istilah (predikat) yang kita pakai untuk membicarakan sesuatu.

Syarat batas menyatakan bahwa elemen yang sedang kita bicarakan pasti

tidak merupakan anggota himpunan kosong dan pasti merupakan anggota dari

semesta pembicaraan.

Sifat monoton menyatakan bahwa derajat kepastian bahwa elemen

tertentu merupakan anggota suatu himpunan haruslah paling sedikit sebesar

derajat kepastian elemen tersebut merupakan anggota dari sebarang himpunan

bagian dari himpunan itu. Dengan perkataan lain, kalau kita mengetahui dengan

derajat kepastian tertentu bahwa suatu elemen merupakan anggota suatu

himpunan, maka derajat kepastian bahwa elemen itu merupakan anggota

himpunan yang memuat himpunan tersebut haruslah lebih besar atau sama (dan

tidak lebih kecil) daripada derajat kepastian yang kita ketahui itu.

Syarat kontinyuitas, yang hanya dapat diberlakukan untuk himpunan

semesta yang takhingga, menyatakan bahwa pemetaan g haruslah suatu pemetaan

Pemetaan yang hanya memenuhi (1), (2), dan (3) atau (1), (2), dan (4)

saja disebut ukuran kabur semikontinyu. Kalau memenuhi (3) disebut kontinyu

dari bawah, dan kalau memenuhi (4) disebut kontinyu dari atas. Ukuran kabur

seperti didefinisikan di atas jelas merupakan generalisasi dari ukuran probabilitas,

bahkan generalisasi dari konsep ukuran. Generalisasi itu pada dasarnya

dilaksanakan dengan mengganti syarat aditif tercacah pada ukuran dengan syarat

yang lebih lemah, yaitu monoton dan kontinyu, atau paling tidak semikontinyu.

Karena (A∩B)⊆A dan (A∩B)⊆B untuk setiap dua himpunan A dan B,

maka dengan sifat monoton ukuran kabur akan kita peroleh

g (A∩B) ≤g (A) dan g (A∩B) ≤g (B)

sehingga g (A∩B) ≤ min {g(A), g(B)}

untuk setiap ukuran kabur g dan setiap dua himpunan A dan B dalam P(X).

Demikian pula karena A⊆ (A∪ B)dan B ⊆ (A∪ B), maka akan kita peroleh

g (A∪B) ≥ max {g(A), g(B)}

untuk setiap ukuran kabur g dan setiap dua himpunan A dan B dalam P(X).

Salah satu cabang khusus dari teori ukuran kabur adalah teori evidensi

yang akan dibahas berikut ini.

2. Teori Evidensi

Definisi 3.2.2.1

Andaikan P(X) adalah keluarga semua himpunan bagian dari X. Suatu

ukuran kepercayaan adalah suatu pemetaan

k : P(X) → [0,1]

yang memenuhi syarat-syarat berikut ini :

1. k(φ) = 0 dan k(X) = 1

sifat monoton dari ukuran kabur.

Jika A∈P(X) dan Ac = X−A, maka

1 = k(X) = k(A∪Ac) ≥k(A) + k(Ac) −k(A∩Ac) = k(A) + k(Ac).

Definisi 3.2.2.2

Hubungan antara ukuran kepercayaan dan ukuran plausibilitas adalah

p(A) = 1−k(Ac)

untuk setiap himpunan bagian A dalam semesta X, sehingga

k(A) = k((Ac)c)

Bila A dan B adalah himpunan bagian dari X, dengan A∈B, maka Bc∈Ac,

sehingga p(A) = 1−k(Ac) < 1−k(Bc) = p(B), yang memperlihatkan bahwa ukuran

plausibilitas juga memenuhi sifat monoton dari ukuran kabur.

Pemetaan di atas disebut pemetaan dasar probabilitas. Untuk setiap himpunan

A∈P(X), bilangan m(A) menyatakan derajat evidensi yang mendukung

keanggotaan suatu elemen tertentu dari X dalam himpunan A berdasarkan semua

informasi yang tersedia. Nilai m(A) tersebut hanya berlaku untuk himpunan A

saja, dan tidak untuk himpunan-himpunan bagian manapun dari A. Karena untuk

pemetaan dasar tersebut

1. Tidak disyaratkan bahwa m(X) = 1

2. Tidak disyaratkan bahwa jika A⊆B maka m(A) ≤ m(B)

3. Tidak disyaratkan ada hubungan antara m(A) dan m(Ac),

maka jelas bahwa m bukan suatu ukuran kabur.

Ukuran kepercayaan dan ukuran plausibilitas dapat didefinisikan secara unik

de-ngan menggunakan pemetaan dasar, yaitu sebagai berikut:

untuk setiap A∈ P(X).

Sebaliknya, ukuran kepercayaan k dapat dipakai untuk mendefinisikan pemetaan

dasar m, yaitu

m(A) = ∑ −

⊆ −

A B B

B A

B k( ) 1

untuk setiap A∈ P(X).

Hubungan antara m(A) dan k(A) yang dinyatakan pada (i) di atas

mempunyai arti sebagai berikut: m(A) menyatakan derajat evidensi bahwa suatu

elemen adalah anggota himpunan A, sedangkan k(A) mewakili keseluruhan

evidensi bahwa elemen itu adalah anggota himpunan A. Ukuran plausibilitas p(A),

seperti dinyatakan pada (ii), mempunyai arti yang berlainan, yaitu bahwa ukuran

plausibilitas tidak hanya mewakili total evidensi bahwa elemen itu adalah anggota

himpunan A atau himpunan bagian dari A, tetapi juga evidensi atau kepercayaan

tambahan yang dikaitkan dengan himpunan-himpunan yang beririsan dengan

himpunan A. Maka

p(A) ≥k(A)

untuk semua A ∈ P(X).

Himpunan A∈P(X) dengan m(A) > 0 disebut elemen fokus dari m, dalam

arti evidensi yang tersedia terfokus pada himpunan bagian dari X yang demikian

itu. Bila ℱ adalah himpunan elemen-elemen fokus dari m maka pasangan (ℱ,m)

Jika kita mengetahui bahwa elemen tertentu berada dalam suatu

himpunan semesta X, namun tidak tahu sama sekali elemen itu berada dalam

himpunan bagian mana dari X, maka kasus ini disebut dengan ketidaktahuan total,

yang dapat dinyatakan dengan

1. Pemetaan dasar:

berbeda dinyatakan dengan dua pemetaan dasar m₁ dan m₂ dan dapat

dikombinasikan untuk memperoleh pemetaan dasar gabungan m1.2. Evidensi dapat

dikombinasikan dalam berbagai macam cara, dengan mempertimbangkan

keandalan sumber-sumbernya dan aspek-aspek lainnya yang relevan. Cara baku

untuk mengombinasikan dua pemetaan dasar adalah

( )

( ) ( )

Aturan ini disebut aturan kombinasi Dempster. Menurut aturan ini, derajat

derajat evidensi m₂(C) dari sumber kedua yang berfokus pada himpunan C∈P(X)

dikombinasikan dengan menggunakan perkalian m₁(B).m₂(C), yang berfokus

pada himpunan B∩C . Tetapi karena mungkin ada irisan-irisan elemen fokus dari

sumber pertama dan sumber kedua yang sama-sama menghasilkan himpunan A,

maka kita harus menjumlahkan perkalian-perkaliannya untuk memperoleh

2 . 1

m (A). Irisan tersebut mungkin pula merupakan himpunan kosong. Karena kita

menyaratkan m_1.2(φ) = 0, maka K dalam rumus di atas tidak dimasukkan dalam

definisi m_1.2. Jumlahan semua perkalian m1(B).m2(C) untuk semua

elemen-elemen fokus B dari m1dan elemen-elemen fokus C dari m2 sedemikian sehingga

B∩C ≠ φ sama dengan 1−K. Untuk menormalkan pemetaan dasar m1.2 kita

membagi jumlahan tersebut dengan 1−K.

Contoh 3.2.2.1

Misalkan sebuah lukisan kuno ditemukan, yang sangat mirip dengan lukisan

Leo-nardo da Vinci. Penemuan seperti itu biasanya menimbulkan berbagai pertanyaan,

yang berhubungan dengan status lukisan itu, misalnya :

1. Apakah lukisan yang ditemukan itu adalah lukisan asli hasil karya Leonardo

da Vinci ?

2. Apakah lukisan yang ditemukan itu adalah hasil karya salah seorang murid

Leonardo da Vinci?

Misalkan semesta X adalah himpunan semua lukisan, dan L, M, dan P adalah

himpunan bagian dari X, yang berturut-turut memuat semua lukisan Leonardo da

Vinci, semua lukisan murid Leonardo da Vinci, dan semua lukisan palsu.

Misal-nya ada dua orang ahli yang memeriksa dengan saksama lukisan itu dan kemudian

memberikan nilai m1 dan m2 (lihat Tabel 3.2.2.1).

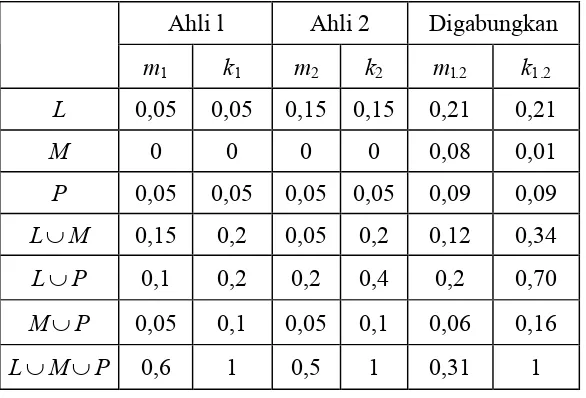
Tabel 3.2.2.1.Kombinasi tingkat evidensi dari dua sumber yang berbeda

Ahli l Ahli 2 Digabungkan

m1 k1 m2 k2 ml.2 k1.2

L 0,05 0,05 0,15 0,15 0,21 0,21

M 0 0 0 0 0,08 0,01

P 0,05 0,05 0,05 0,05 0,09 0,09

L∪M 0,15 0,2 0,05 0,2 0,12 0,34

L∪P 0,1 0,2 0,2 0,4 0,2 0,70

M∪P 0,05 0,1 0,05 0,1 0,06 0,16

L∪M∪P 0,6 1 0,5 1 0,31 1

Ini adalah tingkat evidensi yang diberikan oleh masing-masing ahli dalam

penyelidikan itu dan yang mendukung dugaan bahwa lukisan itu termasuk dalam

salah satu himpunan. Misalnya: m1(L∪M) = 0.15 adalah tingkat evidensi yang

diperoleh dari ahli pertama bahwa lukisan itu dikerjakan oleh Leonardo da Vinci

menghitung evidensi total, k1 dan k2, untuk masing-masing himpunan, seperti

ditunjukkan dalam Tabel 3.2.2.1.

Dengan menggunakan Aturan Dempster untuk m1 dan m2, kita

mendapatkan m1.2 seperti yang terlihat dalan Tabel 3.2.2.1. Untuk menentukan

nilai m1.2, pertama kita menghitung faktor penormal 1−K.

K = m1.(L) m2.(M) + m1.(L) m2.(C) + m1.(L).m2(M∪P) + m1(M).m2(L) +

m1(M).m2(P) + m1(M).m2(L∪P) + m1(P).m2(L) + m1(P).m2(M )+

m1(P).m2(L∪M) + m1(L∪M).m2(P) + m1(L∪P) + m1.m2(M) +

m1(M∪P).m2(L)

= 0,05.0 + 0,05.0,05 + 0,05.0,05 + 0.0,15 + 0.0,05 + 0.0,2 + 0,05.0,15 +

0,05.0 + 0,05.0,05 + 0,15.0,05 + 0,0.0 +0,05.0,15

= 0 + 0,0025 + 0,0025 + 0 + 0 + 0 + 0,0075 + 0 + 0,0025 + 0,0075 + 0 +

0,0075

= 0,03.

Maka didapat faktor penormal 1−K = 1 0,03 = 0,97. Nilai dari − m1.2 dapat

dihitung.

Sebagai contoh,

m1.2 (L) = [m1 (L).m2(L) + m1.(L). m2 (L∪M) + m1.(L).m2(L∪P) +

m1(L).m2(L∪M∪P) + m1(L∪M).m2(L) + m1(L∪M).m2(L∪P)

+m1(L∪P).m2(L) +m1(L∪P).m2(L∪D)+ m1(L∪M∪P).m2(L)]

/0,97

= [0,05.0,15 + 0,05.0,05 + 0,05.0,2 + 0,05.0,5 + 0,15.0,15 +

= [0,0075 + 0,0025 + 0,01 + 0,025 + 0,0225 + 0,03 +0,01 + 0,01

+ 0,09] / 0,97

= 0,2075 / 0,97

= 0,21

m1.2(M) = [m1(M).m2(M + m1(M).m2(L∪M) + m1(M).m2(M∪P) +

m1(M).m2(L∪M∪P)+m1(L∪M).m2(M)+m1(L∪M).m2(M∪P)+

m1(M∪P).m2(M)+m1(M∪P).m2(L∪M)+m1(L∪M∪P).m2(M)]

/ 0,97

= [0.0 + 0.0,05 + 0.0,05 + 0.0,0 + 0,15.0 + 0,15.0,05 + 0,05.0 +

0,05.0,05 + 0,6.0] / 0,97

= [0 + 0 + 0 + 0 + 0 + 0,075 + 0 + 0,0025 + 0] / 0,97

= 0,00775 / 0,97

= 0,08

m1.2(L∪P) = [m1(L∪P).m2(L∪P) + m1(L∪P).m2(L∪M∪P) +

m1(L∪M∪P).m2(L∪P)] / 0,97

= [0,1.0,2 + 0,1.0,5 + 0,6.0,2] / 0,97

= [0,02 + 0,05 + 0,12] / 0,97

= 0,19 / 0,97

= 0,2

= 0,3 / 0,97

= 0,31

k1.2(L∪P) = [ k1 (L∪P).k2(L∪P) + k1(L∪P).k2(L∪M∪P) +

k1(L∪M∪P).k2(L∪P)] / 0,97

= [0,2.0,4 + 0,2.1+ 1.0,4]/0,97

= [0,08 + 0,2 + 0,4] / 0,97

= 0,68 / 0,97

= 0,70

k1.2(L∪M∪P) = [ k1 (L∪M∪P).k2(L∪M∪P)] / 0,97

= [1.1] / 0,97

= 1 / 0,97

= 1.

Sekarang misalkan pemetaan dasar m didefinisikan pada darab Cartesius

Z = X

×

Y

m : P(X × Y) → [0,1].

Setiap elemen fokus dari m adalah relasi biner R pada X ×Y. Jika RX adalah

proyeksi R pada X, maka

(i) RX = {x∈X (∃y∈Y)(x,y)∈R} ⊆X

dan jika R_Y adalah proyeksi R pada Y, maka

Kita dapat mendefinisikan proyeksi _mX dari pemetaan dasar m pada X, yaitu

mX(A) = ∑

=RX

A R

R

m( ) untuk setiap A ∈P(X)

dan proyeksi m pada Y, yaitu

mY(B) = ∑

=RY

B R

R

m( ) untuk setiap B∈ P(Y).

Untuk menghitung mX(A), kita menjumlahkan semua nilai m(R) untuk

elemen fokus R yang proyeksinya pada X adalah A. Fungsi mX dan mY adalah

pemetaan dasar khusus, sedangkan (ℱx, mX) dan (ℱy, mY) adalah badan evidensi

marginal.

Definisi 3.2.2.3

Dua badan evidensi marginal (ℱx, m_X) dan (ℱy, m_Y) dikatakan noninteraktif

jika dan hanya jika untuk semua A∈ ℱx dan semua B∈ ℱy

m (A

×

B) = mX(A).mY(B)

dan

m(R) = 0 untuk semua R≠A

×

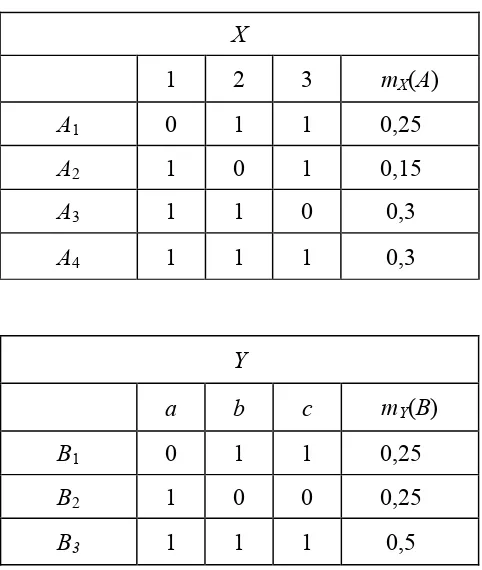
B.

Contoh 3.2.2.2

Diberikan badan evidensi dalam Tabel 3.2.2.2 dengan elemen fokus adalah

him-punan bagian dari darab Cartesisus X

×

Y, di mana X = {1, 2, 3} dan Y ={a, b, c}.

Dengan menggunakan rumus di atas, kita memperoleh badan evidensi marginal

seperti terlihat pada Tabel 3.2.2.3. Sebagai contoh

mX(A1) = mX ({2,3}) = m(R1) + m(R2) + m(R3)

= 0,0625 + 0,0625+0,125

= 0,25

mX(A2) = mX({1,3}) = m(R4) + m(R7) + m(R10)

= 0,0375 + 0,0375 + 0,075

= 0,15

mX (A3) = mX ({2,3}) = m(R5) + m(R8) + m(R11)

= 0,075 + 0,075 + 0,15

= 0,3

mY (B2) = mY ({a}) = m(R2) + m(R7) + m(R8) + m(R9)

= 0,0625 + 0,0375 + 0,075 + 0,075

= 0,25

mY(B3) = mY ({a,b,c}) = m(R3) + m(R10) + m(R11) + m(R12)

= 0,125 + 0,075 + 0,15 + 0,15

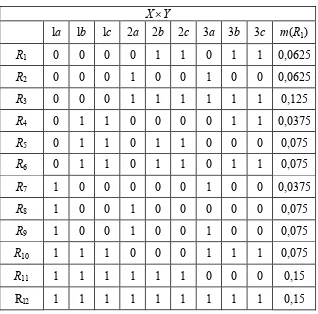
Tabel 3.2.2.2 Badan evidensi

X×Y

la lb lc 2a 2b 2c 3a 3b 3c m(R1)

R1 0 0 0 0 1 1 0 1 1 0,0625

R2 0 0 0 1 0 0 1 0 0 0,0625

R3 0 0 0 1 1 1 1 1 1 0,125

R4 0 1 1 0 0 0 0 1 1 0,0375

R5 0 1 1 0 1 1 0 0 0 0,075

R6 0 1 1 0 1 1 0 1 1 0,075

R7 1 0 0 0 0 0 1 0 0 0,0375

R8 1 0 0 1 0 0 0 0 0 0,075

R9 1 0 0 1 0 0 1 0 0 0,075

R10 1 1 1 0 0 0 1 1 1 0,075

R11 1 1 1 1 1 1 0 0 0 0,15

Tabel 3.2.2.3 Badan Evidensi Marginal

X

1 2 3 mX(A)

A1 0 1 1 0,25

A2 1 0 1 0,15

A3 1 1 0 0,3

A4 1 1 1 0,3

Y

a b c mY(B)

B1 0 1 1 0,25

B2 1 0 0 0,25

B3 1 1 1 0,5

Akan kita lihat apakah badan evidensi marginal bersifat noninteraktif.

m(A1 ×B1) = m(R1)

= 0,0625

= 0,25 . 0,25

= mX(A1).mY(B1)

m(A1 × B2) = m(R2)

= 0,0625

= 0,25 . 0,25

= mX (A1).mY(B2)

Perhatikan bahwa A1 × B2 = {2,3} × {a} = {2a, 3a} = R2.

m(A1×B3) = m(R3)

= 0,125

= 0,25 . 0,5

= mX(A1) .mY(B3)

Perhatikan bahwa A1×B3= {2,3} × {a, b, c} = {2a, 2b, 2c, 3a, 3b, 3c } =R3.

m(A2 × B1) = m(R4)

= 0,0375

= 0,15.0,25

= mX(A2) .mY(B1)

Perhatikan bahwa A2 × B1 = {1,3} × {b, c} = {lb, 1c, 3b, 3c } = R4.

m(A3×B1) = m(R5)

= 0,075

= 0,3 . 0,25

= mX (A3).mY(B1)

m(A4× B1) = m(R6)

= 0,075

= 0,3 . 0,25

= mX(A4).mY(B1)

Perhatikan bahwa A4× B1 ={1,2,3}×{b,c} = {1b, 1c, 2b, 2c, 3b, 3c } = R6.

m(A2× B2) = m(R7)

= 0,0375

= 0,15.0,25

= mX(A3).mY(B2)

Perhatikan bahwa A2× B2 = {1,3} ×{ a} = {la, 3a } = R7.

m(A3 × B2) = m(R8)

= 0,075

= 0,3 . 0,25

= mX(A3).mY(B2)

Perhatikan bahwa A3 × B2 = {1,2} ×{ a) = {la, 2a } =R8.

m(A4×B2) = m(R9)

= 0,075

= 0,3 . 0,25

= mX(A4).mY(B2)

m(A2×B3) = m(R10)

= 0,075

= 0,15.0,5

= mX(A2).mY(B3)

Perhatikan bahwa A2×B3 ={1,3} × {a,b,c} = {la, 1b, 1c, 3a, 3b, 3c} = R10.

m(A3×B3) = m(R11)

= 0,15

= 0,3 . 0,5

= mX(A3).mY(B3)

Perhatikan bahwa A3×B3= {1,3} × {a,b,c} = {la, 1b, 1c, 3a, 3b, 3c} = R11.

m(A3 ×B3) = m(Rl2)

= 0,15

= 0,3 . 0,5

= mX(A4).mY(B3)

Perhatikan bahwa A3 ×B3 ={1,2,3} × {a,b,c}

= {la, 1b, 1c, 2a, 2b, 2c, 3a, 3b, 3c} = Rl2.

Jadi, badan evidensi khusus bersifat noninteraktif karena untuk semua A∈ ℱxdan

Tabel 3.2.2.4 Hubungan antara pemetaan dasar, ukuran kepercayaan,

Suatu cabang dari teori evidensi yang hanya menyangkut badan-badan

evidensi dengan elemen-elemen fokus yang tersarang (nested) dikenal dengan

nama teori posibilitas. Bagian khusus dari ukuran kepercayaan dan ukuran

plausibilitas dalam teori posibilitas adalah ukuran nesesitas dan ukuran

posibilitas.

Bila ℒ ={ A1,A2,...} adalah suatu keluarga himpunan-himpunan

sedemikian sehingga A_i ⊂ A_i+1 untuk setiap i = 1,2,..., maka ℒ disebut keluarga

himpunan-himpunan yang tersarang (nested). Sebelum membahas teori tersebut,

Teorema 3.2.3.1

Bila (ℱ, m) adalah suatu badan evidensi berhingga yang tersarang, maka ukuran

kepercayaan dan ukuran plausibilitas yang berkaitan dengannya mempunyai sifat

(i) k(A∩B) = min {k(A), k(B)}

dan b adalah bilangan positif terbesar i sedemikian sehingga Ai ⊆ B.

yang membuktikan bagian kedua dari teorema tersebut. ■

Definisi 3.2.3.1

Suatu ukuran kepercayaan nes yang berkaitan dengan badan evidensi

yang tersarang disebut ukuran nesesitas.

Berdasarkan Teorema 3.2.3.1 diperoleh

nes( I K

k k

A

∈ ) = infk∈K nes(Ak)

untuk setiap keluarga bagian {Akk∈K} dalam P(X), di mana K adalah suatu

himpunan indeks.

Definisi 3.2.3.2

Suatu ukuran plausibilitas pos yang berkaitan dengan badan evidensi

yang tersarang disebut ukuran posibilitas.

Berdasarkan Teorema 3.2.3.1 diperoleh

pos ( U K

k k

A

∈ ) = k∈K

sup pos(A_k)

untuk setiap keluarga bagian {Ak k∈K } dalam P(X), di mana K adalah suatu

himpunan indeks.

Karena ukuran nesesitas adalah ukuran kepercayaan yang khusus, dan

nes(A) + nes(Ac) ≤ 1

pos(A) + pos(Ac) ≥ l

nes(A) = 1 pos(− Ac)

pos(A) = 1−nes{Ac).

Teorema 3.2.3.2

Untuk setiap himpunan A ∈ P(X)

(i) Bila nes(A) > 0, maka pos(A) = 1

(ii) Bila pos(A) < 1, maka nes(A) = 0.

Bukti:

(i) Dari definisi ukuran nesesitas kita memperoleh

min{nes(A), nes(Ac)} = nes(A∩Ac) = 0.

Jadi jika nes(A) > 0, maka haruslah nes(Ac)=0, sehingga

pos(A) = 1 − nes(Ac) = 1.

(ii) Dari definisi ukuran posibilitas kita memperoleh

max{pos(A), pos(Ac)} = pos(A∪ Ac) = 1

Jadi jika pos(A) < 0, maka haruslah pos(Ac) = 1, sehingga

nes(A) = 1 − pos(Ac) = 0 . ■

Diberikan ukuran posibilitas pos pada P(X). Pemetaan r : X→ [0,1] yang

didefinisikan dengan r(x) = pos({x}) untuk setiap x ∈ X disebut fungsi distribusi

Teorema 3.2.3.3

Setiap ukuran posibilitas pos yang didefinisikan pada himpunan kuasa P(X) yang

berhingga dapat ditentukan secara tunggal oleh fungsi distribusi posibilitas r yang

berkaitan dengannya dengan aturan

max ) (

A x

A pos

∈ = r(x)

untuk setiap A ∈ P(X).

Bukti:

Kita buktikan dengan induksi matematis pada kardinalitas dari himpunan A.

Un-tuk A= 1, maka A = {x}, untuk suatu x ∈ X , sehingga pos (A) = pos ({x}) =

max A x∈

r(x). Selanjutnya andaikan aturan tersebut dipenuhi untuk A= n−1. Untuk

A = {x1,x2,…,xn} berlaku

pos(A) = pos({xl, x2,…, xn-1}∪{xn})

= max{pos({xl, x2,…, xn-1}),pos({xn})}

= max{max{r(x1), r(x2),…, r(xn-l)}, pos({xn})}

= max{max{pos({x1), pos({x2}),…, pos({xn-1}), pos({xn})}

= max {pos({x1), pos({x2}),…, pos{{xn-1}), pos({xn })}

= max{r(x1), r(x2),…,r(xn-1), r(xn)}

= max A x∈

{ r(x)}

Jika X tak berhingga, maka persamaan dalam Teorema 3.2.3.3 diubah menjadi

dengan fungsi r. Banyaknya komponen dalam suatu distribusi posibilitas disebut

panjang distribusi posibilitas itu..

Distribusi posibilitas dapat diurutkan sedemikian sehingga r_i ≥r_j jika

i< j. Misalkan adalah _Rn_{himpunan semua distribusi posibilitas dengan panjang}

n, dan

Jika diberikan dua distribusi posibilitas,

1

dengan join∨ dan meet ∧ didefinisikan sebagai berikut

r

dan

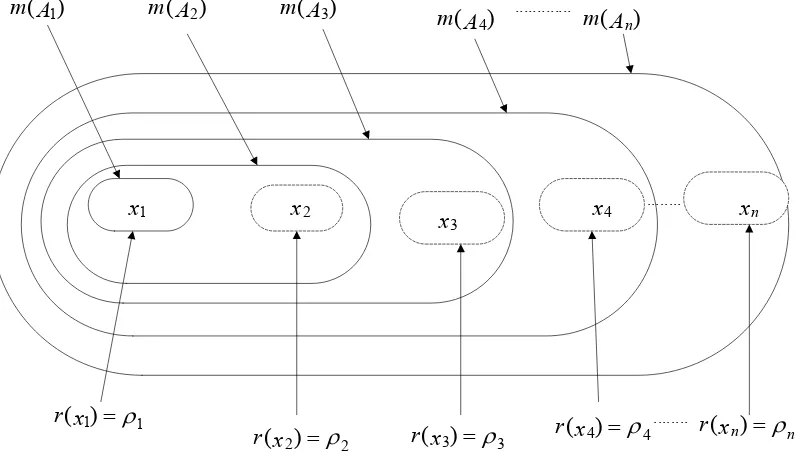
P(X) dengan pemetaan dasar m. Sesuai dengan definisi dari ukuran posibilitas,

semua elemen fokus adalah tersarang. Misalkan elemen-elemen fokus adalah

sebagian atau semua himpunan bagian dalam barisan lengkap

himpunan-himpunan bagian yang tersarang

x2

Gambar 3.2.3.1a Barisan lengkap himpunan-himpunan bagian tersarang dari X

x1 x2 x3 x4

Tidak disyaratkan bahwa m(A_i)≠0 untuk setiap i∈Νn, seperti contoh pada

Gambar 3.2.3.1b.

Sesuai pembicaraan m(A_i)≠0 sebelumnya, setiap ukuran posibilitas

pada himpunan semesta yang berhingga dapat dinyatakan dengan n-tuple

m = m₁,m₂,...,m_n

himpunan semua distribusi dasar dengan panjang n, dan

M

satu distribusi posibilitas r∈R, begitu juga sebaliknya. Berdasarkan Teorema

3.2.3.3 dan definisi ukuran posibilitas sebagai ukuran plausibilitas khusus

diperoleh

dengan satu persamaan untuk setiap i∈Ν_n. Jika ditulis dengan lebih eksplisit

.

mendefinisikan suatu korespondensi satu-satu

M R

t: ↔

antara distribusi posibilitas dan distribusi dasar. Jika diberikan

r = r₁,r₂,...,r_n dan m = m₁,m₂,...,m_n ∈M

untuk suatu n∈N, maka t(r) = m jika dan hanya jika (iv) dipenuhi, dan t−1(m) =

r jika dan hanya jika (iii) dipenuhi.

Fungsi t tersebut memungkinkan kita untuk mendefinisikan urutan parsial

pada himpunan M berdasarkan urutan parsial pada himpunan R. Untuk semua

2

Perhatikan fungsi m pada Gambar 3.2.3.1b. Kita amati bahwa (i) dipenuhi, tetapi

barisan_A1⊂ _A2 ⊂...⊂ _A7 dari himpunan-himpunan bagian yang tersarang.

Menerapkan persamaan (iii) pada distribusi dasar tersebut untuk semua i∈Ν₇,

kita dapatkan distribusi posibilitas

2

seperti terlihat dalam Gambar 3.2.3.1b. Sebagai contoh

7

Derajat posibilitas pos(A) dapat dihitung untuk setiap himpunan bagian A dari X =

{_x1,_x2,..,_x7} dari komponen-komponen distribusi posibilitas r dengan Teorema

3.2.3.3. Sebagai contoh,

Berdasarkan (ii) dan (iii) diperoleh bahwa r₁ =1 untuk setiap distribusi posibilitas

r = r₁,r₂,...,r_n ∈Rn

řn= 1,0,0,...,0

dengan n – 1 nol. Distribusi posibilitas ini dengan pemetaan dasar

t(ř_n) = 1,0,0,...,0,0

yang mempunyai bentuk yang sama, mempresentasikan evidensi sempurna

dengan tanpa ketidakpastian yang terlibat. Distribusi posibilitas terbesar

n

rˆ dengan panjang n terdiri dari 1 semua, dan

t(rˆ ) = _n 0,0,...,0,1

dengan n – 1 nol. Distribusi ini menunjukkan ketidaktahuan total, yaitu suatu

keadaan di mana tidak ada evidensi yang relevan. Pada umumnya, semakin besar

distribusi posibilitas, evidensi semakin kurang spesifik dan akibatnya

ketidaktahuan menjadi lebih besar.

Sekarang kita bahas distribusi posibilitas bersama r yang didefinisikan

pada darab Cartesius X ×Y. Proyeksi rX dan rY dari r, yang disebut distribusi

posibilitas marginal, didefinisikan dengan formula

r (x) maxr(x,y)

Y y

X = _∈ (v)

untuk setiap x∈X dan

r (y) maxr(x,y)

X x

Y = _∈ (vi)

untuk setiap y∈Y.

Formula ini diturunkan langsung dari Teorema 3.2.3.3. Perhatikan bahwa untuk

himpunan {(x,y)y∈Y}, yaitu pasangan dalam X ×Y untuk mana distribusi

bersama didefinisikan. Maka

(vii)

di mana pos_X dan pos adalah ukuran posibilitas yang bersesuaian dengan r_X

dan r. Menurut Teorema 3.2.3.3, ruas kiri persamaan (vii) adalah

)

Jadi diperoleh persamaan (v).

Definisi 3.2.3.4

Badan-badan evidensi tersarang pada X dan Y, yang direpresentasikan

oleh fungsi distribusi posibilitas r_X dan r_Y, disebut noninteraktif jika dan hanya

jika

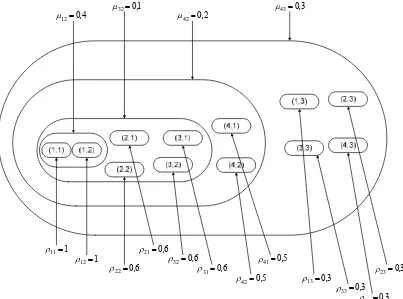
Suatu contoh badan evidensi tersarang noninteraktif diberikan dalam Gambar

3.2.3.2 dan 3.2.3.3. Dalam Gambar 3.2.3.3 terlihat bahwa

) , min( _{i j}

ij r r

r = ′ ,

untuk setiap posibilitas bersama r_ij di mana r_i,r_j′ adalah posibilitas marginal yang

6

Definisi noninteraksi posibilistik ini (Definisi 3.2.3.4) tidak berdasarkan pada

aturan produk dari teori evidensi. Maka definisi itu tidak sesuai dengan definisi

umum dari badan evidensi noninteraktif (seperti pada Definisi 3.2.2.3). Aturan

produk tersebut tidak dapat digunakan untuk mendefinisikan noninteraksi

posibilistik karena aturan itu tidak mempertahankan struktur tersarang dari

elemen-elemen fokus. Hal ini dapat diilustrasikan dalam Contoh 3.2.3.2 di bawah

ini.

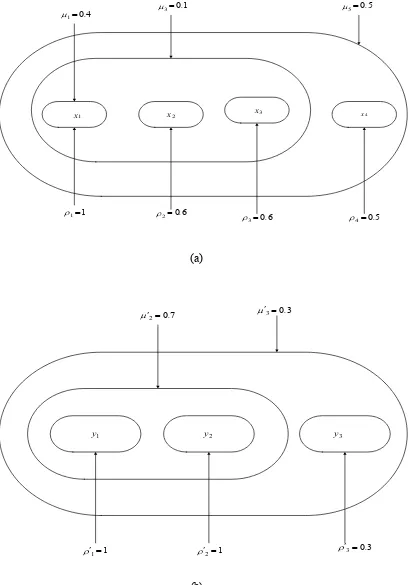
Contoh 3.2.3.2

Perhatikan distribusi posibilitas marginal dan distribusi dasar pada Gambar 3.2.3.2

yang mewakili dua badan evidensi tersarang. Jika kita mengombinasikannya

dengan Definisi 3.2.3.4, maka kita dapatkan distribusi posibilitas bersama, seperti

pada Gambar 3.2.3.5(a). Jadi hasil dari kombinasi dua badan evidensi yang

tersarang dengan operator min adalah tersarang lagi, sehingga kita tetap berada

dalam domain teori posibilitas. Sebaliknya, bila dipakai aturan produk, kita

memperoleh fungsi dasar bersama seperti pada Gambar 3.2.3.5(b). Fungsi dasar

ini tidak mewakili suatu badan evidensi tersarang, sehingga tidak berada dalam

domain teori posibilitas. Berdasarkan (v) dan (vi) diperoleh

x1 x2 x3 x4 4

0

1= .

μ μ3=0.1 μ5=0.5

1

1=

ρ ρ₂=0.6

6 0

3= .

ρ ρ₄=0.5

(a)

y₁ y₂ y₃

7 0

2= .

′

μ μ′3=0.3

1

1=

′

ρ ρ′₂=1 ρ′3=0.3

(b)

4

Gambar 3.2.3.3 Badan evidensi tersarang bersama

x1 x2

y1 y2

(b)

Gambar 3.2.3.4 Distribusi posibilitas marginal

y x1 1

y x2 1

y x1 2

y x2 2

Fungsi dasar bersama Distribusi posibilitas

bersama

y x1 1

y x1 2

y x2 1

y x2 2

(b)

Gambar 3.2.3.5 Fungsi dasar bersama

Ini berarti bahwa distribusi posibilitas bersama yang didefinisikan pada 3.2.3.4

adalah distribusi bersama terbesar yang memenuhi distribusi marginal yang

diberikan.

Misalkan r_X dan r_Y adalah fungsi distribusi posibilitas marginal pada X

dan Y berturut-turut, dan r adalah fungsi distribusi posibilitas bersama pada X ×Y

yang didefinisikan dalam r_X dan r_Y seperti pada Definisi 3.2.3.4.

Jika pos_X,pos_Y dan pos adalah ukuran posibilitas yang bersesuaian dengan r_X,

Y

)]

ukuran nesesitas yang berkaitan dengan ukuran posibilitas pos, pos_X ,pos_Y

berturut-turut, dan A + B adalah kodarab Cartesius A×B. Persamaan ini diperoleh

dari

Selanjutnya kita akan membicarakan konsep fungsi distribusi posibilitas

kondisional, yang penting untuk mendefinisikan kebebasan posibilistik.

Definisi 3.2.3.5

Dua badan evidensi posibilistik marginal dikatakan bebas jika dan hanya jika

posibilitas kondisionalnya tidak berbeda dengan posibilitas marginalnya yang

bersesuaian. Hal tersebut dinyatakan dengan persamaan