LANDASAN TEORI
2.1. Kriptografi
Kriptografi memiliki sejarah yang sangat panjang di mana kriptografi telah ditemukan sejak 3600 tahun yang lalu di lihat dari sudah di temukannya simbol - simbol yang di ukir pada lempeng tanah liat (clay disk) yang disebut dengan phaistos. Meskipun begitu awal mula kriptografi tidak hanya berawal dari bangsa Yunani, namun juga dari bangsa Mesir kuno. Di buktikan dengan di temukannya teks kuno yang di tuliskan oleh Firaun Amanemth II pada tahun 1900 SM. Di mana pesan itu di tuliskan dalam huruf hieroglip (hieroglyphic).(Mollin, 2005). Hieroglyphic merupakan bentuk tulisan dari zaman Mesir kuno yang berupa gambar maupun simbol – simbol yang merupakan sebuah pesan. (Fischer, 1999)
2.2. Tujuan Kriptografi
Tujuan dari kriptografi yang juga merupakan aspek penting dalam proses keamanan data dan informasi adalah sebagai berikut: (Scheiner, 1996).
1. Authentication (Autentikasi)
Berfungsi untuk memberikan kepastian terhadap identitas – identitas yang terlibat,
meyakinkan ke aslian data, sumber data orang yang mengakses dan server yang digunakan.
2. Confidentiality (Kerahasiaan)
Di gunakan untuk menjaga informasi dari semua pihak kecuali pihak yang memiliki otoritas terhadap informasi.
3. Data Integrity (Integritas Data)
Di gunakan untuk memastikan agar informasi yang di kirimkan tidak mengalami modifikasi maupun manipulasi dari pihak yang tidak bersangkutan selama pengiriman.
4. Non-Repudiation (Nipernyangkalan)
Berfungsi untuk menjaga semua entitas – entitas yang saling terhubung sehingga tidak terjadi penyangkalan data yang dikirimkan ataupun yang diterima
2.3. Sistem Kriptografi
Sisem kriptografi klasik umumnya menggunakan metode subtitusi atau transposisi dan telah digunakan jauh sebelum komputer di temukan. Terdapat 5 komponen utama dalam sistem kriptografi klasik, yaitu (Wandani, 1012):
1. Plaintext
Teks asli, dapat berupa pesan atau data sebagai input algoritma enkripsi 2. Kunci Rahasia
Kunci rahasia disebut sebagai penentu output dari algoritma enkripsi. Antar entitas harus saling mengetahui kunci ini agar dapat berkomunikasi.
3. Ciphertext
Hasil proses algoritma enkripsi di mana teks asli dianggap telah tersembunyi. 4. Algoritma Enkripsi
Algoritma enkripsi mengubah teks asli menjadi ciphertext dengan parameter masukan, yaitu teks asli kunci rahasia.
5. Algoritma Dekripsi
Enkripsi adalah suatu proses yang melakukan perubahan kode dari bisa dimengerti (plaintext) menjadi kode yang tidak bisa di mengerti (ciphertext). Proses pembaikannya plaintext dari ciphertext disebut dekripsi. Secara umum operasi enkripsi dan dekripsi secara matematis dapat digambarkan.
EK (M) = C (Proses Enkripsi)
DK (C) = M (Proses Dekripsi)
Dengan Keterangan:
M = Pesan yang dirahasiakan C = Plaintext
D = Dekripsi
E = Mekanisme enkripsi
K = Simbol kuci yang digunakan.
Pembacaan rumus tersebut adalah proses enkripsi E dengan kunci K akan di lakukan pengolahan pesan m menjadi pesan C, dan C adalah ciphertext atau pesan hasil enkripsi yang di harapkan berbeda dan tidak mampu menyikap informasi aslinya dari pesan M.
Proses pembalikannya yaitu proses dekripsi. Pada proses dekripsi dengan kunci K, pesan C akan disandikan kembali menjadi pesan semula yaitu M sehingga di peroleh kembali pesan aslinya. Yang menjadi penting dalam proses enkripsi-dekripsi tidak hanya algoritma yang di gunakan tetapi juga kunci enkripsi. Kunci merupakan kata kunci yang digunakan dalam proses penyandian. Untuk itu walaupun algoritma enkripsi dan dekripsi di ketahui oleh publik, kunci K harus di rahasiakan.
2.4. Kriptosistem
Kriptosistem (cryptosystem atau Cryptographic system) adalah suatu fasilitas untuk mengkonversikan plaintext ke ciphertext dan sebaliknya. Dalam sistem ini, seperangkat parameter yang menentukan transformasi penyandian tertentu disebut satu set kunci. Proses enkripsi atau dekripsi diatur oleh satu atau beberapa kunci kriptorafi.
Gambar 2.2. Proses Enkripsi Dan Dekripsi Asymetric Cryptosystem
2.4.3. Kriptosistem Hibrid (Hybrid Cryptosystem)
Kriptosistem hibrid (Hybrid cryptosystem) merupakan suatu sistem kriptografi yang menggabungkan sistem kriptografi simetri dan sistem keriptografi asimetri (Azizah, 2013) sehingga di dapatlah sebuah kriptosistem dengan fungsi algoritma yang lebih kompleks.
2.5. Teknik Dasar Kriptografi
2.5.1 Teknik Subtitusi
Teknik subtitusi adalah suatu teknik kriptografi di mana pesan yang telah di tulis akan di ganti suatu kode dengan kode yang lain, dengan menggunakan tabel subtitusi. Dapat di tampilkan dalam tabel 2.1.
Tabel 2.1. Teknik subtitusi
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z J X E Q S A M H Z C T L O V F B Y U D W I K G P R N
2.5.2. Teknik Blocking
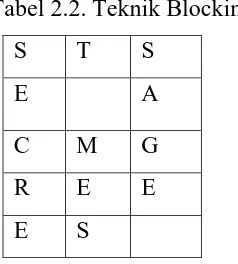
Teknik blocking yaitu membagi pesan plaintext kedalam blok-blok pesan yang kemudian akan di enkripsi secara independen. Misalkan kalimat “SECRET MESSAGE” akan di bagi kedalam blok-blok seperti tabel 2.2.
Tabel 2.2. Teknik Blocking
S T S
E A
C M G
R E E
E S
Selajutnya teknik dapat di enkripsi per-blok, misalkan untuk proses pengacakan sederhana dengan pembacaaan yang terbalik yaitu karena proses penyimpanan pada blok dilakukan per kolom, maka proses enkripsi akan dilakukan dengan cara menaruh kalimat “GNIKCOLB KINKET” pada blok-blok pesan berbaris dan membaca dengan per-kolom dan menjadi kalimat “TEKNIK BLOCKING” kembali.
2.5.3. Teknik permutasi
Teknik permutasi sering juga disebut transposisi. Teknik ini memindahkan atau merotasikan karakter dengan aturan tertentu, prinsipnya adalah berlawanan tetap tapi identitasnya yang diacak. Sebelum dilakukakn permutasi, umumnya plaintext terlebih dahulu di bagi menjadi blok-blok dengan panjang yang sama. Untuk contoh di atas, plaintext dibagi menjadi blok terdiri dari 5 karakter, dengan aturan permutasi berikut:
0 1 2 3 4 5 6 7 8 9
9 3 4 1 2 7 8 5 6 0
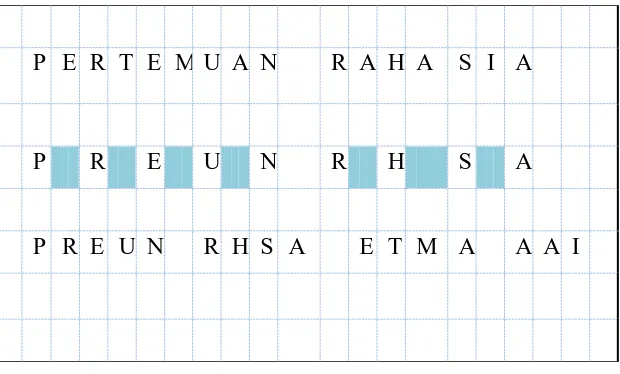
Misalkan kalimat “PERTEMUAN RAHASIA” di enkripsi menjadi “NREETAUMP HARAAIS” dengan cara membaginya kalimat kedalam blok – blok dan melakukan proses permutasi seperti pada gambar di atas dengan teknik pengacakan. Proses dekripsi dilakukan serupa denga membagi kedalam 5 blok pula dan membalik permutasinya.
Gambar 2.4. Teknik Permutasi (Munir, 2008).
2.5.4. Teknik Ekspansi
Teknik akan menambahkan beberapa byte kata kedalam plaintext dengan aturan tertentu. Proses penambahan beberapa byte kata ini diharapkan dapat menyembunyikan informasi dapat plaintext. Salah satu contoh penggunaan teknik ini adalah dengan menukar huruf awal dan akhir kata yang diberi awalan “an” proses enkripsi dengan cara ekspansi terhadap plaintext terjadi sebagai berikut:
Gambar 2.5. Teknik Ekspansi (Munir 2008)
P E R T E M U A N R A H A S I A
N R E E T A U M P H A R A A I S
8 A N P E R T E M U A N A N R A H A S I A A N
Ciphertextnya adalah “8AN NREETAUMPAN HARAAISAN”. Aturan ekspansi dapat dibuat lebih kompleks dan terkadang teknik ekspansi dapat di gabungkan dengan teknik lainnya.
2.5.5. Teknik Pemampatan (Compaction)
Mengurangi panjang pesan atau jumlah bloknya adalah cara lain untuk menyembunyikan isi pesan. Misalkan untuk plaintext “PERTEMUAN RAHASIA” setiap kata ke dua akan di hilangkan dan di sertakan pada akhir kalimat yang sebelumnya di beri tanda “ ”. Proses yang terjadi untuk plaintext tersebut adalah:
Gambar 2.6. Teknik Pemampatan.
Aturan penghilangan karakter dan karakter khusus dan berfungsi sebagai pemisah menjadi dasar untuk proses dekripsi ciphertext menjadi plaintext kembali. Dengan menggunakan kelima menjadi teknik kriptografi diatas, dapat di ciptakan teknik kriptografi yang amat banyak walaupun sekilas terlihat sederhanana, kombinasi teknik dasar kriptografi dapat menghasilkan teknik kriptografi turunan yang cukup kompleks, dan bebrapa teknik dasar kriptografi masih di gunakan dalam kriptografi modern.
2.6. Algoritma Euclid dan Extended Euclid
Salah satu cara untuk menentukan GCD (Greatest Common Divisior) dua bilangan integer a dan b ialah dengan menggunakan algoritma Euclid. Algoritma Euclid merupakan algoritma rekursif yang terdapat dua kasus:
P E R T E M U A N R A H A S I A
P R E U N R H S A
P R E U N R H S A E T M A A A I
I : b = 0 GCD(a,0) = a II : B 0 GCD (a,b) = (b, a mod b)
Algoritma Euclid dapat dikembangkan dan pengembangan dari algoritma Euclid tersebut disebut dengan algoritma Extended Euclid. Algoritma Extended Euclid ini sendiri berfungsi untuk menemukan dua nilai integer x dan y yang unik selain nilai GCD (Greatest Common Divisior) (a,b) sehingga memenuhi relasi (Lipschutz & Lipson, 2007).
a*x +b*y =GCD(a,b)
2.7. Algoritma Extended Polybius Square
Polybius square (kotak polybius) pada dasarnya merupakan algoritma simetris yang di kerjakan secara substitusi. Polybius square merupakan sebuah tabel yang berfungsi untuk membantu dalam proses enkripsi maupun dekripsi pesan.
Pada umumnya Polybius Square menggunakan tabel dengan ukuran 5 x 5 yang di isi oleh 26 huruf alphabetik, dari a hingga z, namun untuk huruf I dan J biasanya di satukan di dalam satu tabel. Polybius square di temukan pertama kali oleh Polybius yang merupakan seorang sejarahwan Yunani pada tahun 200 – 118 SM.
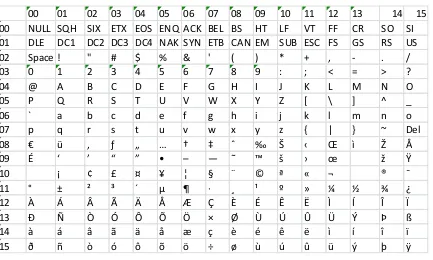
Tabel 2.3 . Tabel Extended Polybius Square 15 x 15
00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 00 NULL SQH SIX ETX EOS ENQ ACK BEL BS HT LF VT FF CR SO SI 01 DLE DC1 DC2 DC3 DC4 NAK SYN ETB CAN EM SUB ESC FS GS RS US 02 Space ! " # $ % & ' ( ) * + , - . / 03 0 1 2 3 4 5 6 7 8 9 : ; < = > ?
04 @ A B C D E F G H I J K L M N O
05 P Q R S T U V W X Y Z [ \ ] ^ _
06 ` a b c d e f g h i j k l m n o
07 p q r s t u v w x y z { | } ~ Del
08 € ü ‚ ƒ „ … ˆ ‰ Š Œ õ Å
09 É • – — ˜ ™ š œ ž ò
10 ¡ ¢ £ ¤ ¥ ¦ ¨ © ª « ¬ ® ¯
11 ° ± ´ µ · ¸ ¹ º » ¼ ½ ¾ ¿
12 â ã ä Ã Ä Å Æ Ç È É è ê Ì Í Î Ï
13 Ð Ñ Ò Ó Ô Õ Ö × Ø Ù Ú Û Ü Ý Þ ß
14 å æ ç ë ï
15 ð ñ ÷ ø ü ý þ ÿ
Contoh 1. Perhitungan manual proses enkripsi dengan plaintext awal “CHITRA” dengan menggunakan Extended Polybius Square.
1.1 Pengenkripsian plainteks : C Plaintext awal : C
Dengan m : 0403
: 110010011
: 11001001111001001 : 206739
1.2 Pengenkripsian plaintext : H Plaintext awal : H
Dengan m : 0408
: 110011000
1.3 Pengenkripsian plaintext : I Plaintext awal : I
Dengan m : 0409
: 110011001
: 110011001110011001 : 209817
1.4 Pengenkripsian plaintext : T Plaintext awal : T
Dengan m : 0504
: 111111000 : 111111000 : 258552
1.5 Pengenkripsian plaintext : R Plaintext awal : R
Dengan m : 0502
: 111110110 : 111110110 : 257526
1.6 Pengenkripsian plaintext : A Plaintext awal : A
Dengan m : 0401
: 110010001
: 110010001110010001 : 205713
Tabel 2.4 Hasil Perhitungan Plaintext “CHITRA”
206739 209304 209817 258552 257526 205713
2.8. Algoritma Rabin Cryptosystem
Algoritma kriptografi Rabin Cryptosystem pertama kali di perkenalkan pada tahun 1979 oleh Michael O Rabin. Algoritma Rabin Cryptosystem pada dasarnya hampir sama dengan algoritma Rivest Shamir Adleman (RSA), hanya saja komputasinya lebih sederhana di bandingkan dengan Rivest Ahamir Adleman (RSA). Algoritma Rabin Cryptosystem merupakan algoritma kriptografi dengan metode kriptografi asimetris pertama di mana untuk mendapatkan plaintext dari ciphertext yang ada sama sulitnya dengan proses pemfaktoran.(Damarjati,2002)
2.8.1. Proses Pembangitan Kunci.
Pembangkitan kunci pada algoritma Rabin Cryptosystem, sama seperti pada sistem kriptografi asimetri lainnya. algoritma Rabin Cryptosystem juga menggunakan sistem kunci publik dan sistem kunci privat. Kunci publik digunakan pada proses enkripsi oleh penerima pesan dan bersifat rahasia. Algoritma pembangkitan kuncinya adalah sebagai berikut :
1. Pilih dua buah bilangan prima besar secara sembarang dan yang saling berbeda (p dan
q).
2. Untuk mempermudah komputasi dari akar kuadrat modulo p dan q, kita bisa lakukan dengan memilih
p ≡ q ≡ 3 (mod) 4 p ≠ q
Contoh 2: penulis ingin menentukan nilai p = 11. Lalu lakukan pengecekan apakah 11
merupakan bilangan prima dengan cara. p ≠ q
p mod 4 = 3
Sehingga
Contoh 3 : penulis ingin menentukan nilai q = 23. Lalu penulis melakukan pengecekan apakah 23 merupakan bilangn prima y ang dimaksud dengan cara.
q mod 4 = 3
Sehingga
23 mod 4 = 3
3. Hitung n= p.q. n adalah kunci publik, bilangan prima p dan q adalah kunci privat. Untuk mengenkripsi hanya membutuhkan kunci publik n, sedangkan untuk dekripsi dibutuhkan bilangan p dan q sebagai kunci privat.
Contoh 3. Penulis menentukan nilai n. Di mana nilai n tersebut akan di dapat dari proses perkalian antara dua bilangan prima, yakni nilai p dan q.
n = p . q
n = 11 . 23
n = 253
2.8.2. Metode Enkripsi
Algoritma Rabin Cryptosystem merupakan algoritma kriptografi kunci publik maka enkripsi di lakukan hanya dengan menggunakan kunci publik yang dapat di ketahui oleh semua orang. Namun proses dekripsinya hanya dapat di lakukan dengan menggunakan kunci privat yang hanya dapat dilakukan oleh orang yang bersangkutan. Untuk proses enkripsi pada algoritma kunci publik Rabin Cryptosystem dapat dilakukan dengan rumus berikut (Schneier, 1996):
C = m² mod n
Dengan keterangan:
C = Ciphertext
m = enkripsi polybius
n = Kunci publik
Setelah itu hitung nilai K yang merupakan nilai kongruen hasil nilai desimal plaintext
m dengan menggunakan rumus:
Contoh 1. Perhitungan manual proses enkripsi dengan plaintext awal “CHITRA” dengan menggunakan algoritma Rabin Cryptosystem .
1.1Enkripsi plaintext awal : C C = mod n
206739² mod n
1444 mod 253
179
Lalu Hitung nilai K
K =
817
1.2Enkripsi plantext awal : H C = mod n
209304² mod n
5329 mod 253 16
Lalu Hitung nilai K
K =
827
1.3Enkripsi plantext awal : I C = mod n
209817² mod n
6400 mod 253 75
Lalu Hitung nilai K
K =
829
1.4Enkripsi plantext awal : T C = mod n
57121 mod 253
Proses dekripsi pada algoritma Rabin Cryptosystem di lakukan dengan menggunakan rumus yang sederhana. Proses dekripsi pada algoritma Rabin Cryptosystem menggunakan kunci
privat p dan q. Selama penerima pesan mengetahui p dan q, penerima pesan dapat menyelesaikan dua kekongruenan menggunakan Chinese Remainder Teorema (CRT)
1. Tentukan nilai dan yang merupakan pembagi GCD (Greatest Common Divisior) dari p dan q dengan menggunakan algoritma Extended Euclidean. Karena bilangan prima GCD (Greatest Common Divisior) adalah 1 maka dapat kita tulis sebagai
*p + *q = 1
2. Hitung nilai akar kuadrat dari ciphertext terhadap nilai p dan q dengan menggunakan rumus
= mod p = mod q
Dengan nilai merupakan nilai akar kuadrat dari ciphertext terhadap nilai p. Dan merupakan nilai akar kuadrat dari ciphertext terhadap nilai q.
3. Hitung nilai r,s,t dan u dengan menggunakan Chinese Remainder Theorem (CRT) dengan rumus:
r =( *p* + *q* ) mod n
s =( *p* - *q* ) mod n t = -( *p* + *q* ) mod n u = -( *p* - *q* ) mod n
4. Tambahkan r,s,t dan u dengan kongruen nilai desimal hasil penggandaan plaintext K yang dikalikan dengan kunci plaintext n
R = (k*n) + r S = (k*n) + s T = (k*n) + t U = (k*n) +u
5. Ubahlah nilai desimal R, S, T, dan U ke dalam bentuk biner. Kemudian nilai biner R, S, T dan U di bagi menjadi 2 bagian. Bandingkan kedua bagian tersebut. Jika kedua bagian tersebut menghasilkan bentuk biner yang sama, maka di dapat hasil dekripsi chipertext dengan mengubah bentuk biner salah satu bagian yang telah di bagi menjadi 2 bagian yang sama.
2.9. Chinese Reminder Theorem
Chinese Reminders Theorem (CRT) atau yang disebut juga dengan Teorema sisa China sudah ada sekitar abad ke 3 – 5 masehi. Teorema ini diperkenalkan oleh seorang matematikawan China yang bernama Sun Zi. Teorema ini pertama kali di tulis dalam sebuah buku yang berjudul Qin Juishan yang di terbitkan pada tahun 1247, di mana dalam buku tersebut di perkenalkan metode mencari solusi sistem linear kongruen.
Berikut adalah bunyi Chinese Reminder Theorem (CRT): berikan bilangan bulat positif yang semuanya saling relatif prima dan bilangan bulat maka sistem linear kongruennya
....
Contoh Chinese Remainder Theorem 1:
Setelah di ketahui nilai dan maka tentukan kunci dekripsi Rabin Cryptosystem yang benar dengan menggunakan banuan metode Chinese Remainder Theorem (CRT). Di mana nantinya pada metode ini akan di temukan 4 kemungkinan plaintext hasil dekripsi algoritma Rabin Cryptosystem yakni nilai (r, s, t, u)
Setelah itu hitung nilai R,S,T dan U dengan menggunakan nilai r,s,t dan u yang di dapat dalam proses sebelumnya.
Contoh 1. Perhitungan manual proses dekripsi dengan plaintext awal “CHITRA”
1.1Dekripsi plaintext awal : C
o Hitung nilai dengan cara:
= mod p = mod 11 27 mod 11
o Hitung nilai dengan cara :
= mod q = mod 23 34012224 mod 23 8
o Hitung nilai Chinesse Remainder Theorem (CRT) dengan
206762
1.2 Dekripsi plaintext awal : H
o Hitung nilai dengan cara:
= mod p
o Hitung nilai Chinesse Remainder Theorem (CRT) dengan
180
o Hitung nilai dengan cara:
= mod p
o Hitung nilai Chinesse Remainder Theorem(CRT) dengan
1.4Dekripsi plaintext awal : T
o Hitung nilai dengan cara:
= mod p
o Hitung nilai Chinesse Remainder Theorem (CRT) dengan
258437
1.5 Dekripsi plaintext awal : R
o Hitung nilai dengan cara:
= mod p
o Hitung nilai Chinesse Remainder Theorem (CRT) dengan
(-396 – 115 ) mod 253
o Hitung nilai dengan cara:
9
o Hitung nilai Chinesse Remainder Theorem (CRT) dengan
T = ( K * n) + t (813 * 253) + 68 205689+ 28 205757
110010001110111101 U = ( K * n) + u
(813 * 253) + 229 205689 + 229 205918
110010010001011110
Maka dari hasil proses perhitungan metode Chinese Remainder Theorem (CRT) maka di dapatkan nilai dekripsi RABIN cryptosystem yang sebenarnya yakni untuk plainiteks “CHITRA” adalah 206739, 209304, 209817, 258552,257526, 205713. nilai. Di mana nilai biner dari nilai tersebut sama dengan nilai kunci enkripsi pada algoritma Extended Polybius Square.
Namun untuk nilai m ( 0000,0003,0006 dan 009 ) terdapat anomali dalam perhitungan algortima dimana perhitungan untuk masing – masing nilai m tersebut akan di jabarkan di dalam contoh enkrips di bawah ini.
Contoh enkripsi 2:
Di mana didalam contoh 2, penulis akan menghitung nilai m yang bernilai 3. Sedangkan untuk nilai p dan q ( 11 dan 23 ) bernilai dan nilai kunci privat ( dan sama seperti contoh enkripsi 1. Oleh karena itu untuk kedua nilai tersebut pada contoh 2 yang akan di masukan akan sama dengan contoh enkripsi 1.
.1. Enkripsi
o Nilai N : 253
o m enkripsi Extended Polybius Square:
Dengan m : 3 : 11 : 1111 : 15
C = mod n
C mod 253
C 225mod 253
C 225
2. Dekripsi
o Hitung nilai dengan cara:
= 3810 mod 253
= 15
= 1111
Contoh 3:
Di mana didalam contoh 3, penulis akan menghitung nilai m yang bernilai 9. Sedangkan untuk nilai p dan q ( 11 dan 23 ) bernilai dan nilai kunci privat ( dan sama seperti contoh enkripsi 1. Oleh karena itu untuk kedua nilai tersebut pada contoh 2 yang akan dimaskan akan sama dengan contoh enkripsi 1.
.1. Enkripsi
o Nilai N : 253
o m enkripsi Extended Polybius:
m : 9
: 1001 : 10011001 : 153
o Enkripsi Rabin Cryptosystem:
C = mod n
C mod 253 C 23409mod 253 C 133
2. Dekripsi
o Hitung nilai dengan cara:
= mod p mod 11 2352637 mod 11 1
o Hitung nilai dengan cara :
o Perhitungan Chinese Remainder Theorem (CRT)
o r = ( * p * + * q * ) mod n
= ( -2 * 11*8 + 1 * 23 * 1 ) mod 253 = (-176 + 23 ) mod 253
= -153 mod 253
= 100
= 1100100
o s = ( * p * - * q * ) mod n
= ( -2 * 11* 8 - 1 * 23 * 1 ) mod 253 = (-176-23 ) mod 253
= -199 mod 253
= 54
= 110110
o t = - ( * p * + * q * ) mod n
= - ( -2 * 11* 8 + 1 * 23 * 1 ) mod 253 = (176 + 23 ) mod 253
= 199 mod 253
= 199
= 11000111
o u = - ( * p * - * q * ) mod n
=- ( -2 * 11*8 - 1 * 23 * 1 ) mod 253 = ( 176 – 23 ) mod 253
= 153 mod 253
= 153
= 10011001
Contoh 4:
contoh enkripsi 1. Oleh karena itu untuk kedua nilai tersebut pada contoh 2 yang akan dimaskan akan sama dengan contoh enkripsi 1.
.1. Enkripsi
o Nilai N : 253
o m enkripsi Extended Polybius Square:
Dengan m : 6 : 110 : 110110 : 54
o Enkripsi Rabin Cryptosystem:
C = mod n
C mod 253 C 2916mod 253 C 133