BAB 3
METODOLOGI PENELITIAN
3.1. Pendahuluan
Pengenalan pola (pattern recognition) adalah proses klasifikasi dari suatu objek atau pola menjadi beberapa kategori atau kelas, yang mana bertujuan untuk memberikan informasi. Pola merupakan bentuk atau model yang dapat dipakai untuk membuat atau menghasilkan suatu bagian dari sesuatu yang ingin dikenal. Salah satu pendekatan pengenalan pola adalah dengan mneggunakan jaringan syaraf tiruan, yang mana jaringan syaraf tiruan memiliki cara kerja yang menyerupai cara kerja otak manusia.
Salah satu metode jaringan syaraf tiruan adalah Learning Vector Quantiztion (LVQ), yang metode pelatihannya pada lapisan kompietitf terawasi yang akan belajar
secara otamatis, untuk meningkatkan akurasi pembelajaran pada LVQ maka parameter-parameter algoritma genetika akan di-input-kan untuk pembentukkan vektor bobot awal pada LVQ.
3.2. Data yang Digunakan
3.3. Analisa Data
Analisa data pengenalan pola alfanumerik dengan pola matriks biner. Adapun tahapan pertama melakukan input data dan parameter jaringan, kemudian melakukan proses menggunakan metode jaringan syaraf tiruan Learning Vector Quantization (LVQ).
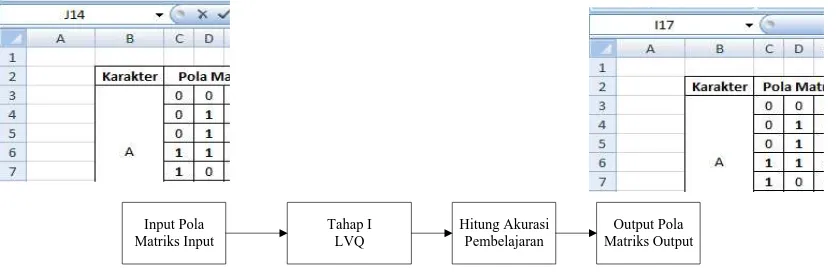
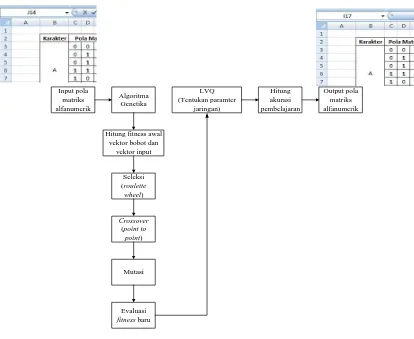
Untuk menganalisa perbedaan akurasi pembelajaran dengan LVQ, dan dengan menggunakan algoritma, maka tahap kedua sebelum di-training dengan LVQ, terlebih dahulu inisialisasi vektor bobot awal LVQ dioptimalisasi dengan algoritma genetika. Untuk lebih jelas dapat dilihat pada Gambar 3.1 dan Gambar 3.2 berikut.
Input Pola Matriks Input
Tahap I LVQ
Output Pola Matriks Output Hitung Akurasi
Pembelajaran
Gambar 3.1. Tahap I Pembelajaran dengan Learning Vector Quantization (LVQ)
Input pola matriks alfanumerik
Algoritma Genetika Hitung fitness awal
vektor bobot dan vektor input
Gambar 3.2. Tahap II Pembelajaran Learning Vector Quantization (LVQ) dengan Menggunakan Algoritma Genetika
3.3.1. Learning Vector Quantization (LVQ)
3.3.1.1. Arsitektur Jaringan
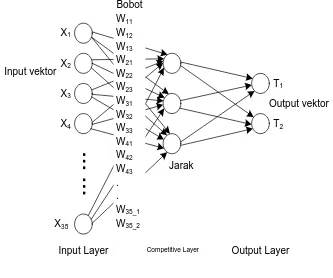
Arsitektur jaringan algoritma LVQ terdiri dari lapisan input (input layer), lapisan kompetitif (terjadi kompetisi pada input berdasarkan kedekatan jaraknya) dan lapisan output (output layer). Bobot yang menguhubungkan lapisan input dengan lapisan kompetitif. Proses pembelajaran merupakan metode jaringan syaraf tiruan supervised (terawasi) pada lapisan kompetitif. Input akan berkompetitif untuk dapat masuk ke dalam suatu kelas.
Ada beberapa variabel dari vektor input dalam penelitian ini, yaitu � = (�1,2,�3,…,�35) dengan neuron output T1 dan T2 serta n vektor bobot yaitu � = (�11,�12,�13,…,�105). Adapun arsitektur jaringan pada algoritma LVQ seperti pada Gambar 3.3.
Gambar 3.3. Arsitektur Jaringan LVQ
… …
3.3.1.2. Algoritma Learning Vector Quantization (LVQ)
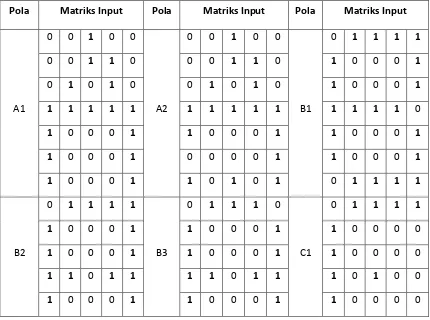
Pembelajaran pada metode LVQ, vektor input adalah pola matriks biner yang dibentuk berupa karakter alfanumerik. Misalnya pola matriks alfanumerik adalah sebagai berikut :
Start
Input pola matriks [A,...Z];
[0,..9] Parameter
jaringan
Training LVQ
Recognition LVQ
Hitung akurasi pembelajaran
Akurasi pembelajaran
End
Adapun tahapan proses pelatihan dengan metode LVQ adalah sebagai berikut:
1. Input pola matiks alfanumerik [A, …, Z] dan [0, …, 9], dan parameter jaringan LVQ. Setiap kelas (kelas 1, kelas 2, dan kelas 3) diambil pada salah satu array vektornya dan dijadikan sebagai inisialisasi bobot (w). Sedangkan array lainnya menjadi data masukan (X). Proses ini terlebih dahulu harus membuat inisialisasi bobot (w), iterasi maksimum (epoch), error minimum (eps), dan learning rate (α). Misalnya, ada 6 data dan target 3 kelas, dan menentukan parameter misalnya nilai-nilai awal yang ditentukan adalah sebagai berikut :
Maksimum epoch = 100
Error minimum = 0,01 Learning rate (α) = 0,05 Pengurangan learning rate (α) = 0,1
Adapun input pola matriks alfanumerik seperti pada Tabel 3.1. dan Tabel 3.2.
Tabel 3.1. Pola matriks input alfanumerik
1 0 0 0 1 1 0 0 0 1 1 0 0 0 0
0 1 1 1 1 0 1 1 1 1 1 1 1 1 1
Tabel 3.2. Inisialisasi Bobot dan Data Input Proses Training LVQ
Input Vektor Kelas
A1 00100001100101011111100011000110001 1
A2 00100001100101011111100010000110101 1
B1 01111100011000111110100011000101111 2
B2 01111100011000111011100011000101111 2
B3 01110100011000111011100011000101111 2
C1 01111100001000010100100001000011111 3
Tiga input pertama akan dijadikan sebagai vektor bobot seperti pada Tabel 3.3 sebagai berikut:
Tabel 3.3. Data Bobot
Input Vektor Kelas
A1 00100001100101011111100011000110001 1
B1 01111100011000111110100011000101111 2
C1 01111100001000010100100001000011111 3
Sedangkan tiga input sisanya akan digunakan sebagai data yang akan dilatih seperti pada Tabel 3.4.
Tabel 3.4. Data Pelatihan
Input Vektor Kelas
A2 00100001100101011111100010000110101 1
B2 01111100011000111011100011000101111 2
2. Pelatihan jaringan syaraf tiruan Learning Vector Quantization (LVQ). Setelah menentukan inisialisa vektor bobot (w) , vektor input, dan parameter-parameter jaringan LVQ, maka untuk tahap pelatihan selanjutnya adalah sebagai berikut:
a. Tahap ini dilakukan selama epoch masih lebih kecil dari maksimum epoch atau learning rate (α) masih lebih besar dari error minimum.
b. Setiap jarak minimum pada data input (X) terhadap setiap data bobot (w) dengan rumus:
�� =�∑ ���− ����
2
�
�=1 (3.1)
Dengan menggunakan palgoritma LVQ berikut adalah perhitungan dari contoh di atas: a. Epoch – 1
Dengan menggunakan persamaan (3,4), jarak pada bobot ke – 1:
Jarak pada bobot ke – 2:
Karena T = J, maka perbaikkan vektor bobotke – 1 menggunakan persamaan (3.2):
��(���)= ��(���)+��� − ��(���)�
Sehingga vektor bobot ke – 1 : A1(new)= [ 0 0 1 0 0 0 0 1 1 0 0 1 0 1 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0.1 0 1]
Untuk data selanjutnya dilakukan seperti tahapan di atas, yang mana dapat dilihat pada Tabel 3.5 untuk epoch – 1:
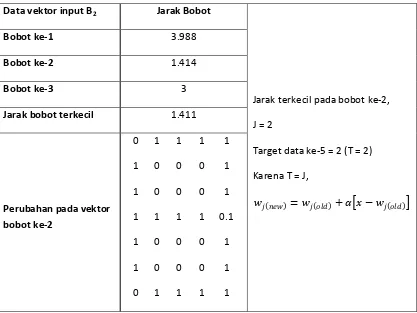
Tabel 3.5. Perhitungan data berikutnya untuk epoch ke – 1.
Data vektor input B2 Jarak Bobot
Jarak terkecil pada bobot ke-2, J = 2
Target data ke-5 = 2 (T = 2) Karena T = J,
��(���) = ��(���)+��� − ��(���)�
Bobot ke-1 3.988
Bobot ke-2 1.414
Bobot ke-3 3
Jarak bobot terkecil 1.411
Perubahan pada vektor
bobot ke-2
0 1 1 1 1 1 0 0 0 1 1 0 0 0 1 1 1 1 1 0.1 1 0 0 0 1
1 0 0 0 1
Data vektor input B3 Jarak Bobot Jarak terkecil pada bobot ke-2, J = 2
Target data ke-6 = 2 (T = 2)
Bobot ke-1 3.860699418
Bobot ke-2 1.674813422
Tabel 3.5. Perhitungan data berikutnya untuk epoch ke – 1. (Lanjutan)
Bobot ke-3 3.16227766
Karena T = J
��(���) = ��(���)+��� − ��(���)� Jarak bobot terkecil 1.674813422
Perubahan pada vektor bobot ke-2
0 1 1 1 1
1 0 0 0 1
1 0 0 0 1
1 1 0.9 1 0.1
1 0 0 0 1
1 0 0 0 1
3. Menghitung akurasi pembelajaran.
Dari proses pengenalan pola dengan menggunakan jaringan syaraf tiruan Learning Vector Quantization (LVQ) dengan menggunakan algoritma genetika, dapat
dianalisa dengan menggunakan persamaan berikut :
% �������= ��ℎ������ℎ������������������������������ × 100% ………..(3.2)
Dengan menggunakan 20 data uji untuk setiap karakter alfanumerik, dan pola matriks alfanumerik yang dikenal adalah 15 pola, maka dengan menggunakan persamaan di atas dapat dihitung akurasi pembelajarannya:
% �������= 15
3.3.2. Pembelajaran LVQ dengan Algoritma Genetika
Adapun algoritma analisis akurasi pembelajaran LVQ dengan menggunakan algoritma genetika adalah sebagai berikut:
Start
Input pola matriks [A,...Z]; [0,..9] Parameter jaringan
Training LVQ
Recognition LVQ
Hitung akurasi pembelajaran
Akurasi Pembelajaran
End
Hitung fitness bobot vektor
Selection Crossover
Optimal?
Vektor bobot yang telah diproses dengan
algoritma genetika
Mutasi
Yes No
1. Tetapkan vektor bobot (w) dan vektor input (x).
2. Pembentukkan parameter algoritma genetika, adalah sebagai berikut: a. Pembentukkan populasi yang diambil dari data pelatihan.
Proses inisialisasi populasi awal dilakukan dengan cara memberikan nilai awal gen. Misalkan ditentukan jumlah populasi adalah 6 kromosom di mana dalam 1 kromosom terdapat 35 gen yang mewakili satu data pelatihan. Dimana terlebih dahulu dihitung nilai fitness suatu indifidu, diasumsikan biner 1 sebagai gen terbaik:
�������= �������ℎ�� ℎ���������� 1 ����� ���� ��������
1 ���� ����� �������� ……….(3.3)
Misal untuk kromosom A1 jumlah biner 1 = 16 dan total biner 1 untuk semua kromosom 106, sehingga fitness untuk kromosom A1 :
�������= 16
106= 0.1509434
Maka, pembentukkan populasi awal dengan nilai fitness terbaik dapat dilihat pada Tabel 3.6.
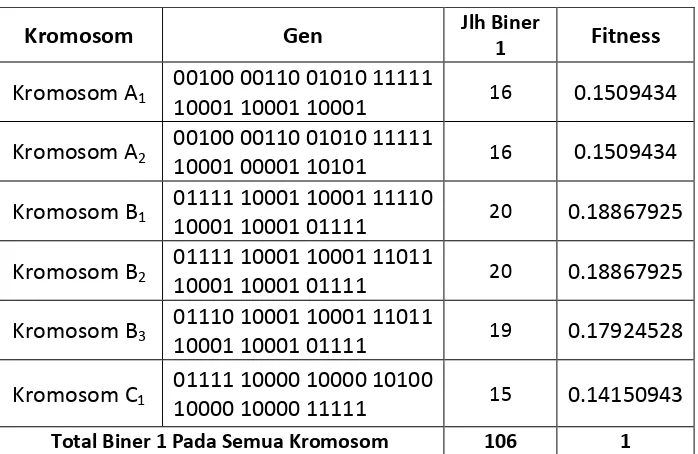
Tabel 3.6. Pembentukkan populasi awal
Kromosom Gen Jlh Biner
1 Fitness
Kromosom A1
00100 00110 01010 11111
10001 10001 10001 16 0.1509434 Kromosom A2
00100 00110 01010 11111
10001 00001 10101 16 0.1509434 Kromosom B1
01111 10001 10001 11110
10001 10001 01111 20 0.18867925 Kromosom B2
01111 10001 10001 11011
10001 10001 01111 20 0.18867925 Kromosom B3
01110 10001 10001 11011
10001 10001 01111 19 0.17924528 Kromosom C1
01111 10000 10000 10100
10000 10000 11111 15 0.14150943
b. Selection, proses seleksi dilakukan dengan cara membuat kromosom yang mempunyai fungsi objektif kecil mempunyai kemungkinan terpilih memiliki nilai probabilitas yang tinggi. Metode seleksi yang digunakan adalah roulette wheel selection.
c. Crossover, untuk menghasilkan kromosom baru yang mewarisi sifat-sifat induknya. Kromosom baru berasal dari dua kromosom induk yang disilangkan. Pada proses ini menggunakan teknik point to point crossover di mana teknik ini akan melakukan persilangan pada dua titik yang ditentukan secara acak dan proses persilangan dilakukan pada seluruh kromosom yang terdapat pada individu secara acak. Kemudian dilakukan pemilihan pasangan kromosom yang akan di crossover untuk seluruh kromosom. Adapun contoh yang dapat diberikan dengan melanjutkan contoh pada proses seleksi, dapat dilihat pada Tabel 3.7 dan 3.8.
d. Mutasi, pada penelitian ini digunakan meotde swapping mutation, yaitu proses pertukaran satu atau beberapa nilai gen di dalam kromosom. Jumlah kromosom yang mengalami mutasi dalam satu populasi ditentukan oleh parameter mutation rate, dimana proses ini dilakukan dengan cara menggantikan satu gen yang terpilih secara acak (random) dengan nilai baru yang didapat juga secara acak. Berikut adalah beberapa tahap proses mutasi:
1. Hitung panjang total gen yang ada dalam satu populasi.
��������������� =��ℎ�������� ×��ℎ�������� ……….. (3.4) Data yang diambil hasil dari proses crossover:
��������������� = 36 × 6 = 216
2. Hitung jumlah gen yang dimutasi dari jumlah kromosom beberapa populasi. Misal mutation rate (Pm) ditentukan 0.01 maka diharapkan ada 0.01 dari total gen yang mengalamai mutasi pada populasi tersebut:
Maka jumlah gen yang akan dimutasi adalah 2 gen dari populasi yang dibentuk.
3. Proses mutasi pada panjang total gen dapat dilihat pada Tabel 3.9
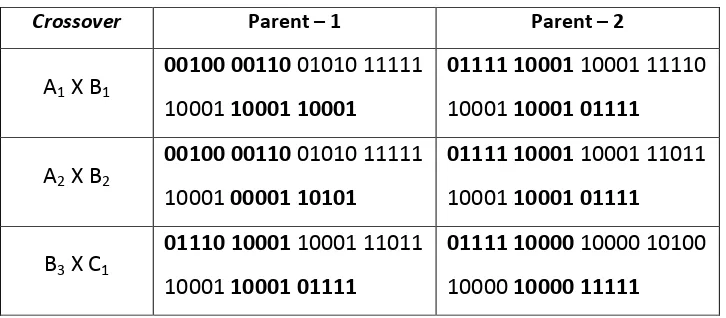
Tabel 3.7 Proses crossover data pelatihan
Crossover Parent – 1 Parent – 2
A1 X B1
00100 00110 01010 11111
10001 10001 10001
01111 10001 10001 11110
10001 10001 01111
A2 X B2
00100 00110 01010 11111
10001 00001 10101
01111 10001 10001 11011
10001 10001 01111
B3 X C1
01110 10001 10001 11011
10001 10001 01111
01111 10000 10000 10100
10000 10000 11111
Sehingga diperoleh generasi baru dari proses crossover tersebut: Tabel 3.8 Generasi baru yang dibentuk dari crossover
Kromosom
Baru Gen Fitness
Kromosom
A’1
01111 10001 01010 11111 10001 10001
01111
0.198113
Kromosom
A’2
01111 10001 01010 11111 10001 10001
01111
0.198113
Kromosom
B’1
00100 00110 10001 11110 10001 10001
10001 0.141509
Kromosom
B’2
00100 00110 10001 11011 10001 00001
10101
0.141509
Kromosom
B’3
01111 10000 10001 11011 10001 10000
11111
0.179245
Kromosom
C’1
01110 10001 10000 10100 10000 10001
Proses mutasi pada panjang total gen adalah sebagai berikut :
01111 10001 01010 11111 10001 10001 01111
01111 10001 01010 11111 10001 10001 01111
0.194
Kromosom A’2
01111 10001 01010 11111 10001 10001 01111
01111 10001 01010 11111 10001 10001 01111
0.194
Kromosom B’1
00100 00110 10001 11110 10001 10001 10001
00100 01110 10001 11110 10001 10001 10001
0.148
Kromosom B’2
00100 00110 10001 11011 10001 00001 10101
00100 00110 10001 11011 10001 01001 10101
0.148
Kromosom B’3
01111 10000 10001 11011 10001 10000 11111
01111 10000 10001 11011 10001 10000 11111
0.175
Kromosom C’1
01110 10001 10000 10100 10000 10001 01111
01110 10001 10000 10100 10000 10001 01111
0.139
Setelah dibentuknya inisialisasi vektor bobot dan vektor input dengan menggunakan algoritma genetika, maka vektor bobot dan vektor input dimasukkan ke dalam pelatihan LVQ. Adapun tahapan proses pelatihan dengan metode LVQ sama halnya dengan tahap sebelumnya adalah sebagai berikut:
Maksimum epoch = 100 Error minimum = 0,01 Learning rate (α) = 0,05 Pengurangan learning rate (α) = 0,1
Tabel 3.10. Inisialisasi Bobot dan Data Input Proses Training LVQ
Input Vektor Kelas
A’1 01111 10001 01010 11111 10001 10001 01111 1
A’2 01111 10001 01010 11111 10001 10001 01111 1
B’1 00100 01110 10001 11110 10001 10001 10001 2
B’2 00100 00110 10001 11011 10001 01001 10101 2
B’3 01111 10000 10001 11011 10001 10000 11111 2
C’1 01110 10001 10000 10100 10000 10001 01111 3
Tiga input pertama akan dijadikan sebagai vektor bobot seperti pada Tabel 3.11 sebagai berikut:
Tabel 3.11 Data Bobot
Input Vektor Kelas
A’1 01111 10001 01010 11111 10001 10001 01111 1
B’1 01111 10001 01010 11111 10001 10001 01111 2
C’1 00100 01110 10001 11110 10001 10001 10001 3
Sedangkan tiga input sisanya akan digunakan sebagai data yang akan dilatih seperti pada Tabel 3.12.
Tabel 3.12. Data Pelatihan
Input Vektor Target
A’2 00100 00110 10001 11011 10001 01001 10101 1
B’2 01111 10000 10001 11011 10001 10000 11111 2
B’3 01111 10000 10000 10100 10000 10000 01111 2
2. Setelah menentukan inisialisa vektor bobot (w) , vektor input, dan parameter-parameter jaringan LVQ, maka untuk tahap pelatihan selanjutnya adalah sebagai berikut:
a. Tahap ini dilakukan selama epoch masih lebih kecil dari maksimum epoch atau learning rate (α) masih lebih besar dari error minimum.
b. Setiap jarak minimum pada data input (X) terhadap setiap data bobot (w) dengan rumus:
�� = �∑ ����=1 �− ����2
Dengan menggunakan palgoritma LVQ berikut adalah perhitungan dari contoh di atas:
Epoch - 1
Data pelatihan untuk vektor input A2: [ 0 1 1 1 1
1 0 0 0 1
0 1 0 1 0
Dengan menggunakan persamaan (3,4), jarak pada bobot ke – 1:
��(���)= ��(���)+��� − ��(���)�
�11 = �11 +�[�11− �11] = 0 + 0.05(0−0) = 0
Sehingga vektor bobot ke – 1 : A1(new)= [ 0 1 1 1 1 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 0 1 1 1 1]
Untuk data selanjutnya dilakukan seperti tahapan di atas, yang mana dapat dilihat pada Tabel 3.13 untuk epoch – 1:
Tabel 3.13. Perhitungan data berikutnya untuk epoch ke – 1.
Data vektor input B2 Jarak Bobot
Jarak terkecil pada bobot ke-2, J = 2
Target data ke-5 = 2 (T = 2) Karena T = J,
��(���) =��(���)
+��� − ��(���)�
Bobot ke-1 4
Bobot ke-2 0
Bobot ke-3 3.7416
Jarak bobot terkecil 0
Perubahan pada vektor
1 0 1 1 0 1 0 0 0 1 1 1 1 1 0 1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
Data vektor input B3 Jarak Bobot
Jarak terkecil pada bobot ke-2, J = 2
Target data ke-6 = 1 (T = 1) Karena T ≠ J
��(���) =��(���)
− ��� − ��(���)�
Bobot ke-1 2.82842712
Bobot ke-2 3.46410162
Bobot ke-3 3.16227766
Jarak bobot terkecil 2.82842712
Perubahan pada vektor
bobot ke-2
0 1 1 1 1
1 0 0 0 1 0.1 0 0 0 0.1
1 1 1 1 1 1 0 0 0 1
1 0 0 0 1
0.1 1 1 1 1
3. Menghitung akurasi pembelajaran.
pola dengan menggunakan 20 data uji untuk setiap karakter alfanumerik, dan pola matriks alfanumerik yang dikenal adalah 17 pola, maka dengan menggunakan persamaan di atas dapat dihitung akurasi pembelajarannya:
% �������= 17
BAB 4
HASIL DAN PEMBAHASAN
4.1. Pendahuluan
Proses pengujian dilakukan untuk mengetahui akurasi pembelajaran Learning Vector Quantization (LVQ) dengan menggunakan algoritma genetika pada pengenalan pola
alfanumerik. Pada penelitian ini ditampilkan hasil dari akurasi pembelajaran yang dihasilkan dari bobot vektor dengan menggunakan algortima genetika yang mana bobot vektor tersebut akan dimasukkan kembali ke dalam embelajaran jaringan syaraf tiruan Learning Vector Quantization (LVQ). Penyajian hasil pengujian akan ditampilkan dalam bentuk table dan grafik.
4.2. Hasil Penelitian
4.2.1. Pengujian Akurasi Pembelajaran Learning Vector Quantization (LVQ)
Pada Pengenalan Pola Alfanumerik
Tabel 4.1. Hasil pengenalan pola alfanumerik dengan LVQ Input
Dikenali
Input
Dikenali
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.1. Hasil pengenalan pola alfanumerik dengan LVQ (Lanjutan – 1) Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.1. Hasil pengenalan pola alfanumerik dengan LVQ (Lanjutan – 2) Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.1. Hasil pengenalan pola alfanumerik dengan LVQ (Lanjutan – 3) Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.1. Hasil pengenalan pola alfanumerik dengan LVQ (Lanjutan – 4) Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
6
0 1 1 1 0
9 8
0 1 1 1 0
8
1 0 0 0 1 1 0 0 0 1
1 0 0 0 0 1 0 0 0 1
1 1 1 1 0 0 1 1 1 0
1 0 0 0 1 1 0 0 0 1
1 0 0 0 1 1 0 0 0 1
0 1 1 1 0 0 1 1 1 0
7
1 1 1 1 1
8 9
0 1 1 1 0
9
0 0 0 0 1 1 0 0 0 1
0 0 0 0 1 1 0 0 0 1
0 0 0 1 0 0 1 1 1 1
0 0 1 0 0 0 0 0 0 1
0 1 0 0 0 1 0 0 0 1
1 0 0 0 0 0 1 1 1 0
Total yang dikenali dengan menggunakan LVQ secara umum: 465 karakter
Sehingga dengan menggunakan persamaan (3.5), persentase akurasi pembelajarannya adalah 65%.
Gambar 4.1. Grafik Pengujian Pengenalan Pola Alfanumerik dengan Learning Vector Quantization (LVQ)
4.2.2. Hasil Pengujian Akurasi Pembelajaran
Learning Vector Quantization (LVQ) Menggunakan Algoritma Genetika
Pada Pengenalan Pola Alfanumerik
Untuk melakukan pembelajaran pada pengenalan pola alfanumerik dengan memasukkan parameter algoritma genetika ke dalam metode jaringan syaraf tiruan Learning Vector Quantization, terlebih dahulu memenentukan bobot vektor (w). Bobot vektor (w) diambil dari pola matriks yang dibangkitkan dari pola matriks LVQ, yang akan dijadikan input pada algoritma genetika.
Pembentukkan parameter algoritma genetika yang dibentuk dibentuk dari bobot vektor LVQ, maka parameter-parameter algoritma genetika adalah sebagai berikut:
3. Tetapkan vektor bobot (w) dan vektor input (x).
4. Pembentukkan parameter algoritma genetika, adalah sebagai berikut: a. Jumlah populasi = 36 kromosom, 1 kromosom terdapat 35 gen.
b. Selection, proses seleksi dilakukan dengan cara roulette wheel selection. c. Crossover, probabilitas crossover (Pc) = 0.5.
d. Mutasi, probabilitas mutasi (Pm) = 0.001. 0
5 10 15 20 25
1 2 3 4 5 6 7 8 9 101112131415161718192021222324252627282930313233343536 Pengujian Pengenalan Pola Alfanumerik dengan
Dengan menggunakan parameter di atas,dilakukan pengejuain sebanyak 20 kali untuk melihat nilai fitness terbaik dari vektor bobot tersebut. Selanjutnya, jika nilai fitness yang dihasilkan dengan algoritma genetika optimal dari pada sebelumnya, maka vektor bobot baru algoritma genetika akan dimasukkan sebagai vektor bobot LVQ, tetapi jika vektor bobot algoritma genetika tidak ada perubahan atau tidak optimal daripada sebelumnya maka dilakukan proses algoritma genetika kembali sampai iterasi 100.
Selanjutnya, vektor bobot yang telah optimal dengan menggunakan algoritma genetika, maka ditentukan kembali tahap jaringan syaraf tiruan metode LVQ dengan menentukan iterasi maksimum (epoch maksimum), error minimum (eps), dan learning rate (α). Pengujian berhenti apabila learning rate (α) mencapai nilai yang cukup kecil. Proses pelatihan dilakukan degan menggunakan data sebanyak 720 karakter pola biner berupa pola alfanumerik, yang terdiri dari alpabet capital [A … Z] dan numeric [0 … 9]. Dari data tersebut diubah ke dalam pola matriks yang mana terdiri dari biner 0 dan 1. Hasil pengenalan pola ditunjukkan pada Tabel 4.2.
Tabel 4.2. Hasil pengenalan pola alfanumerik LVQ dengan Menggunakan Algoritma Genetika
Input Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
A
0 0 1 0 0
18 B
1 1 1 1 0
19
0 1 0 1 0 1 0 0 0 1
0 1 0 1 0 1 0 0 0 1
1 1 1 1 1 1 1 1 1 0
1 0 0 0 1 1 0 0 0 1
1 0 0 0 1 1 0 0 0 1
Tabel 4.2. Hasil pengenalan pola alfanumerik LVQ dengan Menggunakan
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.2. Hasil pengenalan pola alfanumerik LVQ dengan Menggunakan
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.2. Hasil pengenalan pola alfanumerik LVQ dengan Menggunakan Algoritma Genetika (Lanjutan – 3)
Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.2. Hasil pengenalan pola alfanumerik LVQ dengan Menggunakan Algoritma Genetika (Lanjutan – 4)
Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
Tabel 4.2. Hasil pengenalan pola alfanumerik LVQ dengan Menggunakan Algoritma Genetika (Lanjutan – 5)
Input
Dikenali Input Dikenali
Karakter Pola Matriks Karakter Pola Matriks
8
0 1 1 1 0
8 9
0 1 1 1 0
8
1 0 0 0 1 1 0 0 0 1
1 0 0 0 1 1 0 0 0 1
0 1 1 1 0 0 1 1 1 1
1 0 0 0 1 0 0 0 0 1
1 0 0 0 1 1 0 0 0 1
0 1 1 1 0 0 1 1 1 0
Total yang dikenali dengan menggunakan LVQ secara umum: 474 karakter
Sehingga dengan menggunakan persamaan (3.5), persentase akurasi pembelajarannya adalah 66%.
Gambar 4.2. Grafik Pengujian Pengenalan Pola Alfanumerik
Learning Vector Quantization (LVQ) deng Menggunakan Algoritma Genetika
4.3. Pembahasan Penelitian
Pada table 4.3 dan gambar 4.3, menyajikan perbedaan akurasi pembelajaran LVQ secara umum dan akurasi pembelajaran LVQ dengan menggunkan algoritma genetika. Dimana parameter-parameter yang digunakan adalah sebagai berikut :
1. Learning Vector Quantization (LVQ) Learning rate (α) = 0.05
Epoch maksimum = 100
Error minimum = 0.01
Pengurangan learning rate (α) = 0.1 x α 2. Algoritma Genetka
Populasi = 36
Jumlah kromosom dalam 1 gen = 35 Probabiliti crossover (Pc) = 0.5 Probabilitas mutasi (Pm) = 0.001 0
5 10 15 20 25
1 2 3 4 5 6 7 8 9 101112131415161718192021222324252627282930313233343536 Pengujian Pengenalan Pola Alfanumerik Learning Vector
Tabel 4.3. Akurasi Pembelajaran LVQ dan LVQ dengan Menggunakan Algoritma Genetika
Karakter
LVQ
Akurasi Genetika - LVQ Dikenali Akurasi
Pembelajaran Dikenali
Akurasi Pembelajaran
A 15 75% 18 90%
B 10 50% 19 95%
C 10 50% 10 50%
D 17 85% 17 85%
E 13 65% 14 70%
F 16 80% 16 80%
G 18 90% 16 80%
H 13 65% 15 75%
I 18 90% 15 75%
J 8 40% 14 70%
K 19 95% 20 100%
L 20 100% 19 95%
M 13 65% 15 75%
N 16 80% 16 80%
O 6 30% 14 70%
P 14 70% 16 80%
Q 18 90% 12 60%
R 14 70% 18 90%
S 18 90% 10 50%
T 10 50% 4 20%
U 10 50% 15 75%
V 19 95% 14 70%
Tabel 4.3. Akurasi Pembelajaran LVQ dan LVQ dengan Menggunakan Algoritma Genetika (Lanjutan)
Karakter
LVQ Genetika-LVQ
Dikenali Akurasi
Pembelajaran Dikenali
Akurasi
Gambar 4.3. Akurasi Pembelajaran LVQ dan LVQ Menggunakan Algoritma Genetika
1 2 3 4 5 6 7 8 9 101112131415161718192021222324252627282930313233343536
Akurasi Pembelajaran LVQ dan LVQ Menggunakan
Algoritma Genetika
LVQ
Berdasarkan dari hasil analisis pengujan akurasi pembelajaran terhadap Learning Vector Quantization (LVQ) secara umum dan Learning Vector Quantization (LVQ)
BAB 5
KESIMPULAN DAN SARAN
5.1. Kesimpulan
Berdasarkan dari penelitian yang telah dilakukan dapat diambil kesimpulan sebagai berikut:
1. Analisis pengujan akurasi pembelajaran terhadap Learning Vector Quantization (LVQ) secara umum dan Learning Vector Quantization (LVQ)
dengan menggunakan algoritma yang telah dilakukan penulis dari hasil pengujian terhadap data tersebut, dimana masing-masing data uji sebanyak 20 kali dengan nilai parameter pada LVQ sama, setiap tahapnya diperoleh hasil bahwa dengan menggunakan algoritma genetika sebagai inisialisasi awal bobot vektor yang mana memperoleh fitness yang optimal dibandingkan sebelumnya, sehingga diperoleh akurasi pembalajaran yang baik yaitu 66% walau tidak signifikan,
5.2. Saran
Adapaun saran yang diberikan pada penelitian ini adalah sebagai berikut:
1. Penelitian ini dapat dianalisis kembali dengan menggunakan
parameter-parameter LVQ yaitu learning rate (α), epoch maksimum, error minimum, dan
pengurang learning rate (α).
2. Untuk penelitian selanjutnya dapat ditambahkan pengujian terhadap
teknik-teknik dari biologi evolusi, seperti Particle Swarm Optimization (PSO), sehingga