MAKALAH TEORI GRAF KEL 3 jadi

TUGAS MATA KULIAH TEORI GRAF

PEMBUKTIAN DELETION-CONTRACTION THEOREM SERTA PENERAPANNYA DALAM PEMBUATAN JADWAL UJIAN AKHIR

PROGRAM STUDI MATEMATIKA

Disusun oleh:

1. Wigati P. Putri 07305141038 2. Ratnasari Dwi Ambarwati 10305141004 3. Meita Putri Rahayu 10305141005 4. Dwi Prihastuti 10305141020 5. Amalia Sita Nursanti 10305141038

PROGRAM STUDI MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA

BAB I PENDAHULUAN

A. Latar Belakang

Matematika memiliki beberapa pokok bahasan, salah satunya adalah graf. Wilson & Watkins (1990: 10) menyatakan, graf terdiri dari himpunan tak kosong dari elemen yang disebut simpul dan daftar pasangan tak berurutan dari elemen-elemen tersebut yang dinamakan rusuk. Graf biasa digunakan sebagai visualisasi obyek-obyek agar lebih mudah dimengerti. Contoh graf dalam kehidupan sehari-hari antara lain: struktur organisasi, bagan alir pengambilan mata kuliah, peta, rangkaian listrik, dan lain-lain.

Graf merupakan salah satu cabang ilmu Matematika yang dapat diterapkan baik dalam Ilmu Matematika maupun dalam kehidupan sehari-hari. Salah satu topik pada graf adalah pewarnaan graf. Pewarnaan graf dibagi menjadi dua macam, yaitu pewarnaan simpul dan pewarnaan rusuk. Akan tetapi, jika tidak diberikan kualifikasinya, pewarnaan graf diartikan sebagai pewarnaan simpul dan pada makalah ini dikhususkan pada pewarnaan simpul. Mewarnai sebuah graf berarti memberi warna pada setiap simpul graf sedemikian hingga simpul dan rusuk yang berkaitan dapat diwarnai dengan warna yang berbeda.

Misalkan G adalah graf tanpa loop, banyaknya warna yang digunakan untuk mewarnai simpul graf G sedemikian sehingga simpul yang berikatan berlainan warna dinyatakan dengan k-pewarnaan. Jika G memiliki k-pewarnaan, maka G dikatakan dapat diwarna dengan k warna. Pada pewarnaan simpul, jumlah warna yang boleh dipergunakan haruslah seminimal mungkin. Jumlah warna paling minimum yang dapat diterapkan pada Graph ini sering disebut dengan angka kromatik (χ(G)). Salah satu metode yang digunakan untuk mewarnai graf adalah dengan menggunakan polinomial khromatik.

Contoh lainnya adalah saluran televisi ditentukan ke pemancar-pemancar, sedemikian sehingga tidak ada dua pemancar dapat beroperasi pada saluran yang sama dalam jarak tertentu.

Makalah ini, membahas tentang penerapan pewarnaan simpul dalam penjadwalan ujian dengan metode deletion-contraction theorem. Dalam masalah penjadwalan yang dinyatakan dalam bentuk graf, simpul menyatakan mata kuliah dalam jadwal. Rusuk antar dua buah simpul menyatakan bahwa kedua buah mata kuliah tidak dapat dikerjakan secara bersamaan. Warna menunjukkan waktu yang tersedia. Setiap mata kuliah membutuhkan satu waktu. Jadi dapat dituliskan: simpul v menerima mata kuliah i jika dan hanya jika v dieksekusi dalam waktu i. Sehingga graf k-warna berarti semua mata kuliah dapat dikerjakan dalam k waktu secara tidak bersamaan.

Hasil penelitian ini bermanfaat sebagai tambahan literatur bagi mahasiswa yang sedang mempelajari mengenai pewarnaan simpul, khususnya bilangan kromatik dengan metode Deletion-Contraction Theorem serta contoh penerapannya. graf G memiliki V simpul dan E rusuk.

Simpul-simpul pada graf dapat merupakan obyek sembarang seperti kota, nama orang, jenis buah, komponen alat elektronik dan sebagainya. Rusuk dapat menunjukkan hubungan sembarang seperti rute penerbangan, jalan raya, sambungan telepon, ikatan kimia, dan lain-lain.

B. Pewarnaan Graf

Pewarnaan graf terbagi menjadi dua macam yaitu pewarnaan simpul dan pewarnaan rusuk.

1. Pewarnaan simpul didefinisikan sebagai berikut :

Misalkan G adalah graf tanpa loop, k-pewarnaan untuk G menyatakan penggunaan sebanyak k-warna untuk simpul G sedemikian hingga simpil-simpul yang berikatan mendapat warna yang berbeda. Jika G memiliki k-pewarnaan, maka G dikatakan dapat diwarnai dengan k-warna (Wilson dan Watkins, 1989: 235).

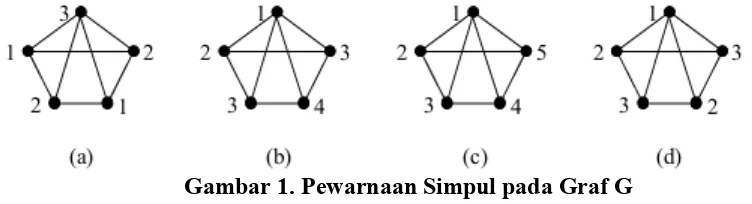
Gambar 1. Pewarnaan Simpul pada Graf G

Gambar 1 (a), (b), dan (c) secara berturut-turut adalah 3-pewarnaan, 4-pewarnaan, dan 5-pewarnaan dari graf G . Gambar 1 (d) bukan merupakan pewarnaan simpul dari graf G , karena terdapat dua simpul berikatan yang memiliki warna sama.

2. Pewarnaan rusuk didefinisikan sebagai berikut :

Misal G adalah graf tanpa loop, k-pewarnaan rusuk untuk G adalah pemberian sebanyak k warna pada rusuk-rusuk G sedemikian hingga setiap dua rusuk yang bertemu dengan simpul yang sama mendapat warna berbeda. Jika G memiliki k-pewarnaan rusuk, maka rusuk graf G dikatakan dapat diwarnai dengan k warna (Wilson dan Watkins, 1989: 240).

Berikut adalah contoh pewarnaan rusuk pada graf G .

Gambar 2. Pewarnaan Rusuk pada Graf G

BAB III PEMBAHASAN

A. Pewarnaan Simpul

Misalkan G adalah graf tanpa loop, k-pewarnaan untuk G menyatakan penggunaan sebanyak k-warna untuk simpul G sedemikian hingga simpul-simpul yang berikatan mendapat warna yang berbeda. Jika G memiliki k-pewarnaan, maka G dikatakan dapat diwarnai dengan k-warna (Wilson dan Watkins, 1989: 235).

Pewarnaan graf dapat dilakukan dengan menggunakan Algoritma Welsh dan Powell. Algoritma ini memberikan cara mewarnai sebuah graph dengan memberi label simpul-simpulnya sesuai dengan derajatnya. Langkah-langkahnya sebagai berikut:

Langkah 1 (melabel simpul dengan derajatnya). Label simpul V1, V2, ..., Vn sedemikian hingga derajat (V1) > derajat (V2) > ... > derajat (Vn).

Langkah 2 (warnai simpul belum berwarna pertama dari simpul-simpul belum berwarna yang berdekatan dengan simpul itu). Berikan warna yang belum digunakan pada simpul belum berwarna yang pertama pada daftar simpul itu. Lakukan hal itu pada semua simpul dalam daftar secara terurut, berikan warna baru ini pada setiap simpul yang tidak berdekatan dengan setiap simpul lain yang telah diwarnai ini.

Langkah 3 (graphnya telah diwarnai?). Jika beberapa simpulnya belum berwarna, maka kembalilah ke langkah 2.

Langkah 4 (selesai). Pewarnaan graph telah dilakukan.

B. Polinomial Khromatik

Misal G merupakan graf sederhana, dan PG(k) adalah banyak cara mewarnai simpul G dengan k warna sedemikian hingga tidak ada dua simpul yang berikatan mendapat warna sama. Fungsi PG(k) disebut polinomial khromatik G atau suku banyak khromatik G .

Contoh 1

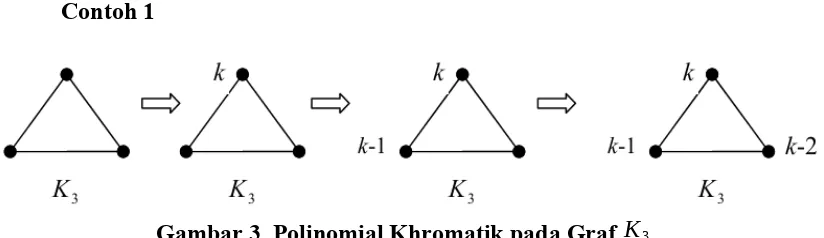
Gambar 3. Polinomial Khromatik pada Graf K3

K_{3 adalah graf lengkap-3. Simpul puncak} K_{3dapat diberi warna sembarang dari}

k warna tersebut. Simpul di sebelah kirinya dapat diberi warna sembarang dari (k-1) warna yang belum diberikan pada simpul puncak. Simpul di sebelah kanan simpul puncak dapat diberi warna sembarang dari (k-2) warna yang belum terpakai.

Sehingga, banyak cara mewarnai K3 adalah k(k−1) (k−2)atau P_K3(k)=k(k−1)(k−2) (Wilson dan Watkins, 1989: 237, 238).

Contoh 2

Gambar 4. Polinomial Khromatik pada Graf P3

Jika G adalah lintasan graf P3 simpul paling kiri dapat diwarnai dengan sebanyak k-warna, simpul tengah dapat diwarnai dengan k-1 warna selain warna yang diberikan pada simpul kiri, dan simpul kanan dapat diwarnai dengan k-1 warna yang sama dengan simpul tengah. Sehingga, banyak cara mewarnai P3 adalah k(k−1)2atau

PP3(k)=k(k−1)

Jika polinomial khromatik diketahui, maka bilangan khromatik suatu graf dapat dihitung dengan mudah, karena bilangan khromatik graf G adalah bilangan bulat positif terkecil k yang memenuhi PG(k)>0.

G _G’’ G’

e

Jika cara untuk menentukan polinomial kromatiknya sudah ditemukan, maka dapat diturunkan sebuah algoritma untuk menentukan bilangan kromatik.

Dari contoh diatas dapat dilihat bahwa k(k−1) (k−2)=k(k−1)2−k(k−1)

Sehingga,

PG(k)=PG'(k)−PG ' '(k)

dimana G,G’, dan G’’ seperti graf berikut:

Gambar 5. G, G’, dan G’’

Dengan G’ didapat dari G dengan menghapus rusuk e. G’’ didapat dari G dengan memampatkan rusuk e. Gagasan tersebut menghasilkan sebuh teorema, yang disebut Deletion-Contraction Theorem.

Berikut diberikan polinomial khromatik beberapa macam graf dalam k. Tabel 1. Polinomial Khromatik Beberapa Macam Graf

C. Pembuktian teorema Deletion-Contraction Theorem

PG(k)=PG¿(k)−PG ο e(k)

Bukti. Misal e = vw adalah rusuk dari G. G \ e adalah graf yang diperoleh dengan menghapus rusuk e dan G ο e adalah graf yang diperoleh dengan mengkontraksi rusuk e.

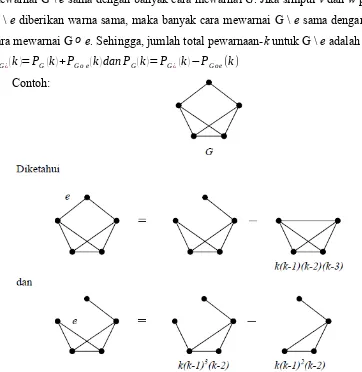
Jika simpul v dan w pada graf G \ e diberikan warna berbeda, maka banyak cara mewarnai G \ e sama dengan banyak cara mewarnai G. Jika simpul v dan w pada graf G \ e diberikan warna sama, maka banyak cara mewarnai G \ e sama dengan banyak cara mewarnai G ο e. Sehingga, jumlah total pewarnaan-k untuk G \ e adalah

PG¿(k)=PG(k)+PG ο e(k)dan PG(k)=PG¿(k)−PG ο e(k) Contoh:

Gambar 6. Pembentukan Polinomial Khromatik Graf G Diperoleh bahwa:

PG(k)=¿

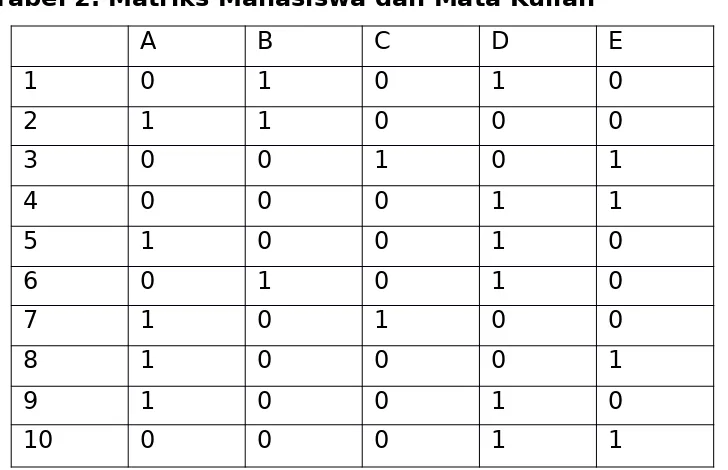
¿k5−7k4+19k3−23k2+10kKarena PG(1)=0,PG(2)=0,dan PG(3)=12, maka FPK, Aljabar Abstrak, Teori Graf, Sistem Geometri, dan Statistika Matematika, mata kuliah tersebut disimbolkan secara berurutan sebagai berikut A, B, C, D, dan E. Terdapat 10 mahasiswa yang akan mengikuti ujian tersebut. Setiap mahasiswa memilih dua mata kuliah yang berbeda, matriks mahasiswa dan mata kuliahnya adalah sebagai berikut:

Tabel 2. Matriks Mahasiswa dan Mata Kuliah

A B C D E

Solusi: Masalah penjadwalan ujian ini dapat diselesaikan dengan menggunakan metode pewarnaan simpul, dengan simpul mewakili mata kuliah dan rusuk antara dua simpul mewakili bahwa ada mahasiswa yang mengambil kedua mata kuliah yang diwakili simpul-simpul tersebut, sehingga ujian kedua mata kuliah yang diambil mahasiswa tersebut tidak dapat dilakukan bersamaan.

Masalah tersebut dapat dibuat dalam bentuk graf, yaitu sebagai berikut

Gambar 7. Graf Representasi Masalah Penjadwalan Ujian Dengan menggunakan metode Deletion-Contraction, maka:

Polinomial Kromatiknya yaitu:

PG(k)=

[

k(k−1) 4

−k(k−1)3

]

−2(k(k−1)3−k(k−1)2

)

+k(k−1) (k−2)

=

[

k(k−1)3(k−1−1)

]

−2¿ = ¿

= k5

−5k4+9k3−7k2+2k−2k4+8k3−10k2+4k+k3−3k2+2k = k5

−7k4+18k3−20k2+8k

Karena PG(0)a =0, PG(1)=0, PG(2)=0, dan PG(3)=6, χ(G) adalah K minimal, sehingga PG(K) > 0.

Jadi, bilangan kromatik dari graf tersebut adalah 3.

Dari kesimpulan tersebut, banyaknya jadwal yang dapat dibuat agar setiap mahasiswa tidak mendapatkan jadwal ujian dua mata kuliah dalam waktu yang bersamaan adalah 3 buah jadwal.

Untuk menentukan pewarnaan graf pada graf tersebut, akan di tentukan dengan menggunakan Algortima Wells-Powell:

2. Memberi warna merah pada simpul v1, karena v1 berikatan dengan v2, v3, v4, dan v5 maka tidak ada simpul lain yang mempunyai warna yang sama dengan v1.

3. Memberi warna biru pada simpul v2, berikan warna yang sama pada simpul-simpul yang tidak berikatan dengan v2 yaitu v5.

4. Memberi warna hijau pada simpul v3, berikan warna yang sama pada simpul-simpul yang tidak berikatan dengan v3 yaitu v4.

BAB IV PENUTUP

A. KESIMPULAN

1. Berdasarkan pembahasan di atas maka Deletion-Contracion Theorem terbukti. 2. Penentuan banyaknya bilangan kromatik dengan metode Deletion-Contracion

yaitu: PG(k)=PG¿(k)−PG ο e(k)

3. Salah satu aplikasi penghitungan banyaknya cara memberikan warna simpul yang menggunakan Deletion-Conttraction Theorem adalah pembuatan jadwal ujian Prodi Matematika FMIPA UNY.

B. SARAN

DAFTAR PUSTAKA

----. ----. Materi Pewarnaan Graf. Diakses dari http://www.itt elkom.ac.id pada Sabtu, 10 November 2012 pukul 7:08 PM

Devadas, Srini dan Eric Lehman. 2005. Graph Teory II. Diakses dari

http://files.myopera.com/m4th03/files/vertex_coloring_graph.pdf pada Sabtu, 10 November 2012 pukul 6:42 PM

Maaruf, Faridah. ----. Pengenalan Teori Graf. Diakses dari http://books.google.co.id/ books?

id=teQ1aMau9i8C&pg=PA113&lpg=PA113&dq=cara+menentukan+polinomial +kromatik&source=bl&ots=p9KCYF0gog&sig=yhqKLURDCZAsqHttx8zDlfd Q5zY&hl=id&sa=X&ei=fTqgUKvklcqVmQW4yYHQCA&ved=0CBoQ6AEw AA#v=onepage&q&f=false pada Rabu, 14 November 2012 pukul 16.00 PM

Priatna, Nanang. ----. Pewarnaan Graf. Diakses dari

http://file.upi.edu/Direktori/FPMIPA/JUR._PEND._MATEMATIKA/196303311

988031-NANANG_PRIATNA/Pewarnaan_Graph.pdf pada Rabu, 14 November

2012 pukul 16.00 PM