STRATEGI THINKING ALOUD PAIR PROBLEM SOLVING(TAPPS) UNTUK MENINGKATKANKEMAMPUAN
KELANCARAN BERPROSEDUR DAN KOMPETENSI STRATEGIS MATEMATIS SISWA SMP
TESIS
Diajukan untuk Memenuhi Sebagian dari Syarat Memperoleh Gelar Magister Pendidikan
Program Studi Pendidikan Matematika
OLEH:
TINA ROSYANA 1007343
PROGRAM STUDI PENDIDIKAN MATEMATIKA SEKOLAH PASCASARJANA
UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG
STRATEGI THINKING ALOUD PAIR PROBLEM SOLVING(TAPPS) UNTUK MENINGKATKANKEMAMPUAN
KELANCARAN BERPROSEDUR DAN KOMPETENSI STRATEGIS MATEMATIS SISWA SMP
Oleh
Tina Rosyana, S.Si. UniversitasPadjadjaran, 2009
Sebuah Tesis yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan (M.Pd.) pada Program Studi Pendidikan Matematika
© Tina Rosyana 2013 Universitas Pendidikan Indonesia
Juli2013
Hak Cipta dilindungi undang-undang.
Tesis ini tidak boleh diperbanyak seluruhya atau sebagian,
ABSTRAK
Tina Rosyana (2013), Strategi Thinking Aloud Pair Problem Solving (TAPPS) untuk Meningkatkan Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis Siswa SMP.
Penelitian ini bertujuan untuk mendeskripsikan dan menelaah peningkatan kemampuan kelancaran berprosedur dan kompetensi strategis matematis antara siswa yang memperoleh pembelajaran dengan strategi TAPPS, dengan siswa yang memperoleh pembelajaran biasa. Metode dalam penelitian ini yaitu metode eksperimen. Populasi dalam penelitian ini adalah seluruh siswa di salah satu SMP Negeri di Bandung semester genap tahun ajaran 2012/2013. Sampel dalam penelitian ini dipilih sebanyak dua kelas dari kelas VIII. Proses penentuan kelas dengan cara purposive sampling. Kelas eksperimen memperoleh pembelajaran dengan strategi TAPPS dan kelas kontrol memperoleh pembelajaran biasa. Instrumen penelitian meliputi tes bentuk uraian untuk kemampuan kelancaran berprosedur dan kompetensi strategis matematis, skala sikap siswa, dan lembar observasi. Pengolahan data untuk uji perbedaan dua rataan menggunakan uji-t dan uji Mann-Whitney. Hasil penelitian menunjukkan bahwa (1) Kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS lebih baik daripada yang memperoleh pembelajaran biasa; (2) Peningkatan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS lebih baik daripada yang memperoleh pembelajaran biasa; (3) Sikap siswa menunjukkan sikap yang positif terhadap matematika, kegiatan pembelajaran dengan strategi TAPPS, dan terhadap soal-soal kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa.
Kata Kunci: Strategi TAPPS, kelancaran berprosedur matematis, kompetensi
ABSTRACT
Tina Rosyana (2013), TAPPS Strategy to Enhancement of Mathematical Procedural Fluency and Strategic Competence of Junior High School Student.
This research aims to describe and to analyze the enhancement of mathematical procedural fluency and strategic competence between students in TAPPS Strategy and conventional learning. This kind of research method is a experiment method. The population of this research is all of the students in one Junior High School in Bandung, the second semester of academic year 2012/2013. The samples of this research are by choosing two classes of VIIIth. Process of selecting samples is purposive sampling. The experiment class obtains the TAPPS Strategy, and the control class obtains the conventional learning. The research of data is obtained by giving a mathematical procedural fluency and strategic competence test, questionnaire, and the observation directive. The data is processed by the t-test and Mann-Whitney test. The result of this research showed that (1) The ability of mathematical procedural fluency and strategic competence between students in TAPPS Strategy better than in conventional learning; (2) The enhancement of mathematical procedural fluency and strategic competence between students in TAPPS Strategy better than in conventional learning; (3) Students showed positive attitude towards mathematics, learning by TAPPS Strategy, and the test of mathematical procedural fluency and strategic competence.
DAFTAR ISI
Halaman
LEMBAR PENGESAHAN ... i
LEMBAR PERNYATAAN ... ii
ABSTRAK ... iii
KATA PENGANTAR ... iv
UCAPAN TERIMA KASIH ... v
DAFTAR ISI ... vii
DAFTAR TABEL ... x
DAFTAR GAMBAR ... xii
DAFTAR LAMPIRAN ... xiii
BAB I PENDAHULUAN A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 15
C. Tujuan Penelitian ... 16
D. Manfaat Penelitian ... 17
E. Definisi Operasional ... 18
BAB II KAJIAN PUSTAKA A. Kemampuan Kelancaran Berprosedur ... 19
B. Kemampuan Kompetensi Strategis ... 21
C. Pemecahan Masalah (Problem Solving) ... 22
D. Strategi Thinking Aloud Pair Problem Solving (TAPPS) ... 25
E. Pemecahan Masalah dengan Strategi Thinking Aloud Pair Problem Solving (TAPPS) ... 27
F. Teori-teori yang Mendukung ... 29
G. Penelitian yang Relevan ... 31
BAB III METODE PENELITIAN
A. Desain Penelitian ... 35
B. Populasi dan Sampel Penelitian ... 36
C. Variabel Penelitian ... 37
D. Instrumen Penelitian ... 38
1. Tes Kemampuan Kelancaran Berprosedur Matematis ... 39
2. Tes Kemampuan Kompetensi Strategis Matematis ... 39
3. Analisis Hasil Ujicoba Tes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 40
4. Bahan Ajar ... 49
5. Skala Sikap ... 50
6. Lembar Observasi ... 51
E. Teknik Pengumpulan Data ... 52
F. Teknik Analisis Data ... 52
G. Prosedur Penelitian ... 55
H. Jadwal Penelitian ... 57
I. Kerangka Penelitian ... 58
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Hasil Penelitian ... 59
1. Data Deskriptif Hasil Pengolahan Data ... 59
2. Analisis Data Pretes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 63
3. Analisis Data Postes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 66
4. Analisis Peningkatan Kemampuan Kelancaran Berprosedur Matematis ... 72
6. Deskripsi Sikap Siswa ... 78
7. Analisis Hasil Observasi ... 83
B. Pembahasan ... 84
1. Pembelajaran dengan Strategi TAPPS ... 84
2. Analisis Peningkatan Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 88
3. Sikap Siswa ... 92
4. Kegiatan Guru dan Siswa ... 92
5. Keterbatasan Penelitian ... 94
BAB V KESIMPULAN DAN SARAN A. Kesimpulan ... 95
B. Saran ... 96
DAFTAR TABEL
Tabel Halaman
3.1 Kriteria Penskoran Tes Kemampuan Kelancaran
Berprosedur Matematis ... 39 3.2 Kriteria Penskoran Tes Kemampuan Kompetensi
Strategis Matematis ... 40 3.3 Klasifikasi Koefisien Korelasi ... 41 3.4 Hasil Analisis Validitas Soal Uji Coba Tes Kemampuan
Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 42 3.5 Klasifikasi Reliabilitas ... 43 3.6 Hasil Analisis Reliabilitas Soal Uji Coba Tes Kemampuan
Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 44 3.7 Klasifikasi Nilai Daya Pembeda ... 45 3.8 Hasil Analisis Daya Pembeda Soal Uji Coba Tes Kemampuan
Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 46 3.9 Klasifikasi Tingkat Kesukaran Soal ... 47 3.10 Hasil Analisis Tingkat Kesukaran Soal Uji Coba Tes Kemampuan
Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 47 3.11 Kesimpulan Hasil Analisis Soal Uji Coba Tes Kemampuan
Kelancaran Berprosedur dan Kompetensi Strategis Matematis ... 48 3.12 Klasifikasi Gain (g) ... 53 3.13 Jadwal Kegiatan Penelitian ... 57 4.1 Statistik Deskriptif Kemampuan Kelancaran
Berprosedur dan Kompetensi Strategis Matematis ... 61 4.2 Rekapitulasi Butir Skala Sikap ... 61 4.3 Hasil Uji Normalitas Data Pretes Kemampuan Kelancaran
Berprosedur dan Kompetensi Strategis Matematis ... 66 4.5 Hasil Uji Normalitas Data Postes Kemampuan Kelancaran
Berprosedur dan Kompetensi Strategis Matematis ... 67 4.6 Hasil Uji Homogenitas Data Postes Kemampuan Kelancaran
Berprosedur dan Kompetensi Strategis Matematis ... 69 4.7 Hasil Uji Perbedaan Rataan Postes Kemampuan Kelancaran
Berprosedur Matematis ... 70 4.8 Hasil Uji Perbedaan Rataan Postes Kemampuan
Kompetensi Strategis Matematis ... 71 4.9 Uji Normalitas Data N-Gain Kemampuan Kelancaran
Berprosedur Matematis ... 73 4.10 Uji Perbedaan Rataan N-Gain Kemampuan Kelancaran
Berprosedur Matematis ... 74 4.11 Uji Normalitas Data N-Gain Kemampuan Kompetensi
Strategis Matematis ... 76 4.12 Uji Perbedaan Rataan N-Gain Kemampuan Kompetensi
Strategis Matematis ... 77 4.13 Distribusi Butir Sikap Siswa terhadap Matematika ... 79 4.14 Distribusi Butir Sikap Siswa terhadap Kegiatan Pembelajaran
dengan Strategi TAPPS ... 80 4.15 Distribusi Sikap Siswa terhadap Soal Kemampuan
Kelancaran Berprosedur dan Kompetensi Strategis
DAFTAR GAMBAR
Gambar Halaman
DAFTAR LAMPIRAN
Halaman
LAMPIRAN A: INSTRUMEN PENELITIAN
A.1 Silabus ... 104 A.2 Rencana Pelaksanaan Pembelajaran (RPP)
Kelas Eksperimen dan Kelas Kontrol ... 106 A.3 Lembar Kerja Siswa (LKS) ... 186 A.4 Kisi-kisi dan Soal Tes Kemampuan Kelancaran
Berprosedur dan Kompetensi Strategis Matematis ... 208 A.5 Kisi-kisi dan Angket Skala Sikap Siswa ... 214 A.6 Pedoman Observasi dalam Pembelajaran Matematika
dengan Strategi TAPPS... 218
LAMPIRAN B: ANALISIS HASIL UJI COBA TES MATEMATIKA
B.1 Skor Uji Coba Tes Kemampuan Kelancaran Berprosedur ... 221 B.2 Skor Uji Coba Tes Kemampuan Kompetensi Strategis ... 222 B.3 Perhitungan Hasil Uji Coba Tes Kemampuan
Kelancaran Berprosedur ... 223 B.4 Perhitungan Hasil Uji Coba Tes Kemampuan
Kompetensi Strategis ... 228
LAMPIRAN C: ANALISIS DATA HASIL PENELITIAN
C.1 Skor Hasil Pretes ... 234 C.2 Skor Hasil Postes ... 238 C.3 Skor Gain Ternormalisasi ... 242 C.4 Perhitungan Data dan Uji Statistik Kemampuan
Kelancaran Berprosedur Matematis ... 246 C.5 Perhitungan Data dan Uji Statistik Kemampuan
LAMPIRAN D: ANALISIS SKOR SKALA SIKAP SISWA
D.1 Distribusi Skala Sikap Siswa ... 254 D.2 Distribusi Skala Sikap Siswa terhadap
Matematika ... 256 D.3 Distribusi Skala Sikap Siswa terhadap
Pembelajaran ... 257 D.4 Distribusi Skala Sikap Siswa terhadap
Soal ... 258
LAMPIRAN E: UNSUR-UNSUR PENUNJANG PENELITIAN
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Perkembangan ilmu pengetahuan dan teknologi di dunia secara global dan kompetitif memerlukan generasi yang memiliki kemampuan memperoleh, mengelola, memanfaatkan informasi, sehingga menjadi sebuah pengetahuan serta menjadi alat untuk bertindak dan mengambil keputusan yang tepat dalam setiap situasi. Ilmu pengetahuan dan teknologi yang terus berkembang pesat memungkinkan kita memperoleh informasi dengan cepat dan mudah yang dapat diperoleh dari berbagai sumber yang seolah-olah tidak dibatasi ruang, jarak dan waktu.
Dalam perkembangan ilmu pengetahuan dan teknologi, matematika sebagai salah satu disiplin ilmu dalam dunia pendidikan mempunyai peranan yang besar. Matematika bermanfaat dalam perkembangan berbagai bidang ilmu pengetahuan lainnya. Oleh karena itu, diperlukan penguasaan matematika sejak dini dan matematika harus dipelajari pada semua jenjang pendidikan, agar kemampuan siswa berkembang sesuai dengan tuntutan kehidupan di masa yang akan datang.
dapat dilihat dari kemampuan berupa kecakapan yang dimiliki oleh siswa dalam penguasaan matematika.
Perumusan tentang kemampuan dan kecakapan matematis yang harus dimiliki siswa diperkenalkan oleh Mathematics Learning Study Committee,
National Research Council (NRC) yang ditulis oleh Kilpatrick, Swafford, dan
Findell tahun 2001, sebagai berikut: 1) Pemahaman konsep; 2) Kelancaran berprosedur; 3) Kompetensi strategis; 4) Penalaran adaptif; 5) Berkarakter Produktif.
Selain itu menurut Sumarmo (2002), kemampuan dasar yang harus dimiliki siswa setelah mempelajari matematika adalah: kemampuan pemahaman matematis, pemecahan masalah matematis, penalaran matematis, koneksi matematis dan komunikasi matematis.
Berdasarkan panduan KTSP (2006) dan pendapat Sumarmo (2002) di atas, salah satu kemampuan dan kecakapan atau kompetensi matematis yang penting yang harus dimiliki siswa yaitu kemampuan pemecahan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh. Selain itu menurut Kilpatrick, Swafford, dan Findell (2001:116) beberapa kemampuan dan kecakapan atau kompetensi matematis yang penting yang harus dimiliki siswa yaitu kelancaran berprosedur (proceduaral fluency), yang meliputi kemampuan siswa menggunakan prosedur secara fleksibel, akurat, efisien dan tepat dalam memecahkan masalah matematika dan kemampuan kompetensi strategis (strategic
competence), yang meliputi kemampuan untuk merumuskan, menyajikan, serta
memecahkan masalah-masalah matematis.
pemecahan masalah diindikasikan dengan kemampuan untuk memahami masalah, menyajikan suatu masalah secara matematik dalam berbagai bentuk (numerik, simbolis, verbal, atau grafis), memilih rumus, pendekatan atau metode yang tepat untuk memecahkan masalah, Widjajanti (2011). Kedua kemampuan matematis tersebut, yaitu kelancaran berprosedur dan kompetensi strategis matematis perlu dikembangkan dalam diri siswa agar dapat memecahkan masalah dalam matematika dan dalam kehidupan sehari-hari bahkan dalam kehidupan mereka di masa depan yang semakin kompetitif.
Namun kenyataan menunjukkan bahwa kemampuan kelancaran berprosedur dan kompetensi strategis siswa saat ini masih rendah. Terbukti dari masih sulitnya siswa untuk menyajikan masalah dalam kehidupan sehari-hari ke dalam model matematis dan menentukan strategi yang tepat untuk menyelesaikannya. Kondisi ini ditunjukkan dari hasil Programme for
International Student Assessment (PISA). PISA adalah studi untuk mengukur
tahun 2006 skor rata-rata naik menjadi 391, yaitu peringkat 50 dari 57 negara, sedangkan tahun 2009 skor rata-rata turun menjadi 371 dengan peringkat 61 dari 65 negara (Balitbang, 2011).
Selain PISA, Indonesia juga menjadi peserta dalam Trends In
International Mathematics and Science Study (TIMSS), survei penilaian
internasional tentang prestasi matematika dan sains siswa SD kelas 4 dan SMP kelas VIII. Selama mengikuti TIMSS tahun 1999, 2003 dan 2007, rata-rata skor prestasi matematika siswa kelas VIII Indonesia berada signifikan di bawah rata-rata internasional, yaitu 500. Pada tahun 1999, Indonesia berada di peringkat ke 34 dari 38 negara, dengan rata-rata skor 403. Tahun 2003 berada di peringkat ke 35 dari 46 negara, dengan rata-rata skor 411, dan tahun 2007 berada di peringkat ke 36 dari 49 negara, dengan rata-rata skor 397 (Balitbang, 2011). Kemudian pada tahun 2011, Indonesia berada di peringkat ke 38 dari 45 negara, dengan rata-rata skor 386 (TIMSS, 2011:487).
Berikut ini adalah contoh soal terkait rendahnya kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa Indonesia di ajang PISA dan TIMSS:
1. Salah satu soal PISA 2003 (Wardhani dan Rumiati, 2011:31) Setelah diterjemahkan, soal tersebut sebagai berikut:
“Sebuah kedai pizza menyajikan dua pilihan pizza dengan ketebalan yang
Sebagai guru matematika, Anda dapat mengasosiasikan bilangan satuan harga dalam “zed” pada soal tersebut dengan bilangan satuan harga dalam rupiah sesuai konteks di lingkungan Anda (Wardhani dan Rumiati, 2011:31).
Pada soal tersebut, siswa dituntut untuk mampu memahami maksud soal, kemudian mampu menghitung luas atau besarnya satu pizza, besarnya pizza yang diperoleh dengan harga 1 zed atau harga setiap cm2 pizza dalam zed, dan menyimpulkan pizza mana yang harganya lebih murah. Dari seluruh siswa Indonesia yang mengikuti tes, hanya 11% yang menjawab benar. Kemungkinan penyebab hal itu adalah banyaknya konten matematika yang termuat di dalamnya, antara lain: kemampuan menghitung luas lingkaran, melakukan operasi hitung perkalian dan pembagian bilangan bulat, dan membandingkan dua bilangan pecahan, jadi banyak prosedur yang harus dilakukan. Kemungkinan penyebab lain adalah siswa kurang terbiasa melakukan proses pemecahan masalah dengan benar, yaitu dengan tahapan memahami masalah, merencanakan pemecahan masalah, melaksanakan pemecahan masalah dan mengecek hasil pemecahan masalah. Pada soal tersebut sebenarnya konteks masalah tampak sederhana dan tidak membutuhkan kemampuan membaca yang tinggi, namun bila siswa tidak dibiasakan untuk memecahkan masalah dengan tahapan proses yang benar maka siswa akan cenderung mengalami kesulitan dalam menyelesaikan soal tersebut.
“Joe mengetahui bahwa harga sebuah pena 1 zed lebih mahal dari harga sebuah pensil. Temannya membeli 2 buah pena dan 3 buah pensil seharga 17 zed. Berapa zed yang dibutuhkan Joe untuk membeli 1 pena dan 2 pensil?”
Soal ini merupakan contoh soal kemampuan kompetensi strategis matematis. Dalam soal ini siswa diminta untuk memecahkan masalah yang berkaitan dengan persamaaan linear dengan dua variabel. Soal tersebut cukup sulit, karena dari semua peserta hanya 18% siswa yang menjawab benar, dan bagi peserta Indonesia hanya 8% siswa yang menjawab benar. Soal ini sulit kemungkinan disebabkan soal ini menguji kemampuan kelancaran berprosedur dan kompetensi strategis matematis dengan diperlukannya kemampuan siswa dalam memecahkan masalah non rutin, bukan sekedar pengetahuan atau penerapan. Tampak bahwa mengubah kalimat biasa menjadi kalimat matematika, dan kemudian menafsirkannya kembali untuk dicari solusinya merupakan salah satu hal yang dianggap sukar dalam pembelajaran matematika.
3. Salah satu soal pada TIMSS tahun 2007 (Wardhani dan Rumiati, 2011:44) Setelah diterjemahkan, soal tersebut sebagai berikut:
Stone Cold. Buatlah sebuah diagram batang yang menggambarkan data yang tersaji pada diagram lingkaran di atas”.
4. Salah satu soal pada TIMSS tahun 2003 (Wardhani dan Rumiati, 2011:56) Setelah diterjemahkan, soal tersebut sebagai berikut:
Tabel di samping merupakan hasil pengamatan Kanti terhadap penurunan suhu air dar 95oC ke 70oC. Ia mencatat waktu yang diperlukan setiap penurunan 5oC. Perkirakan berapa menit jumlah waktu yang diperlukan untuk penurunan suhu 95oC ke 70oC dan jelaskan cara memperoleh perkiraan tersebut.
Soal ini merupakan contoh untuk kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa. Laporan hasil studi menyebutkan bahwa ternyata hanya 4% saja dari siswa Indonesia yang menjawab benar, dan sisanya menjawab salah. Hal ini kemungkinan karena siswa kita kurang antusias, bahkan meninggalkan, dalam mengerjakan soal yang informasinya panjang, dan cenderung tertarik hanya pada soal rutin yang langsung berkaitan dengan rumus.
Berdasarkan uraian di atas, terlihat bahwa kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa SMP di Indonesia masih kurang. Oleh karena itu, perlu dilakukan suatu upaya untuk meningkatkan kedua kemampuan tersebut. Upaya-upaya peningkatan tersebut erat kaitannya dengan proses pembelajaran, seperti cara guru mengajar, kaitan materi dengan kehidupan sehari-hari, jenis soal yang biasa diberikan kepada siswa untuk diselesaikan, sejauhmana keterlibatan siswa dalam pembelajaran dan sebagainya.
Dari hasil PISA yang mengukur kemampuan literasi matematis yang meliputi kemampuan merumuskan, menerapkan dan menafsirkan matematika
Penurunan Waktu
dalam berbagai konteks, penalaran matematis dan penggunaan konsep, prosedur dan fakta untuk menggambarkan, menjelaskan atau memperkirakan kejadian yang dimiliki siswa SMP. Selain itu, hasil TIMSS menunjukkan bahwa kemampuan siswa SMP kelas dua Indonesia dalam menyelesaikan soal-soal matematika, khususnya yang tidak rutin sangat lemah. Pendapat ini sejalan dengan Ruseffendi (2006:156) yang menyatakan bahwa “Banyak anak yang setelah belajar matematika bagian yang sederhana pun banyak yang tidak dipahaminya, bahkan banyak konsep yang dipahami keliru. Matematika dianggap sebagai ilmu yang sukar, ruwet dan banyak memperdayakan”. Ini menunjukkan bahwa banyak anak
yang mengalami kesulitan dalam belajar matematika, karena kebanyakan dari mereka bukan memahami konsepnya, melainkan menghafalnya.
menjadi pengetahuan yang bermakna, pengetahuan tersebut hanya untuk diingat sementara setelah itu dilupakan.
Oleh karena itu, diperlukan suatu strategi pembelajaran untuk dapat meningkatkan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa. Strategi tersebut dapat membuat siswa aktif, melatih siswa berkolaborasi dan saling membantu dalam menyelesaikan masalah yang diberikan serta memberikan peluang kepada siswa untuk menemukan sendiri dan memahami materi lebih mendalam. Reys et. al (1998:75) pemecahan masalah dapat dikerjakan dengan mudah melalui diskusi pada kelompok besar, tetapi proses pemecahan masalah akan lebih praktis bila dilakukan dalam kelompok kecil yang bekerja secara bersama-sama. Hal tersebut juga ditunjang oleh pendapat Damon dan Murray (Slavin, 1995) yang menyatakan bahwa interaksi antar rekan sebaya memegang peranan penting dalam meningkatkan pemahaman suatu konsep. Selain itu sejalan juga dengan pendapat Silberman (2009:10) bahwa apa yang peserta didik diskusikan dengan yang lain dan apa yang peserta didik ajarkan pada yang lain menyebabkan dia memperoleh pemahaman dan menguasai cara belajar.
memungkinkan terjadinya interaksi yang positif antar siswa sehingga dapat meningkatkan kepercayaan diri siswa dalam menyelesaikan masalah-masalah matematis. Salah satu siswa berperan sebagai problem solver yang memecahkan masalah dan menyampaikan semua gagasan dan pemikirannya pasangannya, sedangkan siswa lain yang merupakan pasangannya berperan sebagai listener yang mengikuti dan mengoreksi dengan cara mendengarkan seluruh proses
problem solver. Setelah menyelesaikan masalah, kemudian bertukar peran
sehingga semua siswa memperoleh kesempatan menjadi problem solver dan
listener.
Penelitian menggunakan strategi TAPPS ini telah diterapkan oleh Stice (1987) yang menjanjikan adanya peningkatan kemampuan pemecahan masalah siswa jika dibandingkan dengan pembelajaran secara tradisional. Jeon et al (2005) mengatakan bahwa metode TAPPS lebih efektif dalam mengembangkan kemampuan siswa dalam memecahkan masalah, terutama dalam mengingat kembali konsep-konsep yang terkait dalam menyelesaikan soal matematika. Anita (2007) yang melaporkan adanya peningkatan pemahaman konsep dan pemecahan masalah siswa di tingkat Sekolah Menengah Atas. Selain itu telah diterapkan juga pada penelitian oleh Pestel (1993), Johnson dan Chung (1999) dan Pate et al (2004).
Berdasarkan uraian di atas, maka penulis berpendapat bahwa sangat diperlukan adanya penelitian tentang penerapan strategi Thinking Aloud Pair
Problem Solving (TAPPS) untuk meningkatkan kemampuan kelancaran
aspek kognitif tersebut (kemampuan kelancaran berprosedur dan kompetensi strategis matematis), penulis juga ingin melihat aspek afektifnya yaitu sikap siswa terhadap matematika, pembelajaran dengan strategi Thinking Aloud Pair
Problem Solving (TAPPS) dan terhadap soal-soal kemampuan kelancaran
berprosedur dan kompetensi strategis matematis.
Sikap siswa terhadap matematika merupakan salah satu aspek internal yang berkaitan dengan pelajaran matematika. Saat ini ada kecenderungan bahwa sikap siswa kurang positif terhadap matematika. Mereka masih menganggap bahwa matematika merupakan pelajaran yang sulit dan membosankan. Hal ini tentu mengakibatkan rendahnya hasil belajar siswa. Oleh karena itu, diperlukan upaya untuk mengoptimalkan sikap positif siswa terhadap matematika, termasuk sikap positif siswa terhadap pembelajaran dan soal-soal kemampuan matematis tertentu. Studi tentang sikap siswa terhadap matematika dan pembelajaran matematika biasanya berkaitan erat dengan prestasi siswa dalam matematika (Turmudi, 2008:80).
siswa terhadap pembelajaran matematika. Dalam pembelajaran kelas matematika, domain sikap terkait erat dengan persepsi matematik siswa. Pengalaman menyenangkan yang diperoleh dari pengajaran yang dilakukan guru benar-benar akan memfasilitasi peningkatan sikap positif siswa terhadap matematika.
Sikap siswa terhadap pembelajaran dengan strategi Thinking Aloud Pair
Problem Solving (TAPPS) dapat dipandang sebagai cerminan proses
pembelajaran yang terjadi di kelas. Proses pembelajaran yang memberikan kesempatan kepada siswa untuk aktif memahami dan memecahkan masalah tersebut serta diberi kesempatan untuk berinteraksi serta berdiskusi baik dengan pasangan siswa maupun dengan guru, akan memungkinkan siswa merasa senang dan termotivasi untuk belajar. Bila hal ini benar-benar terjadi dalam proses pembelajaran, bukan mustahil sikap positif siswa terhadap pembelajaran yang diikuti akan tumbuh. Mengingat adanya korelasi positif antara sikap siswa terhadap pembelajaran matematika dan hasil belajar, maka meningkatkan prestasi siswa juga dapat dilakukan melalui pemilihan strategi pembelajaran yang dapat meningkatkan sikap siswa terhadap pembelajaran matematika.
pembelajaran serta kegiatan apa saja yang terjadi selama kegiatan pembelajaran berlangsung, sehingga dapat dilakukan perbaikan untuk setiap pertemuan, maka peneliti merasa perlu untuk meneliti kegiatan siswa dan guru di dalam kelas yang dapat ditunjukkan melalui lembar observasi.
B. Rumusan Masalah
Mengacu pada latar belakang masalah yang sudah diuraikan di atas, maka penelitian ini difokuskan pada penerapan strategi Thinking Aloud Pair Problem
Solving (TAPPS) untuk meningkatkan kemampuan kelancaran berprosedur dan
kompetensi strategis matematis siswa SMP. Dari masalah ini dapat dijabarkan ke dalam beberapa pertanyaan penelitian sebagai berikut:
1. Apakah kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS lebih baik daripada yang memperoleh pembelajaran biasa?
2. Apakah peningkatan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS lebih baik daripada yang memperoleh pembelajaran biasa?
3. Bagaimana sikap siswa terhadap matematika, kegiatan pembelajaran dengan strategi TAPPS, dan terhadap soal-soal kemampuan kelancaran berprosedur dan kompetensi strategis matematis?
C. Tujuan Penelitian
Berdasarkan latar belakang dan rumusan masalah yang telah dipaparkan di atas, maka tujuan penelitian ini adalah:
1. Mengetahui dan menelaah kemampuan kelancaran berprosedur dan kompetensi matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS lebih baik daripada yang memperoleh pembelajaran biasa.
2. Mengetahui dan menelaah peningkatan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS lebih baik daripada yang memperoleh pembelajaran biasa.
3. Mengetahui dan menelaah sikap siswa terhadap matematika, kegiatan pembelajaran dengan strategi TAPPS, dan terhadap soal-soal kemampuan kelancaran berprosedur dan kompetensi strategis matematis.
4. Mengetahui dan menelaah kegiatan guru dan siswa selama pembelajaran dengan strategi TAPPS.
D. Manfaat Penelitian
Hasil penelitian ini diharapkan dapat memberikan manfaat dan masukan yang berarti bagi semua pihak, terutama bagi guru, siswa dan para peneliti selanjutnya yang berkaitan dengan penelitian ini. Adapun manfaat dari penelitian ini secara rinci adalah sebagai berikut:
pembelajaran matematika dengan strategi TAPPS meningkatkan kelancaran berprosedur dan kompetensi strategis matematis siswa, sehingga dapat dijadikan bahan rujukan dalam penelitian selanjutnya.
2. Bagi guru: hasil penelitian ini dapat digunakan sebagai salah satu alternatif strategis pembelajaran matematika di kelas untuk memberikan variasi dalam pembelajaran.
3. Bagi siswa: dapat memberi pengalaman baru bagi siswa dan mendorong siswa untuk meningkatkan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa, sehingga prestasi belajar matematikanya meningkat.
4. Bagi sekolah: hasil penelitian ini dapat meningkatkan mutu sekolah dan dapat digunakan oleh sekolah-sekolah lain sebagai salah satu alternatif dalam rangka meningkatkan hasil belajar matematika dan mutu sekolah.
E. Definisi Operasional
Untuk menghindari terjadinya perbedaan penafsiran terhadap istilah-istilah yang terdapat pada penelitian ini penulis memberikan batasan-batasan definisi operasional yaitu:
1. Strategi Thinking Aloud Pair Problem Solving (TAPPS)
Strategi Thinking Aloud Pair Problem Solving merupakan strategi pembelajaran pemecahan masalah yang melibatkan dua orang siswa yang bekerjasama untuk memecahkan masalah, yang memiliki peran sebagai
2. Kompetensi strategis (strategic competence)
Kompetensi strategis adalah kemampuan untuk merumuskan, merepresentasikan, serta menyelesaikan masalah matematika.
3. Kelancaran berprosedur (procedural fluency)
Kelancaran berprosedur adalah kemahiran siswa dalam menggunakan prosedur secara fleksibel, akurat, efisien dan tepat.
BAB III
METODE PENELITIAN
A. Desain Penelitian
Metode yang digunakan dalam penelitian ini adalah metode eksperimen. Menurut Sudjana (2005) penelitian eksperimen adalah suatu penelitian yang berusaha mencari pengaruh variabel tertentu terhadap variabel lain dalam kondisi yang terkontrol secara ketat. Pada penelitian ini digunakan dua kelas, yaitu kelas eksperimen dan kelas kontrol. Kelas eksperimen diberikan pembelajaran dengan strategi Thinking Aloud Pair Problem Solving (TAPPS), sedangkan kelas kontrol memperoleh pembelajaran biasa. Perlakuan yang diberikan berupa penerapan pembelajaran dengan strategi TAPPS untuk melihat pengaruhnya terhadap peningkatan kemampuan yang diukur yaitu kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa.
Untuk mengetahui besarnya pengaruh terhadap peningkatan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa, maka pada kedua kelas tersebut diberikan pretes dan postes. Pretes diberikan sebelum pembelajaran yang bertujuan untuk mengetahui kesetaraan kemampuan kedua kelas, sedangkan postes sebagai tes akhir untuk mengetahui pengaruh pembelajaran yang diberikan terhadap peningkatan kemampuan siswa.
pengelompokan subjek secara acak, jadi dari kelas yang ada dilakukan pengacakan untuk memilih dua kelas yang dijadikan subjek penelitian. Desain penelitiannya berbentuk:
A O X O
A O O
Keterangan:
A : Pengambilan subjek penelitian dipilih secara acak kelas
O : Pretes dan postes (tes kemampuan kelancaran berprosedur dan kompetensi strategis matematis)
X : Perlakuan pembelajaran dengan strategi TAPPS.
B. Populasi dan Sampel Penelitian
Populasi pada penelitian ini adalah seluruh siswa di salah satu SMP Negeri di Bandung semester genap Tahun Ajaran 2012/2013. Sampel yang diambil dalam penelitian ini adalah siswa kelas VIII.
Di sekolah tersebut terdapat sembilan kelas VIII, kemudian dipilih dua kelas sebagai kelas eksperimen dan kelas kontrol. Pengambilan sampel dilakukan secara
purposive sampling karena pertimbangan tertentu (Sugiyono, 2010:85). Penentuan
C. Variabel Penelitian
Menurut Sugiyono (2010), jika dilihat berdasarkan hubungan antar satu variabel dengan variabel yang lain, maka jenis-jenis variabel dapat dibedakan menjadi dua jenis variabel yaitu variabel bebas (independent variable) dan variabel terikat (dependent variable). Dalam penelitian ini, variabel yang ada terdiri atas variabel bebas dan variabel terikat.
1. Variabel Bebas
Sugiyono (2008:39) berpendapat bahwa variabel bebas merupakan variabel yang akan mempengaruhi dan dapat dikatakan sebagai sebab timbulnya variabel terikat. Berdasarkan pengertian tersebut, maka yang menjadi variabel bebas dalam penelitian ini adalah: (1) Strategi Thinking Aloud Pair Problem
Solving (TAPPS); (2) Pembelajaran biasa.
Dalam pembahasan selanjutnya, pembelajaran dengan strategi Thinking
Aloud Pair Problem Solving (TAPPS) disingkat PTAPPS, sedangkan
pembelajaran biasa disingkat PB. PTAPPS diberikan di kelas eksperimen dan PB diberikan di kelas kontrol.
2. Variabel Terikat
D. Instrumen Penelitian
Pada penelitian ini, instrumen yang digunakan adalah instrumen tes dan non-tes. Instrumen tes berupa tes berbentuk uraian untuk mengukur kemampuan kelancaran berprosedur dan kompetensi strategi matematis siswa. Instrumen non-tes berupa (1) skala sikap untuk mengetahui sikap siswa terhadap matematika, kegiatan pembelajaran dengan strategi TAPPS dan terhadap soal kemampuan kelancaran berprosedur dan kompetensi strategis matematis; (2) lembar observasi, untuk mengetahui kegiatan guru dan siswa selama pembelajaran.
Instrumen tes berupa tes kemampuan kelancaran berprosedur dan tes kompetensi strategis matematis. Tes tertulis ini terdiri dari tes awal (pretes) dan tes akhir (postes). Tes yang diberikan pada setiap kelas eksperimen dan kelas kontrol baik soal-soal untuk pretes maupun postes dibuat sama.
Dalam menyusun dan mengembangkan instrumen tes tertulis ini, peneliti terlebih dahulu membuat kisi-kisi soal disertai dengan alternatif jawaban. Materi tes diambil dari materi pelajaran matematika SMP kelas VIII semester genap dengan mengacu pada Kurikulum 2006 pada materi Teorema Phytagoras.
1. Tes Kemampuan Kelancaran Berprosedur Matematis
Instrumen tes kemampuan kelancaran berprosedur matematis terdiri dari 5 soal uraian. Setiap soal mendapatkan skor tertinggi 4. Setelah diperiksa validitas muka dan isinya oleh dosen pembimbing dan dinyatakan layak untuk diujikan, maka soal tersebut diujicoba. Ujicoba diberikan kepada kelas yang sebelumnya sudah memperoleh materi yang dipilih, yaitu kelas IX. Waktu yang dialokasikan untuk menyelesaikan tes tersebut adalah 80 menit (2 x 40 menit).
[image:36.595.115.529.244.639.2]Untuk memberikan penilaian yang objektif, digunakan pedoman pemberian skor untuk soal tes kemampuan kelancaran berprosedur matematis seperti pada tabel berikut:
Tabel 3.1 Kriteria Penskoran
Tes Kemampuan Kemampuan Kelancaran Berprosedur Matematis
Skor Kriteria
0 Tidak ada jawaban atau jawaban tidak sesuai dengan pertanyaan atau tidak ada jawaban yang benar
1 Prosedur yang digunakan sebagain besar tidak tepat dan masih terdapat perhitungan yang salah
2 Sebagain besar prosedur yang digunakan sudah tepat, namun masih terdapat perhitungan yang salah
3 Prosedur yang digunakan sudah hampir lengkap, namun masih terdapat sedikit kesalahan
4 Prosedur yang digunakan serta perhitungan sudah lengkap dan benar
Suganda (2012)
2. Tes Kemampuan Kompetensi Strategis Matematis
berprosedur, soal tes kemampuan kompetensi strategis juga diujicobakan setelah dinyatakan layak oleh dosen pembimbing untuk diujicobakan.
Untuk penilaian hasil tes, digunakan kriteria pemberian skor untuk soal tes kemampuan kompetensi strategis matematis yang diadaptasi dari buku How to
[image:37.595.114.526.240.631.2]Evaluate Progress in Problem Solving (Charles, 1994) seperti pada tabel berikut:
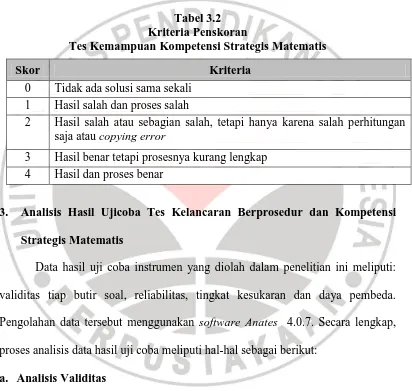
Tabel 3.2 Kriteria Penskoran
Tes Kemampuan Kompetensi Strategis Matematis
Skor Kriteria
0 Tidak ada solusi sama sekali 1 Hasil salah dan proses salah
2 Hasil salah atau sebagian salah, tetapi hanya karena salah perhitungan saja atau copying error
3 Hasil benar tetapi prosesnya kurang lengkap 4 Hasil dan proses benar
3. Analisis Hasil Ujicoba Tes Kelancaran Berprosedur dan Kompetensi
Strategis Matematis
Data hasil uji coba instrumen yang diolah dalam penelitian ini meliputi: validitas tiap butir soal, reliabilitas, tingkat kesukaran dan daya pembeda. Pengolahan data tersebut menggunakan software Anates 4.0.7. Secara lengkap, proses analisis data hasil uji coba meliputi hal-hal sebagai berikut:
a. Analisis Validitas
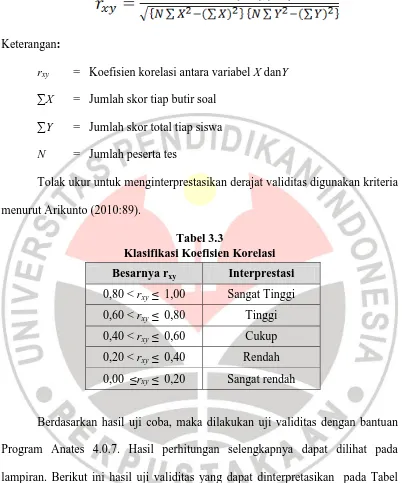
Anderson (Arikunto, 2010:65) menyatakan bahwa sebuah tes dikatakan valid apabila tes tersebut mengukur apa yang hendak diukur. Untuk menentukan perhitungan validitas butir soal digunakan rumus korelasi Product Moment
Keterangan:
rxy = Koefisien korelasi antara variabel X danY ∑X = Jumlah skor tiap butir soal
∑Y = Jumlah skor total tiap siswa
N = Jumlah peserta tes
[image:38.595.112.514.125.608.2]Tolak ukur untuk menginterprestasikan derajat validitas digunakan kriteria menurut Arikunto (2010:89).
Tabel 3.3
Klasifikasi Koefisien Korelasi
Besarnya rxy Interprestasi
0,80 < rxy ≤ 1,00 Sangat Tinggi 0,60 < rxy≤ 0,80 Tinggi 0,40 < rxy ≤ 0,60 Cukup 0,20 < rxy≤ 0,40 Rendah 0,00 ≤rxy≤ 0,20 Sangat rendah
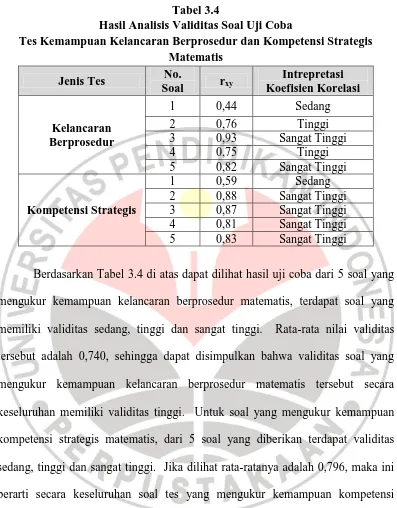
Tabel 3.4
Hasil Analisis Validitas Soal Uji Coba
Tes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis
Jenis Tes No.
Soal rxy
Intrepretasi Koefisien Korelasi
Kelancaran Berprosedur
1 0,44 Sedang
2 0,76 Tinggi
3 0,93 Sangat Tinggi
4 0,75 Tinggi
5 0,82 Sangat Tinggi
Kompetensi Strategis
1 0,59 Sedang
2 0,88 Sangat Tinggi
3 0,87 Sangat Tinggi
4 0,81 Sangat Tinggi
5 0,83 Sangat Tinggi
Berdasarkan Tabel 3.4 di atas dapat dilihat hasil uji coba dari 5 soal yang mengukur kemampuan kelancaran berprosedur matematis, terdapat soal yang memiliki validitas sedang, tinggi dan sangat tinggi. Rata-rata nilai validitas tersebut adalah 0,740, sehingga dapat disimpulkan bahwa validitas soal yang mengukur kemampuan kelancaran berprosedur matematis tersebut secara keseluruhan memiliki validitas tinggi. Untuk soal yang mengukur kemampuan kompetensi strategis matematis, dari 5 soal yang diberikan terdapat validitas sedang, tinggi dan sangat tinggi. Jika dilihat rata-ratanya adalah 0,796, maka ini berarti secara keseluruhan soal tes yang mengukur kemampuan kompetensi strategis matematis memiliki validitas yang tinggi.
b. Analisis Reliabilitas
Koefisien reliabilitas perangkat tes berupa bentuk uraian dapat diketahui menggunakan rumus Alpha (Ruseffendi, 2005:172) sebagai berikut:
Keterangan:
rp = Reliabilitas tes secara keseluruhan
b = Banyak soal
∑DBi2 = Jumlah varians skor tiap butir soal (soal ke-i)
DBj2 = Varians skor total menurut skor tiap siswa
[image:40.595.115.511.171.608.2]Tolak ukur untuk menginterprestasikan derajat reliabilitas alat evaluasi digunakan kriteria menurut Guilford (Ruseffendi, 2005:160) yang telah dimodifikasi sebagai berikut:
Tabel 3.5 Klasifikasi Reliabilitas
Besarnya r11 Interpretasi
0,90 < r11≤ 1,00 Sangat Tinggi 0,70 < r11 ≤ 0,90 Tinggi 0,40 < r11 ≤ 0,70 Sedang 0,20 < r11≤ 0,40 Rendah 0,00 ≤ r11≤ 0,20 Kecil
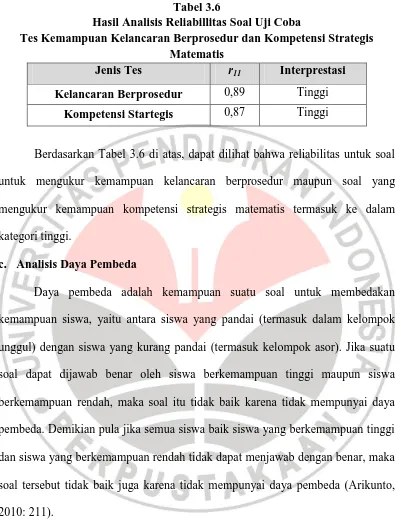
Tabel 3.6
Hasil Analisis Reliabillitas Soal Uji Coba
Tes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis
Jenis Tes r11 Interprestasi
Kelancaran Berprosedur 0,89 Tinggi
Kompetensi Startegis 0,87 Tinggi
Berdasarkan Tabel 3.6 di atas, dapat dilihat bahwa reliabilitas untuk soal untuk mengukur kemampuan kelancaran berprosedur maupun soal yang mengukur kemampuan kompetensi strategis matematis termasuk ke dalam kategori tinggi.
c. Analisis Daya Pembeda
Daya pembeda adalah kemampuan suatu soal untuk membedakan kemampuan siswa, yaitu antara siswa yang pandai (termasuk dalam kelompok unggul) dengan siswa yang kurang pandai (termasuk kelompok asor). Jika suatu soal dapat dijawab benar oleh siswa berkemampuan tinggi maupun siswa berkemampuan rendah, maka soal itu tidak baik karena tidak mempunyai daya pembeda. Demikian pula jika semua siswa baik siswa yang berkemampuan tinggi dan siswa yang berkemampuan rendah tidak dapat menjawab dengan benar, maka soal tersebut tidak baik juga karena tidak mempunyai daya pembeda (Arikunto, 2010: 211).
diambil 27% siswa yang skornya tinggi dan 27% siswa yang skornya rendah (menggunakan Anates Versi 4.0.7). Untuk menentukan daya pembeda, dihunakan rumus:
A B A
J S S
DP
keterangan:
DP = indeks daya pembeda suatu butir soal
A
S = jumlah skor kelompok atas
B
S = jumlah skor kelompok bawah
A
J = jumlah skor ideal kelompok atas
[image:42.595.115.510.190.600.2]Kriteria penafsiran Daya Pembeda suatu butir soal menurut Suherman dan Sukjaya (1990:202) didasarkan pada klasifikasi berikut ini:
Tabel 3.7
Klasifikasi Nilai Daya Pembeda
Nilai DP Klasifikasi
DP ≤ 0,00 Sangat jelek 0,00 < DP ≤ 0,20 Jelek 0,20 < DP ≤ 0,40 Cukup 0,40 < DP ≤ 0,70 Baik 0,70 < DP ≤ 1,00 Sangat baik
Tabel 3.8
Hasil Analisis Daya Pembeda Soal Uji Coba
Tes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis
Jenis Tes No.
Soal DP Intrepretasi
Kelancaran Berprosedur
1 0,25 Cukup
2 0,31 Cukup
3 0,42 Baik
4 0,28 Cukup
5 0,64 Baik
Kompetensi Strategis
1 0,17 Jelek
2 0,56 Baik
3 0,36 Cukup
4 0,56 Baik
5 0,39 Cukup
d. Analisis Tingkat kesukaran
Tingkat kesukaran bertujuan untuk mengetahui bobot soal yang sesuai dengan kriteria perangkat soal yang diharuskan. Jika suatu soal memiliki tingkat kesukaran yang seimbang, artinya soal tersebut tidak terlalu mudah dan juga tidak terlalu sulit, maka dapat dikatakan soal tersebut baik.
Untuk menguji tingkat kesukaran, ditentukan pula kelompok unggul dan kelompok asor. Proses penentuan kelompok unggul dan kelompok asor ini dilakukan dengan cara yang sama ketika menentukan daya pembeda. Untuk menetukan tingkat kesukaran, digunakan rumus:
B A B A J J S S IK Keterangan:
IK = indeks tingkat kesukaran
B
S = jumlah skor kelompok bawah
A
J = jumlah skor ideal kelompok atas
B
J = jumlah skor ideal kelompok bawah
[image:44.595.115.513.252.750.2]Hasil perhitungan tingkat kesukaran diinterpretasikan menggunakan kriteria tingkat kesukaran butir soal yang dikemukakan Suherman dan Sukjaya (1990:213), yang disajikan pada tabel berikut:
Tabel 3.9
Klasifikasi Tingkat Kesukaran Soal
Nilai TK Klasifikasi
TK = 0,00 Terlalu sukar
0,00 < TK ≤ 0,30 Sukar 0,30 < TK ≤ 0,70 Sedang 0,70 < TK < 1,00 Mudah
TK = 1,00 Sangat mudah
Berdasarkan hasil perhitungan dengan menggunakan software Anates
4.0.7 seperti yang tertera pada lampiran, tingkat kesukaran dari soal uji coba
pemahaman konsep dan kompetensi strategis matematis adalah sebagai berikut:
Tabel 3.10
Hasil Analisis Tingkat Kesukaran Soal Uji Coba
Tes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis
Jenis Tes No.
Soal TK Intrepretasi
Kelancaran Berprosedur
1 0,35 Sedang
2 0,15 Sukar
3 0,21 Sukar
4 0,14 Sukar
5 0,32 Sedang
Kompetensi Strategis
1 0,19 Sukar
2 0,31 Sedang
3 0,21 Sukar
5 0,22 Sukar
[image:45.595.109.562.235.689.2]Berdasarkan uraian di atas berupa perhitungan validitas, reliabilitas, daya pembeda dan tingkata kesukaran, maka pada tabel berikut ini disajikan rangkuman hasil analisis uji coba instrumen tes.
Tabel 3.11
Kesimpulan Hasil Analisis Soal Uji Coba
Tes Kemampuan Kelancaran Berprosedur dan Kompetensi Strategis Matematis
Jenis Tes No. Soal
Validitas Reliabilitas Daya
Pembeda Tingkat Kesukaran Keterangan rxy Intre-pretasi
r11
Inter-pretasi DP
Inter-pretasi TK
Inter-pretasi
Kelancaran Berprosedur
1 0,44 Sedang
0,89 Tinggi
0,25 Cukup 0,35 Sedang Dipakai
2 0,76 Tinggi 0,31 Cukup 0,15 Sukar
Dipakai dengan perbaikan
3 0,93 Sangat
Tinggi 0,42 Baik 0,21 Sukar
Dipakai dengan perbaikan
4 0,75 Tinggi 0,28 Cukup 0,14 Sukar
Dipakai dengan perbaikan
5 0,82 Sangat
Tinggi 0,64 Baik 0,32 Sedang Dipakai
Kompetensi Strategis
1 0,59 Sedang
0,87 Tinggi
0,17 Jelek 0,19 Sukar
Dipakai dengan perbaikan
2 0,88 Sangat
Tinggi 0,56 Baik 0,31 Sedang Dipakai
3 0,87 Sangat
Tinggi 0,36 Cukup 0,21 Sukar
Dipakai dengan perbaikan
4 0,81 Sangat
Tinggi 0,56 Baik 0,03 Sukar
Dipakai dengan perbaikan
5 0,83 Sangat
Tinggi 0,39 Cukup 0,14 Sukar
Dipakai dengan perbaikan
Berdasarkan kesimpulan hasil analisis uji coba instrumen tes pada Tabel
berprosedur dan kompetensi strategis semuanya dipakai. Akan tetapi, ada soal-soal yang dipakai dengan catatan dilakukan perbaikan, yaitu:
1) Untuk tes kemampuan kelancaran berprosedur, jika dilihat dari aspek tingkat kesukarannya, maka terdapat tiga soal yang kategorinya sukar. Ketiga soal tersebut yaitu nomor 2, 3 dan 4. Hal tersebut tidak berarti bahwa soal yang diberikan memang benar-benar sukar, tetapi lebih dikarenakan jarangnya siswa mendapatkan soal-soal dengan karakteristik kemampuan ini, yaitu indikator-indikator kelancaran berprosedur matematis. Oleh karena itu atas saran dari ahli, ketiga soal tersebut bisa digunakan dalam penelitian dengan terlebih dahulu dilakukan perubahan redaksi bunyi soal.
2) Soal nomor 1 untuk kemampuan kompetensi strategis tetap dipakai karena diasumsikan rendahnya daya pembeda dan tingkat kesukarannya termasuk kategori sukar, dikarenakan siswa tidak terbiasa dengan soal-soal yang tidak rutin.
3) Soal nomor 3, 4 dan 5 untuk kemampuan kompetensi strategis yang tingkat kesukarannya termasuk kategori sukar telah dilakukan perubahan pada redaksi bunyi soal. Hal tersebut sama dengan soal nomor 2, 3 dan 4 pada kemampuan kelancaran berprosedur.
4. Bahan Ajar
eksperimen adalah bahan ajar yang dibuat dan disiapkan oleh peneliti. Pengembangan bahan ajar tersebut disusun dalam bentuk LKS. LKS tersebut hanya diberikan pada kelas eksperimen. LKS dirancang dan dikembangkan sesuai dengan karakteristik dari pembelajaran melalui strategi TAPPS, serta dengan mempertimbangkan kecakapan matematis (mathematical proficiency) yang ingin dicapai, yaitu kemampuan kelancaran berprosedur dan kompetensi strategis matematis.
5. Skala Sikap
Instrumen ini bertujuan untuk mengetahui dan menelaah sikap siswa terhadap matematika, kegiatan pembelajaran dengan strategi TAPPS dan terhadap soal-soal kelancaran berprosedur dan kompetensi strategis matematis. Oleh karena itu, skala sikap ini hanya diberikan kepada siswa yang berada di kelas eksperimen saja.
Penyusunan skala sikap diawali dengan pembuatan kisi-kisi skala sikap. Untuk mengetahui keterbacaan angket, dilakukan uji coba terhadap 10 siswa kelas VIII di salah satu SMP di Bandung. Hal tersebut dilakukan hanya untuk mengetahui siswa memahami maksud dari pernyataan-pernyataan yang diberikan, sehingga peneliti tidak melakukan pengolahan data atas jawaban siswa. Jumlah pernyataan dalam angket skala sikap yang dipakai dalam penelitian ini berjumlah 30 item. Kisi-kisi serta skala sikap terlampir.
6. Lembar Observasi
Observasi merupakan kegiatan melihat sesuatu secara cermat untuk memperoleh pemahaman yang lebih baik tentang sesuatu itu. Observasi ini digunakan untuk mengamati dan mengumpulkan semua data tentang aktivitas siswa dan guru selama proses pembelajaran berlangsung di kelas eksperimen.
Selain itu juga digunakan lembar observasi untuk mengamati setiap indikator dari kemampuan kelancaran berprosedur dan kompetensi strategis matematis yang dapat dicapai siswa selama proses pembelajaran berlangsung.
E. Teknik Pengumpulan Data
Data dalam penelitian ini dikumpulkan melalui tes, lembar observasi dan angket skala sikap. Data yang berkaitan dengan kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa dikumpulkan melalui tes (pretes dan postes). Kemudian data yang berkaitan dengan sikap siswa dalam pembelajaran dengan strategi TAPPS dikumpulkan melalui angket skala sikap siswa.
F. Teknik Analisis Data
Data-data yang diperoleh dari hasil pretes dan postes dianalisis secara statistik, sedangkan angket skala sikap dan hasil pengamatan dengan menggunakan lembar observasi dianalisis secara deskriptif.
Data yang dianalisis adalah data kuantitatif berupa hasil tes kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa dan data kualitatif berupa angket skala sikap dan hasil observasi. Untuk melakukan uji hipotesis dilakukan pengolahan data dengan menggunakan software SPSS 17 dan
Microsoft Excell 2007.
a. Menghitung skor jawaban siswa sesuai dengan kunci jawaban dan sistem penskoran yang digunakan.
b. Menghitung peningkatan kemampuan yang terjadi sebelum dan sesudah pembelajaran yang dihitung dengan rumus gain ternormalisasi, yaitu:
[image:50.595.115.514.185.626.2]Gain ternormalisasi (g) = (Hake, 1999) Gain ternormalisasi ini untuk melihat kualitas peningkatan kemampuan yang terjadi sebelum dan sesudah pembelajaran. Hasil perhitungan gain kemudian diinterpretasikan dengan menggunakan klasifikasi sebagai berikut:
Tabel 3.12 Klasifikasi Gain (g)
Besarnya Gain (g) Interpretasi
g 0,7 Tinggi
0,3 g < 0,7 Sedang
g <0,3 Rendah
(Hake, 1999)
c. Menyajikan statistik deskriptif skor pretes, skor postes, dan skor N-gain yang meliputi rataan , dan simpangan baku (S) dari masing-masing kemampuan yang diukur .
d. Melakukan uji normalitas pada data pretes, postes dan N-gain kemampuan kelancaran berprosedur dan kompetensi strategis matematis. Uji normalitas digunakan untuk mengetahui normal atau tidaknya distribusi data yang menjadi syarat untuk menentukan jenis statistik yang digunakan dalam analisis selanjutnya.
Hipotesis yang diuji adalah:
Uji normalitas ini menggunakan statistik uji yaitu Kolmogorov- Smirnov atau
Shapiro-Wilk.
Kriteria pengujian, jika nilai signifikansi P-value ≥α = 0,05, maka H0 diterima.
e. Menguji homogenitas varians data skor pretes, postes dan N-gain kemampuan kelancaran berprosedur dan kompetensi strategis matematis. Pengujian homogenitas varians antara dua kelompok data dilakukan untuk mengetahui apakah varians kedua kelompok homogen atau tidak homogen.
Adapun hipotesis yang akan diuji adalah: H0 : variansi pada kedua kelompok sama H1 : variansi pada kedua kelompok tidak sama
Uji statistiknya menggunakan Uji Levene Statistic. Kriteria pengujian H0 diterima jika nilai signifikansi P-value ≥α = 0,05.
Jika kedua data berdistribusi normal, maka uji perbedaan dua rataan menggunakan uji statistik parametrik, yaitu uji Independent-Sample T Test. Jika variansi kedua kelompok data homogen, nilai signifikansi yang
diperhatikan yaitu nilai pada baris “Equal variances assumed”. Jika variansi
kedua kelompok data tidak homogen, nilai signifikansi yang diperhatikan
yaitu nilai pada baris “Equal variances not assumed”. Jika terdapat minimal
Adapun hipotesis yang diuji dalam uji perbedaan dua rataan: Uji dua pihak/arah (2-tailed)
H0 : H1: Atau
Uji sepihak/searah (1-tailed) H0 :
H1:
Adapun diagram alur penganalisisan data yang dilakukan dalam penelitian ini, digambarkan pada diagram berikut:
Gambar 3.1. Diagram Alur Analisis Data
G. Prosedur Penelitian
Prosedur penelitian yang dilaksanakan peneliti dalam penelitian ini adalah sebagai berikut:
tidak homogen homogen
tidak berdistribusi normal berdistribusi normal
Uji Normalitas
Uji Statistik non-parametrik: Uji Mann Whitney Uji Homogenitas Varians
Uji t untuk sampel bebas dengan asumsi varians homogen (Independent Samples T Test
Equal variances assumed)
Uji t’ untuk sampel bebas dengan asumsi varians tidak homogen
(Independent Samples T Test
1. Tahap Persiapan
a. Menyusun jadwal penelitian b. Membuat rencana penelitian c. Menyusun instrumen penelitian
d. Melakukan uji coba instrumen penelitian dan dianalisis validitas, reliabilitas, daya pembeda dan tingkat kesukarannya
2. Tahap Pelaksanaan
a. Menentukan kelas eksperimen dan kelas kontrol dari dua kelas yang telah dipilih.
b. Melakukan pretes di kelas eksperimen dan di kelas kontrol.
c. Melakukan perlakuan (treatment) pembelajaran sesuai dengan rencana pembelajaran untuk masing-masing kelas.
d. Mengisi lembar observasi aktivitas guru dan siswa selama proses pembelajaran berlangsung.
e. Melakukan postes di kedua kelas setelah pembelajaran selesai dilakukan pada masing-masing kelas.
f. Memberikan angket skala sikap pada kelas eksperimen 3. Tahap Analisis Data
a. Melakukan analisis data dan melakukan pengujian hipotesis.
b. Membahas hasil penelitian yang meliputi analisis data, hasil uji hipotesis, observasi, dan hasil penilaian skala sikap.
H. Jadwal Penelitian
[image:54.595.107.518.204.629.2]Penelitian ini dilaksanakan mulai bulan Oktober 2012 sampai Juli 2013. Jadwal kegiatan penelitian selengkapnya dapat dilihat pada tabel berikut ini.
Tabel 3.13
Jadwal Kegiatan Penelitian
No Kegiatan
Okt Nop Des Jan Feb Mar Apr Mei Jun Jul
1. Pembuatan Proposal
2. Seminar Proposal 3. Revisi Proposal 4. Menyusun
Instrumen Penelitian dan bahan ajar
5. Observasi sekolah dan Pelaksanaan pembelajaran di kelas eksperimen dan kelas kontrol 6. Pengumpulan data 7. Pengolahan data 8. Penulisan tesis
I. Kerangka Penelitian
Gambar 3.2 Diagram Alur Penelitian
Postes Observasi dan
skala sikap siswa
Pengembangan dan Validasi:
Bahan Ajar, Instrumen Penelitian dan Ujicoba.
Pemilihan Subjek
Pretes
Pengolahan dan Analisis Data
Kesimpulan
Kelas Kontrol
Pelaksanaan Pembelajaran biasa Kelas Eksperimen
Pelaksanaan Pembelajaran dengan Strategi TAPPS
Analisis Hasil Ujicoba
Temuan Studi Pendahuluan: Identifikasi Masalah, Rumusan Masalah, Studi
Tina Rosyana, 2013
BAB V
KESIMPULAN DAN SARAN
A. Kesimpulan
Dari hasil penelitian ini diperoleh kesimpulan sebagai berikut:
1. Kemampuan kelancaran berprosedur matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS secara signifikan lebih baik daripada yang memperoleh pembelajaran biasa. Kemampuan tersebut termasuk dalam kategori tinggi.
2. Kemampuan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS secara signifikan lebih baik daripada yang memperoleh pembelajaran biasa. Kemampuan tersebut termasuk dalam kategori sedang.
3. Peningkatan kemampuan kelancaran berprosedur matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS secara signifikan lebih baik daripada yang memperoleh pembelajaran biasa. Peningkatan tersebut termasuk dalam ketegori tinggi.
4. Peningkatan kemampuan kompetensi strategis matematis siswa yang memperoleh pembelajaran dengan strategi TAPPS secara signifikan lebih baik daripada yang memperoleh pembelajaran biasa. Peningkatan tersebut termasuk dalam ketegori tinggi.
Tina Rosyana, 2013
soal-soal kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa. Temuan dalam penelitian ini yaitu sikap siswa terhadap soal-soal kemampuan kelancaran berprosedur dan kompetensi strategis matematis siswa merupakan sikap siswa yang paling menonjol. Pada urutan berikutnya adalah sikap siswa terhadap pembelajaran dengan strategi TAPPS. Kemudian yang terakhir yaitu sikap siswa terhadap matematika. Secara umum dapat dikatakan bahwa hasil penilaian sikap siswa, menunjukkan sikap yang positif terhadap keseluruhan aspek pembelajaran dengan strategi TAPPS.
6. Hasil observasi yang telah dilakukan selama berlangsungnya pembelajaran menunjukkan bahwa guru telah melakukan langkah-langkah yang sesuai dalam pembelajaran dengan strategi TAPPS. Kemudian hasil observasi terhadap aktivitas siswa diperoleh bahwa aktivitas dan peran aktif siswa semakin meningkat dari setiap pertemuan yang dilakukan.
B. Saran
Berdasarkan kesimpulan di atas, maka peneliti mengemukakan beberapa saran sebagai berikut:
Tina Rosyana, 2013
2. Pembelajaran matematika dengan strategi TAPPS sebaiknya dapat diterapkan dalam jangka waktu yang lebih lama, dengan tujuan agar proses pembelajaran menjadi lebih optimal.
3. Untuk menerapkan pembelajaran dengan strategi TAPPS, sebaiknya guru membuat sebuah skenario dan perencanaan yang lebih baik, sehingga pembelajaran dapat berjalan secara sistematis sesuai dengan rencana, dan diharapkan guru menyediakan benda nyata atau model yang sesuai dengan pokok bahasan yang diajarkan.
DAFTAR PUSTAKA
Akinsola, M. K., Olowojaiye. (2008). “Teacher Instructional Methods and Students Attitiudes toward Mathematics”. International Electronic Journal of Mathematics Education. 3, (1), 10.
Anita. (2007). Model Pembelajaran Thingking Aloud Pair Problem Solving
(TAPPS) Pada Topik Larutan Penyangga Untuk Meningkatkan Pemahaman Konsep dan Kemampuan Pemecahan Masalah Siswa. Tesis.
UPI: Tidak diterbitkan.
Arikunto, S. (2010). Dasar-dasar Evaluasi Pendidikan. Jakarta: Bumi Aksara. Badan Penelitian dan Pengembangan (Balitbang). (2011). Laporan Hasil TIMSS
2007. Kementrian Pendidikan dan Kebudayaan.
___________. (2011). Laporan Hasil PISA 2009. Kementrian Pendidikan dan Kebudayaan.
Charles, R. (1994). How to Evaluate Progress in Problem Solving. Reston, VA: NCTM.
Hake, R.R. (1999). Analyzing Change/Gain Scores. [Online]. Tersedia: http://www.physics.indiana.edu/~sdi/AnalyzingChange-Gain.pdf. [Mei 2012].
Hartman. (1998). Improving Student’s Problem Solving Skills. [Online]. Tersedia: http://www.ccny.cuny.edu/ctl/handbook/hartman.html. [Juli 2012].
Hidayah, R. N. (2010). Pembelajaran Matematika melalui Metode Thinking
Aloud Pair Problem Solving (TAPPS) dalam Upaya Meningkatkan Kemampuan Siswa dalam Tipe Soal Analisis : Penelitian Eksperimen Terhadap Siswa Kelas VIII SMPN 3 Bandung. Skripsi. UPI: Tidak
diterbitkan.
Izzati, N. (2010). Meningkatkan Kemampuan Berpikir Matematis Pada Tingkat
Koneksi dan Analisis Siswa Mts Negeri Melalui Pembelajaran Kolaboratif Murder. Tesis. UPI: Tidak diterbitkan.
Jhonson, S. D. & Chung, S. P. (1999). The Effect Thingking Aloud Pair Problem Solving (TAPPS) on the troubleshooting Ability of Aviation Technician Students. Journal of Industrial Teacher Education. 37 (1).
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it Up: Helping
Children Learn Mathematics. Washington, DC: National Academy Press.
Meltzer, D.E. (2002). The Relationship between Mathematics Preparation and
Conceptual Learning Gains in Physics: a Possible “Hidden Variable” in
Diagnostic Pretest Score. American Journal of Physics. 70 (12).
Pate, M. et al. (2004). The Effects of Thingking Aloud Pair Problem Solving on The Troubleshooting Performance of Undergraduate Agriculture Students in A Power Technology Course. Journal of Agricultural Education. 45 (4). Pestel, B. C. (1993). Teaching Problem Solving Without Modeling Through Thingking Aloud Pair Problem Solving. Journal of Science Education. 77 (1).
Polya, G. (1957). How to Solve It. [Online]. Tersedia:
http://www.math.utah.edu/~pa/math/polya.html. [Mei 2012].
Rahmawati, I. (2011). Pengaruh Metode Thinking Aloud Pair Problem Solving
(TAPPS) dalam Pembelajaran Matematika Terhadap Kompetensi Strategis (Penelitian Eksperimen terhadap Siswa Kelas VIII SMPN 14 Bandung). Skripsi. UPI: Tidak diterbitkan.
Reys, R. E., Suydam, M. N., Lindquist, M. M., & Smith, N. L. (1998). Helping
Chidren Learn Mathematics (5thed). Massachusetts: Allyn and Bacon. Ruseffendi, E.T. (1991). Pengantar kepada Membantu Guru Mengembangkan
Kompetensinya dalam Pengajaran Matematika untuk Meningkatkan CBSA.
Bandung: Tarsito.
Ruseffendi, E.T. (1993). Statistik Dasar Untuk Penelitian Pendidikan. Bandung: IKIP Bandung Pres.
Ruseffendi, E.T. (2005). Dasar-Dasar Penelitian Pendidikan & Bidang
Non-Eksakta Lainnya. Bandung: Tarsito.
Ruseffendi, E.T. (2006). Pengantar Kepada Guru Mengembangkan
Sanjaya, W. (2008). Strategi Pembelajaran Berorientasi Standar Proses
Pendidikan. Jakarta: Kencana Prenada Media Group.
Silberman, M. L. (2009). Active Learning. 101 Strategi Pembelajaran Aktif. Yogyakarta: Insan Madani dan Yappendis.
Siskandar. (2008). “Sikap dan Motivasi Siswa dalam Kaitan dengan Hasil Belajar Matematika”. Jurnal Pendidikan dan Kebudayaan. 14, (072), 444.
Slavin, R.E. (1995). Cooperatif Learning: Theory, Research, and Practice. Second Edition. Massachussetts: Allyn and Bacon Publishers.
Stice, J.E. (1987). Teaching Problem Solving. [Online]. Tersedia: http://wwwcsi.unian.it/educa/problemsolving/stice_ps.html.[3 Februari 2012].
Sudjana. (2005). Metode Statistika. Bandung: Tarsito.
Sudjono, A. (2001). Pengantar Evaluasi Pendidikan. Jakarta: Raja Grafindo Persada.
Suganda, A.T. (2012). Pembelajaran Matematika dengan Pendekatan Brain
Based Learning untuk Meningkatkan Kemampuan Prosedural dan Pemahaman Konsep Matematis Kelas X Madrasah Aliyah. Tesis. UPI:
Tidak diterbitkan.
Sugiyono. (2008). Metode Penelitian Kuantitatif, Kualitatif dan R & D. Bandung: Alfabeta.
Sugiyono. (2010). Metode Penelitian Pendidikan. Bandung: Alfabeta.
Suparno, P. (1997). Filsafat Konstruktivisme Dalam Pendidikan. Yogyakarta: Kanisius.
Suherman, E. (2003). Strategi Pembelajaran Matematika Kontemporer. Bandung: UPI.
Suherman, E. & Sukjaya, Y. (1990). Petunjuk Praktis untuk Melaksanakan
Evaluasi Pendidikan Matematika. Bandung: Wijayakusumah.
Sumarmo,U. (2002). Alternatif Pembelajaran Matematika dalam Menerapkan
Kurikulum Berbasis Kompetensi. Makalah disajikan pada Seminar
Nasional FPMIPA UPI: Tidak diterbitkan.
TIMSS. (2011). International Result in Mathematics. [Online]. Tersedia:
http://timssandpirls.bc.edu/timss2011/downloads/T11_IR_M_AppendixG. pdf [22 Juni 2013].
Turmudi. (2008). Landasan Filsafat dan Teori Pembelajaran Matematika
(Berparadigma Eksploratif dan Investigatif. Jakarta: Leuser Cita Pustaka.
Uyanto, S. (2009). Pedoman Analisis Data dengan SPSS. Yogyakarta: Graha Ilmu Wardhani, S. dan Rumiati. (2011). Instrumen Penilaian Hasil Belajar Matematika
SMP: Belajar dari PISA dan TIMSS. Yogyakarta: Kementerian Pendidikan
Nasional Badan Pengembangan Sumber Daya Manusia Pendidikan dan Penjaminan Mutu Pendidikan, dan Pusat Pengembangan dan Pemberdayaan Pendidik dan Tenaga Kependidikan (PPPPTK) Matematika.
Widjajanti, D.B. (2011). Mengembangkan Kecakapan Matematis Mahasiswa
Calon Guru Matematika Melalui Strategi Perkuliahan Kolaboratif Berbasis Masalah. Makalah terdapat pada Prosiding Seminar