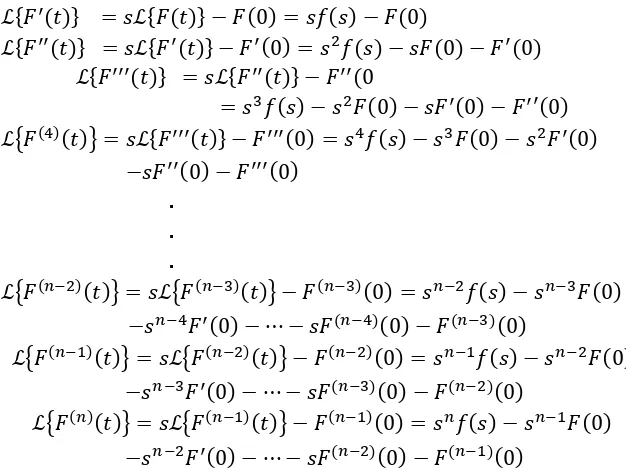PERSAMAAN DIFERENSIAL ORDE DUA UNTUK
PENDULUM SEDERHANA DAN PENDULUM FISIS
Rizqona Maharani
STAIN Kudus, Jawa Tengah, Indonesia [email protected]
Abstract
The purpose of this paper is to determine the solution of second-order linier differential equation for simple and physical pendulum motion. Based on the analysis of force components, the pendulum motion forms a homogeneous second-order linier differential equation with constant coefficients denoted by 𝜃′′+ 𝑔
𝐿𝜃 = 0 . The method used to solve the second-order linier differential equation is the Laplace Transform. The choice of method is based on the ease of solving the initial value problems by changing domain t with domain s using algebraic equations or using tables that contain laplace transform. The result of this study is solution of second-order linier differential equation by using laplace transform which in form
𝜃(𝑡) = ℒ−1{𝜃(𝑠)} = ℒ−1{ 𝑠𝐴
𝑠2+ 𝜔2}
Then, the solution can be used to determine the equation of pendulum motion which include the equation of displacement, velocity, and acceleration of the simple and physical pendulum.
Keywords: Second-Order differential equation, Laplace Transform, and Pendulum
Abstrak
Tujuan paper ini adalah untuk menentukan penyelesaian persamaan diferensial linier orde dua gerak pendulum sederhana dan fisis. Berdasarkan analisis komponen gayanya, maka gerak pendulum membentuk persamaan diferensial linier orde dua homogen dengan koefisien konstan yang dinyatakan dengan 𝜃′′+𝑔
untuk menyelesaikan persamaan linier orde dua tersebut adalah transformasi laplace. Pemilihan metode didasarkan atas kemudahan dalam menyelesaikan masalah nilai awal dengan mengubah domain t dengan domain s menggunakan persamaan aljabar atau menggunakan tabel yang memuat Tranformasi Laplace. Hasil dari penelitian ini adalah solusi persamaan diferensial linier orde dua dengan menggunakan transformasi laplace yang berbentuk:
𝜃(𝑡) = ℒ−1{𝜃(𝑠)} = ℒ−1{ 𝑠𝐴
𝑠2+ 𝜔2}
Sehingga solusi tersebut dapat digunakan untuk menentukan persamaan gerak pendulum yang meliputi persamaan perpindahan, kecepatan, dan percepatan pendulum sederhana dan fisis.
Kata Kunci: Persamaan diferensial orde dua, transformasi laplace, dan pendulum.
A. PENDAHULUAN
Matematika merupakan ilmu pengetahuan yang digunakan secara luas dalam berbagai bidang kehidupan, termasuk dalam m enyelesaikan permasalahan di bidang teknik, fisika, ekonomi dan yang lainnya. Permasalahan pada bidang tersebut kemudian diidentifikasi, dirumuskan, dan dimodelkan untuk dapat ditentukan solusinya. Adapun pemodelan yang menggunakan simbol matematika dan logika untuk menyajikan permasalahan objek disebut pemodelan matematika atau pemodelan simbolik (Susanta, 2008: 1.6).
model berdasarkan teori-teori dalam matematika, dan menginterpretasikan solusi model sehingga diperoleh solusi permasalahan.
Adapun model matematika yang dapat dirumuskan dari suatu permasalahan adalah berbentuk persamaan diferensial linier orde dua homogen dengan koefisien konstan. Untuk menentukan penyelesaian persamaan tersebut, dapat diterapkan transformasi laplace. Hal ini dikarenakan, transformasi laplace dapat mereduksi persamaan diferensial ke masalah aljabar. Aljabar tersebut dapat menjadi rumit pada suatu kejadian dan dapat dengan mudah jika diselesaikan dengan menggunakan transformasi laplace dari pada diselesaikan dengan menggunakan persamaan diferensial secara langsung. Dengan menggunakan transformasi laplace, suatu masalah nilai awal dapat diselesaikan dengan mengubah domain t dengan domain s menggunakan persamaan aljabar atau menggunakan tabel yang memuat Tranformasi Laplace (Nagle et al, 2004: 349). Bentuk umum dari Transformasi Laplace dari 𝐹(𝑡) yang dinyatakan oleh 𝐿{𝐹(𝑡)}, didefinisikan sebagai : 𝐿{𝐹(𝑡)} = 𝑓(𝑠) = ∫ 𝑒0∞ −𝑠𝑡𝐹(𝑡)𝑑𝑡.
gerak yang menunjukkan perpindahan, kecepatan, dan percepatan partikel saat malakukan osilasi.
Berdasarkan latar belakang yang sudah dipaparkan, maka tujuan paper ini adalah untuk mengetahui aplikasi transformasi laplace pada persamaan diferensial linier orde dua homogen dengan koefisien konstan dalam menentukan persamaan gerak pendulum yaitu pada pendulum sederhana dan fisis.
B. PEMBAHASAN
Persamaan Diferensial Linier Orde Dua Homogen dengan Koefisien Konstan
Persamaan diferensial adalah persamaan yang memuat fungsi yang tidak diketahui dan derivatifnya. Persamaan diferensial ditinjau dari banyaknya variabel bebas dari fungsi yang tidak diketahui, dikelompokkan menjadi persamaan diferensial biasa dan persamaan diferensial parsial. Persamaan diferensial biasa adalah persamaan diferensial dimana fungsi yang tidak diketahui adalah fungsi dari satu variabel bebas. Sedangkan persamaan diferensial parsial adalah persamaan diferensial yang memuat derivatif parsial fungsi yang tidak diketahui terhadap dua atau lebih variabel bebas (Suyono, 2003: 1-2). Sedangkan orde dari persamaan diferensial ditunjukkan oleh derivatif tertinggi yang muncul dalam persamaan tersebut (Boyce, 2001: 18).
Selain itu, persamaan diferensial juga dikelompokkan menjadi persamaan linier atau nonlinier. Persamaan diferensial biasa
yang dinyatakan ke dalam bentuk
F
(
t
,
y
,
y
',...,
y
(n))
0
merupakanlinier jika F merupakan fungsi linier dari variabel-variabel
)
real) dan koefisien pertama a0(t) ≠ 0 untuk setiap t ∈ I, y adalah fungsi dalam t, sedangkan y(n) adalah turunan ke-n dari PD. Bila semua koefisien an(t), an−1(t), … , a1(t), a0(t) adalah tetap, persamaan tersebut disebut persamaan diferensial linier orde n dengan koefisien konstan, sedangkan jika nilainya tidak tetap maka disebut persamaan diferensial linier orde n dengan koefisien variabel (Boyce, 2001: 19). Menurut Boyce (2001:130), Persamaan diferensial linier dikatakan homogen jika fungsi g(t) pada persamaan (1) adalah nol untuk setiap t. Sehingga persamaan diferensial linier homogen dengan koefisien konstan dapat dinyatakan dalam bentuk umum:
a0d ny dtn+ a1d
n−1y
dtn−1 + ⋯ + an−1dydt+ any = 0 ...(2)
Dengan a0, a1, ..., an konstan dan ≥ 2
(Suyono, 2003: 34)
Dari persamaan (2) maka persamaan diferensial linier orde dua dengan koefisien konstan dapat dinyatakan dalam bentuk:
a0𝑑 2𝑦
𝑑𝑥2+ a1𝑑𝑦𝑑𝑥+ a2𝑦 = 0 ...(3)
Dengan a0≠ 0, dan a0, a1, a2 adalah konstan real (Boyce, 2001: 131).
Transformasi Laplace
Definisi 1 Transformasi Laplace dari fungsi F(t) didefinisikan sebagai berikut:
ℒ{𝐹(𝑡)} = 𝑓(𝑠) = ∫ 𝑒𝑥 −𝑠𝑡𝐹(𝑡)𝑑𝑡
0 ...(4)
Definisi 2 (Kekontinuan bagian demi bagian) Suatu fungsi dikatakan kontinu bagian demi bagian dalam suatu selang 0 ≤ t ≤ β bila selang ini dapat dibagi-bagi kedalam sejumlah berhingga selang-selang di mana dalam setiap selang ini fungsinya kontinu dan memiliki limit-limit kanan dan kiri yang berhingga.
𝑀𝑒−𝛾 𝑡. Maka dikatakan bahwa 𝐹(𝑡) adalah suatu fungsi eksponensial
berorde 𝛾 apabila 𝑡 → ∞.
Teorema 1 (Syarat cukup untuk keujudan transformasi laplace) Jika 𝐹(𝑡) adalah kontinu secara bagian-bagian dalam setiap selang berhingga 0 ≤ 𝑡 ≤ 𝑁 dan eksponensial berorde 𝛾 untuk 𝑡 > 𝑁, maka transformasi Laplace nya 𝑓(𝑠) ada untuk semua 𝑠 > 𝛾.
Bukti:
Untuk setiap bilangan positif N didapat
𝑓(𝑠) = ℒ{𝐹(𝑡)} = ∫ 𝑒∞ −𝑠𝑡𝐹(𝑡)𝑑𝑡 =
0 ∫ 𝑒−𝑠𝑡𝐹(𝑡)𝑑𝑡 +
𝑁 0
∫ 𝑒𝑁∞ −𝑠𝑡𝐹(𝑡)𝑑𝑡
Karena 𝐹(𝑡) adalah kontinu secara sebagian-sebagian dalam setiap
selang berhingga 0 ≤ 𝑡 ≤ 𝑁, maka ∫ 𝑒0𝑁 −𝑠𝑡𝐹(𝑡)𝑑𝑡 ada
Akan ditunjukkan ∫ 𝑒𝑁∞ −𝑠𝑡𝐹(𝑡)𝑑𝑡 ada
Karena 𝐹(𝑡) adalah eksponensial berorde 𝛾 untuk 𝑡 > 𝑁 atau dapat ditulis dengan
|𝐹(𝑡)| ≤ 𝑀𝑒𝛾𝑡 sehingga:
|∫ 𝑒𝑁∞ −𝑠𝑡𝐹(𝑡)𝑑𝑡| ≤ ∫ 𝑒𝑁∞ −𝑠𝑡|𝐹(𝑡)|𝑑𝑡
≤ ∫ 𝑒𝑁∞ −𝑠𝑡𝑀𝑒𝛾𝑡𝑑𝑡
≤ 𝑀 ∫ 𝑒𝑁∞ −𝑠𝑡𝑒𝛾𝑡𝑑𝑡
≤ 𝑀 [ 1
−(𝑠−𝛾)𝑒−(𝑠−𝛾)𝑡]𝑁 ∞
= −𝑀𝑒−(𝑠−𝛾)𝑁
−(𝑠−𝛾) , untuk 𝑠 > 𝛾
Jadi ∫ 𝑒0∞ −𝑠𝑡𝐹(𝑡)𝑑𝑡 ada untuk semua 𝑠 > 𝛾
Definisi 4 (Invers Transformasi Laplace) Jika ℒ{F(t)} = f(s), maka F(t) disebut suatu invers transformasi Laplace dari f(s) dan secara simbolis ditulis F(t) = ℒ−1{𝑓(𝑠)}.
transformasi Laplace sehingga 𝑓(𝑠) dan 𝑔(𝑠) ada, jika 𝑓(𝑠) = 𝑔(𝑠) untuk 𝑠 > 𝛾 maka 𝐹(𝑡) = 𝐺(𝑡) pada selang kekontinuannya.
Bukti:
𝑓(𝑠) = ∫ 𝑒∞ −𝑠𝑡𝐹(𝑡) 𝑑𝑡
0 ada, jadi konvergen
𝑔(𝑠) = ∫ 𝑒∞ −𝑠𝑡𝐺(𝑡) 𝑑𝑡
0 ada, jadi konvergen
𝑓(𝑠) = 𝑔(𝑠) maka ∫ 𝑒0∞ −𝑠𝑡𝐹(𝑡) 𝑑𝑡= ∫ 𝑒0∞ −𝑠𝑡𝐺(𝑡) 𝑑𝑡 Atau ∫ 𝑒0∞ −𝑠𝑡𝐹(𝑡) 𝑑𝑡− ∫ 𝑒0∞ −𝑠𝑡𝐺(𝑡) 𝑑𝑡= 0
Karena kedua integral tak wajar ini konvergen maka
∫ 𝑒∞ −𝑠𝑡𝐹(𝑡) 𝑑𝑡
0 = ∫ 𝑒0∞ −𝑠𝑡𝐺(𝑡) 𝑑𝑡
∫ 𝑒∞ −𝑠𝑡𝐹(𝑡) 𝑑𝑡
0 − ∫ 𝑒0∞ −𝑠𝑡𝐺(𝑡) 𝑑𝑡= 0
𝑒−𝑠𝑡 ≠ 0 maka 𝐹(𝑡) − 𝐺(𝑡) = 0
Jadi 𝐹(𝑡) − 𝐺(𝑡) dalam selang kekontinuannya
Teorema 3 (sifat linier) Jika c1 dan c2 adalah sebarang konstan sedangkan F1(t) dan F2(t) adalah fungsi-fungsi dengan transformasi-transformasi Laplace nya masing-masing f1(s) dan f2(s) maka
ℒ{𝑐1𝐹1(𝑡) + 𝑐2𝐹2(𝑡)} = 𝑐1ℒ{𝐹1(𝑡)} + 𝑐2ℒ{𝐹2(𝑡)} = 𝑐1𝑓1(𝑠) +
𝑐2𝑓2(𝑠) ...(5)
Bukti:
Misalkan ℒ{𝐹1(𝑡)} = 𝑓1(𝑠) = ∫ 𝑒0𝑥 −𝑠𝑡𝐹1(𝑡)𝑑𝑡 dan ℒ{𝐹2(𝑡) } = 𝑓2(𝑠) = ∫ 𝑒0𝑥 −𝑠𝑡𝐹2(𝑡)𝑑𝑡
Maka ℒ{𝑐1𝐹1(𝑡) + 𝑐2𝐹2(𝑡)} = ∫ 𝑒0∞ −𝑠𝑡{𝑐1𝐹1(𝑡) + 𝑐2𝐹2(𝑡)} 𝑑𝑡
= ∫ 𝑒0∞ −𝑠𝑡𝑐1𝐹1(𝑡) 𝑑𝑡 + ∫ 𝑒0∞ −𝑠𝑡 𝑐2𝐹2(𝑡)𝑑𝑡
= 𝑐1∫ 𝑒0∞ −𝑠𝑡𝐹1(𝑡) 𝑑𝑡 + 𝑐2∫ 𝑒0∞ −𝑠𝑡 𝐹2(𝑡)𝑑𝑡
= 𝑐1ℒ{𝐹1(𝑡)} + 𝑐2ℒ{𝐹2(𝑡)} = 𝑐1𝑓1(𝑠) + 𝑐2𝑓2(𝑠)
Dengan cara yang sama jika ℒ−1{𝑓(𝑠)} = 𝐹(𝑡) maka ℒ−1{𝑐
1𝑓1(𝑠) + 𝑐2𝑓2(𝑠)} = 𝑐1ℒ−1{𝑓1(𝑠)} + 𝑐2ℒ−1{𝑓2(𝑠)}
ℒ{𝐹′(𝑡)} = 𝑠ℒ{𝐹(𝑡)} − 𝐹(0) = 𝑠𝑓(𝑠) − 𝐹(0)
Adapun langkah-langkah dalam menerapkan Transformasi Lapace untuk memecahkan persamaan diferensial linier orde dua dengan koefisien konstan yang kondisi awalnya telah diberikan adalah: 1) Menghitung bayangan Laplace dari kedua ruas persamaan 2) Menggunakan sifat-sifat transformasi Laplace dan kondisi awal
untuk mencari persamaan bayangan Laplace dalam penyelesaiannya.
3) Menyelesaikan persamaan dalam bayangan Laplace yang diperoleh.
5 𝑎
𝑠2− 𝑎2 sin 𝑎𝑡
6 𝑠
𝑠2− 𝑎2 cosh 𝑎𝑡
7
𝑎
𝑠2− 𝑎2 sin 𝑎𝑡
(Spiegel, 1993)
Persamaan Gerak pada Pendulum Sederhana
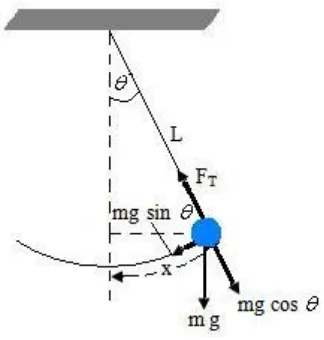
Gerak osilasi yang populer adalah gerak osilasi pendulum (bandul). Pada pendulum sederhana terdiri dari seutas tali ringan dan sebuah bola kecil (bola pendulum) bermassa 𝑚 yang digantungkan pada ujung tali. Pada gerak pendulum biasa, gaya gesekan udara akan diabaikan dan massa tali sangat kecil sehingga dapat diabaikan relatif terhadap bola.
Gambar 1 Sistem Bandul Sederhana
antara panjang busur 𝑥 dengan sudut 𝜃 dinyatakan dengan persamaan 𝑥 = 𝐿𝜃. Bandul tersebut melakukan Gerak Harmonik Sederhana berarti gaya pemulihnya adalah komponen tangensial gaya gravitasi 𝑤 sin 𝜃 atau 𝑚𝑔 sin 𝜃 yang bekerja dengan arah menuju 𝜃 = 0, berlawanan dengan arah simpangannya. Oleh karenanya gaya tegang tali 𝐹𝑇 bernilai −𝑚𝑔 sin 𝜃. Sehingga menurut hukum kedua Newton, percepatan yang dihasilkan oleh pendulum sederhana jika dihubungkan dengan gaya tegang tali dapat dinyatakan dengan:
Persamaan (1.3) adalah persamaan diferensial linear homogen dengan koefisien konstan. Pada permasalahan gerak sebuah pendulum ini, akan diberikan syarat awal yang harus dipenuhi sehingga tidak dapat diselesaikan secara langsung. Oleh karenanya akan digunakan transformasi Lapace. Syarat awal tersebut adalah saat pendulum berada pada simpangan tertentu dengan kecepatan awal nol.
Persamaan (1.3) akan disusun kembali ke dalam bentuk aljabar, sehingga persamaannya menjadi:
𝜃′′+𝑔
𝐿 𝜃 = 0
𝜃′′+ 𝜔2𝜃 = 0 … (1.4)
Dengan 𝜔 adalah frekuensi sudut, 𝜔 = √𝑔
𝐿
Jika diberikan syarat awal 𝜃(0) = 𝐴, 𝜃′(0) = 𝐵 = 0, ℒ{𝜃} = 𝜃(𝑠) maka dengan menggunakan transformasi Laplace pada kedua ruas dari persamaan (1.4) diperoleh:
ℒ{𝜃′′+ 𝜔2𝜃} = ℒ{0}
ℒ{𝜃′′} + ℒ{𝜔2𝜃} = 0
ℒ{𝜃′′} + 𝜔2ℒ{𝜃} = 0
[𝑠2ℒ{𝜃} − 𝑠𝜃(0) − 𝜃′(0)] + 𝜔2ℒ{𝜃} = 0
𝑠2𝜃(𝑠) − 𝑠𝐴 − 𝐵 + 𝜔2𝜃(𝑠) = 0
𝑠2𝜃(𝑠) − 𝑠𝐴 − 𝐵 + 𝜔2𝜃(𝑠) = 0
(𝑠2+ 𝜔2)𝜃(𝑠) = 𝑠𝐴 + 𝐵
𝜃(𝑠) =𝑠𝑠𝐴+02+𝜔2
𝜃(𝑠) = 𝑠𝐴
Untuk mendapatkan persamaan gerak bandul, dikenakan transformasi Laplace invers pada kedua ruas dari persamaan pembantu tersebut.
ℒ−1{𝜃(𝑠)} = ℒ−1{ 𝑠𝐴 𝑠2+𝜔2}
𝜃(𝑡) = ℒ−1{ 𝑠𝐴
𝑠2+𝜔2}
= 𝐴ℒ−1{ 𝑠
𝑠2+𝜔2}
= 𝐴 cos 𝜔𝑡
𝜃(𝑡) = 𝐴 cos(𝜔𝑡 + 0)
𝜃(𝑡) = 𝐴 cos(𝜔𝑡 + ∅)
Berdasarkan persamaan perpindahan gerak pendulum yang sudah diperoleh, maka dapat persamaan kecepatan dan percapatan angularnya adalah
𝜔(𝑡) =𝑑𝜃𝑑𝑡 =𝑑(𝐴 cos(𝜔𝑡 + ∅))𝑑𝑡 = −𝐴 𝑠𝑖𝑛(𝜔𝑡 + ∅) 𝑟𝑎𝑑/𝑠
Dan
𝛼(𝑡) =𝑑𝜔 𝑑𝑡 =
𝑑(−𝐴 𝑠𝑖𝑛(𝜔𝑡 + ∅))
𝑑𝑡 = −𝐴𝜔2cos(𝜔𝑡 + ∅) 𝑟𝑎𝑑2/𝑠
Persamaan Gerak pada Pendulum Fisis
Gambar 2.2 skema bandul fisis
Titik 𝑂 adalah sumbu ayun pada benda yang sering dinamakan pivot, 𝑃 adalah pusat massa, 𝐿 adalah panjang benda, sedangkan ℓ adalah jarak 𝑂 ke 𝑃. Dan yang menyebabkan benda berayun adalah momen gaya atau torsi pemulih (Restoring torque).
Pada gambar bangun datar yang digantung pada sebuah titik berjarak ℓ dari pusat massanya dan disimpangkan dari kesetimbangan sebesar sudut 𝜃. Momen gaya yang bekerja terhadap titik gantung bernilai 𝑚𝑔ℓ sin 𝜃 dan cenderung mengurangi 𝜃. Percepatan sudut 𝛼 yang dihasilkan pada pendulum fisis tersebut dihubungkan dengan momen gaya oleh:
𝜏 = 𝐼𝛼 = 𝐼 𝑑𝑑𝑡2𝜃2 … … … (2.1) Dengan:
𝜏: momen gaya 𝐼: momen inersia 𝛼: percepatan sudut
Karena momen gaya berlawanan dengan arah simpangan dan cenderung mengurangi 𝜃, sehingga momen gaya bernilai −𝑚𝑔ℓ sin 𝜃. Dengan mensubtitusikan −𝑚𝑔ℓ sin 𝜃 untuk momen gaya total pada persamaan (2.1) diperoleh:
−𝑚𝑔ℓ sin 𝜃 = 𝐼 𝑑𝑑𝑡2𝜃2 … … … (2.2)
−𝑚𝑔ℓsin 𝜃 = 𝐼 𝑑2𝜃
Dengan 𝜔 adalah frekuensi sudut yang bernilai√𝑚𝑔ℓ
𝐼
Bentuk persamaan (2.3) adalah termasuk persamaan diferensial linear orde dua homogeny dengan koefisien konstan. Sama halnya dengan permasalahan bandul sederhana, pada bandul fisis ini akan diberikan syarat awal yang harus dipenuhi dan akan diselesaikan dengan transformasi Laplace.
Jika diberikan syarat awal 𝜃(0) = 𝐴, 𝜃′(0) = 𝐵 = 0, ℒ{𝜃} = 𝜃(𝑠) maka dengan menggunakan transformasi Laplace pada kedua ruas dari persamaan (2.3) diperoleh:
ℒ{𝜃′′+ 𝜔2𝜃} = ℒ{0}
Untuk mendapatkan persamaan gerak bandul, dikenakan transformasi Laplace invers pada kedua ruas dari persamaan pembantu tersebut.
= ℒ−1{ 𝑠𝐴
𝑠2+𝜔2}
= 𝐴ℒ−1{ 𝑠
𝑠2+𝜔2}
= 𝐴 cos 𝜔𝑡 𝜃(𝑡) = 𝐴 cos(𝜔𝑡 + 0) 𝜃(𝑡) = 𝐴 cos(𝜔𝑡 + ∅)
Berdasarkan analisis komponen-kompenen gaya yang bekerja pada pendulum biasa dan fisis diperoleh pemodelan matematika yang berbentuk persamaan diferensial linier orde dua yang diberikan syarat awal tertentu. Kemudian dengan menggunakan metode transformasi laplace diperoleh persamaan gerak pendulum biasa dan fisis, yaitu 𝜃(𝑡) = 𝐴 cos(𝜔𝑡 + ∅). Kedua pendulum tersebut memiliki persamaan perpindahan yang sama sehingga untuk persamaan kecepatan dan percepatannya juga sama. Akibatnya jika kedua pendulum diberikan simpangan dan 𝜔𝑡 yang sama, maka diperoleh besar magnitudo perpindahan, kecepatan, dan percepatan yang sama pula.
C. KESIMPULAN
DAFTAR PUSTAKA
Boyce, William E. Diprima, Richard C. (2001). Elementary Differential Equations and Boundary Value Problems. United States of America :John Wiley & Sons, Inc
Halliday, D. Resnick, R. & Walker, J. (2010). Fisika Dasar Edisi 7. Jakarta :Erlangga
Nagle, R. Kent, Edward B. Saff &Arthur David Snider. (2004). Fundamental of Differential Equations and Boundary Value Problems Fourth Edition. United States of America: Pearson Adison Wesley
Spiegel, Murray R.(1993). Transformasi Laplace. Jakarta: Erlangga. Susanta, B. (2008). Cara Mudah menyelesaikan Matematika dengan
Mathematica. Yogyakarta. Universitas Terbuka
Suyono. (2003). Persamaan Diferensial. Surakarta: Sebelas Maret University Press